Analysis of Flight Loads during Symmetric Aircraft Maneuvers Based on the Gradient-Enhanced Kriging Model
Abstract
:1. Introduction
2. Methodology
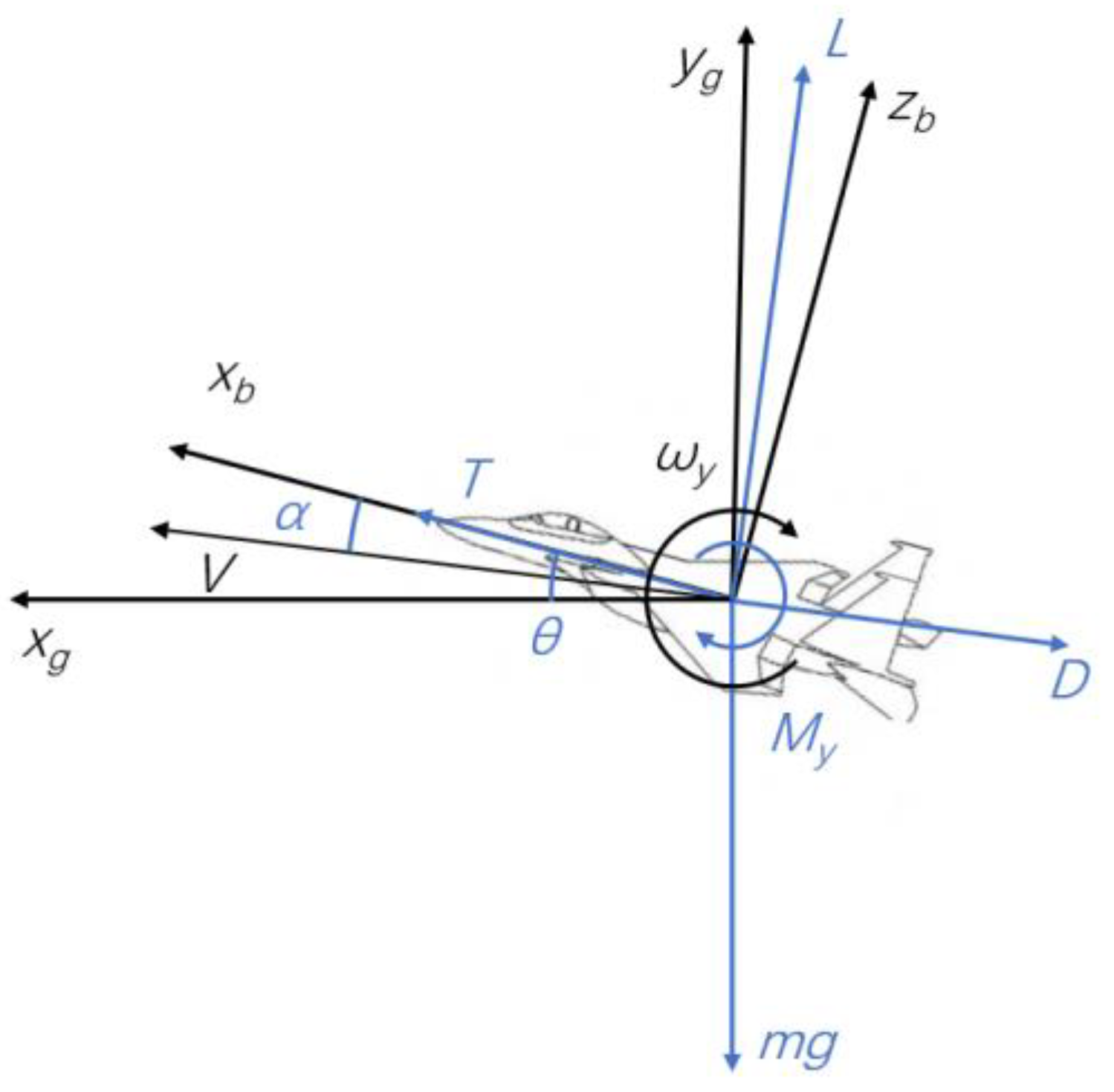
2.1. Analysis Method of Elastic Flight Loads
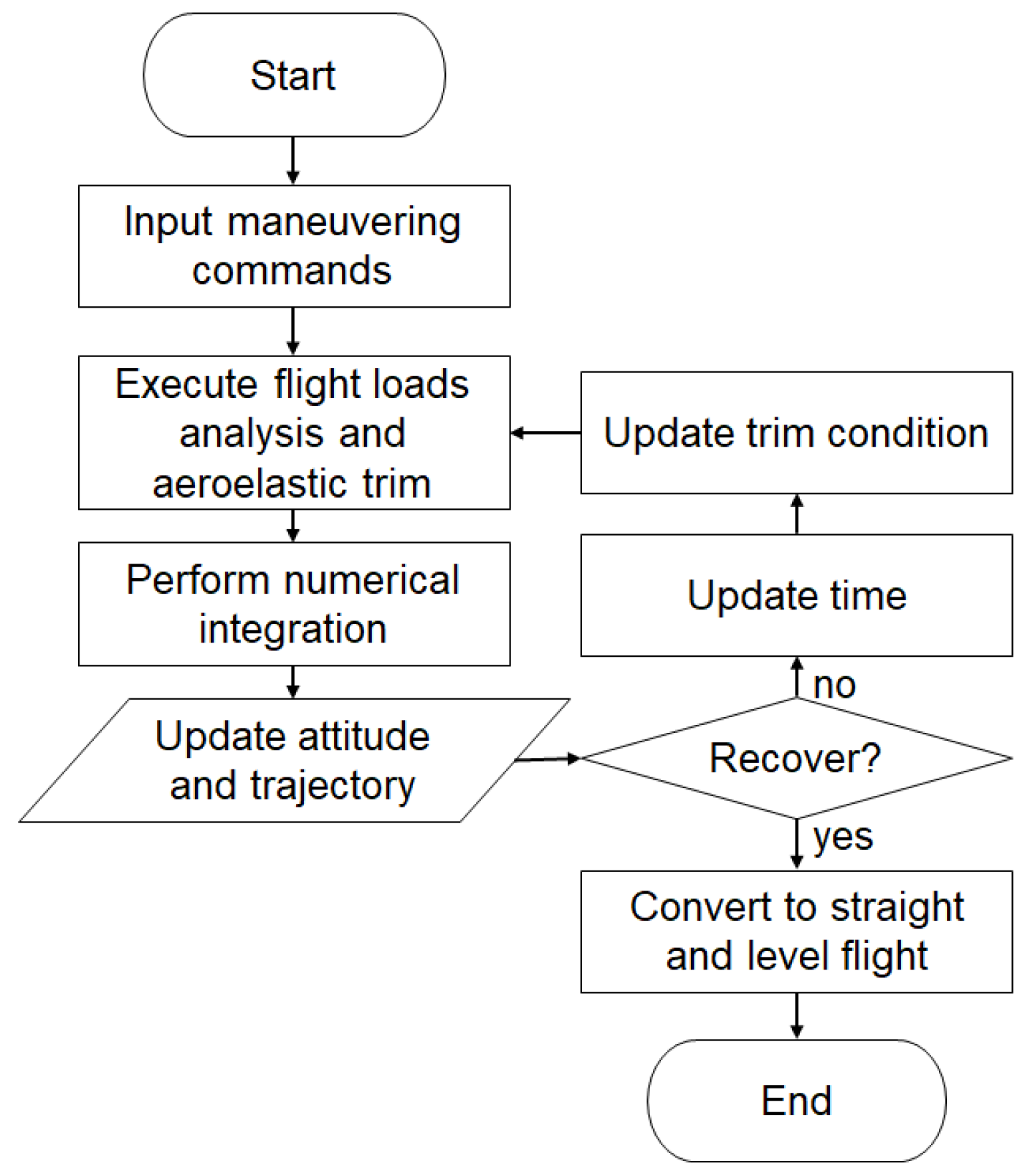
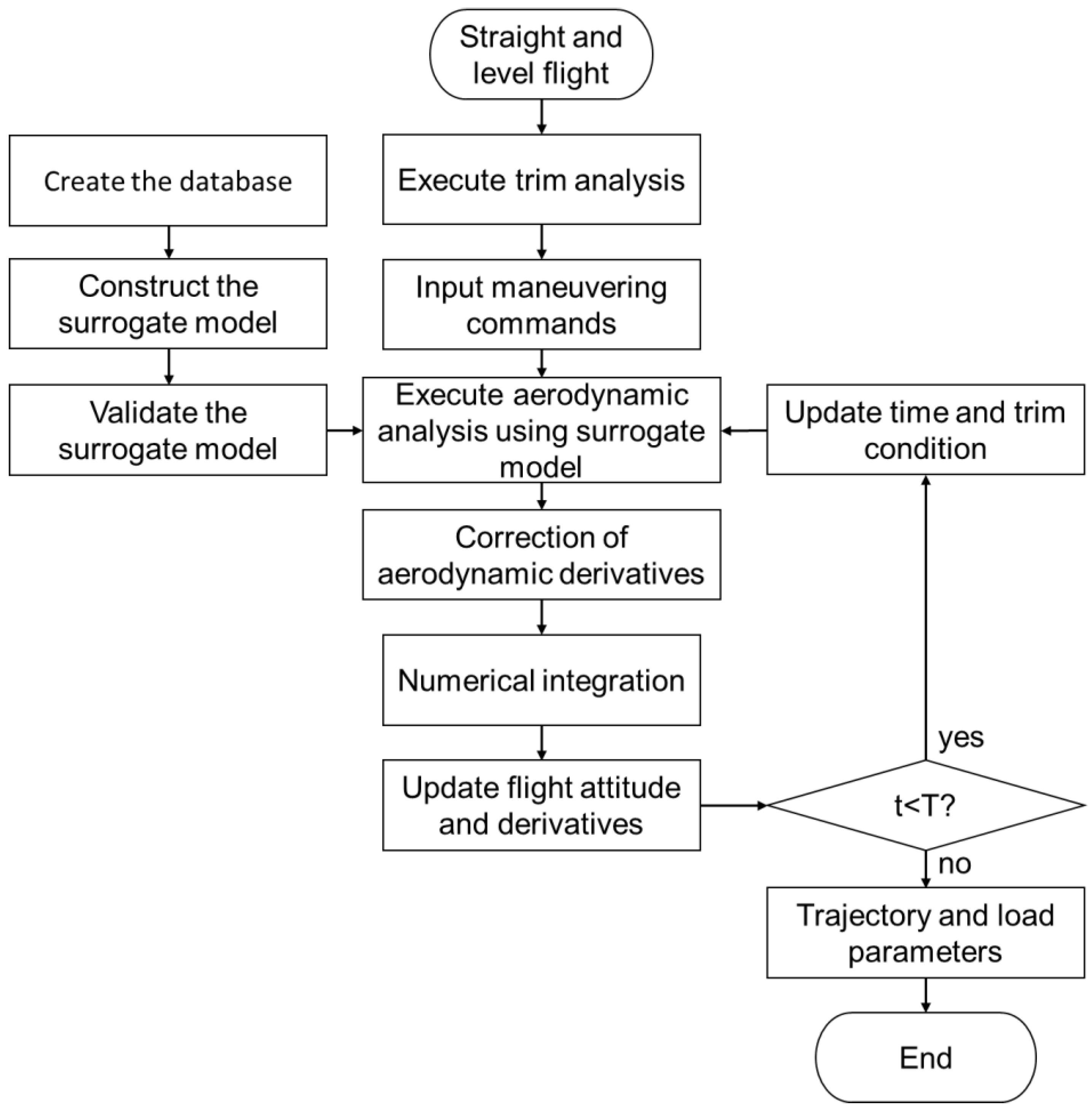
2.2. Simulation of Maneuvering Flight in the Time Domain
- Execute flight loads analysis and aeroelastic trim: calculate the corresponding aerodynamic force distribution according to the maneuver order (deflection law of control surface) and flight parameters (e.g., angle of attack). Obtain elastically corrected maneuvering flight load data through aerodynamic/structural/aerostatic analysis.
- Perform numerical integration: use the aerodynamic parameters and flight load data at that moment and the Runge–Kutta method to solve the longitudinal dynamics equations and obtain the kinematic characteristics in maneuver flight (attitude and trajectory).
- Update attitude and trajectory: update data such as angle of attack, pitching rate, maneuvering load, flight velocity and trajectory, etc.
- Update trim condition: update maneuver instructions and flight parameters.
- Recover: check whether the attitude has corrected the maneuver. If “yes”, the maneuver process ends and returns to the straight and level flight state. If “no”, update time and proceed to the calculation of the next time step.
2.3. Theory of Gradient-Enhanced Kriging
- (1)
- Universal Kriging
- (2)
- Gradient-enhanced Kriging
- (3)
- The comparison of universal Kriging and GEK for nonlinear function prediction
2.4. Analysis Method of Maneuvering Flight Loads Based on GEK Model
- Calculate maneuvering flight loads using linear and nonlinear aerodynamic methods to obtain the range of changes in aerodynamic parameters during the maneuvers. Then, set input and output variables and prepare data for training and calibrating the model. Finally, build the surrogate model for aerodynamic analysis based on the GEK method and check its accuracy.
- Set the initial flight state as straight and level, carry out the trim analysis to obtain parameters, such as angle of attack and angular deflections of control surfaces, and set the initial values of the aerodynamic derivatives.
- Solve the input variables (maneuver commands) for the next moment according to the requirements of the maneuver and perform an aerodynamic analysis using the surrogate model.
- Solve the flight dynamics equations with elastic corrections using the Runge–Kutta method to obtain new aerodynamic derivatives.
- Update the flight attitude according to the new aerodynamic derivatives.
- Determine whether the cycle of the time step ends. If not, update the time, trim the conditions (flight attitude), update the maneuver commands, and repeat steps 3 to 6 in the next time step. If so, the flight trajectory and parameters of aerodynamic loads during the maneuvering flight are obtained.
3. Numerical Validation and Analysis
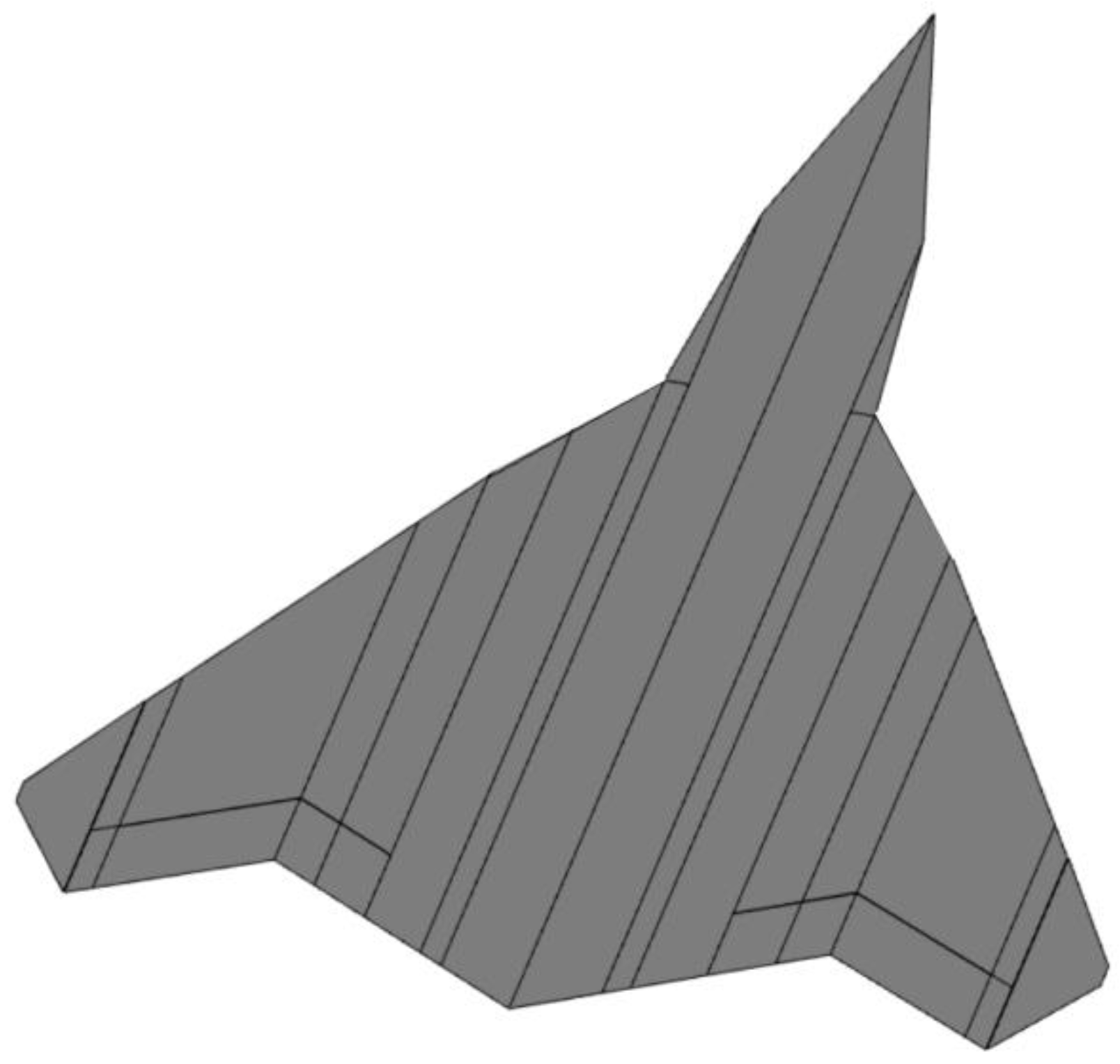
3.1. Models and Flight Conditions for Analysis
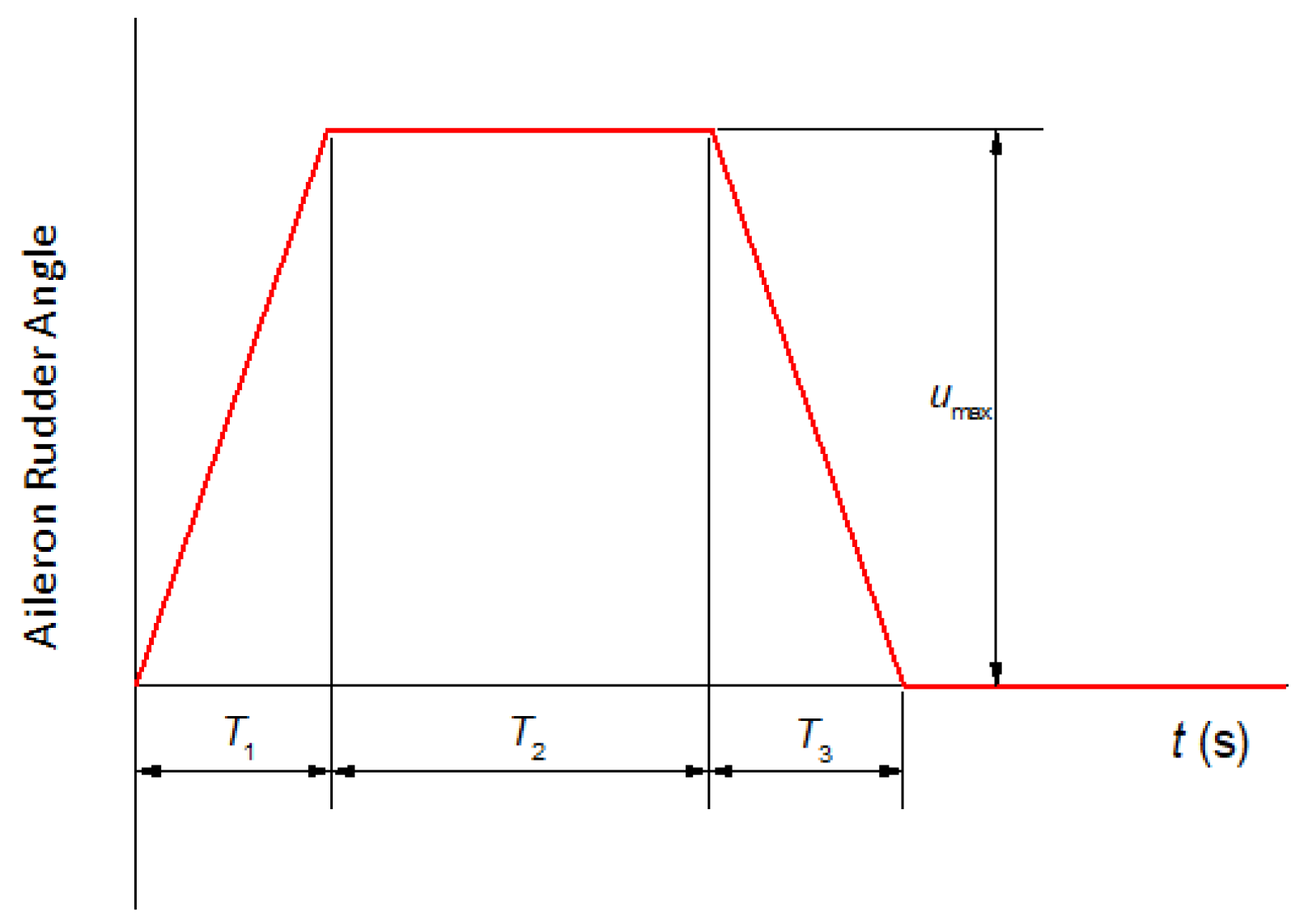
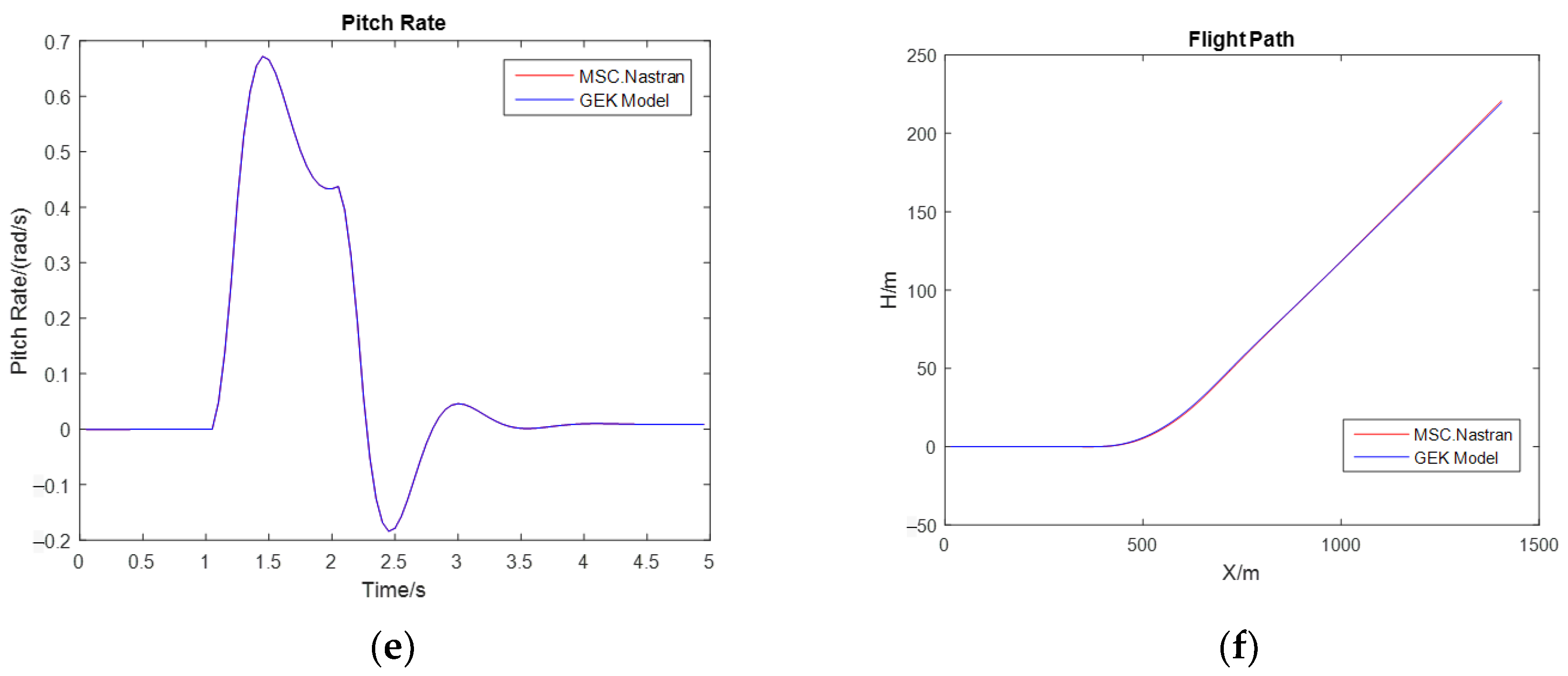
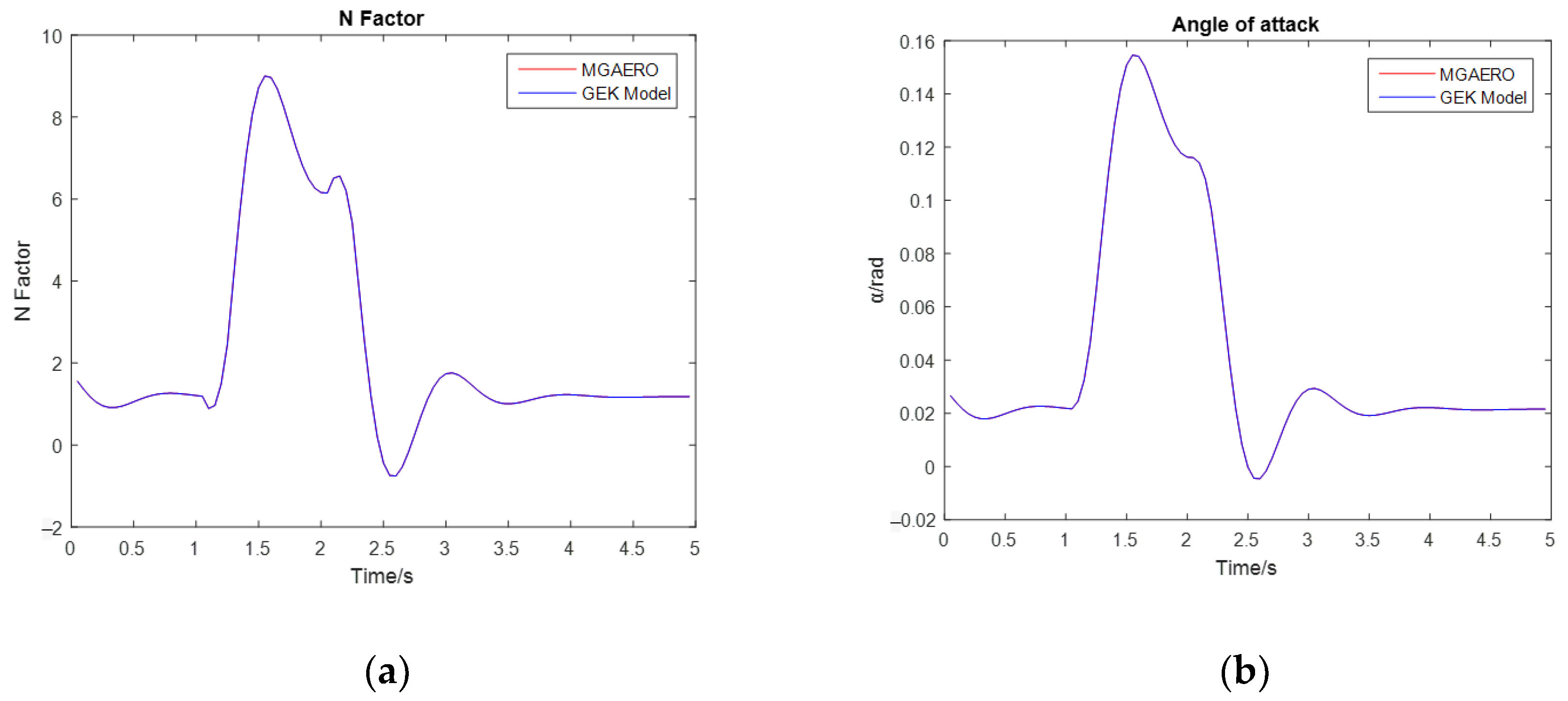
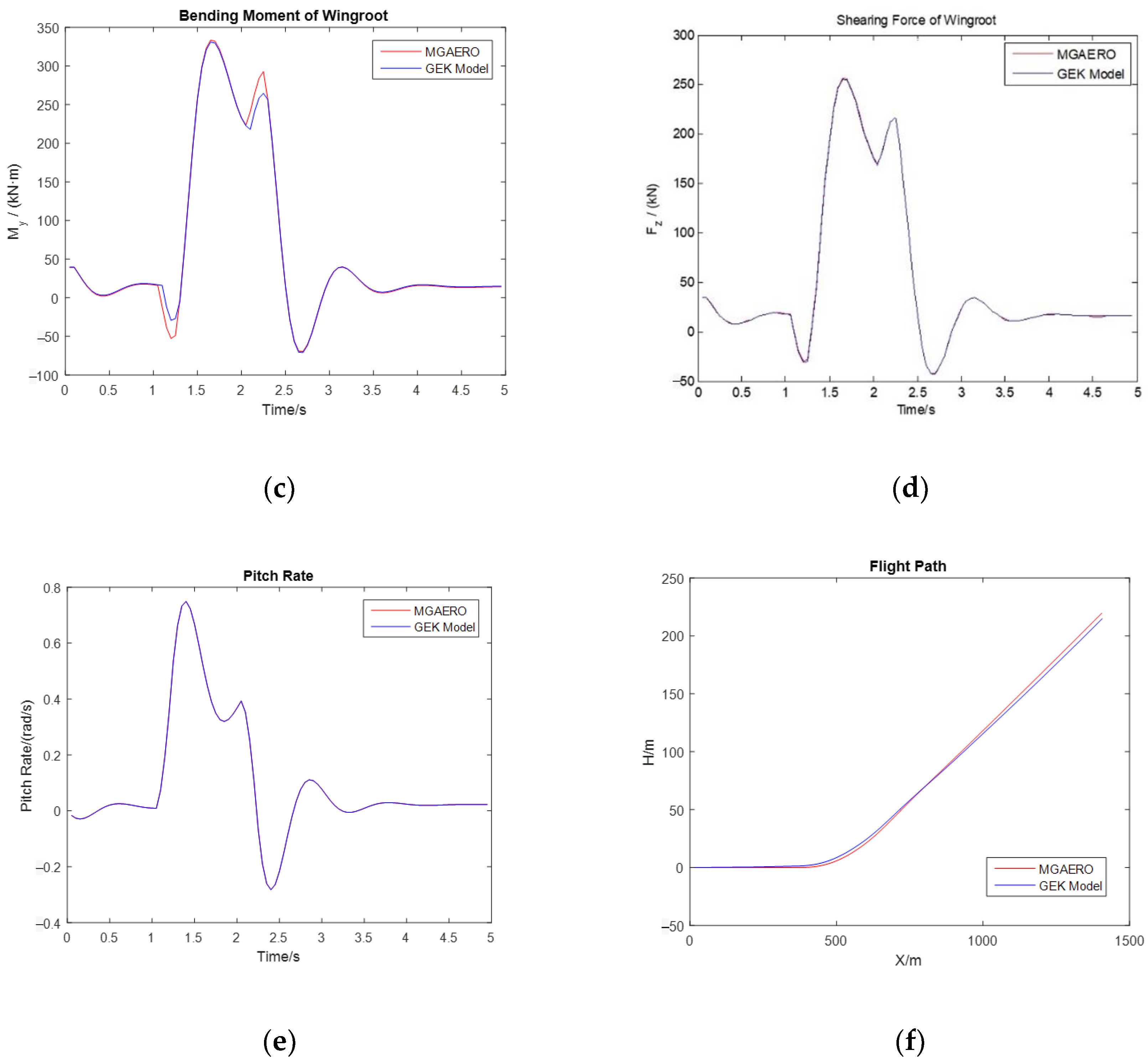
3.2. Prediction of Flight Loads
- (1)
- Steady-state pitch conditions
- (2)
- Abrupt pitch conditions
3.3. Accuracy of the GEK Model
- Both the GEK surrogate models based on linear and nonlinear aerodynamics have a high prediction accuracy, enabling accurate trim calculations and predictions of flight load variation curves during maneuvers.
- Directly solving aerodynamic/structural coupling results in a time expenditure on the order of 100 s for a single load calculation, whereas using the GEK surrogate model for a single load calculation requires less than 1 s, showing a significantly improved computational efficiency.
- The trim calculation results based on nonlinear aerodynamics are superior to those with linear aerodynamics, and the difference between the two is significant. This indicates that conducting analyses based on nonlinear aerodynamics is necessary, especially in flight conditions with strong aerodynamic nonlinearity.
4. Conclusions
- The proposed method exhibits a good fitting accuracy that meets the requirements of flight load analysis and improves computational efficiency significantly.
- The variation in loads corresponds to the maneuvering flight processes. Because of the differences in aerodynamic force distribution, nonlinear aerodynamic forces and their surrogate models represent significant disparities or even inconsistencies in the variation trends of flight loads compared with linear aerodynamic forces. Hence, employing nonlinear aerodynamics for maneuvering flight process calculations is more rational.
- The GEK surrogate model relies on selecting sample databases and the accuracy of gradient calculations during model training. Compared to the Kriging surrogate model, the GEK model is more time-consuming and requires greater computational resources for model training and testing. However, it exhibits a higher fitting accuracy in strongly nonlinear scenarios.
- In future work, more complex maneuvers, such as rolling and other lateral maneuvers, will be analyzed. The existing elastic correction methods of aerodynamic forces will be improved, such as using the more accurate third-order surface panel method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Cai, J.S. Unsteady aerodynamic modeling and identification of airplane at high angles of attack. Acta Aeronaut. Astronaut. Sin. 1996, 17, 391–398. (In Chinese) [Google Scholar]
- Lin, G.-F.; Lan, C.; Brandon, J. A generalized dynamic aerodynamic coefficient model for flight dynamics applications. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar]
- Goman, M.; Khrabrov, A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack. In Proceedings of the Astrodynamics Conference, Hilton Head Island, SC, USA, 10–12 August 1992; pp. 759–766. [Google Scholar]
- Wang, C.; Wang, G.D.; Bai, P. Machine learning method for aerodynamic modeling based on flight simulation data. Acta Aerodyn. Sin. 2019, 37, 488–497. (In Chinese) [Google Scholar]
- Zhang, W.; Wang, B.; Ye, Z.; Quan, J. Efficient Method for Limit Cycle Flutter Analysis Based on Nonlinear Aerodynamic Reduced-Order Models. AIAA J. 2012, 50, 1019–1028. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Reduced-order modeling for nonlinear aeroelasticity with varying Mach numbers. J. Aerosp. Eng. 2018, 31, 04018105. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Multi-kernel neural networks for nonlinear unsteady aerodynamic reduced-order modeling. Aerosp. Sci. Technol. 2017, 67, 309–326. [Google Scholar] [CrossRef]
- Han, Z.H. Kriging surrogate model and its application to design optimization: A review of recent progress. Acta Aeronaut. Astronaut. Sin. 2016, 37, 3197–3225. (In Chinese) [Google Scholar]
- Liu, Y.Z.; Wan, Z.Q.; Li, Q.; Zhang, Q.H. A Corrected Nearest Neighbor Transpotation Method of Aerodynamic Force for Fluid-Structure Interactions. Int. J. Numer. Anal. Model. 2020, 17, 746–765. [Google Scholar]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar] [PubMed]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–423, 415. [Google Scholar] [CrossRef]
- Liu, J.; Han, Z.-H.; Song, W.-P. Efficient kriging-based aerodynamic design of transonic airfoils: Some key issues. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Han, Z.H.; Zhang, K.S.; Song, W.P.; Liu, J. Surrogate-based aerodynamic shape optimization with application to wind turbine airfoils. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 1108. [Google Scholar]
- Wang, X.F.; Xi, G. Aerodynamic optimization design for airfoil based on kriging model. Acta Aeronaut. Astronaut. Sin. 2005, 25, 545–549. (in Chinese). [Google Scholar]
- Zhang, K.S.; Han, Z.H.; Li, W.J.; Li, X. Multidisciplinary aerodynamic/structural design optimization for high subsonic transport wing using approximation technique. Acta Aeronaut. Astronaut. Sin. 2006, 27, 810–815. (In Chinese) [Google Scholar]
- Allen, M.J.; Dibley, R.P. Modeling Aircraft Wing Loads from Flight Data Using Neural Networks; NASA Dryden Flight Research Center: Edwards, CA, USA, 2003. [Google Scholar]
- Haas, D.J.; Milano, J.; Flitter, L. Prediction of Helicopter Component Loads Using Neural Networks. J. Am. Helicopter Soc. 1995, 40, 72–82. [Google Scholar] [CrossRef]
- Wallach, R.; de Mattos, B.S.; da Mota Girardi, R. Aerodynamic coefficient prediction of a general transport aircraft using neural network. In Proceedings of the 25th Congress of the International Council of the Aeronautical Sciences 2006, Hamburg, Germany, 3–8 September 2006; pp. 1199–1214. [Google Scholar]
- He, F.; Shu, C. Application of BP neural networks based on Bayesian regularization to aircraft wing loads analysis. Flight Dyn. 2009, 27, 85–88. [Google Scholar]
- Li, H.; Chen, X.; Zuo, L.; Zhao, Z. Surrogate model for flight load analysis based on random forest. Acta Aeronaut. ET Astronaut. Sin. 2022, 43, 309–318. (In Chinese) [Google Scholar]
- Jameson, A. Optimum aerodynamic design using CFD and control theory. In Proceedings of the 12th Computational Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995; pp. 926–949. [Google Scholar]
- Chung, H.-S.; Alonso, J.J. Using gradients to construct cokriging approximation models for high-dimensional design optimization problems. In Proceedings of the 40th AIAA Aerospace Sciences Meeting and Exhibit 2002, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Chung, H.-S.; Alonsoy, J.J. Design of a low-boom supersonic business jet using cokriging approximation models. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization 2002, Atlanta, GA, USA, 4–6 September 2002. [Google Scholar]
- Liu, W.; Batill, S.M. Gradient-enhanced response surface approximations using kriging models. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization 2002, Atlanta, GA, USA, 4–6 September 2002. [Google Scholar]
- Laurenceau, J.; Sagaut, P. Building Efficient Response Surfaces of Aerodynamic Functions with Kriging and Cokriging. AIAA J. 2008, 46, 498–507. [Google Scholar] [CrossRef]
- Lu, W.; Wang, S.; Ma, Y. Static aeroelastic optimization of a high-aspect-ratio composite wing based on CFD/CSD and Kriging model. Chin. J. Appl. Mech. 2015, 32, 581–585+703–704. (In Chinese) [Google Scholar]
- Chen, L.; Qiu, H.; Gao, L.; Jiang, C.; Yang, Z. Optimization of expensive black-box problems via Gradient-enhanced Kriging. Comput. Methods Appl. Mech. Eng. 2020, 362, 112861. [Google Scholar] [CrossRef]
- MSC.Software. MSC Nastran 2001 Release Guide; MSC Software Corporation: Newport Beach, CA, USA, 2002. [Google Scholar]
- Liu, Y.; Wan, Z.; Yang, C. Quadratic programming equivalent mapping method for external aerodynamic force in flight load analysis. Beijing Hangkong Hangtian Daxue Xuebao/J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 541–547. (In Chinese) [Google Scholar]
- Butcher, J.C. A history of Runge-Kutta methods. Appl. Numer. Math. 1996, 20, 247–260. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Sondergaard, J.; Dace, A. A Matlab Kriging Toolbox; Technical University of Denmark, Informatics Math and Modelling TR 2002-12: Kongens Lyngby, Denmark, 2002. [Google Scholar]
- Dong, G.; Wang, X.; Liu, D. Metaheuristic Approaches to Solve a Complex Aircraft Performance Optimization Problem. Appl. Sci. 2019, 9, 2979. [Google Scholar] [CrossRef]
- Liu, W. Development of Gradient-Enhanced Kriging Approximations for Multidisciplinary Design Optimization; University of Notre Dame: Notre Dame, IN, USA, 2003. [Google Scholar]
- Laurenceau, J.; Meaux, M.; Montagnac, M.; Sagaut, P. Comparison of Gradient-Based and Gradient-Enhanced Response-Surface-Based Optimizers. AIAA J. 2010, 48, 981–994. [Google Scholar] [CrossRef]
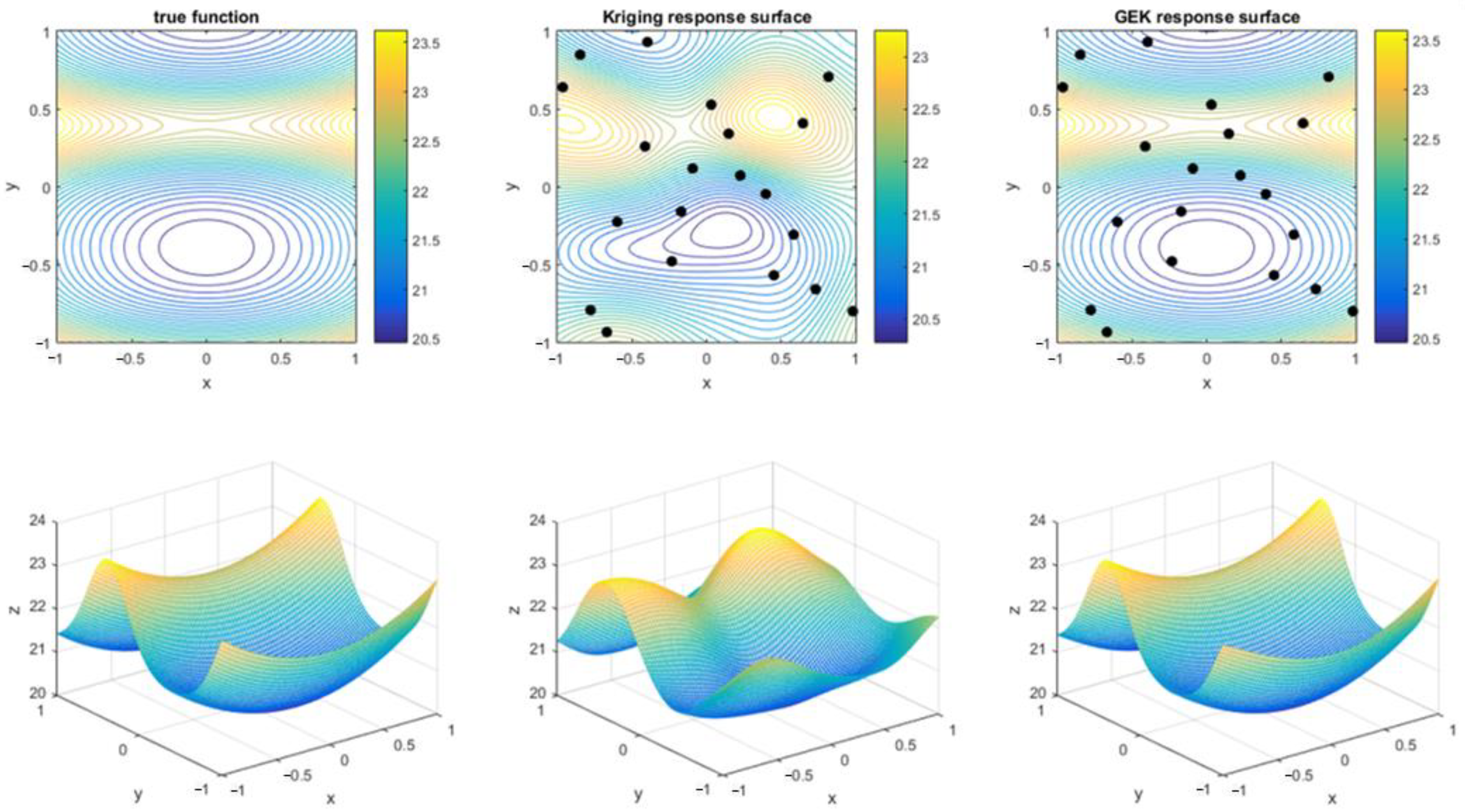
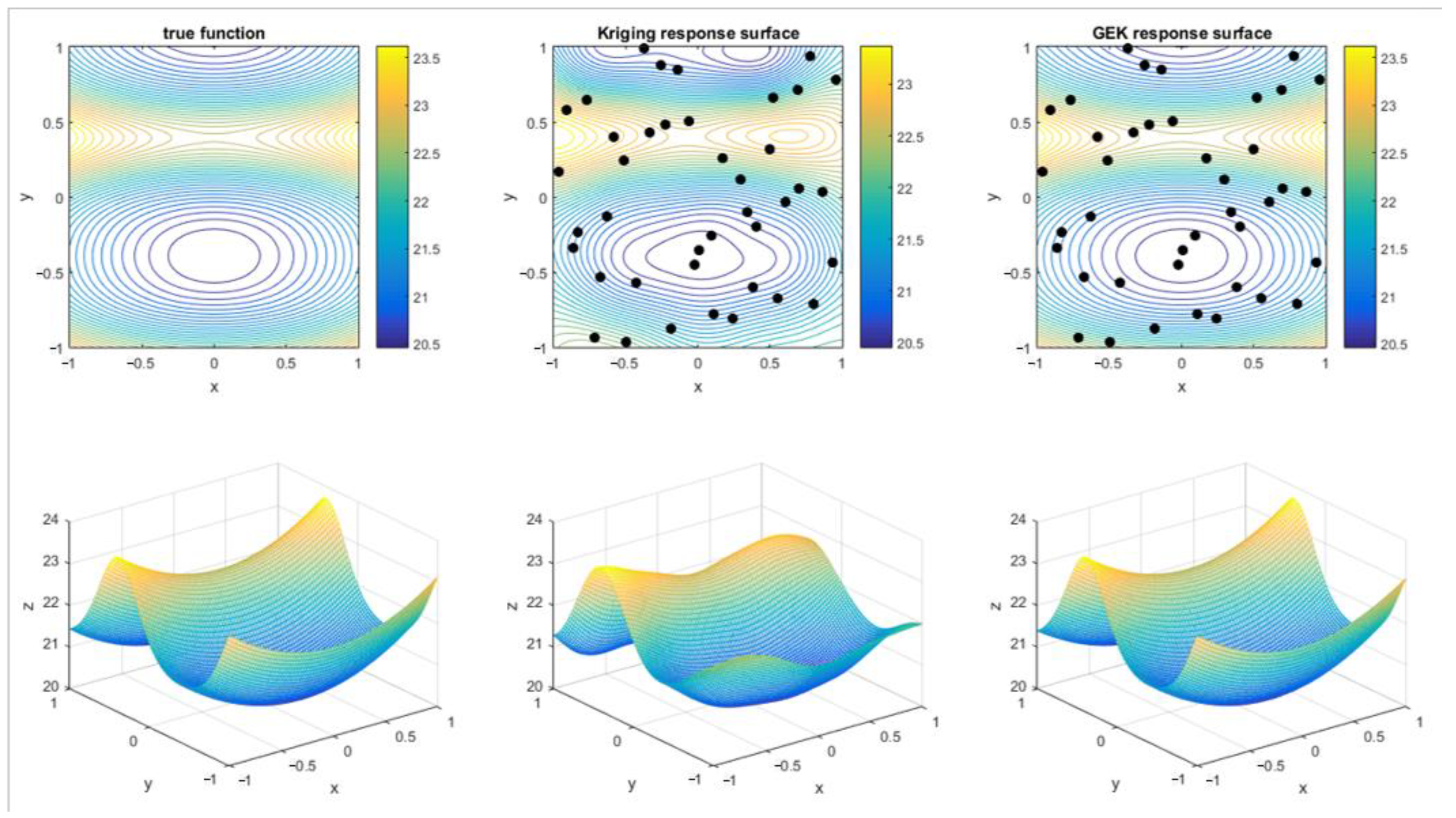



| Number of Samples | MSE of Kriging Model | MSE of GEK Model |
|---|---|---|
| 20 | 0.1549 | 0.0176 |
| 40 | 0.0559 | 0.0024 |
| N Factor | (rad−1) | (rad−1) | (rad−1) | (rad−1) | Shearing Force of Wing Root (kN) | Bending Moment of Wing Root (kN·m) | |
|---|---|---|---|---|---|---|---|
| Rigid linear aerodynamics | 9.04 | −8.31 × 10−1 | −3.48 × 10−2 | −2.53 × 10−1 | −6.00 × 10−2 | 451.8 | 63.8 |
| Elastic linear aerodynamics | 9.89 | −8.66 × 10−1 | −4.06 × 10−2 | −1.95 × 10−1 | −4.80 × 10−2 | 275.1 | 38.8 |
| Rigid nonlinear aerodynamics | 8.72 | −7.86 × 10−1 | −5.59 × 10−2 | −1.94 × 10−1 | −4.76 × 10−2 | 262.6 | 35.3 |
| Elastic nonlinear aerodynamics | 8.83 | −7.70 × 10−1 | −5.59 × 10−2 | −1.39 × 10−1 | −3.61 × 10−2 | 263.8 | 35.1 |
| Input Variables | Output Variables | ||||
|---|---|---|---|---|---|
| Notation | Description | Unit | Notation | Description | Unit |
| H | Flight altitude | km | α | Angle of attack | rad |
| Ma | Mach number | δ | Aileron angle | rad | |
| nz | N factor | ||||
| Input Variables | Output Variables | ||||
|---|---|---|---|---|---|
| Notation | Description | Unit | Notation | Description | Unit |
| α | Angle of attack | rad | nz | N factor | |
| δ | Aileron angle | rad | Pitching rate | rad/s | |
| S-WR | Shearing force of wing root | kN | |||
| BM-WR | Bending moment of wing root | kN·m | |||
| , | Partial derivatives of lift coefficients | rad−1 | |||
| , | Partial derivatives of moments | kN·m/rad | |||
| Linear Aerodynamic Model | Nonlinear Aerodynamic Model | |||
|---|---|---|---|---|
| MSC.Nastran | GEK Model | MGAERO | GEK Model | |
| Angle of attack (rad) | 0.1346 | 0.1346 | 0.1683 | 0.1683 |
| Aileron angle (rad) | −0.1126 | −0.1126 | −0.3370 | −0.3370 |
| Model | Initial Angle of Attack (°) | Initial Aileron Angle (°) | Max Aileron Angle (°) |
|---|---|---|---|
| MSC.Nastran | 0.8567 | −0.7168 | −5.5759 |
| GEK Model | 0.8567 | −0.7168 | −5.5759 |
| Model | N factor | Angle of Attack (rad) | Pitching Rate (rad/s) | Bending Moment of Wing Root (kN·m) | Shearing Force of Wing Root (kN) | Flight Altitude (km) |
|---|---|---|---|---|---|---|
| MSC.NASTRAN | 9.001 | 0.1299 | 0.6102 | 360.500 | 248.0 | 0.2208 |
| GEK model | 9.001 | 0.1299 | 0.6102 | 360.600 | 248.1 | 0.2195 |
| Model | Initial Angle of Attack (°) | Initial Aileron Angle (°) | Max Aileron Angle (°) |
|---|---|---|---|
| MGAERO | 1.6764 | −1.7685 | −8.8808 |
| GEK Model | 1.6764 | −1.7685 | −8.8808 |
| Model | N Factor | Angle of Attack (rad) | Pitching Rate (rad/s) | Bending Moment of Wing Root (kN·m) | Shearing Force of Wing Root (kN) | Flight Altitude (m) |
|---|---|---|---|---|---|---|
| MGAERO | 9.001 | 0.1546 | 0.5944 | 298.9 | 227.1 | 219.5 |
| GEK Model | 9.001 | 0.1546 | 0.5944 | 297.5 | 226.0 | 214.9 |
| N Factor | Angle of Attack | Pitching Rate | Bending Moment of Wing Root | Shearing Force of Wing Root | Flight Path | |
|---|---|---|---|---|---|---|
| GEK model (based on linear aerodynamics) | 0.9999 | 0.9997 | 0.9999 | 0.9979 | 0.9977 | 0.9999 |
| GEK model (based on nonlinear aerodynamics) | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 |
| N Factor | Angle of Attack | Pitching Rate | Bending Moment of Wing Root | Shearing Force of Wing Root | Flight Path | |
|---|---|---|---|---|---|---|
| GEK model (based on linear aerodynamics) | 0.001% | 0.008% | 0.001% | 0.28% | 0.40% | 0.57% |
| GEK model (based on nonlinear aerodynamics) | 0 | 0 | 0 | 0.0047% | 0.0048% | 0.12% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wan, Z.; Wang, X.; Xu, A.; Chen, Z. Analysis of Flight Loads during Symmetric Aircraft Maneuvers Based on the Gradient-Enhanced Kriging Model. Aerospace 2024, 11, 334. https://doi.org/10.3390/aerospace11050334
Zhang S, Wan Z, Wang X, Xu A, Chen Z. Analysis of Flight Loads during Symmetric Aircraft Maneuvers Based on the Gradient-Enhanced Kriging Model. Aerospace. 2024; 11(5):334. https://doi.org/10.3390/aerospace11050334
Chicago/Turabian StyleZhang, Shanshan, Zhiqiang Wan, Xiaozhe Wang, Ao Xu, and Zhiying Chen. 2024. "Analysis of Flight Loads during Symmetric Aircraft Maneuvers Based on the Gradient-Enhanced Kriging Model" Aerospace 11, no. 5: 334. https://doi.org/10.3390/aerospace11050334
APA StyleZhang, S., Wan, Z., Wang, X., Xu, A., & Chen, Z. (2024). Analysis of Flight Loads during Symmetric Aircraft Maneuvers Based on the Gradient-Enhanced Kriging Model. Aerospace, 11(5), 334. https://doi.org/10.3390/aerospace11050334






