Dynamic Encircling Cooperative Guidance for Intercepting Superior Target with Overload, Impact Angle and Simultaneous Time Constraints
Abstract
:1. Introduction
- (1)
- Different from the approaches outlined in refs. [13,14,15,16], the introduced DECG law is based on a feasible dynamic encircling strategy, considering the physical ability of all flight vehicles involved, which can offer a more practical cooperative strategy for the cooperative guidance and ensure the precise interception of the target by at least one interceptor being restricted to low velocity, limited maneuverability and desired impact angle. Noteworthy is the low ability of a single interceptor; the DECG can thereby leverage the group advantage of interceptors and significantly enhance their overall interception performance.
- (2)
- Compared with refs. [11,23], the DECG law employs successive convex optimization to address the guidance problem, which is also tightly coupled with the cooperative strategy. This approach offers improved constraints processing capabilities, control precision and also has good computational efficiency in comparison to existing methodologies. Compared with refs. [30], the proposed DECG improves the time calculation strategy and adopts a more precise solving method.
- (3)
- Compared with refs. [10,22,31], this paper remodels the interception mathematical model using the independent variable of distance, a parameter directly measured by the interceptor’s sensor, thereby enhancing practicality. Furthermore, the chosen independent variable exhibits a monotonically decreasing trend, underscoring the rationale and physical feasibility of the newly proposed interception model. This modification no longer requires the precise calculation of explicit and also aligns the interception model more closely with real-world scenarios, which brings convenience to simultaneous control and realization.
2. Dynamic Encircling Cooperative Guidance Law Design
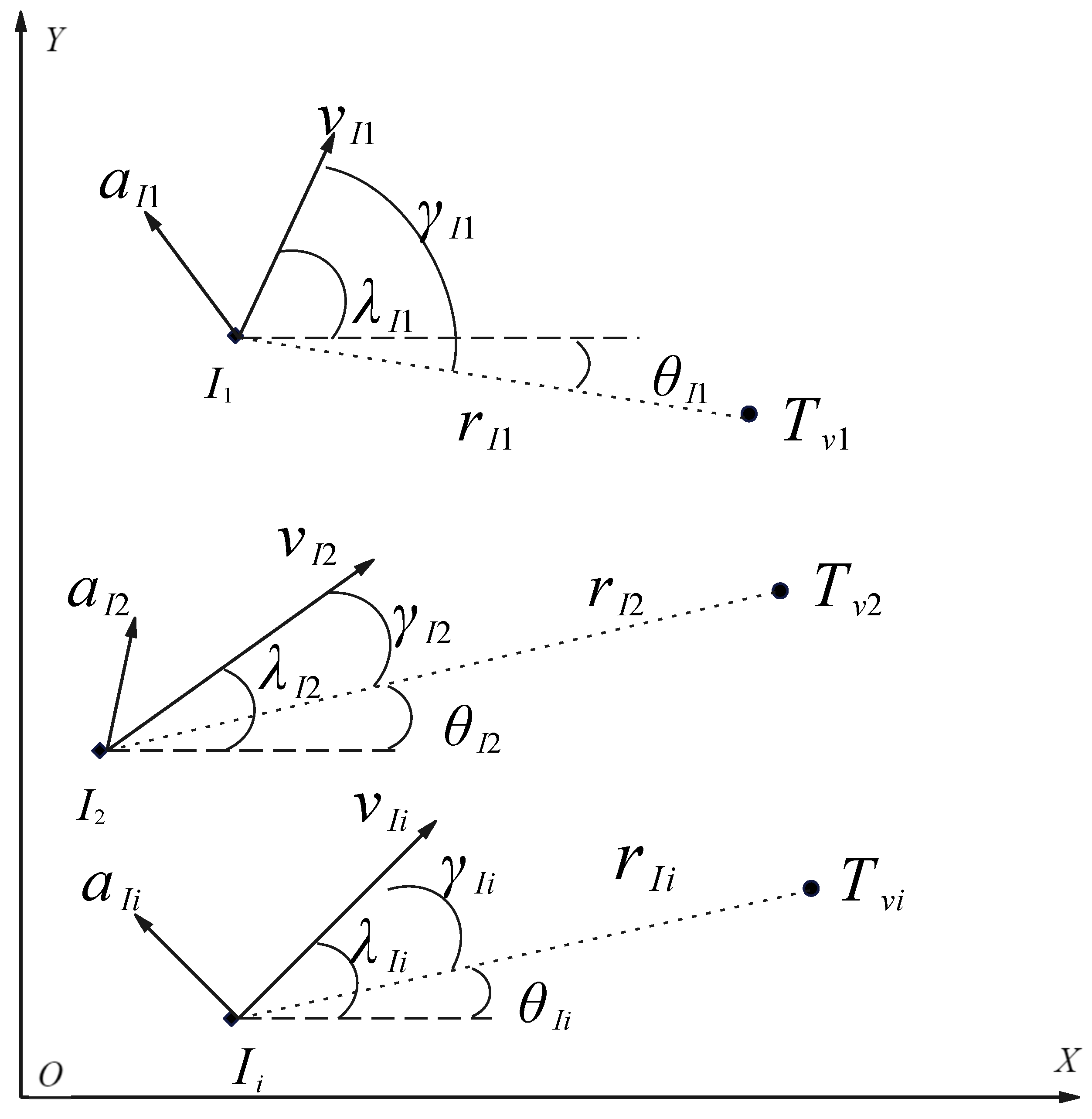
2.1. Problem Formulation
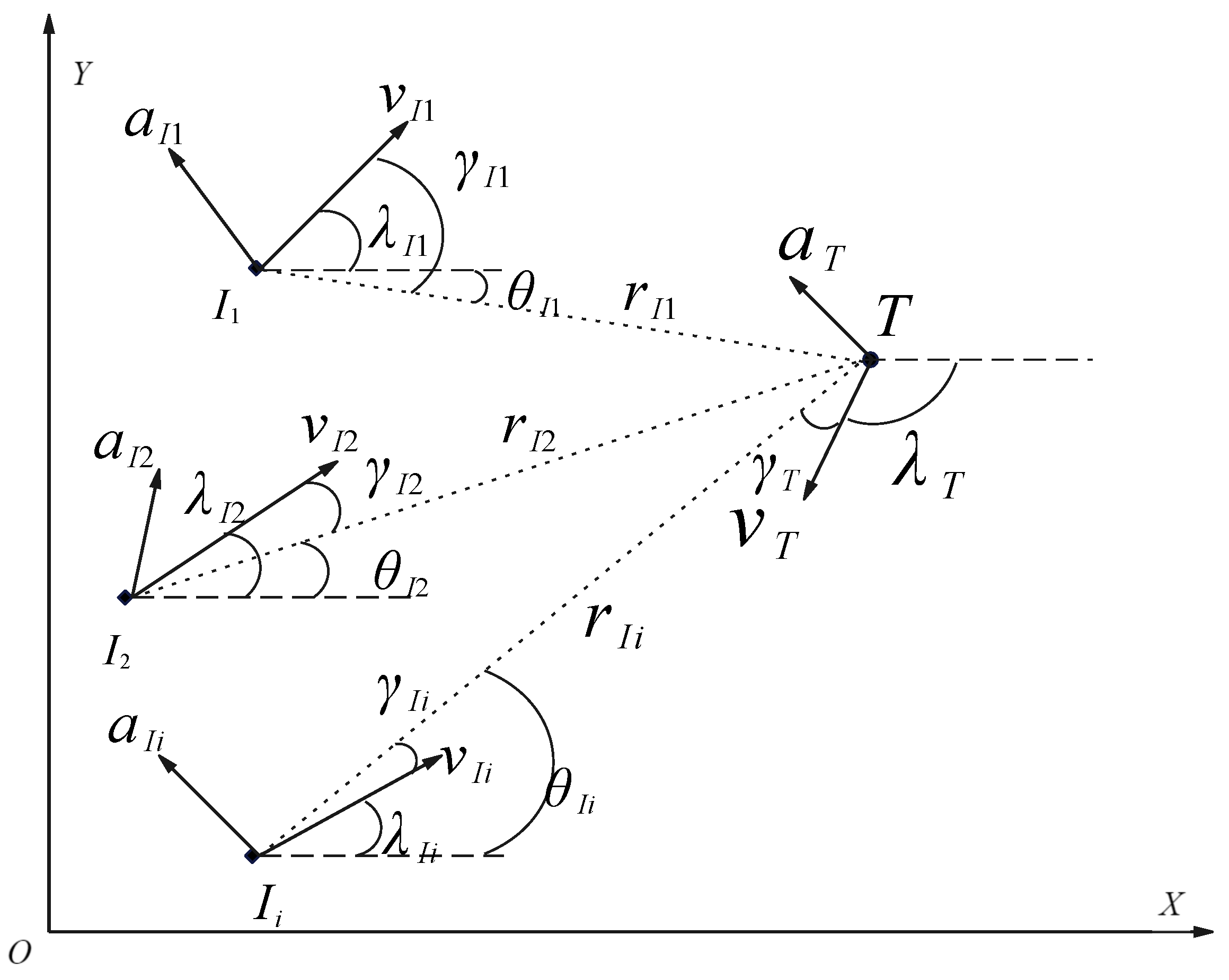
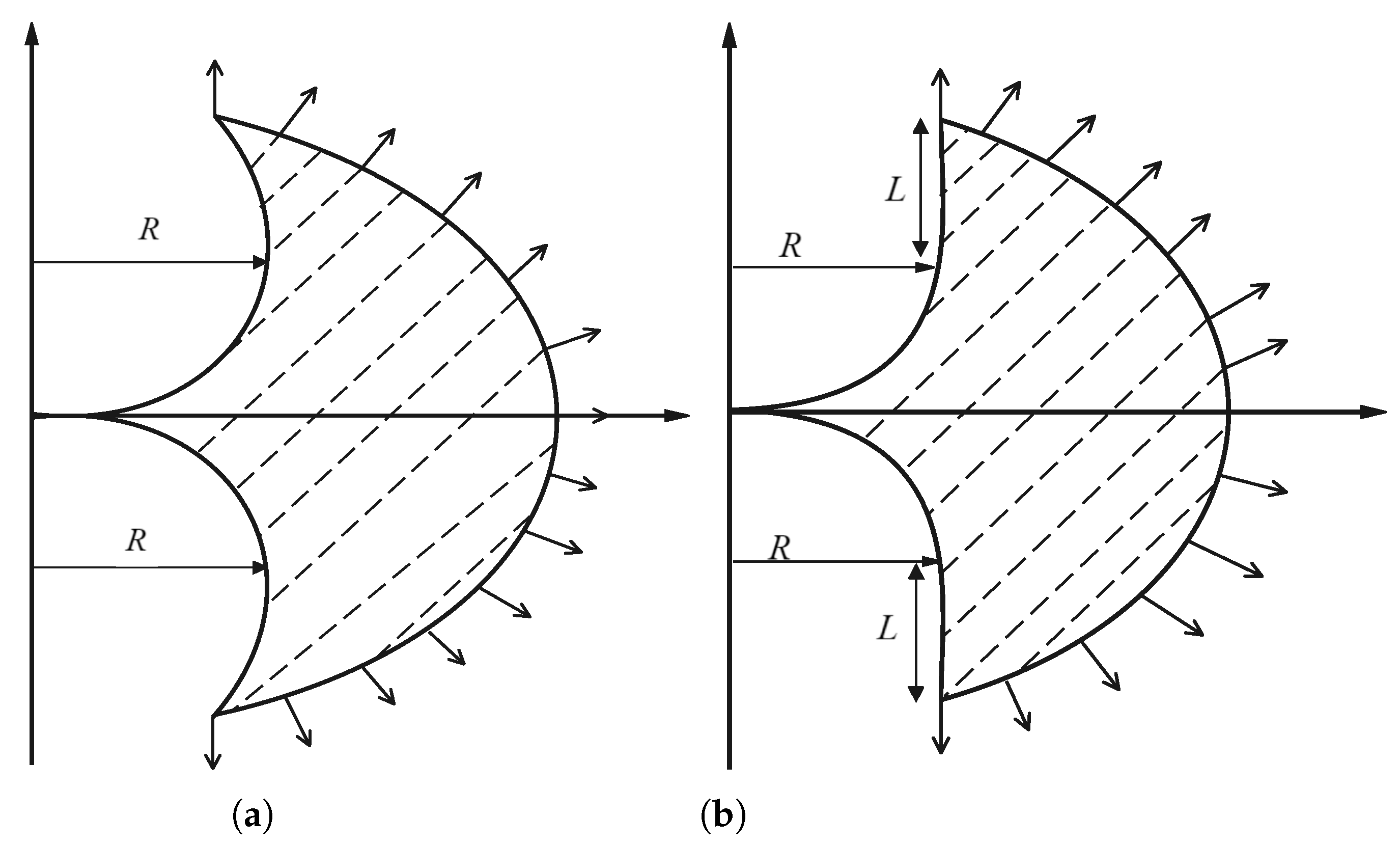
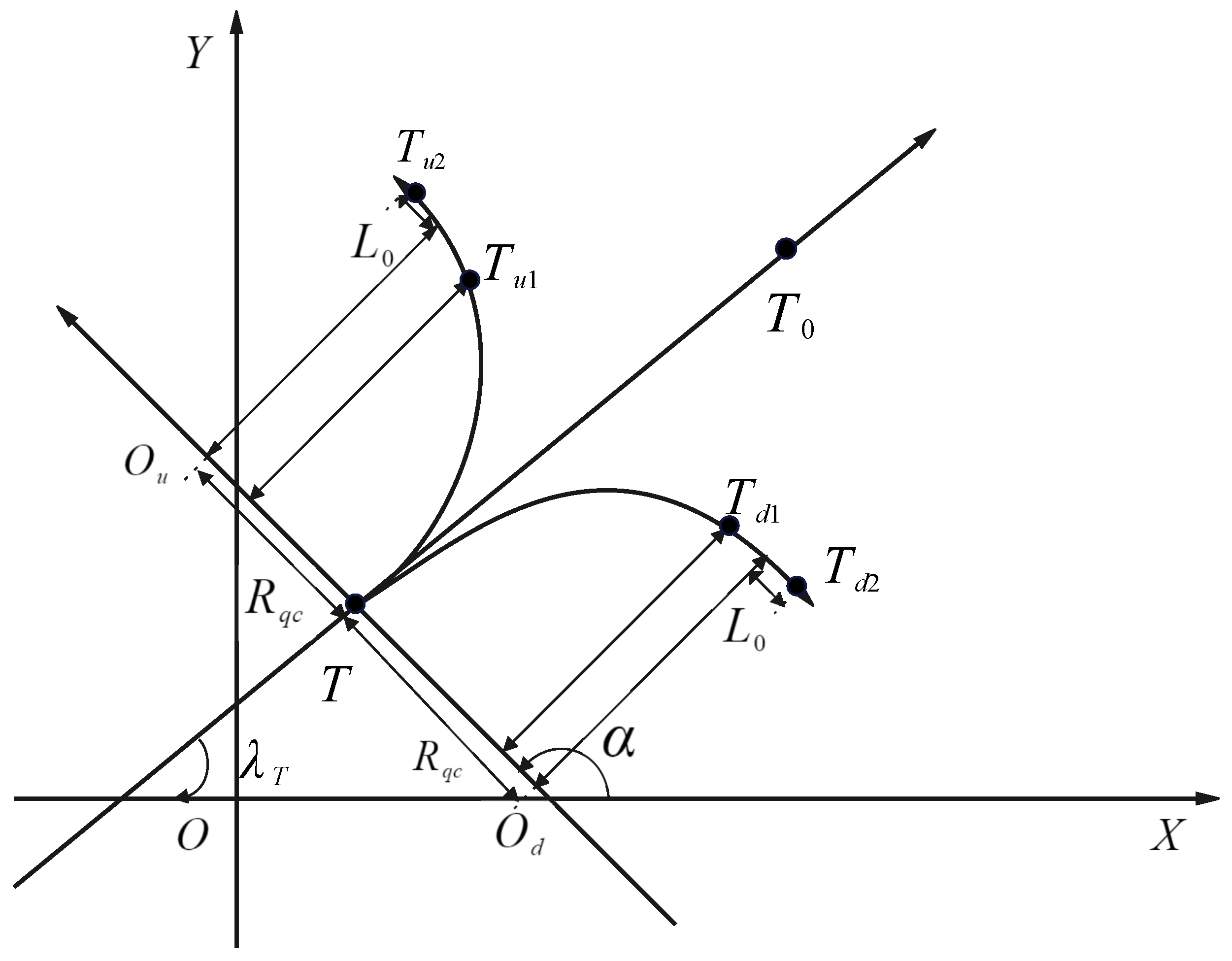
2.2. Dynamic Encircling Strategy and Escaping Points Design
- obj.
- s.t.
2.3. Simultaneous Interception Using Convex Optimization
- obj.
- s.t.
- obj.
- s.t.
- obj.
- s.t.
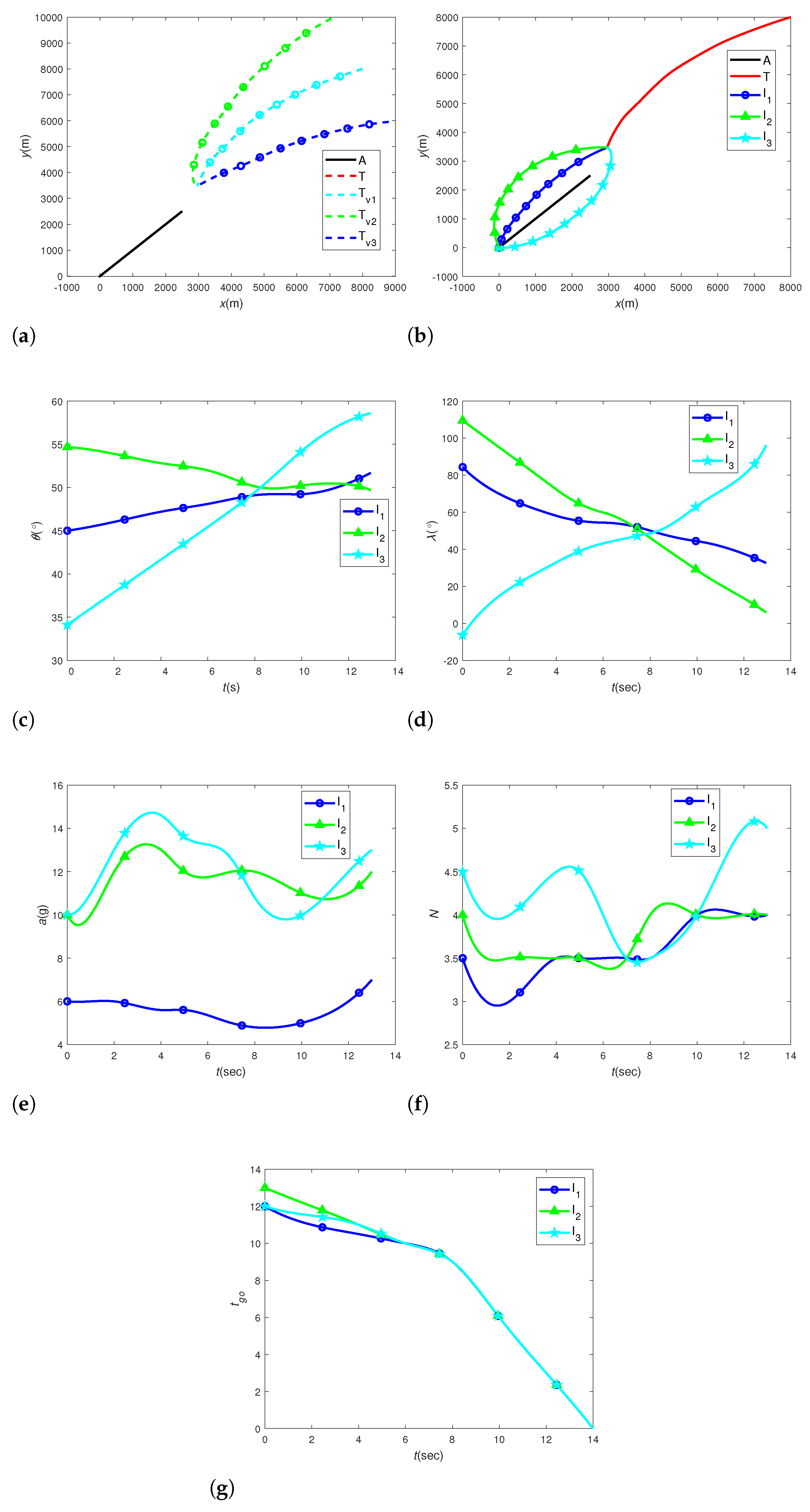
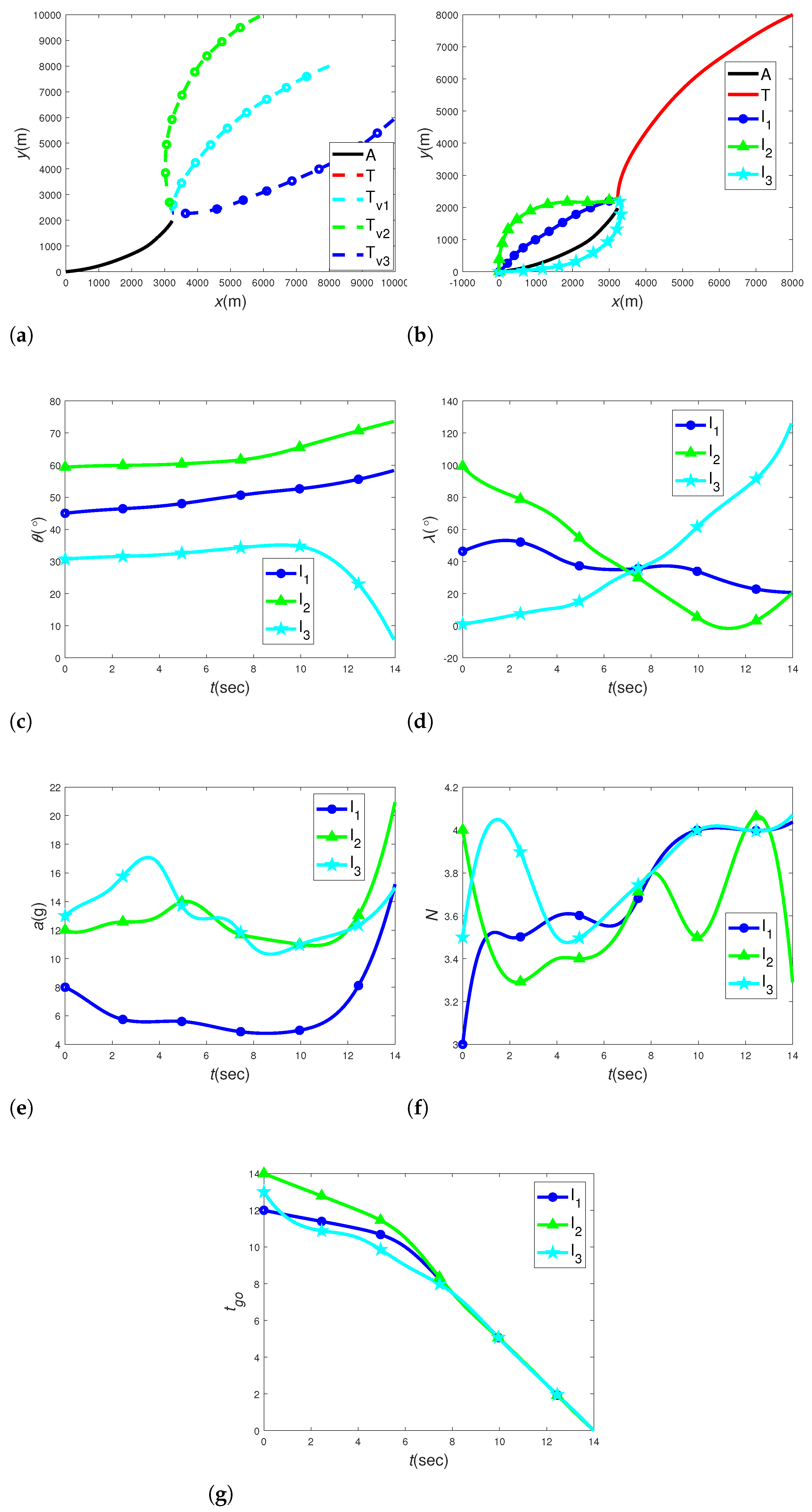
3. Numerical Simulation
3.1. Case 1: Fighter Aircraft Makes No Maneuvers
3.2. Case 2: Fighter Aircraft Makes Evasion Maneuvers
3.3. Case 3: Comparison to the CPNG Guidance
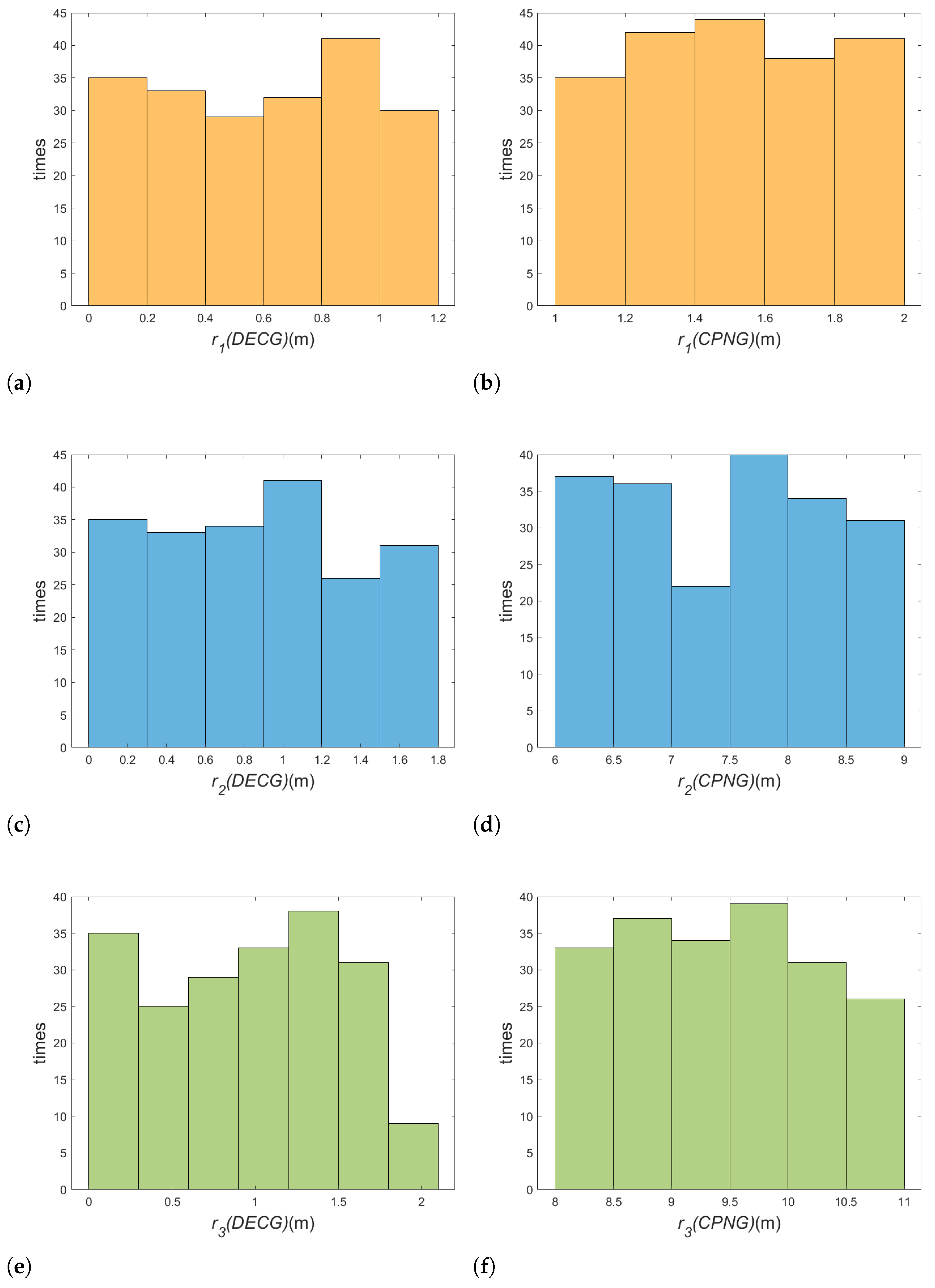
3.4. Case 4: Robustness Analysis
4. Conclusions
- (1)
- The proposed dynamic encircling interception strategy of the DECG law is able to simply and effectively utilize the numerical superiority of the inferior interceptor group, and able to well accomplish the contractual encircling and interception for the superior target. In addition, this strategy can also make the cooperative time constraints easier to process.
- (2)
- The remodeled kinematics and the convex optimization method can satisfy multiple constraints and have better control precision with good computational efficiency, which also makes the guidance problem more practical.
- (3)
- The proposed DECG law has better robustness than the CPNG law in the same simulation conditions, and the interceptors consume less energy under the DECG law, which gives full play to the advantages of the inferior interceptors. What is more, DECG is able to satisfy multiple constraints and still have high control accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garcia, E.; Casbeer, D.W.; Pachter, M. Cooperative Strategies for Optimal Aircraft Defense from an Attacking Missile. J. Guid. Control Dyn. 2015, 38, 1510–1520. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A Differential Game for Cooperative Target Defense. Automatica 2019, 102, 58–71. [Google Scholar] [CrossRef]
- Von Moll, A.; Garcia, E.; Casbeer, D.; Suresh, M.; Swar, S.C. Multiple-Pursuer, Single-Evader Border Defense Differential Game. J. Aerosp. Inf. Syst. 2020, 17, 407–416. [Google Scholar] [CrossRef]
- Liang, H.; Wang, J.; Liu, J.; Liu, P. Guidance Strategies for Interceptor against Active Defense Spacecraft in Two-on-Two Engagement. Aerosp. Sci. Technol. 2020, 96, 105529. [Google Scholar] [CrossRef]
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Robust Multi-Agent Differential Games with Application to Cooperative Guidance. Aerosp. Sci. Technol. 2021, 111, 106568. [Google Scholar] [CrossRef]
- Liu, F.; Dong, X.; Li, Q.; Ren, Z. Cooperative Differential Games Guidance Laws for Multiple Attackers against an Active Defense Target. Chin. J. Aeronaut. 2022, 35, 374–389. [Google Scholar] [CrossRef]
- Yan, X.; Lyu, S. A Two-Side Cooperative Interception Guidance Law for Active Air Defense with a Relative Time-to-Go Deviation. Aerosp. Sci. Technol. 2020, 100, 105787. [Google Scholar] [CrossRef]
- Song, J.; Song, S.; Xu, S. Three-Dimensional Cooperative Guidance Law for Multiple Missiles with Finite-Time Convergence. Aerosp. Sci. Technol. 2017, 67, 193–205. [Google Scholar] [CrossRef]
- Weiss, M.; Shima, T. Minimum Effort Pursuit/Evasion Guidance with Specified Miss Distance. J. Guid. Control. Dyn. 2016, 39, 1069–1079. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S.R.; Mukherjee, D. Cooperative Salvo Based Active Aircraft Defense Using Impact Time Guidance. IEEE Control Syst. Lett. 2021, 5, 1573–1578. [Google Scholar] [CrossRef]
- Kang, S.; Wang, J.; Li, G.; Shan, J.; Petersen, I.R. Optimal Cooperative Guidance Law for Salvo Attack: An MPC-Based Consensus Perspective. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2397–2410. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, H.; Chen, W. Three-Dimensional Impact Time and Angle Control Guidance Based on MPSP. Int. J. Aerosp. Eng. 2019, 2019, e5631723. [Google Scholar] [CrossRef]
- Li, G.Y.; Yu, Z.; Zhang, Y. Cooperative Guidance Law with Angle Constraint to Intercept Maneuvering Target. J. Syst. Eng. Electron. 2019, 41, 626–635. [Google Scholar]
- Lyu, T.; Lyu, Y.Y.; Li, C.J.; Guo, Y.N. Finite Time Cooperative Guidance Law for Multiple Missiles with Line-of-sight Angle Constraint. Acta Armamentarii 2018, 39, 305. [Google Scholar]
- Kumar, S.R.; Mukherjee, D. Cooperative Active Aircraft Protection Guidance Using Line-of-Sight Approach. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 957–967. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Huang, P. Optimal Cooperative Line-of-Sight Guidance for Defending a Guided Missile. Aerospace 2022, 9, 232. [Google Scholar] [CrossRef]
- Su, W.; Li, K.; Chen, L. Coverage-Based Cooperative Guidance Strategy against Highly Maneuvering Target. Aerosp. Sci. Technol. 2017, 71, 147–155. [Google Scholar] [CrossRef]
- Su, W.; Shin, H.S.; Chen, L.; Tsourdos, A. Cooperative Interception Strategy for Multiple Inferior Missiles against One Highly Maneuvering Target. Aerosp. Sci. Technol. 2018, 80, 91–100. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, D.; Li, J.; Yao, Y. Coverage-Based Cooperative Guidance Strategy by Controlling Flight Path Angle. J. Guid. Control Dyn. 2022, 45, 972–981. [Google Scholar] [CrossRef]
- Yan, X.; Kuang, M.; Zhu, J.; Yuan, X. Reachability-Based Cooperative Strategy for Intercepting a Highly Maneuvering Target Using Inferior Missiles. Aerosp. Sci. Technol. 2020, 106, 106057. [Google Scholar] [CrossRef]
- Garcia, E. Cooperative Target Protection from a Superior Attacker. Automatica 2021, 131, 109696. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S.R. Supertwisting Control-Based Cooperative Salvo Guidance Using Leader–Follower Approach. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3556–3565. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, W.; Chen, W. Reinforcement Learning-based Intelligent Guidance Law for Cooperative Attack of Multiple Missiles. Acta Armamentarii 2021, 42, 1638. [Google Scholar] [CrossRef]
- Yujie, S.; Hua, X.; Zhe, L. Three-Dimensional Adaptive Neural Network Guidance Law against Maneuvering Targets. J. Syst. Simul. 2021, 33, 453. [Google Scholar] [CrossRef]
- Luo, D.; Fan, Z.; Yang, Z.; Xu, Y. Multi-UAV Cooperative Maneuver Decision-Making for Pursuit-Evasion Using Improved MADRL. Def. Technol. 2023, in press. [Google Scholar] [CrossRef]
- Xia, J.; Luo, Y.; Liu, Z.; Zhang, Y.; Shi, H.; Liu, Z. Cooperative Multi-Target Hunting by Unmanned Surface Vehicles Based on Multi-Agent Reinforcement Learning. Def. Technol. 2023, 29, 80–94. [Google Scholar] [CrossRef]
- Jiang, H.; An, Z.; Yu, Y.; Chen, S.; Xiong, F. Cooperative Guidance with Multiple Constraints Using Convex Optimization. Aerosp. Sci. Technol. 2018, 79, 426–440. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, X.; Lv, Y.; Li, X.; Liu, Z. Recent Progress on the Study of Multi-vehicle Coordination in Cooperative Attack and Defense: An Overview. Asian J. Control 2022, 24, 794–809. [Google Scholar] [CrossRef]
- Pachter, M.; Moll, A.V.; Garcia, E.; Casbeer, D.; Milutinović, D. Cooperative Pursuit by Multiple Pursuers of a Single Evader. J. Aerosp. Inf. Syst. 2020, 17, 371–389. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, W.; Fang, Y.; Wu, Z.; Wang, M. Cooperative Guidance Law against Highly Maneuvering Target with Dynamic Surrounding Attack. Int. J. Aerosp. Eng. 2021, 2021, 6623561. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, R. Unified Approach to Cooperative Guidance Laws against Stationary and Maneuvering Targets. Nonlinear Dyn. 2015, 81, 1635–1647. [Google Scholar] [CrossRef]




| Par | Values | Units | Par | Values | Units |
|---|---|---|---|---|---|
| [8000 8000] | m | [0 0] | m | ||
| [0 0] | m | [0 0] | m | ||
| [0 0] | m | 1000 | |||
| [300 300] | 600 | ||||
| 5 | g | 30 | g | ||
| 20 | g | −180 | deg | ||
| [45 100 0] | deg | 45 | deg | ||
| 4 | / | 4 | / | ||
| 12 | s | 2 | s | ||
| [0.01 0.01 0.01] | / | 1.57 | rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Yan, X. Dynamic Encircling Cooperative Guidance for Intercepting Superior Target with Overload, Impact Angle and Simultaneous Time Constraints. Aerospace 2024, 11, 375. https://doi.org/10.3390/aerospace11050375
Yang D, Yan X. Dynamic Encircling Cooperative Guidance for Intercepting Superior Target with Overload, Impact Angle and Simultaneous Time Constraints. Aerospace. 2024; 11(5):375. https://doi.org/10.3390/aerospace11050375
Chicago/Turabian StyleYang, Dengfeng, and Xiaodong Yan. 2024. "Dynamic Encircling Cooperative Guidance for Intercepting Superior Target with Overload, Impact Angle and Simultaneous Time Constraints" Aerospace 11, no. 5: 375. https://doi.org/10.3390/aerospace11050375
APA StyleYang, D., & Yan, X. (2024). Dynamic Encircling Cooperative Guidance for Intercepting Superior Target with Overload, Impact Angle and Simultaneous Time Constraints. Aerospace, 11(5), 375. https://doi.org/10.3390/aerospace11050375






