Operational Reliability Analysis of Turbine Blisk Using an Enhanced Moving Neural Network Framework
Abstract
:1. Introduction
2. Enhanced Moving Neural Network Framework for Reliability Evaluation
2.1. Structural Reliability Estimation Procedures with MNNF
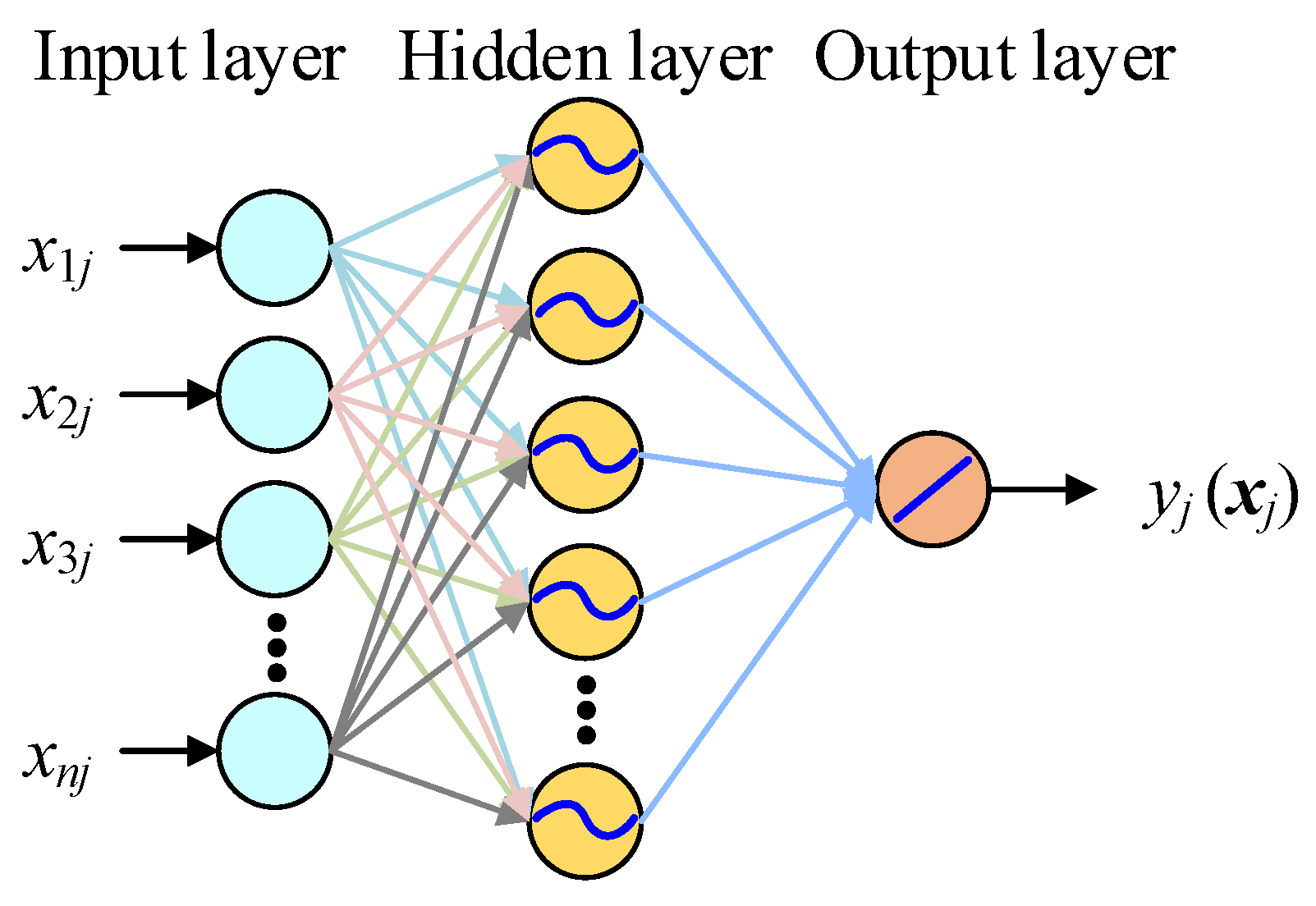
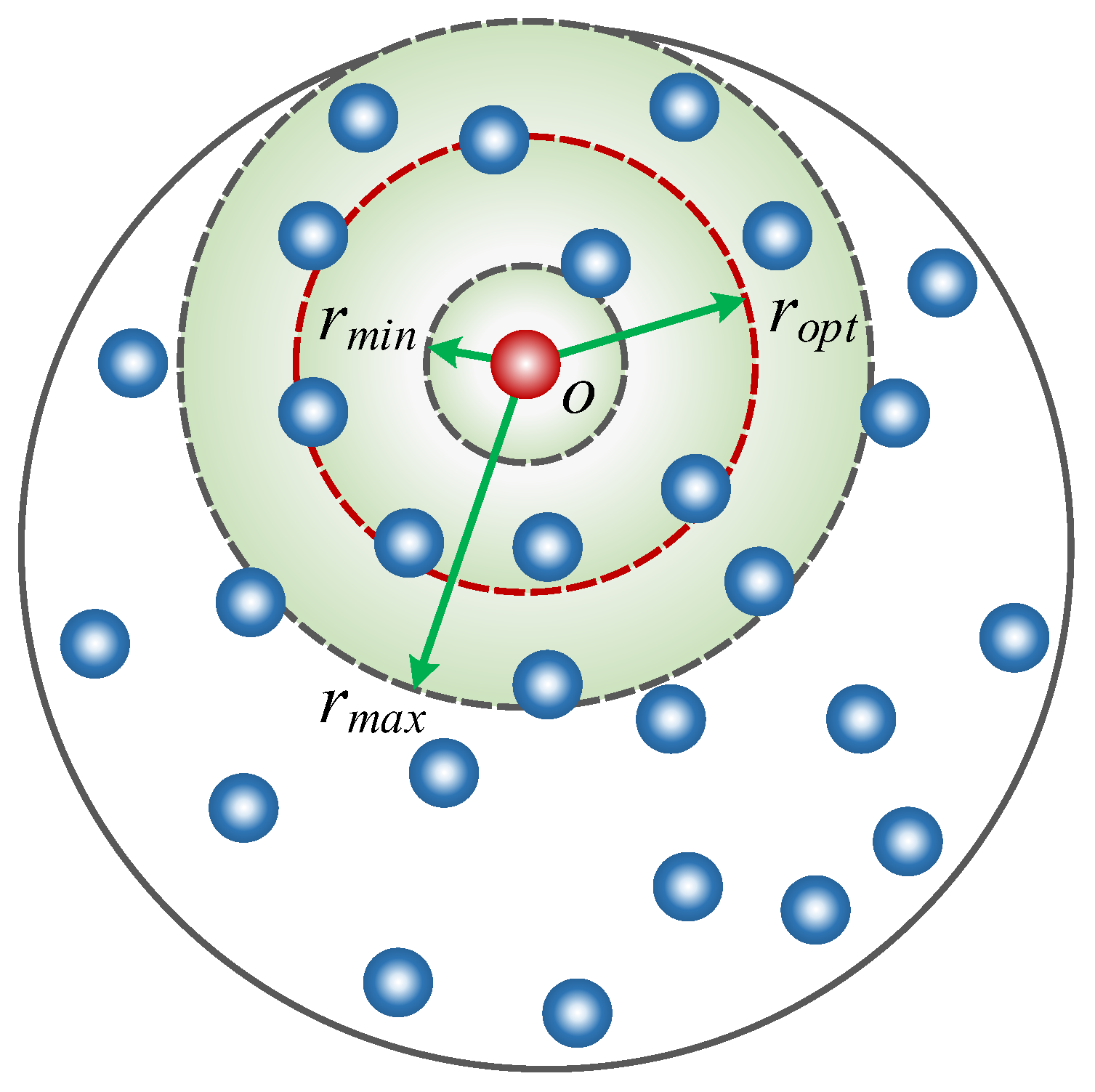
2.2. MNNF Mathematical Modeling
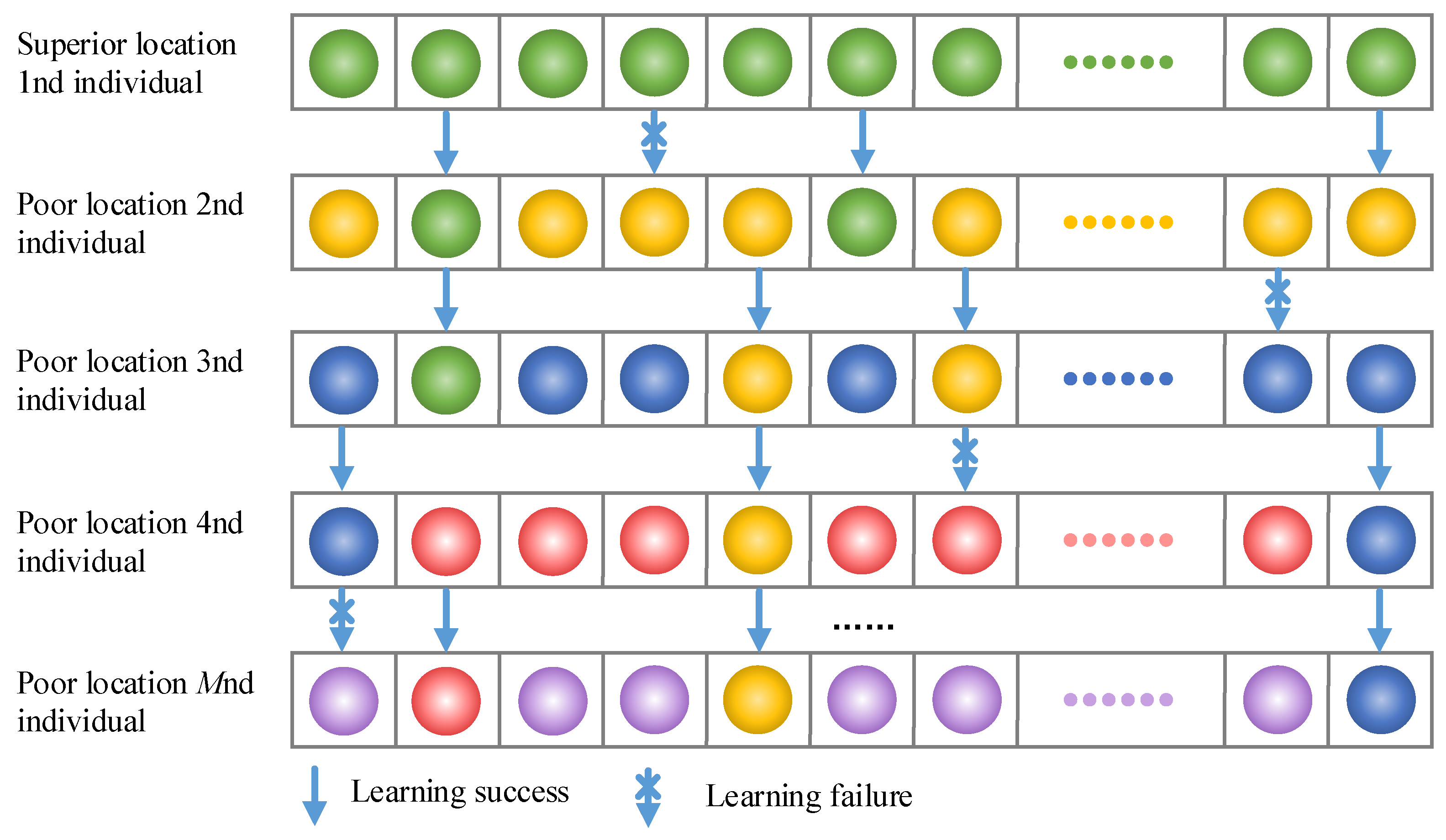
2.3. Reliability Approach with MNNF
3. Reliability Assessment of Turbine Blisk with the MNNF Model
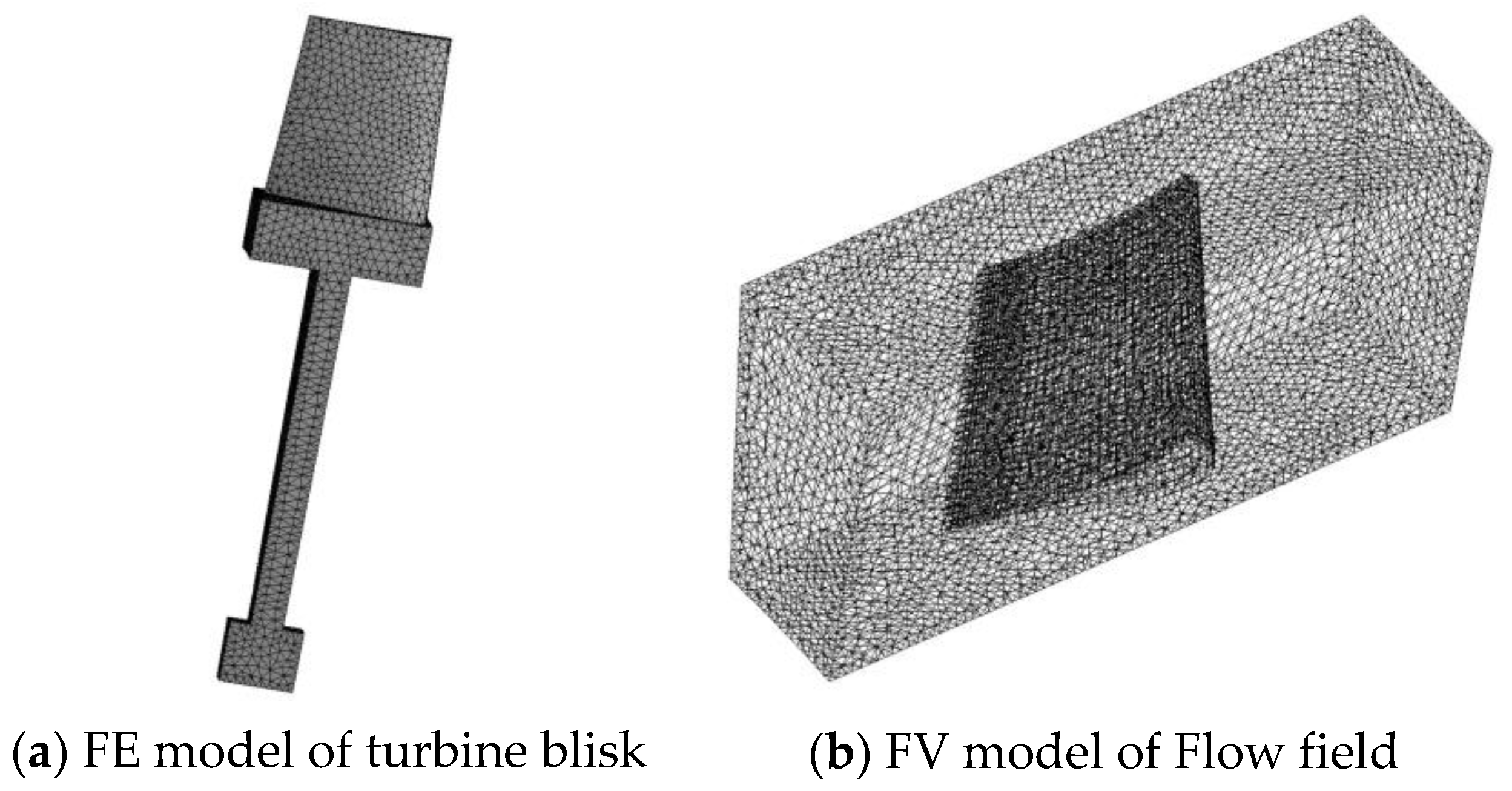
3.1. Deterministic Analysis of Turbine Blisk
3.2. MNNK Modeling for Turbine Blisk Strain Failure
3.3. Reliability Analysis for Turbine Blisk Strain
4. Enhanced Moving Neural Network Framework Validation
4.1. Modeling Properties
4.2. Simulation Performances
5. Conclusions
- (i)
- The MNNF method is developed by introducing the compact support region theory, ISTOA, and Bayesian regularization strategy into the artificial neural network model for the reliability analysis of turbine blisk strain.
- (ii)
- The reliability degree of turbine blisk strain is 0.9984 when the allowable value is 5.2862 × 10−3 m according to the reliability evaluation of turbine blisk strain with the proposed MNNF model.
- (iii)
- The modeling properties of the MNNF model are verified by comparing the RSM, Kriging, SVM, BP-NN, and BP-PSO approaches. The modeling accuracy and efficiency with the RMSE of 0.99738, R2 of 3.1634 × 10−4 m and modeling time of 0.423 s are superior to other methods.
- (iv)
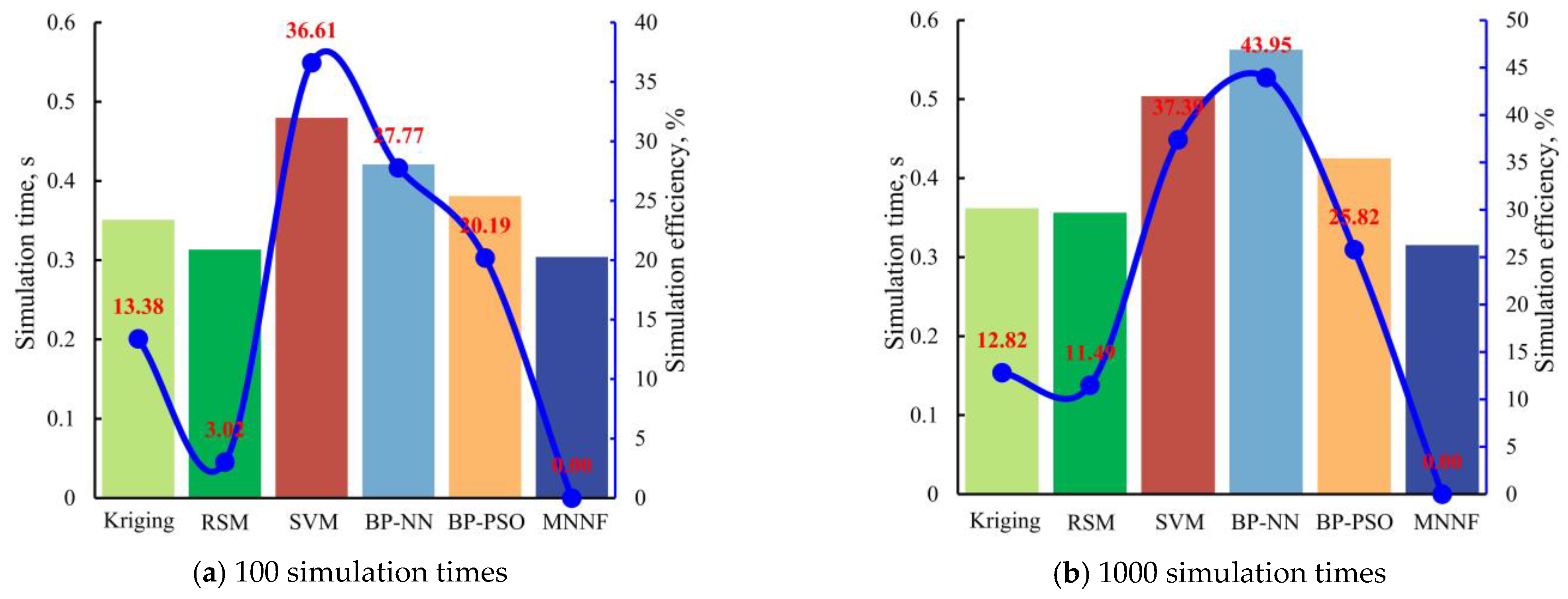
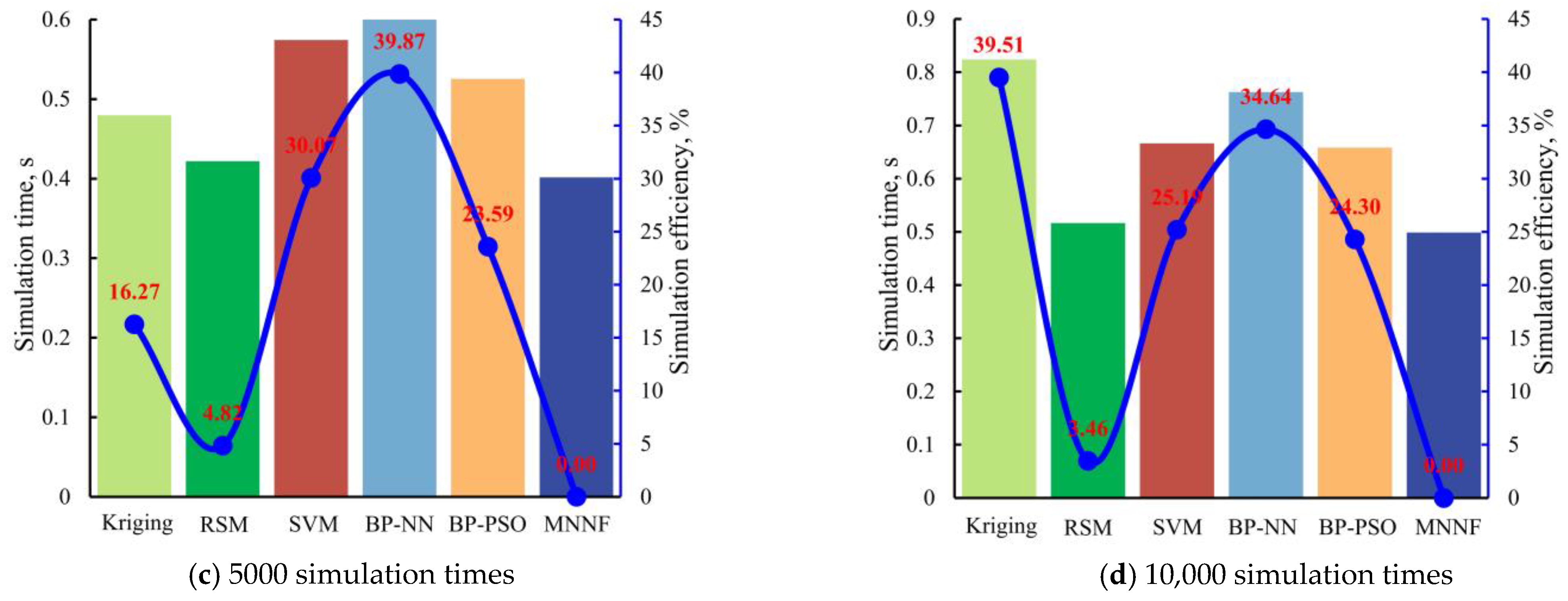
- The simulation performances of the MNNF model are demonstrated by different MC simulation times with multiple methods. The simulation precision of the MNNF model (99.99%) is higher than these of different approaches (i.e., RSM of 99.96%, Kriging of 99.91%, SVM of 99.93%, BP-NN of 99.97%, and BP-PSO methods of 99.97%. Compared with the RSM, Kriging, SVM, BP-NN, and BP-PSO methods, the simulation efficiency of the proposed MNNF is improved by 16.27%, 4.82%, 30.07%, 39.87%, and 23.59%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| MNNF | Moving Neural Network Framework |
| ISTOA | Improve sooty tern Optimization algorithm |
| MC | Monte Carlo |
| FOSM | First-order second-moment |
| RSM | Response surface method |
| SVM | Support vector machine |
| FE | Finite element |
| BP-NN | Back propagation-artificial neural network |
| BP-PSO | BP-NN based on particle swarm optimization |
| RMSE | Root means square error |
| R2 | R-Square |
| LHS | Latin hypercube sampling |
References
- Qian, C.; Li, W.; Ren, Y.; Hu, Z.; Yang, L.; Zhao, X.; Wang, X. Monte-Carlo simulation-based analysis for structural reliability of the crane rail beam under stochastic crane movements and irradiation conditions. Qual. Reliab. Eng. Int. 2023, 39, 1704–1719. [Google Scholar] [CrossRef]
- Jensen, H.A.; Jerez, D.J.; Valdebenito, M. An adaptive scheme for reliability-based global design optimization: A Markov chain Monte Carlo approach. Mech. Syst. Signal Process. 2020, 143, 106836. [Google Scholar] [CrossRef]
- Tabandeh, A.; Jia, G.; Gardoni, P. A review and assessment of importance sampling methods for reliability analysis. Struct. Saf. 2022, 97, 102216. [Google Scholar] [CrossRef]
- Tokdar, S.T.; Kass, R.E. Importance sampling: A review. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 54–60. [Google Scholar] [CrossRef]
- Qin, Q.; Cao, X.; Zhang, S. AWK-TIS: An improved AK-IS based on whale optimization algorithm and truncated importance sampling for reliability analysis. CMES Comput. Model. Eng. Sci. 2023, 135, 1457–1480. [Google Scholar] [CrossRef]
- Zhang, H.; Song, L.K.; Bai, G.C. Moving-zone renewal strategy combining adaptive Kriging and truncated importance sampling for rare event analysis. Struct. Multidiscip. Optim. 2022, 65, 285. [Google Scholar] [CrossRef]
- Song, J.; Wei, P.; Valdebenito, M.; Beer, M. Active learning line sampling for rare event analysis. Mech. Syst. Signal Process. 2021, 147, 107113. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Cheng, K. AK-DS: An adaptive Kriging-based directional sampling method for reliability analysis. Mech. Syst. Signal Process. 2021, 156, 107610. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, Y.; Chen, B.; Zhao, Y. An active learning Kriging model combined with directional importance sampling method for efficient reliability analysis. Probabilistic Eng. Mech. 2020, 60, 103054. [Google Scholar] [CrossRef]
- Ricardo, A.S.; de Santana Gomes, W.J. Structural reliability methods applied in analysis of steel elements subjected to fire. J. Eng. Mech. 2021, 147, 04021108. [Google Scholar] [CrossRef]
- Dey, P.; Walbridge, S.; Narasimhan, S. Evaluation of design provisions for pedestrian bridges using a structural reliability framework. J. Bridge Eng. 2018, 23, 04017132. [Google Scholar] [CrossRef]
- Breitung, K. SORM, design points, subset simulation, and Markov chain Monte Carlo. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021052. [Google Scholar] [CrossRef]
- Lu, Z.H.; Hu, D.Z.; Zhao, Y.G. Second-order fourth-moment method for structural reliability. J. Eng. Mech. 2017, 143, 06016010. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Ang, A.H.S. On the first-order third-moment reliability method. Struct. Infrastruct. Eng. 2012, 8, 517–527. [Google Scholar] [CrossRef]
- Teng, D.; Feng, Y.W.; Chen, J.Y.; Lu, C. Structural dynamic reliability analysis: Review and prospects. Int. J. Struct. Integr. 2022, 13, 753–783. [Google Scholar] [CrossRef]
- Feng, G.; Wen, J.; Fei, C. LCF Lifetime Reliability Prediction of Turbine Blisks Using Marine Predators Algorithm-Based Kriging Method. Aerospace 2023, 10, 875. [Google Scholar] [CrossRef]
- Afshari, S.S.; Enayatollahi, F.; Xu, X.; Liang, X. Machine learning-based methods in structural reliability analysis: A review. Reliab. Eng. Syst. Saf. 2022, 219, 108223. [Google Scholar] [CrossRef]
- Fei, C.W.; Han, Y.J.; Wen, J.R.; Li, C.; Han, L.; Choy, Y.S. Deep learning-based modeling method for probabilistic LCF life prediction of turbine blisk. Propuls. Power Res. 2024, 13, 12–25. [Google Scholar] [CrossRef]
- Lehký, D.; Šomodíková, M.; Lipowczan, M. A utilization of the inverse response surface method for the reliability-based design of structures. Neural Comput. Appl. 2022, 34, 12845–12859. [Google Scholar] [CrossRef]
- Cheng, W.F.; Guang, C.B.; Tian, C. Extremum response surface method for casing radial deformation probabilistic analysis. J. Aerosp. Inf. Syst. 2013, 10, 47–52. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z.; Li, Y. Time and space-variant system reliability analysis through adaptive Kriging and weighted sampling. Mech. Syst. Signal Process. 2022, 166, 108443. [Google Scholar] [CrossRef]
- Teng, D.; Feng, Y.W.; Chen, J.Y. Intelligent moving extremum weighted surrogate modeling framework for dynamic reliability estimation of complex structures. Eng. Fail. Anal. 2022, 138, 106364. [Google Scholar] [CrossRef]
- Roy, A.; Chakraborty, S. Support vector machine in structural reliability analysis: A review. Reliab. Eng. Syst. Saf. 2023, 233, 109126. [Google Scholar] [CrossRef]
- Chen, J.Y.; Feng, Y.W.; Teng, D.; Lu, C.; Fei, C.W. Support vector machine-based similarity selection method for structural transient reliability analysis. Reliab. Eng. Syst. Saf. 2022, 223, 108513. [Google Scholar] [CrossRef]
- Zhang, X.; Pandey, M.D.; Luo, H. Structural uncertainty analysis with the multiplicative dimensional reduction–based polynomial chaos expansion approach. Struct. Multidiscip. Optim. 2021, 64, 2409–2427. [Google Scholar] [CrossRef]
- Yang, B.; Cheng, C.; Wang, X.; Bai, S.; Long, K. Robust reliability-based topology optimization for stress-constrained continuum structures using polynomial chaos expansion. Struct. Multidiscip. Optim. 2023, 66, 88. [Google Scholar] [CrossRef]
- Lu, C.; Teng, D.; Keshtegar, B.; Alkabaa, A.S.; Taylan, O.; Fei, C.W. Extremum hybrid intelligent-inspired models for accurate predicting mechanical performances of turbine blisk. Mech. Syst. Signal Process. 2023, 190, 110136. [Google Scholar] [CrossRef]
- Song, L.K.; Fei, C.W.; Bai, G.C.; Yu, L.C. Dynamic neural network method-based improved PSO and BR algorithms for transient probabilistic analysis of flexible mechanism. Adv. Eng. Inform. 2017, 33, 144–153. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, X. Global sensitivity analysis of the reliability of the slope stability based on the moment-independent combine with the Latin hypercube sampling technique. Stoch. Environ. Res. Risk Assess. 2023, 37, 2159–2171. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.W.; Teng, D. EMR-SSM: Synchronous surrogate modeling-based enhanced moving regression method for multi-response prediction and reliability evaluation. Comput. Methods Appl. Mech. Eng. 2024, 421, 116812. [Google Scholar] [CrossRef]
- Shi, Y.; Behrensdorf, J.; Zhou, J.; Hu, Y.; Broggi, M.; Beer, M. Network reliability analysis through survival signature and machine learning techniques. Reliab. Eng. Syst. Saf. 2024, 242, 109806. [Google Scholar] [CrossRef]
- Dhiman, G.; Kaur, A. STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Eng. Appl. Artif. Intell. 2019, 82, 148–174. [Google Scholar] [CrossRef]
- Pan, W.; Feng, Y.W.; Liu, J.Q. Parameter-Influencing Analysis of Aeroengine Operation Reliability. J. Aerosp. Eng. 2023, 36, 04023030. [Google Scholar] [CrossRef]
- Teng, D.; Feng, Y.W.; Lu, C.; Keshtegar, B.; Xue, X.F. Generative adversarial surrogate modeling framework for aerospace engineering structural system reliability design. Aerosp. Sci. Technol. 2023, 144, 108781. [Google Scholar] [CrossRef]
- Fei, C.W.; Li, H.; Lu, C.; Han, L.; Keshtegar, B.; Taylan, O. Vectorial surrogate modeling method for multi-objective reliability design. Appl. Math. Model. 2022, 109, 1–20. [Google Scholar] [CrossRef]
- Lu, C.; Teng, D.; Chen, J.Y.; Fei, C.W.; Keshtegar, B. Adaptive vectorial surrogate modeling framework for multi-objective reliability estimation. Reliab. Eng. Syst. Saf. 2023, 234, 109148. [Google Scholar] [CrossRef]
- Teng, D.; Feng, Y.W.; Chen, J.Y.; Liu, J.Q.; Lu, C. Multi-polynomial chaos Kriging-based adaptive moving strategy for comprehensive reliability analyses. Reliab. Eng. Syst. Saf. 2024, 241, 109657. [Google Scholar] [CrossRef]
- Lu, C.; Fei, C.W.; Liu, H.T.; Li, H.; An, L.Q. Moving extremum surrogate modeling strategy for dynamic reliability estimation of turbine blisk with multi-physics fields. Aerosp. Sci. Technol. 2020, 106, 106112. [Google Scholar] [CrossRef]



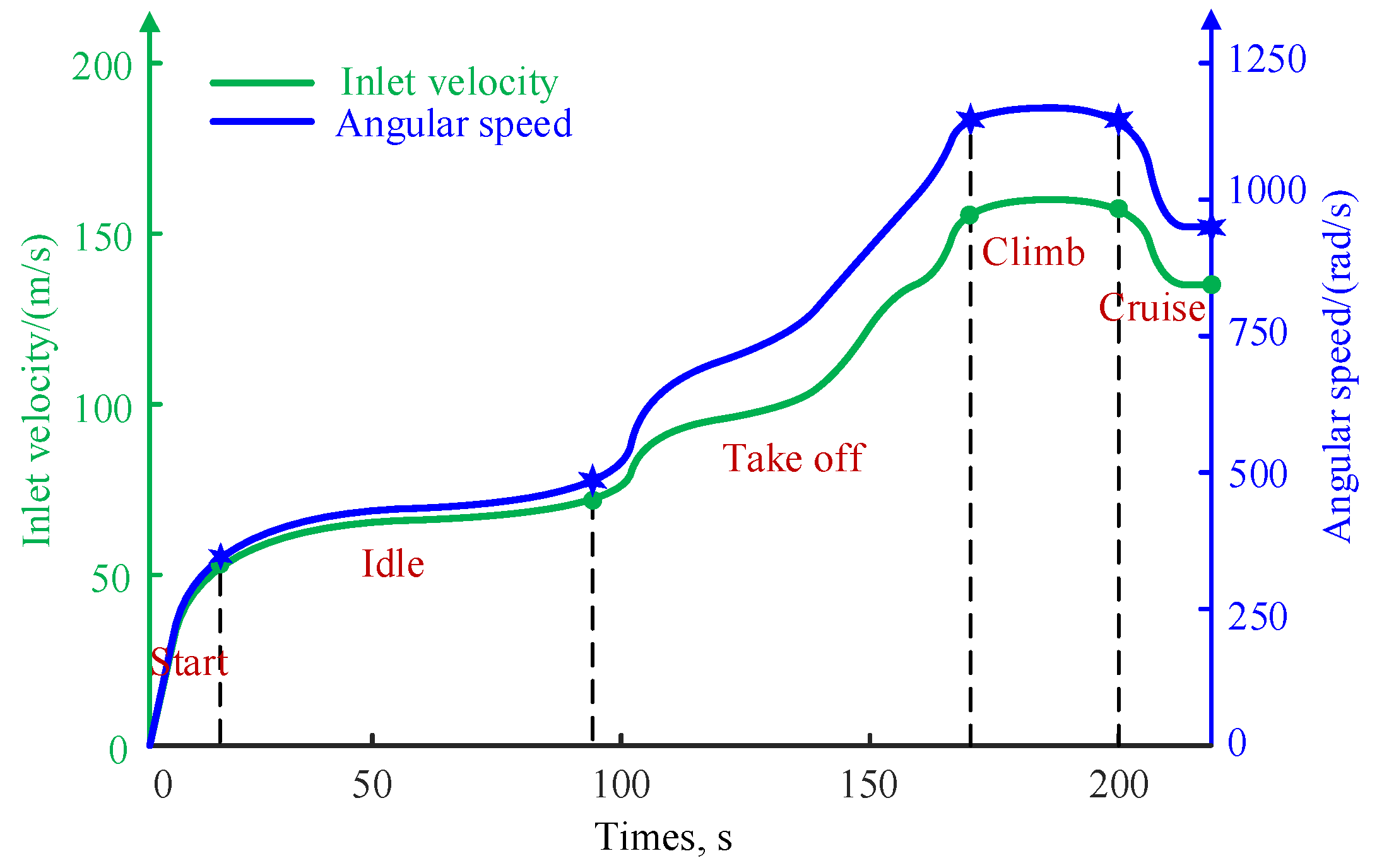

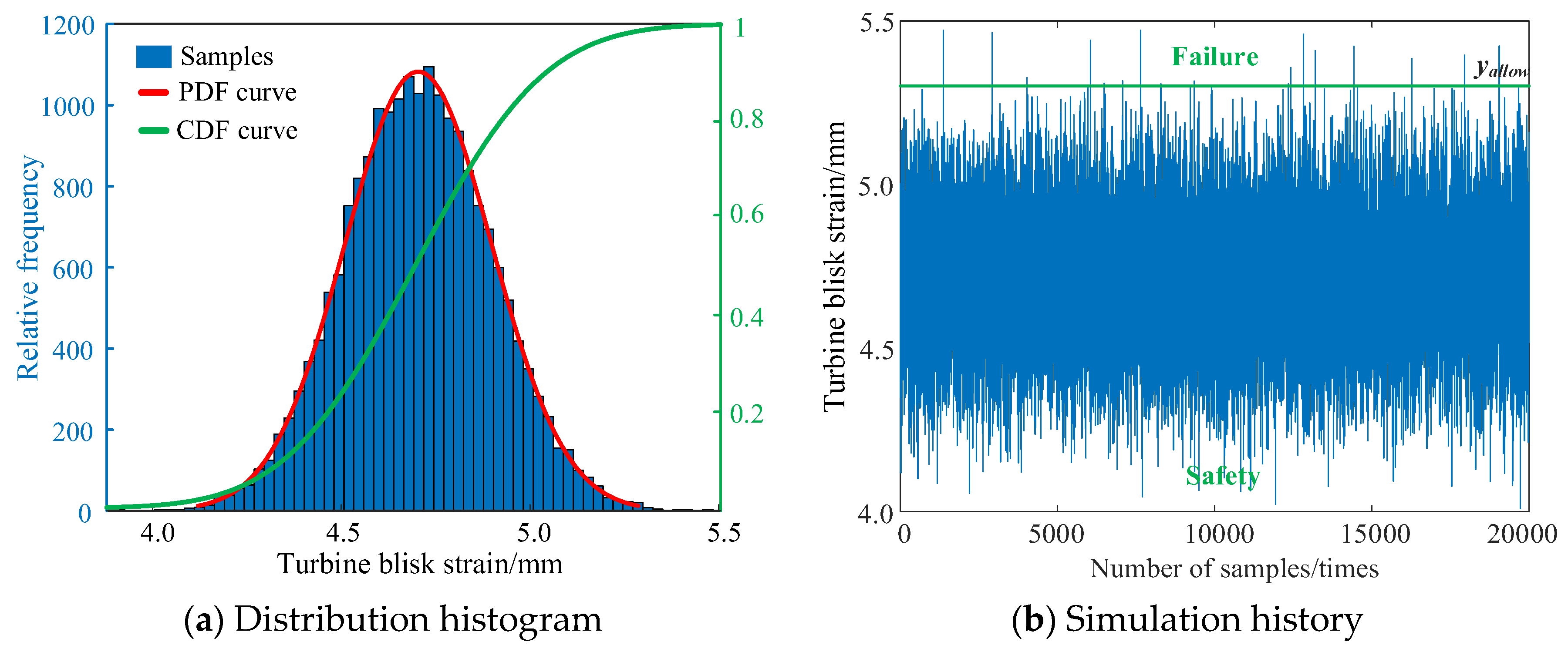
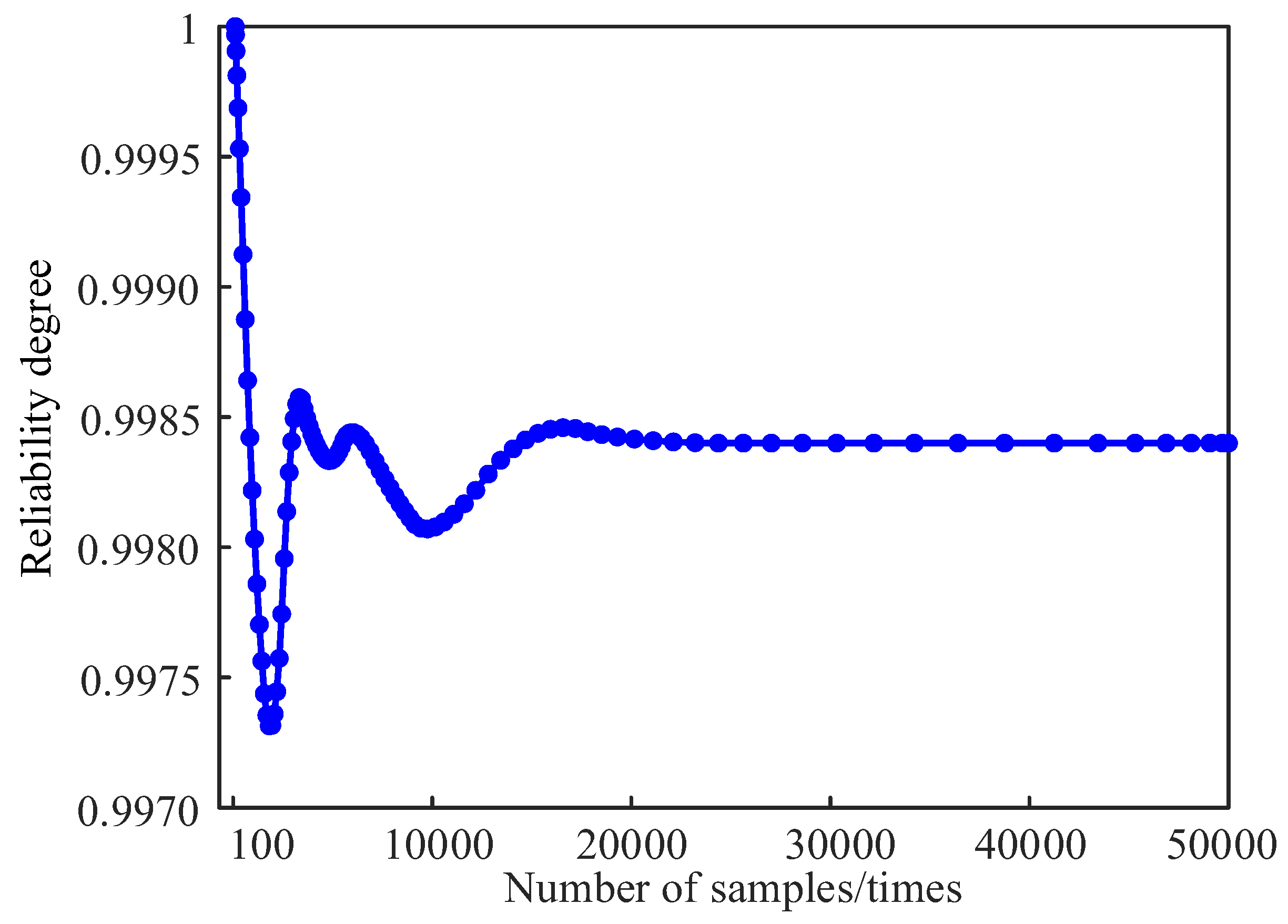


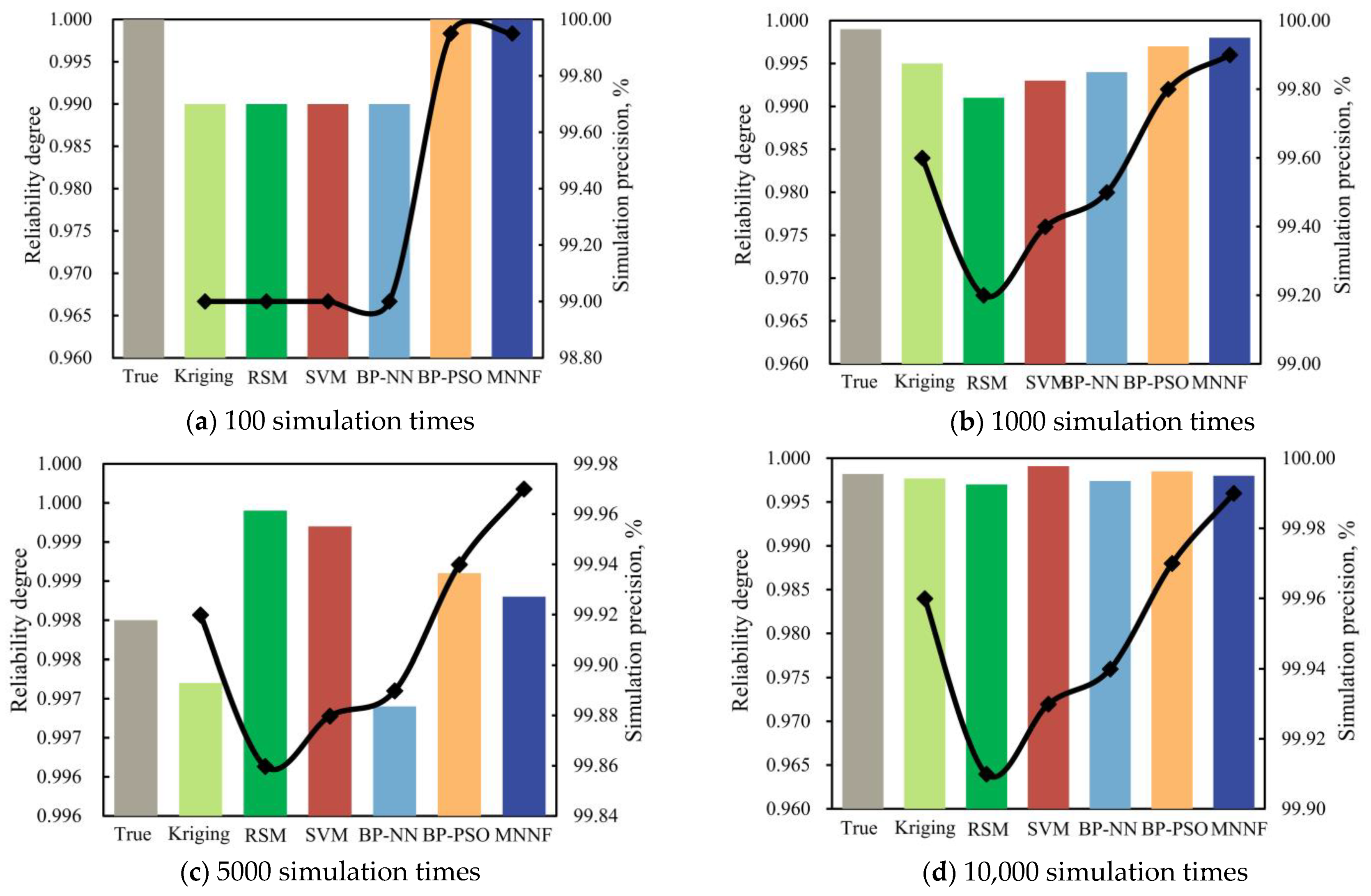
| Material Type | Parameter |
|---|---|
| Material name | Nickel-based superalloy GH4133 |
| Density | 8.56 × 103 kg/m3 |
| Elastic modulus | 1.61 × 1011 Pa |
| Poisson ratio | 0.3224 |
| Input Variables | Mean | Standard Deviation |
|---|---|---|
| v, m/s | 160 | 3.2 |
| pin, Pa | 2,000,000 | 60,000 |
| pout, Pa | 588,000 | 17,600 |
| ρ, kg/m3 | 8560 | 171.2 |
| ω, rad/s | 1168 | 23.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, X.; Sun, W.; Sun, Q.; Fei, C. Operational Reliability Analysis of Turbine Blisk Using an Enhanced Moving Neural Network Framework. Aerospace 2024, 11, 382. https://doi.org/10.3390/aerospace11050382
Liang X, Sun W, Sun Q, Fei C. Operational Reliability Analysis of Turbine Blisk Using an Enhanced Moving Neural Network Framework. Aerospace. 2024; 11(5):382. https://doi.org/10.3390/aerospace11050382
Chicago/Turabian StyleLiang, Xiao, Wei Sun, Qingchao Sun, and Chengwei Fei. 2024. "Operational Reliability Analysis of Turbine Blisk Using an Enhanced Moving Neural Network Framework" Aerospace 11, no. 5: 382. https://doi.org/10.3390/aerospace11050382
APA StyleLiang, X., Sun, W., Sun, Q., & Fei, C. (2024). Operational Reliability Analysis of Turbine Blisk Using an Enhanced Moving Neural Network Framework. Aerospace, 11(5), 382. https://doi.org/10.3390/aerospace11050382








