Design and Rate Control of Large Titanium Alloy Springs for Aerospace Applications
Abstract
:1. Introduction
2. Design and Preparation of Titanium Alloy Spring
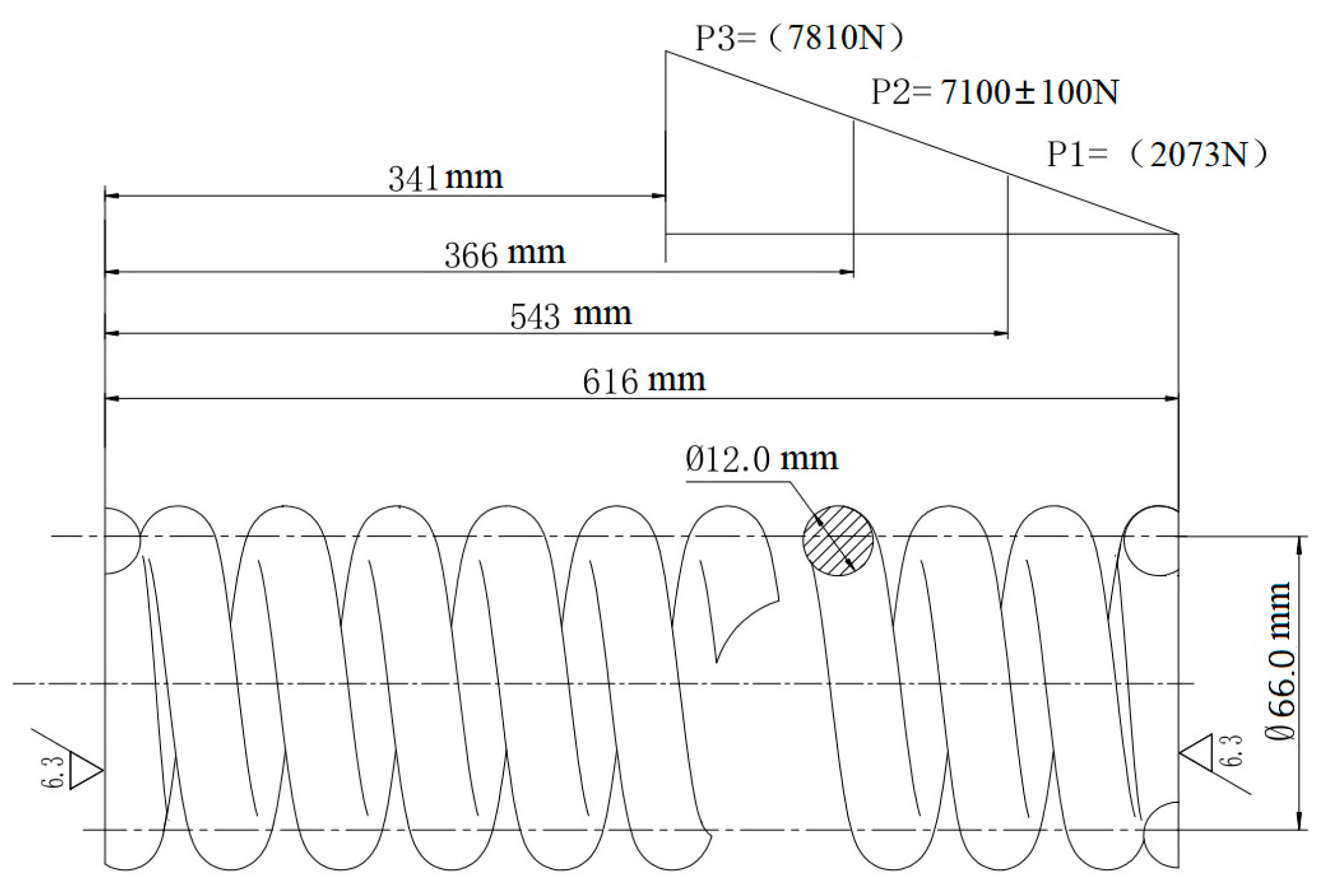
2.1. Parameters of Original Steel Spring
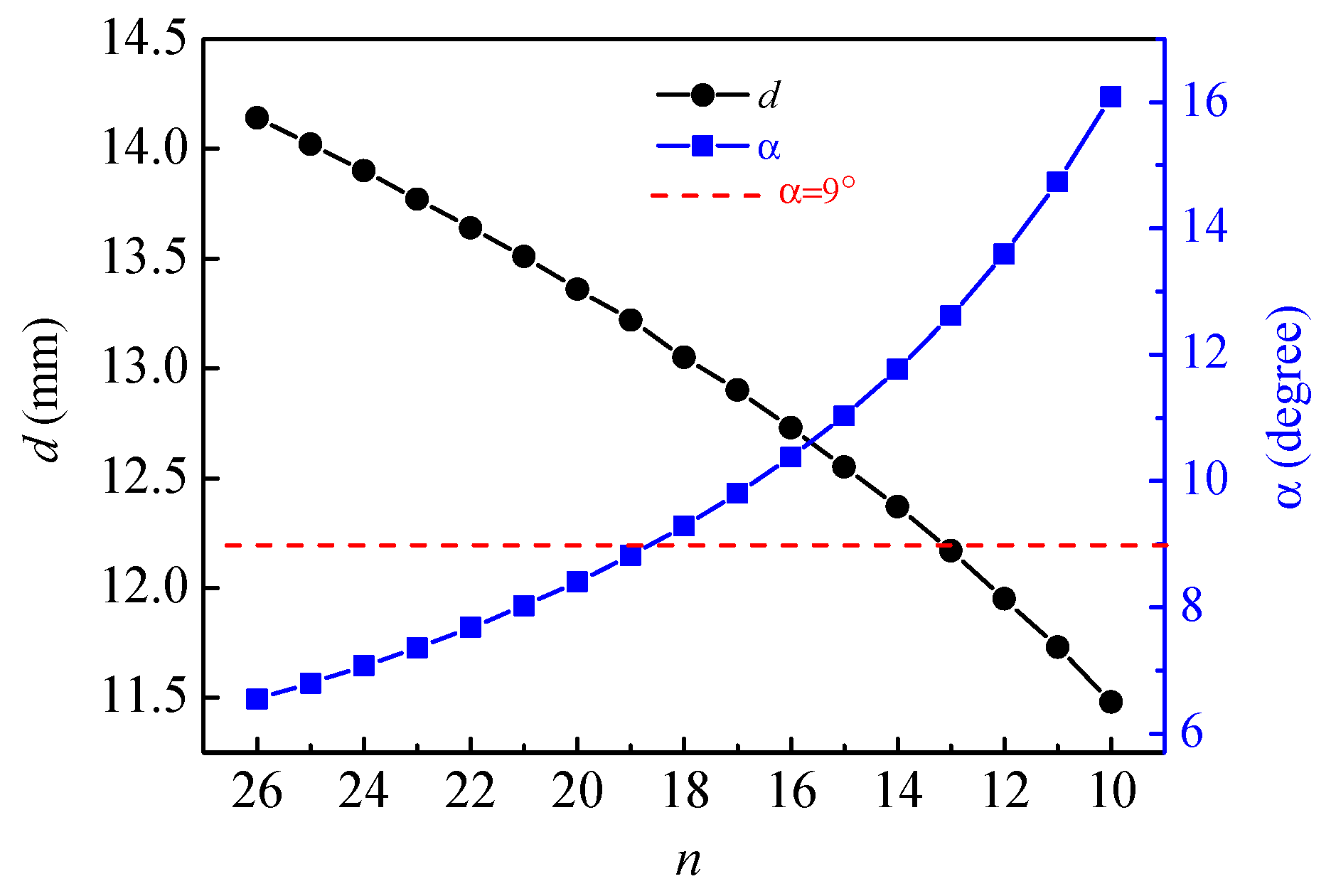
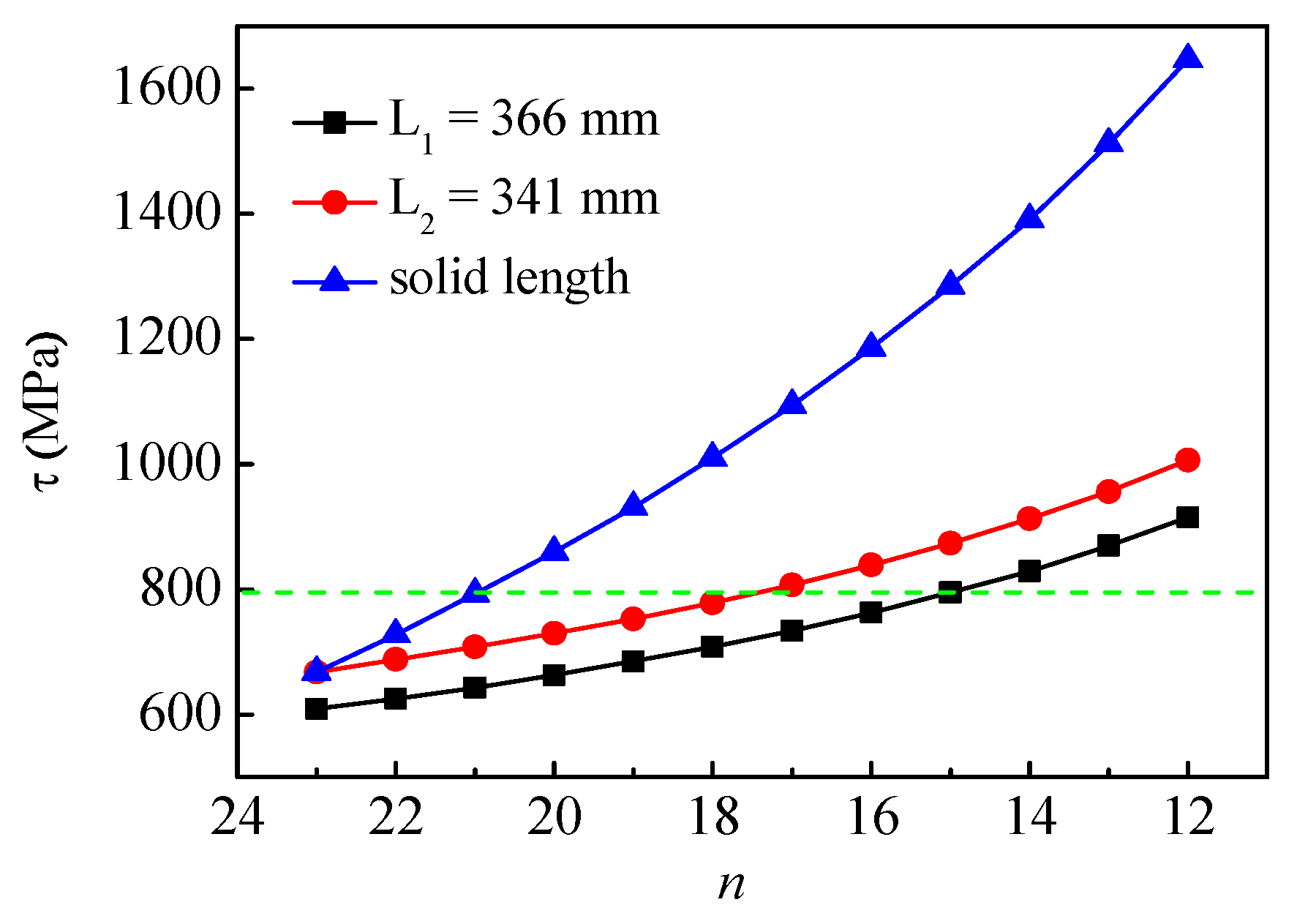
2.2. Design of Titanium Spring
2.3. Preparation of Titanium Springs
3. Rate Control of Titanium Spring by Heat Treatment
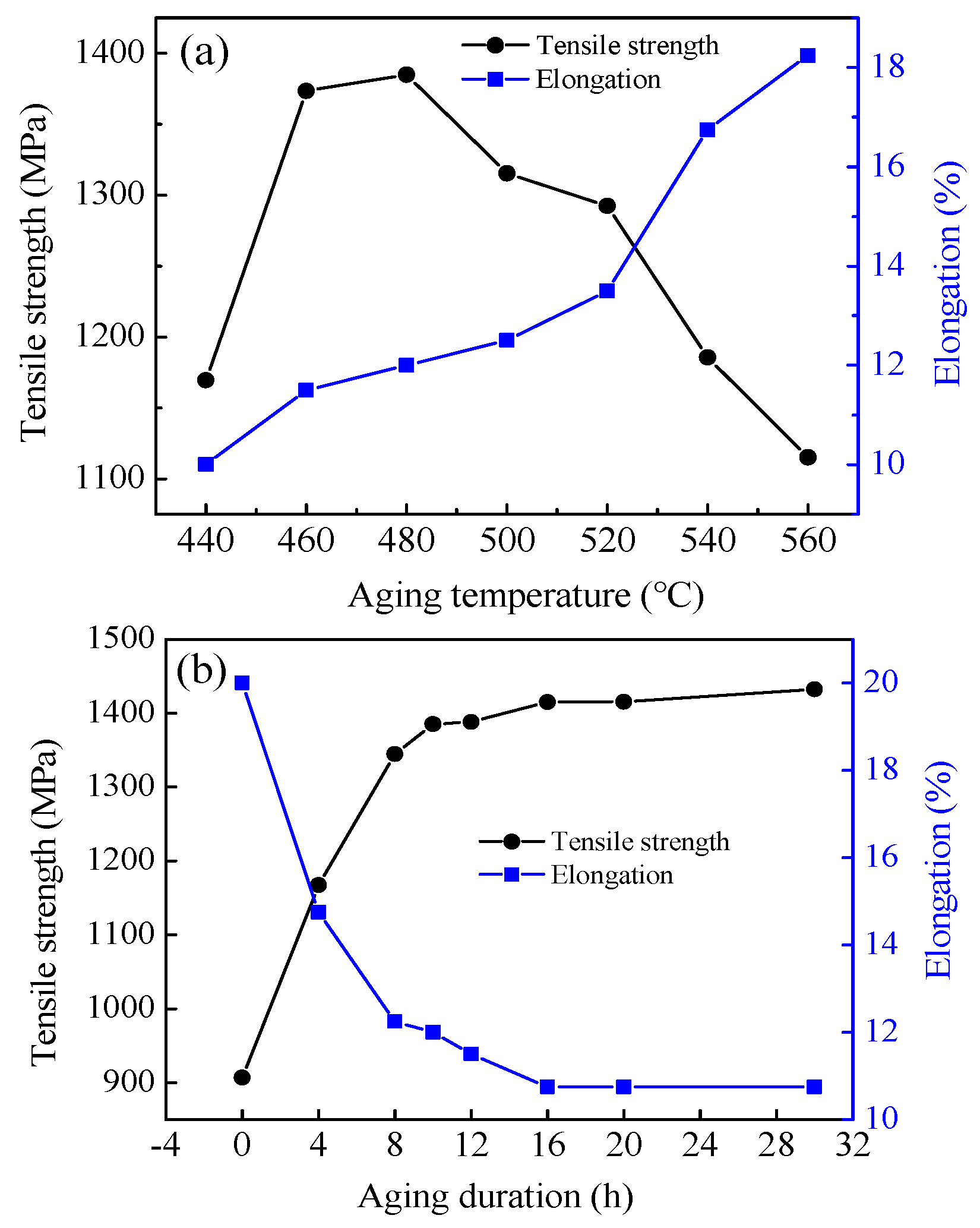
3.1. Influence of Heat Treatment Process on Mechanical Properties
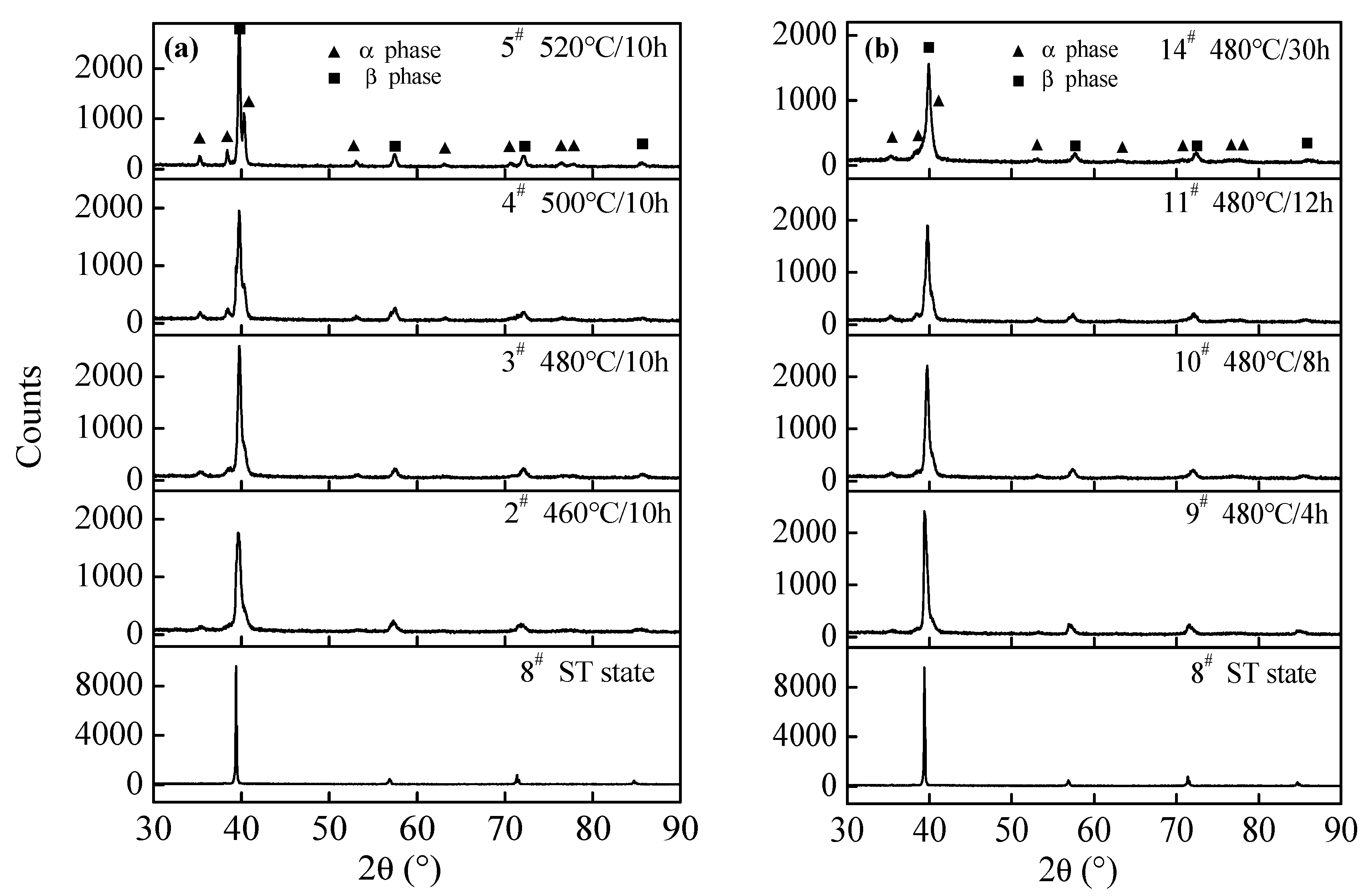
3.2. The Influence of Heat Treatment on the Moduli of β-C Alloy
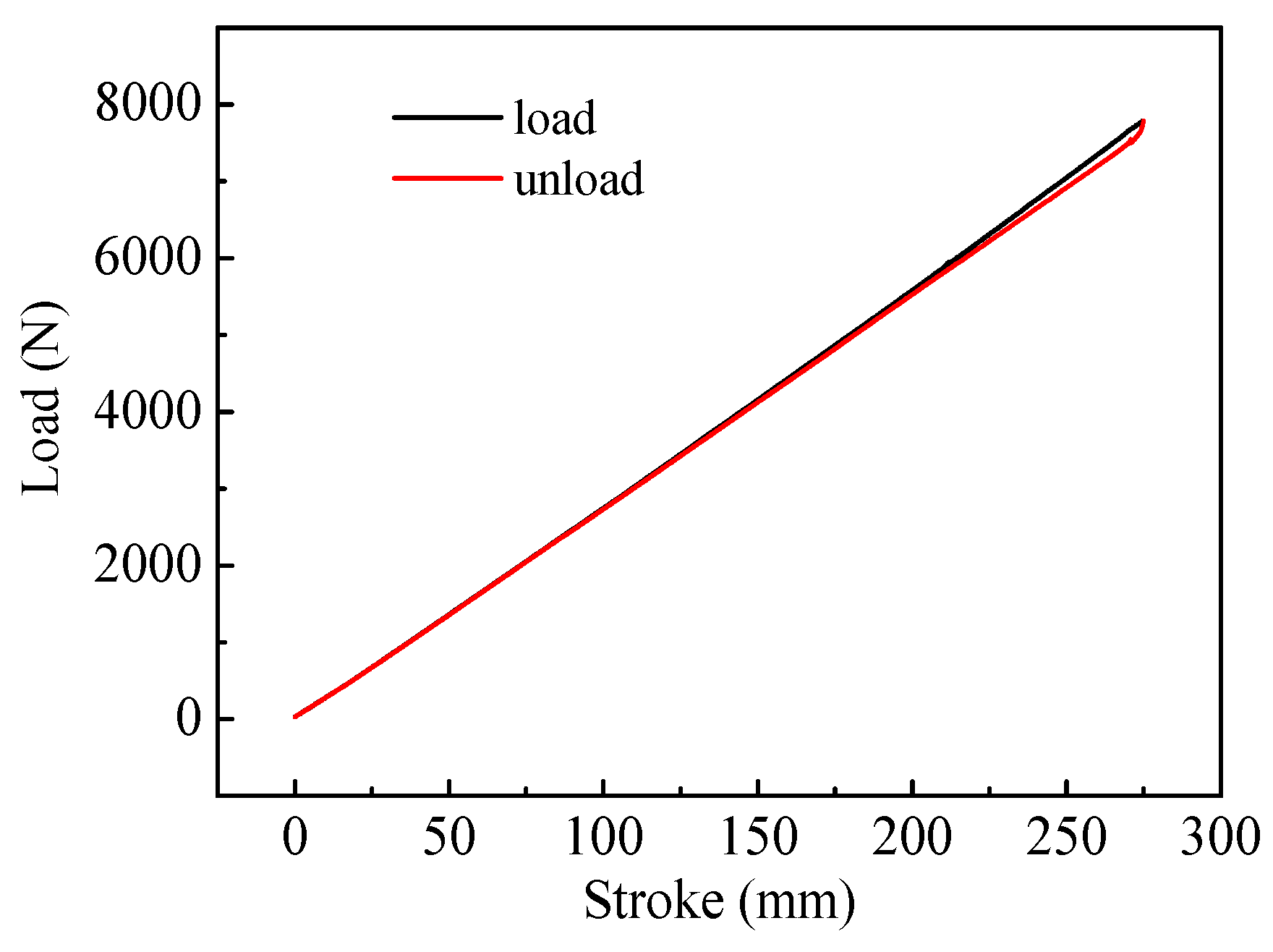
3.3. Control of Spring Rate by Heat Treatment
4. The Influence of Ambient Temperature on the Rate of Titanium Alloy Springs
5. Conclusions
- (1)
- The current spring design standards are not applicable to big helix angle springs. The helix angle of titanium alloy springs is often greater than 9°, so new variables of E and α should be added to spring rate calculation equation.
- (2)
- As the aging temperature increases, the elastic modulus gradually increases until 480 °C, then the elastic modulus slowly decreases. As the aging duration increases, the elastic modulus rapidly increases within the initial 8 h and then increases slowly. By adjusting the aging temperature and duration, the rate of titanium alloy springs can be controlled within a certain range. The rate of the β-C alloy compression separation spring can meet design requirements after aging at 480 °C/12 h.
- (3)
- The tensile strength and elastic modulus of β-C alloy bars decrease with an increase in temperature. The rate of the β-C spring gradually decreases with increasing temperature below 300 °C. When the temperature exceeds 300 °C, the spring rate drops rapidly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boyer, R.R.; Bajoraitis, R.; Greenwood, D.W.; Mild, E.E. Symposium on Beta Titanium Alloys in the 80’s; The Metallurgical Society of AIME: Atlanta, GA, USA, 1983; pp. 295–305. [Google Scholar]
- Royer, R.R.; Briggs, R.D. The use of βtitanium alloy in the aerospace industry. J. Mater. Eng. Perform. 2005, 14, 681–685. [Google Scholar]
- Seagle, S.R.; Bajoraitis, R.; Pepka, C.F. Titanium alloy springs. Mater. Des. 1989, 10, 215–216. [Google Scholar] [CrossRef]
- Williams, J.C.; Boyer, R.R. Opportunities and Issues in the Application of Titanium Alloys for Aerospace Components. Metal 2020, 10, 705. [Google Scholar] [CrossRef]
- Gui, N.; Song, T.; Qian, M. Titaniu for Consumer Applications: Real World Use of Titanium; Froes, F.H., Qian, M., Niinomi, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 297–319. [Google Scholar]
- Cao, S.; Zhou, X.G.; Chao VS, L.; Boyer, R.R.; Williams, J.C.; Wu, X. A strong and ductile Ti-3Al-8V-6Cr-4Mo-4Zr (Beta-C) alloy achieved by introducing trace carbon addition and cold work. Scr. Mater. 2020, 178, 124–128. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Q.; Yang, F.; Yue, H.; Yang, X.; Li, H. Design and analysis of a compression and separation device for multi-satellite deployment. Aerospace 2022, 9, 446. [Google Scholar] [CrossRef]
- Sallam, A.M.F. Effect of Separation Springs on the Design of a Spacecraft-Launcher Separation System. J. Multidiscip. Eng. Sci. Technol. 2022, 9, 15031–15036. [Google Scholar]
- Hu, X.; Chen, X.; Zhao, Y.; Yao, W. Optimization design of satellite separation systems based on Multi-Island Genetic Algorithm. Adv. Space Res. 2014, 53, 870–976. [Google Scholar] [CrossRef]
- GB/T 23935-2009; Design of Cylindrical Helical Springs. National Standardization Administration of China: Beijing, China, 2009.
- EN 13906-1; Cylindrical Helical Springs Made from Round Wire and Bar—Calculation and Design. CEN: Brussels, Belgium, 2013.
- IS-7907-1; Design and Calculation for Springs Made from Circular Section Wire and Bar. Bureau of Indian Standards: New Delhi, India, 2004.
- Liu, B.; Cao, F.; Zeng, Y.; Wu, W. Numerical and experimental study on temperature and springback control of U-shape titanium extrusion hot stretch bending. Int. J. Lightweight Mater. Manuf. 2022, 5, 453–469. [Google Scholar] [CrossRef]
- Hu, J.; Chen, X.; Wang, Y. Stress relaxation mechanism and life evaluation of titanium alloy springs under long-term thermo-mechanical coupling conditions. Mater. Today Commun. 2024, 38, 109472. [Google Scholar] [CrossRef]
- QJ 1787-89; Technical Conditions for Cylindrical Compression Springs. Ministry of Aerospace Industry of China: Beijing, China, 1989.
- SAE International. Spring Design Manual, 2nd ed.; Society of Automotive Engineers: Warrendale, PA, USA, 1996. [Google Scholar]
- AMS4957E; Titanium Alloy, Round Bar and Wire 3Al-8V-6Cr-4Mo-4Zr Consumable Electrode Melted Cold Drawn. SAE International: Warrendale, PA, USA, 2011.
- GB/T 228; Metallic Materials—Tensile Testing at Ambient Temperature. General Administration of Quality Supervision, Inspection and Quarantine of China: Beijing, China, 2002.
- Wang, J.; Huang, L.; Jin, W. The effect of heat treatment on mechanical properties and microstructure of TB9 alloy. Rare Met. Mater. Eng. 2017, 46, 129–133. [Google Scholar] [CrossRef]
- Okamoto, T.; Wakita, M.; Muramatsu, H.; Saruki, K. Effect of Microstructure on Torsional Fatigue Strength of Titanium Alloy for High Strength Spring. Trans. Jpn. Soc. Spring Eng. 2009, 54, 35–40. [Google Scholar] [CrossRef]
- GB/T 10128-2007; Metallic Materials—Torsion Testing at Ambient Temperature. General Administration of Quality Supervision, Inspection and Quarantine of China: Beijing, China, 2007.
- Keene, K.H.; Hartman JRJ, T.; Wolfenden, A.; Ludtka, G.M. Determination of dynamic young’s modulus, shear modulus, and poisson’s ration as a function of temperature for depleted uranium-0.75wt% titanium using the piezoelectric ultrasonic composite oscillator technique. J. Nucl. Mater. 1987, 149, 218–226. [Google Scholar] [CrossRef]
- Tane, M.; Akita, S.; Nakano, T.; Hagihara, K.; Umakoshi, Y.; Niinomi, M.; Mori, H.; Nakajima, H. Low Young’s modulus of Ti-Nb-Ta-Zr alloys caused by softening in shear moduli c’ and c44 near lower limit of body-centered cubic phase stability. Acta Mater. 2010, 58, 6790–6798. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, J.; Huo, Y.; Sui, Y.; Zhang, J.; Guo, S.; Zhao, X. Design of low modulus β-type titanium alloys by tuning shear modulus C44. J. Alloys Compd. 2018, 745, 579–585. [Google Scholar] [CrossRef]
- Makarov, A.S.; Mitrofanov, Y.P.; Afonin, G.V.; Kobelev, N.P.; Khonik, V.A. Predicting temperature dependence of the shear modulus of metallic glasses using calorimetric data. Scr. Mater. 2019, 168, 10–13. [Google Scholar] [CrossRef]
- Huang, Z.; Jiang, X.; Lin, B. Study on heat treatment and strengthening process of titanium alloy spring for railway vehicle. Vibroengineering Procedia 2022, 41, 165–172. [Google Scholar] [CrossRef]
- Berg, A.; Kises, J.; Wagner, L. Microstructural gradients in Ti–3Al–8V–6Cr–4Zr–4Mo for excellent HCF strength and toughness. Mater. Sci. Eng. A 1998, 243, 146–149. [Google Scholar] [CrossRef]
- Yumak, N.; Aslantas, K. A review on heat treatment efficiency in metastable β titanium alloys: The role of treatment process and parameters. J. Mater. Res. Technol. 2020, 9, 15360–15380. [Google Scholar] [CrossRef]
- Ren, D.; Liu, Y.; Zhang, H.; Wang, J.; Jin, W.; Yang, R. Influence of cold deformation and aging heat treatment on microstructure and mechanical property of TB9 titanium alloy. Rare Met. Mater. Eng. 2020, 49, 1083–1089. [Google Scholar]
- Rateick, R.G.; McCool, K.C.; Leonard, E.C.; Hoeffer, J.H. Metastable beta titanium spring performance at elevated temperature. SAE Trans. 2002, 111, 638–646. [Google Scholar]
- HB 7571-1997; Metallic Materials—Compression Testing at High-Temperature. Ministry of Aerospace Industry of China: Beijing, China, 1997.





| Al | V | Cr | Zr | Mo | Fe | O | N | H |
|---|---|---|---|---|---|---|---|---|
| 3.54 | 8.18 | 6.08 | 4.13 | 4.01 | 0.05 | 0.097 | 0.01 | 0.0011 |
| No | Temperature | Duration | No | Temperature | Duration |
|---|---|---|---|---|---|
| 1 | 440 °C | 10 h | 8 | 480 °C | 0 |
| 2 | 460 °C | 10 h | 9 | 480 °C | 4 h |
| 3 | 480 °C | 10 h | 10 | 480 °C | 8 h |
| 4 | 500 °C | 10 h | 11 | 480 °C | 12 h |
| 5 | 520 °C | 10 h | 12 | 480 °C | 16 h |
| 6 | 540 °C | 10 h | 13 | 480 °C | 20 h |
| 7 | 560 °C | 10 h | 14 | 480 °C | 30 h |
| Temperature | Rm/MPa | Rp0.2/MPa | A/% | Z/% | E/GPa |
|---|---|---|---|---|---|
| RT | 1388 | 1287.5 | 11.5 | 27.5 | 106 |
| 100 °C | 1307 | 1174 | 11.5 | 33 | 98.1 |
| 200 °C | 1271 | 1130 | 10.5 | 38 | 94.3 |
| 300 °C | 1247 | 1068 | 11.0 | 38 | 88.7 |
| 380 °C | 1238 | 1051 | 12.5 | 44 | 85.6 |
| Temperature | RT | 100 °C | 200 °C | 300 °C | 350 °C | 380 °C |
|---|---|---|---|---|---|---|
| Rate (N/mm) | 156.8 | 154.5 | 150.5 | 145.0 | 138.6 | 134.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Xu, Q.; Yang, H.; Ying, Y.; Cao, Z.; Guo, D.; Ji, V. Design and Rate Control of Large Titanium Alloy Springs for Aerospace Applications. Aerospace 2024, 11, 514. https://doi.org/10.3390/aerospace11070514
Li L, Xu Q, Yang H, Ying Y, Cao Z, Guo D, Ji V. Design and Rate Control of Large Titanium Alloy Springs for Aerospace Applications. Aerospace. 2024; 11(7):514. https://doi.org/10.3390/aerospace11070514
Chicago/Turabian StyleLi, Lei, Qiufa Xu, Haiying Yang, Yang Ying, Zuhan Cao, Dizi Guo, and Vincent Ji. 2024. "Design and Rate Control of Large Titanium Alloy Springs for Aerospace Applications" Aerospace 11, no. 7: 514. https://doi.org/10.3390/aerospace11070514
APA StyleLi, L., Xu, Q., Yang, H., Ying, Y., Cao, Z., Guo, D., & Ji, V. (2024). Design and Rate Control of Large Titanium Alloy Springs for Aerospace Applications. Aerospace, 11(7), 514. https://doi.org/10.3390/aerospace11070514






