Abstract
This study presents an enhanced exploration path planning for unmanned aerial vehicles. The primary goal is to increase the chances of survival of missing people in forest environments. Exploration path planning is an essential methodology for exploring unknown three-dimensional spaces. However, previous studies have mainly focused on underground environments, not forest environments. The existing path planning methods for underground environments are not directly applicable to forest environments. The reason is that multiple open spaces exist with various obstacles, such as trees, foliage, undergrowth, and rocks. This study mainly focused on improving the safety and efficiency to be suitable for forests rather than underground environments. Paths closer to obstacles are penalized to enhance safety, encouraging exploration at a safer distance from obstacles. A potential field function is applied based on explored space to minimize overlapping between existing and new paths to increase efficiency. The proposed exploration path planning method was validated through an extensive simulation analysis and comparison with state-of-the-art sampling-based path planning. Finally, a flight experiment was conducted to verify further the feasibility of the proposed method using onboard real hardware implementation in a cluttered and complex forest environment.
1. Introduction
The use of UAVs (Unmanned Aerial Vehicles) in intelligent agriculture, search and rescue, security, advanced natural disaster surveillance, and other applications has increased tremendously because they can perform time-consuming, complex, and dangerous tasks in place of humans. However, achieving full autonomy in UAV operations remains challenging, and current UAVs require the intervention of a skilled human operator. To achieve full autonomy, technological and algorithmic developments are required for localization [1], environment mapping [2], path planning [3,4], trajectory generation [5], and flight control [6,7]. Of these various technologies, path planning holds the key to determining the performance of exploration.
The primary purpose of this study is to design path planning for autonomous UAVs that increases the chances of survival of missing people in forest environments by ensuring rapid and accurate search operations. In particular, this study focuses on modifying and supplementing state-of-the-art sampling-based exploration path planning to suit forest environments. The enhanced path planning can autonomously search the unknown three-dimensional space while maintaining both safety and efficiency. First, the state-of-the-art does not distinguish between narrow and wide spaces, as the environment of interest is underground with a single open space except for junctions. Consequently, the state-of-the-art cannot be directly applied to forest environment exploration, where multiple open spaces exist with scattered obstacles such as trees and bushes. This study improves the exploration gain so the UAV can select safer and wider spaces when exploring forest environments. Second, the randomness of the sampling-based method may result in overlooked areas that have not been entirely explored [8] and may cause unnecessary visits to previously explored spaces of the environment [9]. To address this issue, this study proposes a new application of the potential field methods [10,11,12] that generates repulsive forces from the already explored space in the exploration gain to increase the exploration efficiency. Some researchers have researched operating multiple UAVs to overcome the small payload capacity and short operating range of a single UAV. Zhou et al. designed the online hgrid decomposition and pairwise interaction that allocates decomposed distinct areas to distributed UAVs while balancing the workload without causing interference between UAVs [13]. Bartolomei et al. proposed a decentralized exploration strategy using multiple UAVs capable of switching modes between cautious exploration and aggressive exploitation [14]. Unlike these attempts, this study focuses on enhancing the exploration efficiency of a single UAV.
The main contributions of this study can be summarized as follows. First, this is the first study to expand state-of-the-art sampling-based path planning to explore forest environments by enhancing safety and efficiency. Second, an extensive simulation analysis demonstrated improved safety (i.e., greater distance from surrounding obstacles) and efficiency (i.e., reduced flight time and distance) of the proposed method compared to the state-of-the-art method. Third, the feasibility of the proposed method was validated through a challenging flight experiment conducted in a real forest environment.
The remainder of this study is organized as follows. Section 2 provides a literature review of exploration path planning. Section 3 introduces the overall system architecture and details the local planner of the state of the art. Section 4 presents the proposed improvements for the safety and efficiency of exploration path planning. Section 5 shows an extensive simulation analysis and comparison to evaluate our enhanced exploration path planning method. Section 6 provides the challenging flight experiment results as the most thorough performance validation. Finally, Section 7 concludes this study and suggests directions for future research.
2. Related Work
Exploration path planning differs from traditional path planning. First, the goal position is not predefined. Therefore, traditional path planning, which usually finds the shortest path between the start and the goal positions, cannot be applied in exploration. Second, exploration path planning is performed under unknown environments. In other words, exploration path planning enables UAVs to reveal an unknown environment and gather new information incrementally.
Exploration path planning can be broadly classified into frontier- and sampling-based approaches. Frontier-based exploration identifies frontiers (that is, boundaries between known and unknown spaces) and guides a UAV toward the frontier until the entire environment has been explored [8,15,16,17]. In contrast, sampling-based exploration spans random trees within a known free space, evaluates the exploration gain of each branch, and selects the branch that facilitates the exploration of unknown space [18,19,20,21,22]. In general, sampling-based exploration offers several advantages. First, it has been proven that sampling-based exploration can be applied regardless of the complexity of environments, allowing for them to scale effectively to various types of terrain, obstacles, and environmental conditions [23,24]. Second, sampling-based exploration is computationally efficient and has been argued for effectively solving complex problems at relatively low computational costs [25]. For these reasons, this study adopted sampling-based exploration.
As we considered sampling-based exploration, we analyze related work focused on this approach. Bircher et al. [18] proposed a receding-horizon NBVPlanner (Next-Best View Planner) that incrementally constructs RRT (Rapidly exploring Random Tree) and formulates the exploration gain as the maximum amount of unknown space explored at the end of a branch. NBVPlanner successfully explores locally bounded spaces but tends to get stuck in dead ends, undermining global exploration [9]. Witting et al. [19] extended NBVPlanner to operate in large environments by using previously visited positions to build a history graph and reseeding RRT if the UAV path hits a dead end. Similarly, Batinovic et al. [20] modified NBVPlanner by evaluating the exploration gain along a branch rather than at the branch endpoint in a short computation time based on a recursive shadow-casting algorithm. Dang et al. developed GBPlanner (Graph-Based exploration Path planner), cited as the state-of-the-art methodology in this study [21]. GBPlanner uses a bifurcated local/global planning architecture to explore subterranean environments. The GBPlanner’s local planner gradually reveals unknown spaces. Unlike NBVPlanner, GBPlanner’s local planner constructs rapidly exploring random graphs and computes the exploration gain by considering the amount of unknown space and the distance and direction of the reachable area. Otherwise, GBPlanner’s global planner performs autonomous homing and repositioning of a UAV to achieve resilient exploration of large and complex underground environments.
As discussed above, exploration path planning has been studied extensively, but most have focused on underground environments. Only a few studies have addressed UAV path planning in forest environments. Jarin-Lipschitz et al. [26] studied search-based motion planning for UAVs in cluttered forest environments, while Lu et al. [27] generated collision-free and dynamic feasible trajectory based on RRT* in a GPS-denied environment. However, their research goals differ from ours in that they focused on achieving rapid access to a predefined goal point rather than exploration in an unknown environment. Lin and Stol [28] performed autonomous coverage planning in plantation forests consisting of waypoint selection, trajectory generation, and trajectory following. However, the waypoint selection method only applies to semi-structured plantation forests as it generates a set of waypoints along the corridor between two adjacent rows of trees. Zhou et al. [29] proposed to solve a variant of the traveling salesman problem that visits all frontiers by using incremental frontier information. However, they conducted field tests in a small, sparse forest environment with few trees. To the best of our knowledge, no existing studies have implemented sampling-based exploration path planning for dense forest environments.
3. Problem Statement
3.1. System Overview
Although we focus on exploration path planning, path planning alone does not allow for a UAV to fly autonomously. This section describes the overall system architecture to discuss the elements and their interactions required for a UAV to perform fully autonomous flight for exploration in forest environments. Figure 1 shows a diagram of the overall system architecture. The system comprises localization, mapping, exploration path planning, trajectory refinement, and flight control. First, localization is required to obtain precise position information of a UAV. Second, mapping aims to recognize environmental information. Third, exploration path planning aims to generate a set of waypoints for a UAV to navigate unexplored space while avoiding obstacles. Fourth, trajectory refinement provides a smooth and dynamically executable trajectory by connecting the generated waypoints. Finally, flight control generates motor commands to follow the refined trajectory.

Figure 1.
Overall system architecture.
In this study, we implement each of the above-mentioned elements as follows. First, localization is performed based on the EKF2 (the second-order Extended Kalman Filter) and by fusing inertial measurement unit, magnetometer, barometer, and GPS (Global Positioning System) measurements through the PX4 (Pixhawk Project 4) firmware. Second, an occupancy map determines the voxel status as occupied, free, or unknown. Third, the proposed exploration path planning is based on GBPlanner [21] and adapted to forest environments. Lastly, we use minimum snap trajectory generation [30,31] for trajectory refinement and the PX4 v1.14.0 firmware, an open-source autopilot software, for flight control. The system elements are iteratively executed until the exploration is completed.
3.2. GBPlanner
Since this study enhances the capability of GBPlanner’s local planner, a brief description of GBPlanner is provided to clarify the differences as follows. As shown in Figure 1, when the UAV’s position and occupancy map are given, GBPlanner’s local planner rapidly explores random graphs by sampling a collision-free configuration within a specific radius from the UAV. Once a graph is constructed with n leaf nodes (i.e., the far end of the graph), Dijkstra’s algorithm computes the shortest paths from the root node to each leaf node. The exploration gain per path is calculated, and the path with the highest exploration gain is selected as the optimal path. The exploration gain of the i-th path for can be redefined as follows:
where represents the j-th node on the path . When j equals 1, the symbol represents the root node of the path . When j equals , the symbol represents the leaf node of the path because represents the number of nodes from the root node to the leaf node on the i-th path. In addition, and are the weights of and , respectively. is the similarity metric between the i-th path, , and pseudo-path, . The pseudo-path has the same length of path and is straight along the current UAV flight direction. Therefore, is aimed at preventing sudden changes in the flight direction by penalizing a path that differs from the current UAV flight direction. is the cumulative Euclidean distance from node to root node along the i-th path, . A small allows for quickly exploring the environment before filling in details, whereas a large makes the UAV proceed slowly and explore the area meticulously [32]. Variable represents the number of voxels that can be newly explored when a UAV is located at node . In summary, GBPlanner selects the path with the highest exploration gain as the next path for the UAV. This path leads the UAV toward unexplored spaces and typically has a similar direction to the current path while keeping its length relatively short.
4. Proposed Method
We improve the GBPlanner’s local planner regarding two aspects. First, the distance to the nearest obstacle is included in the exploration gain for the UAV to safely fly far from obstacles. Second, to reduce the time required to complete exploration, newly generated paths close to previous ones are penalized in the exploration gain. Each improvement is detailed below.
4.1. Safety Improvement
The original GBPlanner was intended for underground environments without obstacles other than inner walls. Therefore, GBPlanner cannot be applied to forest environments with multiple open spaces and various obstacles, such as trees and bushes. If the path is evaluated using the exploration gain in Equation (1), the UAV cannot distinguish between a dangerous path close to an obstacle and a safe path far from an obstacle. Therefore, we modify GBPlanner to allow for a UAV to safely explore forest environments. To this end, we adapt the exploration gain to increase safety as follows:
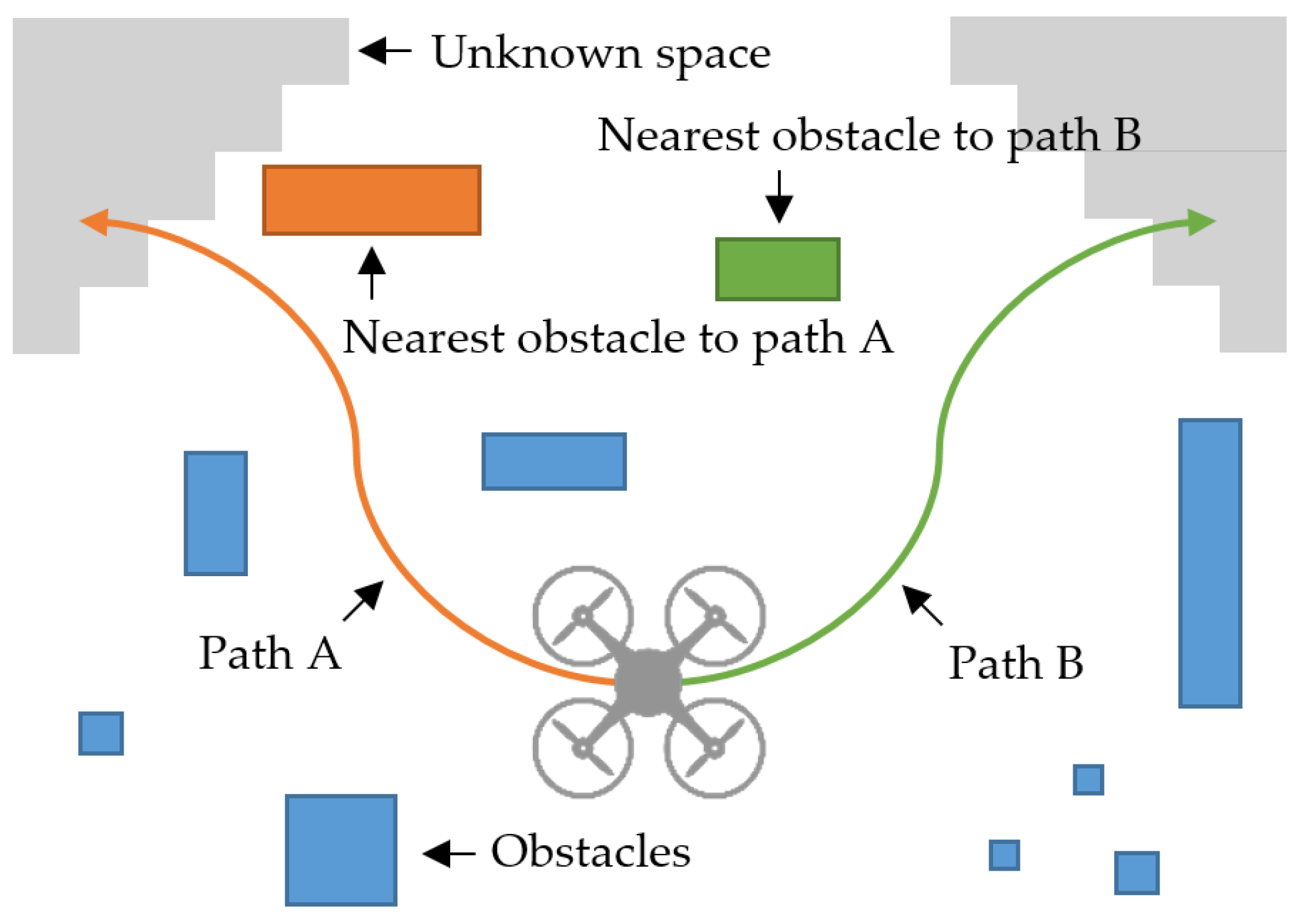
where is the weight for , which is the distance between node and the closest obstacle. To determine , the occupancy is organized into a K-dimensional tree, and the distance to the nearest obstacle from the node is then queried and returned. The reciprocal of is considered to penalize the proximity to an obstacle. As illustrated in Figure 2, the improved exploration gain directs the UAV into larger open spaces when multiple paths have similar exploration gains, as defined in Equation (1).
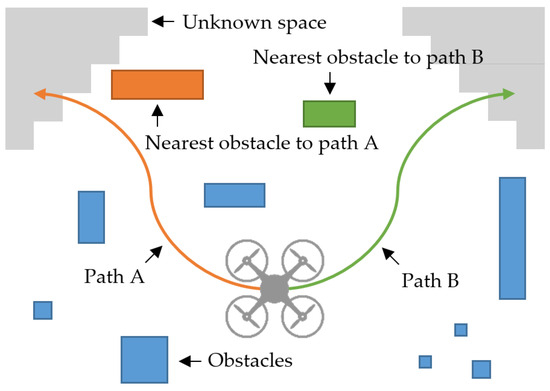
Figure 2.
Safety improvement required to avoid narrow spaces: there are two candidate paths. Path B (green) is safer because path A (orange) is closer to the nearest obstacle than path B.
4.2. Efficiency Improvement
The GBPlanner’s global planner repositions the UAV toward unexplored areas when its local planner can no longer proceed with exploration. The local planner cannot continue exploration when there is no path with an exploration gain above a predefined threshold [21]. This occurs when a few unexplored voxels remain within a specific radius of the UAV. However, a critical limitation of GBPlanner is that the exploration performance of the local planner deteriorates until decision-making triggers the global planner. This results in the UAV tending to wander in previously explored areas. We consider that exploration typically proceeds to quickly find an unexplored voxel. To minimize overlapping between new and existing paths, the exploration gain can be modified as follows:
where is the weight of potential function for new path . can be expressed as
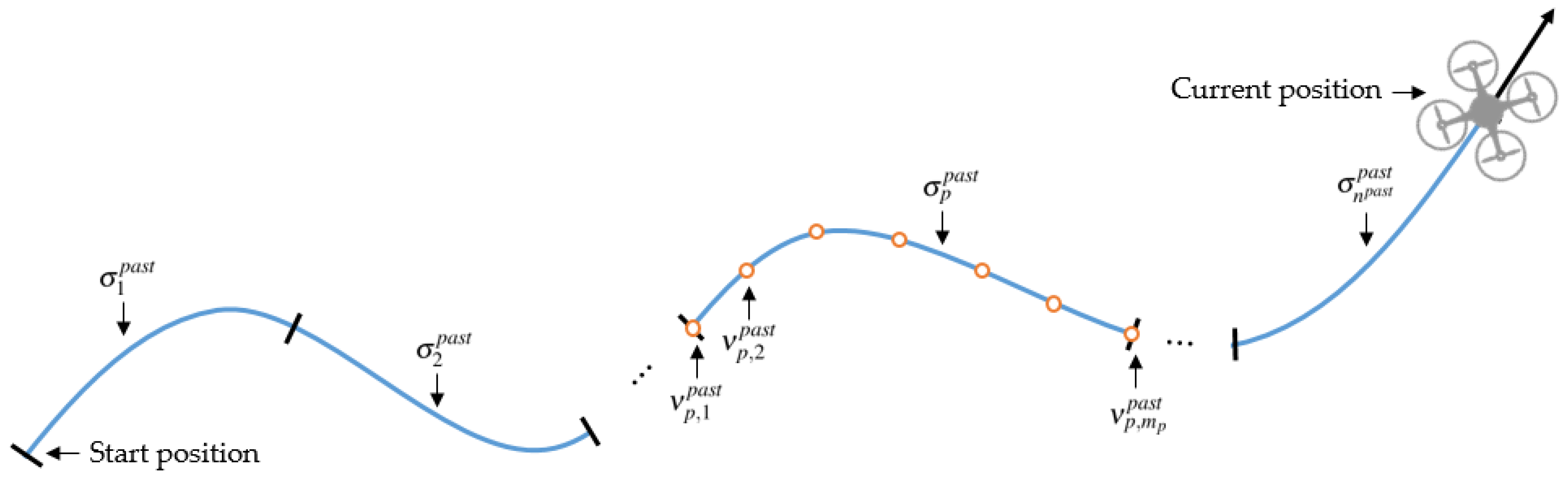
where represents the q-th node on the existing path . Figure 3 illustrates the existing paths for and the nodes from the root node and the leaf node consisting of the path . When p equals 1, the symbol represents the first existing path (i.e., the oldest path). When p equals , the symbol represents the last existing path (i.e., the most recently generated path). When q equals 1, the symbol represents the root node of the existing path . When q equals , the symbol represents the leaf node of the existing path . A potential field function is generally defined as the sum of attractive and repulsive forces, but we only consider the repulsive force to push the UAV away from already explored paths. In Equation (4), denotes a decaying factor that gradually weakens the repulsive force caused by the existing path as exploration proceeds. Consider the improved exploration gain in Equation (3). Because the overlapping between the new and existing paths is minimized, the UAV does not wander in the same space, accelerating exploration.
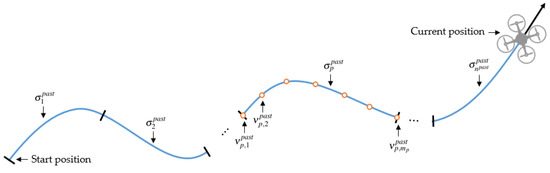
Figure 3.
Diagram of existing paths.
5. Simulation Experiment
In this section, we evaluate the performance of the proposed method through two different simulations. In the first simulation, our goal was to compare the performance of the proposed method with the original GBPlanner in various environments and across multiple runs. The second simulation was the final verification step before the actual experiment and aimed to verify the feasibility of the proposed method in a realistic forest environment. PX4 software in the loop for the Gazebo simulator was used with a 3DR IRIS drone as a UAV model for all simulations. A customized LiDAR (light detection and ranging) sensor was included to generate 180 × 40 samples at 10 Hz. Also, the field of view was and on the horizontal and vertical planes, respectively. The proposed path planning determines the best path at 4 Hz. We employed the MAVROS interface between the path planning and flight control in the simulator. The computed values were transmitted to a flight controller at 50 Hz. The simulator was run on a computer running the Linux Ubuntu operating system. It was equipped with a 2.6 GHz Intel core i7 processor and 16 GB of memory.
5.1. Performance Comparison
This simulation mainly focused on comparing the performance of the proposed exploration method with that of the original GBPlanner’s local planner [21]. The methods were compared in terms of safety and efficiency. The closest distance to an obstacle quantified safety, while efficiency was evaluated by measuring the flight time and distance depending on the exploration rate. Specifically, we defined the exploration rate as follows.
where , , and are the numbers of unknown, occupied, and free voxels, respectively. The exploration rate also served as a measure of the degree of exploration completeness. Exploration terminated at a rate of instead of due to the residual space. The residual space corresponds to hollow spaces or narrow pockets not being explored, given the perception of most sensors that stop on surfaces [18]. As the actual value of the residual space could not be determined, it was set to for this simulation. However, future work requires a more detailed analysis of how to determine the actual value of the residual space.
For the simulation environment, we created a finite configuration of 50 m (length) × 50 m (width) × 5 m (height) with different tree densities. We randomly placed tree-like cylinder obstacles with a height of 5 m and a radius of 0.25 m. The tree density was varied from 0.1 to 0.4 trees/ as proposed in [33]. The simulation was repeated 200 times. Each trial randomly generated the initial UAV take-off position for different tree densities.
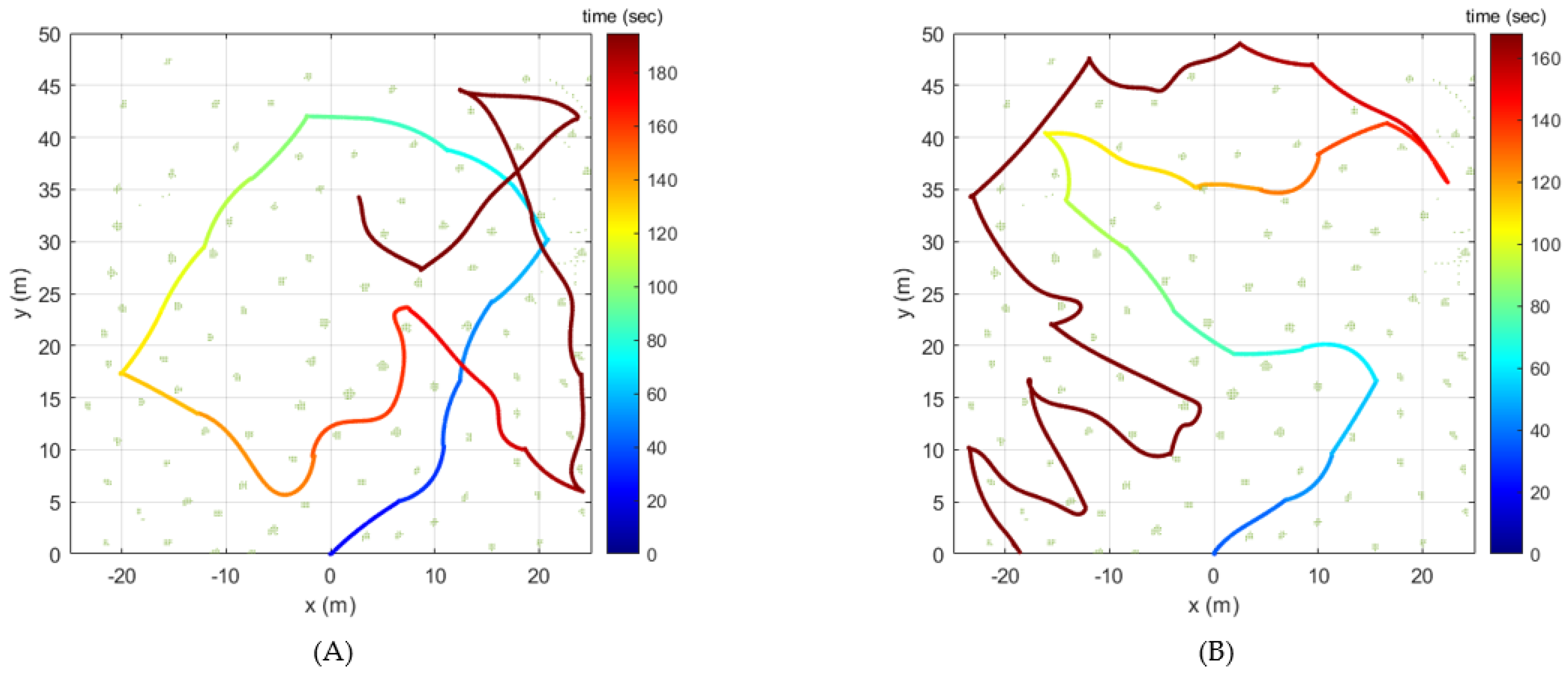
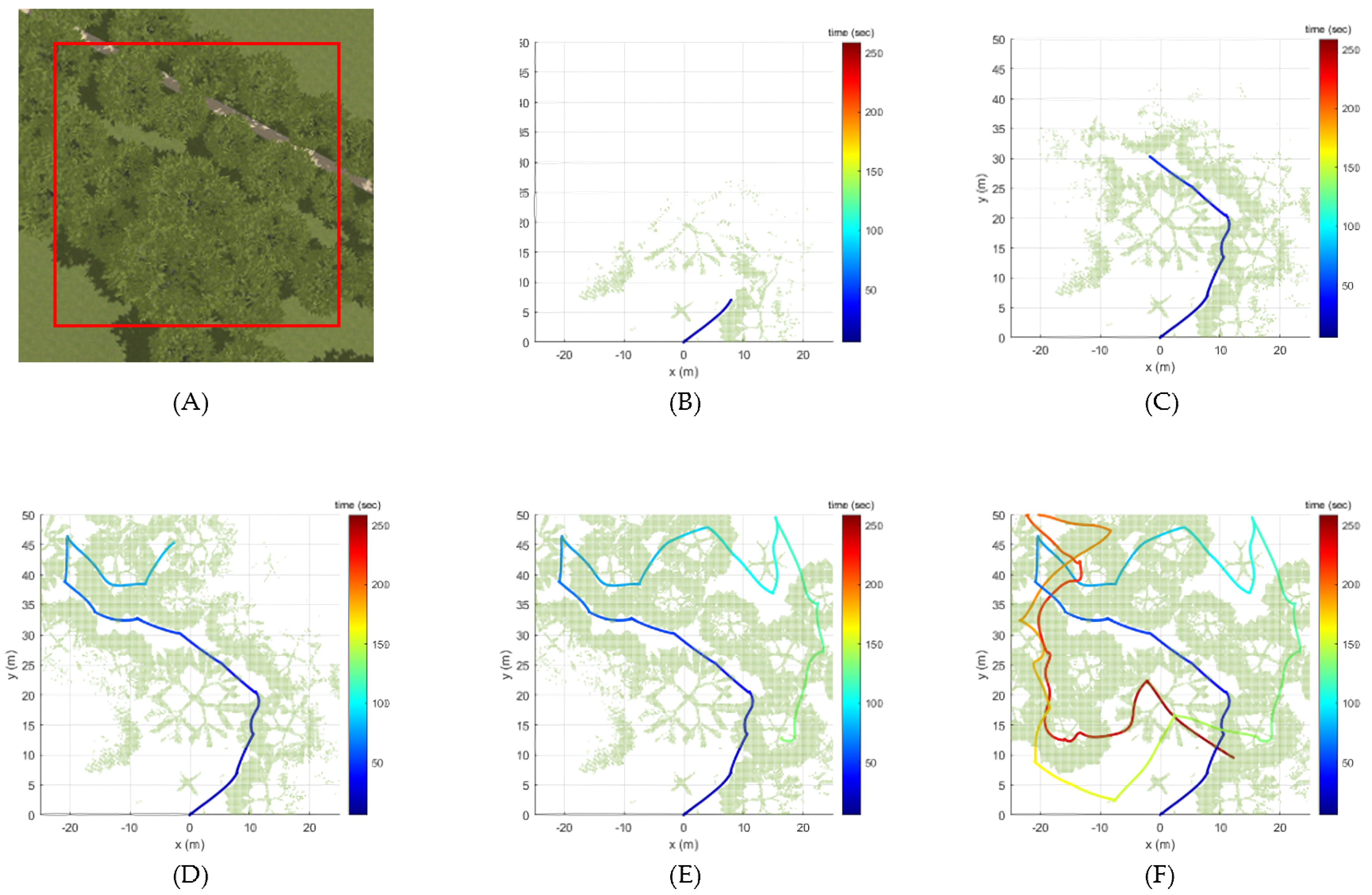
Figure 4 presents the exploration simulation result for one sample configuration. In this sample configuration, the tree density was set to 0.1 tree/, and the UAV started its exploration at the origin and flew until the exploration rate reached .
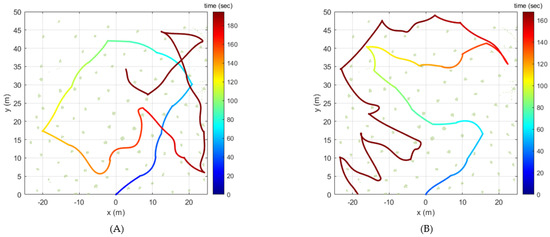
Figure 4.
Flight trajectory over time for a sample configuration: (A) GBPlanner (B) Proposed method.
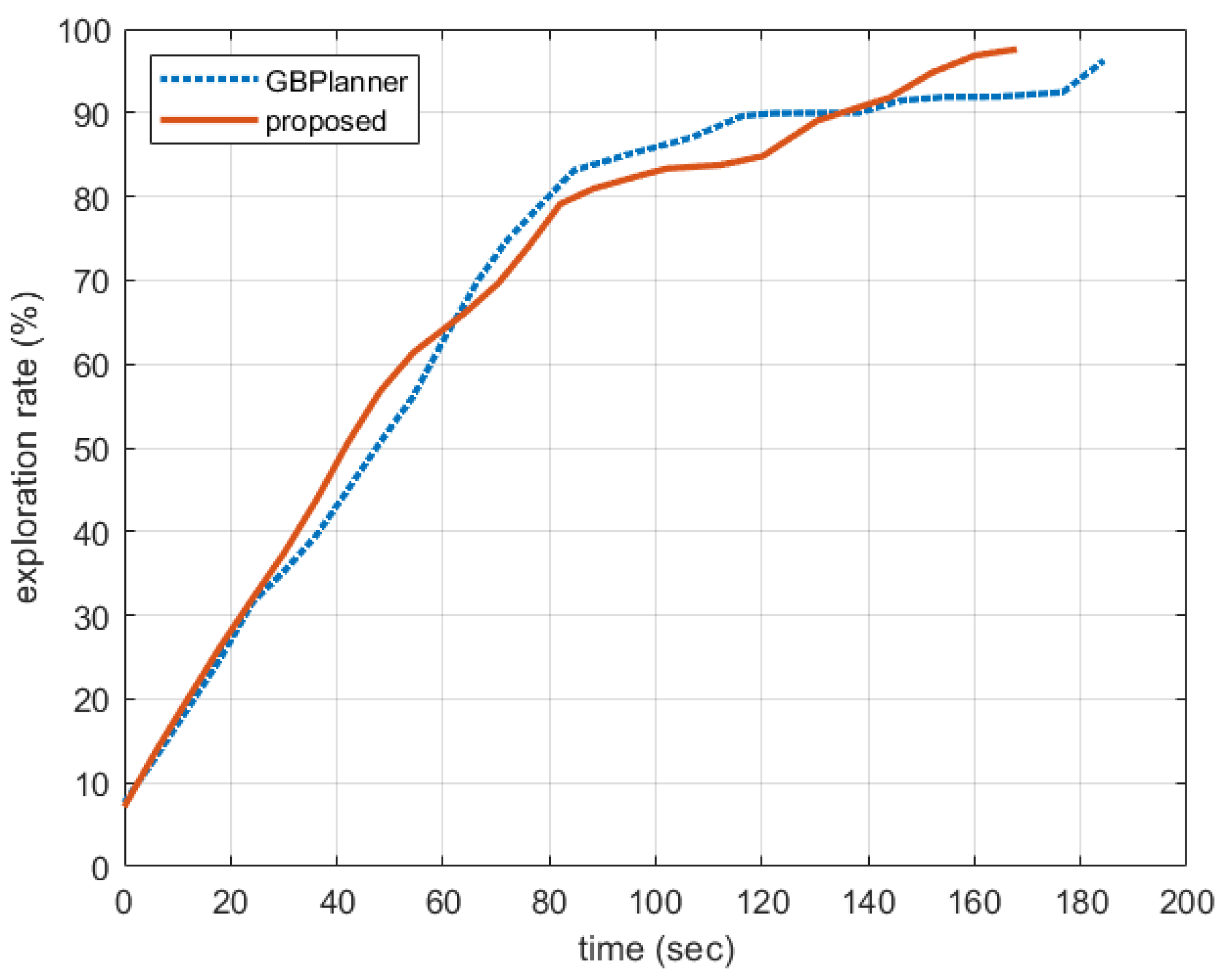
In Figure 4, the colored solid line represents the flight trajectory over time, and the green dots denote the point cloud data detected as obstacles. As shown in Figure 4A, the flight time and distance achieved by the GBPlanner were 194.72 s and 312.48 m, respectively. On the other hand, as shown in Figure 4B, the flight time and distance determined by the proposed method were 168.00 s and 272.87 m, respectively. Additionally, GBPlanner’s closest distance to the obstacle was 0.40 m, while the proposed method’s was 0.57 m. Figure 5 shows the exploration rate over time for this sample configuration. The GBPlanner and proposed method showed a linear increase in the exploration rate to approximately . However, the GBPlanner local planner required more time than the proposed method to increase the rate from approximately up to . From Figure 4 and Figure 5, it can be seen that GBPlanner encountered situations where it intersected with the past trajectory several times during exploration, but this was not the case with the proposed method. For this reason, GBPlanner’s flight time and flight distance were increased until the exploration rate reached 97% compared to the proposed method.

Figure 5.
Exploration rate over time for sample configuration.
Table 1 shows the overall results for the 200 simulation configurations for each tree density. In Table 1, the flight distance and flight time represent the total time and distance the UAV flies after takeoff until it reaches an exploration rate of . In addition, the nearest obstacle distance represents the closest distance between the UAV and the obstacle in reaching the exploration rate of . Each value represents the mean and standard deviation for the 200 trials. As the tree density increases, GBPlanner and the proposed method show an increasing flight time and distance trend. This result indicates that a complex environment requires a longer time and greater distance for exploration. However, applying the proposed method shortened the flight time and distance required for the exploration rate to reach . This improvement is likely owing to the proposed exploration gain that considers previous paths in the potential field function and minimizes overlapping between existing and new paths. Additionally, in the case of the nearest obstacle distance, as tree density increases, the distance tends to decrease. This result implies that as tree density increases, the proximity to obstacles decreases, resulting in reduced safety. However, the proposed method increased the value of the nearest obstacle distance. This result is likely owing to the enhanced exploration gain, which penalizes paths close to obstacles. Therefore, our performance comparison shows that the proposed method is more efficient and offers greater safety.

Table 1.
Performance comparison for all configurations depending on the different tree densities.
5.2. Performance Verification
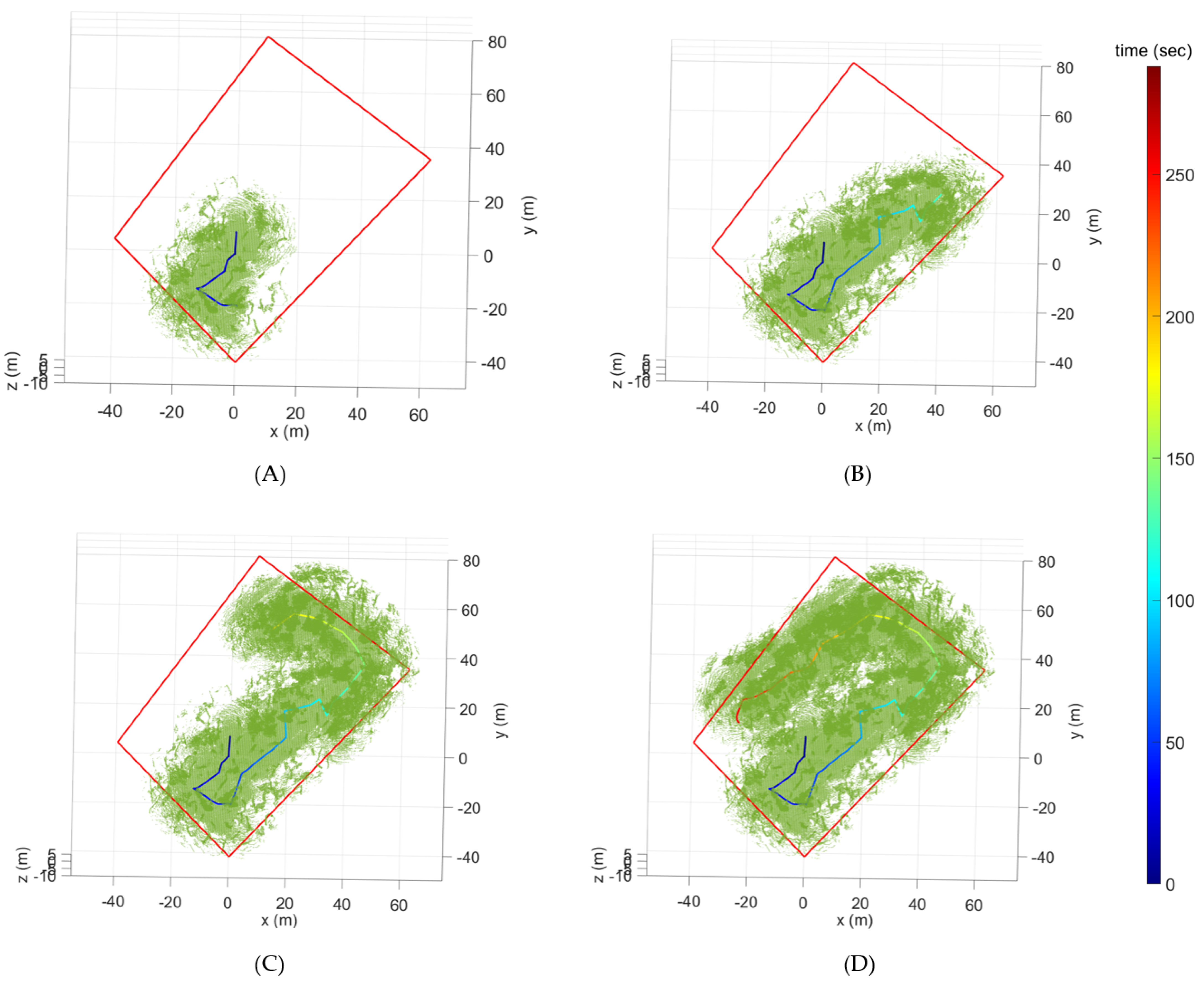
This simulation adopted the Baylands scenario for the Gazebo environment, mimicking the real Baylands Park in Sunnyvale, California. The performance verification of the proposed method is reliable in that it was performed in an officially released scenario in PX4, not in a scenario self-constructed in this study. As shown in Figure 6A, Baylands is an artificial forest-like environment with relatively flat elevations and stylized trees. We selected an area 50 m (length) × 50 m (width) × 5 m (height) with the highest tree density across all areas of the Baylands environment. Because there were many trees, exploration was carried out up to 95%. We focused on the final validation of the proposed method before performing actual experiments.
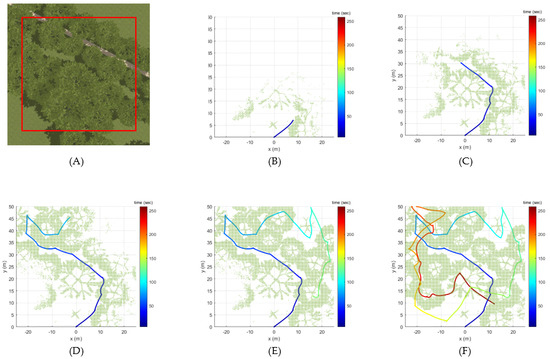
Figure 6.
Explorarion results of the proposed method for Baylands scenario within the selected area (A) at exploration rates of (B) 10.23%, (C) 30.44%, (D) 50.18%, (E) 70.5%, and (F) 95.61%.
Figure 6B–F show the simulation results for the Bayland scenario. As shown in Figure 6B–F, the flight trajectory and the point cloud data were obtained over time with exploration rates of 10.23%, 30.44%, 50.18%, 70.5%, and 95.61%, respectively. The flight times for each exploration rate were 30.57 s, 54.80 s, 92.63 s, 142.72 s, and 264.74 s, respectively. Additionally, the flight distances for each exploration rate were 13.71 m, 45.61 m, 102.67 m, 184.09 m, and 391.87 m, respectively. The closest distance to any obstacle during the entire flight was 0.49 m. These results verify the robustness of the proposed method in that it can successfully perform exploration even in diverse and complex simulation scenarios.
6. Flight Experiment
Our flight experiment was conducted at Pine Forest, Gongju-si, Chung Cheong Nam-do, Republic of Korea. As shown in Figure 7A, this forest features a variety of obstacles, including thick and straight trees, leaning trees, bushes, and thin and short young trees, along with an uneven terrain. We selected the 6065 two-dimensional area, which is represented as a red polygon in Figure 7B, with the highest tree density throughout the forest. Considering the height from 1 m to 3 m above the terrain as the flight altitude, the size of the three-dimensional space to be explored was 14,556 . The quadrotor automatically took off vertically from a random starting position and began the exploration path planning when it reached a specified altitude of 2 m. The exploration was carried out up to 94% (i.e., the residual space was assumed to be 6%).

Figure 7.
Photos of test site: (A) field photo, (B) satellite photo. The quadrotor in flight is inside the yellow circle. The red square is the selected area.
Figure 8 shows a custom quadrotor built for this flight experiment. For localization and mapping, 3D LiDAR (Ouster OS0) and AHRS (Microstrain 3DM-CV7) sensors were installed at the bottom of the quadrotor. Additionally, the quadrotor was equipped with Pixhawk 6C Mini running PX4 firmware (v1.13.3) as a flight control computer and Jetson Orion NX as a mission computer. Including all the onboard peripheral devices, the quadrotor hardware platform’s tip-to-tip length was 0.66 m, and its weight was 3.30 kg. Assuming the quadrotor only performs hovering, the maximum expected flight time was about 23 min. All the quadrotor hardware platform details are listed in Table 2.

Figure 8.
Quadrotor hardware platform.

Table 2.
Qaudrotor hardware platform specification.
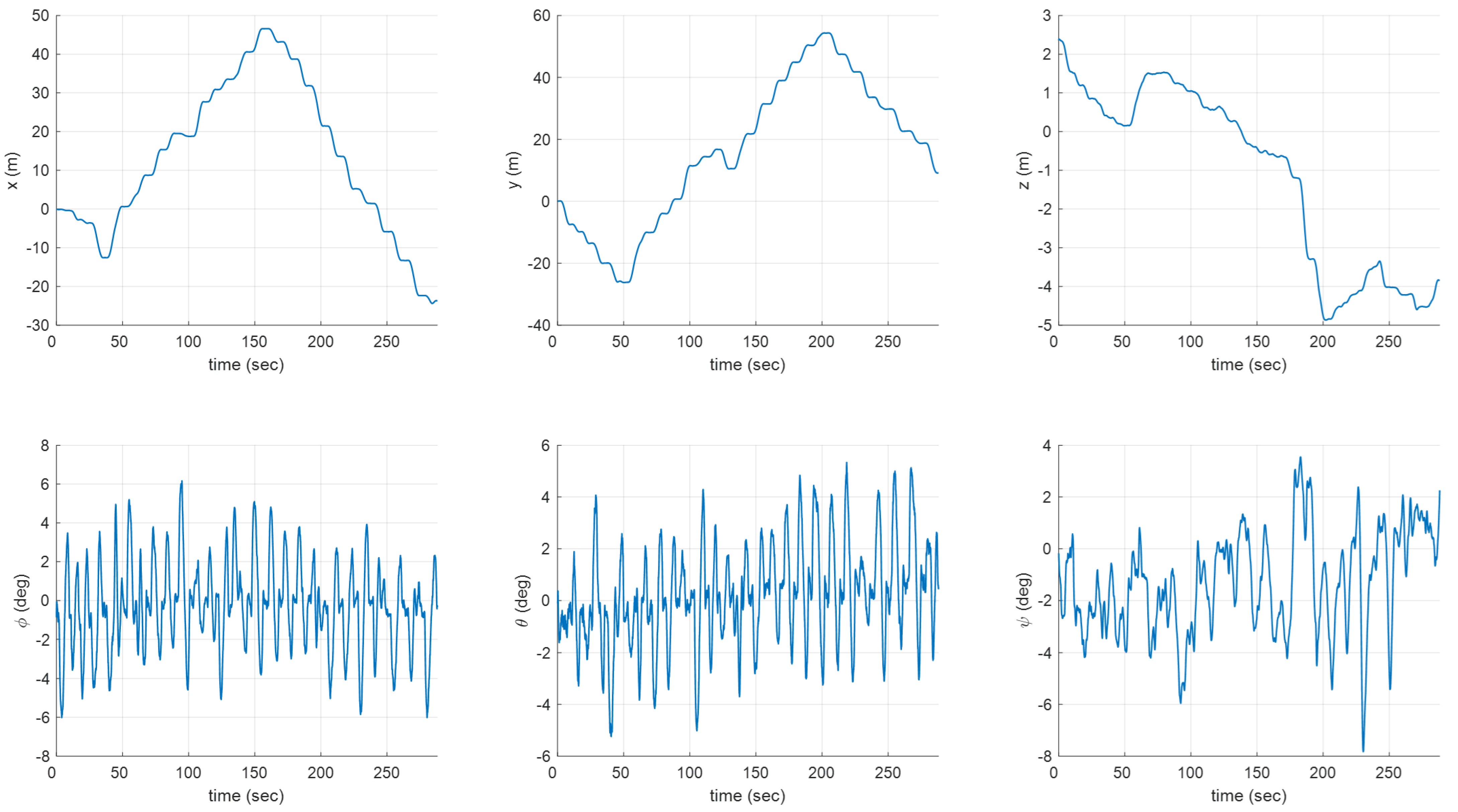
Figure 9 shows the flight experiment results, including time-dependent flight trajectories and obtained point cloud data for each exploration rate of 25.12%, 52.63%, 73.64%, and 94.6%, respectively. The flight times for each exploration rate were 50.63 s, 144.64 s, 213.85 s, and 288.16 s, respectively. Additionally, the flight distances for each exploration rate were 42.42 m, 122.30 m, 181.34 m, and 241.00 m, respectively. The distance to the nearest obstacle during the entire flight was 0.50 m. Figure 10 shows the time histories of the quadrotor’s states, including the position and attitude recorded in the flight experiment. These results demonstrate that the proposed method can be used successfully for exploration even in a forest environment with dense and scattered obstacles.
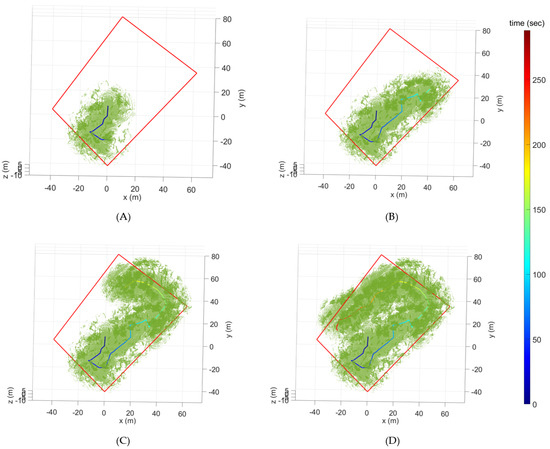
Figure 9.
Flight trajectories and point cloud data for each exploration rate of (A) 25.12%, (B) 52.63%, (C) 73.64%, and (D) 94.6%. The red square is the selected area.
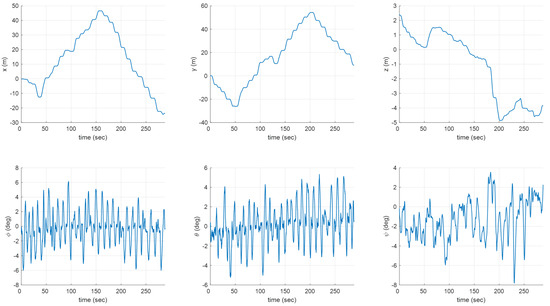
Figure 10.
Time histories of states.
7. Conclusions
We proposed a safe and efficient exploration path planning method for UAVs (Unmanned Aerial Vehicles) in forest environments. First, the distance to the nearest obstacle was incorporated into the exploration gain to enhance safety. Hence, proximity to obstacles was penalized, allowing for the UAV to fly far from obstacles and pass through wider spaces instead of narrow spaces. Second, to increase efficiency, previous flight trajectories were integrated into a potential field function to penalize the overlapping between existing and new paths. By minimizing overlapping paths, the UAV shortened the flight time required to complete exploration without wandering into previously visited space. The proposed method’s performance was thoroughly validated through extensive simulation analysis and a challenging flight experiment in a real dense forest.
Our study can be further developed in the following aspects. First, although this study was focused on using a single UAV for exploration, multiple UAVs can overcome limitations such as a small payload and short operating range. However, to achieve multiagent exploration, in addition to implementing the proposed path planning method, high-level decision-making problems, such as mission area assignments, should be addressed. Future work should investigate the feasibility of integrating multiple UAVs into exploration and development strategies for efficient assignment and coordination. Second, this study only aimed to strengthen the local planner’s capability of GBPlanner (Graph-Based exploration Path planner) without relying on the global planner. However, the global planner’s function, such as homing and repositioning of UAV, may be required to facilitate exploration in more complex or more extensive environments. Therefore, in future studies, it would be more meaningful to compare the performance with the complete GBPlanner by additionally implementing the functions of the global planner.
Author Contributions
Conceptualization, Y.H. and S.K.; methodology, Y.H. and S.K.; software, Y.H., S.K., Y.K. and S.C.; validation, Y.H., S.K., Y.K. and S.C.; formal analysis, Y.H., S.K. and Y.K.; investigation, Y.H.; resources, J.C.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H.; visualization, Y.H.; supervision, J.C.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2022-0-00021, Development of Core Technologies for Autonomous Searching Drones).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hashim, H.A. A geometric nonlinear stochastic filter for simultaneous localization and mapping. Aerosp. Sci. Technol. 2021, 111, 106569. [Google Scholar] [CrossRef]
- Oleynikova, H.; Taylor, Z.; Fehr, M.; Siegwart, R.; Nieto, J. Voxblox: Incremental 3d euclidean signed distance fields for on-board mav planning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1366–1373. [Google Scholar]
- Tsai, Y.J.; Lee, C.S.; Lin, C.L.; Huang, C.H. Development of flight path planning for multirotor aerial vehicles. Aerospace 2015, 2, 171–188. [Google Scholar] [CrossRef]
- Aslan, S.; Oktay, T. Path Planning of an Unmanned Combat Aerial Vehicle with an Extended-Treatment-Approach-Based Immune Plasma Algorithm. Aerospace 2023, 10, 487. [Google Scholar] [CrossRef]
- Yao, P.; Cai, Y.; Zhu, Q. Time-optimal trajectory generation for aerial coverage of urban building. Aerosp. Sci. Technol. 2019, 84, 387–398. [Google Scholar] [CrossRef]
- Hou, Z.; Lu, P.; Tu, Z. Nonsingular terminal sliding mode control for a quadrotor UAV with a total rotor failure. Aerosp. Sci. Technol. 2020, 98, 105716. [Google Scholar] [CrossRef]
- Eliker, K.; Grouni, S.; Tadjine, M.; Zhang, W. Practical finite time adaptive robust flight control system for quad-copter UAVs. Aerosp. Sci. Technol. 2020, 98, 105708. [Google Scholar] [CrossRef]
- Cao, C.; Zhu, H.; Choset, H.; Zhang, J. TARE: A Hierarchical Framework for Efficiently Exploring Complex 3D Environments. In Proceedings of the Robotics: Science and Systems, Virtual, 12–16 July 2021; Volume 5. [Google Scholar]
- Selin, M.; Tiger, M.; Duberg, D.; Heintz, F.; Jensfelt, P. Efficient autonomous exploration planning of large-scale 3-d environments. IEEE Robot. Autom. Lett. 2019, 4, 1699–1706. [Google Scholar] [CrossRef]
- Hao, G.; Lv, Q.; Huang, Z.; Zhao, H.; Chen, W. Uav path planning based on improved artificial potential field method. Aerospace 2023, 10, 562. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, E. Hybrid path planning using positioning risk and artificial potential fields. Aerosp. Sci. Technol. 2021, 112, 106640. [Google Scholar] [CrossRef]
- Woo, J.W.; An, J.Y.; Cho, M.G.; Kim, C.J. Integration of path planning, trajectory generation and trajectory tracking control for aircraft mission autonomy. Aerosp. Sci. Technol. 2021, 118, 107014. [Google Scholar] [CrossRef]
- Boyu, Z.; Hao, X.; Shaojie, S. Racer: Rapid collaborative exploration with a decentralized multi-uav system. IEEE Trans. Robot. 2023, 39, 1816–1835. [Google Scholar]
- Bartolomei, L.; Teixeira, L.; Chli, M. Fast multi-UAV decentralized exploration of forests. IEEE Robot. Autom. Lett. 2023, 8, 5576–5583. [Google Scholar] [CrossRef]
- Dai, A.; Papatheodorou, S.; Funk, N.; Tzoumanikas, D.; Leutenegger, S. Fast frontier-based information-driven autonomous exploration with an MAV. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 9570–9576. [Google Scholar]
- Cieslewski, T.; Kaufmann, E.; Scaramuzza, D. Rapid exploration with multi-rotors: A frontier selection method for high speed flight. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2135–2142. [Google Scholar]
- Heng, L.; Gotovos, A.; Krause, A.; Pollefeys, M. Efficient visual exploration and coverage with a micro aerial vehicle in unknown environments. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1071–1078. [Google Scholar]
- Bircher, A.; Kamel, M.; Alexis, K.; Oleynikova, H.; Siegwart, R. Receding horizon “next-best-view” planner for 3D exploration. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1462–1468. [Google Scholar]
- Witting, C.; Fehr, M.; Bähnemann, R.; Oleynikova, H.; Siegwart, R. History-aware autonomous exploration in confined environments using mavs. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–9. [Google Scholar]
- Batinovic, A.; Ivanovic, A.; Petrovic, T.; Bogdan, S. A shadowcasting-based next-best-view planner for autonomous 3D exploration. IEEE Robot. Autom. Lett. 2022, 7, 2969–2976. [Google Scholar] [CrossRef]
- Dang, T.; Mascarich, F.; Khattak, S.; Papachristos, C.; Alexis, K. Graph-based path planning for autonomous robotic exploration in subterranean environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), The Venetian Macao, Macau, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3105–3112. [Google Scholar]
- Dharmadhikari, M.; Dang, T.; Solanka, L.; Loje, J.; Nguyen, H.; Khedekar, N.; Alexis, K. Motion primitives-based path planning for fast and agile exploration using aerial robots. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, May 31–August 31 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 179–185. [Google Scholar]
- Elbanhawi, M.; Simic, M. Sampling-based robot motion planning: A review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Zhuang, X.; Li, F.; Liang, Y. A Sampling-Based Distributed Exploration Method for UAV Cluster in Unknown Environments. Drones 2023, 7, 246. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Jarin-Lipschitz, L.; Liu, X.; Tao, Y.; Kumar, V. Experiments in adaptive replanning for fast autonomous flight in forests. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 8185–8191. [Google Scholar]
- Lu, H.; Shen, H.; Tian, B.; Zhang, X.; Yang, Z.; Zong, Q. Flight in GPS-denied environment: Autonomous navigation system for micro-aerial vehicle. Aerosp. Sci. Technol. 2022, 124, 107521. [Google Scholar] [CrossRef]
- Lin, T.J.; Stol, K.A. Autonomous Surveying of Plantation Forests Using Multi-Rotor UAVs. Drones 2022, 6, 256. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, Y.; Chen, X.; Shen, S. Fuel: Fast uav exploration using incremental frontier structure and hierarchical planning. IEEE Robot. Autom. Lett. 2021, 6, 779–786. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2520–2525. [Google Scholar]
- Lou, J.; Yuksek, B.; Inalhan, G.; Tsourdos, A. Real-Time On-the-Fly Motion Planning for Urban Air Mobility via Updating Tree Data of Sampling-Based Algorithms Using Neural Network Inference. Aerospace 2024, 11, 99. [Google Scholar] [CrossRef]
- González-Banos, H.H.; Latombe, J.C. Navigation strategies for exploring indoor environments. Int. J. Robot. Res. 2002, 21, 829–848. [Google Scholar] [CrossRef]
- Junior, B.M.R.; Pereira, G.A. Fast path computation using lattices in the sensor-space for forest navigation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1117–1123. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).