Optimal Design of High-Power Density Medium-Voltage Direct Current Bipolar Power Cables for Lunar Power Transmission
Abstract
1. Introduction
2. Challenges Related to the Lunar Environment
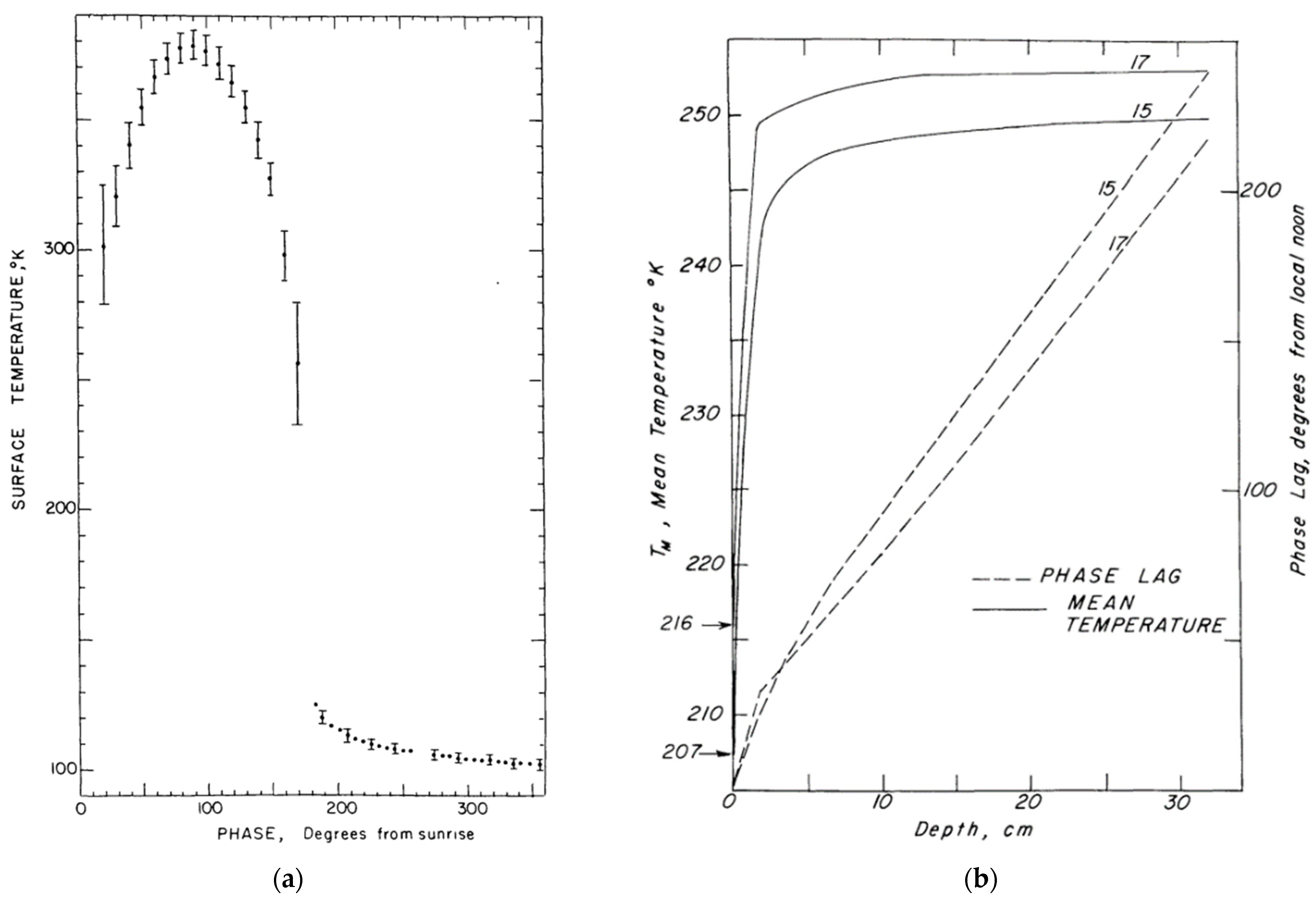
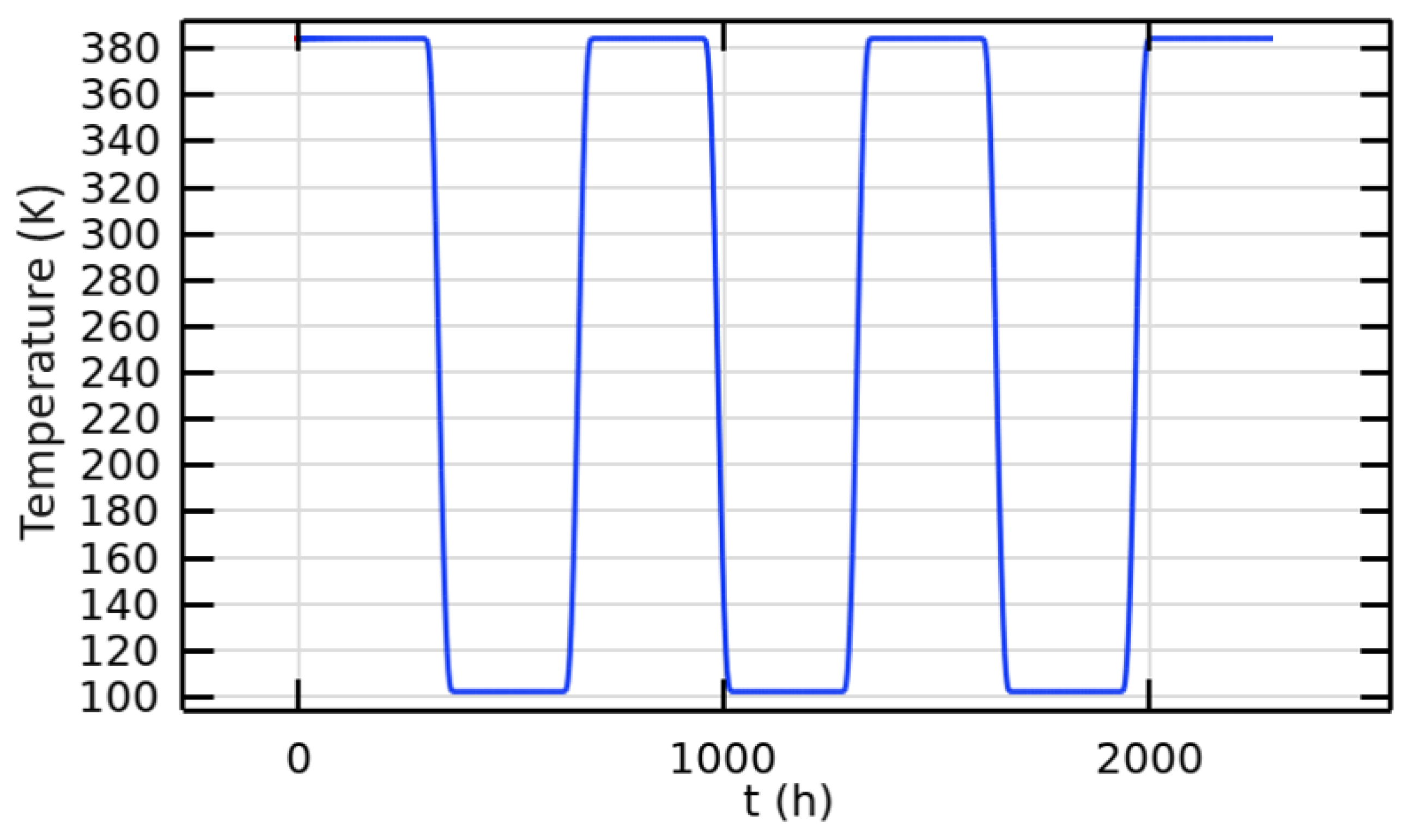
2.1. The Lunar Environment
2.2. Specifications of Power Lines
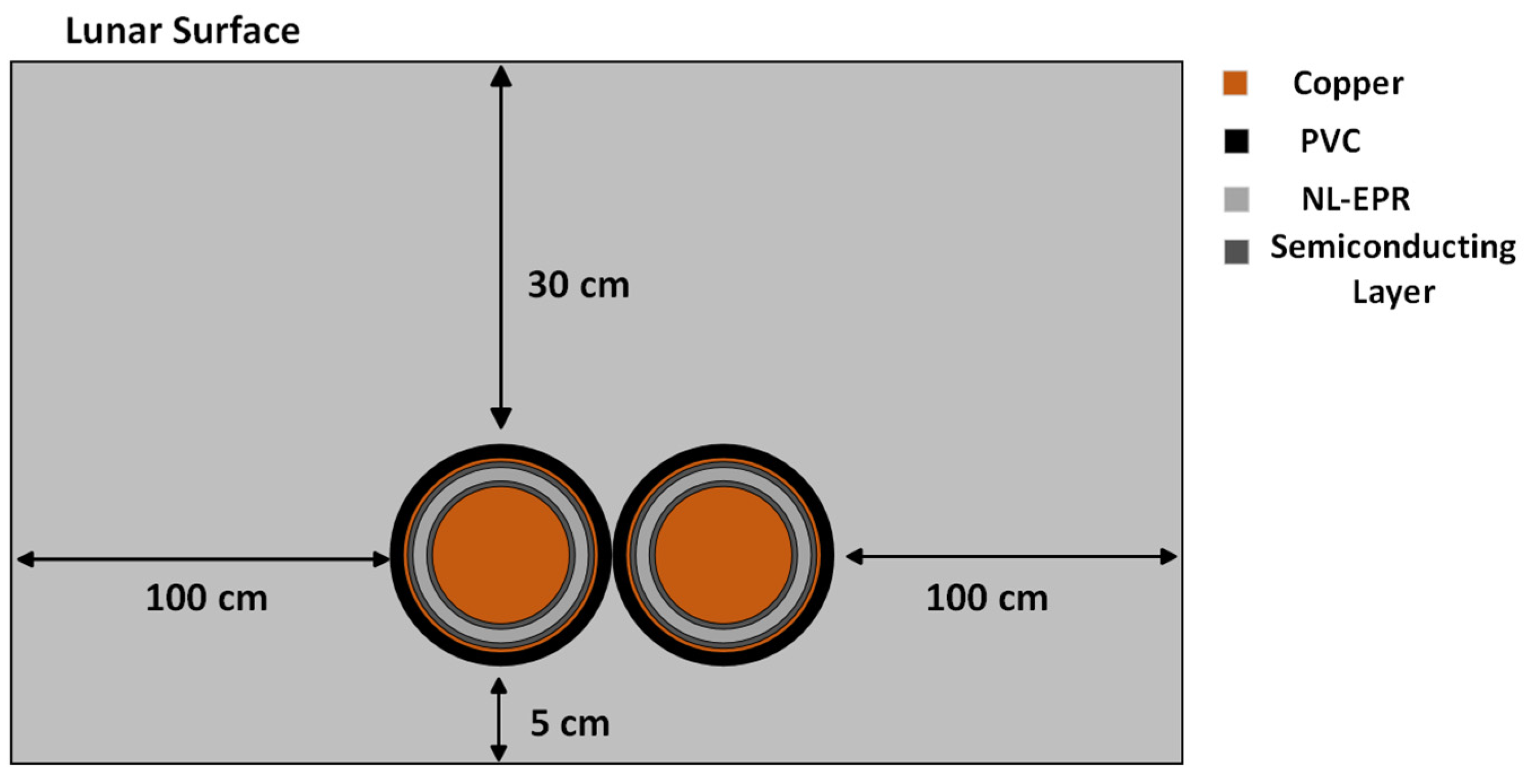
3. Model and Design
3.1. Coupled Electrothermal Model
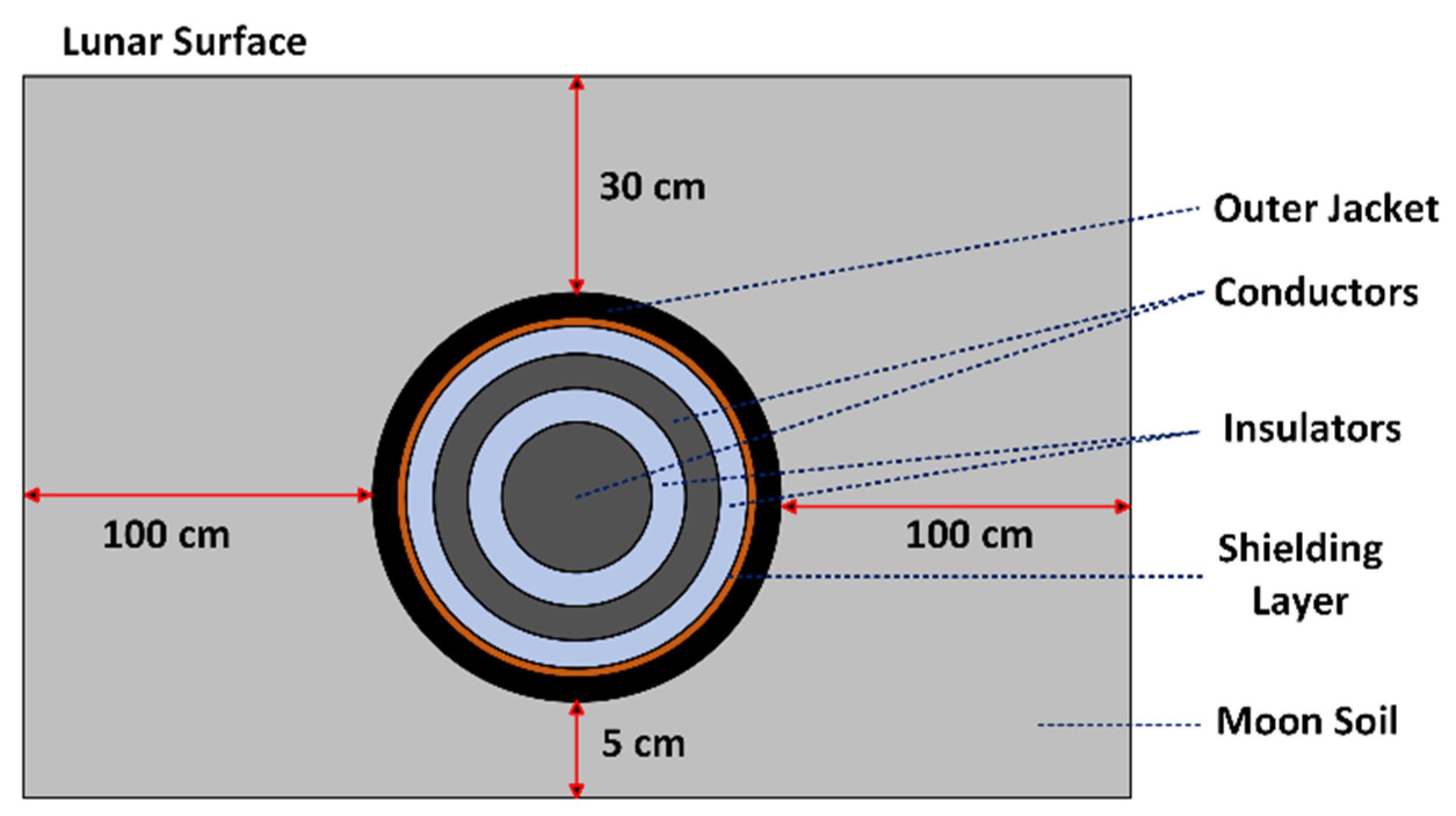
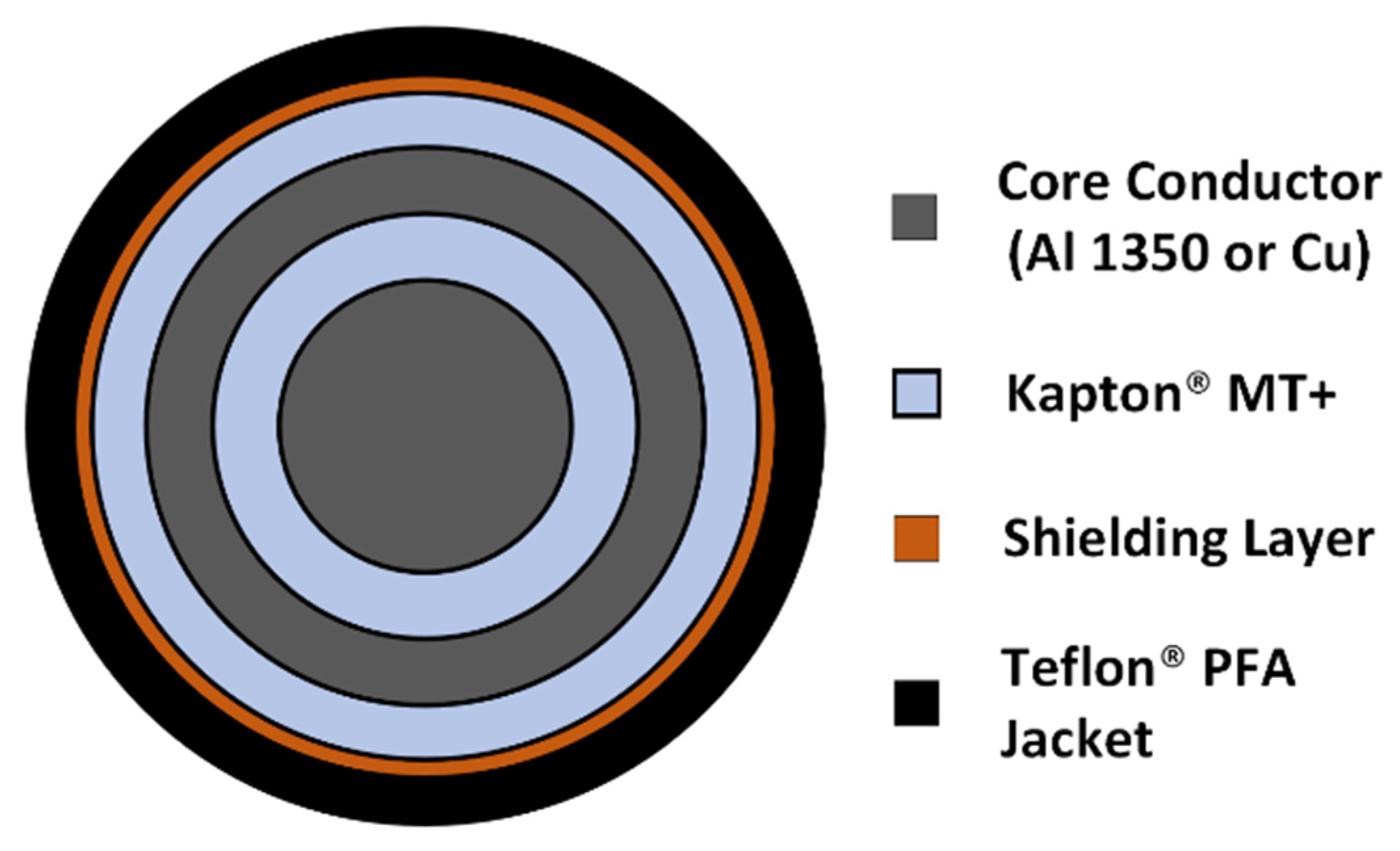
3.2. Proposed Insulation Designs
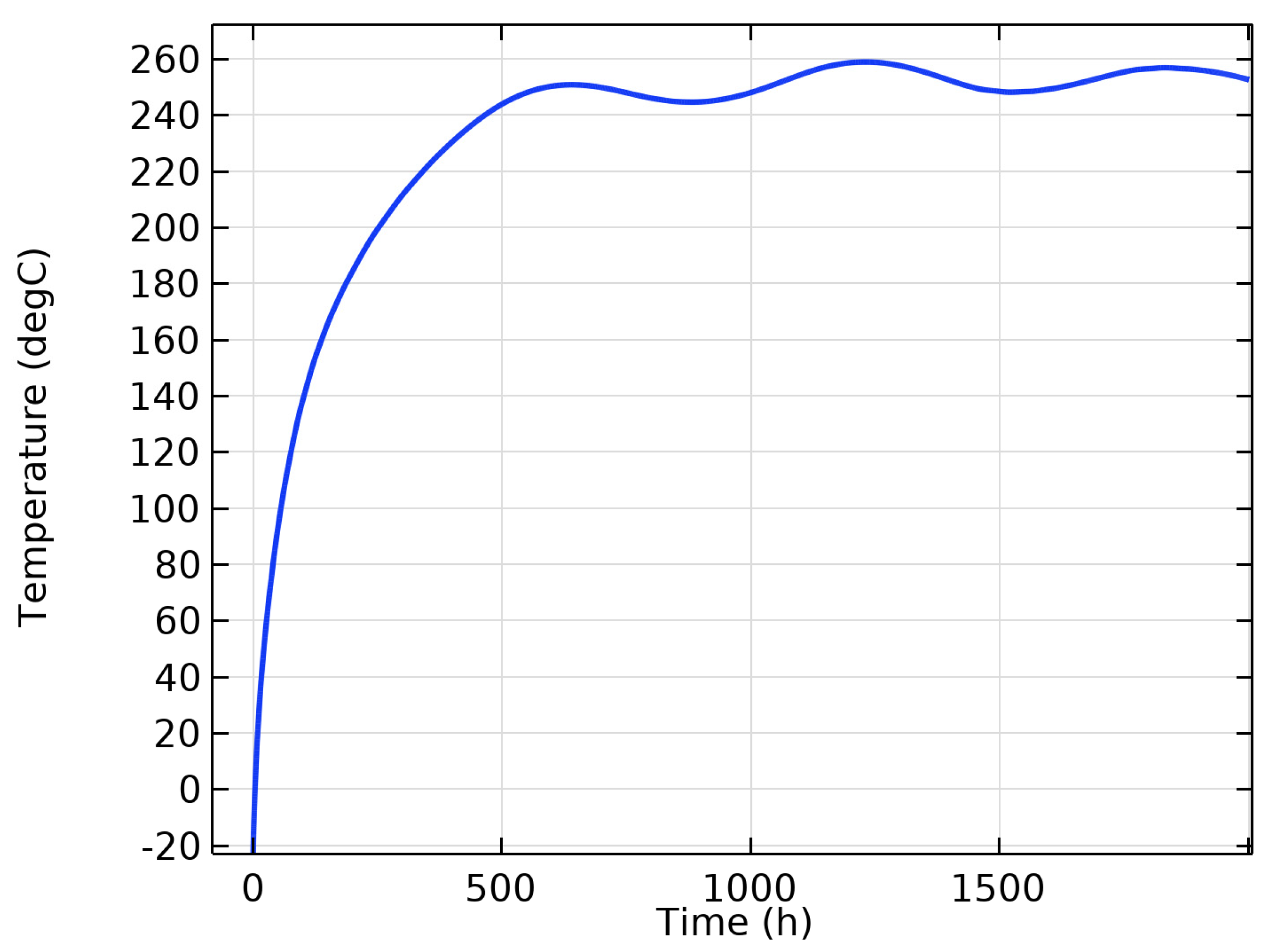
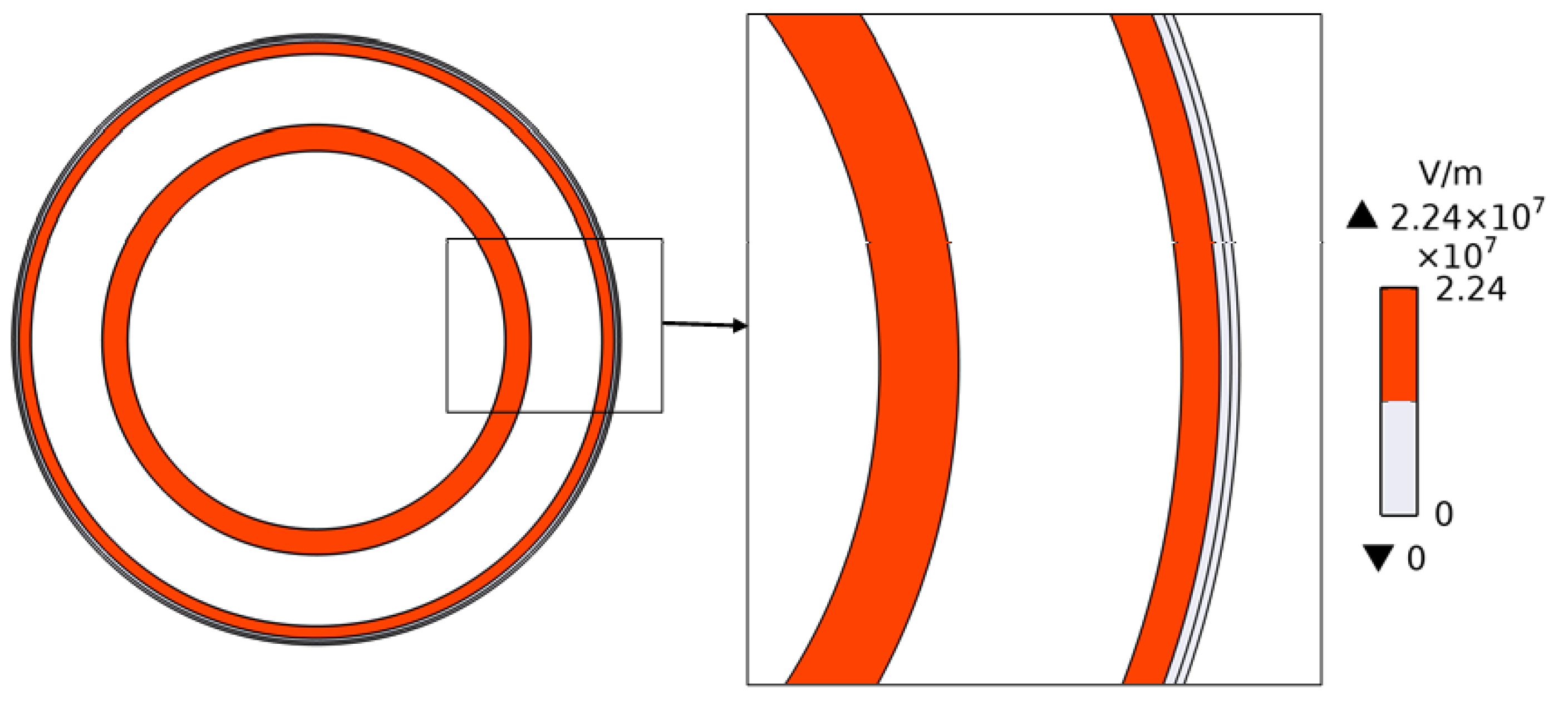
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, Z.; Vranis, A.; Zavoico, A.; Freid, S.; Manners, B. Power system concepts for the lunar outpost: A review of the power generation, energy storage, power management and distribution (PMAD) system requirements and potential technologies for development of the lunar outpost. AIP Conf. Proc. 2006, 813, 1083–1092. [Google Scholar]
- Gordon, L.B. Electrical Transmission on the Lunar Surface Part I—DC Transmission. 2001. Available online: https://ntrs.nasa.gov/api/citations/20040191588/downloads/20040191588.pdf (accessed on 13 April 2024).
- Gordon, L.B.; Gaustad, K.L. Vacuum insulation for a lunar-based power system. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 299–311. [Google Scholar] [CrossRef]
- Boretz, J.; Koslover, M. Synthesis of an electrical power system for a manned lunar base. IEEE Trans. Aerosp. Electron. Syst. 1969; AES-5, 770–788. [Google Scholar]
- IEC 60287-1-1:2006; Electric Cables-Calculation of the Current Rating-Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses-General. IEC: Geneva, Switzerland, 2006; pp. 1–136.
- IEC 60853-1:1985; Calculation of the Cyclic and Emergency Current Rating of Cables. Part 1: Cyclic Rating Factor for Cables up to and Including 18/30(36) kV. IEC: Geneva, Switzerland, 1985; pp. 1–39.
- IEC 60986:2000; Short-Circuit Temperature Limits of Electric Cables with Rated Voltages from 6 kV (Um = 7.2 kV) up to 30 kV (Um = 36 kV). IEC: Geneva, Switzerland, 2000; pp. 1–19.
- IEC TR 62095:2003; Electric Cables-Calculations for Current Ratings-Finite Element Method. IEC: Geneva, Switzerland, 2003; pp. 1–69.
- Smith, R.E.; West, G.S. Space and Planetary Environment Criteria Guidelines for Use in Space Vehicle Development. Volume 1: 1982 Revision; 1983; Volume 83, p. 18816. Available online: https://ntrs.nasa.gov/api/citations/19830019790/downloads/19830019790.pdf (accessed on 13 April 2024).
- Podnieks, E.R. Environmental Considerations for Lunar Base Engineering. In Engineering, Construction, and Operations in Space; ASCE: Reston, VA, USA, 1988; pp. 55–66. [Google Scholar]
- Johnson, F.S.; Carroll, J.M.; Evans, D.E. Vacuum Measurements on the Lunar Surface. J. Vac. Sci. Technol. 1972, 9, 450–456. [Google Scholar] [CrossRef]
- Hoffman, J.H.; Hodges, R.R.; Evans, D.E. Lunar Orbital Mass Spectrometer Experiment. Lunar Planet. Sci. Conf. Proc. 1972, 3, 2205. [Google Scholar]
- Hodges, R.R.; Hoffman, J.H.; Evans, D.E. Apollo 16—Lunar Orbital Mass Spectrometer Experiment. 1972. Available online: https://www.lpi.usra.edu/lunar/documents/NASA%20SP%20315.pdf (accessed on 13 April 2024).
- Strangway, D.W. Moon: Electrical Properties of the Uppermost Layers. Science 1969, 165, 1012–1013. [Google Scholar] [CrossRef] [PubMed]
- Keihm, S.J.; Langseth, M.G. Surface Brightness Temperatures at the Apollo 17 Heat Flow Site—Thermal Conductivity of the Upper 15 Cm of Regolith. Lunar Planet. Sci. Conf. Proc. 1973, 4, 2503. [Google Scholar]
- Langseth, M.G.; Clark, S.P.; Chute, J.L.; Keihm, S.J.; Wechsler, A.E. Heat Flow Experiment. Sci. Rep. 1972, 289, 11. [Google Scholar]
- General Cable Catalogs, Electric Utility (U.S.) Products. Available online: https://prysmian-group.dcatalog.com/v/Electric-Utility-(US)/ (accessed on 13 April 2024).
- Cour-Palais, B.G.; Flaherty, R.E.; Brown, M.L. Apollo Window Meteoroid Experiment. Available online: https://ntrs.nasa.gov/citations/19720015188 (accessed on 13 April 2024).
- Cour-Palais, B.G.; Brown, M.L.; Mckay, D.S. Apollo Window Meteoroid Experiment. Available online: https://ntrs.nasa.gov/citations/19730013033 (accessed on 13 April 2024).
- Brownlee, D.; Bucher, W.; Hodge, P. Micrometeorite impact analyses. In Analysis of Surveyor 3 Material and Photographs Returned by Apollo 12; NASA: Washington, DC, USA, 1972. [Google Scholar]
- Kirkici, H.; Rose, M.F.; Chaloupka, T. Experimental study on simulated lunar soil, high voltage breakdown and electrical insulation characteristics. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 119–125. [Google Scholar] [CrossRef]
- Kirkici, H.; Rose, M.F. High voltage transmission line operation in simulated lunar environment. In Proceedings of the Ninth IEEE International Pulsed Power Conference, Albuquerque, NM, USA, 21–23 June 1993. [Google Scholar]
- Heiken, G.; Vaniman, D.; French, B.M. Lunar Sourcebook; Cambridge University Press: New York, NY USA, 1991. [Google Scholar]
- Jordan, A.P.; Stubbs, T.J.; Zeitlin, C.; Spence, H.E.; Schwadron, N.A.; Zimmerman, M.I.; Farrell, W.M. On the Interaction Between Highly Energetic Charged Particles and the Lunar Regolith. In Proceedings of the Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2012; p. 2619. [Google Scholar]
- Baferani, M.A.; Li, C.; Shahsavarian, T.; Ronzello, J.; Cao, Y. High temperature insulation materials for dc cable insulation—Part I: Space charge and conduction. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 223–230. [Google Scholar] [CrossRef]
- Shin, E.E.; Scheiman, D.A.; Lizcano, M. Lightweight, durable, and multifunctional electrical insulation material systems for high voltage applications. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018; pp. 1–21. [Google Scholar]
- Saha, A.; Azizi, A.; Ghassemi, M. Optimal Bipolar MVDC Power Cable Designs for Future Wide-Body All Electric Aircraft. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2074–2083. [Google Scholar] [CrossRef]
- Saha, A.; Ghassemi, M. Challenges in Electrical Insulation Materials and Thermal Management for Medium Voltage Power Cables for Envisaged Wide-Body All-Electric Aircraft. In Aeronautics-Characteristics and Emerging Technologies; Li, L., Ed.; IntechOpen: London, UK, 2024; Available online: https://www.intechopen.com/online-first/1194193 (accessed on 18 August 2024).
- Saha, A.; Azizi, A.; Ghassemi, M. Optimized Design of ±5 kV, 1 kA Rectangular Power Cable for a Low Pressure of 18.8 kPa for Envisioned All-Electric Wide-Body Aircraft. IEEE Access 2024, 12, 28654–28665. [Google Scholar] [CrossRef]
- Saha, A.; Ghassemi, M. High power density, cost-effective HVDC cables for power transmission on the moon. In Proceedings of the IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 12–13 February 2024; pp. 1–5. [Google Scholar]
- DuPont™ Kapton® MT+. Available online: https://materials-direct.com/wp-content/uploads/2021/05/K-MT-Eng-2019.pdf (accessed on 3 May 2024).
- DuPont™ Teflon® PFA. Available online: https://catalog.cshyde.com/Asset/Data%20Sheet%2023-__PFA%20DuPont%20PFA%20Film%20Data%20Sheet.pdf (accessed on 3 May 2024).
- Saha, A.; Ghassemi, M. MVDC Bipolar Power Cables with Rectangular Geometry Design for Envisaged All-Electric Wide-Body Aircraft. In Proceedings of the IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 12–13 February 2024; pp. 1–5. [Google Scholar]
- Available online: https://www.sanghviaerospace.com/pdf/polyimide-cable-partnumbering381-27500.pdf (accessed on 13 April 2024).
- Available online: https://americandurafilm.com/film-distribution/kapton-film/ (accessed on 13 April 2024).
- 1/0-19 CU 90 MILS NL-EPR 5KV 100% T/S BLACK SIMpull PVC JACKET UL|Southwire. Available online: https://www.southwire.com/wire-cable/medium-voltage-power-cable/spec46101-cu-compressed-5kv-nlepr-insulation-100-il-pvc-jacket-mv-105-tray-rated-sunlight-resistant-for-direct-burial/p/55565699 (accessed on 3 August 2024).


| Parameter | (K) | (mm/kV) | (S/m) |
|---|---|---|---|
| ETFE | 4061 | 0.03097 | 2.027 × 10−10 |
| PI | 3319 | 0.05558 | 1.677 × 10−9 |
| Material | Density (kg·m−3) | Thermal Conductivity (W·m−1·K−1) | Dielectric Constant | Dielectric Strength (V·m−1) |
|---|---|---|---|---|
| Aluminum | 2705 | 237 | - | - |
| Copper | 8960 | 400 | - | - |
| Kapton® MT+ (500 MT+) | 1420 | 0.75 | 4.2 | 114.173 × 106 |
| Teflon® PFA | 2150 | 0.195 | 2 | 256 × 106 |
| XLPE | 930 | 0.46 | 2.5 | - |
| NL-EPR | 860 | 0.3 | 2.5 | - |
| Semiconducting layer | 1055 | 10 | - | - |
| PVC | 1350 | 0.19 | - | - |
| Moon’s Soil | - | 0.010 | - | - |
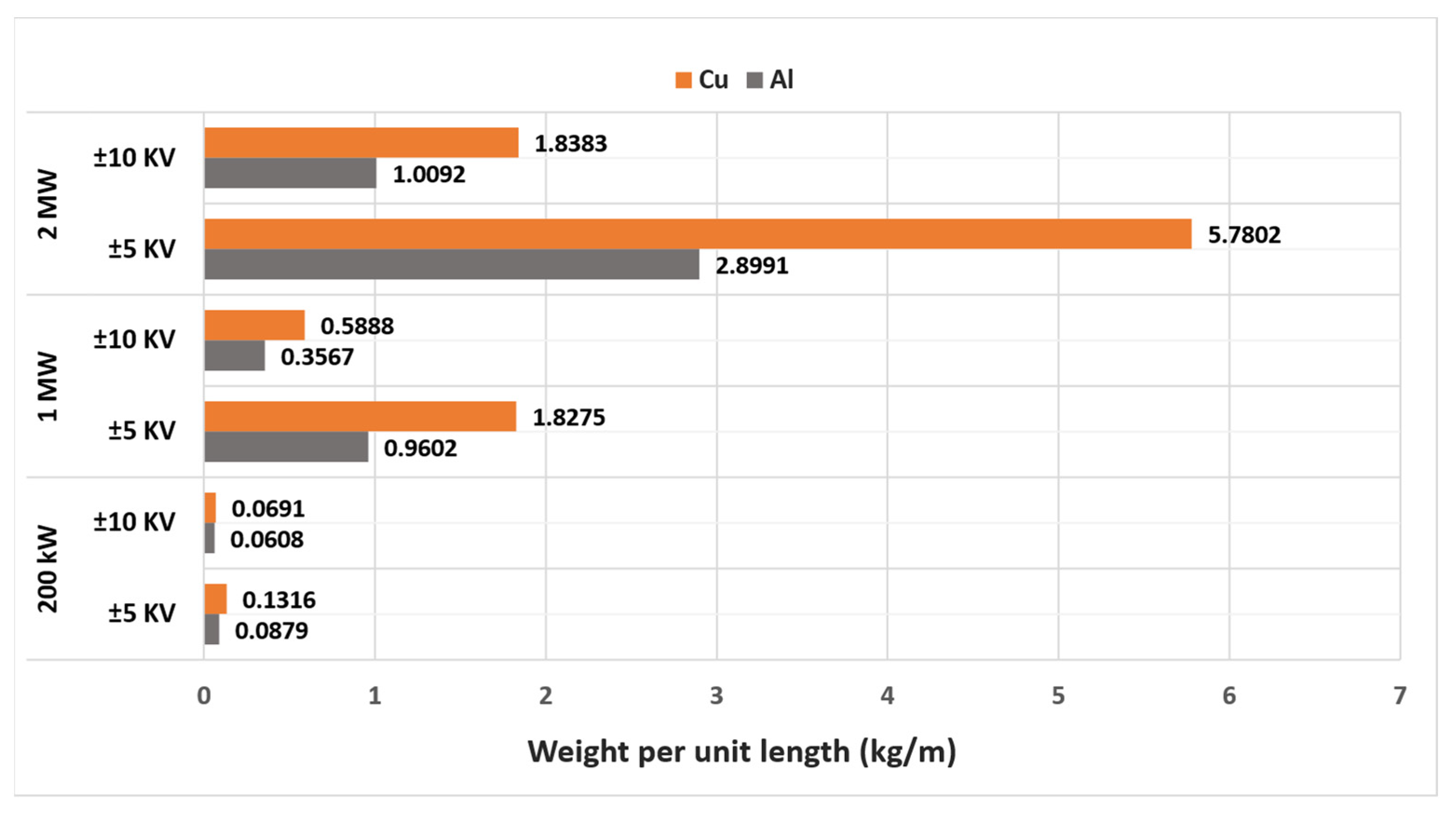
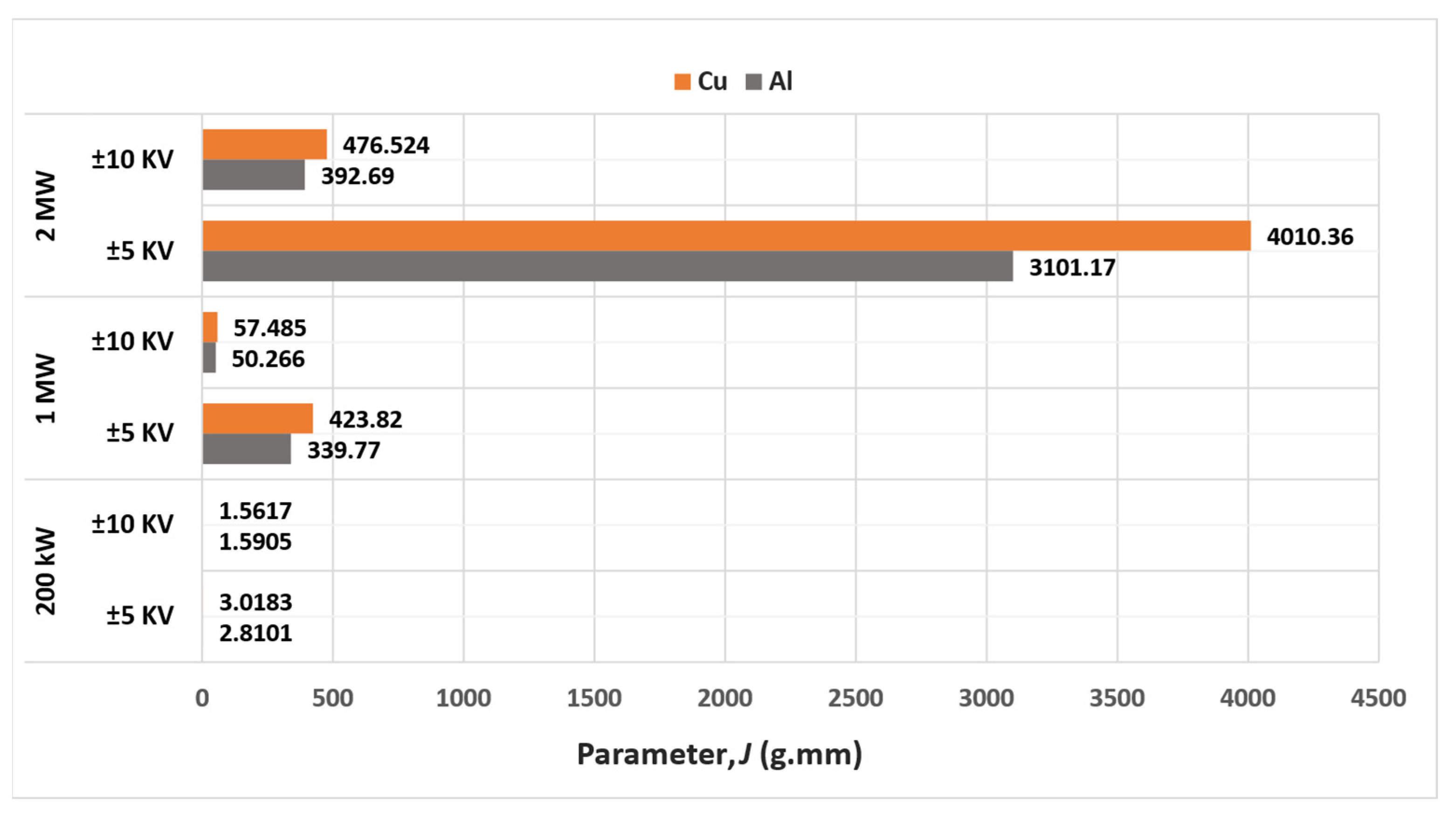
| Power Level (kW) | Core Conductor Material | Radius of the Core Conductor (mm) | Thickness of the Inner Insulator (mm) | Thickness of the Outer Conductor (mm) | Thickness of the Outer Insulator (mm) | Overall Radius of the Cable (mm) |
|---|---|---|---|---|---|---|
| 200 | Al | 1.68 | 0.48 | 0.5764 | 0.225 | 6.38 |
| Cu | 1.32 | 0.50 | 0.4283 | 0.225 | 5.40 | |
| 1000 | Al | 6.95 | 0.46 | 2.7495 | 0.225 | 10.61 |
| Cu | 5.52 | 0.46 | 2.158 | 0.225 | 8.59 | |
| 2000 | Al | 12.5 | 0.45 | 5.0485 | 0.225 | 18.45 |
| Cu | 9.96 | 0.45 | 3.9975 | 0.225 | 14.86 |
| Power Level (kW) | Core Conductor Material | Radius of the Core Conductor (mm) | Thickness of the Inner Insulator (mm) | Thickness of the Outer Conductor (mm) | Thickness of the Outer Insulator (mm) | Overall Radius of the Cable (mm) |
|---|---|---|---|---|---|---|
| 200 | Al | 0.86 | 1.14 | 0.1771 | 0.48 | 2.89 |
| Cu | 0.66 | 1.2 | 0.1137 | 0.48 | 2.68 | |
| 1000 | Al | 3.76 | 0.94 | 1.319 | 0.45 | 6.70 |
| Cu | 2.96 | 0.94 | 0.9961 | 0.45 | 5.57 | |
| 2000 | Al | 6.91 | 0.93 | 2.6105 | 0.45 | 11.13 |
| Cu | 5.46 | 0.93 | 2.015 | 0.45 | 9.08 |
| Cable Type | Core Conductor Material | Radius of the Core Conductor (mm) | Overall Radius of the Cable (mm) | Weight per Unit Length for 2 Poles (kg/m) | Total Cross-Sectional Area (mm2) |
|---|---|---|---|---|---|
| NL-EPR 5 kV Cable | Cu | 10.65 | 16.6825 | 7.7157 | 1748.6 |
| Designed Coaxial Cable | Cu | 9.96 | 14.861 | 5.7802 | 693.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, A.; Ghassemi, M. Optimal Design of High-Power Density Medium-Voltage Direct Current Bipolar Power Cables for Lunar Power Transmission. Aerospace 2024, 11, 685. https://doi.org/10.3390/aerospace11080685
Saha A, Ghassemi M. Optimal Design of High-Power Density Medium-Voltage Direct Current Bipolar Power Cables for Lunar Power Transmission. Aerospace. 2024; 11(8):685. https://doi.org/10.3390/aerospace11080685
Chicago/Turabian StyleSaha, Anoy, and Mona Ghassemi. 2024. "Optimal Design of High-Power Density Medium-Voltage Direct Current Bipolar Power Cables for Lunar Power Transmission" Aerospace 11, no. 8: 685. https://doi.org/10.3390/aerospace11080685
APA StyleSaha, A., & Ghassemi, M. (2024). Optimal Design of High-Power Density Medium-Voltage Direct Current Bipolar Power Cables for Lunar Power Transmission. Aerospace, 11(8), 685. https://doi.org/10.3390/aerospace11080685







