Rutting Caused by Grouser Wheel of Planetary Rover in Single-Wheel Testbed: LiDAR Topographic Scanning and Analysis
Abstract
:1. Introduction
1.1. Relevance
1.2. Contributions
- Employing LiDAR technology to characterize wheel-induced terrain deformation in a SWT.
- Modeling ruts using curve-fitted sine waves to extract their average dimensions.
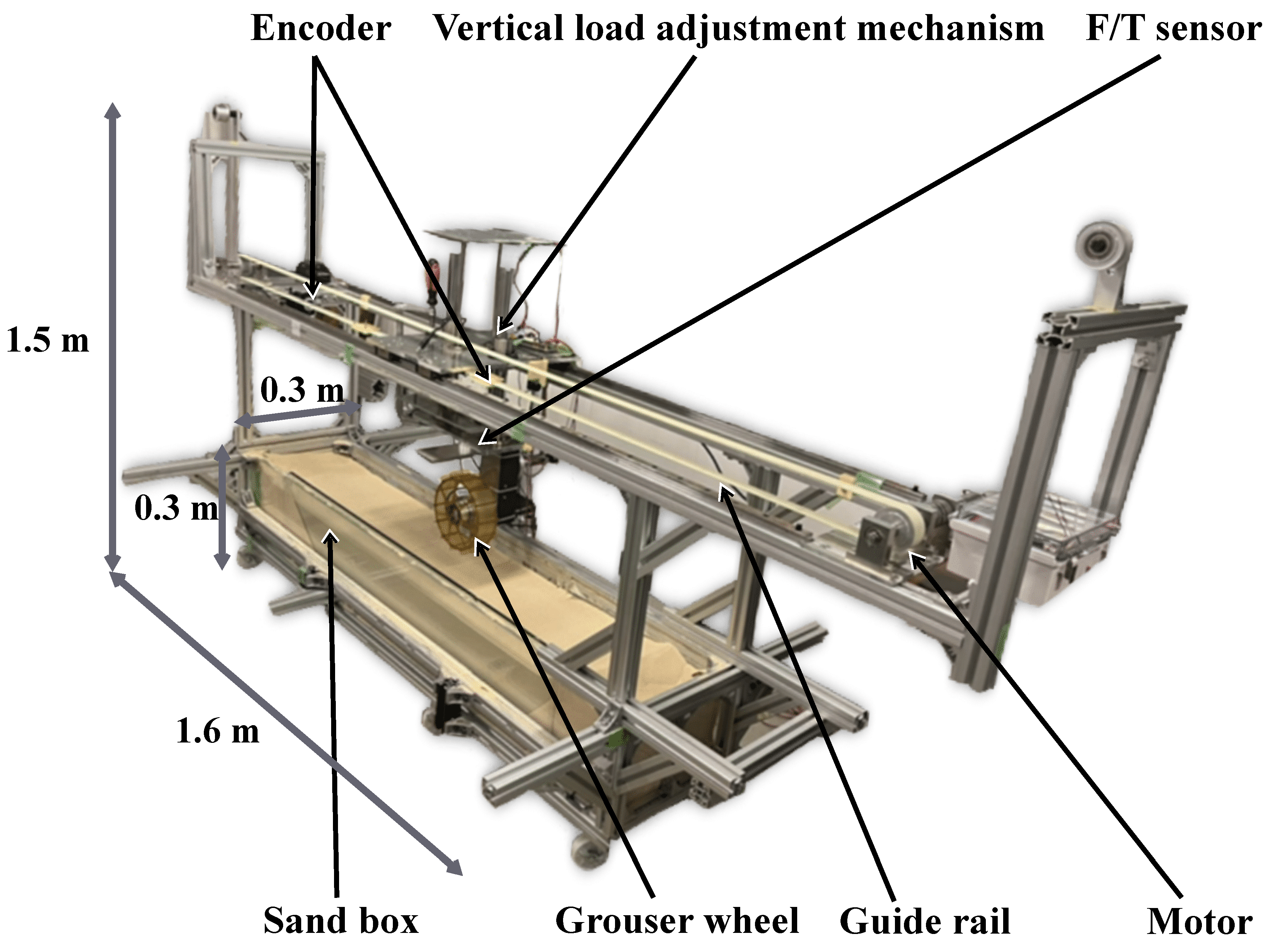
2. Experimental Description
- Terrain preparation: the sandbed is plowed to establish a loose state and is then leveled to ensure a consistent starting surface for the experiment.
- Initial setup: the wheel unit is positioned at the starting point, and the wheel is lowered until it makes contact with the sand surface.
- Track creation: the running parameters (rotational and horizontal velocities) are set, and the wheel is driven forward for the first time across the sandbed to create tracks.
- Locking the wheel up: with the help of a clamp, the wheel unit is locked in the up position so it does not disturb the created tracks.
- Cart returning: after completing the first run, the wheel unit is returned to the starting point.
- LiDAR data acquisition: in the second forward movement, the LiDAR sensor is activated, the horizontal velocity is set, and the cart performs the movement while recording LiDAR data.
- Repetition: the sandbed is reset to the initial conditions, and the experiment is repeated as required.
LiDAR Accuracy Experiment
3. Datasets
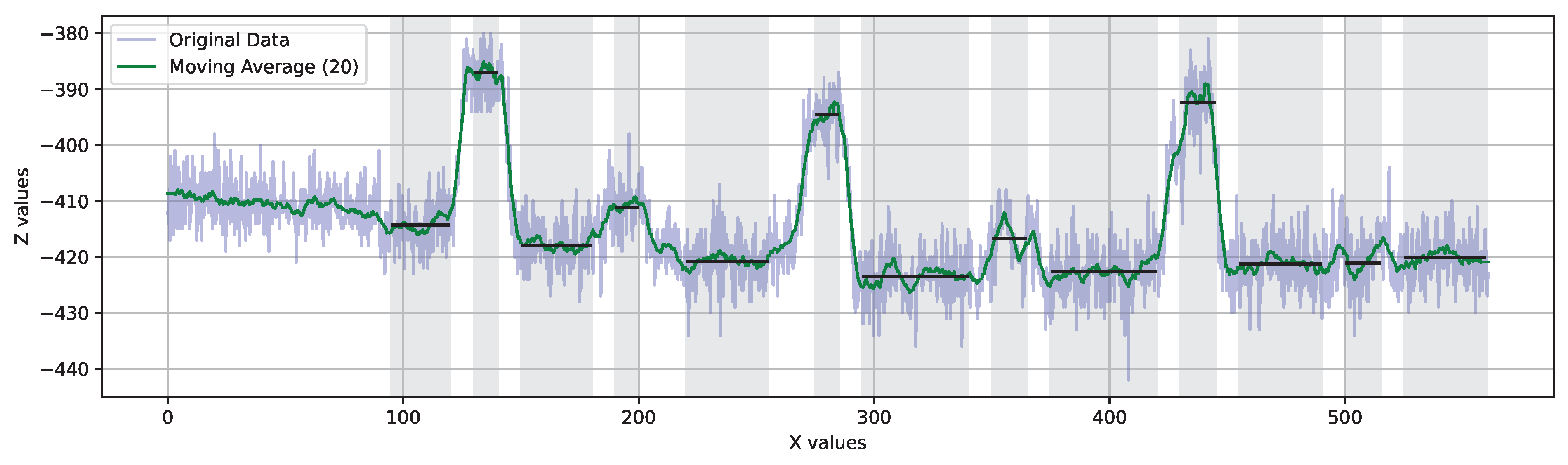
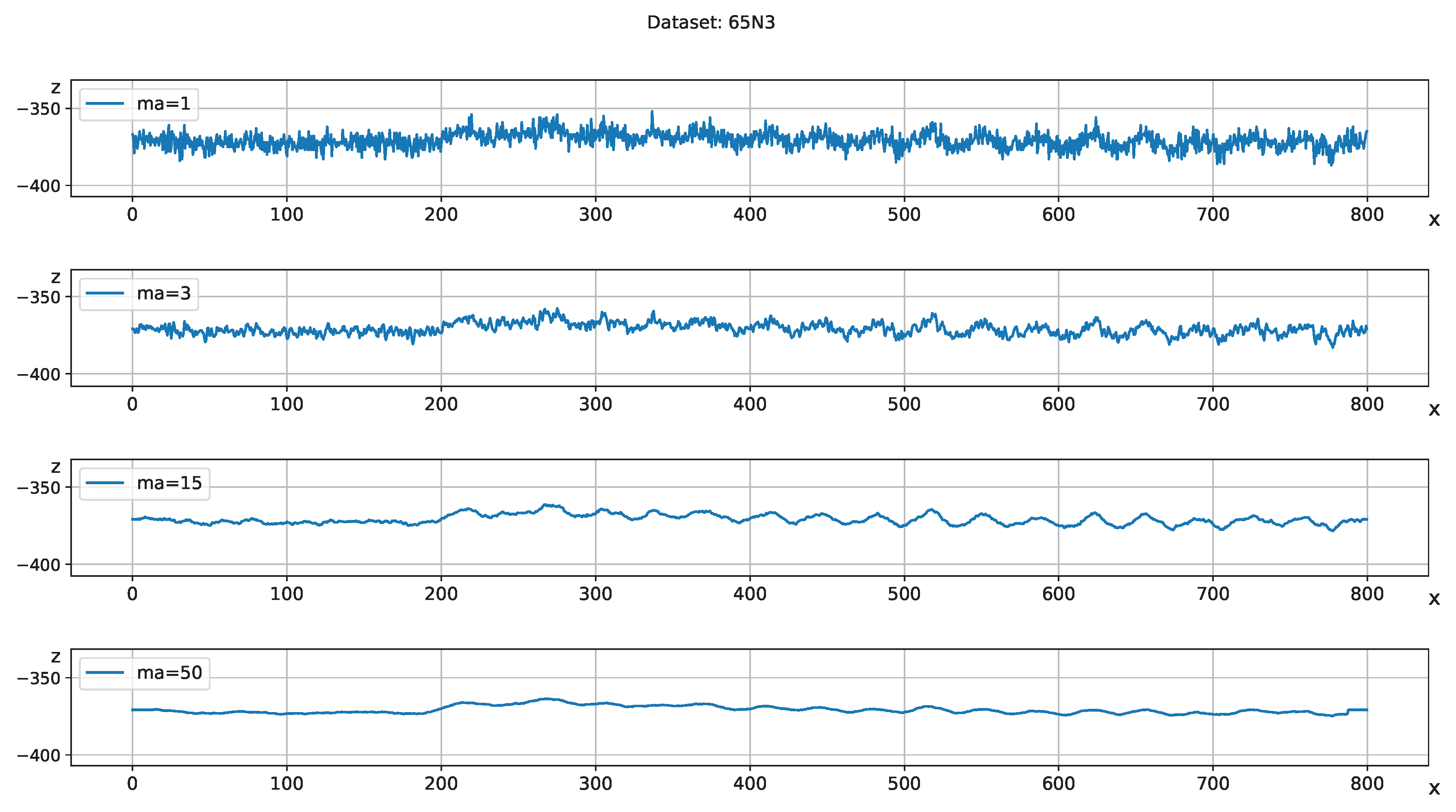
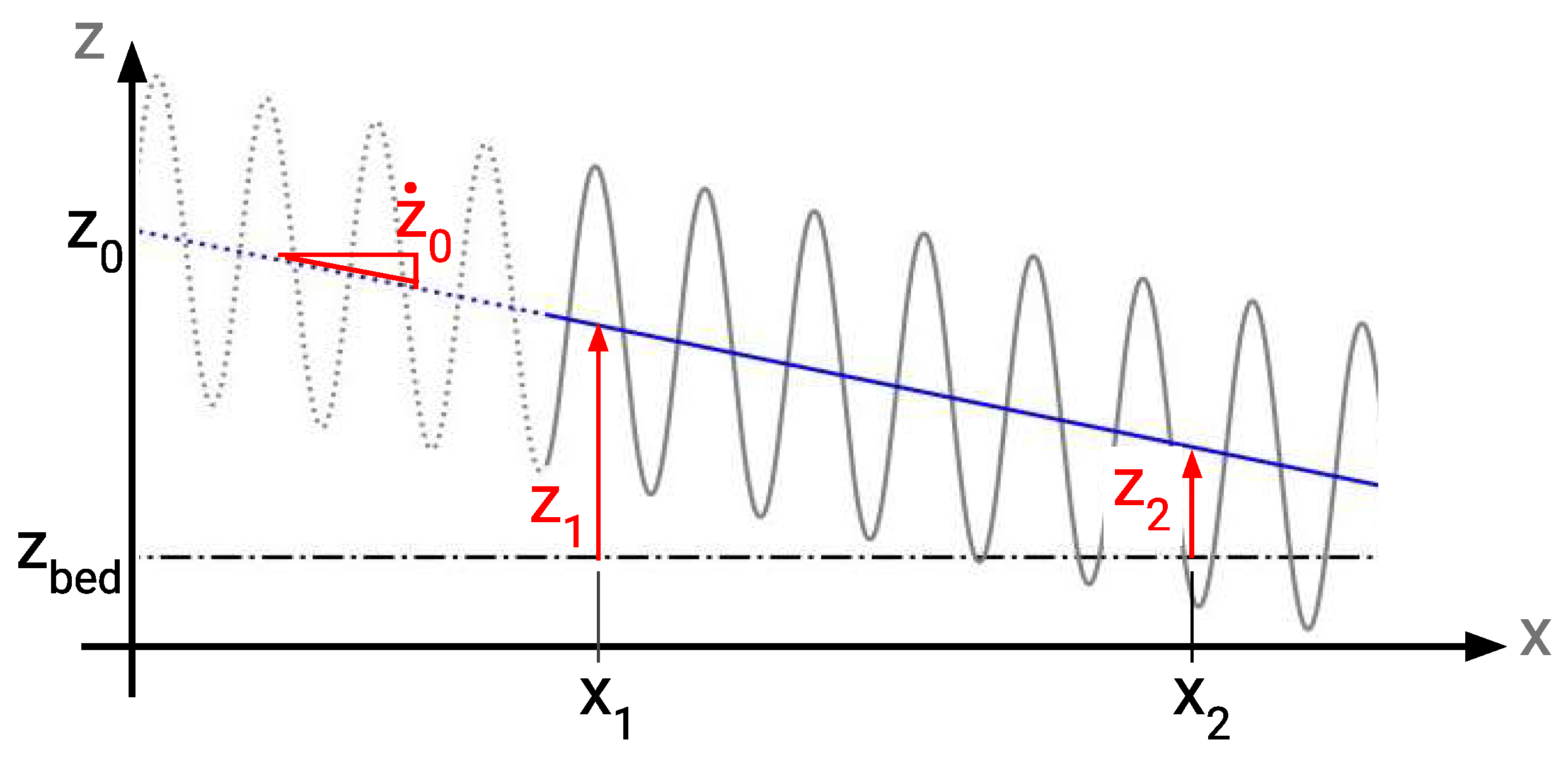
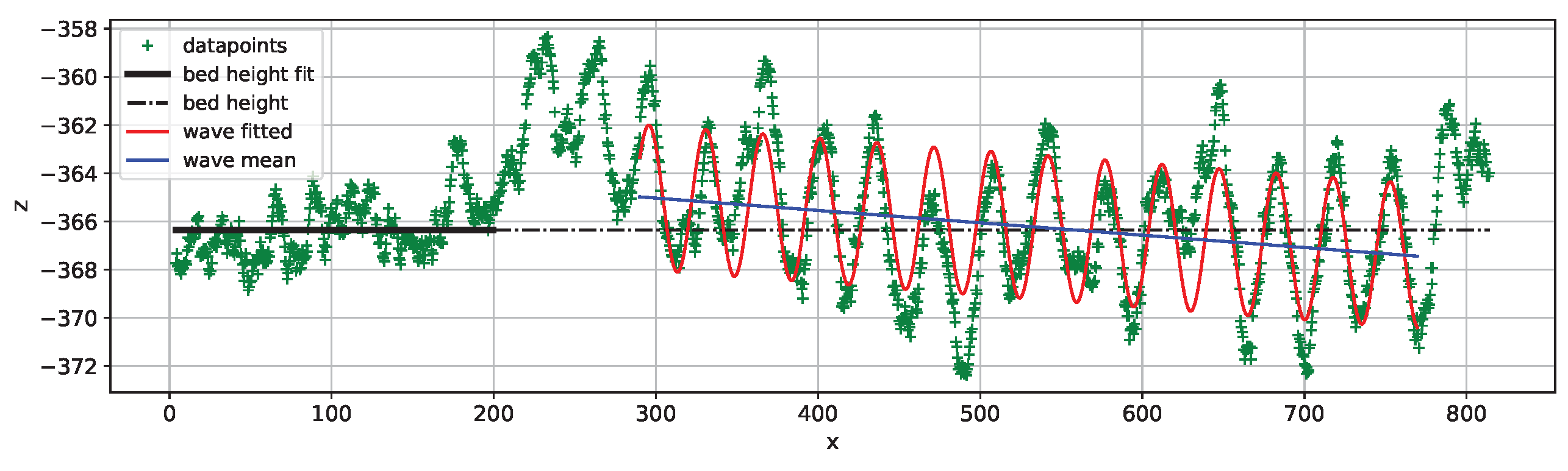
4. Data Analysis Methods
Processes of Curve Fitting and Extraction of Coefficients
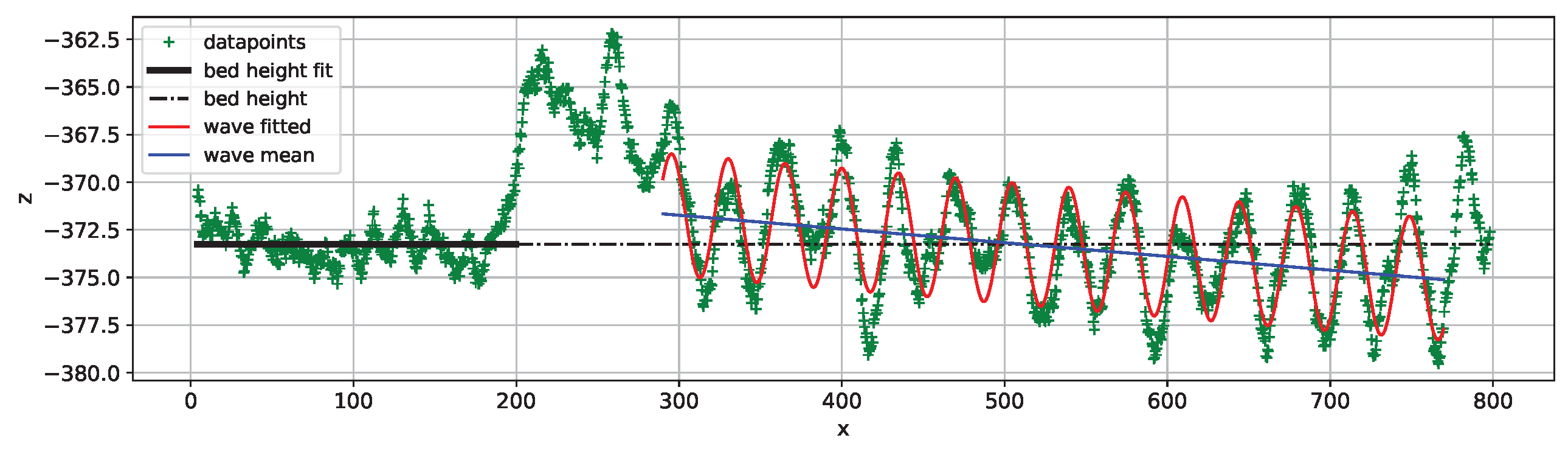
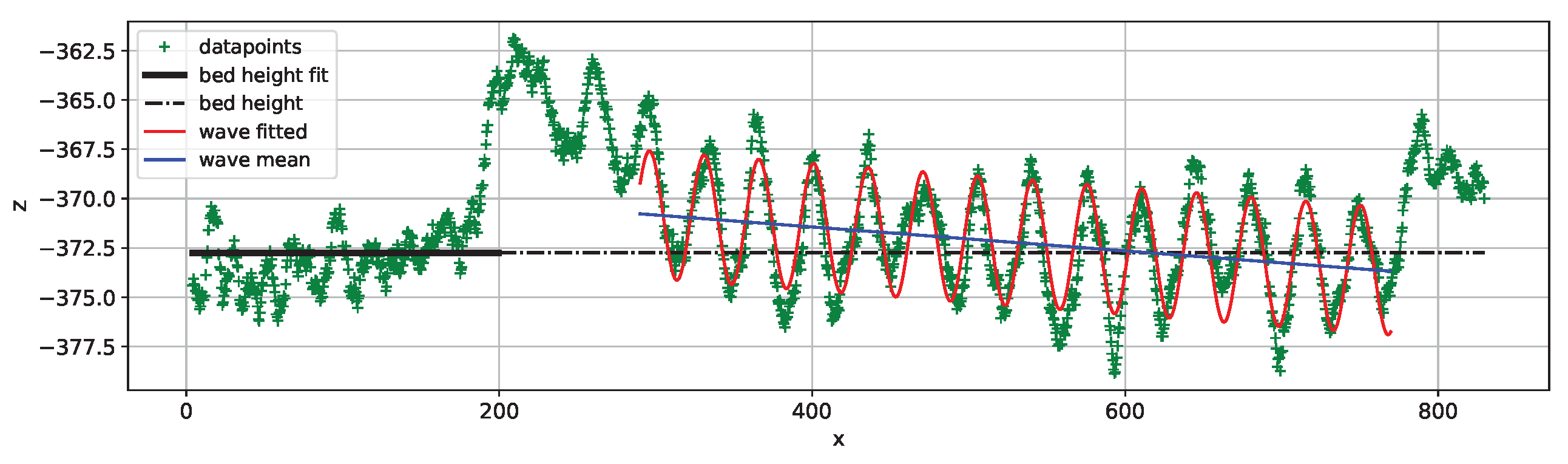
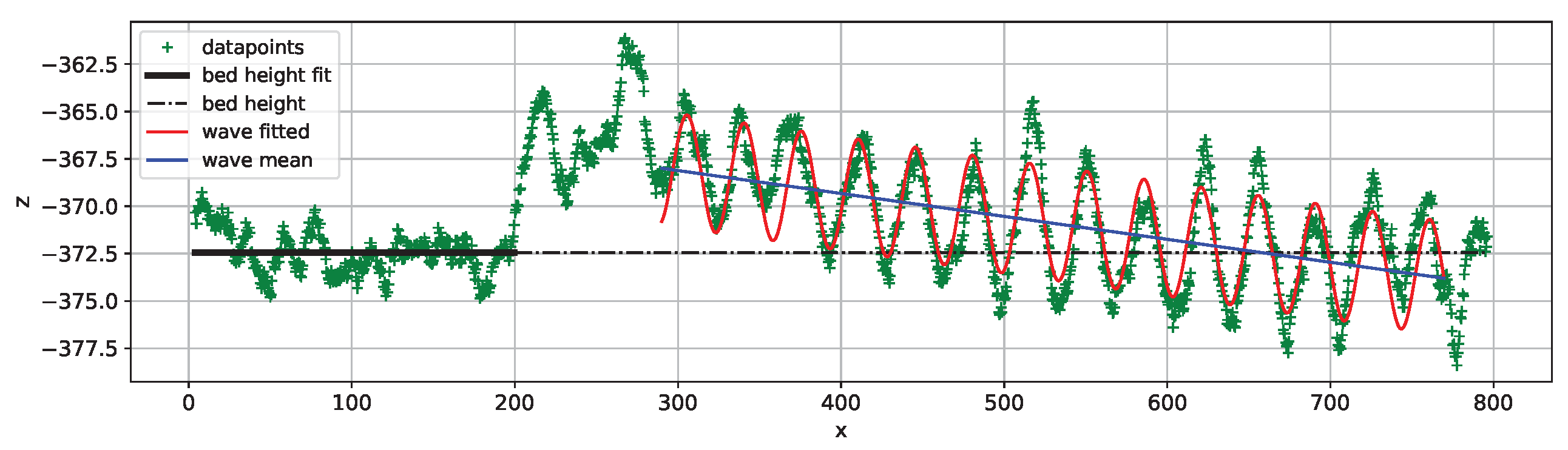
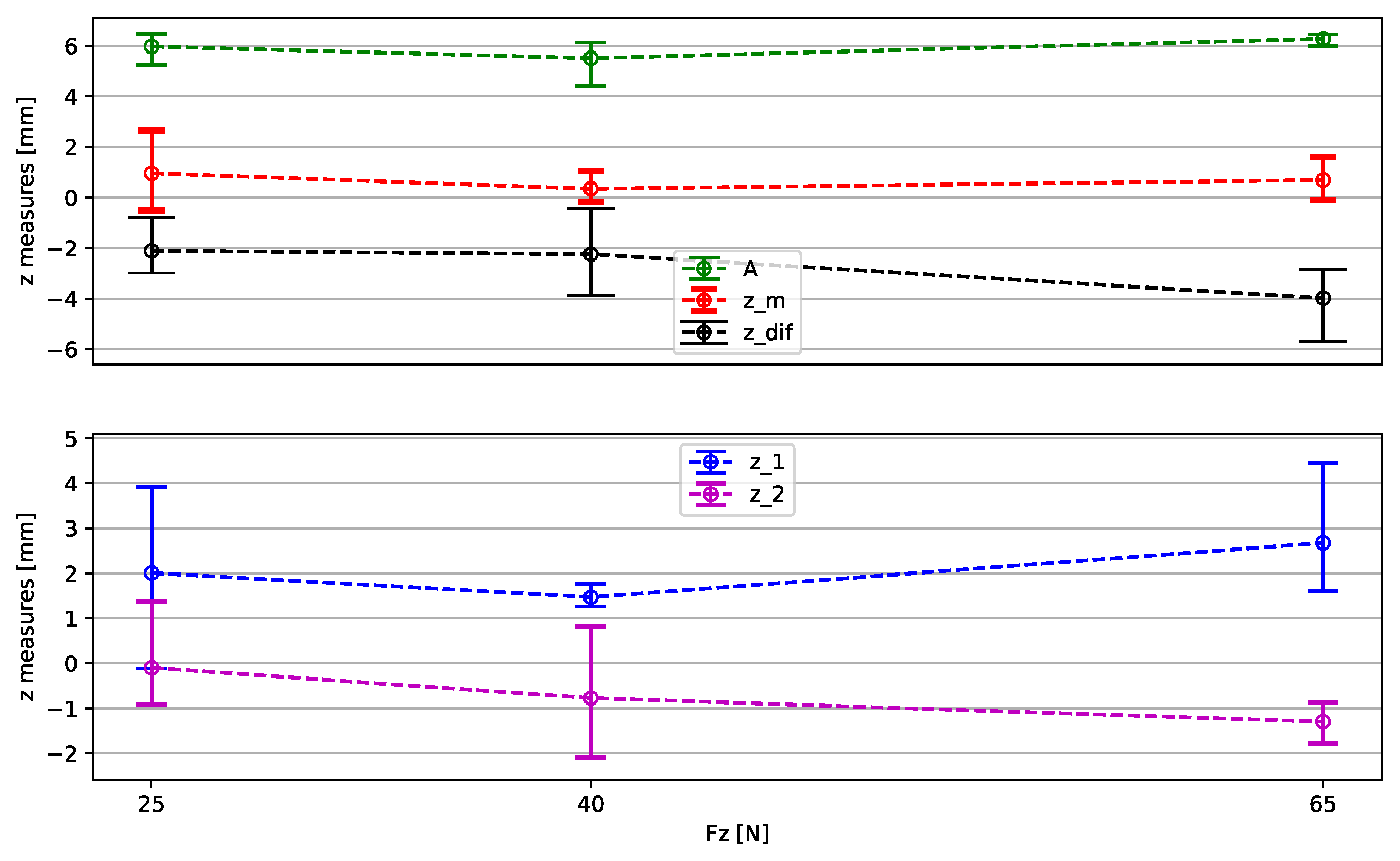
5. Data Analysis and Results
5.1. Considerations About Each Dataset
5.2. Discussion About Each Parameter
6. Conclusions
Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McKay, D.S.; Heiken, G.; Basu, A.; Blanford, G.; Simon, S.; Reedy, R.; French, B.M.; Papike, J. The lunar regolith. In Lunar Sourcebook: A User’s Guide to the Moon; Heiken, G.H., Vaniman, D.T., French, B.M., Eds.; Cambridge University Press: Cambridge, UK, 1991; pp. 285–356. [Google Scholar]
- Shkuratov, Y.G.; Bondarenko, N.V. Regolith layer thickness mapping of the Moon by radar and optical data. Icarus 2001, 149, 329–338. [Google Scholar] [CrossRef]
- Wilcox, B.B.; Robinson, M.S.; Thomas, P.C.; Hawke, B.R. Constraints on the depth and variability of the lunar regolith. Meteorit. Planet. Sci. 2005, 40, 695–710. [Google Scholar] [CrossRef]
- Kerr, R.A. Mars Rover Trapped in Sand, But What Can End a Mission? Science 2009, 324, 998. [Google Scholar] [CrossRef]
- Wirkus, M.; Hinck, S.; Backe, C.; Babel, J.; Riedel, V.; Reichert, N.; Kolesnikov, A.; Stark, T.; Hilljegerdes, J.; Küçüker, H.D.; et al. Comparative study of soil interaction and driving characteristics of different agricultural and space robots in an agricultural environment. J. Field Robot. 2024, 41, 2009–2042. [Google Scholar] [CrossRef]
- Chen, L.; Zou, M.; Chen, Z.; Liu, Y.; Xie, H.; Qi, Y.; He, L. The applications of soil bin test facilities to terramechanics: A review. Rend. Lincei. Sci. Fis. Nat. 2024, 35, 683–703. [Google Scholar] [CrossRef]
- Stitch, M.L.; Woodbury, E.J.; Morse, J.H. Optical Ranging System Uses Laser Transmitter. Electronics 1961, 34, 51–53. [Google Scholar]
- Saku, Y.; Ishigami, G. Slip Estimation Using Machine Learning of Wheel Trace Patterns for Mobile Robot on Loose Soil. In Proceedings of the 15th European-African Regional Conference of the International Society of Terrain Vehicle Systems (ISTVS), Prague, Czech Republic, 8–11 September 2019. [Google Scholar]
- Reina, G.; Ishigami, G.; Nagatani, K.; Yoshida, K. Vision-based estimation of slip angle for mobile robots and planetary rovers. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 486–491. [Google Scholar] [CrossRef]
- Gao, H.; Xia, K.; Ding, L.; Deng, Z.; Liu, Z.; Liu, G. Optimized control for longitudinal slip ratio with reduced energy consumption. Acta Astronaut. 2015, 115, 1–17. [Google Scholar] [CrossRef]
- Ding, C.; Chang, Y.; Su, Y.; Wang, J.; Xie, M. Rover-Mounted Radar Observation of Discrete Layers Within the Top 4 Meters of Regolith at the Chang’E-3 Landing Site, the Moon. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Allan, M.; Wong, U.Y.; Furlong, P.M.; Rogg, A.; McMichael, S.T.; Welsh, T.M.; Chen, I.; Peters, S.C.; Gerkey, B.P.; Quigley, M.; et al. Planetary Rover Simulation for Lunar Exploration Missions. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–19. [Google Scholar]
- Bingham, L.; Kincaid, J.; Weno, B.; Davis, N.; Paddock, E.; Foreman, C. Digital Lunar Exploration Sites Unreal Simulation Tool (DUST). In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–12. [Google Scholar] [CrossRef]
- Crues, E.Z.; Lawrence, S.J.; Bielski, P.; Jacobs, A.B.; Schlueter, J.; Jagge, A.; Foreman, C.; Raymond, C.; Davis, N. Digital Lunar Exploration Sites (DLES). In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–13. [Google Scholar]
- Kamohara, J.; Ares, V.E.; Hurrell, J.; Takehana, K.; Richard, A.; Santra, S.; Uno, K.; Rohmer, E.; Yoshida, K. Modelling of Terrain Deformation by a Grouser Wheel for Lunar Rover Simulation. In Proceedings of the 21st International and 12th Asia-Pacific Regional Conference of the ISTVS, Yokohama, Japan, 28–31 October 2024. [Google Scholar]
- Pieczyński, D.; Ptak, B.; Kraft, M.; Drapikowski, P. LunarSim: Lunar Rover Simulator Focused on High Visual Fidelity and ROS 2 Integration for Advanced Computer Vision Algorithm Development. Appl. Sci. 2023, 13, 12401. [Google Scholar] [CrossRef]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An open source multi-physics dynamics engine. In Proceedings of the High Performance Computing in Science and Engineering: Second International Conference, HPCSE 2015, Soláň, Czech Republic, 25–28 May 2015; Revised Selected Papers 2. Springer: Berlin/Heidelberg, Germany, 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Higa, S.; Nagaoka, K.; Yoshida, K. Reaction force/torque sensing wheel system for in-situ monitoring on loose soil. In Proceedings of the 19th International and 14th European-African Regional Conference of the International Society for Terrain-Vehicle Systems (ISTVS), Budapest, Hungary, 25–27 September 2017. [Google Scholar]
- Takehana, K.; Kizaki, S.; Uno, K.; Tanaka, T.; Suda, G.; Yoshida, K. Evaluation and Comparison of Driving Performance of Lunar Exploration Rover Wheel in Different Soils. In Proceedings of the 16th European-African Regional Conference of the ISTVS, Lublin, Poland, 11–13 October 2023. [Google Scholar]
- Ozaki, S.; Ishigami, G.; Otsuki, M.; Miyamoto, H.; Wada, K.; Watanabe, Y.; Nishino, T.; Kojima, H.; Soda, K.; Nakao, Y.; et al. Granular flow experiment using artificial gravity generator at International Space Station. NPJ Microgravity 2023, 9, 61. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.; Houston, W.; Carrier III, W.; Costes, N. Apollo Soil Mechanics Experiment S-200; Final Report. Technical Report 15, Issue 7; Space Sciences Laboratory: Berkeley, CA, USA, 1974; NASA Contract NAS 9–11266. [Google Scholar]
- Fa, W. Bulk Density of the Lunar Regolith at the Chang’E-3 Landing Site as Estimated From Lunar Penetrating Radar. Earth Space Sci. 2020, 7, e2019EA000801. [Google Scholar] [CrossRef]
- Almaeeni, S.; Els, S.; Almarzooqi, H. To a Dusty Moon: Rashid’s Mission to Observe Lunar Surface Processes Close-Up. In Proceedings of the 52nd Lunar and Planetary Science Conference, The Woodlands, TX, USA, 15–19 March 2021; p. 1906. Available online: https://www.hou.usra.edu/meetings/lpsc2021/pdf/1906.pdf (accessed on 19 September 2024).






| Quantity | Toyoura Sand [20] | Regolith Simulant (<425 μm) [20] | Lunar Samples [21] |
|---|---|---|---|
| Particle size 50% (μm) | 262 | 139 | 42–128 |
| Particle size max (μm) | 675 | 675 | - |
| Bulk density (g/cm3) | 1.378–1.631 | 1.497–1.908 | 0.85–2.25 [22] |
| Particle density (g/cm3) | 2.661 | 2.899 | - |
| Angle of repose (deg) | 36.0 | - | - |
| Friction angle (deg) | 31.0–40.4 | 33.9–46.7 | 35–1.5 |
| Cohesion (kPa) | 0.6–2.8 | 0.3–3.2 | 0.03–2.1 |
| Object | Left Height (mm) | Deviation (mm) | Right Height (mm) | Deviation (mm) |
|---|---|---|---|---|
| Big, sand | 27.37 | −2.63 | 30.96 | 0.96 |
| Small, sand | 6.80 | −3.20 | 9.75 | −0.25 |
| Big, green | 26.32 | −3.68 | 28.98 | −1.02 |
| Small, green | 6.71 | −3.29 | 5.84 | −4.16 |
| Big, white | 30.25 | 0.25 | 28.88 | −1.12 |
| Small, white | 0.18 | −9.82 | 1.00 | −11.00 |
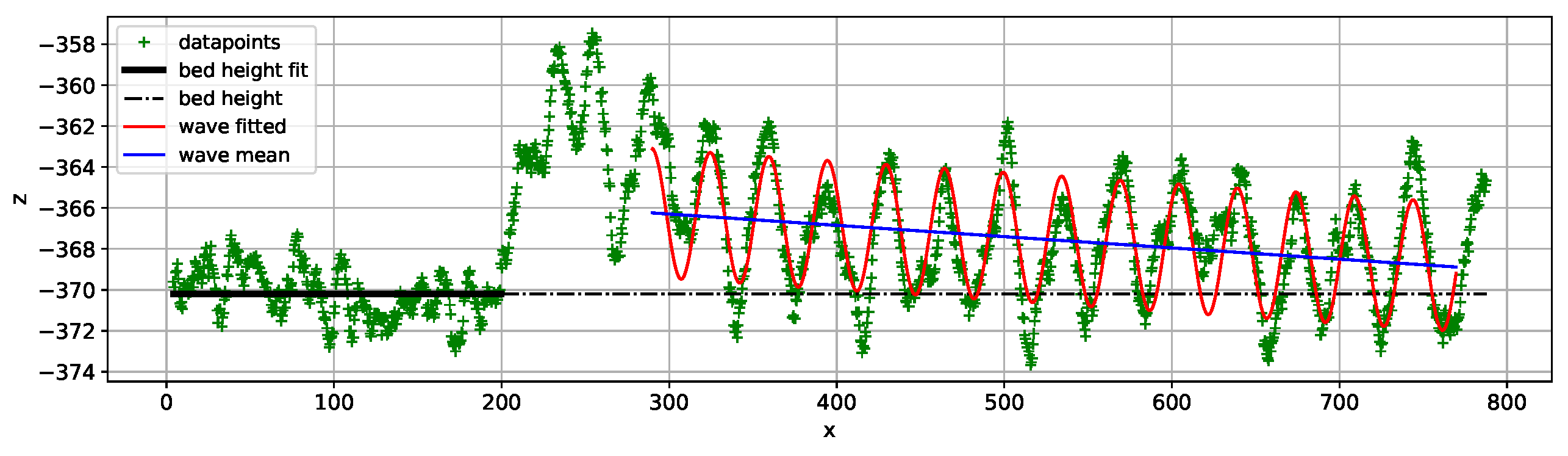
| Sample | Bed Height (mm) | Mean Square Error (mm) |
|---|---|---|
| 25N 1 | −369.04 | 2.43 |
| 25N 2 | −370.19 | 1.45 |
| 25N 3 | −368.63 | 4.60 |
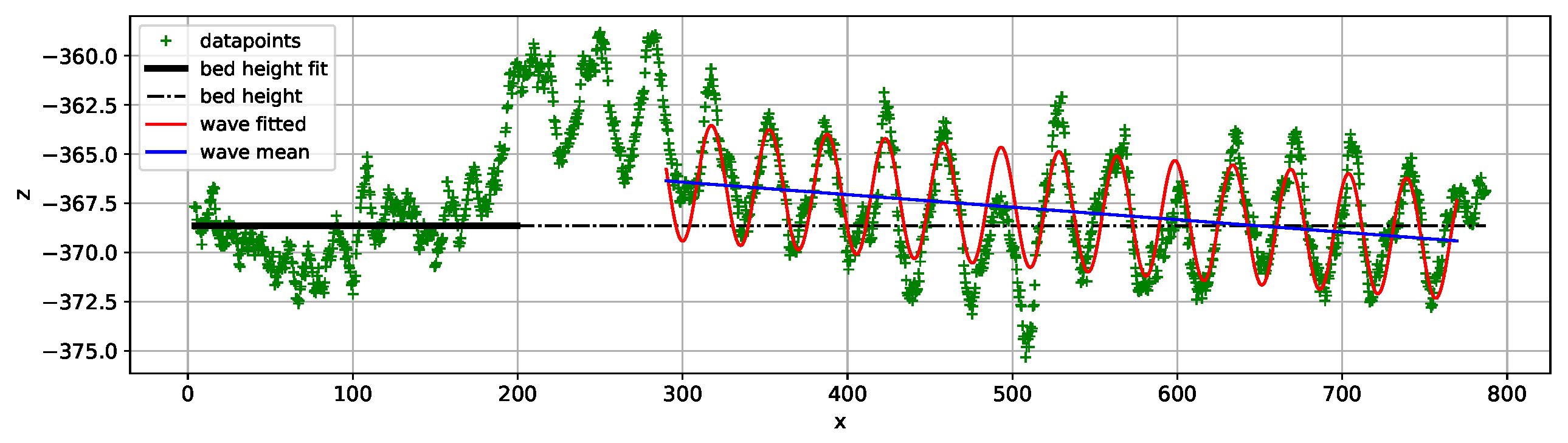
| 40N 1 | −366.51 | 1.85 |
| 40N 2 | −370.54 | 1.40 |
| 40N 3 | −366.36 | 1.44 |
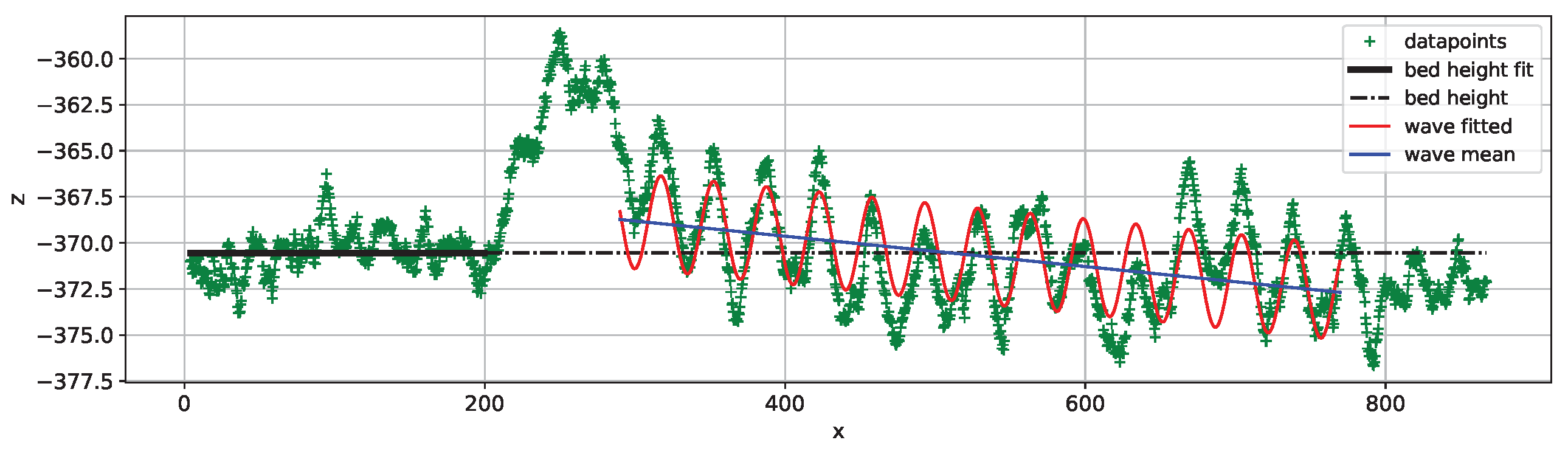
| 65N 1 | −373.26 | 1.02 |
| 65N 2 | −372.74 | 4.97 |
| 65N 3 | −372.45 | 1.45 |
| Intercept | Incline | Amplitude A | Phase | Period T | |
|---|---|---|---|---|---|
| Lower bound | −380 | −0.01220 | 5.1 | −1.5 | 34.86 |
| Upper bound | −355 | −0.00093 | 6.5 | 34 | 35.18 |
| Sample | (mm) | (mm/mm) | A (mm) | (mm) | T (mm) |
|---|---|---|---|---|---|
| 25N 1 | −368.67 | −0.00169 | 6.458 | 21.36 | 35.03 |
| 25N 2 | −364.64 | −0.00551 | 6.272 | −1.47 | 34.95 |
| 25N 3 | −364.52 | −0.00636 | 5.998 | 8.33 | 35.13 |
| 40N 1 | −364.97 | −0.00094 | 6.124 | 28.00 | 35.13 |
| 40N 2 | −366.34 | −0.00824 | 5.170 | 8.78 | 35.16 |
| 40N 3 | −363.49 | −0.00513 | 6.005 | 33.36 | 35.17 |
| 65N 1 | −369.57 | −0.00720 | 6.372 | 30.84 | 34.88 |
| 65N 2 | −369.01 | −0.00607 | 6.452 | 30.86 | 34.96 |
| 65N 3 | −364.49 | −0.01210 | 5.991 | 20.70 | 35.02 |
| Sample | Mean Square Error (mm) | Mean Error (mm) | Maximum Error (mm) |
|---|---|---|---|
| 25N 1 | 2.86 | 1.40 | 4.16 |
| 25N 2 | 2.20 | 1.20 | 4.38 |
| 25N 3 | 2.14 | 1.16 | 4.91 |
| 40N 1 | 1.64 | 1.04 | 3.63 |
| 40N 2 | 3.32 | 1.53 | 5.02 |
| 40N 3 | 2.65 | 1.30 | 4.72 |
| 65N 1 | 1.81 | 1.12 | 3.41 |
| 65N 2 | 1.60 | 1.04 | 3.61 |
| 65N 3 | 1.90 | 1.09 | 4.67 |
| Sample | A (mm) | (mm) | T (mm) | (mm) | (mm) |
|---|---|---|---|---|---|
| 25N 1 | 6.458 | 21.36 | 35.03 | −0.11 | −0.91 |
| 25N 2 | 6.272 | −1.47 | 34.95 | 3.95 | 1.36 |
| 25N 3 | 5.998 | 8.33 | 35.13 | 2.27 | −0.72 |
| 40N 1 | 6.124 | 28.00 | 35.13 | 1.26 | 0.82 |
| 40N 2 | 5.170 | 8.78 | 35.16 | 1.81 | −2.06 |
| 40N 3 | 6.005 | 33.36 | 35.17 | 1.38 | −1.04 |
| 65N 1 | 6.372 | 30.84 | 34.88 | 1.60 | −1.78 |
| 65N 2 | 6.452 | 30.86 | 34.96 | 1.97 | −0.88 |
| 65N 3 | 5.991 | 20.70 | 35.02 | 4.45 | −1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takehana, K.; Ares, V.E.; Santra, S.; Uno, K.; Rohmer, E.; Yoshida, K. Rutting Caused by Grouser Wheel of Planetary Rover in Single-Wheel Testbed: LiDAR Topographic Scanning and Analysis. Aerospace 2025, 12, 71. https://doi.org/10.3390/aerospace12010071
Takehana K, Ares VE, Santra S, Uno K, Rohmer E, Yoshida K. Rutting Caused by Grouser Wheel of Planetary Rover in Single-Wheel Testbed: LiDAR Topographic Scanning and Analysis. Aerospace. 2025; 12(1):71. https://doi.org/10.3390/aerospace12010071
Chicago/Turabian StyleTakehana, Keisuke, Vinicius Emanoel Ares, Shreya Santra, Kentaro Uno, Eric Rohmer, and Kazuya Yoshida. 2025. "Rutting Caused by Grouser Wheel of Planetary Rover in Single-Wheel Testbed: LiDAR Topographic Scanning and Analysis" Aerospace 12, no. 1: 71. https://doi.org/10.3390/aerospace12010071
APA StyleTakehana, K., Ares, V. E., Santra, S., Uno, K., Rohmer, E., & Yoshida, K. (2025). Rutting Caused by Grouser Wheel of Planetary Rover in Single-Wheel Testbed: LiDAR Topographic Scanning and Analysis. Aerospace, 12(1), 71. https://doi.org/10.3390/aerospace12010071


_Zhu.png)



