A Sample Average Approximation Approach for Aircraft Product Configuration Optimization with Customer Order Uncertainty

Abstract

Commercial aircraft manufacturers often face order uncertainty in particular situations, such as quantity or demand change, or lack of confirmed customer options. As a countermeasure, aircraft manufacturers can adopt a two-stage strategy to produce batch General-Configuration Aircraft (GCA), so as to maintain continuous aircraft production. Nevertheless, additional work on disassembling and re-assembling must be performed, to convert the GCA into specific configurations specified later by the customer. Thus, an appropriate GCA that leads to a minimal overall manufacturing workload is essential. In this paper, a Sample Average Approximation (SAA) model for GCA optimization is proposed, to obtain a robust GCA whose prediction results can help minimize the total production time. Compared with the empirical method, the proposed SAA approach significantly accelerates the production operation and is adaptive to various scenarios. The robustness of the SAA approach was evaluated, and the results prove that the general configuration obtained by the SAA approach has sustainable variances in the manufacturing workload.

1. Introduction

Recent global economic and societal progress has fostered rapid growth in the aircraft manufacturing industry [1]. Developing commercial aircraft intended for long operation cycles is a complex and time-consuming process [2]. Commercial aircraft consist of multiple functional systems, including structure, propulsion, hydraulics, flight control, fuel, avionics, and environmental management. Furthermore, each system comprises multiple subsystems, and there are numerous physical, functional, and other interfaces within and between the systems.

The production of commercial aircraft, consisting of parts manufacturing and aircraft assembly, constitutes a complex, long-cycle process that is perpetually challenged by demand fluctuations and order uncertainties. These persistent operational dilemmas have led to the development of a dual-track coordination process, as illustrated in Figure 1. In the order-driven track, manufacturers generate a customized Bill of Materials (BOM) based on validated customer configurations, to execute production. Concurrently, aircraft manufacturers can adopt a two-stage strategy. The forecast-guided track enables engineering teams to establish pre-production baselines through General-Configuration Aircraft (GCA) predefined by market pattern mining, documented in default BOM protocols. This pre-configured inventory subsequently incorporates structural or interior decoration modifications after customer orders are confirmed.

General-Configuration Aircraft (GCA) is a production concept that offers aircraft with a specific or intermediate configuration and incomplete functions. In an ideal scenario, where the demands of customers can be clearly understood, a GCA-derived product should be the greatest common divisor of all potential customers’ needs. However, in practice, constraints such as regulations, safety, test flights, production capacity and efficiency, costs, and technology must be considered. A GCA often needs to perform outfield flights and partial production flight tests to meet subsequent modification requirements and deliveries to other places. Alternatively, to cope with uncertainty related to customer orders, manufacturers usually produce GCA, having equipment sufficient for safe operation but without cabin accessories, most of the associated equipment, and electronic devices.

Based on the above discussions, a GCA must undergo additional dismantling and re-assembly to ultimately transform it into an aircraft meeting all the customer’s specifications. Considering the entire process and workload distribution, it is expected that the major work will be completed in the main production phase, while less work will be done in the dismantling and re-assembly phase, to reduce the total manufacturing labor cost. Therefore, it is particularly important to determine the optimal GCA and continuously optimize it to minimize the overall manufacturing workload and cost.

To optimize the production time and costs, an appropriate general configuration that leads to a minimal overall workload—including assembly, disassembly, and re-assembly—is critical. However, GCA are currently empirically determined. And it is difficult to consider factors—e.g., customer adaptability, costs at each stage, disassembly sequence, subsequent changes globally, etc.—globally. It is critical to develop an optimization approach to determining the optimal GCA, which can help overcome the problem of uncertain orders and reduce the overall production costs.

The remainder of this paper is organized as follows. Section 2 reviews the related literature. The stochastic GCA optimization problem is formulated and the SAA approach is developed in Section 3. The results of the aircraft manufacturing industry application are presented in Section 4. Finally, Section 5 provides concluding remarks and some research perspectives.

2. Literature Review

The following section reviews the related literature about the article. Section 2.1 reviews research on the uncertainty management approach. Section 2.2 reviews production configuration in aircraft manufacturing. Section 2.3 is a summary of the innovative contributions of this article.

2.1. Uncertainty Management Approach

The uncertainty of customer orders poses a huge challenge to manufacturing companies. Studying uncertainty management in the production field creates possibilities for coping with related issues and provides a path for improving enterprise resilience and creating higher profits [3]. Orders are the link between sales and production and can influence other logistics objectives, such as the utilization of production. For Make-To-Order (MTO) companies, delivery time and delivery reliability are key evaluation criteria for customers [4]. Therefore, a model-based procedure that uses a diagram with early available information, such as the offer requests, in the planning process to determine delivery time is favorable for addressing the challenge of confirming binding delivery times with customers in the early stages of the ordering process [4]. To maintain the stable and robust production of Multistate Manufacturing Systems (MMS) under various kinds of disruptions, a comprehensive production-and-maintenance scheduling method oriented towards overall interruptions resilience was proposed, and a performance loss-based resilience measurement considering operational uncertainty was developed, to enhance adaptability to changes in production demand [5]. In an environment of uncertain market demand and spot prices, retailers can order products before demand updates by signing wholesale price contracts (known as contract orders), or they can order products from manufacturers in the spot market after demand updates (known as spot orders). A dynamic decision model was constructed to derive the optimal equilibrium solution for production and order quantities under the contract order strategy and spot order strategy, to achieve the maximum profit in uncertain environments [6].

Supply chain disruption is another type of uncertainty faced by manufacturing enterprises. To enhance supply chain resilience and effectively manage disturbances, implementing flexible/hybrid manufacturing systems is a feasible strategy that uses dedicated machinery to meet regular demand and Flexible Manufacturing Systems (FMSs) to respond to demand surges. A scenario-based method was used to model demand uncertainty, enabling instant and adaptive decision making using the cost-effectiveness of standard production and the responsiveness of FMSs [7]. Hu et al. [8] proposed a two-stage stochastic programming model to minimize the cost of business relations establishment with upstreaming supply enterprises, as well as production costs, inventory costs, transportation costs, and penalty costs for unfulfilled demands. They designed an improved Benders decomposition algorithm by incorporating a heuristic searching mechanism to enhance its problem-solving efficiency.

A hybrid manufacturing system that uses raw materials and returns components for further production is easily affected by inventory, market demand, and return uncertainties. The Kalman-based estimation control method provides a path to dealing with uncertainties by estimating inventory levels and demands and forecasting return components, allowing cost estimation over a long period; it also allows for determining production and disposal policies that adapt to market changes and possible uncertainties [9]. Wu [10] studied the production load problem of a global clothing manufacturing company facing uncertainties in demand and import quotas; Wu [10] constructed a two-stage stochastic programming model and used two-stage production planning to rapidly respond to constantly changing market information while minimizing total production costs. Fuqiang zhang and Ding [11] studied the impact mechanism of the uncertain demands of enterprises on the profit decision making of the Warehouse Product Service System (WPSS) based on intelligent warehouses and “centralized procurement + shared storage + JIT distribution” services. Lin [12] studied the batch size issue in an economic production quantity model that considered the existence of backlogs and incomplete rework processes, to address uncertain demands, determine the optimal production batch size and delayed delivery level, and minimize the long-term expected costs of the system.

2.2. Production Configuration in Aircraft Manufacturing

The product configuration process refers to all activities that lead to a custom product from a set of predefined components, respecting a set of well-defined constraints that restrict item selection and combination [13,14]. Once the customer’s order is confirmed, the product configuration process involves selecting common components/modules, which are usually combined into options for individualized products. The selection of aircraft options includes model introduction (aerodynamic shape, fuel consumption, weight, etc.) and the selection of airborne products. The product option selection usually considers certain constraint indicators (e.g., reliability and economy) to meet and maximize the aircraft performance through equipment selection. The option selection’s result is a list of items containing aircraft configuration information [15]. Since customers’ aircraft orders are highly uncertain, enormous challenges are presented. The focus of some previous studies was on predicting potential customer orders, e.g., to satisfy customers’ diversified and personalized demands and optimize the product configuration design scheme under the constraints of the product configuration design cycle. Yang et al. [16] proposed a customer demand evaluation and decision-making method based on network planning technology.

A series of studies was conducted to address the customer-oriented aircraft configuration process. For example, Airbus elaborated a service that offers customers the flexibility to choose each option at the last possible moment, depending on its lead, referred to as Just-In-Time Specification [17]. Hochdörffer et al. [18] introduced a decision support model that integrates product configuration and production supply network redesign, customer order allocation, and local rescheduling, seeking a holistic approach to designing, planning, and controlling production networks. Most studies on product configuration processes have been conducted in deterministic environments, assuming that customer orders are pre-determined [19,20], and scenarios in which customer orders are uncertain have not been fully considered in the existing literature. However, some studies have contributed to the field of general product configuration, taking uncertainty into account. Buergin et al. [21] introduced a robust optimization model developed on the basis of potential customer-specific order configurations to provide enough flexibility to handle the maximum work overload caused by potential order configurations at specific locations, which guarantees a robust assignment of orders, avoiding undesirable delays and additional costs. Considering uncertainties (e.g., component supplies and lead-time uncertainty) in the product configuration setting, Yang et al. [22] proposed a new stochastic decision model using a two-stage stochastic programming approach to handle the uncertainty in the component replenishment lead time. Song et al. [23,24] developed an uncertain product configuration model based on uncertain lead time and time-sensitive demand using uncertain programming, and they proposed a new uncertain decision model to anticipate product configuration using redundancy and standardization in an uncertain environment.

2.3. Contributions of This Research

A commercial aircraft, which consist of millions of components [25], is constructed by implementing various customer requirements and by complex product composition, and is intended to have a long life cycle. This paper thoroughly elaborates on current aspects of aircraft production configuration optimization with respect to the existing research, providing multiple invaluable contributions.

Firstly, this paper analyzes situations where an aircraft Original Equipment Manufacturer (OEM) encounters uncertainty in customer flow and order confirmation, and it provides details on the concept of GCA, which is applicable in resolving the issue of general product configuration in the field of commercial aircraft manufacturing.

Secondly, the SAA approach is developed for GCA optimization given uncertain customer order conditions. By developing the SAA approach, a robust general aircraft configuration can be obtained, to reduce the overall production time costs when issuing a specific aircraft configuration. A quantitative analysis is conducted on the robustness of the proposed approach.

Finally, the effectiveness of the proposed SAA approach is verified, based on the real production data of a certain type of commercial aircraft. By comparing the SAA approach with the empirical method, it is shown that the SAA GCA optimization approach can significantly reduce production time.

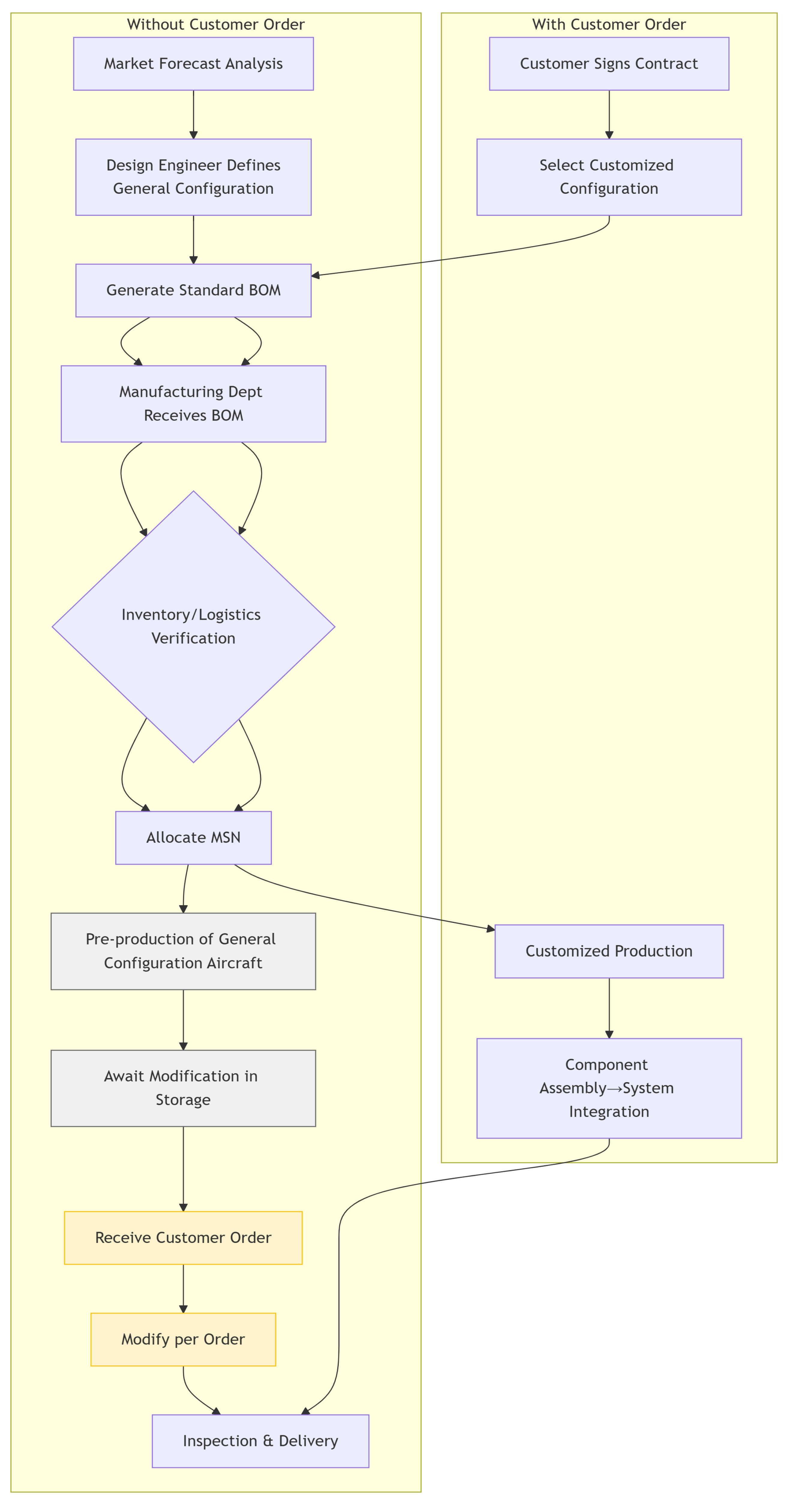
3. General-Configuration Aircraft Optimization Approach

3.1. Problem Definition

Commercial aircraft are usually highly customized, due to specific airlines’ business strategies, geographical locations, passenger preferences, and many other reasons [26,27]. Commercial aircraft products consist of a series of functional option units, and customers select options from the list of functional option units provided by the OEM, based on the customers’ needs when confirming the order. The functional option unit is a configurable product combination composed of various parts, components, modules, software, etc.

Table 1. A configurable options unit list.

Number	Identification	Description	Mandatory?
1	OPT_XX-YY-ZZ-001	normal range	No
2	OPT_XX-YY-ZZ-002	long range	No
3	OPT_XX-YY-WW-001	90 seats cabin furnishing	Yes
…	…	…	…

shows a configurable option unit list. Until the order is confirmed by a customer, the OEM cannot determine all the functional option units for a certain aircraft, so the purpose of the GCA concept is to provide a relatively optimal option selection to guide OEMs to start production ahead of schedule for customers while waiting on the order confirmation.

Figure 2 shows the schematic illustration of the study framework used in this paper. Firstly, starting from the current configurable option selection results of the aircraft, the cost composition and constraint composition in the aircraft assembly process are determined by analyzing the selected options and the workstation situation. Then, by combining various costs and constraints, a GCA optimization model that determines the optimal GCA based on the input combinations of options by minimizing the total assembly time is established. Finally, uncertain scenarios are generated by sampling historical orders, and some deterministic scenarios are combined as model inputs to obtain the optimal GCA scheme, i.e., the aircraft configuration that can adapt to different potential customers and order quantities, using the Gurobi solver. This GCA scheme can support the OEM’s production preparation. As more aircrafts are delivered, changes in historical orders and option selection results caused by customers will drive the continuous iterative optimization of the GCA.

3.2. Stochastic Optimization Model for GCA

To deal with the uncertainty related to customer orders, OEMs usually choose to produce aircraft with general configurations. The problem lies in deciding the optimal GCA to minimize the total production time (including assembly time and reworking time) of the aircraft, given uncertain orders, while considering the coupling relationships between aircraft options and workstation labor resources.

We propose a stochastic optimization model for GCA, in which orders are uncertain and are represented by random variables. The notation used for the mathematical formulation is presented in

Table 2. Notation.

Indices	Representation
i	Index of product option groups.
I	Number of configurations in the product.
$m_i$	Index of options in the option group i.
$M_i$	Number of options associated with the option group i.
$v_i$	The least number of options should be chosen for the option group i.
$D_i$	Disassemble time of options for the option group i.
$A_i$	Re-assemble time of options for the option group i.
j	Index of customers.
J	Number of customers.
${\tilde{o}}_{ji{m}_i}$	Binary random variable, equal to 1 if option $m_i$ is chosen for the option
	group i by the customer j.
$\tilde{\mathit{o}}$	Random matrix with three dimensions (customers, option groups, and
	options), a combination of orders.
k	Index of stations.
K	Number of stations in the production line.
$T_{i{m}_{i}k}$	Duration time of the configuration i performed as the option $m_i$
	at the station k.
$W_k$	Maximal duration times reserved for options of option groups
	at the station k.
$x_{i{m}_i}$	Binary variable equals 1 if the option $m_i$ is chosen for
	the option group i.

:

In the objective function, multiple criteria are integrated for the optimization of the GCA. For the sake of the model results’ perception, and due to the difficulty in estimating the weight placed on the evaluation criteria by the decision maker, only those criteria corresponding to the production time in the assembly line are considered in the following objective function:

$$\begin{array}{cc}\hfill & \underset{\mathit{x}\in X}{min}f\left(\mathit{x}\right)=C^{AS}\left(\mathit{x}\right)+{\mathbb{E}}_{\tilde{\mathit{o}}}[C^{RD}(\mathit{x},\tilde{\mathit{o}})+C^{RA}(\mathit{x},\tilde{\mathit{o}})]\hfill \end{array}$$

(1)

where $\mathit{x}$ is the vector of the binary decision variables $x_{i{m}_i}$, which describes the combination of options chosen for all option groups, and where $\tilde{\mathit{o}}$ is the random matrix of the orders’ options for all the option groups.

The assembly time is the total duration used to assemble the configuration options in a GCA, which is not relevant to uncertain customer orders:

$$\begin{array}{cc}\hfill & C^{AS}\left(\mathit{x}\right)=J\times \sum _i\sum _{m_i}{x}_{i{m}_i}\sum _k{T}_{i{m}_{i}k}\hfill \end{array}$$

(2)

The rework time of detachment is the total duration used to detach the options of general-configuration planes that are not in the customer’s order. Therefore, the detachment time is calculated based on uncertain customer orders and is defined as below:

$$\begin{array}{cc}\hfill & C^{RD}(\mathit{x},\tilde{\mathit{o}})=\sum _j\sum _i\sum _{m_i}{D}_i(1-{\tilde{o}}_{ji{m}_i})x_{i{m}_i}\hfill \end{array}$$

(3)

The rework time of re-assembly is the total duration used to re-assemble the options that are in the orders but are not in the GCA. The re-assembly time is also calculated regarding the uncertain customer orders. The re-assembly time is defined as below:

$$\begin{array}{cc}\hfill & C^{RA}(\mathit{x},\tilde{\mathit{o}})=\sum _j\sum _i\sum _{m_i}{A}_i{\tilde{o}}_{ji{m}_i}(1-x_{i{m}_i})\hfill \end{array}$$

(4)

In addition to the objective function, the stochastic optimization model for GCA also consists of constraints, which are briefly described in the following part. Each option group has to choose at least the corresponding number of options:

$$\begin{array}{cc}\hfill & \sum _{m_i}{x}_{i{m}_i}\ge v_i,1\le i\le I\hfill \end{array}$$

(5)

The coupling relationships between the options of the option groups are divided into three types of constraints: assembly constraints, supplier constraints, and customer-oriented constraints. The assembly constraints originate from the assembly order of the options or option groups. Supplier constraints mainly refer to preferences toward options from the same supplier. The insufficient supply capacity of a supplier is also considered a supplier constraint. Customer-oriented constraints refer to factors such as product characteristics, customer preferences, and adaptability. The above three types of constraints are summarized and represented by two forbidden sets, an option coupling set $F^O$, and an option group coupling set $F^G$. Correspondingly, coupling constraints are described as follows:

$$\begin{array}{cc}\hfill & x_{i{m}_i}+x_{j{m}_j}\le 1,\forall (i,m_i,j,m_j)\in F^O\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \sum _{m_i}{x}_{i{m}_i}+\sum _{m_j}{x}_{j{m}_j}\le 1,\forall (i,j)\in F^G\hfill \end{array}$$

(7)

The Aircraft Moving Assembly Line (AMAL) is a new production model that replaces the traditional fixed assembly method in the aircraft industry. There are multiple work stations in the AMAL. The particular choice of option groups is assembled in one or several work stations. Considering the cycle time of the AMAL, the workforce of each station is limited. The workforce constraints in each station can be described as follows:

$$\begin{array}{cc}\hfill & \sum _i\sum _{m_i}{T}_{i{m}_{i}k}{x}_{i{m}_i}\le C_k,1\le k\le K\hfill \end{array}$$

(8)

Moreover, decision variables that represent the option choices should have binary values:

$$\begin{array}{cc}\hfill & x_{i{m}_i}\in \{0,1\},1\le i\le I,1\le m_i\le M_i\hfill \end{array}$$

(9)

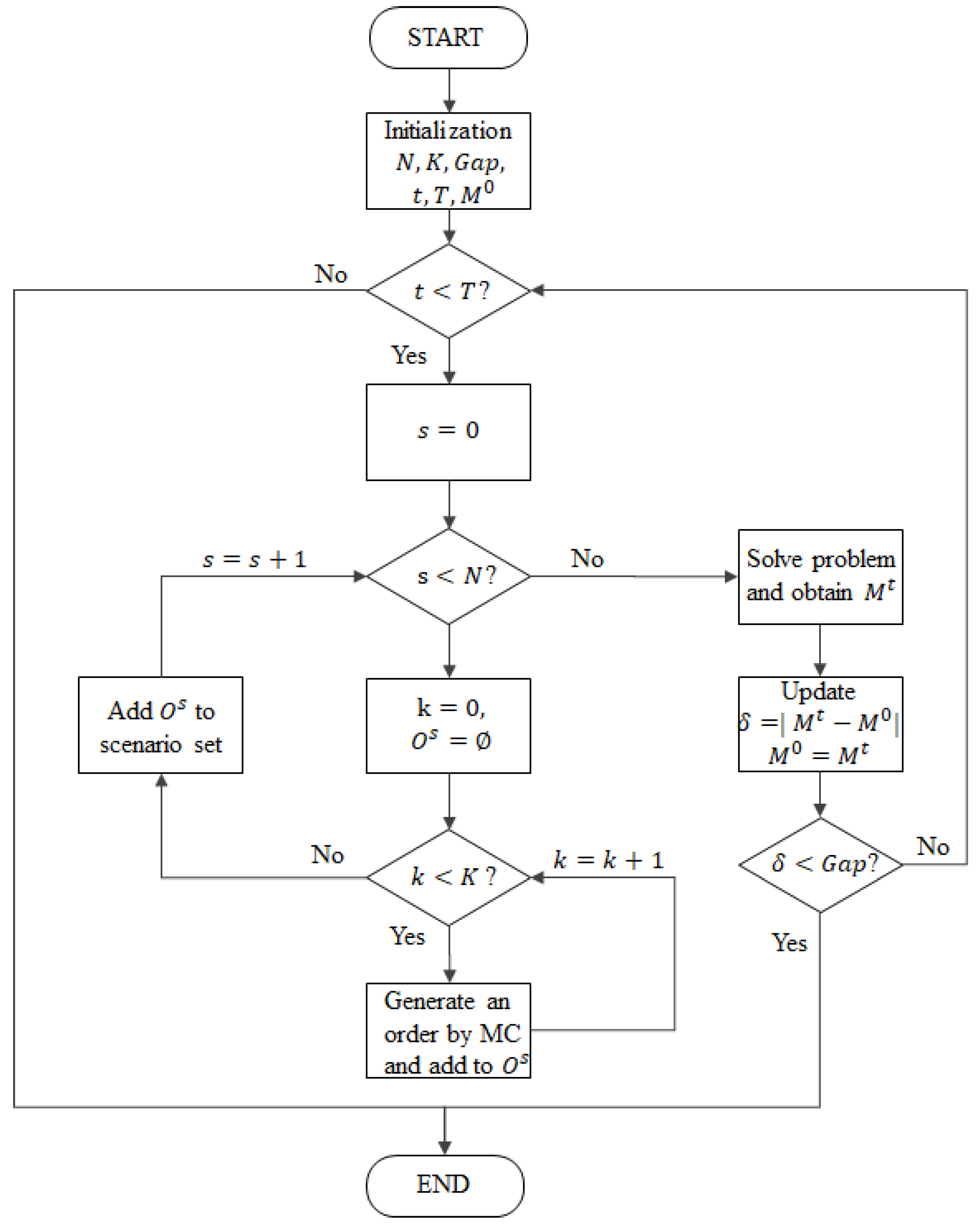
3.3. A Sample Average Approximate Approach

Analytical methods require the use of an assumed Probability Distribution Function (PDF) of stochastic variables for the conversion from stochastic to deterministic variables.

Some researchers have assumed that random variables follow known PDFs such as normal distribution and Weibull distribution. These previously assumed PDFs are overly dependent on the subjective judgment of researchers, and errors between the assumed and actual PDFs result in inaccurate solutions.

It is difficult to solve the stochastic optimization model for GCA using analytical methods. On the one hand, the number of random variables is too large to characterize. On the other hand, the distribution of the high-dimension random binary variable cannot easily be generated from historical orders.

Alternatively, instead of assuming a PDF, simulation methods do not rely on the PDFs of stochastic variables and are entirely data-driven, making the process of solving the stochastic optimization model of GCA simpler and easier.

It is worth noticing that random variables are not included in the constraints. Therefore, chance constraints are not included, and we can use Monte Carlo (MC)-based methods to improve the approximation accuracy by using many MC samples. Thus, the objective can be approximated by the sample average function.

In other words, the SAA approach is an exterior sampling approach that repeatedly generates several scenarios and solves several related optimization problems, in which the expected value of the objective Function (1) is approximated by the sample average function:

$$\begin{array}{cc}\hfill & \underset{\mathit{x}\in X}{min}f\left(\mathit{x}\right)=C^{AS}\left(\mathit{x}\right)+{\displaystyle \frac{1}{S}}\sum _{s\in S}[C^{RD}(\mathit{x},{\mathit{o}}^s)+C^{RA}(\mathit{x},{\mathit{o}}^s)]\hfill \end{array}$$

(10)

where S is the total number of scenarios, and where ${\mathit{o}}^s$ is the realization of uncertain customer orders in the scenario s. A scenario is a possible production situation with a combination of orders from customers, including certain orders and the realization of uncertain orders.

The stochastic optimization model is then converted into a deterministic model with the objective of the average production time in all scenarios. The procedure of the approach is shown as Figure 3 and Algorithm 1:

Algorithm 1: The MC-based SAA approach.

START

1. Initialize historical data set $O^H$, sampling times N, number of orders K, converge gap $Gap$, iteration time $t=0$, initial objective $M^0=0$.

2. While $\delta <Gap$ Do

3.    Set $t=t+1$, $s=0$.

4.    For $s<N$ Do

5.       Generate scenario s, set $o^s=\varnothing$, $k=0$

6.       For $k<K$ Do

7.          Generate order k using Monte Carlo sampling in $O^H$ and add it to $o^s$. Set $k=k+1$.

8.       End for

9.       Add the scenario s with the orders $o^s$ to the objective Formula (10). Set $s=s+1$.

10.    End For

11.    Solve Problem with the updated objective Formula (10) and obtain the optimal objective $M^t$

12.    Set $Gap=M^t-M^0$, and set $M^0=M^t$.

13. End while

14. Return $M^0$

END

4. Application Analysis and Results

4.1. Application Background Description

The SAA model for the general-configuration design was applied to aircraft manufacturing. We assumed that a batch of 50 aircraft were put into production. We considered nearly 20 option groups, with a major dependency between their options and their respective impact on the workload of the workstations on the assembly line. The option groups included the decoration of aircraft (e.g., the type of the cockpit window frame decorative cover) and airborne devices (e.g., the music playback system and emergency equipment).

It was assumed that there were contracts promising delivery times for 20% of orders at the planned time. These orders were indicated as certain orders, a specially designed aircraft version for a specific customer.

The options for the remaining 80% of orders were considered uncertain. Each scenario had 50 customer orders, of which 20% were certain orders and 80% were uncertain orders.

There were seven workstations on the aircraft assembly line, each of which was responsible for different assembly tasks. Considering the balance of workstation assembly, the proportion of assembly time reserved for optional configurations within the production cycle varied accordingly. Based on the current production schedule, the proportion of the reserved time for each workstation is shown in

Table 3. Reserved time for optional configurations in different workstations.

Workstation	Reserved Time (h)
1	560
2	800
3	320
4	400
5	80
6	720
7	80

:

It is worth mentioning that a dedicated workstation is set up for reworking and modifying the produced aircraft. The assembly time in the rework workstation was considered as the reworking time in our optimization model.

4.2. Application Results

As the input for the SAA approach, the solving time limit was set to 3600 s. The number of scenarios was set to 100. The SAA approach was coded in Python 3.9.13 and the deterministic model was solved by Gurobi 11.1.2, with the optimal gap for the mixed integer programming problem set to 0.01. The experiments were performed on a computer with an Intel(R) Xeon(R) Gold 6254 CPU 3.10 Ghz RAM 128 GB.

4.2.1. Effectiveness Analysis

To evaluate the effectiveness of the SAA approach, we considered the following three strategies:

(1)

The ideal situation of applying the MTO strategy.

(2)

An empirical method in real production.

(3)

The GCA strategy obtained by the SAA approach.

The MTO strategy is the best way to organize aircraft manufacturing and assembly. However, MTO realization is not straightforward, due to the uncertainty of customer orders. An empirical method, which is a substitute used in real production now, can construct GCA by choosing the most popular options of the option groups.

According to empirical methods, option units for navigation, communication, and related functions that affect basic flight safety must be installed in the GCA, while highly customized functions of customers, such as cabin layout and interior, are not required. Taking a certain type of aircraft as an example, among the 55 option units of the 32 systems in the aircraft, functions such as cockpit door monitoring, music playback system, life raft, life jacket, etc., are not installed in the GCA. In addition, the following three types of customer options may not be installed:

(1) Option units for additional functions, such as a second set of high-frequency and satellite communication systems;

(2) Option units for cabin decoration, such as cabin layout, door curtains, carpets, seats, portable oxygen cylinders, and passenger oxygen units;

(3) Option units for cabin function, such as kitchen plug-ins, second-attendant seats, dog kennels, and a dressing room.

The GCA must ultimately meet specific customer requirements and must not be repaired before delivery (e.g., repairing holes after large openings). Therefore, determining its configuration requires consideration of the following constraints:

(1) The drawings in enclosed areas, such as the aircraft head and at the front of the production process, need to be installed in advance, such as certain cables;

(2) The mandatory customized functional structure and equipment must be easy to disassemble in the future, without causing any structural damage;

(3) Necessary structures and equipment that depend on customized option units, such as kitchens, bathrooms, passenger-announcement systems, etc., which are affected by cabin layout, must be identified.

From this, the basic configuration of the GCA can be determined, and the decision-making process is shown in Figure 4.

Figure 5 shows the production time according to the three strategies. Each pillar represents the production time of a specific strategy, and it consists of the assembly time, disassembly time, and re-assembly time. The gap between the total production time and the reworking time is marked in the figure.

Figure 5 indicates the following:

(1)

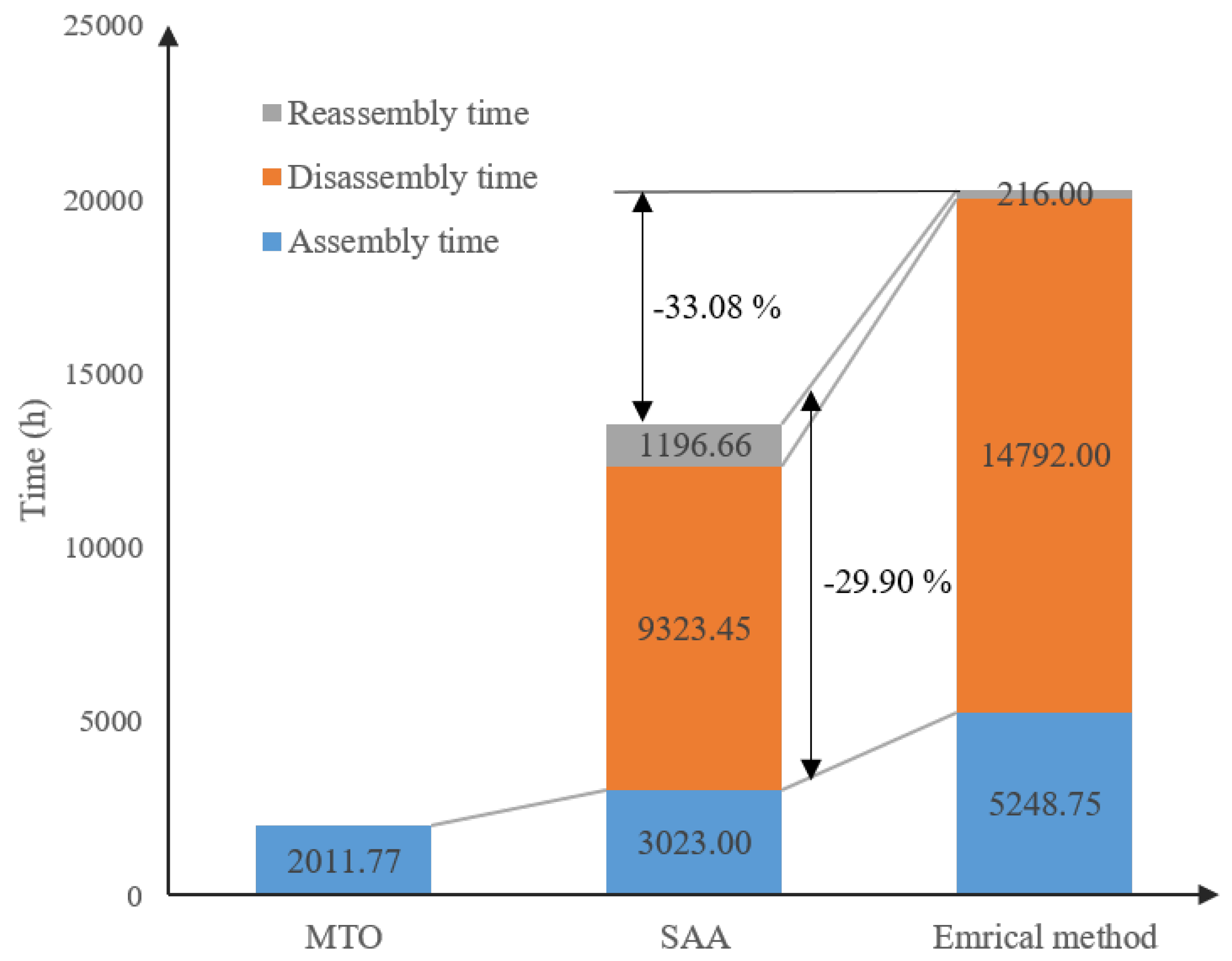
The MTO strategy had a production time of 2011.77 h with no reworking time, which was the least of the three modes. Aircraft OEMs usually hope for a proper and fixed pace of aircraft production. However, due to changes in the airline’s product business strategy, operational status, etc., the aircraft delivery time to the airline is highly uncertain. The MTO strategy is inapplicable under uncertainty conditions because the MTO production is usually idealized for each order.

(2)

When the aircraft order is highly uncertain and the MTO strategy is no longer applicable, OEMs adopt a GCA approach for aircraft production. OEMs apply the SAA approach solution with the total production time reduced by 33.08% compared to the empirical method solution for the same orders, as demonstrated in Figure 5. The reason is that the empirical method generates the configuration by individually optimizing each option group; thus, it cannot optimize the configuration from a global perspective or considering the uncertainty of orders.

(3)

Additional work has to be conducted after planning; a rework workstation is set to take pro-active actions to convert the GCA into an order-specific configuration. However, the workload in the rework station in real production often exceeds the limit. As shown in Figure 5, the total time (including disassembly and re-assembly periods) of the SAA approach was 29.90% lower than the empirical method, confirming that the SAA solution gives a more reasonable aircraft configuration.

These results indicate that the MTO strategy is optimal but inapplicable for uncertainty orders and that the GCA determined by the SAA approach is better than that obtained by the traditional empirical method.

4.2.2. Robustness and Sensitivity Analysis

Moreover, the robustness of the SAA-derived solution was quantified and the sensitivity of the model to the weight of the scenarios was also analyzed. The solution of the SAA approach was robust but not optimal for all scenarios. For comparison, the GCA optimization model was optimized for each scenario. The average processing time, including the assembly time, the disassembly time, and the re-assembly time, for the robust solution obtained by the SAA approach and the solutions obtained by certain order optimization with a single scenario are shown in

Table 4. Average times needed for the robust solution and scenario optimal solutions.

	Robust Solution	Scenario Optimal Solutions	Gap
AS (h)	3023.00	3026.22	−0.11%
RD (h)	9323.45	9315.89	0.08%
RA (h)	1196.66	1194.14	0.21%
Total (h)	13,543.11	13,536.25	0.05%
$Va{r}_D$	1136.76	1391.05	−18.28%
$Va{r}_A$	4168.04	4202.06	−0.81%

. Note that the weight of the scenarios was determined in the SAA approach, while in the model with certain order optimization with a single scenario, the weight of the exact scenario was changed to 1, with the others changed to 0. We report the average assembly time, disassembly time, re-assembly time, and total production time for all scenarios in rows AS, RD, RA, and Total. The variances of the disassembly time and re-assembly time instances are given in rows $Va{r}_D$ and $Va{r}_A$.

The following can be observed in Table 4:

(1)

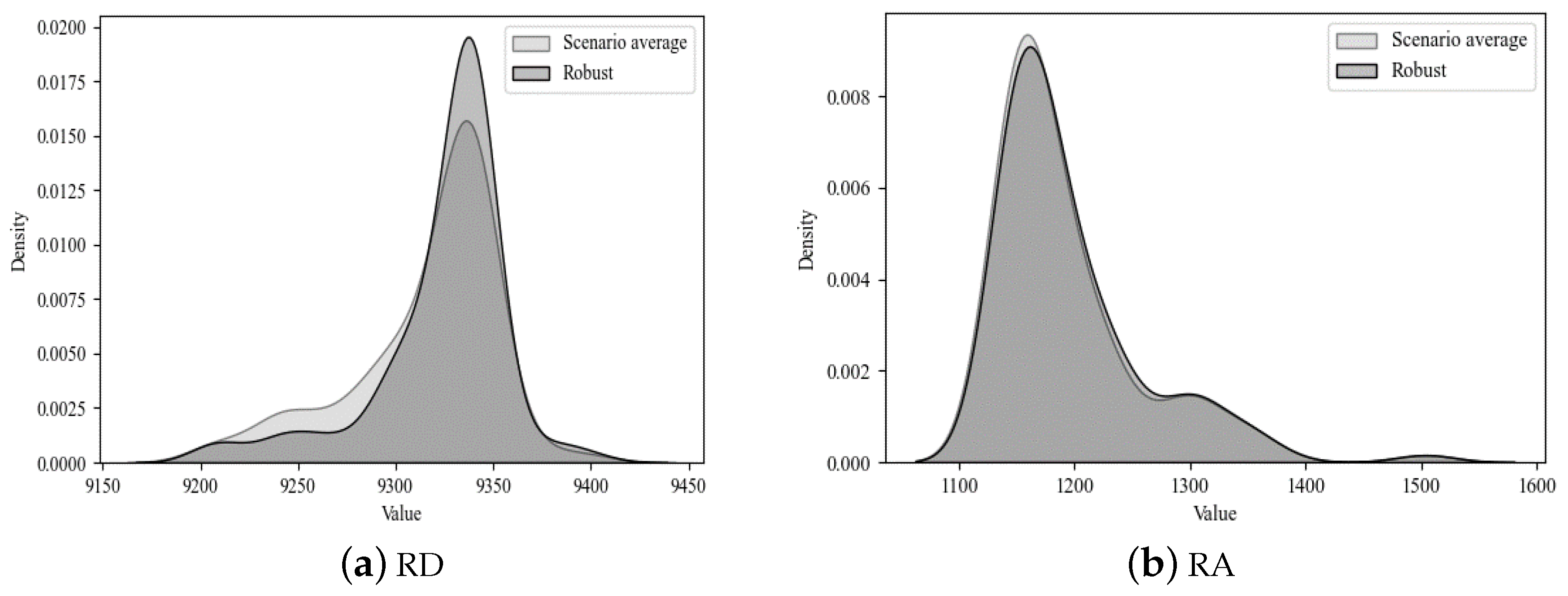
The gap between the robust solution and the single scenario optimal solutions was 0.05%, implying that these costs are expected to be saved if orders are predicted accurately or are known. This result confirms that the objective of the robust solution is very close to the optimal solutions of each scenario; thus, the robust solution is acceptable.

(2)

The variances of the disassembly time and re-assembly time for the robust solution were 18.28 and 0.81% less than that of the scenario optimal solutions, which was an expected trend. The robust solution obtained by the SAA approach could achieve higher production stability.

The reworking time reveals that the scenario optimal solution is superior to the robust solution in most scenarios. The distribution of reworking time, including the disassembling and re-assembling times, in the two models is presented in Figure 6 for the 100 scenarios:

It can be observed in Figure 6 that, due to the volatility of the scenarios, the results of the optimal solution exhibited significant differences. Thus, whatever the GCA decided, the re-assembly time was higher than for other scenarios that had similar orders. Moreover, the disassembly times for the robust solution were more concentrated on the average value, which indicates that applying the robust solution can achieve lower and more stable average disassembly times.

The above results show the comparison of the three production strategies: MTO, the SAA approach, and an empirical method. The proposed SAA GCA optimization approach can save 33.08% of production time. Moreover, the robustness of the proposed approach was evaluated, and the results show that the GCA obtained by the proposed approach had low variances in the reworking time.

5. Conclusions and Outlook

This study addresses production planning challenges in the aircraft industry, given order uncertainty, and it proposes a two-step production strategy that incorporates GCA. This strategy helps maintain production stability while significantly shortening order lead times, allowing for rapid modifications from GCA to meet customer delivery requirements after order acceptance. Based on the possible generated scenarios, an SAA GCA optimization model is further proposed, to obtain a robust GCA that can deal with the uncertainty of orders. A comparison of the three production strategies, i.e., MTO, the SAA approach, and an empirical method, is presented, confirming that the proposed SAA GCA optimization approach can save 33.08% of the production time. Moreover, the robustness of the proposed approach was evaluated, and the results show that the GCA obtained by the proposed approach exhibited low variances in the reworking times, being robust for all the order combinations. It should be noted that this study primarily focused on production time minimization for specific aircraft batches, while not fully addressing real-world constraints, such as operational costs, workstation loads, or dynamic production cycle adjustments. Further research in these dimensions remains necessary.