Performance Monitoring Based on Improved Adaptive Kalman Filtering for Turboshaft Engines Under Network Uncertainties
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. The Main Contribution of This Paper
2. Network Uncertainty Analysis of the Distributed Control Architecture
2.1. Distributed Kalman Filter
- (a)
- Time update:
- (b)
- Measurement update:where and are the covariance matrixes of and . The Jacobian matrixes A and C are calculated as follows:
- (a)
- Information fusion:
- (b)
- Information distribution:
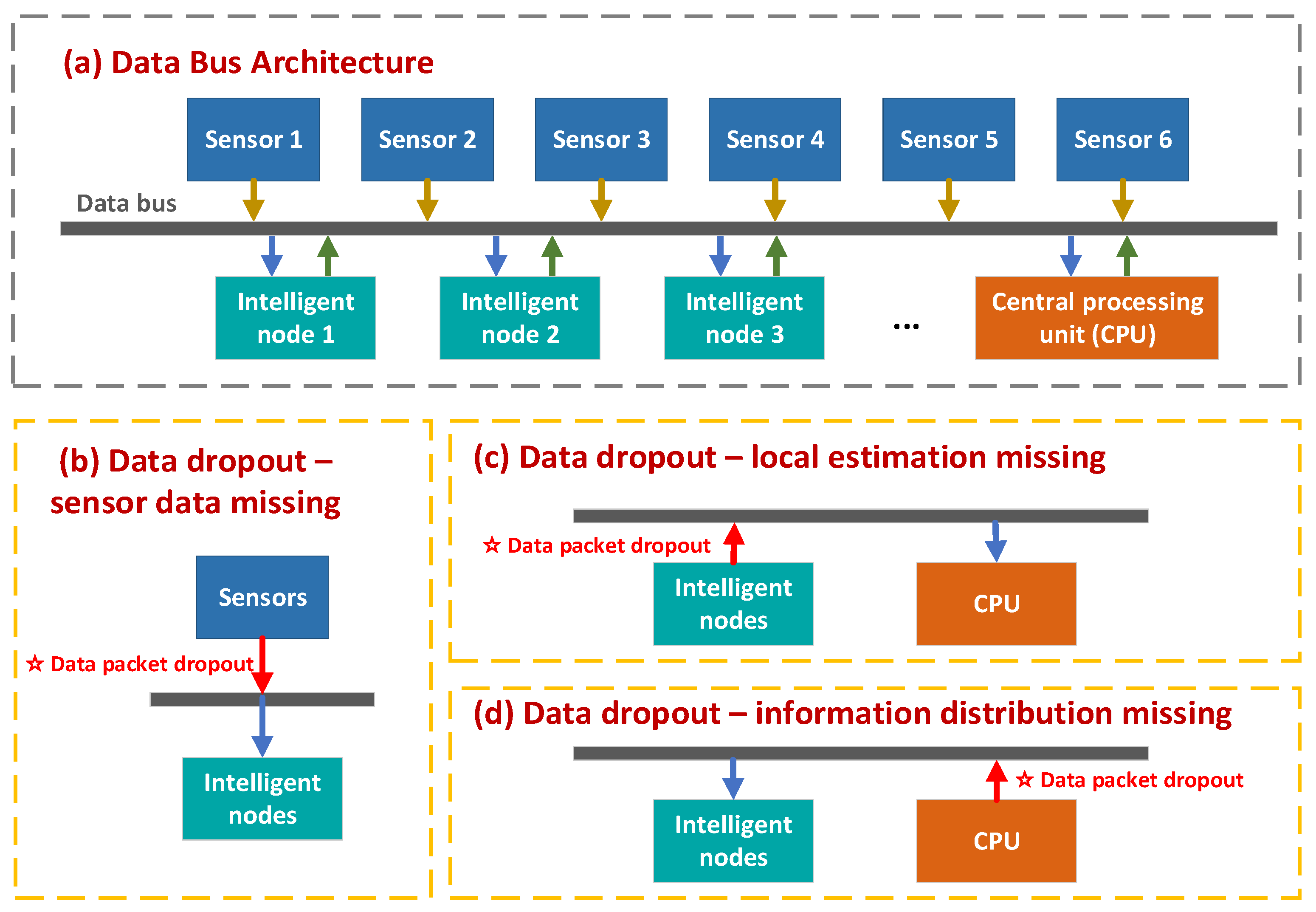
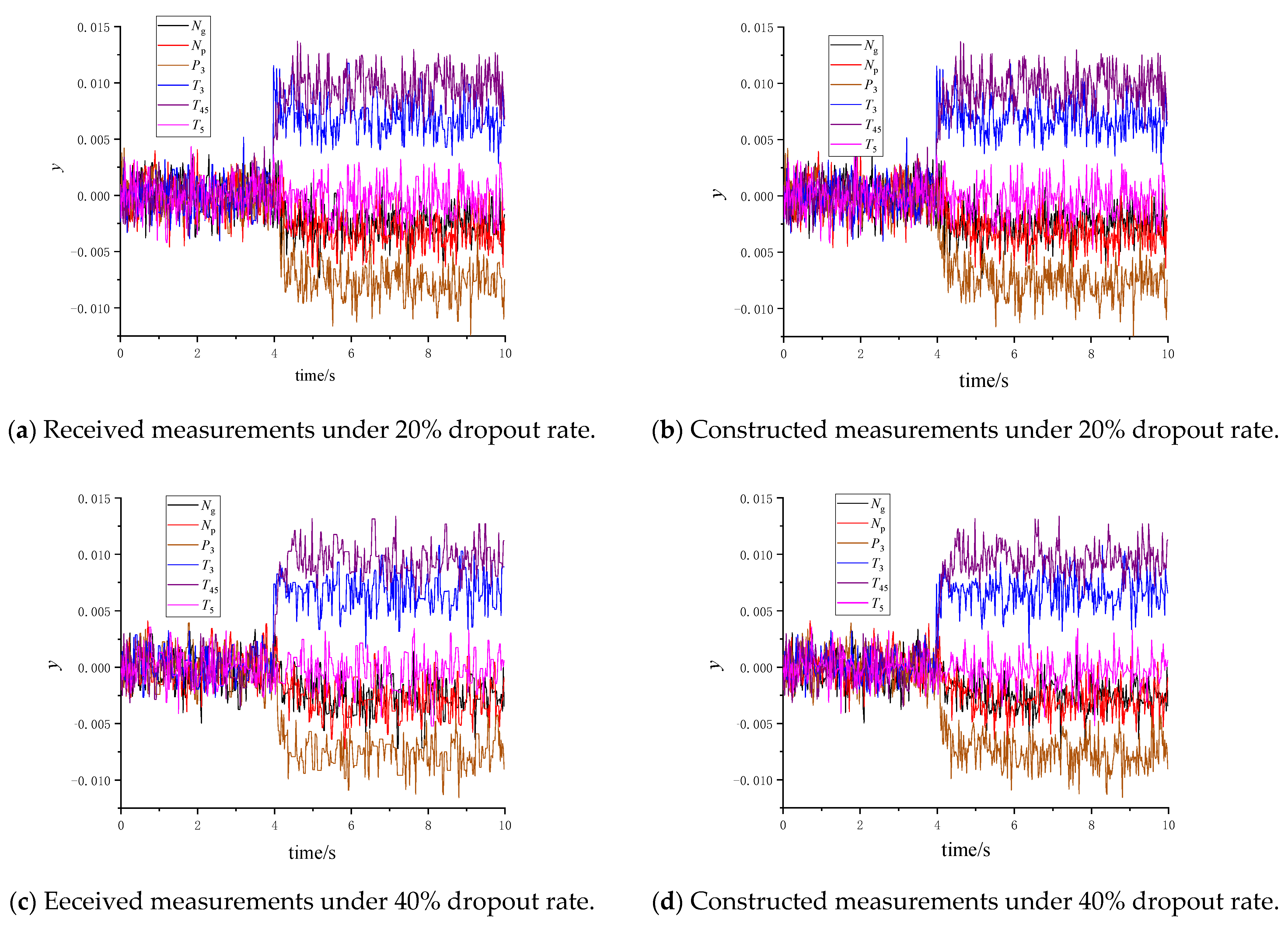
2.2. Data Packet Dropout Problem Under the Network Control
3. Performance Monitoring Based on the Improved Distributed Adaptive Kalman Filter
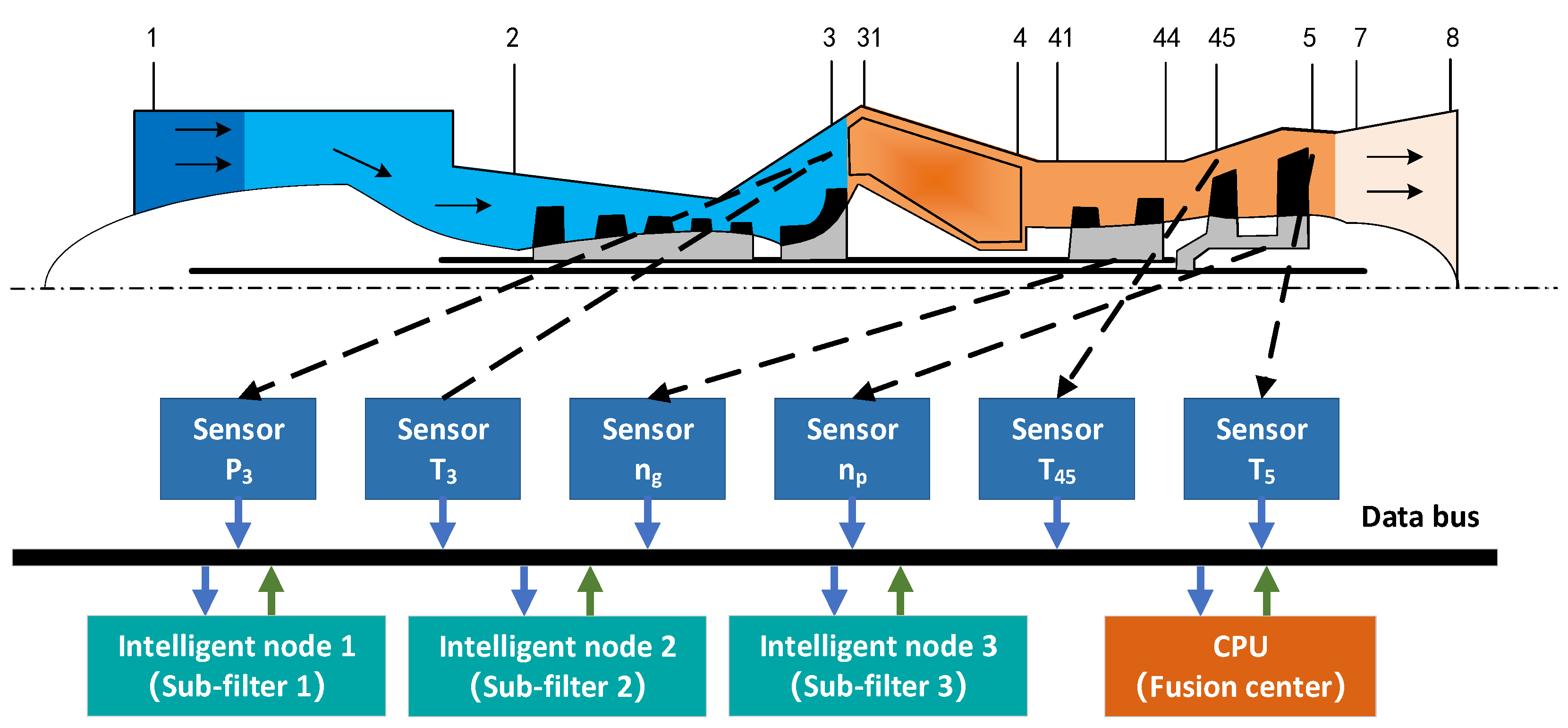
3.1. Distributed Performance Monitoring of the Turboshaft Engine
3.2. Adaptive Kalman Filtering Based on Measurement Reconstruction
| Algorithm 1: Sub-filter calculation in DAKF. |
| (1) Initialize state parameters; |
| according to Equation (5); |
| according to Equation (16) based on the data packet dropout; |
| ; (5) Update Kalman gain matrix and posterior error covariance matrix according to Equation (26); |
| and go to step (2). |
3.3. Signals’ Fusion Based on the Intelligent Buffer
| Algorithm 2: State buffer-based fusion. |
| (1) Initialize state variables and error covariance matrix; |
| (2) Receive the local state estimation results from the sub-filters via the bus and check for data dropout: If the dropout occurs |
| Fuse the local estimation results in the corresponding buffer of the filter to obtain the local estimation results at this time step; Else Store the sub-filter local estimation results into the state buffer; End |
| (3) Perform global fusion and allocation of the integrated local estimation results and integrated local error covariance matrices obtained from different sub-filters, and upload the allocation results to the data bus; |
| , return to step 2 until the simulation ends. |
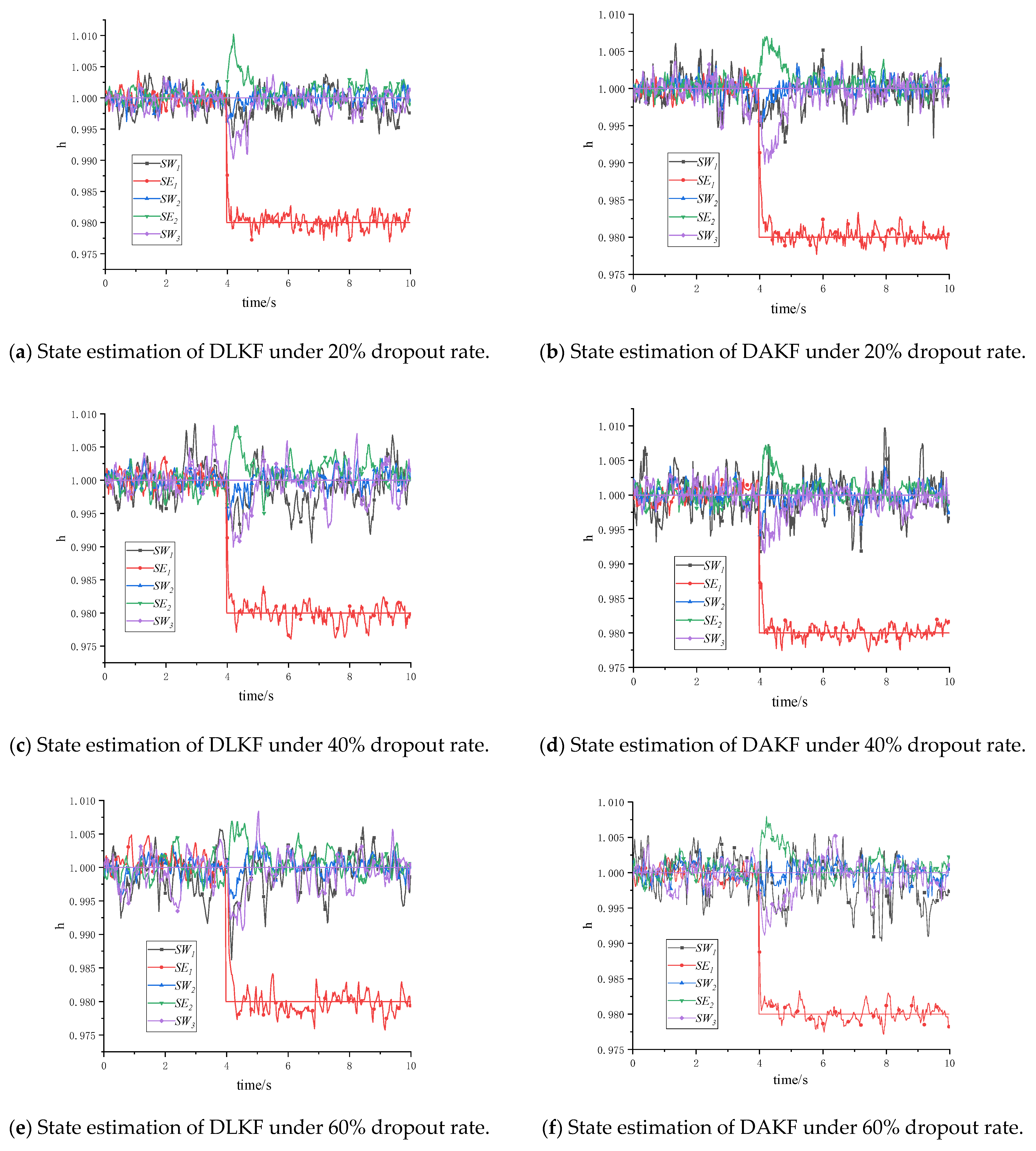
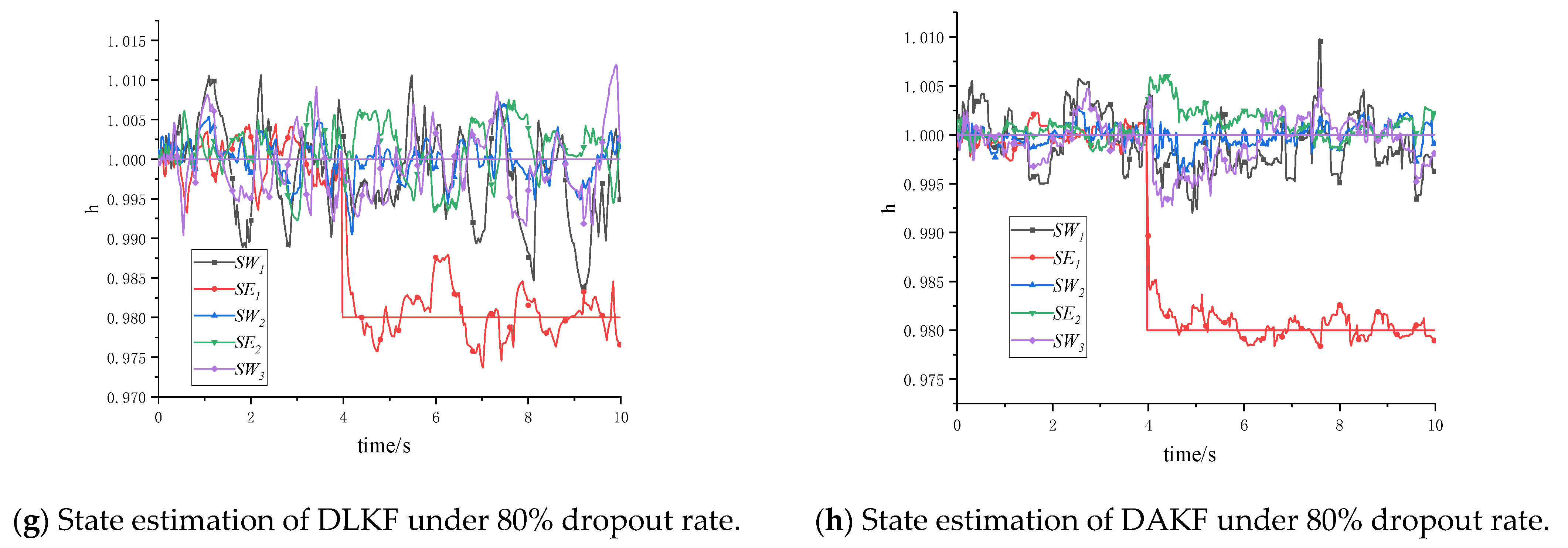
3.4. Data Packet Dropout Coping Strategies
| Algorithm 3: State buffer-based fusion. |
| (1) Initialize the prior estimate; |
| (2) Determine whether data dropout has occurred between the central control node and the intelligent simulation node: If the dropout occurs and from the previous step to calculate the prior estimate; Else received from the bus to calculate the prior estimate; End |
| (3) Perform local state estimation as in Algorithm 2; |
| ; return to step 2 until the simulation ends. |
4. Construction of Distributed Control Simulation Platform
4.1. TTP/C Communication Scheduling
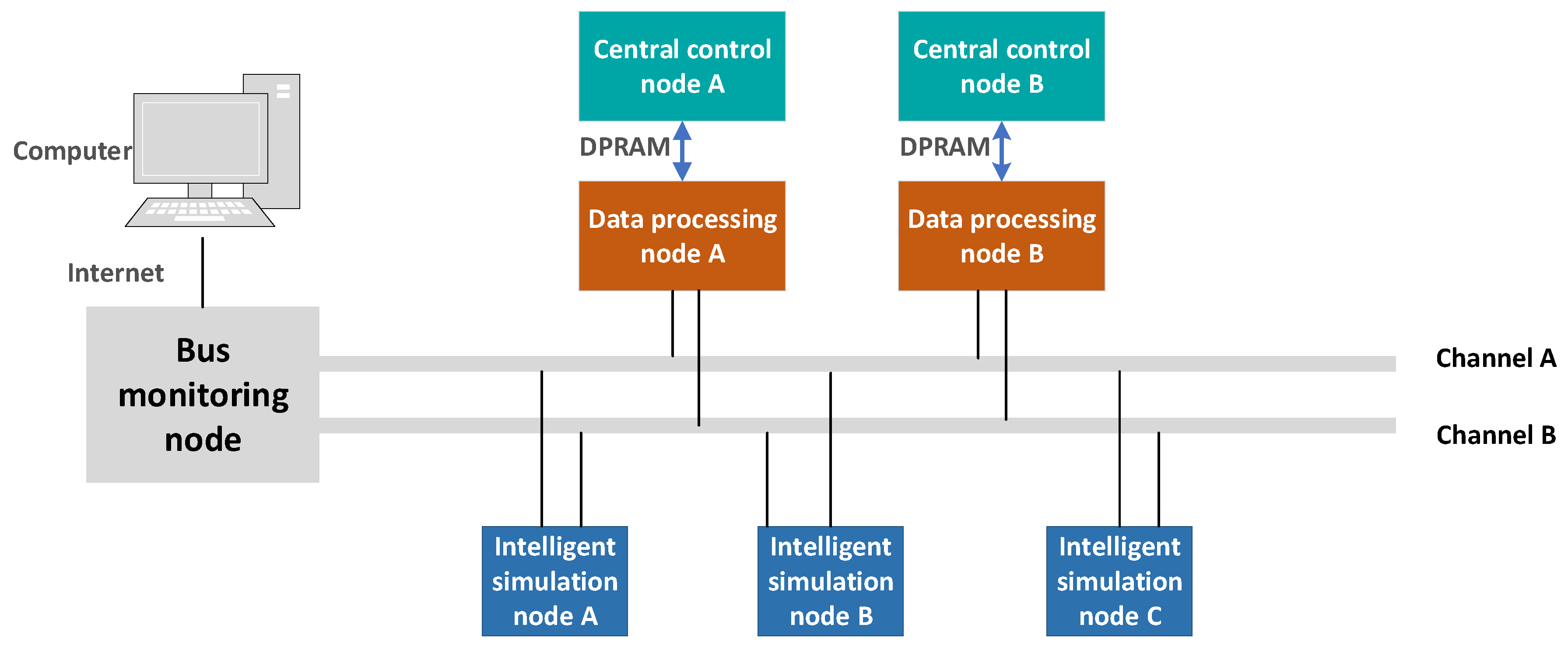
4.2. Hardware Platform Construction
- (a)
- Central control nodes: Each central control node is equipped with a P2020 processor with a main frequency of 800 MIPS (millions of instructions per second), providing strong computational capability. The P2020 chip is produced by Freescale (now part of NXP Semiconductors, headquartered in Eindhoven, The Netherlands). To enable data exchange, the central control nodes use dual-ported random-access memory (DPRAM) and establish the independent data transmission bus to communicate with the data processing nodes. The DPRAM has dedicated read/write addresses, and in this study, the read/write address range of the DPRAM is defined as 0×0000-0×1FFE (hexadecimal expression).
- (b)
- Intelligent simulation nodes: Each intelligent simulation node is equipped with an MPC5566 processor, with a main frequency of 132 MIPS. TTP/C driver chips are used in the intelligent simulation nodes to facilitate communication with the data bus.
- (c)
- Data processing node: Each data processing node is equipped with an MPC5674 processor (manufactured by NXP Semiconductors), with a main frequency of 264 MIPS. Like intelligent simulation nodes, the data processing nodes also use TTP/C driver chips to enable communication with the data bus.
- (d)
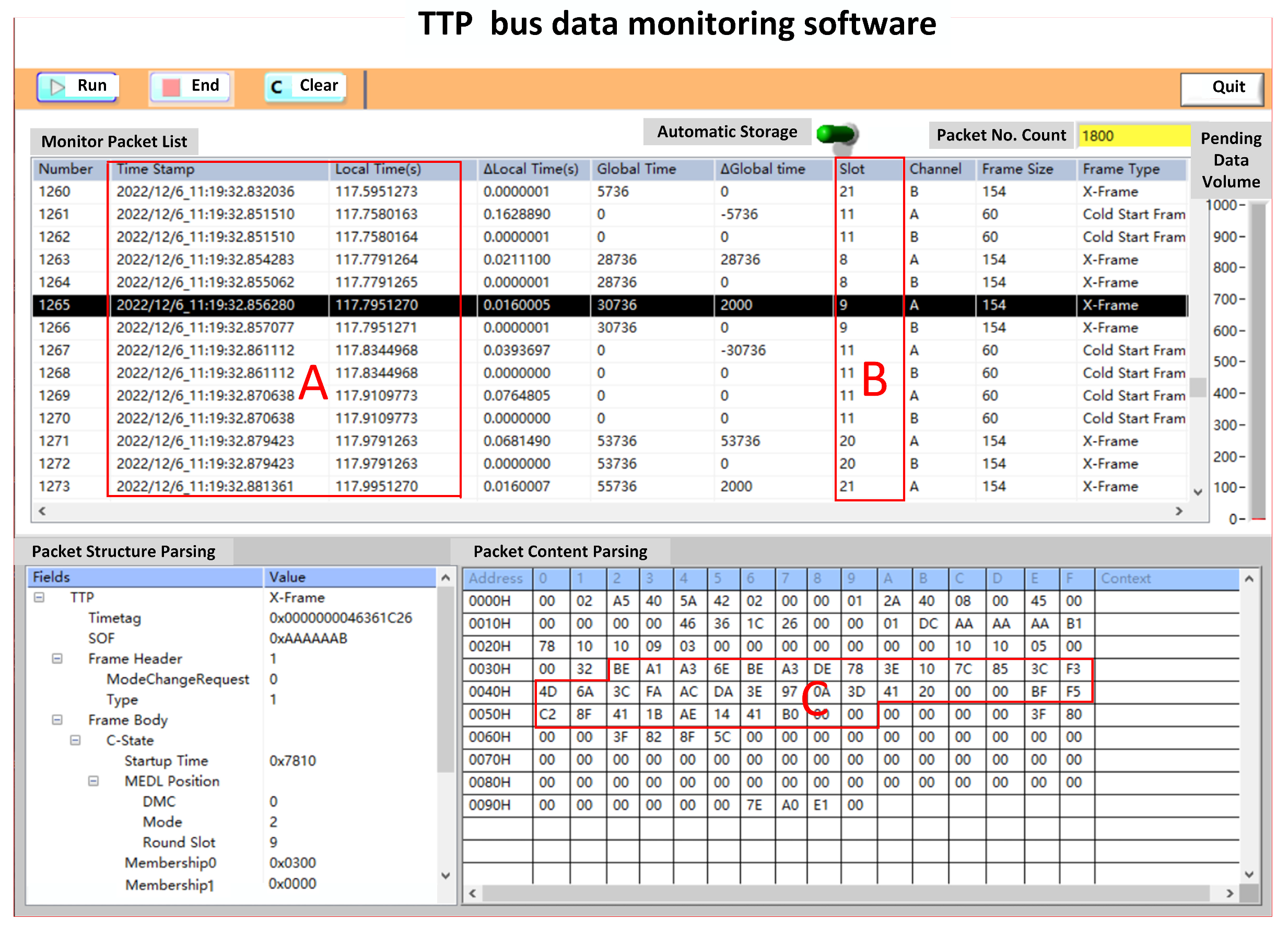
- Bus monitoring node: The data on the data bus can be read by the bus monitoring node and sent to the host computer for data collection by signal acquisition software. The data monitoring interface is shown in Figure 7. It consists of several parts:
- Area A displays the time at which each node sends data to the bus.
- Area B shows the node information of the data sender at that moment.
- Area C shows the specific data sent by the node to the bus.
5. Test and Analysis
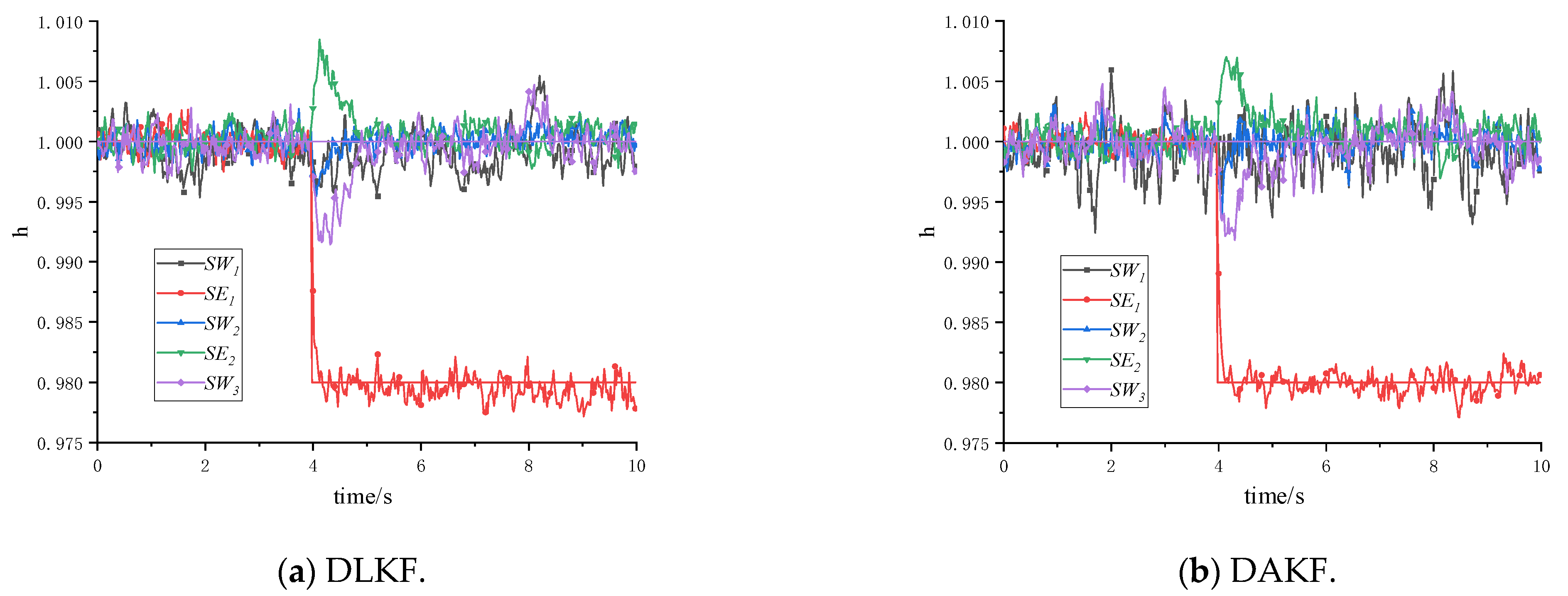
5.1. Full Digital Simulation
5.2. Experimental Verification Under Distributed Architecture
6. Conclusions
Nomenclature List
| Nomenclature | |
| DAKF | Distributed Adaptive Kalman Filter |
| DEKF | Distributed Extended Kalman Filter |
| DLKF | Distributed Linear Kalman Filter |
| DPRAM | Dual-ported random-access memory |
| EHM | Engine health management |
| EKF | Extended Kalman Filter |
| H | Altitude |
| KCF | Kalman Consensus Filter |
| Ma | Mach number |
| MEDL | Message Description List |
| MIPS | Millions of instructions per second |
| RMSE | Root mean square error |
| SUKF | Spherical Unscented Kalman Filter |
| TDMA | Timing division multiple access |
| TTP/C | Time-triggered protocol/category C |
| Subscripts | |
| d | Design point |
| f | Fuel |
| g | Gas turbine |
| p | Power turbine |
| 3 | Compressor exit |
| 45 | Power turbine inlet |
| 5 | Power turbine exit |
| 8 | nozzle exit |
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tegtmeier, L.A. 10-year global MRO forecast. Overhaul Maint. 2011, 17, 28–31. [Google Scholar]
- Amare, F.D.; Gilani, S.I.; Aklilu, B.T.; Mojahid, A. Two-shaft stationary gas turbine engine gas path diagnostics using fuzzy logic. J. Mech. Sci. Technol. 2017, 31, 5593–5602. [Google Scholar] [CrossRef]
- Li, Y.G.; Korakiantis, T. Nonlinear Weighted-Least-Squares Estimation Approach for Gas-Turbine Diagnostic Applications. J. Propuls. Power 2012, 27, 337–345. [Google Scholar] [CrossRef]
- Lee, S.-M.; Choi, W.-J.; Roh, T.-S.; Choi, D.-W. A study on separate learning algorithm using support vector machine for defect diagnostics of gas turbine engine. J. Mech. Sci. Technol. 2008, 22, 2489–2497. [Google Scholar] [CrossRef]
- Depold, H.R.; Gass, F.D. The application of expert systems and neural networks to gas turbine prognostics and diagnostics. J. Eng. Gas Turbines Power-Trans. ASME 1999, 121, 607–612. [Google Scholar] [CrossRef]
- Zhao, N.; Wen, X.; Li, S. A review on gas turbine anomaly detection for implementing health management. Turbo Expo Power Land Sea Air 2016, 49682, V001T22A009. [Google Scholar]
- Tolani, D.; Yasar, M.; Chin, S.; Ray, A. Anomaly detection for health management of aircraft gas turbine engines. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Lu, F.; Jin, P.; Huang, J.; Wang, C.; Qin, H. Aircraft engine hot-section virtual sensor creation and gas path performance monitoring. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 879–899. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, J.; Lu, F. Reduced kernel recursive least squares algorithm for aero-engine degradation prediction. Mech. Syst. Signal Process. 2017, 95, 446–467. [Google Scholar] [CrossRef]
- Chen, Q.; Sheng, H.; Zhang, T. An improved nonlinear onboard adaptive model for aero-engine performance control. Chin. J. Aeronaut. 2023, 36, 317–334. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, J.; Luo, C.; Xiong, L.; Pan, Q. Aero-engine health degradation estimation based on an underdetermined extended Kalman filter and convergence proof. ISA Trans. 2022, 125, 528–538. [Google Scholar] [CrossRef]
- Wang, P.; Cheng, N.; Li, Q. The estimation algorithm for component health parameter of turbofan engine. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 75–80. [Google Scholar] [CrossRef]
- Chen, C.; Zheng, Q.; Zhang, H. Research on selection method of aero-engine health parameters based on correlation and condition number. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2939–2951. [Google Scholar] [CrossRef]
- Liu, B.; Ma, Y.; Wu, Y.; Sun, X. An improved Kalman filter based on neural network for turbofan engine gas-path health estimation. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 4135–4140. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Jin, H.-J.; Liu, H. Gas Path Fault Diagnosis of Turboshaft Engine Based on Novel Transfer Learning Methods. J. Dyn. Sys. Meas. Control 2024, 146, 031010. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Y.; Zhang, G.; Wang, J. Research of Fault Feature Extraction and Analysis Method Based on Aeroengine Fault Data. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 2960–2965. [Google Scholar] [CrossRef]
- Willsky, A.S.; Bello, M.; Castanon, D.A.; Levy, B.C.; Verghese, G. Combining and updating of local estimates and regional maps along sets of one-dimensional tracks. IEEE Trans. Autom. Control 1982, 27, 799–813. [Google Scholar] [CrossRef]
- Carlson, N.A. Federated square root filter for decentralized parallel processors. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 517–525. [Google Scholar] [CrossRef]
- Ribeiro, A.; Giannakis, G.B.; Roumeliotis, S.I. SOI-KF: Distributed Kalman filtering with low-cost communications using the sign of innovations. IEEE Trans. Signal Process. 2006, 54, 4782–4795. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, W.A.; Yu, L. Distributed finite-horizon fusion Kalman filtering for bandwidth and energy constrained wireless sensor networks. IEEE Trans. Signal Process. 2014, 62, 797–812. [Google Scholar] [CrossRef]
- Safari, S.; Shabani, F.; Simon, D. Multirate multisensor data fusion for linear systems using Kalman filters and a neural network. Aerosp. Sci. Technol. 2014, 39, 465–471. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Emzir, M.F. State estimation with asynchronous multi-rate multi-smart sensors. Inf. Sci. 2012, 196, 15–27. [Google Scholar] [CrossRef]
- Liu, L.; Yang, A.; Tu, X.; Fei, M.; Naeem, W. Distributed weighted fusion estimation for uncertain networked systems with transmission time-delay and cross-correlated noises. Neurocomputing 2017, 270, 54–65. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Distributed Kalman filtering for sensor networks. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar]
- Olfati-Saber, R. Kalman-consensus filter: Optimality, stability, and performance. In Proceedings of the Joint 48th IEEE Conference on Decision and Control (CDC)/28th Chinese Control Conference (CCC), Shanghai, China, 16–18 December 2009. [Google Scholar]
- Kamal, A.T.; Ding, C.; Song, B.; Farrell, J.A.; Roy-Chowdhury, A.K. A generalized Kalman consensus filter for wide-area video networks. Proccedings of the 50th IEEE Conference of Decision and Control (CDC)/European Control Conference (ECC), Orlando, FL, USA, 12–15 December 2011. [Google Scholar]
- Xiong, J.; Lam, J. Stabilization of linear systems over networks with bounded packet loss. Automatica 2007, 43, 80–87. [Google Scholar] [CrossRef]
- Xie, L.; Xie, L. Peak covariance stability of a random Riccati equation arising from Kalman filtering with observation losses. J. Syst. Sci. Complex. 2007, 20, 262–272. [Google Scholar] [CrossRef]
- Huang, M.; Dey, S. Stability of Kalman filtering with Markovian packet losses. Automatica 2007, 43, 598–607. [Google Scholar] [CrossRef]
- Qian, H.; Qiu, Z.; Wu, Y. Robust extended Kalman filtering for nonlinear stochastic systems with random sensor delays, packet dropouts and correlated noises. Aerosp. Sci. Technol. 2017, 66, 249–261. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Deng, Z. Robust weighted fusion Kalman estimators for systems with multiplicative noises, missing measurements and uncertain-variance linearly correlated white noises. Aerosp. Sci. Technol. 2017, 68, 331–344. [Google Scholar] [CrossRef]
- Rezaei, H.; Esfanjani, R.M.; Sedaaghi, M.H. Improved robust finite-horizon Kalman filtering for uncertain networked time-varying systems. Inf. Sci. 2015, 293, 263–274. [Google Scholar] [CrossRef]
- Schenato, L. Optimal estimation in networked control systems subject to random delay and packet drop. IEEE Trans. Autom. Control. 2008, 53, 1311–1317. [Google Scholar] [CrossRef]
- Rezaei, H.; Mahboobi Esfanjani, R.; Farsi, M. Robust filtering for uncertain networked systems with randomly delayed and lost measurements. IET Signal Process. 2015, 9, 320–327. [Google Scholar] [CrossRef]
- Nikfetrat, A.; Esfanjani, R.M. Adaptive Kalman filtering for systems subject to randomly delayed and lost measurements. Circuits Syst. Signal Process. 2018, 37, 2433–2449. [Google Scholar] [CrossRef]
- Shi, L.; Xie, L.; Murray, R.M. Kalman filtering over a packet-delaying network: A probabilistic approach. Automatica 2009, 45, 2134–2140. [Google Scholar] [CrossRef]
- Zhu, C.; Xia, Y.; Yan, L.; Fu, M. Centralized fusion over unreliable networks. Int. J. Control. 2012, 85, 409–418. [Google Scholar] [CrossRef]
- Xing, Z.; Xia, Y. Distributed federated Kalman filter fusion over multi-sensor unreliable networked systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1714–1725. [Google Scholar] [CrossRef]
- Pakmehr, M.; Fitzgerald, N.; Paduano, J.; Feron, E.; Behbahani, A. Dynamic Modeling of a Turboshaft Engine Driving a Variable Pitch Propeller: A Decentralized Approach. AIAA 2011-6149. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Han, X.; Huang, J.; Zhou, X.; Zou, Z.; Lu, F.; Zhou, W. A novel, reduced-order optimization method for nonlinear model correction of turboshaft engines. J. Mech. Sci. Technol. 2024, 38, 2103–2122. [Google Scholar] [CrossRef]





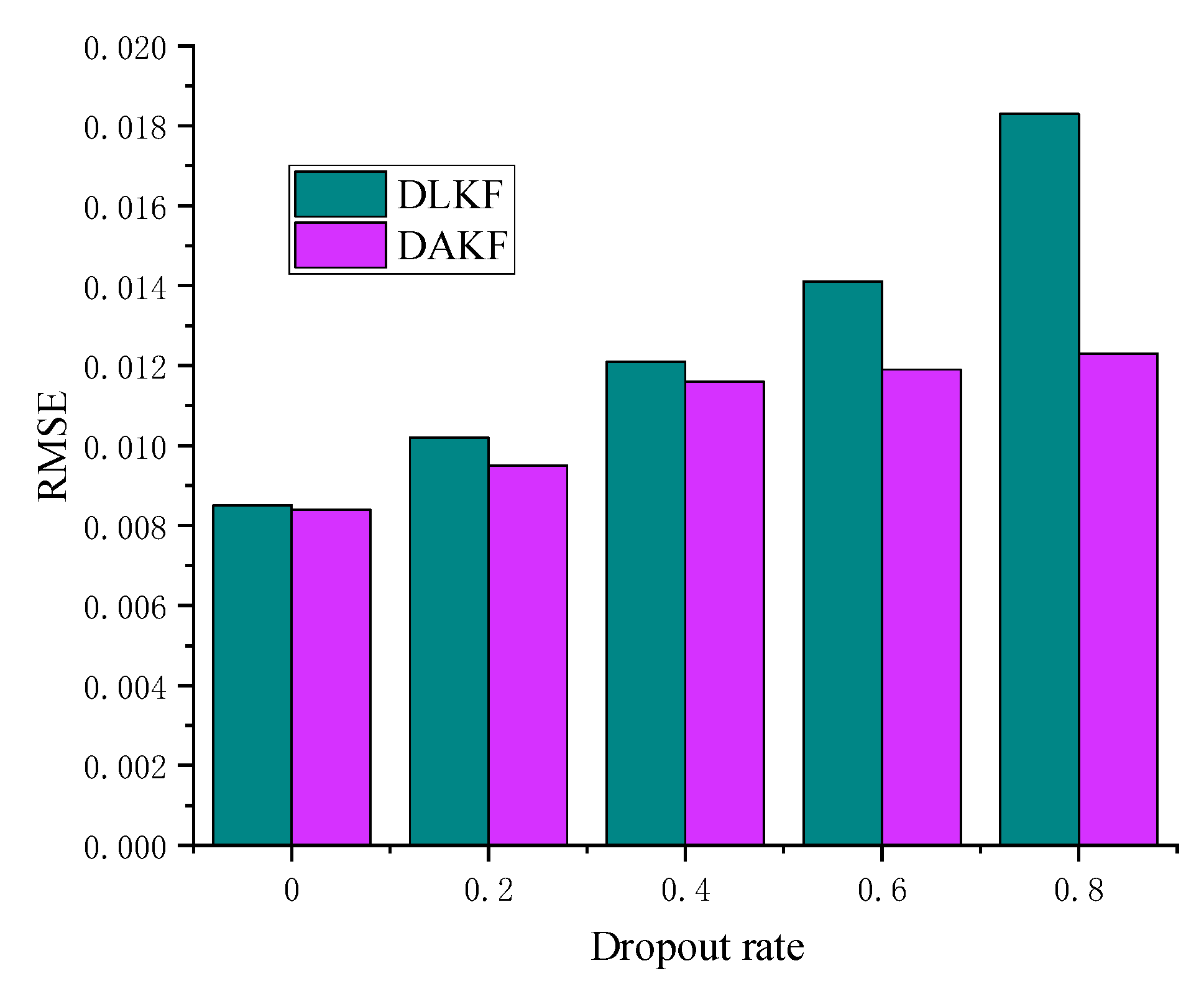

| Measurement | Abbreviation | Standard Deviation |
|---|---|---|
| Gas turbine rotor speed | ng | 0.0015 |
| Power turbine rotor speed | np | 0.0015 |
| Compressor exit temperature | T3 | 0.0015 |
| Compressor exit pressure | P3 | 0.0020 |
| Power turbine inlet temperature | T45 | 0.0015 |
| Power turbine exit temperature | T5 | 0.0015 |
| Health Parameters | ng | np | P3 | T3 | T45 | T5 |
|---|---|---|---|---|---|---|
| SW1 −2% | 0.0034 | −0.0009 | −0.0016 | −0.0003 | 0.0004 | −0.0001 |
| SE1 −2% | −0.0037 | −0.0039 | −0.0094 | 0.0060 | 0.0114 | −0.0004 |
| SW2 +2% | −0.0018 | −0.0007 | −0.0204 | −0.0060 | 0.0039 | −0.0001 |
| SE2 −2% | −0.0051 | −0.0056 | −0.0154 | −0.0058 | 0.0153 | −0.0006 |
| SW3 +2% | 0.0030 | −0.0028 | 0.0088 | 0.0029 | −0.0088 | 0.0004 |
| (a) Group #1 | (b) Group #2 | ||||||||||
| Health parameters | SW1 − 2% | SE1 − 2% | SW2 + 2% | SE2 − 2% | SW3 + 2% | Health parameters | SW1 − 2% | SE1 − 2% | SW2 + 2% | SE2 − 2% | SW3 + 2% |
| SW1 − 2% | 1 | — | — | — | — | SW1 − 2% | 1 | — | — | — | — |
| SE1 − 2% | 0.1220 | 1 | — | — | — | SE1 − 2% | 0.1808 | 1 | — | — | — |
| SW2 + 2% | 0.0737 | 0.1743 | 1 | — | — | SW2 + 2% | 0.3645 | 0.7472 | 1 | — | — |
| SE2 − 2% | 0.0613 | 0.7164 | 0.8061 | 1 | — | SE2 − 2% | 0.2180 | 0.9952 | 0.8072 | 1 | — |
| SW3 + 2% | 0.2190 | 0.5690 | 0.7318 | 0.8259 | 1 | SW3 + 2% | 0.1123 | 0.8889 | 0.7964 | 0.8954 | 1 |
| (c) Group #3 | (d) Group #4 | ||||||||||
| Health parameters | SW1 − 2% | SE1 − 2% | SW2 + 2% | SE2 − 2% | SW3 + 2% | Health parameters | SW1 − 2% | SE1 − 2% | SW2 + 2% | SE2 − 2% | SW3 + 2% |
| SW1 − 2% | 1 | — | — | — | — | SW1 − 2% | 1 | — | — | — | — |
| SE1 − 2% | 0.0880 | 1 | — | — | — | SE1 − 2% | 0.1402 | 1 | — | — | — |
| SW2 + 2% | 0.3585 | 0.6231 | 1 | — | — | SW2 + 2% | 0.3706 | 0.5725 | 1 | — | — |
| SE2 − 2% | 0.2068 | 0.6712 | 0.9358 | 1 | — | SE2 − 2% | 0.2293 | 0.8139 | 0.8198 | 1 | — |
| SW3 + 2% | 0.0695 | 0.5247 | 0.9259 | 0.8281 | 1 | SW3 + 2% | 0.1254 | 0.7345 | 0.8069 | 0.9003 | 1 |
| ng | np | P3 | T3 | T45 | T5 | |
|---|---|---|---|---|---|---|
| Sub-filter 1 | ✓ | ✓ | — | ✓ | ✓ | ✓ |
| Sub-filter 2 | ✓ | ✓ | ✓ | ✓ | — | ✓ |
| Sub-filter 3 | ✓ | ✓ | ✓ | ✓ | ✓ | — |
| Buffer Length | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| Additional computation time-consuming per cycle (ms) | 0.386 | 0.416 | 0.429 | 0.439 | 0.460 |
| RMSE | 0.0131 | 0.0117 | 0.0114 | 0.0112 | 0.0111 |
| Parameter | Value |
|---|---|
| Number_slot | 12 |
| Period_round | 20 ms |
| Fixed_round_number | 4 |
| Length of Transmission Time | Maximum Size of Transmitted Packet | Cold Start or Not | Host Synchronization Node or Not | |
|---|---|---|---|---|
| Intelligent node #1 | 2500 us | 120 × 16 bit | yes | yes |
| Intelligent node #2 | 2000 us | 50 × 16 bit | yes | no |
| Intelligent node #3 | 2200 us | 50 × 16 bit | no | no |
| Hardware Node | CPU-Equipped | Number | Frequency |
|---|---|---|---|
| Central control node | P2020 | 2 | 800 MIPS |
| Intelligent simulation node | MPC5566 | 3 | 132 MIPS |
| Data processing node | MPC5674 | 2 | 264 MIPS |
| Data monitoring node | — | 1 | — |
| Failure Mode | Fault Component | Flow Capacity Coefficient | Efficiency Coefficient |
|---|---|---|---|
| 1 | Compressor | −4% | −3.2% |
| 2 | Compressor | — | −2% |
| 3 | Compressor | −5% | — |
| 4 | Gas turbine | +1.5% | −1.2% |
| 5 | Gas turbine | +2% | — |
| 6 | Gas turbine | — | −2% |
| 7 | Power turbine | +2% | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhu, X.; Zhou, X.; Huang, J.; Lu, F. Performance Monitoring Based on Improved Adaptive Kalman Filtering for Turboshaft Engines Under Network Uncertainties. Aerospace 2025, 12, 241. https://doi.org/10.3390/aerospace12030241
Wang C, Zhu X, Zhou X, Huang J, Lu F. Performance Monitoring Based on Improved Adaptive Kalman Filtering for Turboshaft Engines Under Network Uncertainties. Aerospace. 2025; 12(3):241. https://doi.org/10.3390/aerospace12030241
Chicago/Turabian StyleWang, Chengjiu, Xinyu Zhu, Xin Zhou, Jinquan Huang, and Feng Lu. 2025. "Performance Monitoring Based on Improved Adaptive Kalman Filtering for Turboshaft Engines Under Network Uncertainties" Aerospace 12, no. 3: 241. https://doi.org/10.3390/aerospace12030241
APA StyleWang, C., Zhu, X., Zhou, X., Huang, J., & Lu, F. (2025). Performance Monitoring Based on Improved Adaptive Kalman Filtering for Turboshaft Engines Under Network Uncertainties. Aerospace, 12(3), 241. https://doi.org/10.3390/aerospace12030241






