Aerodynamics of Corrugated Wings: Past, Present, and Future
Abstract
:1. Introduction
1.1. Corrugated Wing Flight
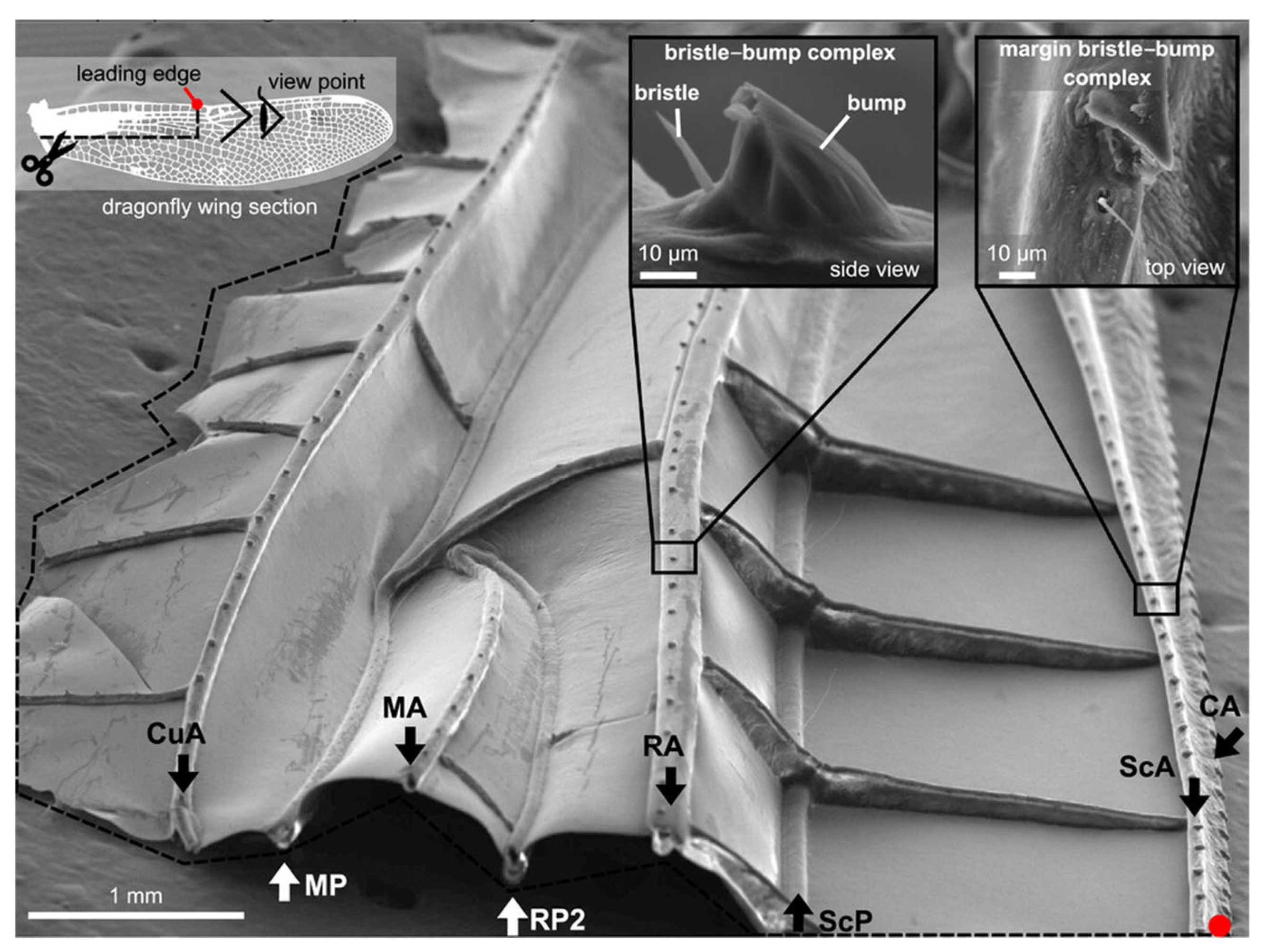
1.1.1. Corrugation in Nature
1.1.2. History of Corrugated Wing Research Leading to Technical Advances
1.1.3. Evolutionary Traits
1.1.4. Aerodynamic Design and Application
1.1.5. Scope
1.1.6. Parameters of Interest
2. Experimental and Numerical Research Methods
2.1. Experimental Methods
2.2. Numerical Methods
2.2.1. Boundary Layer Treatment and Transition to Turbulence
2.2.2. Overview of CFD Methods
2.2.3. Verification and Validation
3. Multiphysics Effects on Corrugated Wings: FSI (One Way and Two-Way Coupling), Aeroacoustics, and Tandem vs. Isolated Wings
3.1. Aeroacoustics
3.2. Fluid–Structure Interactions (FSI)
3.3. Tandem vs. Isolated Wing Configuration
4. Effects of Corrugation on Aerodynamic Performance
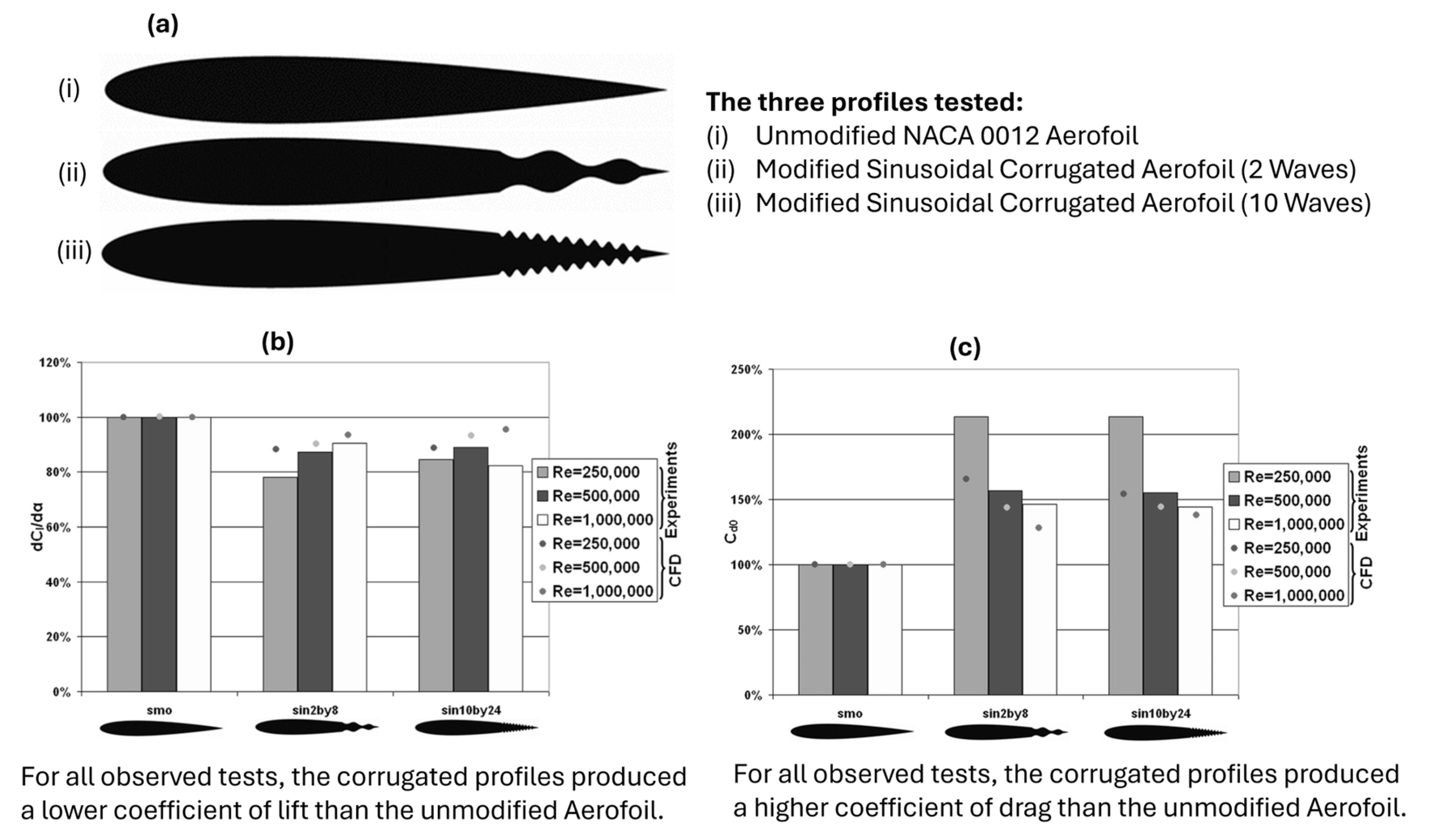
4.1. Effects on Lift Enhancement
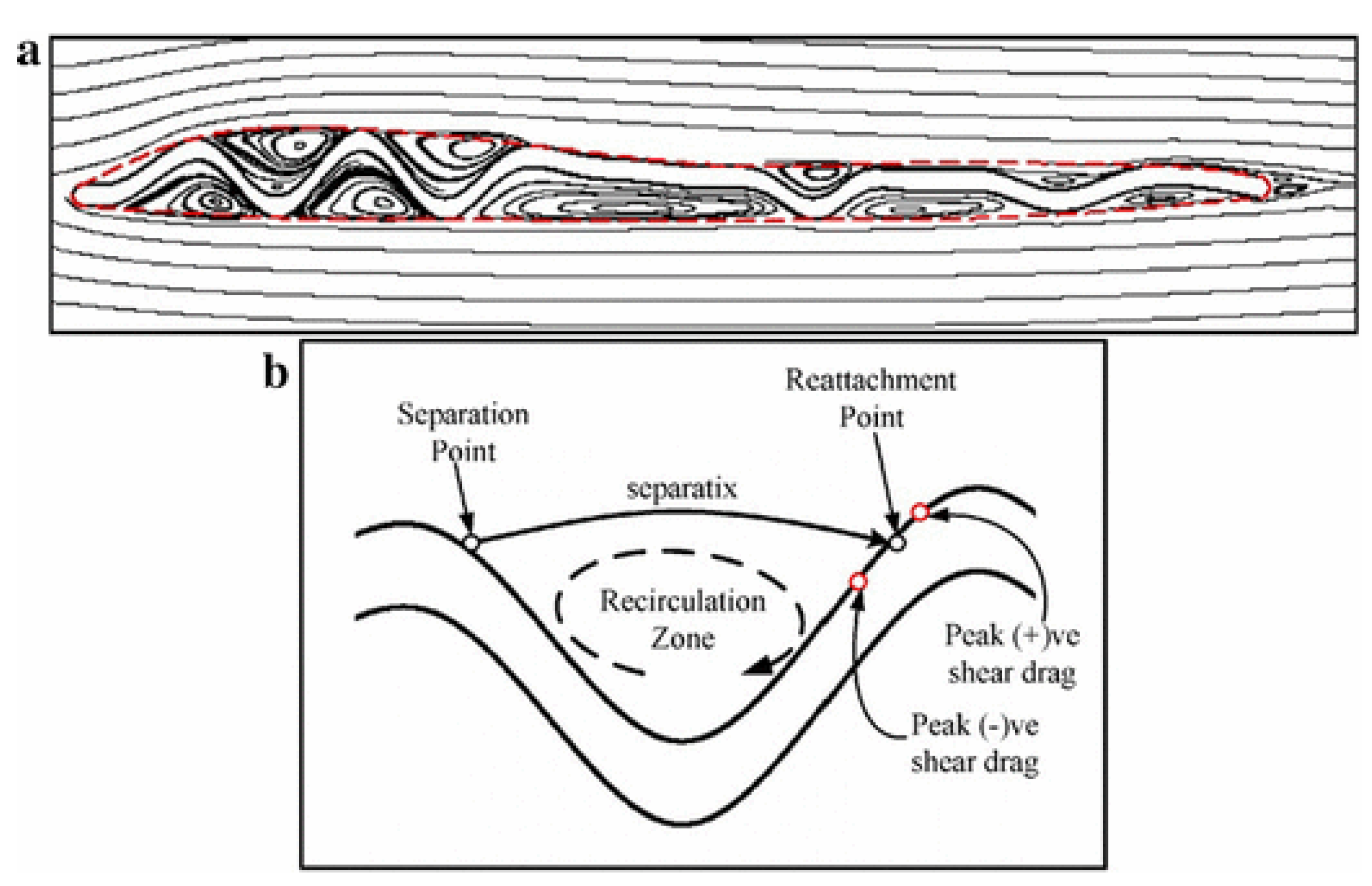
4.1.1. Recirculation Zones
4.1.2. Leading Edge Vortex (LEV)
4.1.3. Lambda Vortex Breakdown
4.1.4. Effect on Drag Reduction
4.2. Flow Separation and Stall
4.2.1. Boundary Layer Control
4.2.2. Functionality
5. Consequence of Angle of Attack (AoA)
5.1. Role of AoA in Manoeuvrers
5.2. Effect of AoA on Boundary Layer Flow
5.3. Critical Angles of Attack
5.4. Consequence of AoA on Pressure Distribution
5.5. A Brief Note on Induced Errors
5.6. Vortex Shedding
5.7. AoA on Tandem Wings
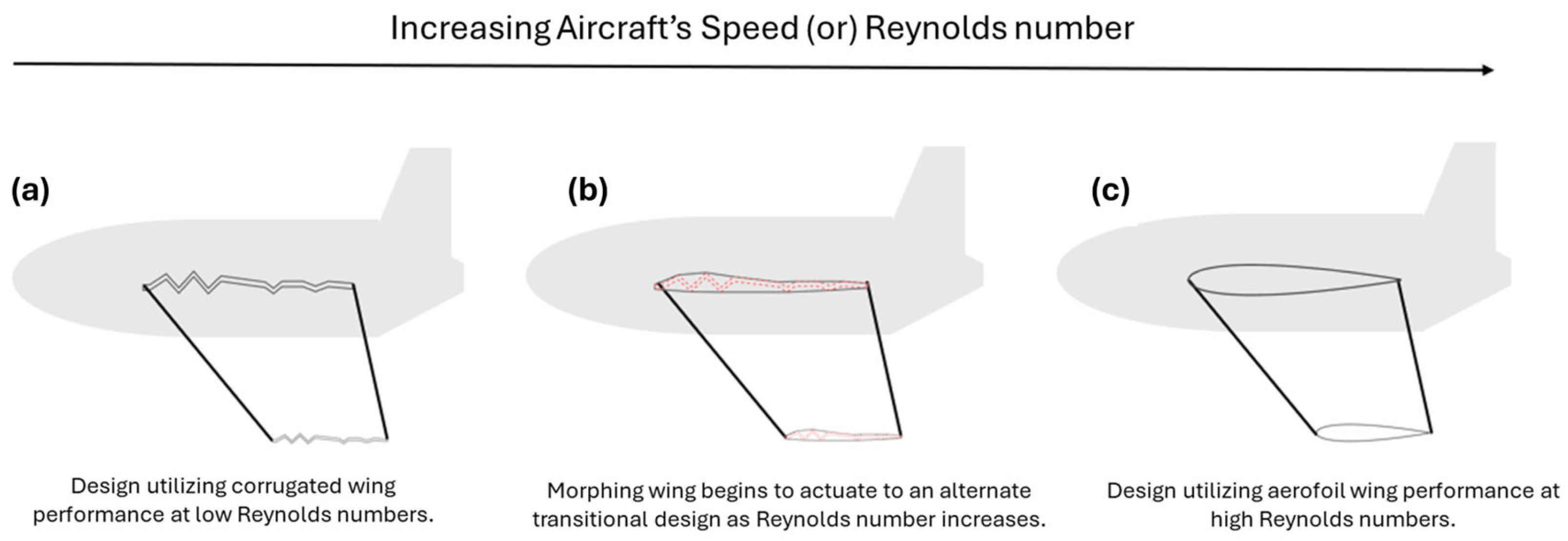
6. Morphing Wings
6.1. Morphing with Corrugation in Nature
Flow Sensing, Active Flow Control, and Application to Wing Morphing
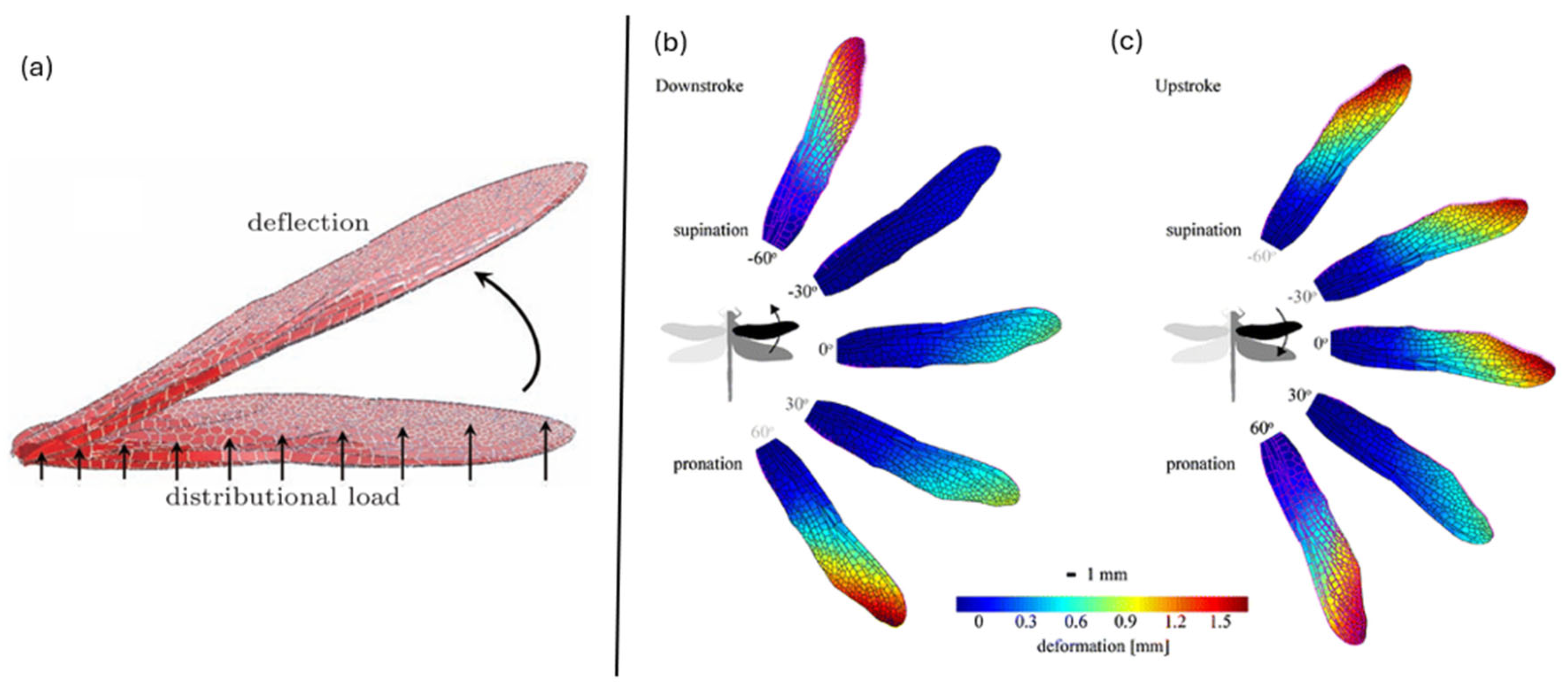
6.2. Aerodynamic Coefficients of Corrugated Morphing Wings
6.3. Structural Considerations of Corrugated Morphing Wings from an Aerodynamic Perspective
7. Concluding Reflections, Challenges, and Visions for the Future
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| UAV | Unmanned Aerial Vehicle |
| MAV | Micro Aerial Vehicle |
| CFD | Computational Fluid Dynamics |
| PIV | Particle Image Velocimetry |
| AoA | Angle of Attack |
| FSI | Fluid Structure Interaction |
| DDQN | Double Deep Q-Networks |
| ML | Machine Learning |
| AI | Artificial Intelligence |
| LEV | Leading Edge Vortex |
| TEV | Trailing Edge Vortex |
| FVM | Finite Element Method |
| FEA | Finite Element Analysis |
| CT | Computed Tomography |
| LES | Large Eddy Simulation |
| ILES | Implicit Large Eddy Simulation |
| GPU | Graphics Processing Unit |
| IBM | Immersed Boundary Method |
| FW-H | Ffowcs-Williams and Hawkings |
| 2D | Two dimensions |
| 3D | Three dimensions |
| Coefficient of drag | |
| Coefficient of lift | |
| Pressure coefficient | |
| Skin friction coefficient | |
| Reynolds number | |
| Strouhal number | |
| Drag force | |
| Lift force | |
| Area | |
| Pressure | |
| Ambient pressure | |
| Density of the fluid | |
| Wall shear stress | |
| Characteristic length scale | |
| Frequency of vortex shedding | |
| Flow velocity | |
| Phase angle | |
| Horizontal force coefficient |
References
- Kesel, A.B. Aerodynamic Characteristics of Dragonfly Wing Sections Compared with Technical Aerofoils. J. Exp. Biol. 2000, 203, 3125–3135. [Google Scholar] [CrossRef] [PubMed]
- Abd El-Latief, M.E.; Elsayed, K.; Madbouli Abdelrahman, M. Aerodynamic study of the corrugated airfoil at ultra-low Reynolds number. Adv. Mech. Eng. 2019, 11, 1687814019884164. [Google Scholar] [CrossRef]
- Xia, Y.; Bilgen, O.; Friswell, M.I. The effect of corrugated skins on aerodynamic performance. J. Intell. Mater. Syst. Struct. 2014, 25, 786–794. [Google Scholar] [CrossRef]
- Tamai, M.; Wang, Z.; Rajagopalan, G.; Hu, H.; He, G. Aerodynamic Performance of a Corrugated Dragonfly Airfoil Compared with Smooth Airfoils at Low Reynolds Numbers. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Vargas, A.; Mittal, R.; Dong, H. A computational study of the aerodynamic performance of a dragonfly wing section in gliding flight. Bioinspir. Biomim. 2008, 3, 026004. [Google Scholar] [CrossRef]
- Kim, W.-K.; Ko, J.H.; Park, H.C.; Byun, D. Effects of corrugation of the dragonfly wing on gliding performance. J. Theor. Biol. 2009, 260, 523–530. [Google Scholar] [CrossRef]
- Li, Q.; Zheng, M.; Pan, T.; Su, G. Experimental and Numerical Investigation on Dragonfly Wing and Body Motion during Voluntary Take-off. Sci. Rep. 2018, 8, 1011. [Google Scholar] [CrossRef]
- Brodskij, A.K.; Brodskij, A.K. The Evolution of Insect Flight; Oxford science publications; Oxford University Press: Oxford, UK, 1996; ISBN 978-0-19-850089-6. [Google Scholar]
- Wakeling, J.M.; Ellington, C.P. Dragonfly Flight: I. Gliding Flight and Steady-State Aerodynamic Forces. J. Exp. Biol. 1997, 200, 543–556. [Google Scholar] [CrossRef]
- Liu, C.; Chen, G.; Wang, Q.; Sun, L.; Wang, K. A study on the aerodynamic behaviors learned from microscopy imaging of beetle corrugated hindwing. Microsc. Res. Techol. 2024, 87, 1822–1835. [Google Scholar] [CrossRef]
- Jongerius, S.R.; Lentink, D. Structural Analysis of a Dragonfly Wing. Exp. Mech. 2010, 50, 1323–1334. [Google Scholar] [CrossRef]
- Forbes, W.T.M. The Origin of Wings and Venational Types in Insects. Am. Midl. Nat. 1943, 29, 381. [Google Scholar] [CrossRef]
- Fage, A. The Smallest Size of a Spanwise Surface Corrugation Which Affects Boundary Layer Transition on an Aerofoil. Aeronautical Research Council Reports & Memoranda 1943. Available online: https://reports.aerade.cranfield.ac.uk/handle/1826.2/3987 (accessed on 14 February 2025).
- Wood, D. Tests of Large Airfoils in the Propeller Research Tunnel, Including Two with Corrugated Surfaces; Technical Report; NASA: Greenbelt, MD, USA, 1930. Available online: https://ntrs.nasa.gov/citations/19930091406 (accessed on 11 March 2025).
- Barnes, C.J.; Visbal, M.R. Numerical exploration of the origin of aerodynamic enhancements in [low-Reynolds number] corrugated airfoils. Phys. Fluids 2013, 25, 115106. [Google Scholar] [CrossRef]
- Moscato, G.; Romano, G. Biomimetic Wings for Micro Air Vehicles. Biomimetics 2024, 9, 553. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Krings, A.W.; Hiromoto, R.E. Dragonfly as a model for UAV/MAV flight and communication controls. In Proceedings of the 2009 IEEE Aerospace conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–8. [Google Scholar]
- Adak, R.; Mandal, A.; Saha, S. Aerodynamic Performance of a Tandem Wing Configuration Inspired from Dragonfly Gliding Flight for MAV Application. In Fluid Mechanics and Fluid Power; Singh, K.M., Dutta, S., Subudhi, S., Singh, N.K., Eds.; Lecture Notes in Mechanical Engineering; Springer Nature: Singapore, 2024; Volume 2, pp. 409–418. ISBN 978-981-9957-51-4. [Google Scholar]
- Gaissert, N.; Mugrauer, R.; Mugrauer, G.; Jebens, A.; Jebens, K.; Knubben, E.M. Inventing a Micro Aerial Vehicle Inspired by the Mechanics of Dragonfly Flight. In Towards Autonomous Robotic Systems; Natraj, A., Cameron, S., Melhuish, C., Witkowski, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8069, pp. 90–100. ISBN 978-3-662-43644-8. [Google Scholar]
- Hu, Y.; Ru, W.; Liu, Q.; Wang, Z. Design and Aerodynamic Analysis of Dragonfly-like Flapping Wing Micro Air Vehicle. J. Bionic Eng. 2022, 19, 343–354. [Google Scholar] [CrossRef]
- Zoell, W. Leonardo Da Vinci’s Mechanical Dragonfly. The Great Canadian Model Builders Web Page. 2016. Available online: https://thegreatcanadianmodelbuilderswebpage.blogspot.com/2016/03/leonardo-da-vincis-mechanical-dragonfly.html (accessed on 11 March 2025).
- Chitsaz, N.; Siddiqui, K.; Marian, R.; Chahl, J. An experimental study of the aerodynamics of micro corrugated wings at low Reynolds number. Exp. Therm. Fluid Sci. 2021, 121, 110286. [Google Scholar] [CrossRef]
- Chahl, J.; Chitsaz, N.; McIvor, B.; Ogunwa, T.; Kok, J.-M.; McIntyre, T.; Abdullah, E. Biomimetic Drones Inspired by Dragonflies Will Require a Systems Based Approach and Insights from Biology. Drones 2021, 5, 24. [Google Scholar] [CrossRef]
- Du, G.; Sun, M. Effects of wing deformation on aerodynamic forces in hovering hoverflies. J. Exp. Biol. 2010, 213, 2273–2283. [Google Scholar] [CrossRef]
- Calafate, C.T.; Tropea, M. Unmanned Aerial Vehicles—Platforms, Applications, Security and Services. Electronics 2020, 9, 975. [Google Scholar] [CrossRef]
- Badrya, C.; Govindarajan, B.; Chopra, I. Basic Understanding of Unsteady Airfoil Aerodynamics at Low Reynolds Numbers. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Astronautics, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Winslow, J.; Otsuka, H.; Govindarajan, B.; Chopra, I. Basic Understanding of Airfoil Characteristics at Low Reynolds Numbers (104–105). J. Aircr. 2018, 55, 1050–1061. [Google Scholar] [CrossRef]
- Murphy, J.; Hu, H. An Experimental Investigation on a Bio-inspired Corrugated Airfoil. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Salami, E.; Ward, T.A.; Montazer, E.; Ghazali, N.N.N. A review of aerodynamic studies on dragonfly flight. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6519–6537. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, G. Review on the Structure Design of Morphing Winglets. Aerospace 2024, 11, 1004. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Liu, T. Vortices and Forces in Biological Flight: Insects, Birds, and Bats. Annu. Rev. Fluid Mech. 2024, 56, 147–170. [Google Scholar] [CrossRef]
- Shyy, W. Aerodynamics of Low Reynolds Number Flyers; Cambridge aerospace series; Cambridge University Press: Cambridge, UK, 2008; ISBN 978-0-521-20401-9. [Google Scholar]
- Rees, C.J.C. Aerodynamic properties of an insect wing section and a smooth aerofoil compared. Nature 1975, 258, 141–142. [Google Scholar] [CrossRef] [PubMed]
- Rees, C.J.C. Form and function in corrugated insect wings. Nature 1975, 256, 200–203. [Google Scholar] [CrossRef]
- Azuma, A.; Watanabe, T. Flight Performance of a Dragonfly. J. Exp. Biol. 1988, 137, 221–252. [Google Scholar] [CrossRef]
- Wakeling, J.M.; Ellington, C.P. Dragonfly Flight: II. Velocities, Accelerations and Kinematics of Flapping Flight. J. Exp. Biol. 1997, 200, 557–582. [Google Scholar] [CrossRef]
- Wakeling, J.M.; Ellington, C.P. Dragonfly Flight: III. Lift and Power Requirements. J. Exp. Biol. 1997, 200, 583–600. [Google Scholar] [CrossRef]
- Hu, H.; Tamai, M. Bioinspired Corrugated Airfoil at Low Reynolds Numbers. J. Aircr. 2008, 45, 2068–2077. [Google Scholar] [CrossRef]
- Murphy, J.T.; Hu, H. An experimental study of a bio-inspired corrugated airfoil for micro air vehicle applications. Exp. Fluids 2010, 49, 531–546. [Google Scholar] [CrossRef]
- Guilarte Herrero, A.; Noguchi, A.; Kusama, K.; Shigeta, T.; Nagata, T.; Nonomura, T.; Asai, K. Effects of compressibility and Reynolds number on the aerodynamics of a simplified corrugated airfoil. Exp. Fluids 2021, 62, 63. [Google Scholar] [CrossRef]
- Placek, R. Errors and problems while conducting research studies in a wind tunnel—selected exaples. Pr. Inst. Lotnictwa 2016, 245, 169–177. [Google Scholar] [CrossRef]
- Özer, Ö.; Quinn, M.K. Progress towards a Miniaturised PIV System. Sensors 2022, 22, 8774. [Google Scholar] [CrossRef] [PubMed]
- Basri, E.I.; Basri, A.A.; Ahmad, K.A. Computational Fluid Dynamics Analysis in Biomimetics Applications: A Review from Aerospace Engineering Perspective. Biomimetics 2023, 8, 319. [Google Scholar] [CrossRef] [PubMed]
- Levy, D.-E.; Seifert, A. Simplified dragonfly airfoil aerodynamics at Reynolds numbers below 8000. Phys. Fluids 2009, 21, 071901. [Google Scholar] [CrossRef]
- Levy, D.-E.; Seifert, A. Parameter study of simplified dragonfly airfoil geometry at Reynolds number of 6000. J. Theor. Biol. 2010, 266, 691–702. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, X.-Y. Aerodynamic performance due to forewing and hindwing interaction in gliding dragonfly flight. Phys. Rev. E 2009, 80, 017302. [Google Scholar] [CrossRef]
- Hord, K.; Liang, Y. Numerical Investigation of the Aerodynamic and Structural Characteristics of a Corrugated Airfoil. J. Aircr. 2012, 49, 749–757. [Google Scholar] [CrossRef]
- Meng, X.G.; Sun, M. Aerodynamic effects of wing corrugation at gliding flight at low Reynolds numbers. Phys. Fluids 2013, 25, 071905. [Google Scholar] [CrossRef]
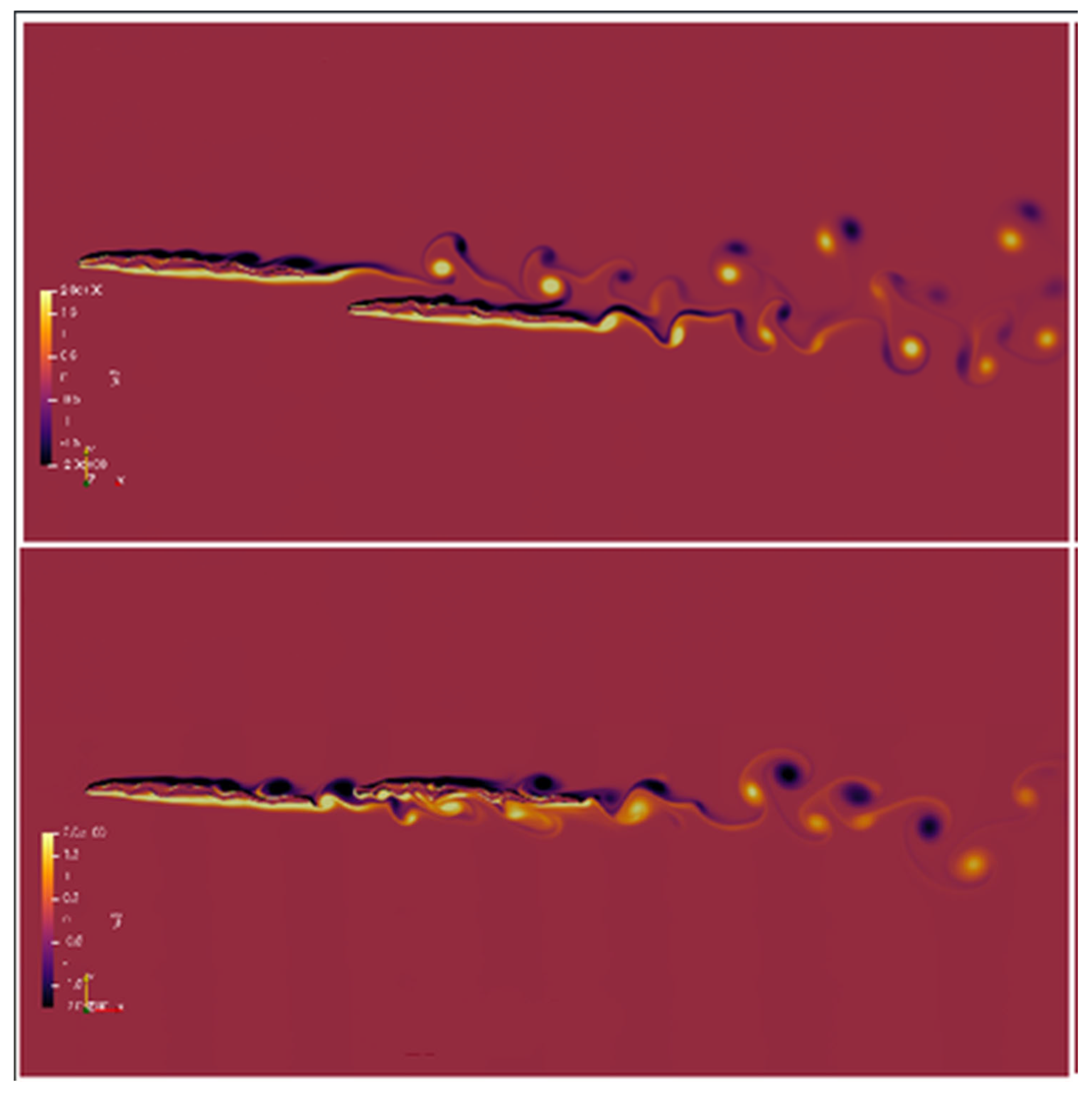
- Lian, Y.; Broering, T.; Hord, K.; Prater, R. The characterization of tandem and corrugated wings. Prog. Aerosp. Sci. 2014, 65, 41–69. [Google Scholar] [CrossRef]
- Chen, Y.H.; Skote, M. Gliding performance of 3-D corrugated dragonfly wing with spanwise variation. J. Fluids Struct. 2016, 62, 1–13. [Google Scholar] [CrossRef]
- Ho, W.; New, T. Unsteady numerical investigation of two different corrugated airfoils. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 2423–2437. [Google Scholar] [CrossRef]
- Khan, M.A.; Padhy, C. Aerodynamic and structural analysis of bio-mimetic corrugated wing. Fluid Mech. Res. Int. J. 2019, 3, 61–67. [Google Scholar] [CrossRef]
- Stelzer, V.; Krenkel, L. 2D numerical investigations derived from a 3D dragonfly wing captured with a high-resolution micro-CT. Technol. Health Care 2021, 30, 283–289. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, R.; Li, H. Aerodynamic Exploration for Tandem Wings with Smooth or Corrugated Surfaces at Low Reynolds Number. Aerospace 2023, 10, 427. [Google Scholar] [CrossRef]
- Au, L.T.K.; Phan, H.V.; Park, S.H.; Park, H.C. Effect of corrugation on the aerodynamic performance of three-dimensional flapping wings. Aerosp. Sci. Technol. 2020, 105, 106041. [Google Scholar] [CrossRef]
- Abbott, I.H.; von Doenhoff, A.E. Theory of Wing Sections: Including a Summary of Airfoil Data; Correc. rep. of: McGraw-Hill Book, 1949; Dover Publications: New York, NY, USA,, 1959; ISBN 978-0-486-60586-9. [Google Scholar]
- Mueller, T.J.; DeLaurier, J.D. Aerodynamics of Small Vehicles. Annu. Rev. Fluid Mech. 2003, 35, 89–111. [Google Scholar] [CrossRef]
- Bauerheim, M.; Chapin, V. Route to chaos on a dragonfly wing cross section in gliding flight. Phys. Rev. E 2020, 102, 011102. [Google Scholar] [CrossRef]
- Liu, Y.; Li, P.; Jiang, K. Comparative assessment of transitional turbulence models for airfoil aerodynamics in the low Reynolds number range. J. Wind Eng. Ind. Aerodyn. 2021, 217, 104726. [Google Scholar] [CrossRef]
- Abdizadeh, G.R.; Farokhinejad, M.; Ghasemloo, S. Numerical investigation on the aerodynamic efficiency of bio-inspired corrugated and cambered airfoils in ground effect. Sci. Rep. 2022, 12, 19117. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Graduate texts in physics; Springer International Publishing: Cham, Swizterland, 2017; ISBN 978-3-319-83103-9. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Numerical mathematics and scientific computation; Oxford University Press: Oxford, UK, 2001; ISBN 978-0-19-850398-9. [Google Scholar]
- Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [CrossRef]
- McCroskey, W.J.; Carr, L.W.; McAlister, K.W. Dynamic Stall Experiments on Oscillating Airfoils. AIAA J. 1976, 14, 57–63. [Google Scholar] [CrossRef]
- Oberkampf, W.; Trucano, T. Verification and Validation in Computational Fluid Dynamics; Sandia National Laboratories: Albuquerque, NM, USA, 2002.
- Oberkampf, W.L.; Roy, C.J. Verification and Validation in Scientific Computing, 1st ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-11360-1. [Google Scholar]
- Zheng, H.; Mofatteh, H.; Hablicsek, M.; Akbarzadeh, A.; Akbarzadeh, M. Dragonfly-Inspired Wing Design Enabled by Machine Learning and Maxwell’s Reciprocal Diagrams. Adv. Sci. 2023, 10, 2207635. [Google Scholar] [CrossRef]
- Rajabi, H.; Moghadami, M.; Darvizeh, A. Investigation of microstructure, natural frequencies and vibration modes of dragonfly wing. J. Bionic. Eng. 2011, 8, 165–173. [Google Scholar] [CrossRef]
- Jiang, S.; Hu, Y.; Li, Q.; Wang, H.; Lin, Y.; Zhou, X.; Liu, Q. The Noise-Reduction Characteristics of Microstructure of Dragonfly Wing Leading Vein. Appl. Sci. 2021, 11, 2970. [Google Scholar] [CrossRef]
- Moslem, F.; Babaie, Z.; Masdari, M.; Fedir, K. A review on insects flight aerodynamics, noise sources, and flow control mechanisms. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2907–2917. [Google Scholar] [CrossRef]
- Viswanathan, H.; Chode, K.K. The Role of Forebody Topology on Aerodynamics and Aeroacoustics Characteristics of Squareback Vehicles using Computational Aeroacoustics (CAA). Flow Turbul. Combust. 2024, 112, 1055–1081. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, S.; Farris, S.; Chennuri, N.; Wang, N.; Shinsato, S.; Demir, K.; Horii, M.; Gu, G.X. Towards silent and efficient flight by combining bioinspired owl feather serrations with cicada wing geometry. Nat. Commun. 2024, 15, 4337. [Google Scholar] [CrossRef]
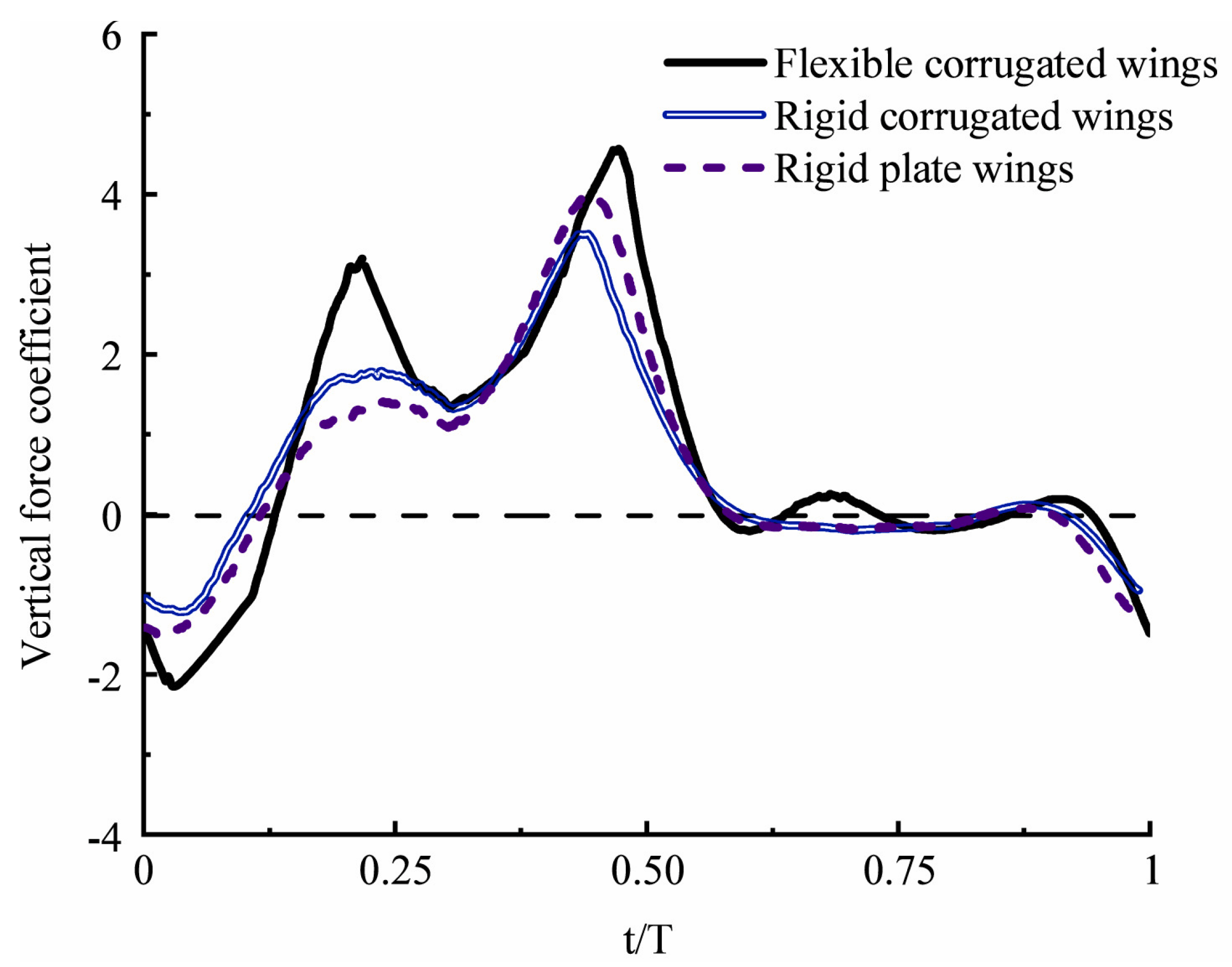
- Sun, W.; Wang, Y.; He, G.; Wang, Q.; Yu, F.; Song, W. Effects of kinematic parameters and corrugated structure on the aerodynamic performance of flexible dragonfly wings. J. Fluids Struct. 2024, 125, 104058. [Google Scholar] [CrossRef]
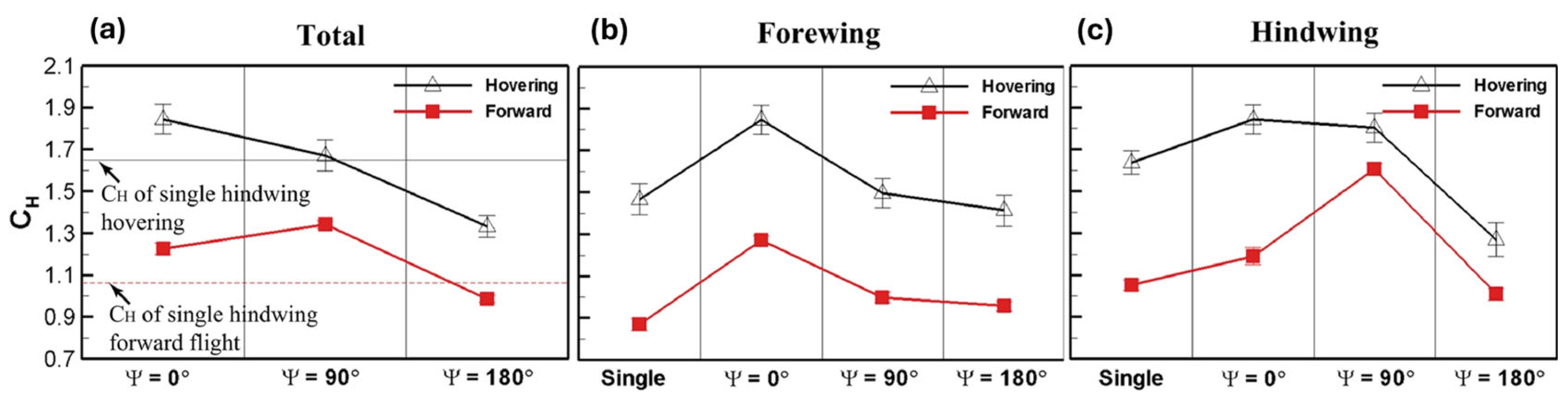
- Peng, L.; Zheng, M.; Pan, T.; Su, G.; Li, Q. Tandem-wing interactions on aerodynamic performance inspired by dragonfly hovering. R. Soc. Open Sci. 2021, 8, 202275. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.; Guo, S.; Tong, M.; Ji, B. Unsteady aerodynamic model of flexible flapping wing. Aerosp. Sci. Technol. 2018, 80, 354–367. [Google Scholar] [CrossRef]
- Yoon, S.-H.; Cho, H.; Lee, J.; Kim, C.; Shin, S.-J. Effects of camber angle on aerodynamic performance of flapping-wing micro air vehicle. J. Fluids Struct. 2020, 97, 103101. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Z.; Zhang, X.; Wang, S. Optimal reduced frequency for the power efficiency of a flat plate gliding with spanwise oscillations. Phys. Fluids 2021, 33, 111908. [Google Scholar] [CrossRef]
- Lehmann, F.-O. Wing–wake interaction reduces power consumption in insect tandem wings. Exp. Fluids 2009, 46, 765–775. [Google Scholar] [CrossRef]
- Shumway, N.; Gabryszuk, M.; Laurence, S. The impact of dragonfly wing deformations on aerodynamic performance during forward flight. Bioinspir. Biomim. 2020, 15, 026005. [Google Scholar] [CrossRef] [PubMed]
- Salami, E.; Montazer, E.; Ward, T.A.; Nik Ghazali, N.N.; Anjum Badruddin, I. Aerodynamic Performance of a Dragonfly-Inspired Tandem Wing System for a Biomimetic Micro Air Vehicle. Front. Bioeng. Biotechnol. 2022, 10, 787220. [Google Scholar] [CrossRef]
- Cho, H.; Gong, D.; Lee, N.; Shin, S.; Lee, S. Combined co-rotational beam/shell elements for fluid–structure interaction analysis of insect-like flapping wing. Nonlinear Dyn. 2019, 97, 203–224. [Google Scholar] [CrossRef]
- Lagopoulos, N.S.; Weymouth, G.D.; Ganapathisubramani, B. Deflected wake interaction of tandem flapping foils. J. Fluid Mech. 2020, 903, A9. [Google Scholar] [CrossRef]
- Wang, Z.J.; Russell, D. Effect of Forewing and Hindwing Interactions on Aerodynamic Forces and Power in Hovering Dragonfly Flight. Phys. Rev. Lett. 2007, 99, 148101. [Google Scholar] [CrossRef]
- Sivasankaran, P.N.; Ward, T.A.; Salami, E.; Viyapuri, R.; Fearday, C.J.; Johan, M.R. An experimental study of elastic properties of dragonfly-like flapping wings for use in biomimetic micro air vehicles (BMAVs). Chin. J. Aeronaut. 2017, 30, 726–737. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, Y.; Tang, H. An experimental study on the forewing–hindwing interactions in hovering and forward flights. Int. J. Heat Fluid Flow 2016, 59, 62–73. [Google Scholar] [CrossRef]
- Broering, T.; Lian, Y. The Effect of Wing Spacing on Tandem Wing Aerodynamics. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar]
- Lua, K.B.; Lu, H.; Zhang, X.H.; Lim, T.T.; Yeo, K.S. Aerodynamics of two-dimensional flapping wings in tandem configuration. Phys. Fluids 2016, 28, 121901. [Google Scholar] [CrossRef]
- Bie, D.; Li, D. Numerical analysis of the wing–wake interaction of tandem flapping wings in forward flight. Aerosp. Sci. Technol. 2022, 121, 107389. [Google Scholar] [CrossRef]
- Rudolph, R. Aerodynamical properties of Libellula quadrimaculata L. (Anisoptera: Libellulidae) and the flow around smooth and cor-rugated wing section models during gliding flight. Odonatologica 1978, 7, 49–58. [Google Scholar]
- Newman, B.; Savage, S.; Schouella, D. Model Tests on a Wing Section of an Aeschna Dragonfly. In Scale Effects in Animal Locomotion; Pedley, T.J., Ed.; Academic Press: London, UK, 1977. [Google Scholar]
- Fujita, Y.; Iima, M. Aerodynamic performance of dragonfly wing model that starts impulsively: How vortex motion works. J. Fluid Sci. Technol. 2023, 18, JFST0013. [Google Scholar] [CrossRef]
- Chin, D.D.; Lentink, D. Flapping wing aerodynamics: From insects to vertebrates. J. Exp. Biol. 2016, 219, 920–932. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, P.; Mehdi, H. Numerical analysis of aerodynamic performance and fluid flow of dragonfly wing section at low Reynold numbers. In AIP Conference Proceedings; AIP Publishing: Rapid City, SD, USA, 2023; p. 020026. [Google Scholar]
- Shi, S.; Liu, Y.; Chen, J. An Experimental Study of Flow Around a Bio-Inspired Airfoil at Reynolds Number 2.0×103. J. Hydrodyn. 2012, 24, 410–419. [Google Scholar] [CrossRef]
- Sun, X.; Gong, X.; Huang, D. A review on studies of the aerodynamics of different types of maneuvers in dragonflies. Arch. Appl. Mech. 2017, 87, 521–554. [Google Scholar] [CrossRef]
- Thomas, A.L.R.; Taylor, G.K.; Srygley, R.B.; Nudds, R.L.; Bomphrey, R.J. Dragonfly flight: Free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms, controlled primarily via angle of attack. J. Exp. Biol. 2004, 207, 4299–4323. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Crowther, W.J. The role of the leading edge vortex in lift augmentation of steadily revolving wings: A change in perspective. J. R. Soc. Interface. 2017, 14, 20170159. [Google Scholar] [CrossRef]
- Shahzad, A.; RCMS NUST; Hamdani, H.R. National University of Sciences & Technology; Aizaz, A. National University of Sciences & Technology Investigation of Corrugated Wing in Unsteady Motion. J. Appl. Fluid Mech. 2017, 10, 833–845. [Google Scholar] [CrossRef]
- Han, C.-S.; Kang, J.-H.; Park, E.H.; Lee, H.-J.; Jeong, S.-J.; Kim, D.-W.; Park, C.-W. Corrugated surface microparticles with chitosan and levofloxacin for improved aerodynamic performance. Asian J. Pharm. Sci. 2023, 18, 100815. [Google Scholar] [CrossRef]
- Sooraj, P.; Sharma, A.; Agrawal, A. Dynamics of co-rotating vortices in a flow around a bio-inspired corrugated airfoil. Int. J. Heat Fluid Flow 2020, 84, 108603. [Google Scholar] [CrossRef]
- Shah, S.H.R.; Mckinney, M.; Shabbir, Z.; Ahmed, A. An Investigation of Varying Peak Height and Leading Edge Roundness on the Aerodynamic Performance of Corrugated Wings at Low Reynolds Number. American Institute of Aeronautics and Astronautics. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Yd, D. Aerodynamic characterization of bio inspired corrugated wings. MOJ Appl. Bionics Biomech. 2019, 3, 1–10. [Google Scholar] [CrossRef]
- Fujita, Y.; Iima, M. Dynamic lift enhancement mechanism of dragonfly wing model by vortex-corrugation interaction. Phys. Rev. Fluids 2023, 8, 123101. [Google Scholar] [CrossRef]
- Ren, H.-H.; Wang, X.-S.; Chen, Y.-L.; Li, X.-D. Biomechanical behaviors of dragonfly wing: Relationship between configuration and deformation. Chin. Phys. B 2012, 21, 034501. [Google Scholar] [CrossRef]
- Xuan, H.; Hu, J.; Yu, Y.; Zhang, J. Aerodynamic effects of corrugation configurations in sweeping- pitching flight. MATEC Web Conf. 2020, 306, 05005. [Google Scholar] [CrossRef]
- Mulligan, R.; Rasool, A. Aerodynamic Performance of Dragonfly-Inspired Corrugated Airfoils. In Proceedings of the 2020 IEEE 23rd International Multitopic Conference (INMIC), Bahawalpur, Pakistan, 5–7 November 2020; pp. 1–5. [Google Scholar]
- Benedetti, L.; Bianchi, G.; Cinquemani, S.; Belloli, M. A numerical study about the flight of the dragonfly: 2D gliding and 3D hovering regimes. bioRxiv 2020. [Google Scholar] [CrossRef]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef]
- Alexander, D.E. Unusual Phase Relationships Between The Forewings And Hindwings In Flying Dragonflies. J. Exp. Biol. 1984, 109, 379–383. [Google Scholar] [CrossRef]
- Anderson, D.F.; Eberhardt, S. Understanding Flight; McGraw-Hill: New York, NY, USA, 2001; ISBN 978-0-07-136377-8. [Google Scholar]
- Lavimi, R.; Hojaji, M.; Dehghan Manshadi, M. Investigation of the aerodynamic performance and flow physics on cross sections of Dragonfly wing on flapping and pitching motion in low Reynolds number. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 589–603. [Google Scholar] [CrossRef]
- Biradar, G.S.; Khan, M.H.; Bankey, S.; Mishra, A.; Joshi, G.; Agrawal, A. Separated Flow Around Dragonfly Inspired Corrugated Airfoil at Large Angle of Attack in Freestream Turbulence. In Recent Advancements in Mechanical Engineering; Sudarshan, T.S., Sharma, A.K., Misra, R.D., Patowari, P.K., Eds.; Lecture Notes in Mechanical Engineering; Springer Nature: Singapore, 2024; pp. 235–246. ISBN 978-981-9708-99-4. [Google Scholar]
- Narita, Y.; Chiba, K. Aerodynamics on a faithful hindwing model of a migratory dragonfly based on 3D scan data. J. Fluids Struct. 2024, 125, 104080. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Li, X.; Fu, Y. Numerical Investigation of the Aerodynamic Characteristics and Attitude Stability of a Bio-Inspired Corrugated Airfoil for MAV or UAV Applications. Energies 2019, 12, 4021. [Google Scholar] [CrossRef]
- Steinle, F.W.; Stanewsky, E. Wind Tunnel Flow Quality and Data Accuracy Requirements; Technical Report; Advisory Group for Aerospace Research and Development (AGARD) [NATO]: Neuilly sur Seine, France, 1982; Available online: https://apps.dtic.mil/sti/tr/pdf/ADA129881.pdf (accessed on 11 March 2025).
- Gorbachev, N.A.; Gorbushin, A.R.; Krapivina, E.A.; Sudakova, I.A. Use of accelerometers for measurement of pitch and bank angles in an aerodynamic experiment. Meas. Sci. Technol. 2012, 55, 883–889. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Nakata, T.; Henningsson, P.; Lin, H.-T. Flight of the dragonflies and damselflies. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150389. [Google Scholar] [CrossRef] [PubMed]
- Hou, D.; Zhong, Z. Comparative analysis of deformation behaviors of dragonfly wing under aerodynamic and inertial forces. Comput. Biol. Med. 2022, 145, 105421. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 4112–4130. [Google Scholar] [CrossRef]
- Norberg, R.Å. The pterostigma of insect wings an inertial regulator of wing pitch. J. Comp. Physiol. 1972, 81, 9–22. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. VI. Lift and power requirements. Phil. Trans. R. Soc. Lond. B 1984, 305, 145–181. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Götz, K.G. The Active Control of Wing Rotation by Drosophila. J. Exp. Biol. 1993, 182, 173–189. [Google Scholar] [CrossRef]
- Uhrhan, M.J.; Bomphrey, R.J.; Lin, H. Flow sensing on dragonfly wings. Ann. N. Y. Acad. Sci. 2024, 1536, 107–121. [Google Scholar] [CrossRef]
- Liu, D. Implications of Passive and Active Pitching on Dragonfly’s Flapping Aerodynamics. Ph.D. Thesis, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong, 2022; p. 991013106348003412. [Google Scholar]
- Liu, D.; Hefler, C.; Shyy, W.; Qiu, H. Implications of dragonfly’s muscle control on flapping kinematics and aerodynamics. Phys. Fluids 2022, 34, 081902. [Google Scholar] [CrossRef]
- Shyy, W.; Aono, H.; Kang, C.; Liu, H. An Introduction to Flapping Wing Aerodynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-1-139-58391-6. [Google Scholar]
- Meng, X.G.; Xu, L.; Sun, M. Aerodynamic effects of corrugation in flapping insect wings in hovering flight. J. Exp. Biol. 2011, 214, 432–444. [Google Scholar] [CrossRef]
- Thill, C.; Etches, J.A.; Bond, I.P.; Potter, K.D.; Weaver, P.M. Composite corrugated structures for morphing wing skin applications. Smart Mater. Struct. 2010, 19, 124009. [Google Scholar] [CrossRef]
- Thill, C.; Downsborough, J.D.; Lai, S.J.; Bond, I.P.; Jones, D.P. Aerodynamic study of corrugated skins for morphing wing applications. Aeronaut. J. 2010, 114, 237–244. [Google Scholar] [CrossRef]
- Tsushima, N.; Yokozeki, T.; Su, W.; Arizono, H. Geometrically nonlinear static aeroelastic analysis of composite morphing wing with corrugated structures. Aerosp. Sci. Technol. 2019, 88, 244–257. [Google Scholar] [CrossRef]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development and Wind Tunnel Test of Variable Camber Morphing Wing. In Proceedings of the 22nd AIAA/ASME/AHS Adaptive Structures Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Dayyani, I.; Ziaei-Rad, S.; Friswell, M.I. The mechanical behavior of composite corrugated core coated with elastomer for morphing skins. J. Compos. Mater. 2014, 48, 1623–1636. [Google Scholar] [CrossRef]
- Dayyani, I.; Khodaparast, H.H.; Woods, B.K.; Friswell, M.I. The design of a coated composite corrugated skin for the camber morphing airfoil. J. Intell. Mater. Syst. Struct. 2015, 26, 1592–1608. [Google Scholar] [CrossRef]
- Bai, J.-B.; Liu, T.-W.; Yang, G.-H.; Xie, C.-C.; Mao, S. A variable camber wing concept based on corrugated flexible composite skin. Aerosp. Sci. Technol. 2023, 138, 108318. [Google Scholar] [CrossRef]
- Ursache, N.M.; Melin, T.; Isikveren, A.T.; Friswell, M.I. Technology Integration for Active Poly-Morphing Winglets Development. In Proceedings of the Smart Materials, Adaptive Structures and Intelligent Systems; ASMEDC: Ellicott City, MD, USA, 2008; Volume 1, pp. 775–782. [Google Scholar]
- Fincham, J.H.; Ajaj, R.M.; Friswell, M.I. Aerodynamic Performance of Corrugated Skins for Spanwise Wing Morphing. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Rechenberg, I. Cybernetic solution path of an experimental problem. R. Aircr. Establ. Libr. Transl. 1965, 1122. [Google Scholar]
- Rechenberg, I. Evolution Strategy: Optimization of Technical Systems by Means of Biological Evolution; Fromman-Holzboog: Stuttgart, Germany, 1973. [Google Scholar]
- Krishna, S.; Cho, M.; Wehmann, H.-N.; Engels, T.; Lehmann, F.-O. Wing Design in Flies: Properties and Aerodynamic Function. Insects 2020, 11, 466. [Google Scholar] [CrossRef]
- Hirooka, S.; Kurahashi, T.; Toyama, S.; Nonami, R. Shape optimization of a corrugated wing to improve lift force. JSIAM Lett. 2024, 16, 117–120. [Google Scholar] [CrossRef]
- Rose, J.B.R.; Natarajan, S.G.; Gopinathan, V.T. Biomimetic flow control techniques for aerospace applications: A comprehensive review. Rev. Envron. Sci. Biotechnol. 2021, 20, 645–677. [Google Scholar] [CrossRef]
- Wehmann, H.-N. Corrugation, Flexibility and Wear of Fly Wings. Doctoral Dissertation, Universität Rostock, Rostock, Germany, 2023. [Google Scholar] [CrossRef]
- Wang, L.; Song, B.; Sun, Z.; Yang, X. Review on ultra-lightweight flapping-wing nano air vehicles: Artificial muscles, flight control mechanism, and biomimetic wings. Chin. J. Aeronaut. 2023, 36, 63–91. [Google Scholar] [CrossRef]
- Najmon, J.C.; Raeisi, S.; Tovar, A. Review of additive manufacturing technologies and applications in the aerospace industry. In Additive Manufacturing for the Aerospace Industry; Elsevier: Amsterdam, The Netherlands, 2019; pp. 7–31. ISBN 978-0-12-814062-8. [Google Scholar]
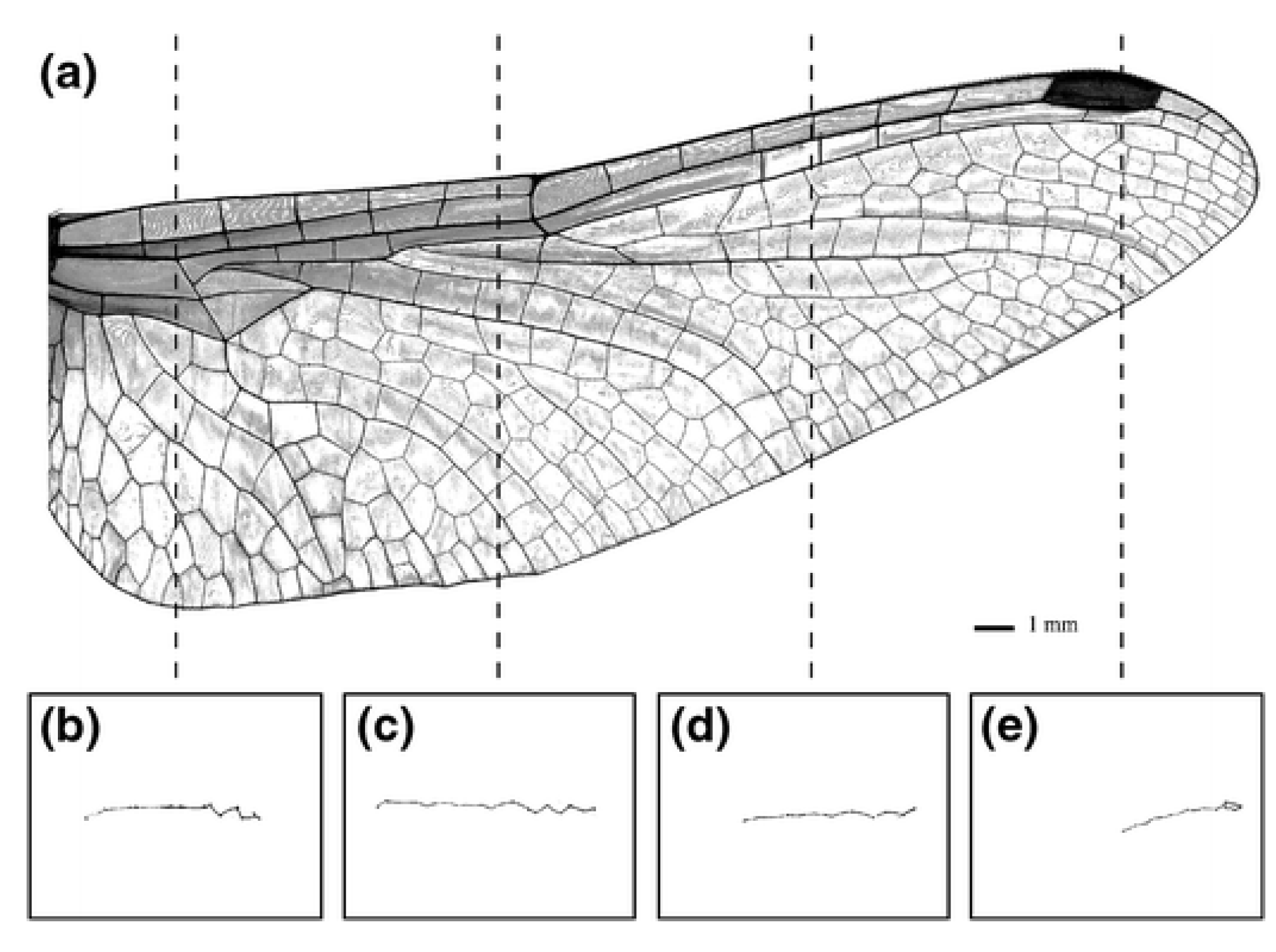
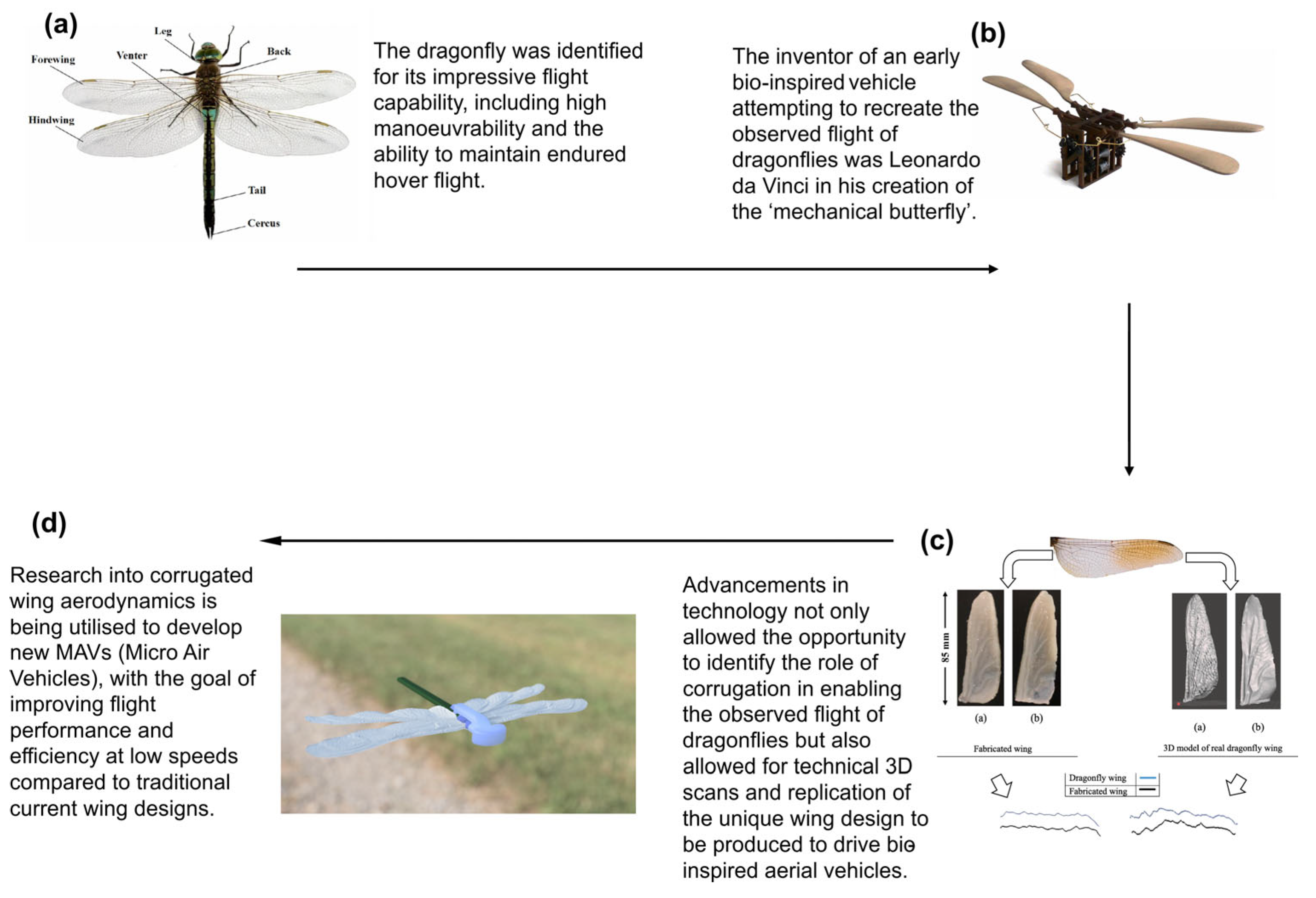

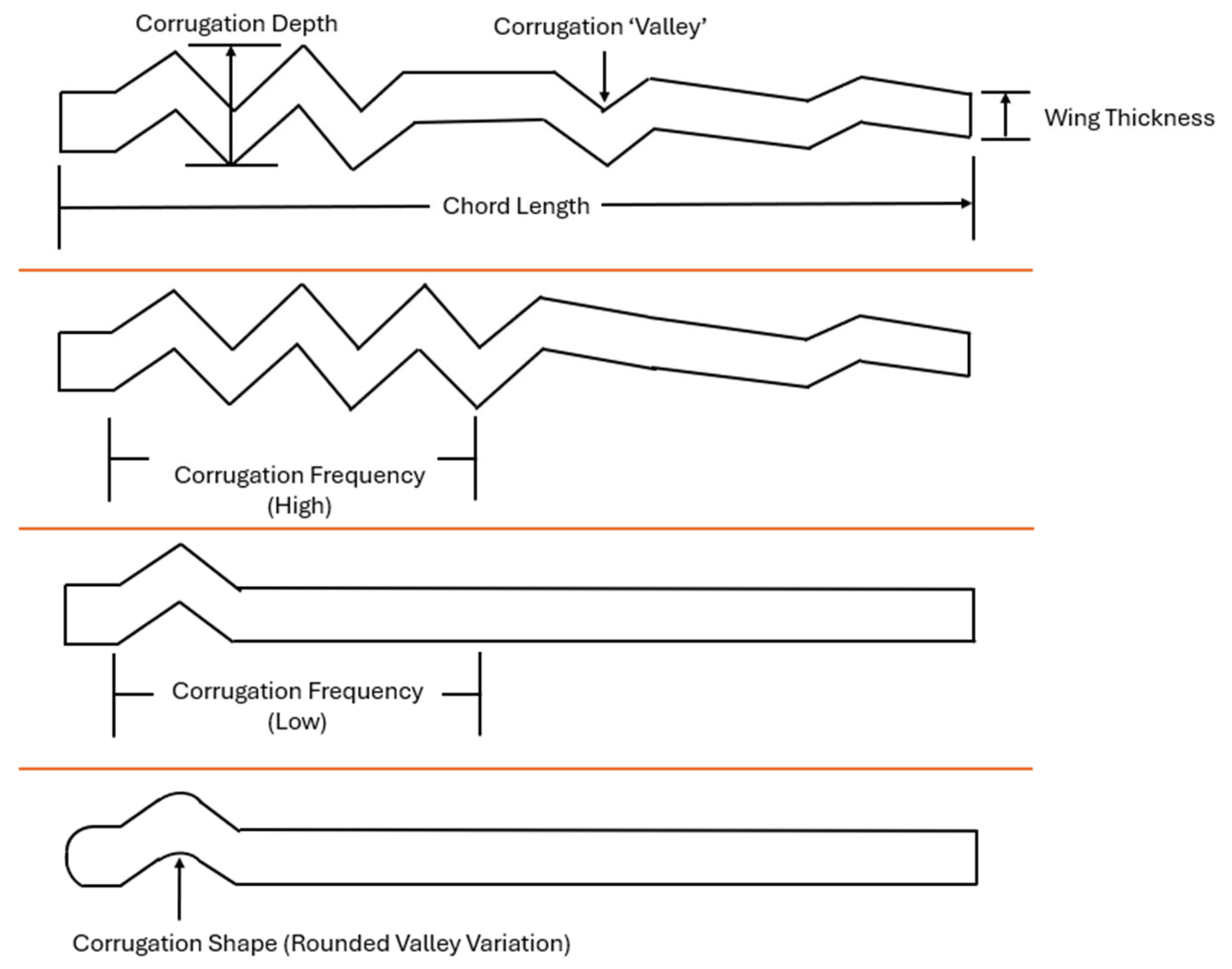
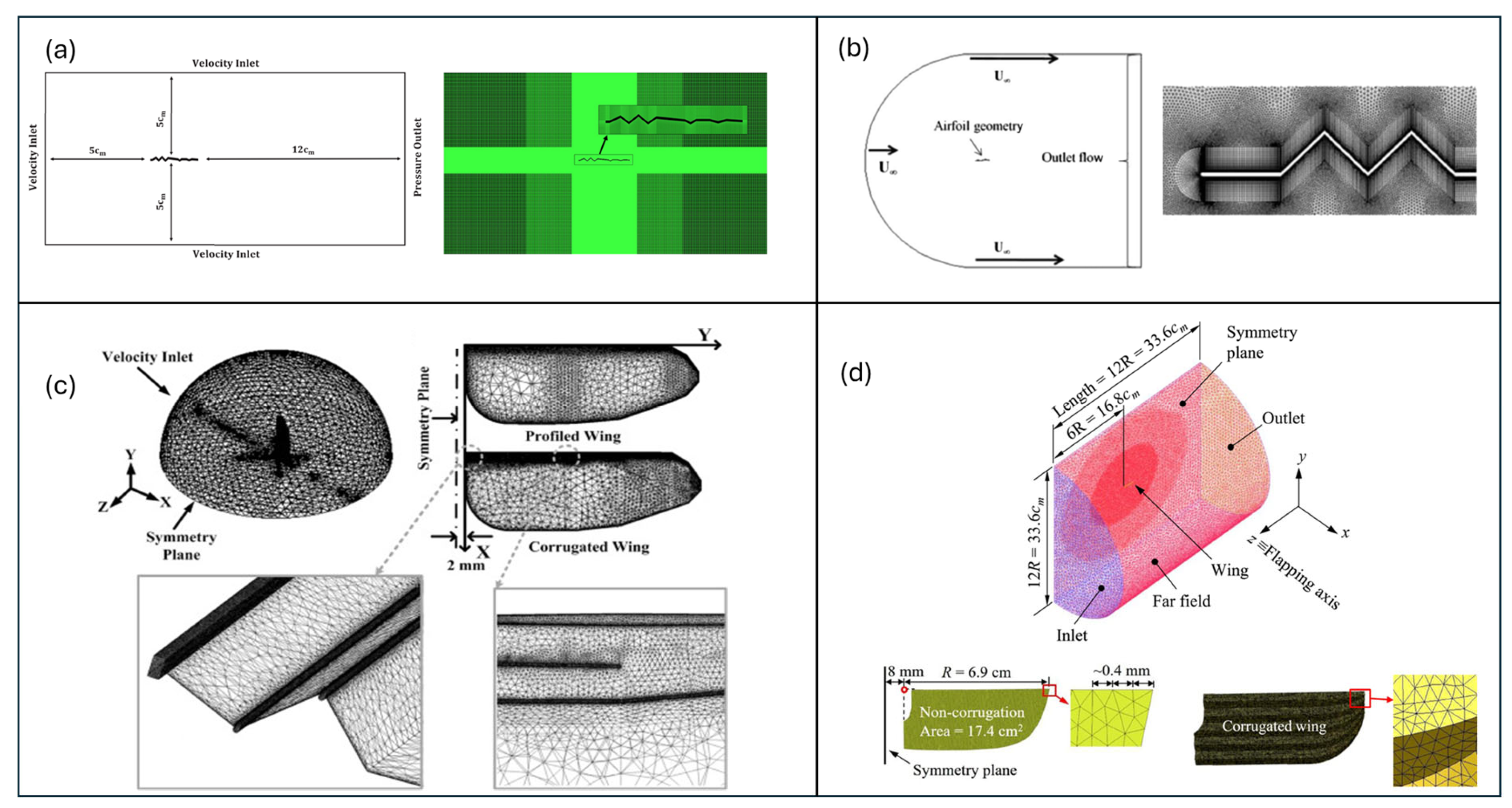

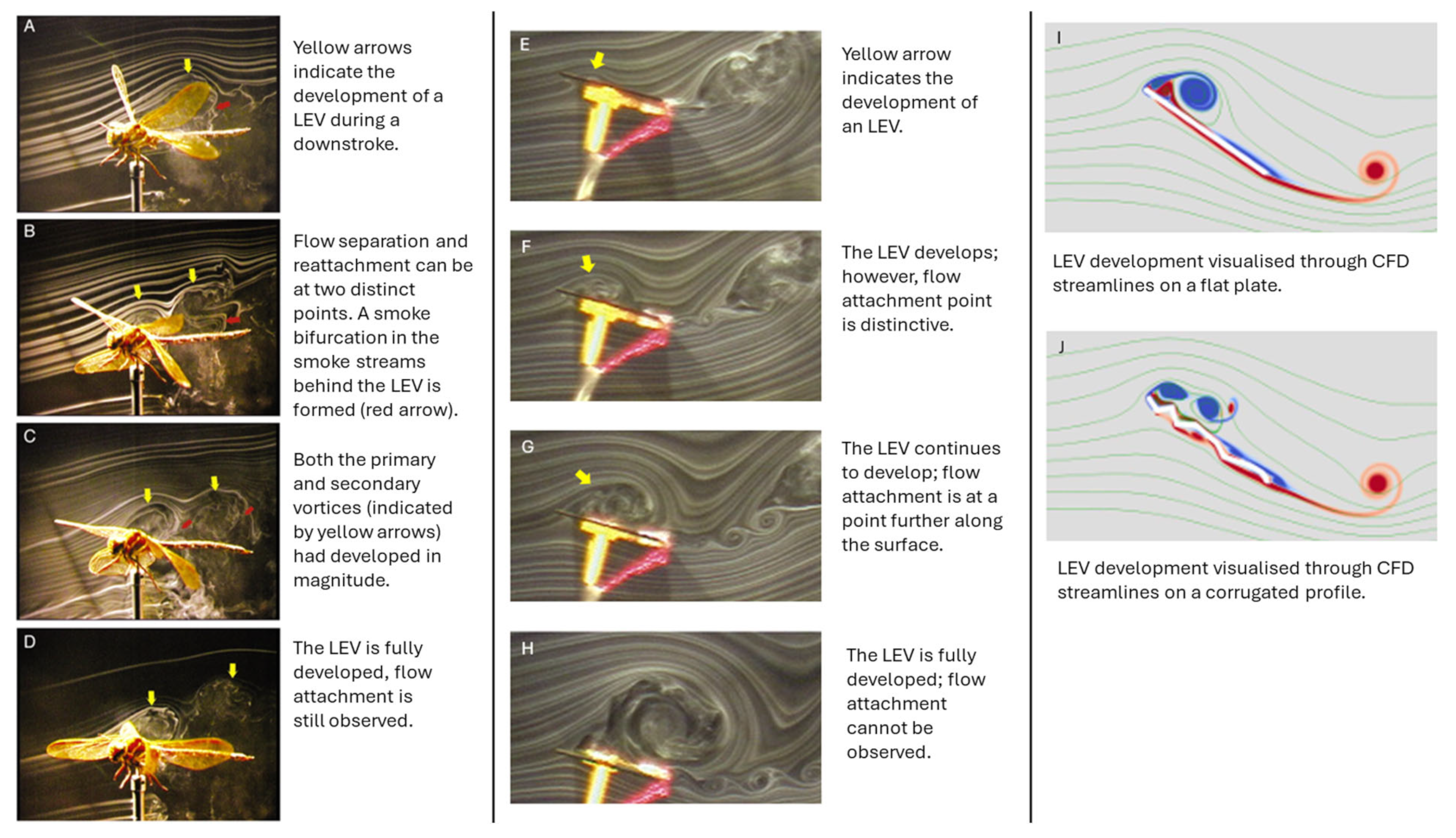
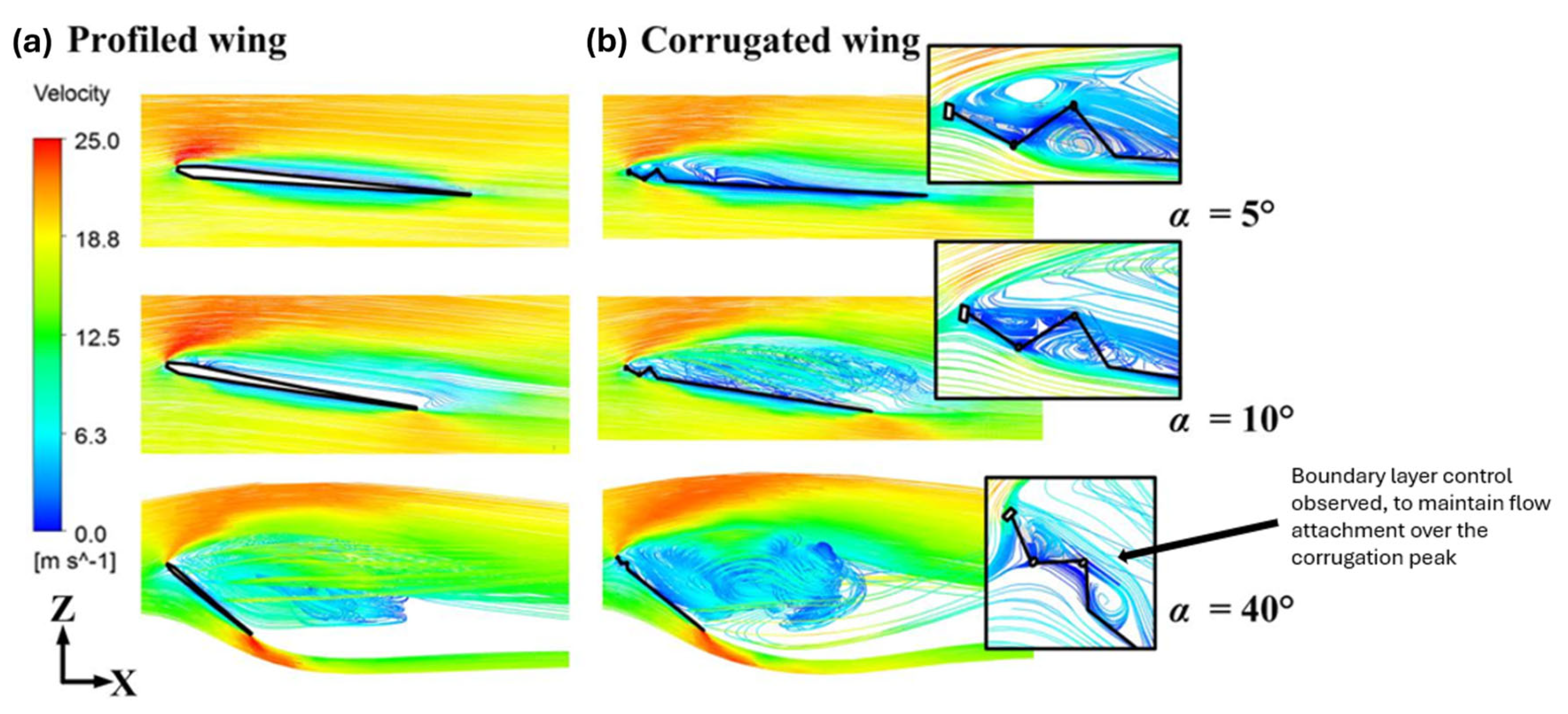


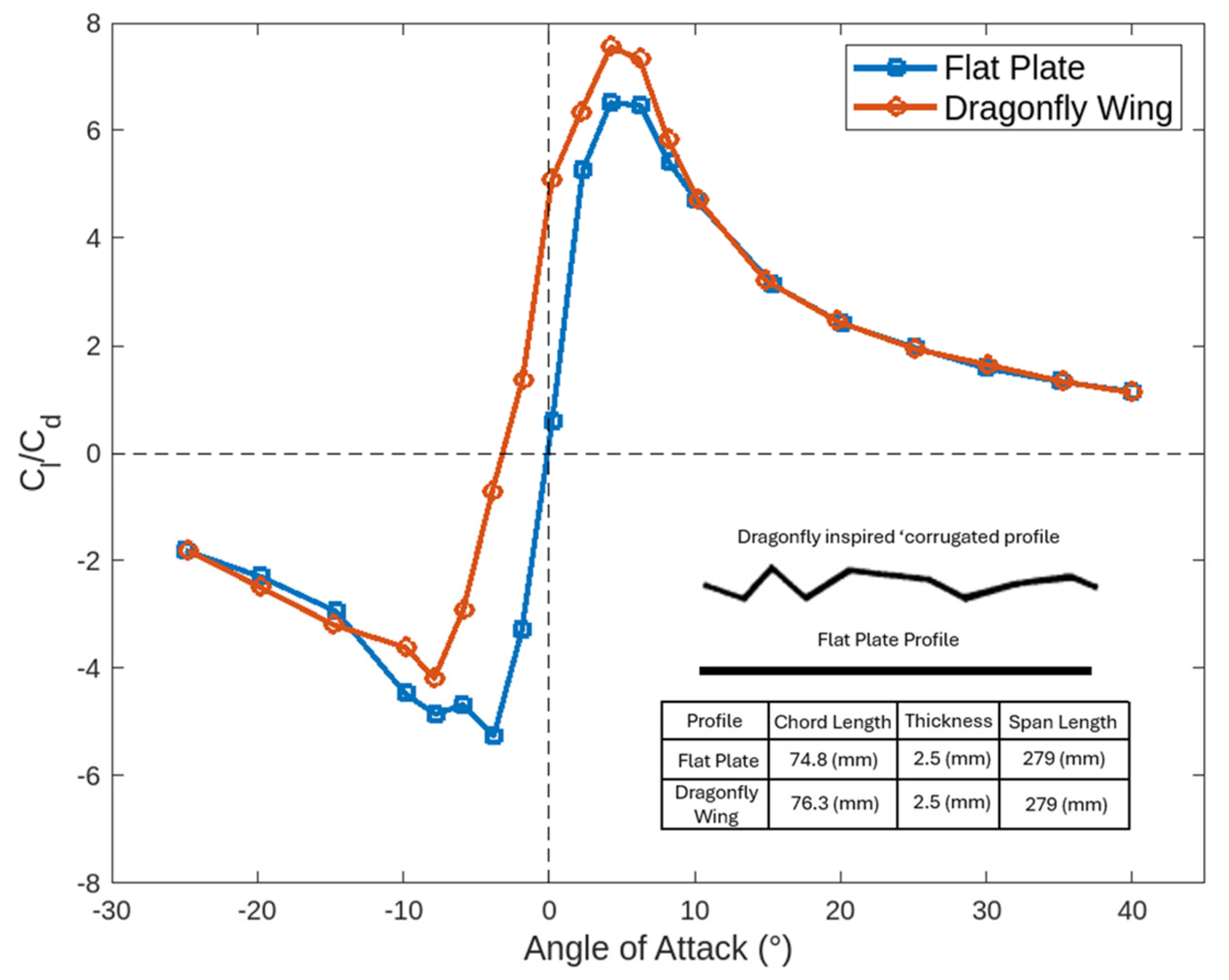
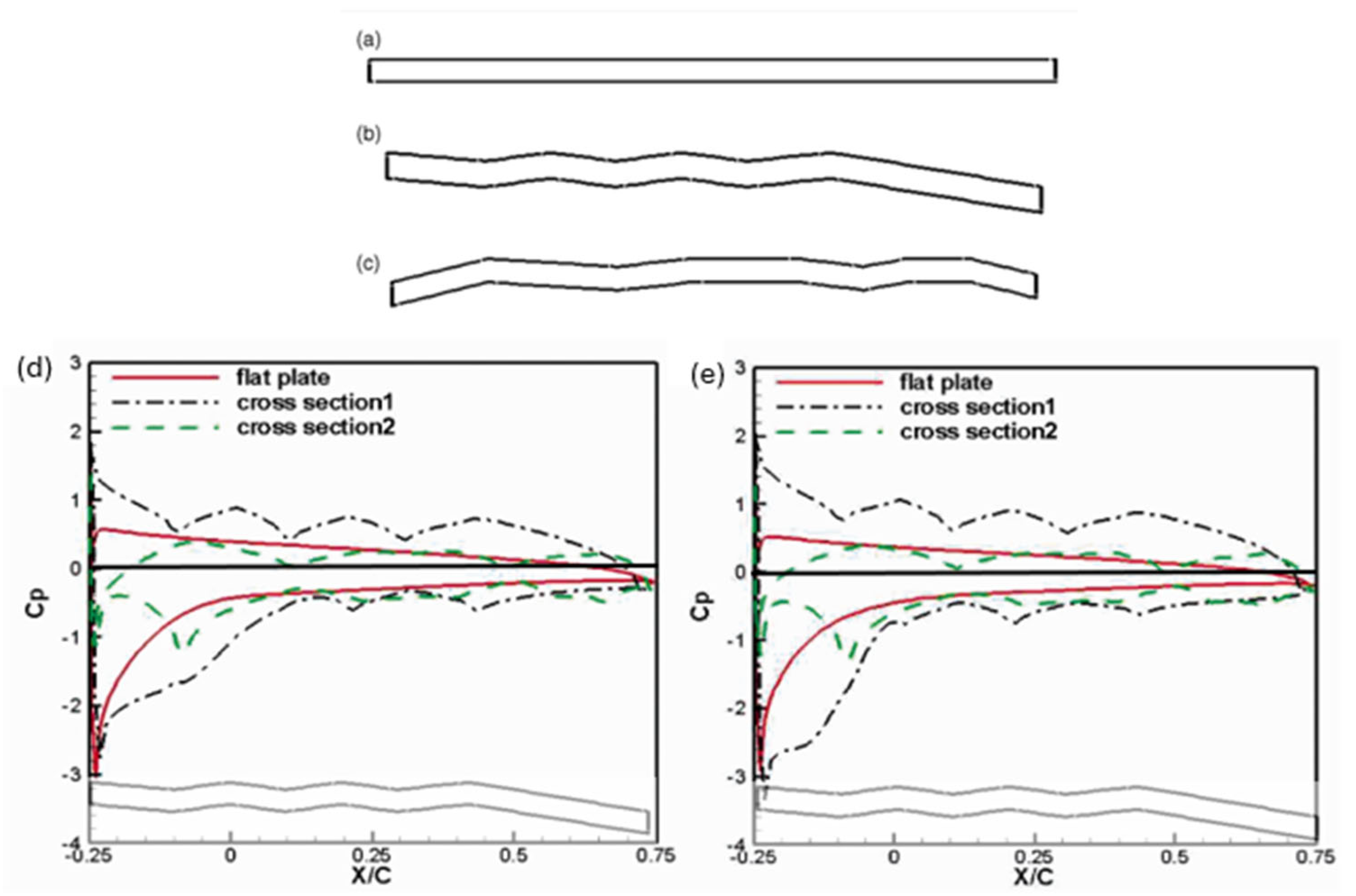

| Parameter | Metrics and Importance | Equation |
|---|---|---|
| Coefficient of Lift—() | Quantifies a wing’s ability to generate lift relative to the dynamic pressure and wing area. It is a critical parameter for assessing aerodynamic performance, particularly in achieving sufficient lift during various flight conditions. | |
| Coefficient of Drag—() | Quantifies the aerodynamic resistance experienced by a wing or body as it moves through air. It is a critical measure for evaluating and minimizing drag forces, directly impacting energy efficiency and overall aerodynamic performance. | |
| Gliding Ratio—() | Represents aerodynamic efficiency, indicating the amount of lift generated relative to drag. A higher ratio signifies better performance, as more lift is produced for a given amount of drag, crucial for optimizing gliding and energy efficiency in flight designs. | |
| Pressure Coefficient—() | Allows for the analysis of pressure distribution across a surface, identifying regions of low pressure and pinpointing critical areas like flow separation points. This information is essential for understanding aerodynamic performance and optimizing designs to minimize drag and enhance lift. | |
| Skin Friction Coefficient—() | Skin friction significantly impacts aerodynamic efficiency by influencing the behavior of the boundary layer, particularly its transition from laminar-to-turbulent flow. This, in turn, affects drag and overall performance, making it a critical factor in optimizing aerodynamic designs. | |
| Reynolds Number—() | A dimensionless number quantifies the ratio of inertial forces to viscous forces in a fluid flow. It characterizes the flow behavior (laminar or turbulent) and facilitates direct comparisons across varying flow conditions, including chord lengths, velocity, and fluid properties. | |
| Strouhal Number—() | A dimensionless number that is important for predicting unsteady flow phenomena such as vortex shedding. It relates the oscillatory frequency of a flow structure to its characteristic length and velocity, providing insights into flow stability and periodicity in aerodynamics. | |
| Stall Angle—(°) | The stall angle refers to the critical angle of attack at which a wing operates efficiently before experiencing a rapid loss of lift due to flow separation. Identifying this angle is essential for optimizing aerodynamic performance and avoiding stall in flight conditions. | - |
| Parameter | Metrics and Description |
|---|---|
| Corrugation Depth | The height of the valleys impacts boundary layer control mechanisms. |
| Corrugation Frequency | The number of corrugations along the chord affects flow behavior. |
| Corrugation Shape | The edge and peak shapes, from rounded to sharp, influence flow separation and lift. |
| Material of the Wing | Impacts skin friction and boundary layer dynamics. |
| Wing Thickness | Affects structural integrity and aerodynamic drag. |
| Wing Configuration | Tandem or isolated configurations influence overall aerodynamic efficiency. |
| Study Parameters and Experimental Description | Reynolds Number | References |
|---|---|---|
| Scaled model in a water channel for fluid flow with beam analysis (structural). | 450, 800, 900 | [33,34] |
| Flight performance of a dragonfly using wind tunnel and high-speed videography. | 35,000–60,000 | [35] |
| Dragonfly flight (gliding, flapping flight and power requirements) using wind tunnel and high-speed videography. | 700–2400 | [9,36,37] |
| Comparison between dragonfly wing sections and technical aerofoils using an open-circuit wind tunnel. | 10,000 | [1] |
| Detailed quantitative flow measurements of the flow over a corrugated aerofoil using a low-speed wind tunnel and PIV for MAV applications. | 34,000 | [38] |
| Similar to [38], but considered a wider range of Reynolds number. | 58,000–125,000 | [39] |
| Developed a method for the 3D reconstruction of a dragonfly wing and tested the fabricated model in a low-speed wind tunnel with PIV. | 5000, 8000, 12,000 | [22] |
| Effects of compressibility on the aerodynamics of a simplified corrugated aerofoil using a “Mars Wind Tunnel” with force measurements, pressure sensitive paint, and schlieren imagery. | 10,000–25,000 | [40] |
| Wind tunnel experiments with MAVs equipped with bio-inspired corrugated and profiled wings, using PIV for flow analysis. | 80,000–130,000 | [16] |
| Study Parameters and Numerical Methodology | Reynolds Number | References |
|---|---|---|
| Corrugated wing from [1]. 2D—Unsteady (CFD) | 500–10,000 | [5] |
| Simplified dragonfly aerofoil of Newman’s gliders. 2D—Unsteady (CFD) | 2000–8000 | [44,45] |
| The interaction between forewing and hindwing in gliding dragonfly flight. 2D—Unsteady (CFD) | 300–2000 | [46] |
| Corrugated wing from [1]. 2D (CFD)—Unsteady and static 3D (FEA) | 500–2000 | [47] |
| Simplified corrugated wing sections. 3D—Unsteady (CFD) | 200–2400 | [48] |
| Corrugated wing from [1]. 3D—Unsteady (CFD) | 1000–10,000 | [15] |
| Flapping Tandem wings (aerofoil and flat plate) and corrugated wing form [1]. 2D—Unsteady (CFD) and static 3D (FEA) | 1000 | [49] |
| Reconstruction of the model from [1]. 3D—Unsteady (CFD) | 1400, 10,000 | [50] |
| Two corrugated wings from [1,45]. 2D—Unsteady (CFD) | 14,000 | [51] |
| Corrugated wing form [1] in gliding and flapping phases. 2D—Unsteady (CFD) | 200, 4000 | [2] |
| Newly designed corrugated structure. 2D—Steady (CFD) and static 3D (FEA) | 15,632 | [52] |
| A realistic dragonfly wing. 2D—Unsteady (CFD) | 10,000 | [53] |
| Aerofoils with corrugated skin in tandem. 3D—Unsteady (CFD) | 120,000 | [54] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lurans, E.; Alhinai, A.; Viswanathan, H. Aerodynamics of Corrugated Wings: Past, Present, and Future. Aerospace 2025, 12, 262. https://doi.org/10.3390/aerospace12030262
Lurans E, Alhinai A, Viswanathan H. Aerodynamics of Corrugated Wings: Past, Present, and Future. Aerospace. 2025; 12(3):262. https://doi.org/10.3390/aerospace12030262
Chicago/Turabian StyleLurans, Eduards, Almajd Alhinai, and Harish Viswanathan. 2025. "Aerodynamics of Corrugated Wings: Past, Present, and Future" Aerospace 12, no. 3: 262. https://doi.org/10.3390/aerospace12030262
APA StyleLurans, E., Alhinai, A., & Viswanathan, H. (2025). Aerodynamics of Corrugated Wings: Past, Present, and Future. Aerospace, 12(3), 262. https://doi.org/10.3390/aerospace12030262







