Conjugate Heat Transfer Characteristics in a Highly Thermally Loaded Film Cooling Configuration with TBC in Syngas
Abstract
:1. Introduction
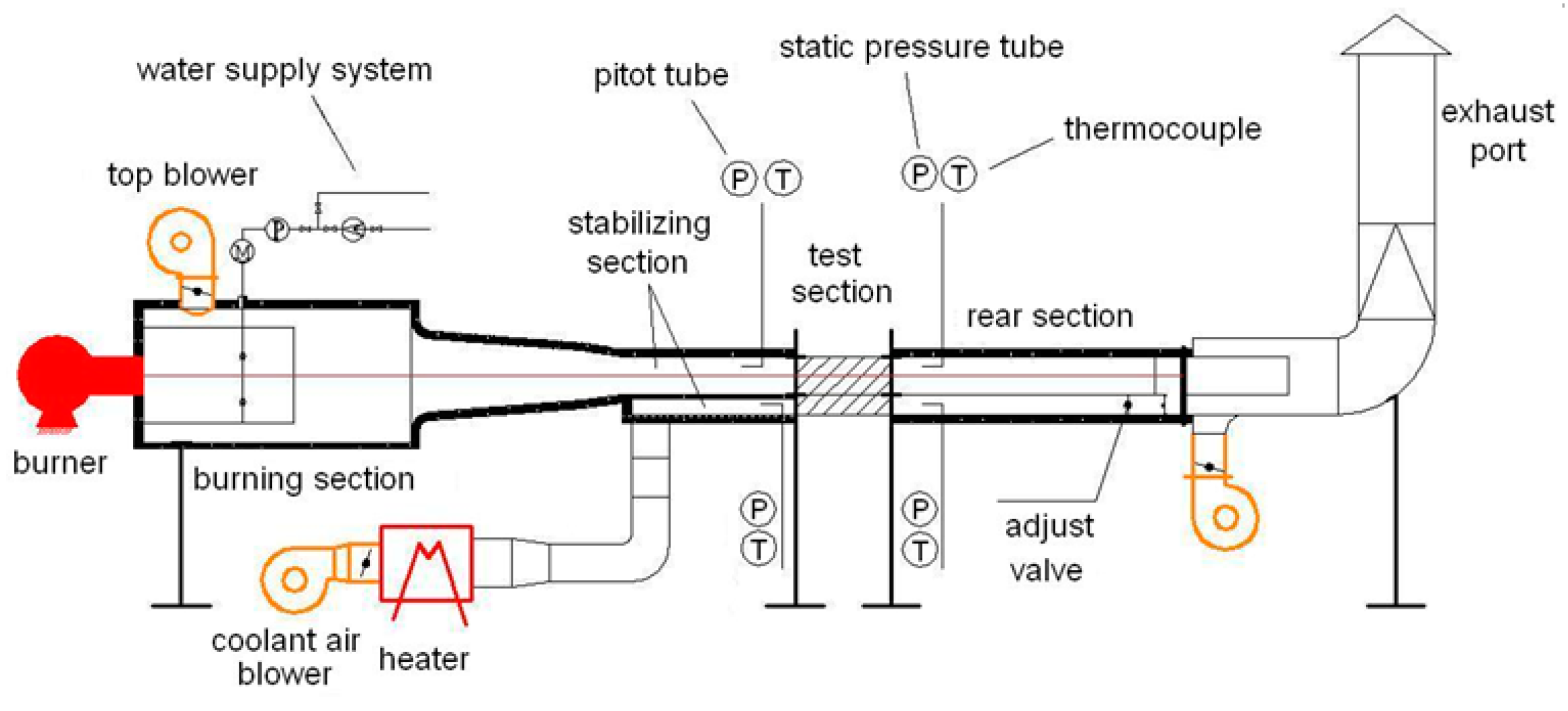
2. Experimental Apparatus
2.1. Hot Gas and Coolant Air Supply Systems
2.2. Test Section
2.3. Measurement System
3. Numerical Methodology
3.1. Test Section Radiation Model
3.2. Spectral Model
3.3. Computational Geometry and Domain
3.4. Turbulence Model and Boundary Conditions
3.5. Material Parameters
3.6. Validation of the Numerical Algorithm
4. Results and Discussion
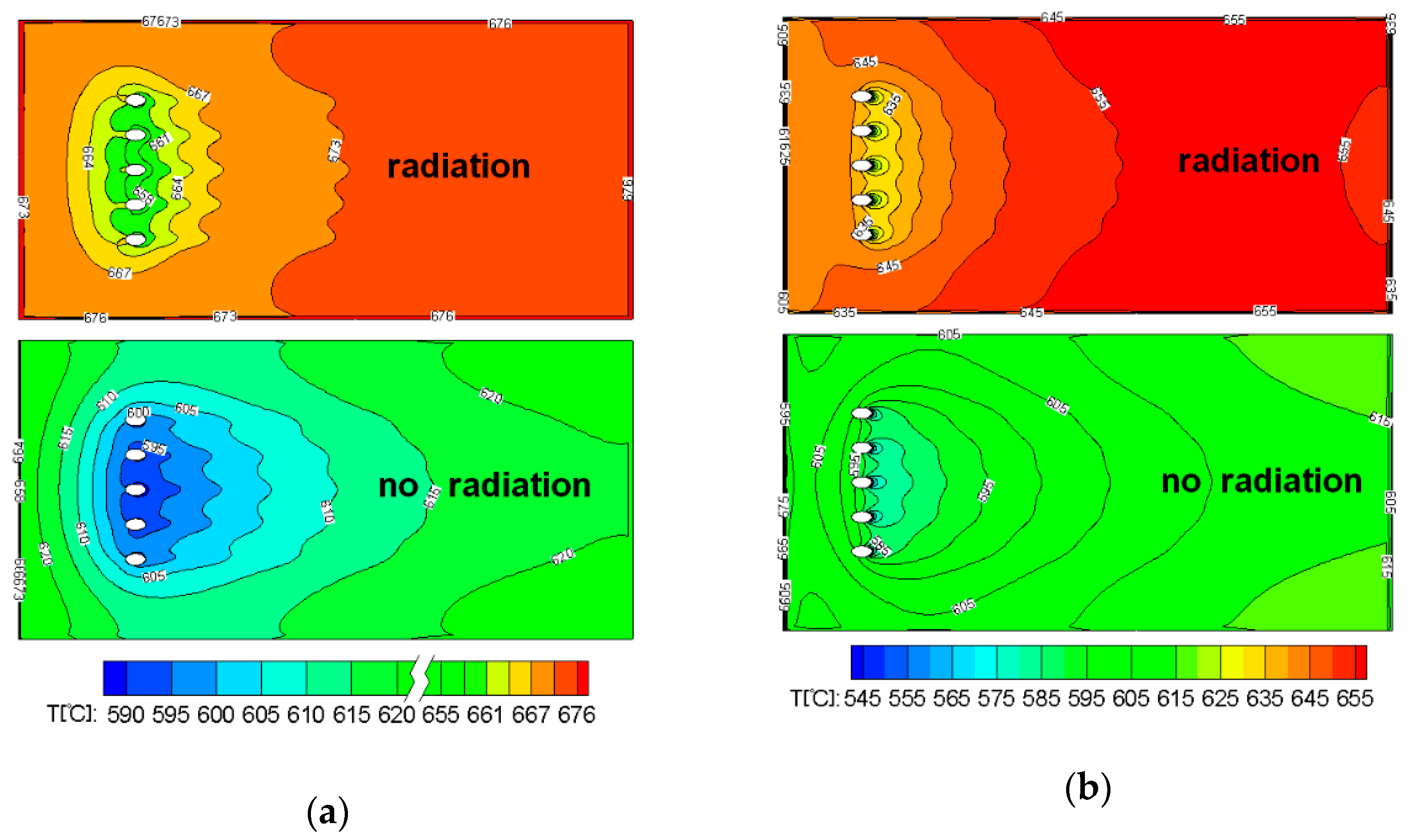
4.1. Effect of Radiative Heat Transfer
4.2. Effect of Hot Gas Composition
4.3. Effect of Thermal Barrier Coating (TBC)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Emission weighting factor | (-) | |
| Diameter of the hole | (m) | |
| Spectral black body emission intensity | (Wm−3sr−1) | |
| Spectral radiation intensity | (Wm−3sr−1) | |
| Radiation Intensity leaving the boundary | (Wm−3sr−1) | |
| Spectral absorption coefficient | (m−1) | |
| Spectral scattering coefficient | (m−1) | |
| Absorption coefficient | (m−1) | |
| Length of the hole | (m) | |
| Number of gray gases | (-) | |
| Position vector | (m) | |
| S | Radiation intensity source term | (Wm−4sr−1) |
| Path length | (m) | |
| Direction vector | (m) | |
| T | Temperature | (K) |
| Cartesian coordinates | (m) | |
| Dimensionless wall distance | (-) |
Greeks
| ε | Total gas emissivity | (-) |
| η | Normalized temperature | (-) |
| Frequency | (s−1) | |
| Solid angle | (sr) |
Subscripts
| Coolant flow | |
| Gas | |
| Index | |
| w | Wall |
Acronyms
| DTM | Discrete transfer model |
| RTE | Radiation transport equation |
| WSGG | Weighted sum of gray gases |
References
- Mazzotta, D.W.; Chyu, M.K.; Alvin, M.A. Airfoil Heat Transfer Characteristics in Syngas and Hydrogen Turbines; ASME Paper, No. GT2007-28296; ASME: New York, NY, USA, 2007. [Google Scholar]
- Bohn, D.; Bonhoff, C. Combined Aerodynamic and Thermal Analysis of a Turbine Nozzle Guide Vane; IGTC Paper 95-108; Gas Turbine Society of Japan: Tokyo, Japan, 1995. [Google Scholar]
- Bohn, D.; Heuer, T. Conjugate Flow and Heat Transfer Calculation of a High Pressure Turbine Nozzle Guide Vane. In Proceedings of the 37th Joint Propulsion Conference and Exhibit, Salt Lake City, UT, USA, 8–11 July 2001. [Google Scholar]
- Bohn, D.; Becker, V.; Kusterer, K.; Otsuki, Y.; Sugimoto, T.; Tanaka, R. 3-D Internal Conjugate Calculations of a Convectively Cooled Turbine Blade with Serpentine-Shaped Ribbed Channels. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar]
- Bohn, D.; Ren, J.; Kusterer, K. Conjugate Heat Transfer Analysis for Film Cooling Configurations with Different Hole Geometry. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003. [Google Scholar]
- Hansmann, T.; Wilhelmi, H.; Bohn, D. An Experimental Investigation of the Film-Cooling Process at High Temperatures and Velocities. In Proceedings of the 5th International Aerospace Planes and Hypersonics Technologies Conference, Munich, Germany, 30 November–3 December 1993. [Google Scholar]
- Bohn, D.; Becker, V. 3-D Conjugate Flow and Heat Transfer Calculations of Film-Cooled Turbine Guide Vane at Different Operation Conditions. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, Florida, USA, 2–5 June 1997. [Google Scholar]
- Mansour, M.L.; Hosseini, K.M.; Liu, J.S. Assessment of the Impact of Laminar-Turbulent Transition on the Accuracy of Heat Transfer Coefficient Prediction in High Pressure Turbines. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Heidmann, J.D.; Kassab, A.; Divo, E.A.; Rodriguez, F.; Steinthorsson, E. Conjugate Heat Transfer Effects on a Realistic Film-Cooled Turbine Vane. In Proceedings of the ASME Turbo Expo 2003, collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA,, 16–19 June 2003. [Google Scholar]
- Hylton, L.D.; Milhec, M.S.; Turner, E.R.; Nealy, D.A.; York, R.E. Analytical and Experimental Evaluation of the Heat Transfer Distribution Over the Surface of Turbine Vanes; NASA CR-168015; NASA: Washington, DC, USA, 1983.
- Hylton, L.D.; Nirmalan, V.; Sultanian, B.K.; Kaufman, R.M. The Effects of Leading Edge and Downstream Film Cooling on Turbine Vane Heat Transfer; NASA CR-182133; NASA: Washington, DC, USA, 1988.
- Dees, J.E.; Bogard, D.G.; Ledezma, G.A.; Laskowski, G.M. Overall and Adiabatic Effectiveness Values on a Scaled Up, Simulated Gas Turbine Vane: Part I—Experimental Measurements. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 571–582. [Google Scholar]
- Ledezma, G.A.; Laskowski, G.M.; Dees, J.E.; Bogard, D.G. Overall and Adiabatic Effectiveness Values on a Scaled Up, Simulated Gas Turbine Vane: Part II—Numerical Simulations. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June; pp. 595–605.
- Dees, J.E.; Bogard, D.G.; Ledezma, G.A.; Laskowski, G.M. The Effects of Conjugate Heat Transfer on the Thermal Field above a Film Cooled Wall. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 607–617. [Google Scholar]
- Kumar, A.; Kale, S.R. Numerical simulation of steady state heat transfer in a ceramic-coated gas turbine blade. Int. J. Heat Mass Transf. 2002, 45, 4831–4845. [Google Scholar] [CrossRef]
- He, Z.H.; Tan, H.P.; Liu, L.H.; Feng, G.T.; Ruan, L.M. Numerical computation on blade channel radiation in engine. J. Propuls. Technol. 2001, 22, 65–68, 88. [Google Scholar]
- Zhang, L.; Liu, Z.; Lian, X. Numerical study of 3D heat transfer for turbine blade with air cooling. J. Aerosp. Power 2007, 22, 1268–1272. [Google Scholar]
- Akwaboa, S.; Mensah, P.; Diwan, R. Effects of Thermal Radiation on Air Plasma Spray (APS) Coated Gas Turbine Blade. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Mazzotta, D.W.; Karaivanov, V.G.; Chyu, M.K.; Slaughter, W.S. Gas-Side Heat Transfer in Syngas, Hydrogen-Fired and Oxy-Fuel Turbines. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Na, S.; Dennis, R.A.; Alsup, C.; Bryden, K.M.; Shih, T.I.-P. Effects of Hot-Gas Composition on Temperature Distribution in a Flat Plate Cooled by Internal and Film Cooling. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009. [Google Scholar]
- Moliere, M. Hydrogen-fuelled gas turbines: Status and prospects. In Proceedings of the 2nd CAME-GT conference, Bled, Slovenia, 29–30 April 2004. [Google Scholar]
- Feuerstein, A.; Knapp, J.; Taylor, T.; Ashary, A.; Bolcavage, A.; Hitchman, N. Technical and economical aspects of current thermal barrier coating systems for gas turbine engines by thermal spray and EBPVD: A review. J. Therm. Spray Technol. 2008, 17, 199–213. [Google Scholar] [CrossRef]
- Bohn, D.; Krewinkel, R. Influence of a Broken-Away TBC on the Flow Structure and Wall Temperature of an Effusion Cooled Multi-Layer Plate Using the Conjugate Calculation Method. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 351–362. [Google Scholar]
- Davidson, F.T.; Dees, J.E.; Bogard, D.G. An Experimental Study of Thermal Barrier Coatings and FilmCooling on an Internally Cooled Simulated Turbine Vane. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 559–570. [Google Scholar]
- Cui, Y.F.; Xu, G.; Yu, B.; Nie, C.Q.; Huang, W.G. The Effects of Pressure on Gas Turbine Combustor Performance: An Investigation via Numerical Simulation. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Smith, T.F.; Shen, Z.F.; Friedman, J.N. Evaluation of Coefficients for the Weighted Sum of Gray Gases Model. Trans. ASME 1982, 104, 602–608. [Google Scholar] [CrossRef]
- Krishnamoorthy, G. A New Weighted-Sumof-Gray-Gases Model for CO2-H2O Gas Mixtures. Int. Commun. Heat Mass Transf. 2010, 37, 1182–1186. [Google Scholar] [CrossRef]
- Sun, P.; Wang, W.; Ren, J.; Jiang, H. Effect of the Hot Gas Composition on a Highly Thermally Loaded Film Cooling System. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Kermanpur, A.; Varahram, N.; Davami, P.; Rappaz, M. Thermal and Grain-Structure Simulation in a Land-Based Turbine Blade Directionally Solidified with the Liquid Metal Cooling Process. Metall. Mater. Trans. B 2000, 31, 1293–1304. [Google Scholar] [CrossRef]
- Hottel, H.C.; Noble, J.J.; Sarofim, A.F.; Green, D.W.; Perry, R.H. Chapter 5: Heat and Mass Transfer. In Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- ‘‘REFPROP: (NIST).”. Available online: http://www.boulder.nist.gov/div838/theory/refprop/Frequently_asked_questions.htm#Updates. (accessed on 12 November 2018).
- Wang, W.; Sun, P.; Ren, J.; Jiang, H. Radiative Effectiveness on the Aero- and Thermodynamics in a Highly Thermally Loaded Film Cooling System. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Li, M.; Yin, H.; Ren, J.; Jiang, H. Conjugate Heat Transfer Characteristics of a Highly Thermal-Loaded Film Cooling System in Hot and Multicomposition Gas Condition. J. Heat Transf. 2015, 138, 024503. [Google Scholar] [CrossRef]












| Thermal Couple Positions | 1 | 2 | 3 | 4 | 5 | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|---|---|---|---|---|
| Distance from the trailing edge of the hole to the thermocouple | 1 D | 2 D | 5 D | 10 D | 17 D | 20 D | 25 D | 30 D | 35 D | 40 D |
| Compositions (Volume %) | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| H2O | 11.86 | 22.34 | 26.15 |
| CO2 | 5.28 | 7.14 | 7.80 |
| O2 | 10.26 | 5.55 | 3.87 |
| N2 | 72.60 | 64.97 | 62.18 |
| Parameters | Mainstream | Coolant Flow |
|---|---|---|
| Inlet Temperature (°C) | 800 | 389 |
| Inlet Mass Flow Rate (kg/s) | 0.217 | 0.140 |
| Outlet Pressure (pa) | 101,407 | 101,428 |
| Type of Fuel | Mole fraction (%) | ||||
|---|---|---|---|---|---|
| CO2 | H2O | N2 | Ar | O2 | |
| LPG | 4.44 | 12.34 | 71.50 | 0.00 | 11.72 |
| NG | 5.66 | 11.08 | 74.66 | 0.00 | 8.60 |
| syn | 9.27 | 8.50 | 72.80 | 0.80 | 8.63 |
| H2 | 1.40 | 17.30 | 72.20 | 0.90 | 8.20 |
| oxy | 16.00 | 82.00 | 1.10 | 0.80 | 0.10 |
| Compostions (Volume %) | Case 1 without TBC | Case 1 with TBC | Case 2 without TBC | Case 2 with TBC | Case 3 without TBC | Case 3 with TBC |
|---|---|---|---|---|---|---|
| H2O | 11.86 | 11.27 | 22.34 | 22.66 | 26.15 | 25.01 |
| CO2 | 5.28 | 6.13 | 7.14 | 6.23 | 7.80 | 8.65 |
| O2 | 10.26 | 10.07 | 5.55 | 5.25 | 3.87 | 4.94 |
| N2 | 72.60 | 72.53 | 64.97 | 65.86 | 62.18 | 61.40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Li, X.; Jiang, H. Conjugate Heat Transfer Characteristics in a Highly Thermally Loaded Film Cooling Configuration with TBC in Syngas. Aerospace 2019, 6, 16. https://doi.org/10.3390/aerospace6020016
Ren J, Li X, Jiang H. Conjugate Heat Transfer Characteristics in a Highly Thermally Loaded Film Cooling Configuration with TBC in Syngas. Aerospace. 2019; 6(2):16. https://doi.org/10.3390/aerospace6020016
Chicago/Turabian StyleRen, Jing, Xueying Li, and Hongde Jiang. 2019. "Conjugate Heat Transfer Characteristics in a Highly Thermally Loaded Film Cooling Configuration with TBC in Syngas" Aerospace 6, no. 2: 16. https://doi.org/10.3390/aerospace6020016
APA StyleRen, J., Li, X., & Jiang, H. (2019). Conjugate Heat Transfer Characteristics in a Highly Thermally Loaded Film Cooling Configuration with TBC in Syngas. Aerospace, 6(2), 16. https://doi.org/10.3390/aerospace6020016





