An Insight on the Crashworthiness Behavior of a Full-Scale Composite Fuselage Section at Different Impact Angles
Abstract
:1. Introduction
2. Theoretical Background
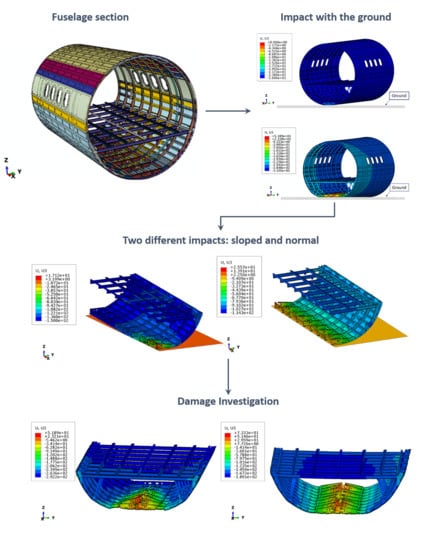
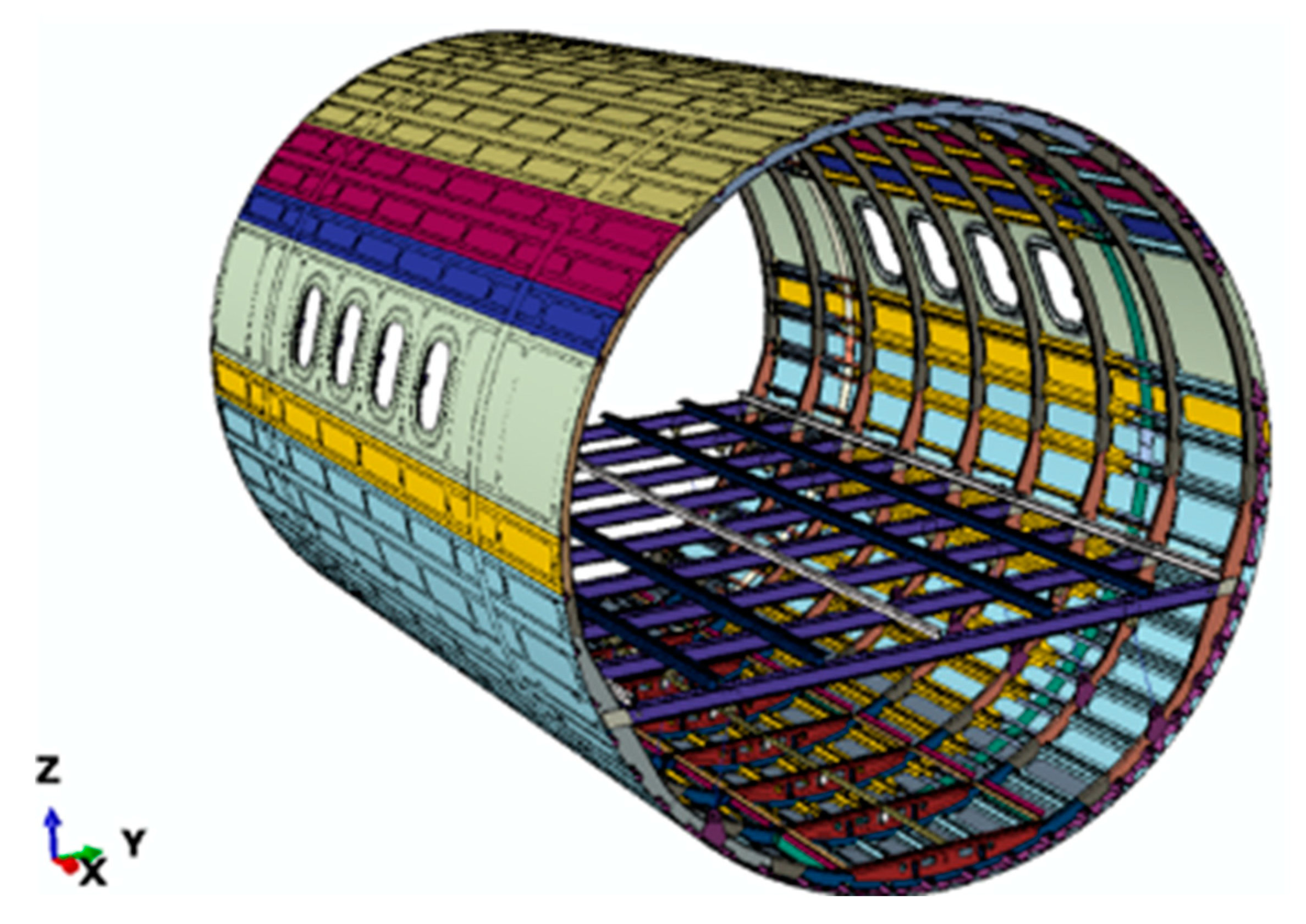
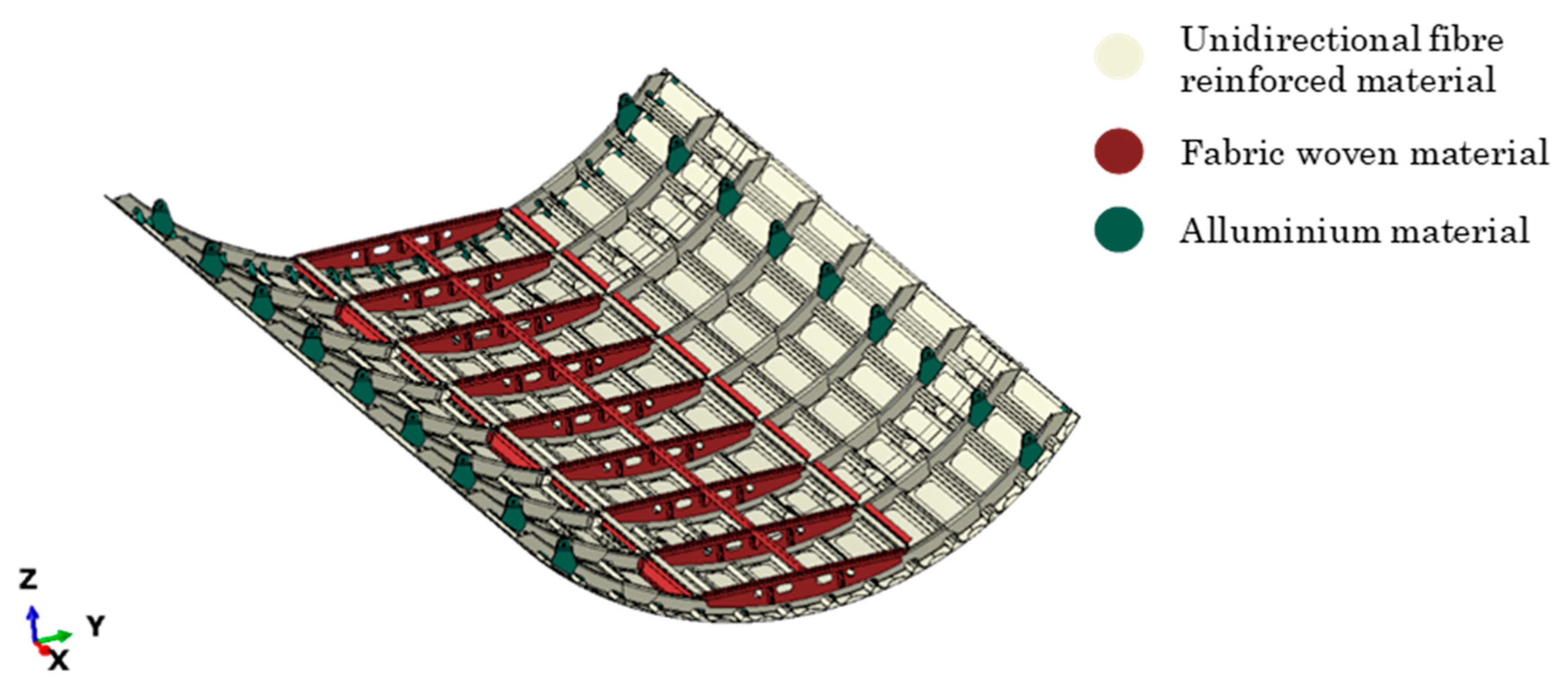
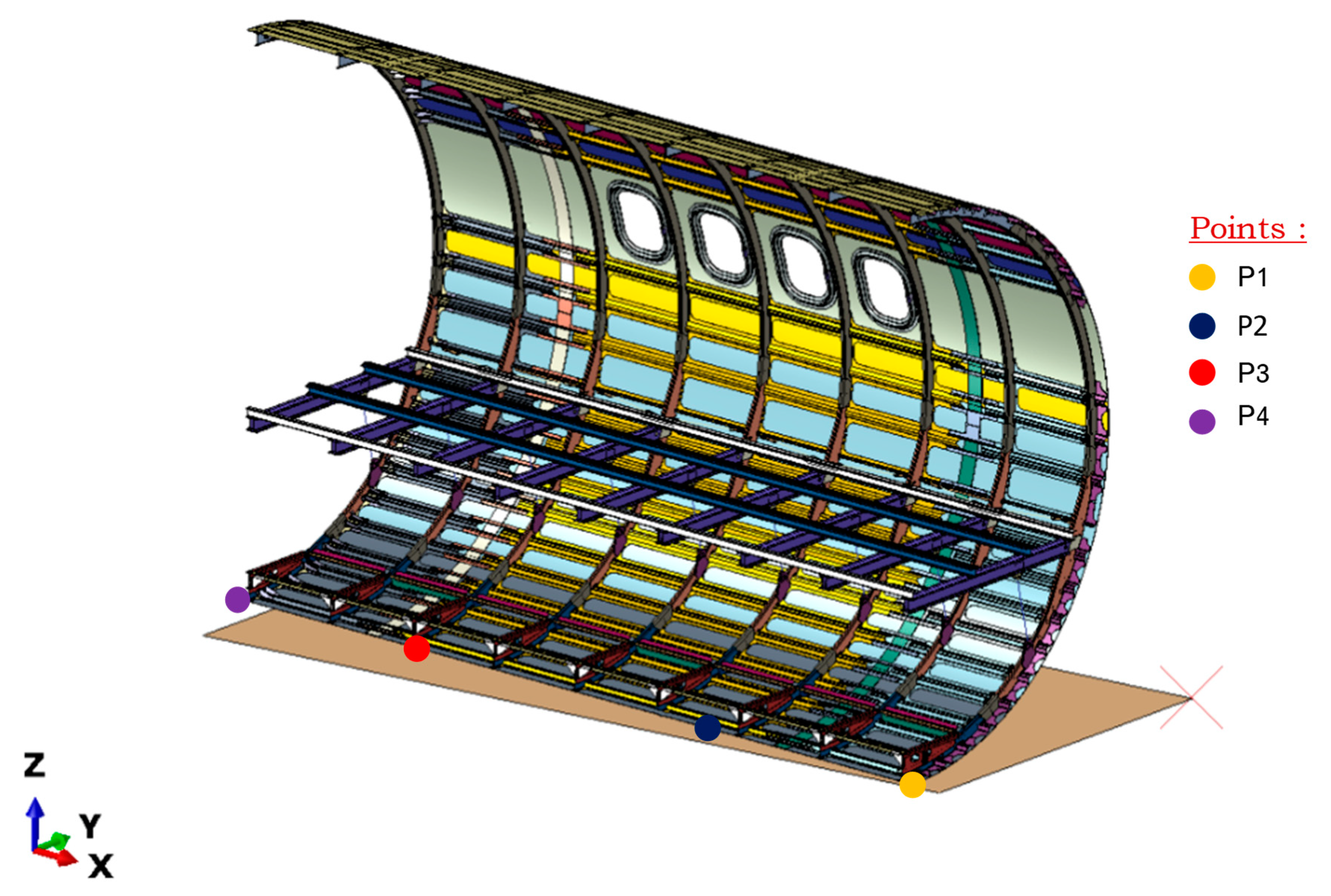
3. Geometrical Model and Numerical FEM Model Description
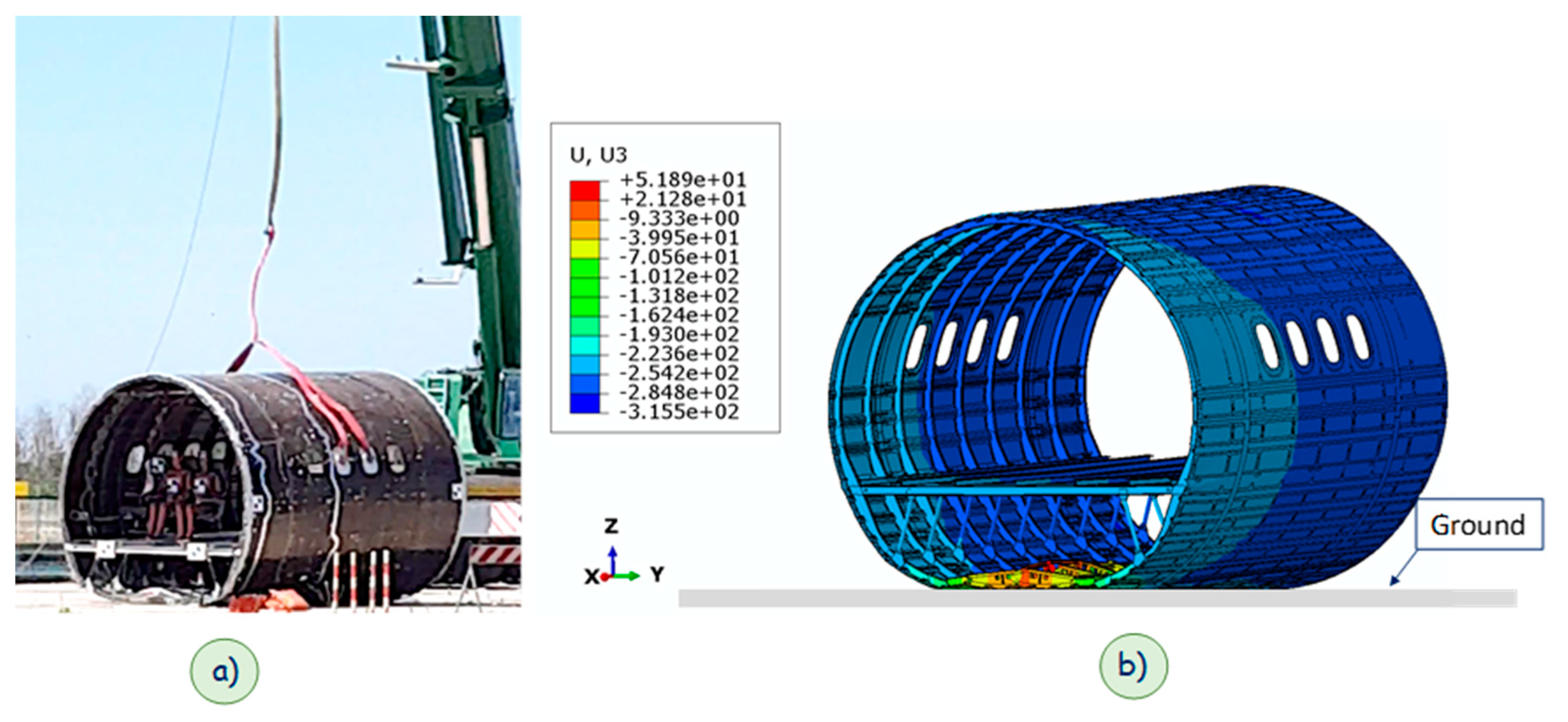
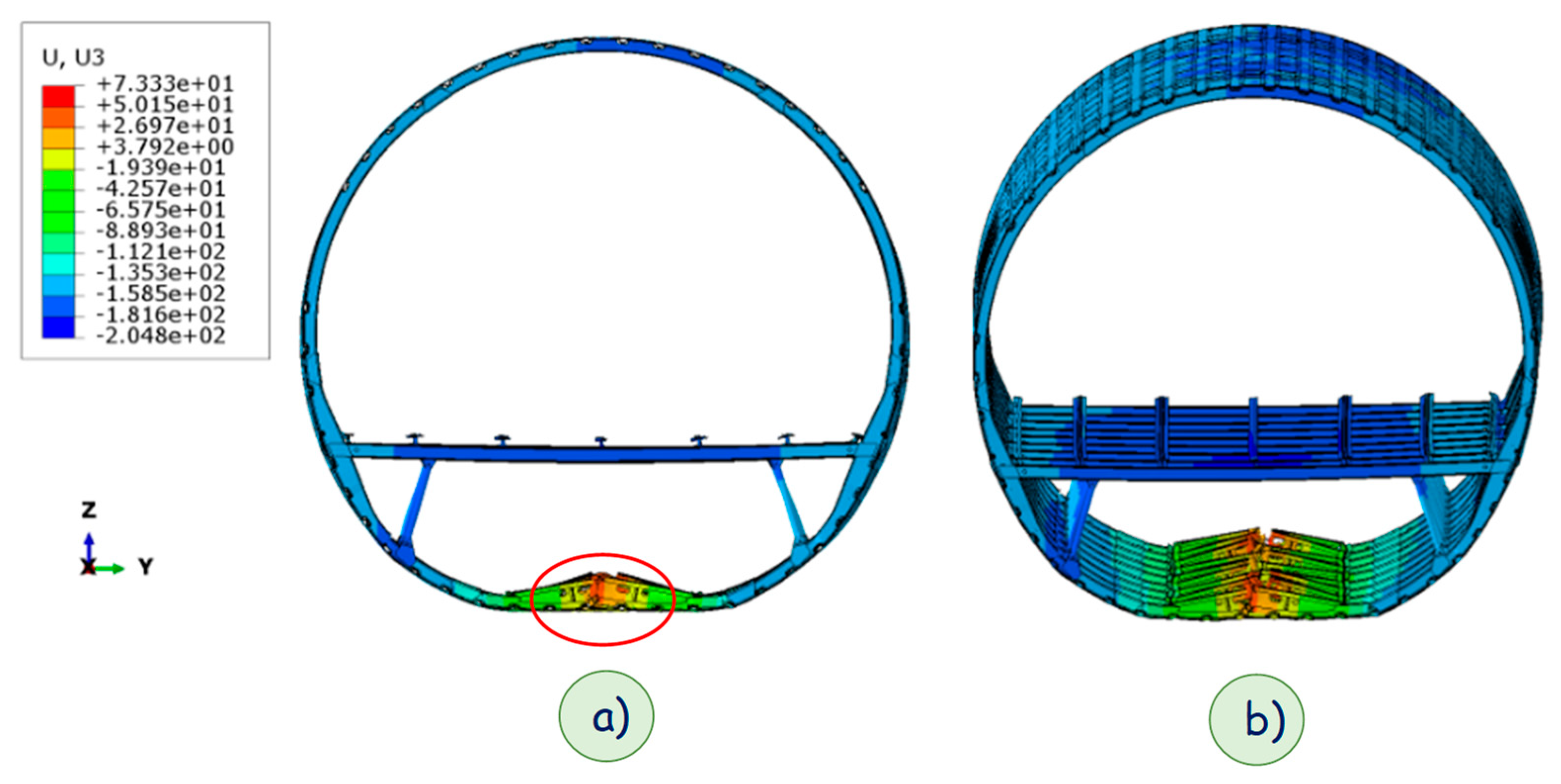
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Federal Aviation Regulations. Part 25—Aircrashworthiness Standards: Transport Category Airplanes; Federal Aviation Adminstration, Department of Transportation: Washington, DC, USA, 2003.
- Cronkhite, J.D.; Berry, V.L. Crashworthy Airframe Design Concepts—Fabrication and Testing; NASA Contractor, Report 3603; NASA: Washington, DC, USA, 1982.
- Guida, M.; Manzoni, A.; Zuppardi, A.; Caputo, F.; Marulo, F.; De Luca, A. Development of a multibody system for crashworthiness certification of aircraft seat. Multibody Syst. Dyn. 2018, 44, 191–221. [Google Scholar] [CrossRef]
- Caputo, F.; De Luca, A.; Marulo, F.; Guida, M.; Vitolo, B. Numerical-experimental assessment of a hybrid FE-MB model of an aircraft seat sled test. Int. J. Aerospace Eng. 2018, 8943826. [Google Scholar] [CrossRef]
- Riccio, A.; Caputo, F.; Di Felice, G.; Saputo, S.; Toscano, C.; Lopresto, V. A Joint Numerical-Experimental Study on Impact Induced Intra-laminar and Inter-laminar Damage in Laminated Composites. Appl. Compos. Mater. 2016, 23, 219–237. [Google Scholar] [CrossRef]
- Riccio, A.; Ricchiuto, R.; Saputo, S.; Raimondo, A.; Caputo, F.; Antonucci, V.; Lopresto, V. Impact behaviour of omega stiffened composite panels. Prog. Aerosp. Sci. 2016, 81, 41–48. [Google Scholar] [CrossRef]
- Ren, Y.R.; Xiang, J.W. Crashworthiness uncentainty analysis of typical civil aircraft based on Box-Behnken method. Chin. J. Aeronaut. 2014, 27, 253–262. [Google Scholar] [CrossRef]
- Caputo, F.; De Luca, A.; Greco, A.; Maietta, S.; Marro, A.; Apicella, A. Investigation on the static and dynamic structural behaviours of a regional aircraft main landing gear by a new numerical methodology. Frattura ed Integrità Strutturale 2018, 12, 191–204. [Google Scholar] [CrossRef]
- Riccio, A.; Cristiano, R.; Saputo, S.; Sellitto, A. Numerical methodologies for simulating bird-strike on composite wings. Compos. Struct. 2018, 202, 590–602. [Google Scholar] [CrossRef]
- Perfetto, D.; De Luca, A.; Lamanna, G.; Chiariello, A.; Di Caprio, F.; Di Palma, L.; Caputo, F. Drop test simulation and validation of a full composite fuselage section of a regional aircraft. Procedia Struct. Integr. 2018, 12, 380–391. [Google Scholar] [CrossRef]
- Jackson, K.E.; Fasanella, E.L. NASA Langley Research Center impact dynamics research facility research survey. J. Aircraft 2004, 41, 511–522. [Google Scholar] [CrossRef]
- Bisagni, C. Crashworthiness of helicopter subfloor structures. Int. J. Impact Eng. 2002, 27, 1067–1082. [Google Scholar] [CrossRef]
- Adams, A.; Lankarani, H.M. A modern aerospace modelling approach for evaluation of aircraft fuselage crashworthiness. Int. J. Crashworthiness 2003, 8, 401–413. [Google Scholar] [CrossRef]
- Sellitto, A.; Riccio, A.; Russo, A.; Zarrelli, M.; Toscano, C.; Lopresto, V. Compressive behaviour of a damaged omega stiffened panel: Damage detection and numerical analysis. Compos. Struct. 2019, 209, 300–316. [Google Scholar] [CrossRef]
- McGuire, R.J.; Nissley, W.J.; Newcomb, J.E. Vertical Drop Test of a Fairchild Metro III; FAA Report DOT/FAA/CT-93/1; U.S. G.P.O.: Washington, DC, USA, 1993.
- Abramowitz, A.; Ingraham, P.A.; McGuire, R. Vertical Drop Test of a Shorts 3-30 Airplane; FAA Report DOT/FAA/AR-99/87; U.S. G.P.O.: Washington, DC, USA, 1999.
- Federal Aviation Administration. Special Conditions: Boeing Model 787-8 Airplane; Crashworthiness, Docket No. NM368 Special Conditions No. 25-362-SC, US Federal Register 72; U.S. G.P.O.: Washington, DC, USA, 2007.
- Federal Aviation Administration. Special Conditions: Airbus A350-900 Airplane; Crashworthiness, Emergency Landing Conditions, Docket No. FAA-2013-0892 Special Conditions No. 25-537-SC, US Federal Register 79; U.S. G.P.O.: Washington, DC, USA, 2014.
- Maia, L.G.; de Oliveira, P.H.I.A. Crashworthy Composite Fuselage Section Concept for Next Generation General Aviation; SAE Technical Paper 2005-01-4011; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Riccio, A.; Raimondo, A.; Di Caprio, F.; Fusco, M.; Sanità, P. Experimental and numerical investigation on the crashworthiness of a composite fuselage subfloor support system. Compos. Part B Eng. 2018, 150, 93–103. [Google Scholar] [CrossRef]
- Kumakura, I.; Minegishi, M.; Iwasaki, K. Impact Simulation of Simplified Structural Models of Aircraft Fuselage; SAE Technical Paper 2000-01-5586; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Zheng, J.; Xiang, J.; Luo, Z.; Ren, Y. Crashworthiness design of transport aircraft subfloor using polymer foams. Int. J. Crashworthiness 2011, 16, 375–383. [Google Scholar] [CrossRef]
- Shoji, H.; Miyaki, H.; Iwasaki, K.; Minegishi, M. Crashworthiness research on cabin structure at JAXA. In Proceedings of the 5th Triennial International Aircraft Fire and Cabin Safety Research Conference, Atlantic City, NJ, USA, 30 October 2007. [Google Scholar]
- Ren, Y.; Xiang, J. A comparative study of the crashworthiness of civil aircraft with different strut configurations. Int. J. Crashworthiness 2010, 15, 321–330. [Google Scholar] [CrossRef]
- Hu, D.Y.; Meng, K.P.; Yang, Z.Y. Numerical investigation of the energy absorption characteristics of a fan shaped deployable energy absorber. Int. J. Crashworthiness 2014, 19, 126–138. [Google Scholar] [CrossRef]
- Huculak, R.D.; Lankarani, H.M. Methods of evaluating ES-2 leg flail in dynamic evaluation and certification tests of side-facing aircraft seats. Int. J. Crashworthiness 2015, 20, 613–628. [Google Scholar] [CrossRef]
- Liu, X.C.; Guo, J.; Bai, C.Y.; Sun, X.S.; Mou, R.K. Droptest and crash simulation of a civil airplane fuselage section. Chin. J. Aeronaut. 2015, 28, 447–456. [Google Scholar] [CrossRef]
- Paz, J.; Diaz, J.; Romera, L.; Costas, M. Size and shape optimization of aluminum tubes with GFRP honeycomb reinforcements for crashworthy aircraft structures. Compos. Struct. 2015, 133, 499–507. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.R.; Xiang, J.W. The crashworthiness of civil air Craft using different quadrangular tubes as cabin-floor struts. Int. J. Crashworthiness 2011, 16, 253–262. [Google Scholar] [CrossRef]
- Ren, Y.R.; Xiang, J.W. Energy absorption structures design of civil aircraft to improve crashworthiness. Aeronaut. J. 2014, 118, 383–398. [Google Scholar] [CrossRef]
- Ren, Y.R.; Xiang, J.W.; Zheng, J.Q.; Luo, Z.P. Crashworthiness analysis of aircraft fuselage with sine-wave beamstructure. Chin. J. Aeronaut. 2016, 29, 403–410. [Google Scholar] [CrossRef]
- Schatrow, P.; Waimer, M. Crash concept for composite transport aircraft using mainly tensile and compressive absorption mechanisms. CEAS Aeronaut. J. 2016, 7, 471–482. [Google Scholar] [CrossRef]
- Shi, Q.H.; Dai, D.; Cao, Z.H. Tensile failure strength analysis and Experimental confirmation of stitch reinforced composite of T-stiffened structure. Polym. Compos. 2012, 20, 307–311. [Google Scholar] [CrossRef]
- Sturma, R.; Klett, Y.; Kindervater, C.; Voggenreiter, H. Failure of CFRP airframe sandwich panels under crash relevant loading conditions. Compos. Struct. 2014, 112, 11–21. [Google Scholar] [CrossRef]
- Riccio, A.; Raimondo, A.; Saputo, S.; Sellitto, A.; Battaglia, M.; Petrone, G. A numerical study on the impact behaviour of natural fibres made honeycomb cores. Compos. Struct. 2018, 202, 909–916. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Soroush, M.; Davar, A.; Rahmani, O. Finite element modeling of low-velocity impact on laminated composite plates and cylindrical shells. Compos. Struct. 2011, 93, 1363–1375. [Google Scholar] [CrossRef]
- Chattopadhyay, S. Response of elastic plates to impact including the effects of shear deformation. In Recent Advances in Engineering Science; Springer: Berlin, Germany, 1977; pp. 127–138. [Google Scholar]
- Shivakumar, K.N.; Elber, W.; Illg, W. Prediction of impact force and duration due to low-velocity impact on circular composite laminates. J. Appl. Mech. Trans. ASME 1985, 52, 674–680. [Google Scholar] [CrossRef]
- Dassault System Abaqus 2016 User’s Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2016.









| Failure | Equivalent Stress | Equivalent Displacement |
|---|---|---|
| Fiber tension | ||
| Fiber compression | ||
| Matrix tension | ||
| Matrix compression |
| Unidirectional CFRP | |
|---|---|
| Young’s Modulus, E11 [MPa] | 137,500 |
| Young’s Modulus, E22 [MPa] | 8200 |
| Shear Modulus, G12 [MPa] | 3950 |
| Shear Modulus, G13 [MPa] | 3950 |
| Shear Modulus, G23 [MPa] | 3950 |
| Poisson’s ratio, ν12 = ν13 = ν23 [-] | 0.35 |
| Fiber Tensile Strength, F1t [MPa] | 1890 |
| Fiber Compressive Strength, F1c [MPa] | 1008 |
| Matrix Tensile Strength, F2t [MPa] | 86.5 |
| Matrix Compressive Strength, F2c [MPa] | 112 |
| In-Plane Shear Strength, S12 [MPa] | 95 |
| Out-Plane Shear Strength, S23 [MPa] | 100 |
| Density, ρ [ton/mm3] | 1.9 × 10−9 |
| Ply thickness, tp [mm] | 0.129 |
| Woven Fabric | |
|---|---|
| Young’s Modulus, E11 [MPa] | 55,000 |
| Young’s Modulus, E22 [MPa] | 55,000 |
| Shear Modulus, G12 [MPa] | 3363 |
| Shear Modulus, G13 [MPa] | 3363 |
| Shear Modulus, G23 [MPa] | 3363 |
| Poisson’s ratio, ν12 = ν13 = ν23 [-] | 0.30 |
| Fiber Tensile Strength, F1t [MPa] | 650 |
| Fiber Compressive Strength, F1c [MPa] | 650 |
| Matrix Tensile Strength, F2t [MPa] | 650 |
| Matrix Compressive Strength, F2c [MPa] | 650 |
| In-Plane Shear Strength, S12 [MPa] | 150 |
| Out-Plane Shear Strength, S23 [MPa] | 150 |
| Density, ρ [ton/mm3] | 1.97 × 10−9 |
| Ply thickness, tp [mm] | 0.25 mm |
| Al2024 | |
|---|---|
| Young’s Modulus, E [MPa] | 70,000 |
| Poisson’s ratio, ν [-] | 0.33 |
| Yield stress, σy [MPa] | 369 |
| Ultimate Tensile stress, σf [MPa] | 469 |
| Density, ρ [ton/mm3] | 2.7 × 10−9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riccio, A.; Saputo, S.; Sellitto, A.; Russo, A.; Di Caprio, F.; Di Palma, L. An Insight on the Crashworthiness Behavior of a Full-Scale Composite Fuselage Section at Different Impact Angles. Aerospace 2019, 6, 72. https://doi.org/10.3390/aerospace6060072
Riccio A, Saputo S, Sellitto A, Russo A, Di Caprio F, Di Palma L. An Insight on the Crashworthiness Behavior of a Full-Scale Composite Fuselage Section at Different Impact Angles. Aerospace. 2019; 6(6):72. https://doi.org/10.3390/aerospace6060072
Chicago/Turabian StyleRiccio, Aniello, Salvatore Saputo, Andrea Sellitto, Angela Russo, Francesco Di Caprio, and Luigi Di Palma. 2019. "An Insight on the Crashworthiness Behavior of a Full-Scale Composite Fuselage Section at Different Impact Angles" Aerospace 6, no. 6: 72. https://doi.org/10.3390/aerospace6060072
APA StyleRiccio, A., Saputo, S., Sellitto, A., Russo, A., Di Caprio, F., & Di Palma, L. (2019). An Insight on the Crashworthiness Behavior of a Full-Scale Composite Fuselage Section at Different Impact Angles. Aerospace, 6(6), 72. https://doi.org/10.3390/aerospace6060072