A Novel Control Allocation Method for Yaw Control of Tailless Aircraft
Abstract
:1. Introduction
2. Theoretical Background
3. Method
3.1. Wing Aerodynamic Models
3.2. Validation of Model Predictions Due to Control Surface Deflection
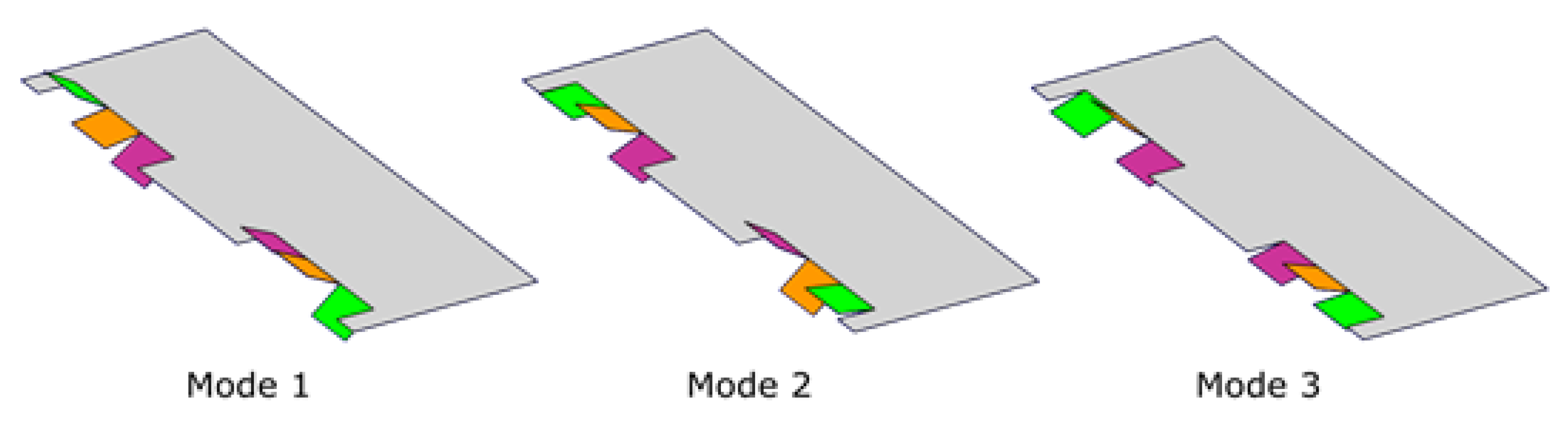
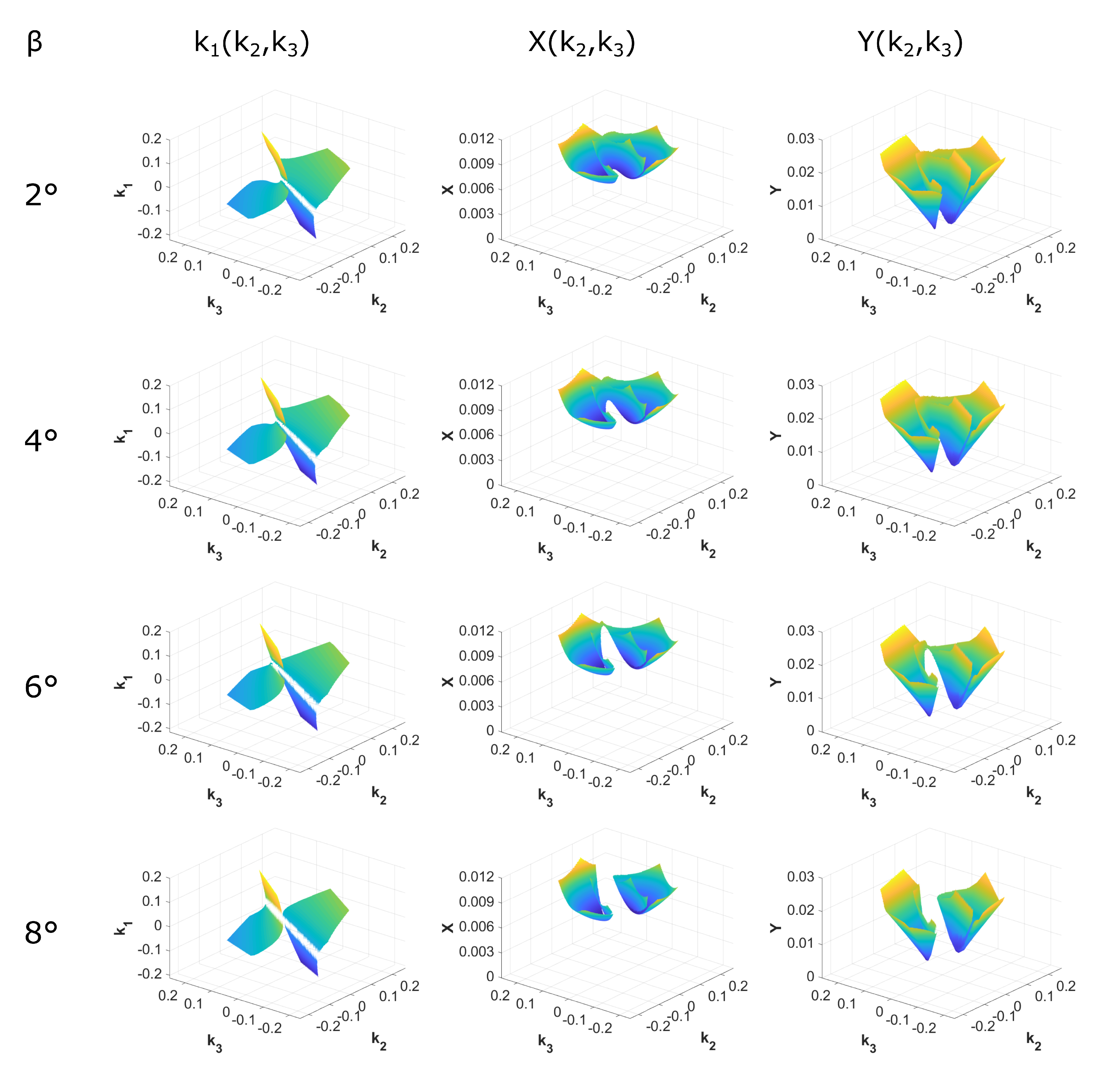
3.3. Control Allocation
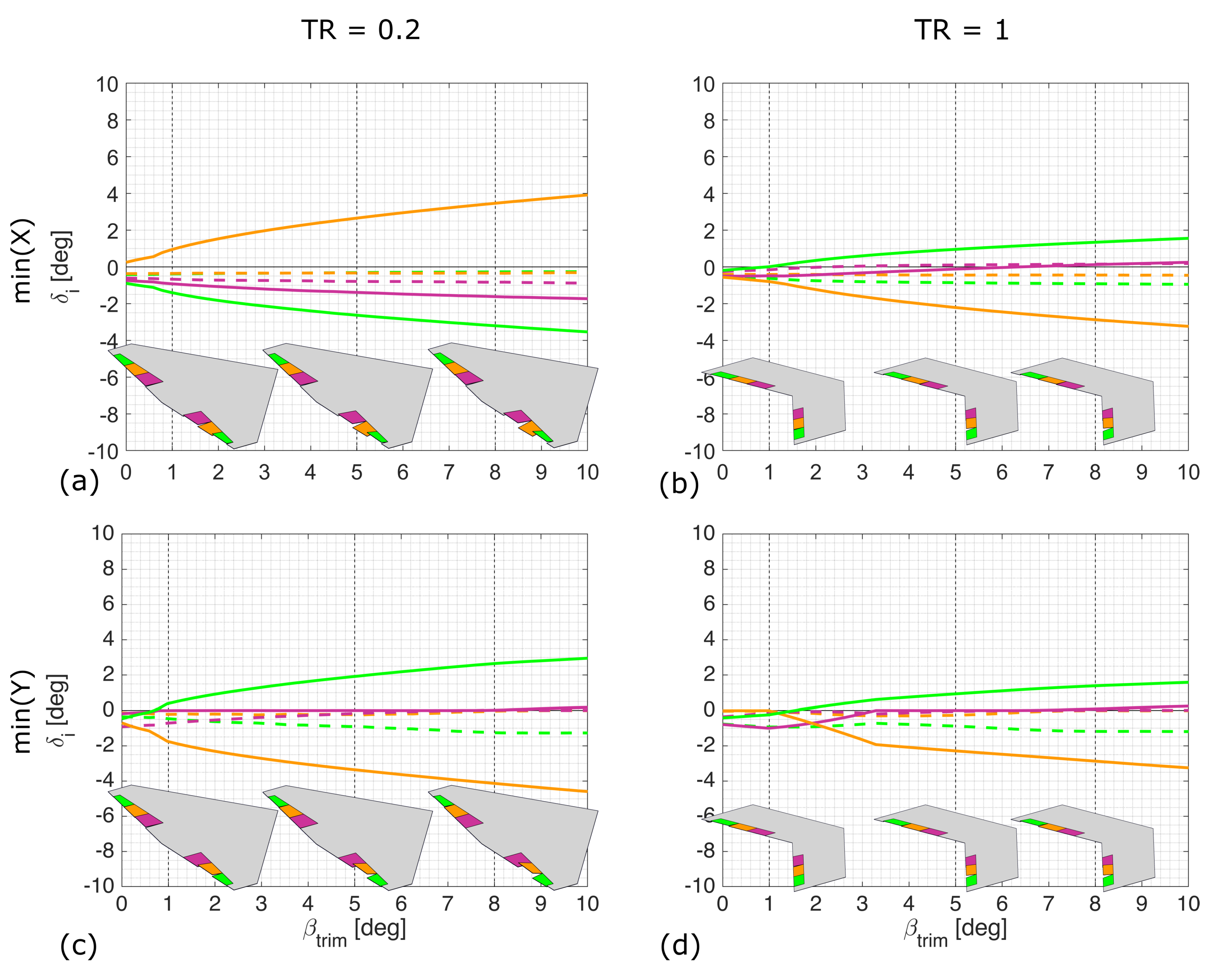
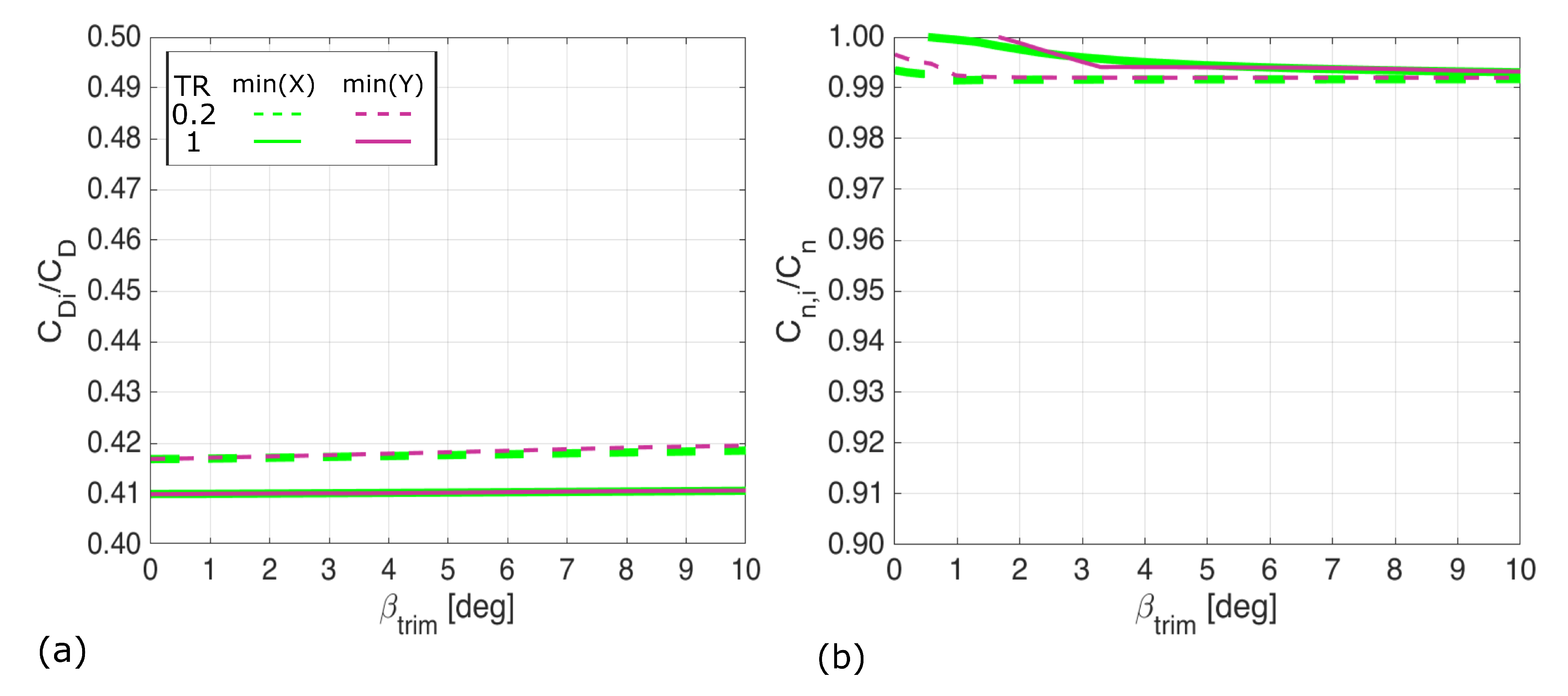
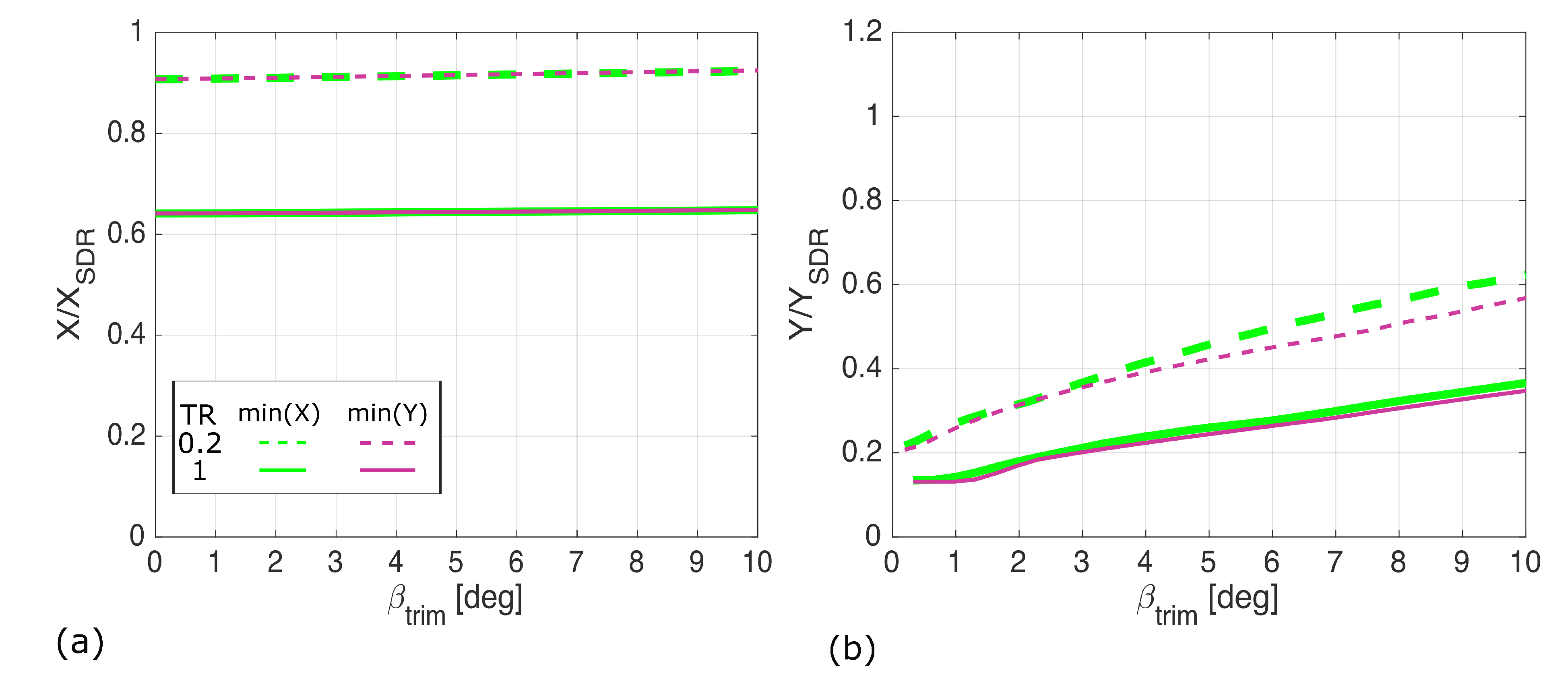
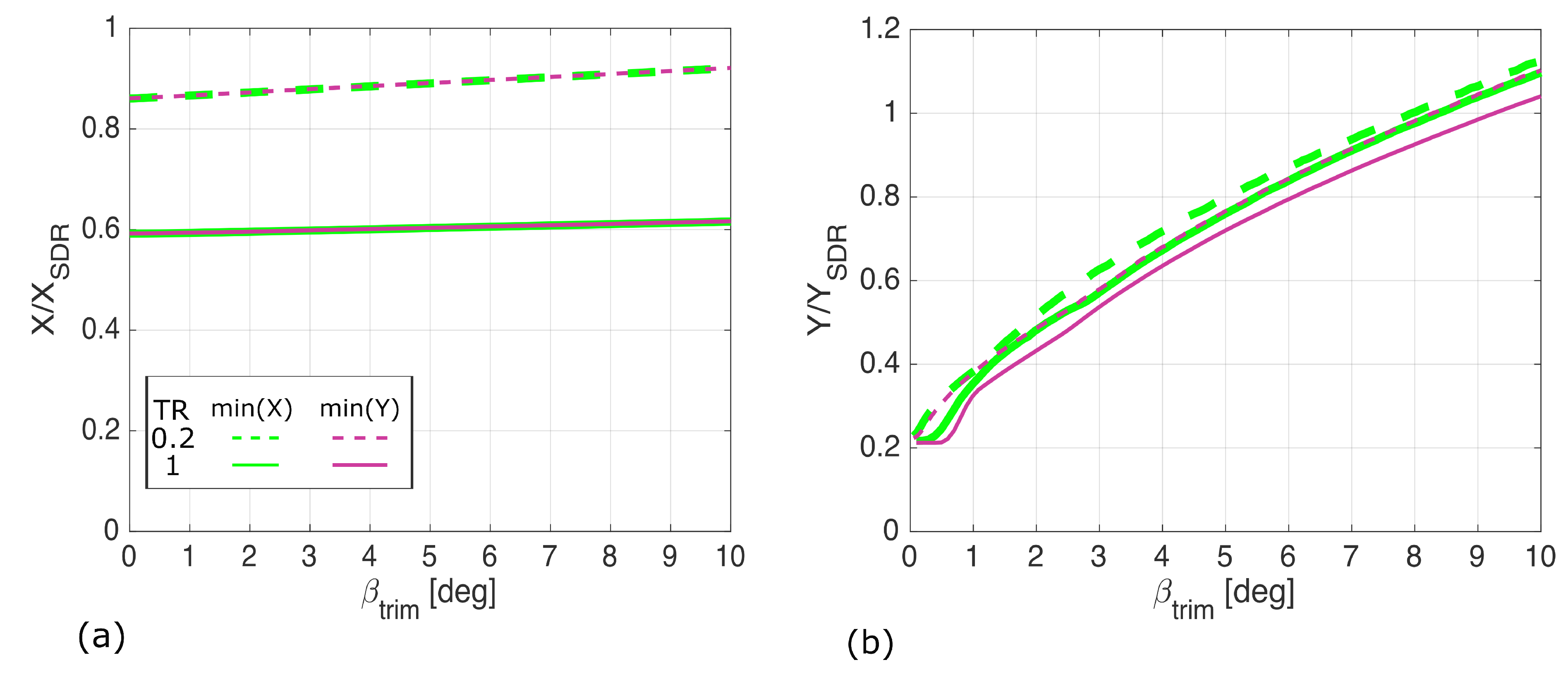
4. Results and Discussion
4.1. Wing Geometries
4.2. Unswept Wing
4.3. Thirty Degree Sweep
4.4. Forty-Five Degree Sweep
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RCS | Radar Cross Section |
| TEU | Trailing Edge Up |
| TED | Trailing Edge Down |
| SDR | Split Drag Rudder |
Appendix A. Model Selection
Appendix A.1. Overview
Appendix A.2. Straight Rectangular Wing

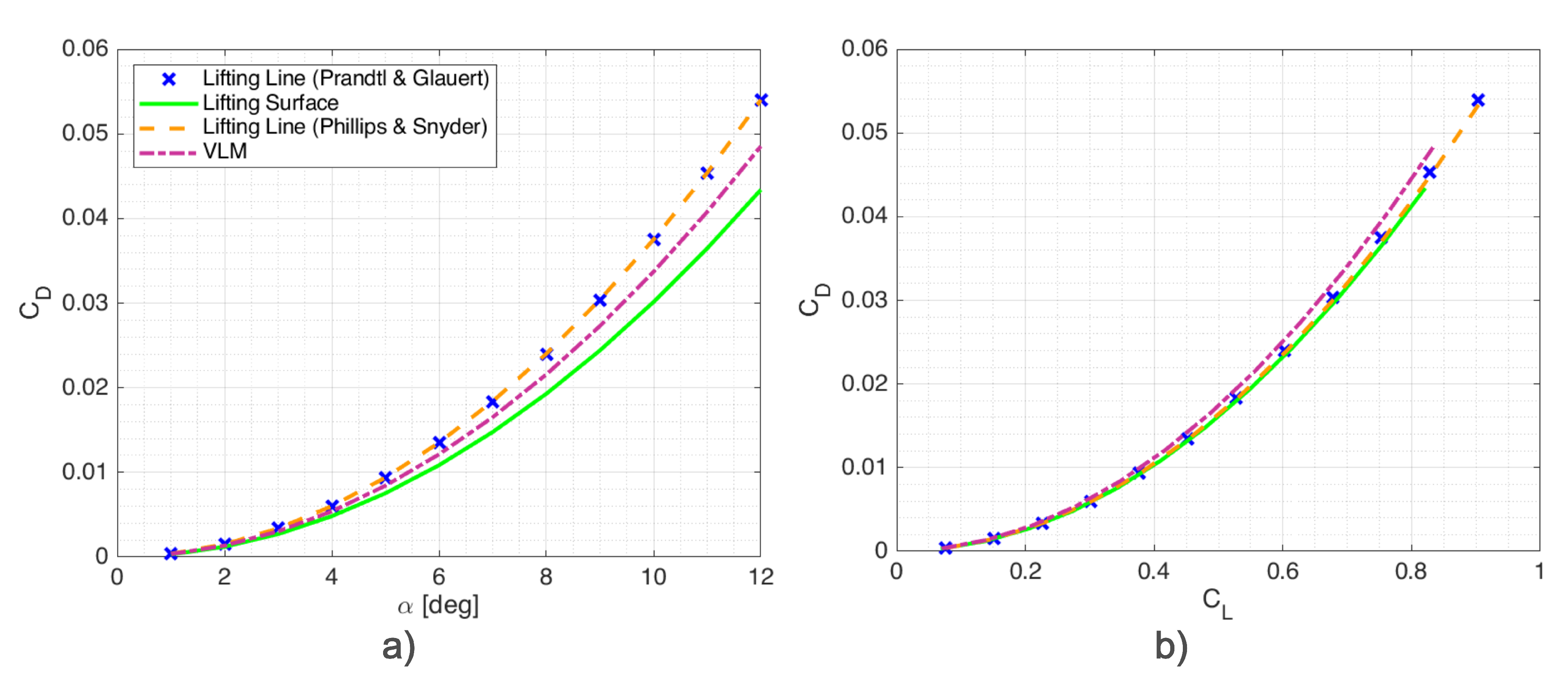
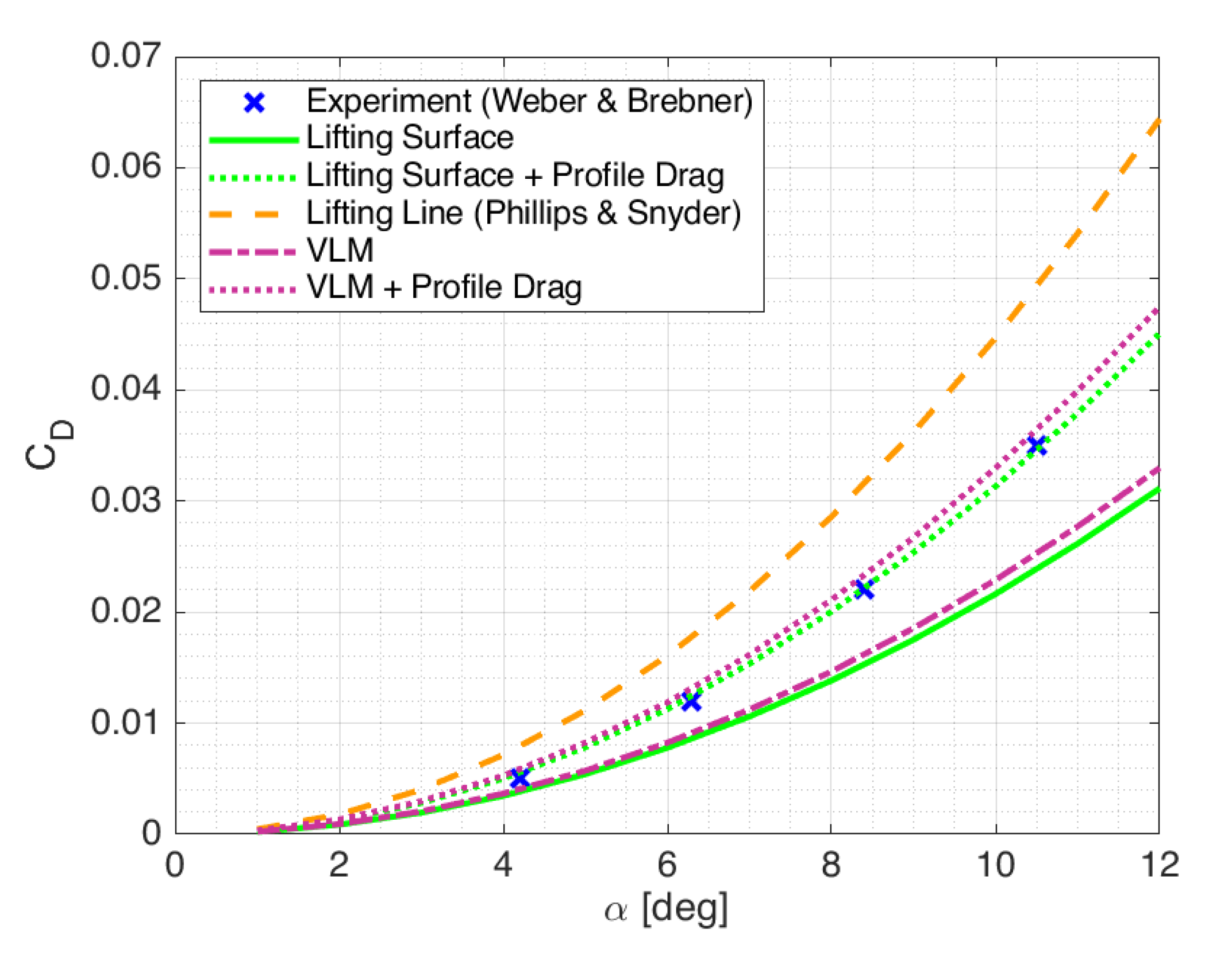
Appendix A.3. Forty-Five Degree Swept, Untapered Wing

References
- Löchert, P.; Huber, K.C.; Ghoreyshi, M.; Allen, J. Control device effectiveness studies of a 53∘ swept flying wing configuration. Experimental, computational, and modeling considerations. Aerosp. Sci. Technol. 2019, 1, 105319. [Google Scholar] [CrossRef] [Green Version]
- Grellmann, H. B-2 aerodynamic design. In Proceedings of the Aerospace Engineering Conference and Show, Los Angeles, CA, USA, 13–15 February 1990. [Google Scholar] [CrossRef]
- Denisov, V.; Shkadov, L.; Chernyshev, S. The Flying Wing Concept—The Challenge for the Future. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; pp. 1–11. [Google Scholar] [CrossRef]
- Tomac, M.; Stenfelt, G. Predictions of stability and control for a flying wing. Aerosp. Sci. Technol. 2014, 39, 179–186. [Google Scholar] [CrossRef]
- Rajput, J.; Zhang, W.G.; Qu, X.B. A Differential Configuration of Split Drag-Rudders with Variable Bias for Directional Control of Flying-Wing. In Applied Mechanics and Materials; Engineering Providing of Industrial Development; Trans Tech Publications: Zurich, Switzerland, 2014; Volume 643, pp. 54–59. [Google Scholar] [CrossRef]
- Li, Z.J.; Ma, D.L. Control characteristics analysis of split-drag-rudder. In Applied Mechanics and Materials; Engineering Providing of Industrial Development; Trans Tech Publications: Zurich, Switzerland, 2014; Volume 472, pp. 185–190. [Google Scholar] [CrossRef]
- Hong, W.J.; Ma, D.L. Influence of Control Coupling Effect on Landing Performance of Flying Wing Aircraft. In Applied Mechanics and Materials; Engineering Providing of Industrial Development; Trans Tech Publications: Zurich, Switzerland, 2016; Volume 829, pp. 110–117. [Google Scholar] [CrossRef]
- Li, Z.; Yong, C.; Duo, L. Multi-effectors distribution of flying wing with stealthy optimization. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 2864–2869. [Google Scholar] [CrossRef]
- Paterson, J. Overview of Low Observable Technology and Its Effects on Combat Aircraft Survivability. J. Aircr. 1999, 36, 380–388. [Google Scholar] [CrossRef]
- Härkegård, O.; Glad, S.T. Resolving actuator redundancy—Optimal control vs. control allocation. Automatica 2005, 41, 137–144. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, L.; Li, F. Research on multi-task command allocation method for flying wing aircraft. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020. [Google Scholar] [CrossRef]
- Zhang, N. Research on Command Allocation Method for Flying Wing Aircraft. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020. [Google Scholar] [CrossRef]
- Handelman, D.A.; Stengelj, R.F. Combining Expert System and Analytical Redundancy Concepts for Fault-Tolerant Flight Control. J. Guid. 1989, 12, 39–45. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, W.; Shi, J.; Lyu, Y. A novel yaw control method for flying-wing aircraft in low speed regime. Aerosp. Sci. Technol. 2017, 69, 636–649. [Google Scholar] [CrossRef]
- Huber, K.C.; Vicroy, D.D.; Schuette., A.; Huebner, V. UCAV model design and static experimental investigations to estimate control device effectiveness and S&C capabilities. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; pp. 1–20. [Google Scholar]
- Yue, T.; Zhang, X.; Wang, L.; Ai, J. Flight dynamic modeling and control for a telescopic wing morphing aircraft via asymmetric wing morphing. Aerosp. Sci. Technol. 2017, 70, 328–338. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z. Analytical study on the synthetic jet control of asymmetric flow field of flying wing unmanned aerial vehicle. Aerosp. Sci. Technol. 2016, 56, 90–99. [Google Scholar] [CrossRef]
- Keidel, D.; Fasel, U.; Ermanni, P. Control Authority of a Camber Morphing Flying Wing. J. Aircr. 2020, 1–10. [Google Scholar] [CrossRef]
- Guiler, R.; Huebsch, W. Wind tunnel analysis of a morphing swept wing tailless aircraft. In Proceedings of the AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 6–9 June 2005; Volume 2, pp. 946–959. [Google Scholar] [CrossRef]
- Hunsaker, D.F.; Montgomery, Z.S.; Joo, J.J. Control of Adverse Yaw During Roll for a Class of Optimal Lift Distributions. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–24. [Google Scholar] [CrossRef]
- Richter, J.; Hainline, K.; Louis, S.; Agarwal, R.K.; Richter, J.; Hainline, K. Examination of Proverse Yaw in Bell-Shaped Spanload Aircraft Examination of Proverse Yaw in Bell-Shaped Spanload Aircraft; Mechanical Engineering and Materials Science Independent Study; Washington University: St. Louis, MO, USA, 2019. [Google Scholar]
- Montgomery, Z.S.; Hunsaker, D.F.; Joo, J.J. A Methodology for Roll Control of Morphing Aircraft. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Gamble, L.L.; Inman, D.J. Yaw Control of a Smart Morphing Tailless Aircraft Concept. Adv. Sci. Technol. 2016, 101, 127–132. [Google Scholar] [CrossRef]
- Phillips, E.; Jentzsch, M.; Menge, M.; Heinritz, C.; Taubert, L.; Forster, M.; Wygnanski, I.; Ladd, J. NATO AVT-239 Task Group: On the Use of Active Flow Control (AFC) on Tailless Aircraft Models to Affect their Trim and Control. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Cusher, A.A.; Gopalarathnam, A. Drag reduction on aircraft configurations with adaptive lifting surfaces. Aerosp. Sci. Technol. 2014, 34, 35–44. [Google Scholar] [CrossRef]
- Multhopp, H. Methods for Calculating the Lift Distribution of Wings (Subsonic Lifting-Surface Theory); Technical Report; Ministry of Supply: London, UK, 1955. [Google Scholar]
- Stenfelt, G.; Ringertz, U. Lateral Stability and Control of a Tailless Aircraft Configuration. J. Aircr. 2009, 46, 2161–2164. [Google Scholar] [CrossRef]
- ESDU. Zero-Lift Drag Coefficient Increment Due to Full-Span Plain Flaps; ESDU: London, UK, 2006. [Google Scholar]
- Oppenheimer, M.W.; Doman, D.B. A method for including control effector interactions in the control allocation problem. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; Volume 1, pp. 1074–1083. [Google Scholar] [CrossRef] [Green Version]
- Fruchter, G.; Srebro, U.; Zeheb, E. On Several Variable Zero Sets and Application to MIMO Robust Feedback Stabilization. IEEE Trans. Circuits Syst. 1987, 34, 1208–1220. [Google Scholar] [CrossRef]
- Stein, M. Large sample properties of simulations using latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Robinson, A.; Laurmann, J.A. Wing Theory; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- ESDU. Drag of a Smooth Flat Plate at Zero Incidence; ESDU: London, UK, 2000. [Google Scholar]
- Myers, R.H. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; Wiley Series in Probability and Mathematical Statistics; Applied Probability Section; Wiley: New York, NY, USA, 2016. [Google Scholar]
- Lei, W.; Lixin, W. Reconfigurable Flight Control Design for Combat Flying Wing with Multiple Control Surfaces. Chin. J. Aeronaut. 2012, 25, 493–499. [Google Scholar] [CrossRef] [Green Version]
- ESDU. Lift and Rolling Moment Due to Spoilers on Wings at Subsonic Speeds with Trailing-Edge Flaps Undeployed; ESDU: London, UK, 2015. [Google Scholar]
- ESDU. Drag and Yawing Moment Due to Spoilers; ESDU: London, UK, 2015. [Google Scholar]
- Phillips, W.F.; Snyder, D.O. Modern Adaptation of Prandtl’s Classic Lifting-Line Theory. J. Aircr. 2000, 37, 662–670. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 1991; p. 351. [Google Scholar] [CrossRef]
- Prandtl, L. Applications of Modern Hydrodynamics to Aeronautics; Technical Report; NACA: Washington, DC, USA, 1922. [Google Scholar] [CrossRef]
- Schlichting, H. Aerodynamics of the Airplane; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- Nabawy, M.R.A.; ElNomrossy, M.M.; Abdelrahman, M.M.; ElBayoumi, G.M. Aerodynamic shape optimisation, wind tunnel measurements and CFD analysis of a MAV wing. Aeronaut. J. 2012, 116, 685–708. [Google Scholar] [CrossRef] [Green Version]
- Nabawy, M.R.A.; Crowthe, W.J. A Quasi-Steady Lifting Line Theory for Insect-Like Hovering Flight. PLoS ONE 2015, 10, e0134972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmed, M.R.; Abdelrahman, M.M.; ElBayoumi, G.M.; ElNomrossy, M.M. Optimal wing twist distribution for roll control of MAVs. Aeronaut. J. 2011, 115, 641–649. [Google Scholar] [CrossRef]
- Weber, J.N.; Brebner, G.G.; Kuchemann, D. Low-Speed Tests on 45.deg Swept-Back Wings; Technical Report; Aeronautical Research Council: London, UK, 1958. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shearwood, T.R.; Nabawy, M.R.A.; Crowther, W.J.; Warsop, C. A Novel Control Allocation Method for Yaw Control of Tailless Aircraft. Aerospace 2020, 7, 150. https://doi.org/10.3390/aerospace7100150
Shearwood TR, Nabawy MRA, Crowther WJ, Warsop C. A Novel Control Allocation Method for Yaw Control of Tailless Aircraft. Aerospace. 2020; 7(10):150. https://doi.org/10.3390/aerospace7100150
Chicago/Turabian StyleShearwood, Thomas R., Mostafa R. A. Nabawy, William J. Crowther, and Clyde Warsop. 2020. "A Novel Control Allocation Method for Yaw Control of Tailless Aircraft" Aerospace 7, no. 10: 150. https://doi.org/10.3390/aerospace7100150
APA StyleShearwood, T. R., Nabawy, M. R. A., Crowther, W. J., & Warsop, C. (2020). A Novel Control Allocation Method for Yaw Control of Tailless Aircraft. Aerospace, 7(10), 150. https://doi.org/10.3390/aerospace7100150






