The Contrail Mitigation Potential of Aircraft Formation Flight Derived from High-Resolution Simulations
Abstract
:1. Introduction
2. Methods
2.1. Model
2.2. Numerical Set-Up
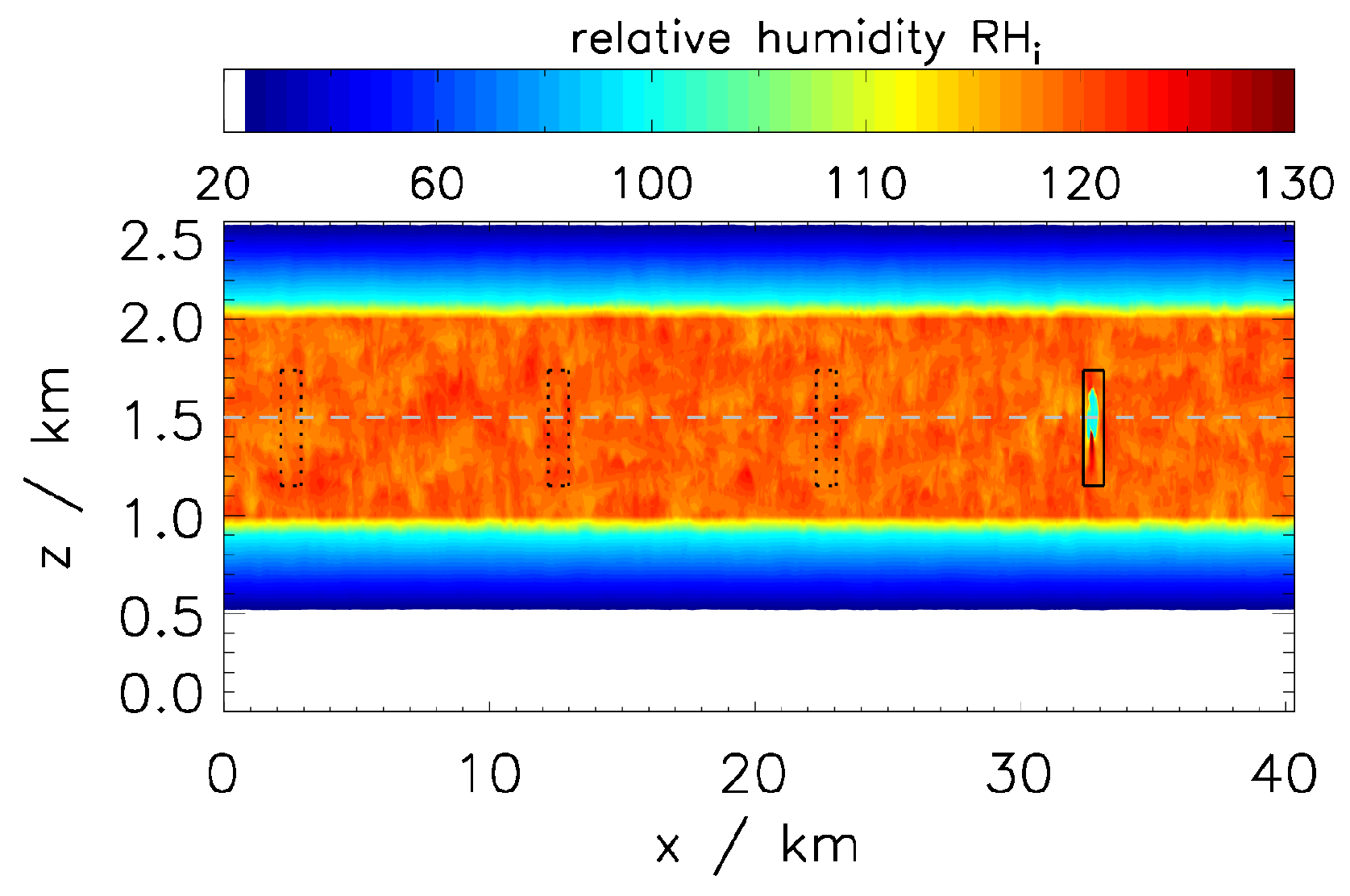
2.3. Contrail Initialisation
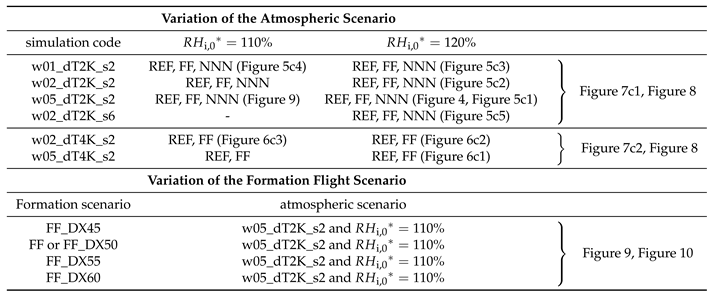
2.4. Set of Simulations
2.5. Analysed Quantities
3. Results
3.1. Exemplary Simulation
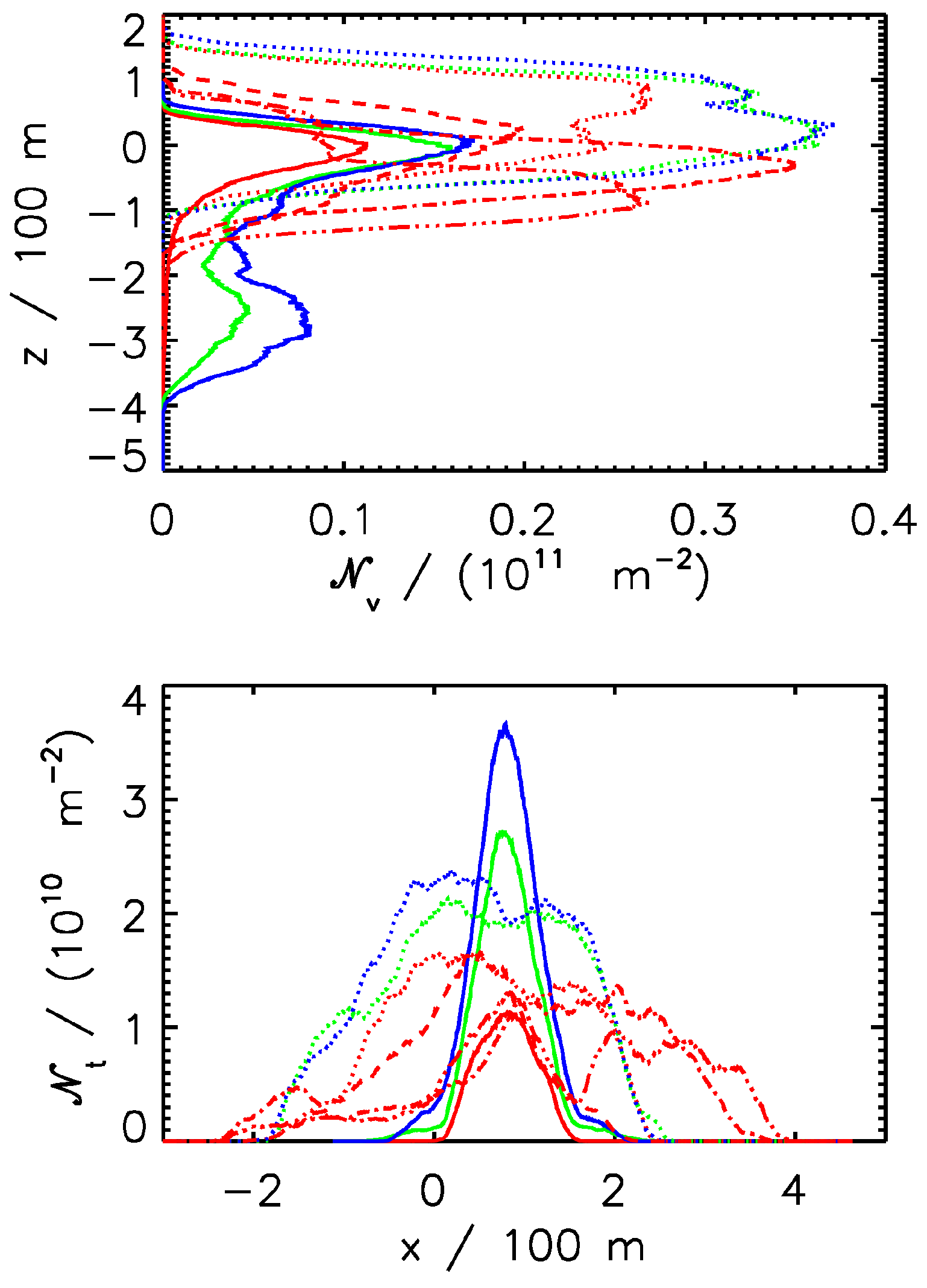
3.2. Contrail-Cirrus Evolution
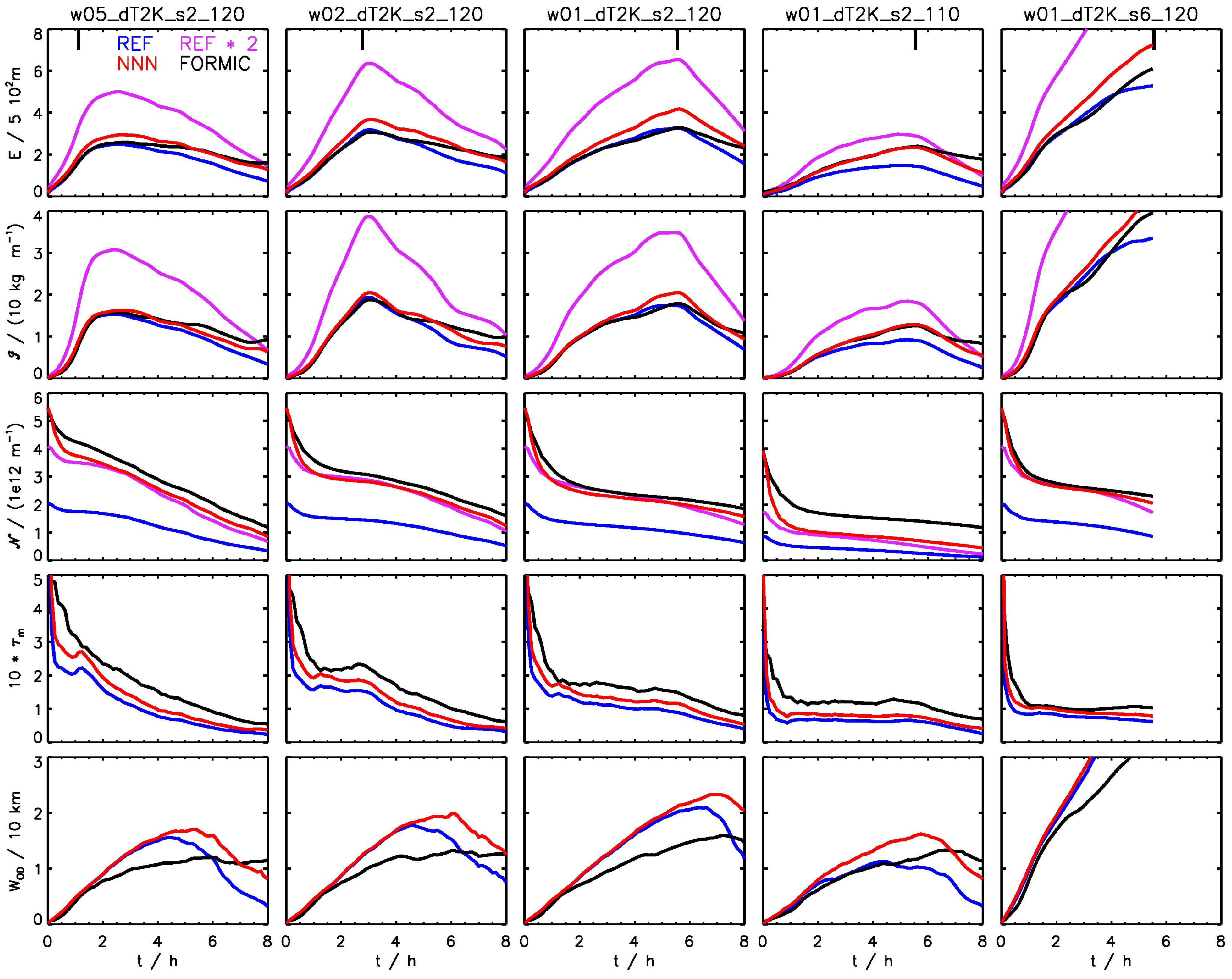
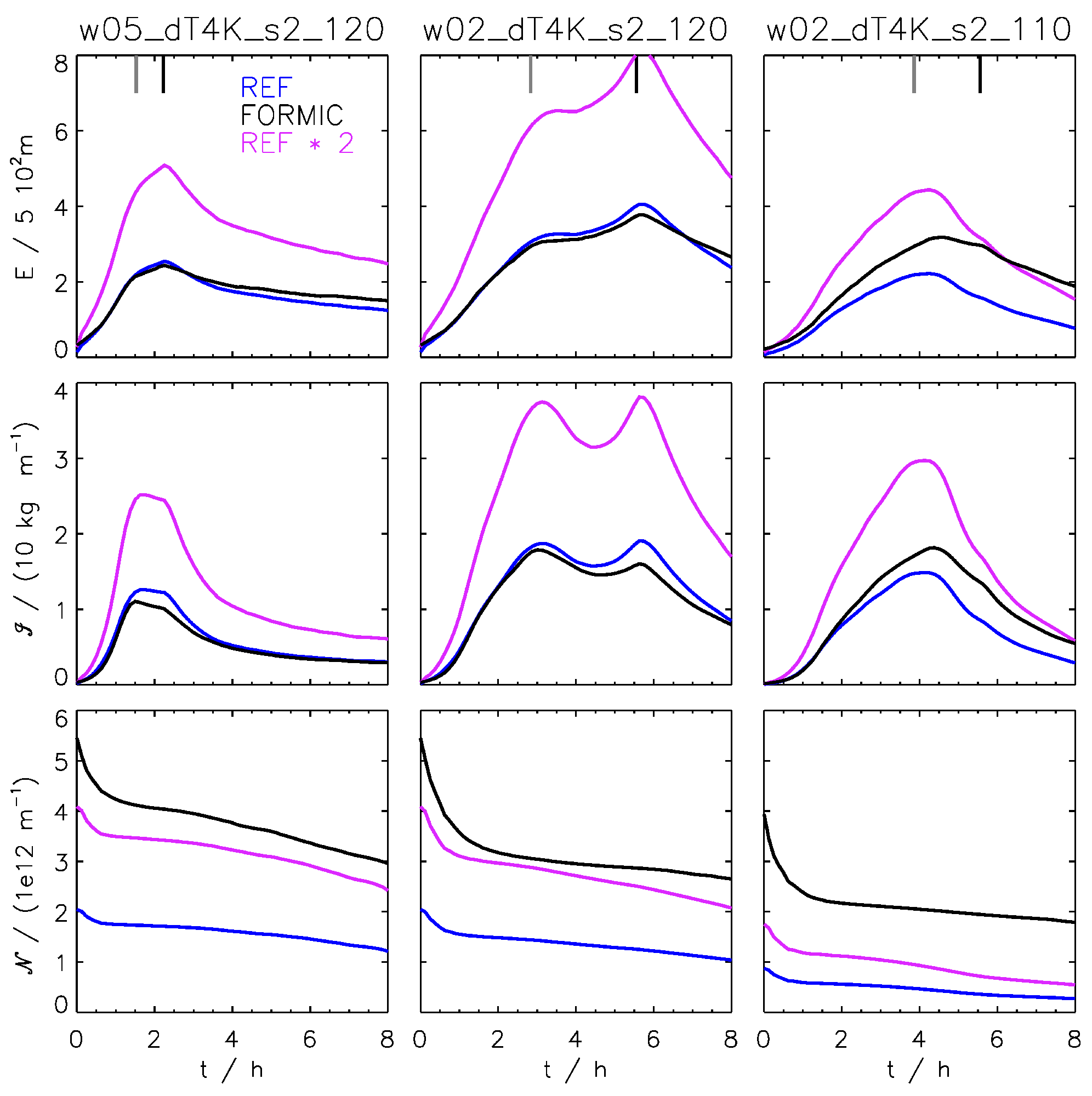
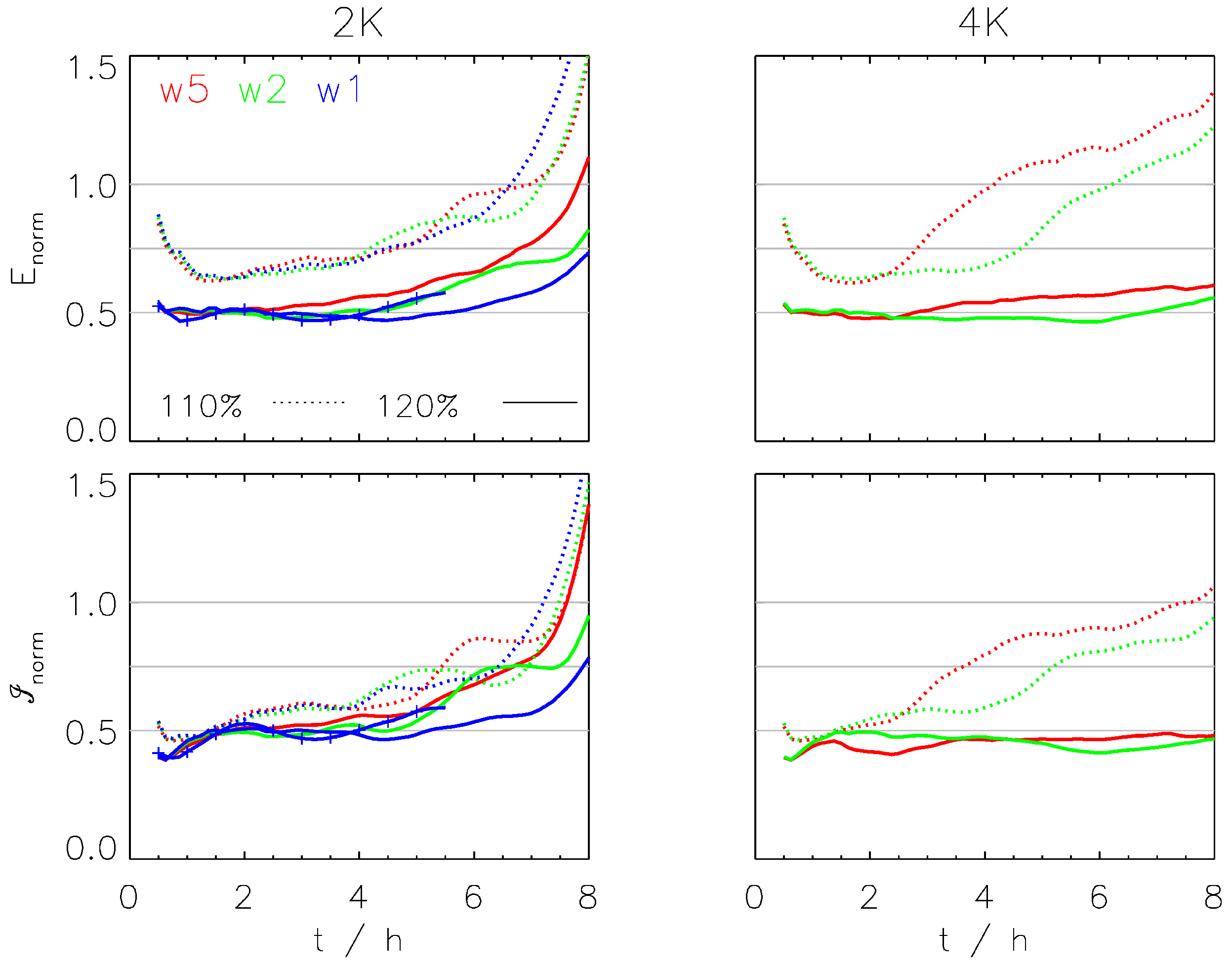
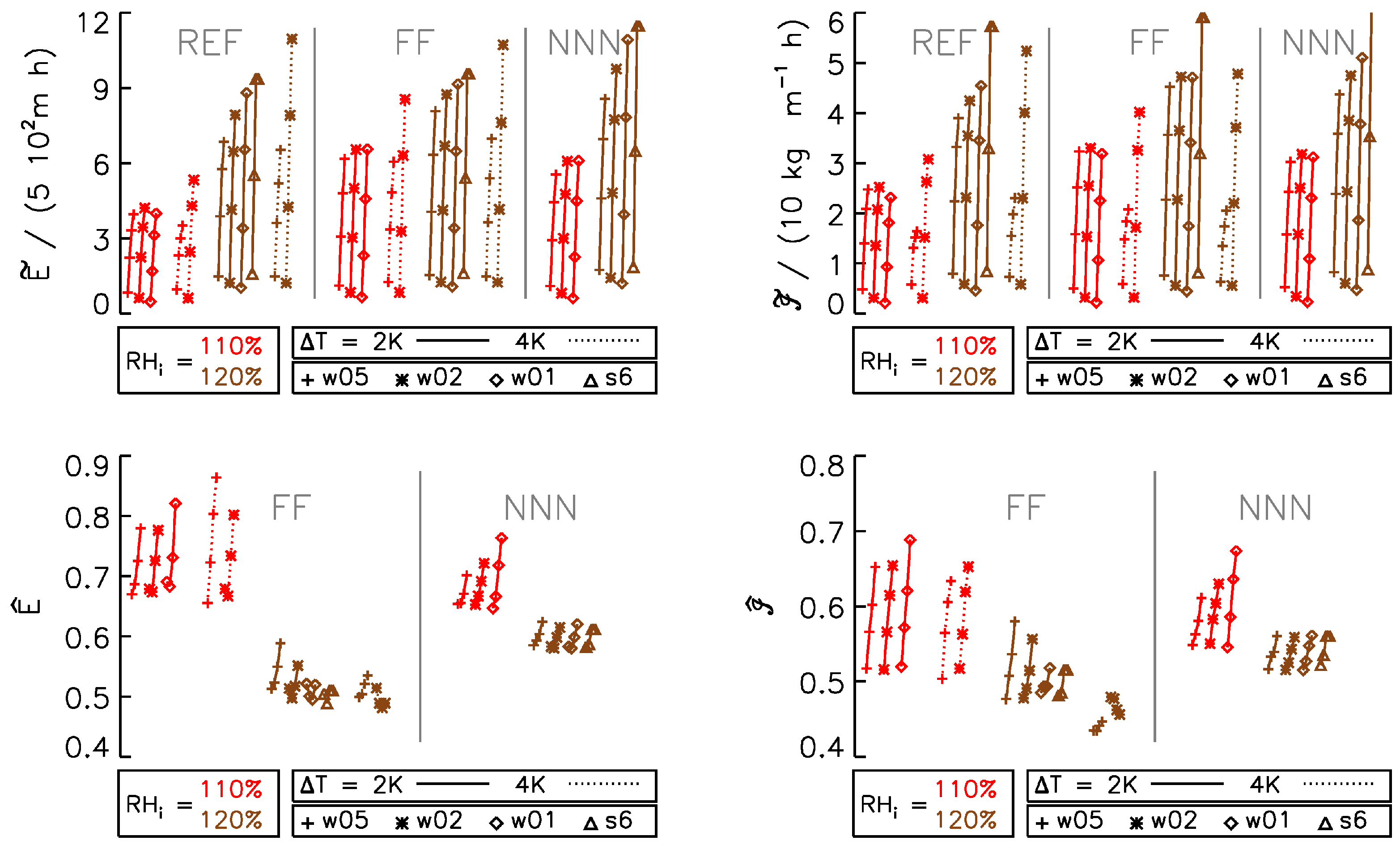
3.3. Time-Integrated Contrail Properties
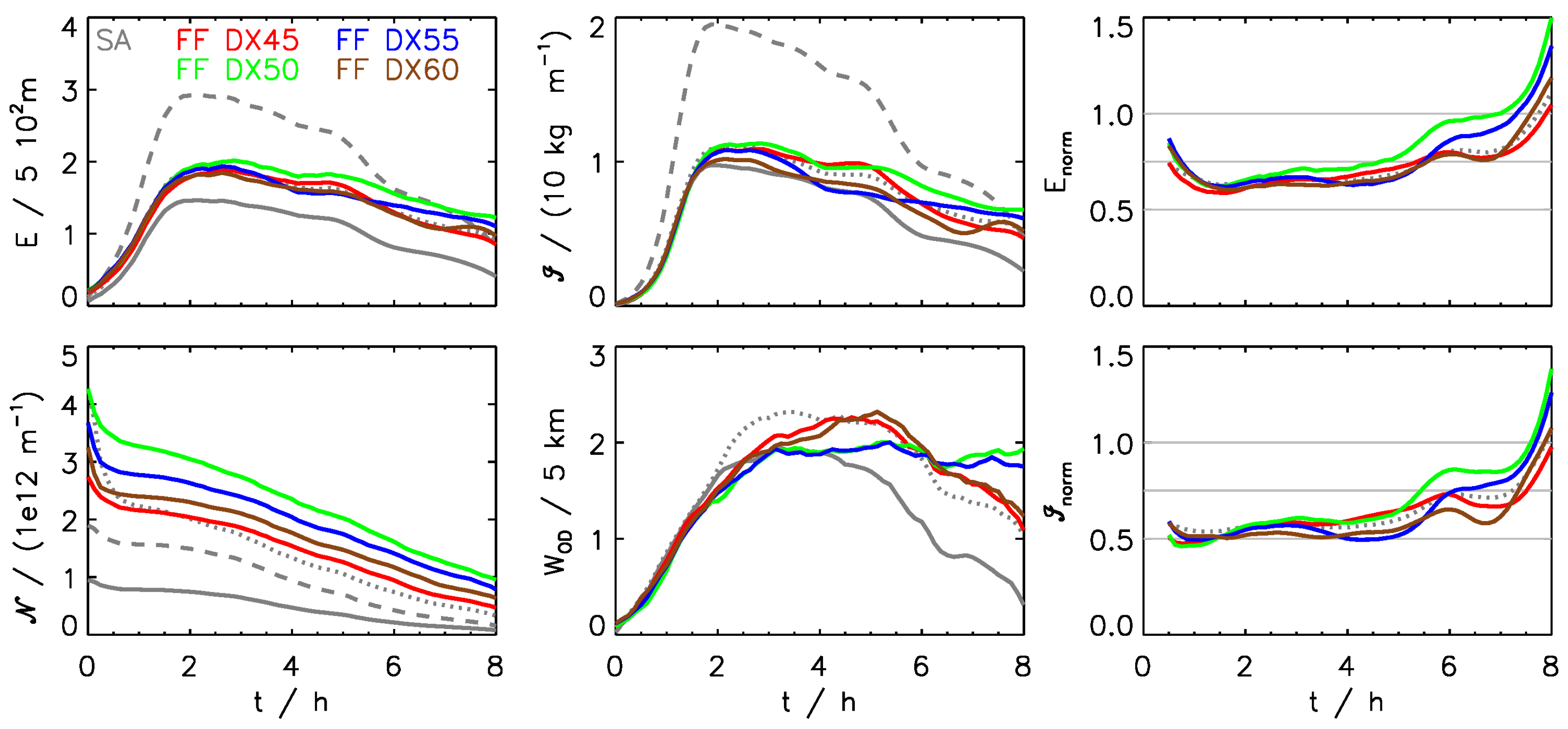
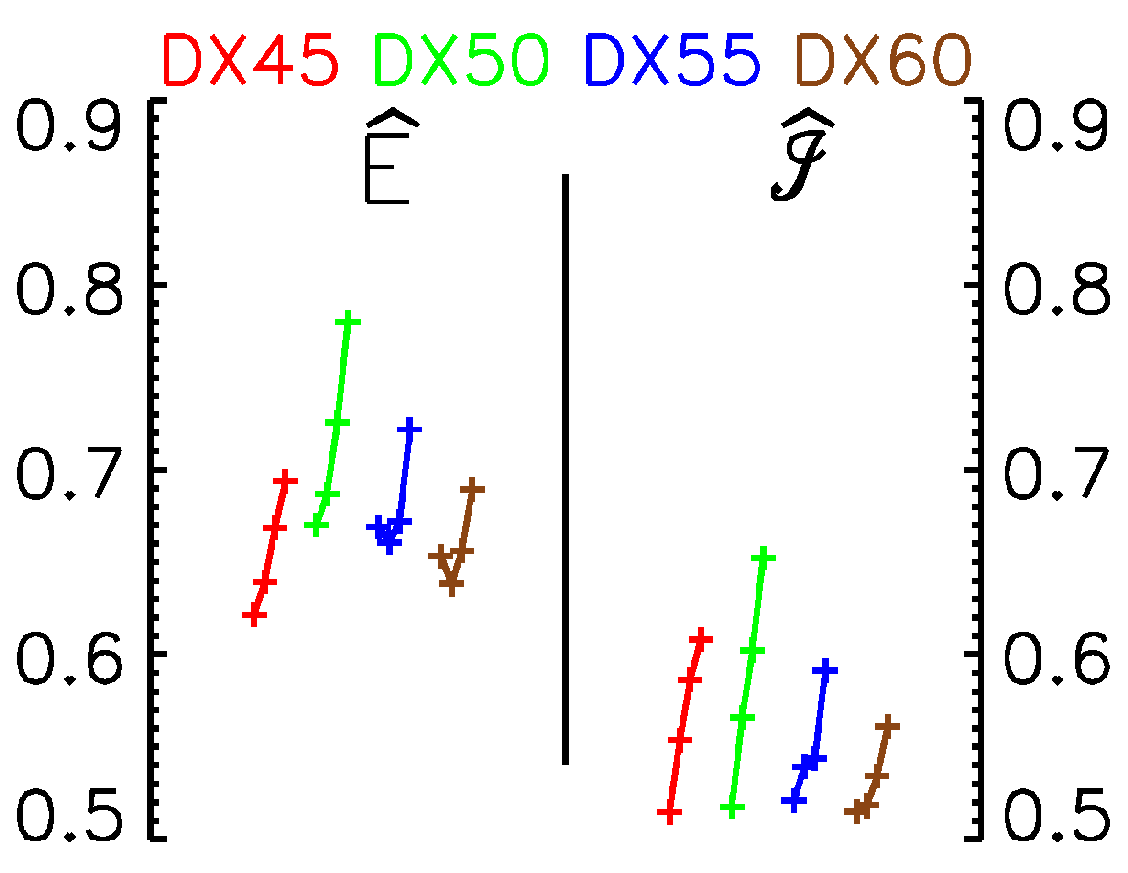
3.4. Sensitivity to Formation Flight Geometry
4. Discussion
5. Summary
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | aircraft |
| CC | contrail-cirrus |
| EULAG | name of the LES model |
| FF | formation flight |
| IC | ice crystal |
| ISS | ice-supersaturated |
| LCM | name of the ice microphysical model |
| LES | large-eddy simulation |
| NNN | type of REF simulation with upscaled IC number |
| RHi | relative humidity with respect to ice |
| initial background RHi in the ISS layer | |
| hypothetic background RHi in the ISS layer after the synoptic cooling | |
| REF | reference |
| RF | radiative forcing |
| SA | single aircraft |
| SIP | simulation particle |
| WV | water vapour |
References
- Lissaman, P.; Shollenberger, C. Formation flight of birds. Science 1970, 168, 1003–1005. [Google Scholar] [CrossRef] [PubMed]
- Hummel, D. Aerodynamic aspects of formation flight in birds. J. Theor. Biol. 1983, 104, 321–347. [Google Scholar] [CrossRef]
- Weimerskirch, H.; Martin, J.; Clerquin, Y.; Alexandre, P.; Jiraskova, S. Energy saving in flight formation. Nature 2001, 413, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Beukenberg, M.; Hummel, D. Aerodynamics, Performance and Control of Airplanes in Formation Flight. In Proceedings of the 17th Congress of the ICAS, Stockholm, Sweden, 9–14 September 1990; Volume 2, pp. 21777–21794. [Google Scholar]
- Blake, W.; Multhopp, D. Design, performance and modeling considerations for close formation flight. In Proceedings of the Guidance, Navigation, and Control and Co-located Conferences, Boston, MA, USA, 10–12 August 1998; AIAA: Reston, VA, USA, 1998; p. 4343. [Google Scholar] [CrossRef]
- Wagner, E.; Jacques, D.; Blake, W.; Pachter, M. Flight Test Results of Close Formation Flight for Fuel Savings. In Proceedings of the Guidance, Navigation, and Control and Co-located Conferences, Monterey, CA, USA, 5 August 2002; AIAA: Reston, VA, USA, 2002; p. 4490. [Google Scholar] [CrossRef]
- Iglesias, S.; Mason, W. Optimum spanloads in formation flight. In Proceedings of the Aerospace Sciences Meetings, Reno, NV, USA, 14–17 January 2002; AIAA: Reston, VA, USA, 2002; p. 258. [Google Scholar] [CrossRef]
- Frazier, J.W.; Gopalarathnam, A. Optimum Downwash Behind Wings in Formation Flight. J. Aircraft 2003, 40, 799–803. [Google Scholar] [CrossRef]
- Bangash, Z.; Sanchez, R.; Ahmed, A.; Khan, M. Aerodynamics of formation flight. J. Aircraft 2006, 43, 907–912. [Google Scholar] [CrossRef]
- Nangia, R.; Palmer, M. Formation Flying of Commercial Aircraft, Variations in Relative Size/Spacing—Induced Effects & Control Induced Effects & Control. In Proceedings of the Fluid Dynamics and Co-located Conferences, Miami, FL, USA, 25–28 June 2007; AIAA: Reston, VA, USA, 2007; p. 4163. [Google Scholar] [CrossRef]
- Kless, J.E.; Aftosmis, M.J.; Ning, S.A.; Nemec, M. Inviscid Analysis of Extended-Formation Flight. AIAA J. 2013, 51, 1703–1715. [Google Scholar] [CrossRef] [Green Version]
- Okolo, W.; Dogan, A.; Blake, W.B. A Modified Analysis of Alternate Lateral Trimming Methods for Flying Wing Aircraft at Sweet Spot in Formation Flight. In Proceedings of the AIAA SciTech Forum, National Harbor, MD, USA, 13–17 January 2014; AIAA: Reston, VA, USA, 2014; p. 0543. [Google Scholar] [CrossRef]
- Xu, J.; Ning, S.; Bower, G.; Kroo, I. Aircraft Route Optimization for Formation Flight. J. Aircraft 2014, 51, 490–501. [Google Scholar] [CrossRef] [Green Version]
- Sausen, R.; Isaksen, I.; Grewe, V.; Hauglustaine, D.; Lee, D.; Myhre, G.; Köhler, M.; Pitari, G.; Schumann, U.; Stordal, F.; et al. Aviation radiative forcing in 2000: An update on IPCC (1999). Meteorol. Z. 2005, 14, 555–561. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Pitari, G.; Grewe, V.; Gierens, K.; Penner, J.; Petzold, A.; Prather, M.; Schumann, U.; Bais, A.; Berntsen, T.; et al. Transport impacts on atmosphere and climate: Aviation. Atmos. Environ. 2010, 44, 4678–4734. [Google Scholar] [CrossRef] [Green Version]
- Burkhardt, U.; Kärcher, B. Global radiative forcing from contrail cirrus. Nat. Clim. Chang. 2011, 1, 54–58. [Google Scholar] [CrossRef] [Green Version]
- Bock, L.; Burkhardt, U. Reassessing properties and radiative forcing of contrail cirrus using a climate model. J. Geophys. Res. 2016, 121, 9717–9736. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S.; Gierens, K. Numerical simulations of contrail-to-cirrus transition—Part 1: An extensive parametric study. Atmos. Chem. Phys. 2010, 10, 2017–2036. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S.; Sölch, I. Numerical Modeling of contrail cluster formation. In Proceedings of the 3rd International Conference on Transport, Atmosphere and Climate, Prien, Deutschland, 25–28 June 2012; pp. 114–119. [Google Scholar]
- Sussmann, R.; Gierens, K. Lidar and numerical studies on the different evolution of vortex pair and secondary wake in young contrails. J. Geophys. Res. 1999, 104, 2131–2142. [Google Scholar] [CrossRef]
- Lewellen, D.; Lewellen, W. The effects of aircraft wake dynamics on contrail development. J. Atmos. Sci. 2001, 58, 390–406. [Google Scholar] [CrossRef]
- Unterstrasser, S. Properties of young contrails—A parametrisation based on large-eddy simulations. Atmos. Chem. Phys. 2016, 16, 2059–2082. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S.; Stephan, A. Far field wake vortex evolution of two aircraft formation flight and implications on young contrails. Aeronaut. J. 2020, 124, 667–702. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S.; Görsch, N. Aircraft-type dependency of contrail evolution. J. Geophys. Res. 2014, 119, 14,015–14,027, 2014JD022642. [Google Scholar] [CrossRef]
- Unterstrasser, S.; Gierens, K.; Sölch, I.; Lainer, M. Numerical simulations of homogeneously nucleated natural cirrus and contrail-cirrus. Part 1: How different are they? Meteorol. Z. 2017, 26, 621–642. [Google Scholar] [CrossRef]
- Unterstrasser, S.; Gierens, K.; Sölch, I.; Wirth, M. Numerical simulations of homogeneously nucleated natural cirrus and contrail-cirrus. Part 2: Interaction on local scale. Meteorol. Z. 2017, 26, 643–661. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.; Margolin, L. On Forward-in-Time Differencing for Fluids: An Eulerian/Semi-Lagrangian Non-Hydrostatic Model for Stratified Flows. In Numerical Methods in Atmospheric and Oceanic Modelling: The André J. Robert Memorial Volume; Lin, C., Laprise, R., Ritchie, H., Eds.; Canadian Meteorological and Oceanographical Society: Ottawa, ON, Canada, 1997; Volume 35, pp. 127–152. [Google Scholar]
- Smolarkiewicz, P.; Kühnlein, C.; Wedi, N. A consistent framework for discrete integrations of soundproof and compressible PDEs of atmospheric dynamics. J. Comput. Phys. 2014, 263, 185–205. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.; Margolin, L. MPDATA: A Finite-Difference Solver for Geophysical Flows. J. Comput. Phys. 1998, 140, 459–480. [Google Scholar] [CrossRef] [Green Version]
- Smolarkiewicz, P.K. Multidimensional positive definite advection transport algorithm: An overview. Int. J. Numer. Methods Fluids 2006, 50, 1123–1144. [Google Scholar] [CrossRef]
- Sölch, I.; Kärcher, B. A large-eddy model for cirrus clouds with explicit aerosol and ice microphysics and Lagrangian ice particle tracking. Q. J. R. Meteorol. Soc. 2010, 136, 2074–2093. [Google Scholar] [CrossRef] [Green Version]
- Sölch, I.; Kärcher, B. Process-oriented large-eddy simulations of a midlatitude cirrus cloud system based on observations. Q. J. R. Meteorol. Soc. 2011, 137, 374–393. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S. Large eddy simulation study of contrail microphysics and geometry during the vortex phase and consequences on contrail-to-cirrus transition. J. Geophys. Res. 2014, 119, 7537–7555. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, P.; Schlesinger, R. A Numerical Study of Cirrus Clouds. Part II: Effects of Ambient Temperature, Stability, Radiation, Ice Microphysics, and Microdynamics on Cirrus Evolution. J. Atmos. Sci. 2003, 60, 1097–1119. [Google Scholar] [CrossRef] [Green Version]
- Spichtinger, P.; Gierens, K. Modelling of cirrus clouds—Part 2: Competition of different nucleation mechanisms. Atmos. Chem. Phys. 2009, 9, 2319–2334. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S.; Gierens, K. Numerical simulations of contrail-to-cirrus transition—Part 2: Impact of initial ice crystal number, radiation, stratification, secondary nucleation and layer depth. Atmos. Chem. Phys. 2010, 10, 2037–2051. [Google Scholar] [CrossRef] [Green Version]
- Lewellen, D.C. Persistent contrails and contrail cirrus. Part 2: Full Lifetime Behavior. J. Atmos. Sci. 2014, 71, 4420–4438. [Google Scholar] [CrossRef] [Green Version]
- Unterstrasser, S.; Sölch, I. Optimisation of simulation particle number in a Lagrangian ice microphysical model. Geosci. Model Dev. 2014, 7, 695–709. [Google Scholar] [CrossRef] [Green Version]
- Paoli, R.; Shariff, K. Contrail Modeling and Simulation. Annu. Rev. Fluid Mech. 2016, 48, 393–427. [Google Scholar] [CrossRef] [Green Version]
- Kaufmann, S.; Voigt, C.; Jeßberger, P.; Jurkat, T.; Schlager, H.; Schwarzenboeck, A.; Klingebiel, M.; Thornberry, T. In situ measurements of ice saturation in young contrails. Geophys. Res. Lett. 2014, 41, 702–709. [Google Scholar] [CrossRef]
- Grewe, V.; Dahlmann, K. How ambiguous are climate metrics? Furthermore, are we prepared to assess and compare the climate impact of new air traffic technologies? Atmos. Environ. 2015, 106, 373–374. [Google Scholar] [CrossRef] [Green Version]
- Bickel, M.; Ponater, M.; Bock, L.; Burkhardt, U.; Reineke, S. Estimating the Effective Radiative Forcing of Contrail Cirrus. J. Clim. 2020, 33, 1991–2005. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U.; Graf, K.; Mannstein, H. Potential to reduce the climate impact of aviation by flight level changes. In Proceedings of the 3rd AIAA Atmospheric and Space Environments Conference, Honolulu, HI, USA, 27–30 June 2011; Volume 3376, pp. 1–22. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U.; Heymsfield, A.J. On the Life Cycle of Individual Contrails and Contrail Cirrus. Meteorol. Monogr. 2017, 58, 3.1–3.24. [Google Scholar] [CrossRef]
- Schumann, U.; Mayer, B.; Graf, K.; Mannstein, H. A Parametric Radiative Forcing Model for Contrail Cirrus. J. Appl. Meteor. Climatol. 2012, 51, 1391–1406. [Google Scholar] [CrossRef] [Green Version]
- Crow, S. Stability theory for a pair of trailing vortices. AIAA J. 1970, 8, 2172–2179. [Google Scholar] [CrossRef]
- Bier, A.; Burkhardt, U.; Bock, L. Synoptic Control of Contrail Cirrus Life Cycles and Their Modification Due to Reduced Soot Number Emissions. J. Geophys. Res. 2017, 122, 11584–11603. [Google Scholar] [CrossRef] [Green Version]
- Paoli, R.; Thouron, O.; Cariolle, D.; García, M.; Escobar, J. Three-dimensional large-eddy simulations of the early phase of contrail-to-cirrus transition: Effects of atmospheric turbulence and radiative transfer. Meteorol. Z. 2017, 26, 597–620. [Google Scholar] [CrossRef]
- Grewe, V.; Stenke, A. AirClim: An efficient tool for climate evaluation of aircraft technology. Atmos. Chem. Phys. 2008, 8, 4621–4639. [Google Scholar] [CrossRef] [Green Version]
- Marks, T.; Dahlmann, K.; Grewe, V.; Gollnick, V.; Linke, F.; Matthes, S.; Stumpf, E.; Unterstrasser, S.; Yamashita, H.; Zumegen, C. Climate Impact Mitigation Potential of Formation Flight. Aerospace 2020. in review. [Google Scholar]
- Dahlmann, K.; Matthes, S.; Yamashita, H.; Unterstrasser, S.; Grewe, V.; Marks, T. Assessing the climate impact of formation flights. Aerospace 2020. in review. [Google Scholar]


| Default Parameter Settings | |||||
|---|---|---|---|---|---|
| Quantity | Value | Quantity | Value | Quantity | Value |
| Numerical parameters | |||||
| or | |||||
| Atmospheric parameters | |||||
| hPa | |||||
| 217 K | ≈1200 m | ≈600 m | |||
| Atmospheric Updraught Scenarios | ||||
|---|---|---|---|---|
| wsyn | tupdr,2K | tupdr,4K | tnuc/ s | tnuc/ s |
| in | in | in | ||
| 1 | 20,000 | – | – | – |
| 2 | 10,000 | 20,000 | 10,200 | 13,900 |
| 5 | 4000 | 8000 | 4000 | 5500 |
| Final | ||||
| Contrail Parameters | ||||||
|---|---|---|---|---|---|---|
| # 1 | # 2 | # 3 | # 4 | # 5 | ||
| scenario | W/m | H/m | (kg/m) | |||
| 110% | 140 | 345 | 0.94 | 28% | 0.05 | |
| SA case REF @ | 120% | 250 | 420 | 2.22 | 66% | 0.15 |
| 110% | 415 | 260 | 4.27 | 64% | 0.17 | |
| FF case @ | 120% | 430 | 260 | 5.91 | 89% | 0.32 |
| DX45 | 400 | 260 | 2.74 | 41% | 0.16 | |
| FF case | DX55 | 590 | 250 | 3.68 | 55% | 0.16 |
| DX60 | 610 | 270 | 3.33 | 49% | 0.16 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unterstrasser, S. The Contrail Mitigation Potential of Aircraft Formation Flight Derived from High-Resolution Simulations. Aerospace 2020, 7, 170. https://doi.org/10.3390/aerospace7120170
Unterstrasser S. The Contrail Mitigation Potential of Aircraft Formation Flight Derived from High-Resolution Simulations. Aerospace. 2020; 7(12):170. https://doi.org/10.3390/aerospace7120170
Chicago/Turabian StyleUnterstrasser, Simon. 2020. "The Contrail Mitigation Potential of Aircraft Formation Flight Derived from High-Resolution Simulations" Aerospace 7, no. 12: 170. https://doi.org/10.3390/aerospace7120170
APA StyleUnterstrasser, S. (2020). The Contrail Mitigation Potential of Aircraft Formation Flight Derived from High-Resolution Simulations. Aerospace, 7(12), 170. https://doi.org/10.3390/aerospace7120170





