Abstract
This paper presents the issues concerning calibration of a measurement system for monitoring the cross-sectional forces and moments of an unmanned aircraft’s wing. A composite cantilever wing with built-in measurement systems based on electrical resistance and Fibre Bragg Grating strain gauges has been made for the purpose of the study. Measurement systems placed along the span of the wing consist of strain gauges arranged in a manner that allows the monitoring of shear force, bending and twisting moments. The calibration process was described in terms of both experimental tests and mathematical formalism. The calibration results were compared for the complete system, consisting of three sensor units, and for various combinations of separated measuring points. For each case, a reading inaccuracy analysis was carried out and conclusions, including recommendations for the design of this kind of measurement system, were formulated.
1. Introduction
Currently, there is a significantly growing interest in Unmanned Aircraft Systems (UASes). The load-bearing structures of this kind of aeroplane are largely built as composite structures. With respect to their fatigue life, such structures are relatively poorly understood. In this regard, it would be appropriate to intensify the work leading to the fullest understanding of the nature of load on the particular elements of UAS structures. The continuous development of numerical methods, including the finite element method, can help to develop more and more accurate and fuller strength analyses. However, in order to reach the full potential of modern computational methods, one should use experimental testing. Correct numerical results are determined by, more than anything else, the knowledge of material constants, which allow us to, among other things, reproduce the stiffness of the analysed structure as accurately as possible. As far as aircraft structures are concerned, there is an additional problem in the numerical calculations: proper discretization of the pressure distribution on lifting surfaces, caused by the aerodynamic loads [1]. This issue is particularly important in numerical fatigue tests, in which the determination of the actual load spectrum present during the operation of the aircraft conditions the correctness of the results obtained.
Many experimental testing methods have been used to determine the load spectrum acting on the aircraft structure [2,3,4,5,6]. For manned aircrafts, electrical resistance strain gauges have been successfully used for many years in cases of load monitoring. Their appropriate arrangement allows monitoring of the current load level of the structure. In the aircraft’s wing, the major load is induced by the bending moment, shear force and torsional moments that appear in the structure as the effects of aerodynamic forces (Figure 1a). The values of section loads differ along the wingspan (Figure 1b) and are also connected with the actual load factor depending on the flight conditions and manoeuvre of the aircraft.
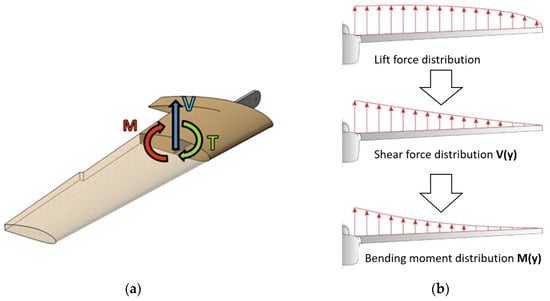
Figure 1.
Wing main section load (a) and sample spanwise distribution of lift force, shear force and bending moment acting on the wing (b).
The idea of measurements taken using strain gauges is connected with the assumption of the work of the structure as a semi-monocoque structure [7,8]. Under such conditions, the wing spar caps transmit axial loads only, which are the effect of the bending moment, while the spar wall and the other part of the skin work for shear only. It, thus, becomes possible to connect the occurrence of the essential cross-sectional forces and moments with the strains in the semi-monocoque structure elements. The system of three strain gauge bridges, as presented in Figure 2, enables us, once it is calibrated, to determine the section load components using Equation (1):
where V is the shear force, M is the bending moment, T is the torsional moment; μj is the strain gauge bridge readings (j = 1, 2, 3). Coefficients βij (i,j = 1, 2, 3) in Equation (1) are the values to be determined during the experimental calibration tests according to Equation (2), involving at least three specific load cases.
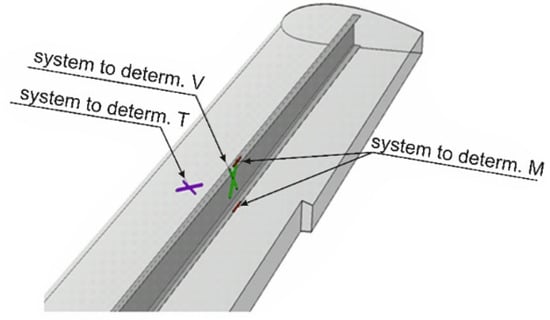
Figure 2.
Typical positions of strain gauges making up a system for measuring cross-sectional forces and moments in the wing structure.
This measurement method was first outlined in the literature as a NASA report [9] and, later, repeatedly applied in tests on aircraft structures [10,11,12,13,14]. However, there is a lack in the literature of such tests on unmanned structures, in particular on mini- or micro-class aircraft. The fact that no such tests have been performed on UASes so far is probably due to the considerable weight of the measuring systems based on strain gauges in relation to the weight of the UAS structure, which does not allow their use during the actual operation.
However, special attention needs to be paid to the development of alternative measuring techniques based on fibre optic strain gauges called Fibre Bragg Grating (FBG) sensors, which are low in weight and can thus be used in the classes of the structure in question. There are many examples in the literature of using this kind of sensor in research, including fatigue crack growth measurements [15], detection of the delamination [16,17], stress and strain state monitoring [18,19,20] and life cycle monitoring of composite structures [21,22]. There are also examples of the testing of aircraft structures. Iadicicco et al. [23] presented the application of FBG sensors to monitor the strain state of composite aircraft landing gear. Orkisz et al. [24] used FBG sensors to measure strain level change due to fatigue tests of the composite spar of a motor sailplane. Ramly et al. [25] described the design and development of a part of a vertical stabilizer in the form of a composite sandwich panel with embedded FBG. Ruzek et al. [26] and Tserpes et al. [27] published papers devoted to strain and damage monitoring in Carbon Fibre Reinforced Plastics (CFRP) fuselage panels using FBG sensors. Ryu et al. [28] used numerous built-in FBG sensors to carry out buckling behaviour monitoring of a composite wing box. Recently, Ma and Chen [29] summarized applications of FBG to wing shape measurement. Nicolas et al. [30] published research results based on the testing of a composite wing with hundreds of built-in types of constant FBG sensors.
This study explores the issues of the calibration of the above-described measurement system. As mentioned above, the measuring method is closely linked with the theory of how a semi-monocoque structure works, so the full version of the system in question is based on the simultaneous measurement of three values, i.e., shear force, bending moment and torsional moment, using three sensor sets. Bearing in mind that it is also possible to measure these values individually, an attempt was made to determine the reading accuracy level according to the number of gauges used. This issue seems essential given the cost of a measurement system and the possibility of reducing its weight in the case of using fewer gauges.
2. Tested Structure
For the purpose of the study, a single-spar composite cantilever wing with a constant aerodynamic profile (NACA 4415) was made. The channel-sectioned spar was built from carbon fabric and additionally reinforced with carbon roving on the junctions of the shelves and wall. The wing skin was a sandwich-thin shell made of four carbon fabric layers, with an axial configuration of ±45° and with a core of polyurethane foam. The whole spar was covered with one glass fabric layer.
The wing was connected to the UAS fuselage through the bayonet portion of the spar, which had two supports to take the reaction in the form of shear force and bending moment. The third support was attached to the rear portion of the wing, by the so-called anti-flap wall, to prevent the rotation of the wing on the aircraft’s lateral axis. The solution details of the technical realization of the test stand are presented in Figure 3.

Figure 3.
CAD geometry of tested wing (a) and details of carry through structures and attachment part of the test stand (b).
3. Measurement System
The measurement system used was built on the basis of electrical resistance and fibre optic strain gauges. The strain gauges were grouped under four measuring sections (Figure 4). Systems I, II and III comprised three strain gauge bridges each.
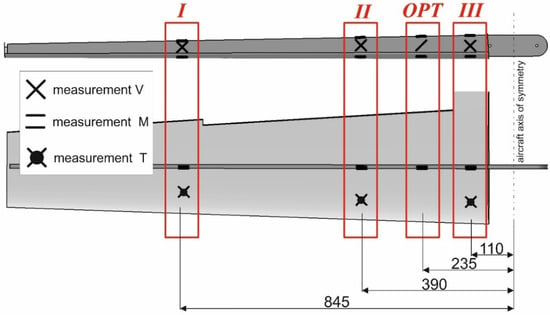
Figure 4.
Strain gauges positions inside the wing structure (dimensions in mm).
Shear force was measured with the use of the gauges connected in a full bridge system positioned on the spar wall, according to the assumption that the essential task of the wall was to transmit transverse forces.
The occurrence of the bending moment is linked to the loading of the spar caps with normal forces, and that is why half-bridge gauges were placed on the surface of those elements. According to the idea of the work of the semi-monocoque structure, the wing skin elements are only subjected to loads in the form of shear stress.
The front portion of the wing, separated by the spar, is a torque box, the task of which is to transmit torsional moment. In order to determine this value, full bridge systems integrated with the skin were used.
Systems I, II and III comprised 30 electrical resistance strain gauges in total (Figure 4 and Figure 5). All used electrical sensors were manufactured by HBM company (Hottinger Baldwin Messtechnik GmbH, Darmstadt, Germany), they were general purpose strain gauges with 10 mm gauge length and 120 Ω nominal resistance. Electrical strain gauges were bonded to the composite structure of the wing using HBM Z70 cyanoacrylate adhesive.

Figure 5.
Strain gauges integrated into the wing structure.
As already emphasized for UAS structures, the weight of the measurement system is the key factor and that is why fibre optic strain gauges were additionally embedded in the structure tested (OPT Section, Figure 4). The optical strain gauge chain used was an HBM OptiMet-OMF single-mode optical fibre with four Bragg gratings acting as the strain measuring points. In general, it allows us to place up to 13 Bragg gratings a minimum of 60 cm apart with a Bragg wavelength distance of 5 nm. The diameter of the fibre core is 6 μm and the outer diameter of the fibre with cladding is approximately 195 μm. Opticla strain gauges were bonded to the tested structure with the use of a HBM X120 bi component cold-curing epoxy adhesive, specially selected for installing optical fibres. According to the data sheets, such a glued connection allows the fibre to strain up to 0.7% in both positive and negative directions and its expected fatigue life should be above 107 load cycles.
Shear force was measured using one gauge placed on the spar wall at the angle of 45 degrees in relation to the spar caps. The measurement system design included two such gauges placed on the opposite sides of the spar wall; however, one of the gauges was damaged during installation.
The system for measuring bending moment was built from two gauges placed along the spar caps on the inner sides. Additionally, one strain gauge was used to compensate for the effect of temperature. No temperature compensation is required for electrical resistance strain gauges, as half-bridge and full bridge systems are self-compensating.
The measurement data acquisition system (Figure 6) consisted of the HBM Quantum MX840B strain gauge amplifier and the HBM SI405 interrogator for FBG sensors. The used amplifier for electrical strain gauges has a mass of approximately 1 kg and is equipped with eight channels with sample rates up to 40 kHz for each of them. The interrogator is capable of capturing data with a measuring range up to 10 Hz from four optical chains connected, which gives us the possibility of recording data from up to 52 measuring points. The mass of the device is approximately 2 kg, but it can be assumed that, with time, this value will decrease with the introduction of subsequent generations of equipment. Both devices were connected to a PC with installed HBM Catman Easy AP 4.2 software (Hottine Baldwin Messtechnik GmbH, Darmstadt, Germany), which allows for the recording and time synchronization of the measurement results.

Figure 6.
Complete tested wing and acquisition systems.
4. Measurement System Calibration
The measurement system was calibrated through applying concentrated loads in a gravitational manner, one by one, at five points spanwise and chordwise of the wing (Figure 7). In this way, fifteen load cases (Table 1) with different values of shear force (V), bending moment (M) and torsional moment (T) acting on the wing were considered.
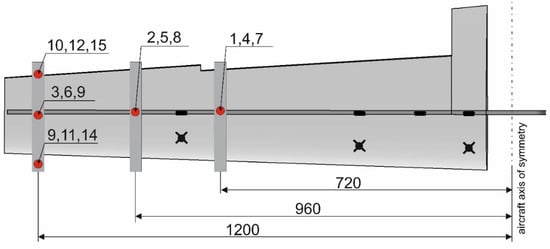
Figure 7.
Points of application of force (The digits in the figure refer to the load cases in Table 1).

Table 1.
Experimental load cases.
In Table 1, each load value is normalized and refers to the values of shear force and bending moment that occurred in the first loading phase at Section III.
The strain measurement results obtained in the tests were used to calibrate the system, that is, to determine the β coefficients in Equations (1) and (2), which, for n measurements is generally expressed, is as follows:
After appropriate transformation, the β values can be obtain according to Equations (6)–(8):
where, for one bridge j = 1, for two bridges j = 1, 2; while for one full measurement system (three bridges) j = 1, 2, 3.
5. Measurement Results
5.1. Calibration Cases
The results obtained in the tests were used to consider the following three calibration cases:
- Calibration with the use of one full measurement system: System A
- Calibration with the use of only the bridges for the measurement of shear force and bending moment: System B
- Calibration with the use of individual bridges—individual measurements of shear force, bending moment and torsional moment: System C
Each case led to the calculation of the β coefficients according to Equations (6)–(8) and to the determination of the cross-sectional forces and moments. The graphics below make up a comparison between the measurement errors (absolute values) for each load case under consideration. The absolute error values were calculated according to Equations (9), where subscript calib means values obtained with the use of Equations (3)–(5) and values without subscripts are the actual loads the structure is subjected to.
5.2. System Calibration for Resistance Strain Gauges (Sections II and III)
Figure 8, Figure 9, Figure 10 and Figure 11 show the distribution of errors in strain gauge readings for Sections II and III. The analysis of the results leads to the conclusion that the systems and the numerical calibration procedure applied to provide information on the bending moment acting in the section have a margin of error not exceeding 5%. The calibration results also show that the accuracy of the measured value is slightly dependent on the measurement system used.
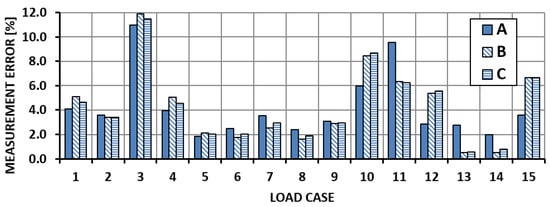
Figure 8.
Shear force measurement error—Section II.
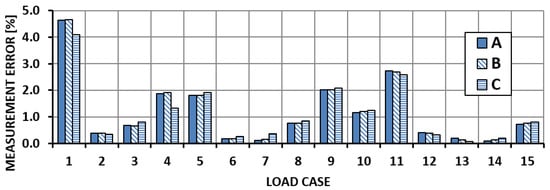
Figure 9.
Bending moment measurement error—Section II.
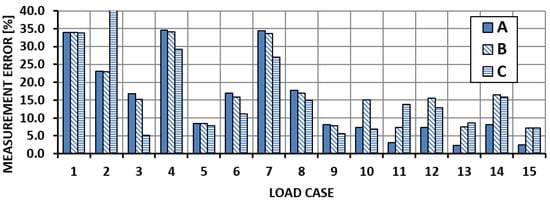
Figure 10.
Shear force measurement error—Section III.
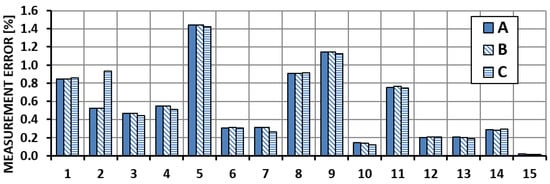
Figure 11.
Bending moment measurement error—Section III.
For the determination of the shear force, the errors in Section II did not exceed 12%, whereas the error of measurement in Section III reached 40%. When analysing the graphs in Figure 7 and Figure 9, one can conclude that the measurement errors deviate significantly from the mean in only a few measurements. Figure 12 and Figure 13 present the results of the calibration performed after removing measurements 3, 10 and 11 (System A1). The elimination of the clearly incorrect readings had a positive effect on the calibration process; however, it should be noted that the mean square error deviation increased for the whole series of measurements.
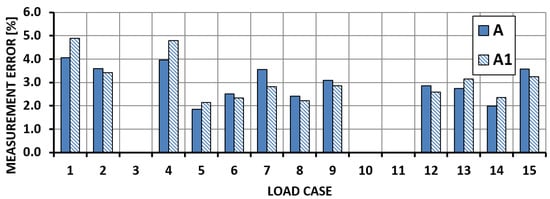
Figure 12.
Shear force measurement error—Section II.
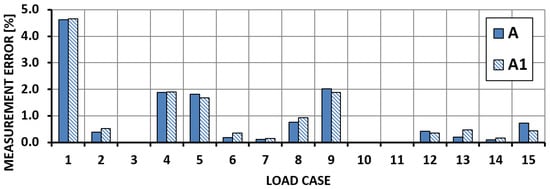
Figure 13.
Bending moment measurement error—Section II.
The assessment of the results obtained also leads to the conclusion that the distribution of measurement errors is accidental in character and results rather from the mathematical roots of the method than from the load cases considered.
Table 2 shows calibration errors for the torsional moment measurement. The use of the full measurement system (System A) results in a satisfactory reading accuracy, one that does not exceed 10% of the actual load values. System B or the measurement with the use of only one bridge embedded in the wing’s torque box skin leads to completely incorrect readings (absolute error above 100%).

Table 2.
Torsional moment measurement errors.
5.3. System Calibration for BRAGG FIBRE STRAIN GAUGES (OPT Section)
The calibration results for fibre optic strain gauges are presented in Figure 14 and Figure 15. The results of the bending moment measurement for both System B and System C should be considered satisfactory (error below 3%) when compared to results obtained for electrical strain gauges (Figure 9, Figure 11 and Figure 13).
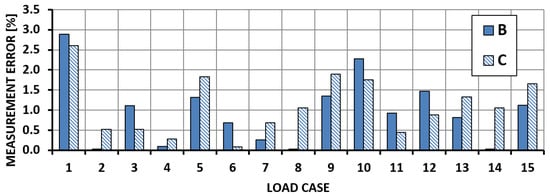
Figure 14.
Bending moment measurement error—OPT Section.
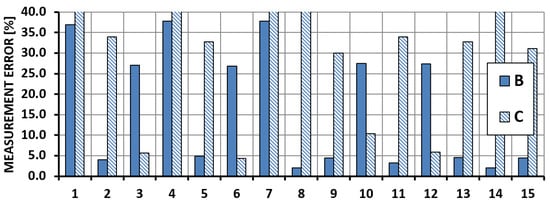
Figure 15.
Shear force measurement error—OPT Section.
The results of the shear force measurements for System B show an error rate of 40%. However, it should be noted that the measurements were taken using only one gauge (Section 3), which probably has affected the measurement accuracy. Using the readings of only one gauge placed on the spar wall (System C) to calibrate the system leads to discrepancies between the actual and measured values at a rate of 140% (beyond the scale in Figure 15). Obtained results indicate that the monitoring of shear force level based on the measurement of strain in the wall of the wing spar cannot be conducted with the use of only one sensor. This phenomenon is probably connected with local deformations of the structure which affect calibration accuracy. To achieve acceptable accuracy, a complete measuring system (Figure 2) should be used.
6. Summary and Conclusions
The paper has presented the results of the calibration of the measurement systems used to determine cross-sectional forces and moments of an unmanned aircraft’s wing. The measurements were taken using both electrical resistance and fibre optic strain gauges based on the Bragg grating method.
The tests have proven that it is not necessary to use a full measurement system consisting of three sensor groups (schematically presented in Figure 2) to measure a bending moment. A system built from only the gauges embedded in the wing spar caps enables measurements with accuracies sufficient to assess the behaviour of the structure during operation. The introduction of the results of measurements from sensors placed on the skin of the wing, and the wall of the wing spar, into the calibration procedure do not indicate a significant impact on calibration errors.
The analysis of the measurement results for shear force shows that there are significant discrepancies in the actual values (error between 12% and 40% depending on the measuring section). The obtained results also lead to the conclusion that it is only possible to determine the wing’s torsional moment with the use of a full measurement system, as presented in Figure 2.
In conclusion, linked to the fact that the bending moment is, in most cases, a load that determines the dimensions of the wing structure is the basis for the construction of simple and relatively low-cost measurement systems. If the intention is monitoring the shear force or all cross-sectional forces and moments, a complete measurement should be used.
It should also be noted that, at present, the mass of interrogators used to record data from optical strain gauges is greater than the mass of devices used for electrical strain sensors. This disadvantage is less significant if it is planned that more optical sensors will be used, because the mass of one FBG deformation sensor is insignificant compared to the mass of electric strain gauges.
Funding
The research was conducted under the Maintaining Research Potential funds for the Department of Aircraft and Aircraft Engines of Rzeszów University of Technology, but some results used are from a project on Modern Material Technologies in Aerospace Industry (No. POIG.01.01.02-00-015/08-00) with Financial support from Structural Funds in the Operational Programme–Innovative Economy (IE–OP) financed from the European Regional Development Fund.
Conflicts of Interest
The author declares no conflict of interest.
References
- Schrenk, O. A Simple Approximation Method for Obtaining the Spanwise Lift Distribution. J. R. Aeronaut. Soc. 1941, 45, 331–336. [Google Scholar] [CrossRef]
- Aoki, Y.; Ishikawa, T.; Takeda, S.-I.; Hayakawa, Y.; Harada, A.; Kikukawa, H. Fatigue test of lightweight composite wing structure. Int. J. Fatigue 2006, 28, 1109–1115. [Google Scholar] [CrossRef]
- Baraniecki, R.; Kaniewska, M.; Leski, A. Fatigue Life Assessment of Selected Structural Elements of MI-24 Helicopter. Fatigue Aircr. Struct. 2010, 2010, 5–13. [Google Scholar] [CrossRef][Green Version]
- Diamanti, K.; Soutis, C. Structural health monitoring techniques for aircraft composite structures. Prog. Aerosp. Sci. 2010, 46, 342–352. [Google Scholar] [CrossRef]
- Reymer, P. Validation of the FEM model of the Mi-24 tail boom and vertical stabilizer. J. KONES Powertrain Transp. 2011, 18. [Google Scholar]
- Takeda, S.-I.; Aoki, Y.; Ishikawa, T.; Takeda, N.; Kikukawa, H. Structural health monitoring of composite wing structure during durability test. Compos. Struct. 2007, 79, 133–139. [Google Scholar] [CrossRef]
- Brzoska, Z. Statyka i Stateczność Konstrukcji Prętowych i Cienkościennych; PWN: Warsaw, Poland, 1965. [Google Scholar]
- Megson, T.H.G. Introduction to Aircraft Structural Analysis, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Skopinski, T.; Aiken, W.; Huston, W. Calibration of Strain-Gauge Installation in Aircraft Structures for the Measurements of Flight Loads; NACA Technical Note 2993; NACA: Washington, DC, USA, 1953. [Google Scholar]
- Eckstorm, C. Flight Loads Measurements Obtained from Calibrated Strain-Gage Bridges Mounted Externally on Skin of Low-Aspect-Ratio Wing; NASA TN D-8349; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Hovell, P.; Webber, D.; Roberts, T. The use of Calibrated Strain Gauges for Flight Load Determination; Aeronautical Research Council Technical Report 1041; NASA: Washington, DC, USA, 1969. [Google Scholar]
- Jenkins, J.; DeAngelis, V. A Summary of Numerous Strain-Gauge Load Calibrations on Aircraft Wings and Tails in a Technology Format; NASA Technical Memorandum 4804; NASA: Washington, DC, USA, 1997. [Google Scholar]
- Lokos, W.; Stauf, R. Strain-Gage Calibration Parametric Study; NASA TM 212853; NASA: Washington, DC, USA, 2004. [Google Scholar]
- Monaghan, R.; Fields, R. Experiments to Study Strain-Gage Load Calibrations on Wing Structure at Elevated Temperatures; NASA TN D-7390; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Bao, P.; Yuan, M.; Dong, S.; Song, H.; Xue, J. Fiber Bragg grating sensor fatigue crack real-time monitoring based on spectrum cross-correlation analysis. J. Sound Vib. 2013, 332, 43–57. [Google Scholar] [CrossRef]
- Grouve, W.; Warnet, L.; de Boer, A.; Akkerman, R.; Vlekken, J. Delamination detection with fibre Bragg gratings based on dynamic behavior. Compos. Sci. Technol. 2008, 68, 2418–2424. [Google Scholar] [CrossRef]
- Takeda, N.; Okabe, Y.; Kuwahara, J.; Kojima, S.; Ogisu, T. Development of smart composite structures with small-diameter fiber Bragg grating sensors for damage detection: Quantitative evaluation of delamination length in CFRP laminates using Lamb wave sensing. Compos. Sci. Technol. 2005, 65, 2575–2587. [Google Scholar] [CrossRef]
- Mulle, M.; Zitoune, R.; Collombet, F.; Robert, L.; Grunevald, Y.-H. Embedded FBGs and 3-D DIC for the stress analysis of a structural specimen subjected to bending. Compos. Struct. 2009, 91, 48–55. [Google Scholar] [CrossRef]
- Rao, Y. Recent progress in applications of in-fibre Bragg grating sensors. Opt. Lasers Eng. 1999, 31, 297–324. [Google Scholar] [CrossRef]
- Antonucci, V.; Esposito, M.; Ricciardi, M.; Giordano, M.; Zarrelli, M. Strain monitoring of composite elements by fibre Bragg grating sensors during a quasi-static indentation. Compos. Part B Eng. 2014, 56, 34–41. [Google Scholar] [CrossRef]
- Minakuchi, S.; Takeda, N.; Takeda, S.-I.; Nagao, Y.; Franceschetti, A.; Liu, X. Life cycle monitoring of large-scale CFRP VARTM structure by fiber-optic-based distributed sensing. Compos. Part A Appl. Sci. Manuf. 2011, 42, 669–676. [Google Scholar] [CrossRef]
- Papantoniou, A.; Rigas, G.; Alexopoulos, N.D.; Rigas, G.-P. Assessment of the strain monitoring reliability of fiber Bragg grating sensor (FBGs) in advanced composite structures. Compos. Struct. 2011, 93, 2163–2172. [Google Scholar] [CrossRef]
- Iadicicco, A.; Natale, D.; Di Palma, P.; Spinaci, F.; Apicella, A.; Campopiano, S. Strain Monitoring of a Composite Drag Strut in Aircraft Landing Gear by Fiber Bragg Grating Sensors. Sensors 2019, 19, 2239. [Google Scholar] [CrossRef] [PubMed]
- Orkisz, M.; Święch, Ł.; Zacharzewski, J. Fatigue tests of motor glider wing’s composite spar. Maint. Reliab. 2012, 14, 228–232. [Google Scholar]
- Ramly, R.; Kuntjoro, W.; Rahman, M.K.A. Using Embedded Fiber Bragg Grating (FBG) Sensors in Smart Aircraft Structure Materials. Procedia Eng. 2012, 41, 600–606. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Karachalios, V.; Giannopoulos, I.; Prentzias, V.; Ruzek, R. Strain and damage monitoring in CFRP fuselage panels using fiber Bragg grating sensors. Part I: Design, manufacturing and impact testing, Compos. Struct. 2014, 107, 726–736. [Google Scholar]
- Růžek, R.; Kudrna, P.; Kadlec, M.; Karachalios, V.; Tserpes, K. Strain and damage monitoring in CFRP fuselage panels using fiber Bragg grating sensors. Part II: Mechanical testing and validation. Compos. Struct. 2014, 107, 737–744. [Google Scholar] [CrossRef]
- Ryu, C.; Lee, J.; Kim, C.; Hong, C. Buckling behaviour monitoring of composite wing box using multiplexed and multi-channeled built-in fiber Bragg grating strain sensor. NDT&E Int. 2008, 41, 534–543. [Google Scholar]
- Ma, Z.; Chen, X. Fiber Bragg Gratings Sensors for Aircraft Wing Shape Measurement: Recent Applications and Technical Analysis. Sensors 2018, 19, 55. [Google Scholar] [CrossRef] [PubMed]
- Nicolas, M.; Sullivan, R.W.; Richards, W.L. Large Scale Applications Using FBG Sensors: Determination of In-Flight Loads and Shape of a Composite Aircraft Wing. Aerospace 2016, 3, 18. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).