Dual-Satellite Lunar Global Navigation System Using Multi-Epoch Double-Differenced Pseudorange Observations
Abstract
:1. Introduction
2. Algorithm
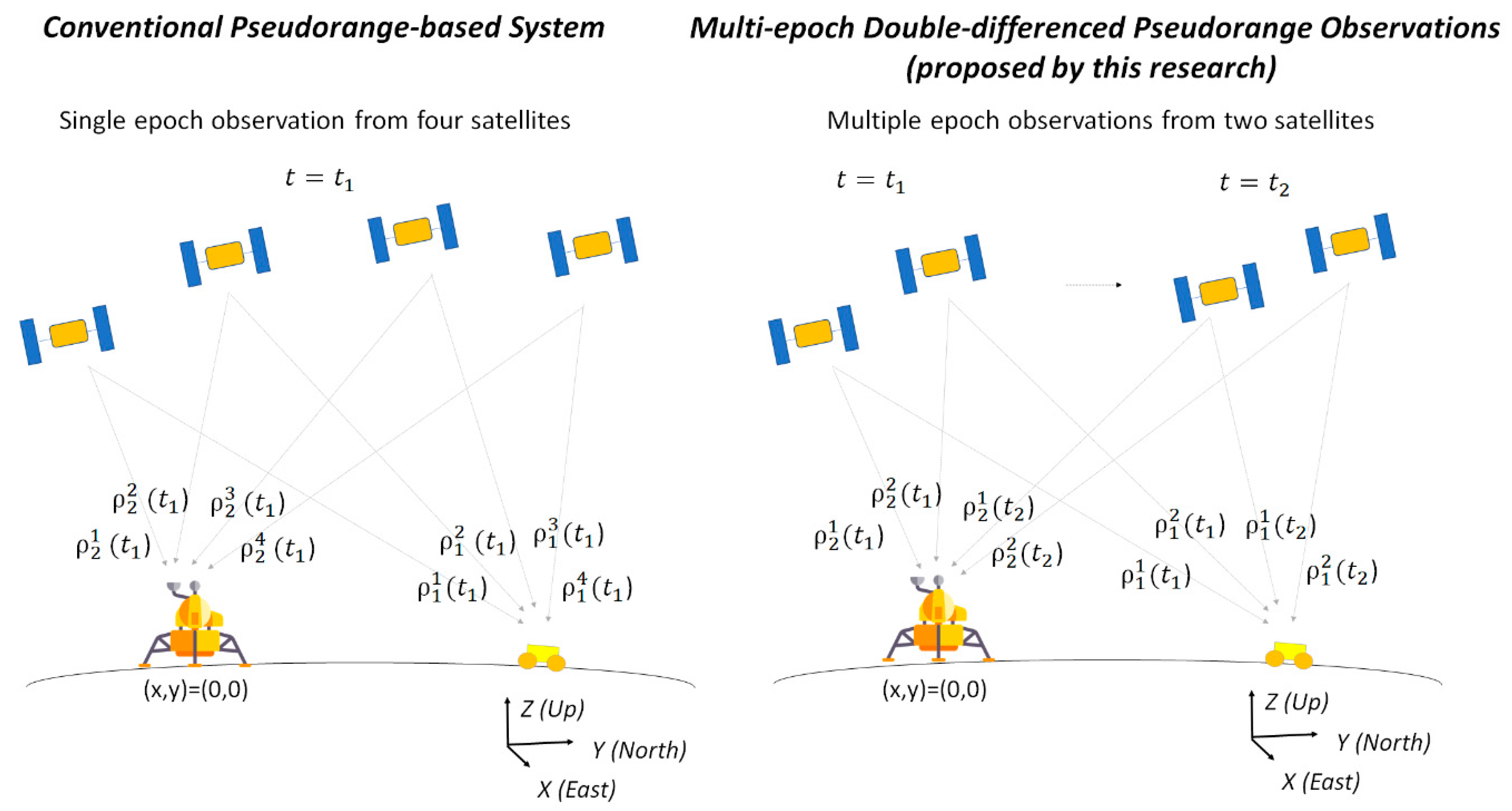
2.1. Multi-Epoch Double-Differenced Pseudorange Observations (MDPO) Algorithm
2.2. Two-Dimentional MDPO Algorithm Using a Pre-Known User Altitude
2.3. Other Systematic Errors
2.3.1. Satellite Orbit Determination Error
2.3.2. Time Tag Error
2.3.3. DEM Information Error
2.3.4. Other System Errors
2.4. Design Parameters
3. Simulation
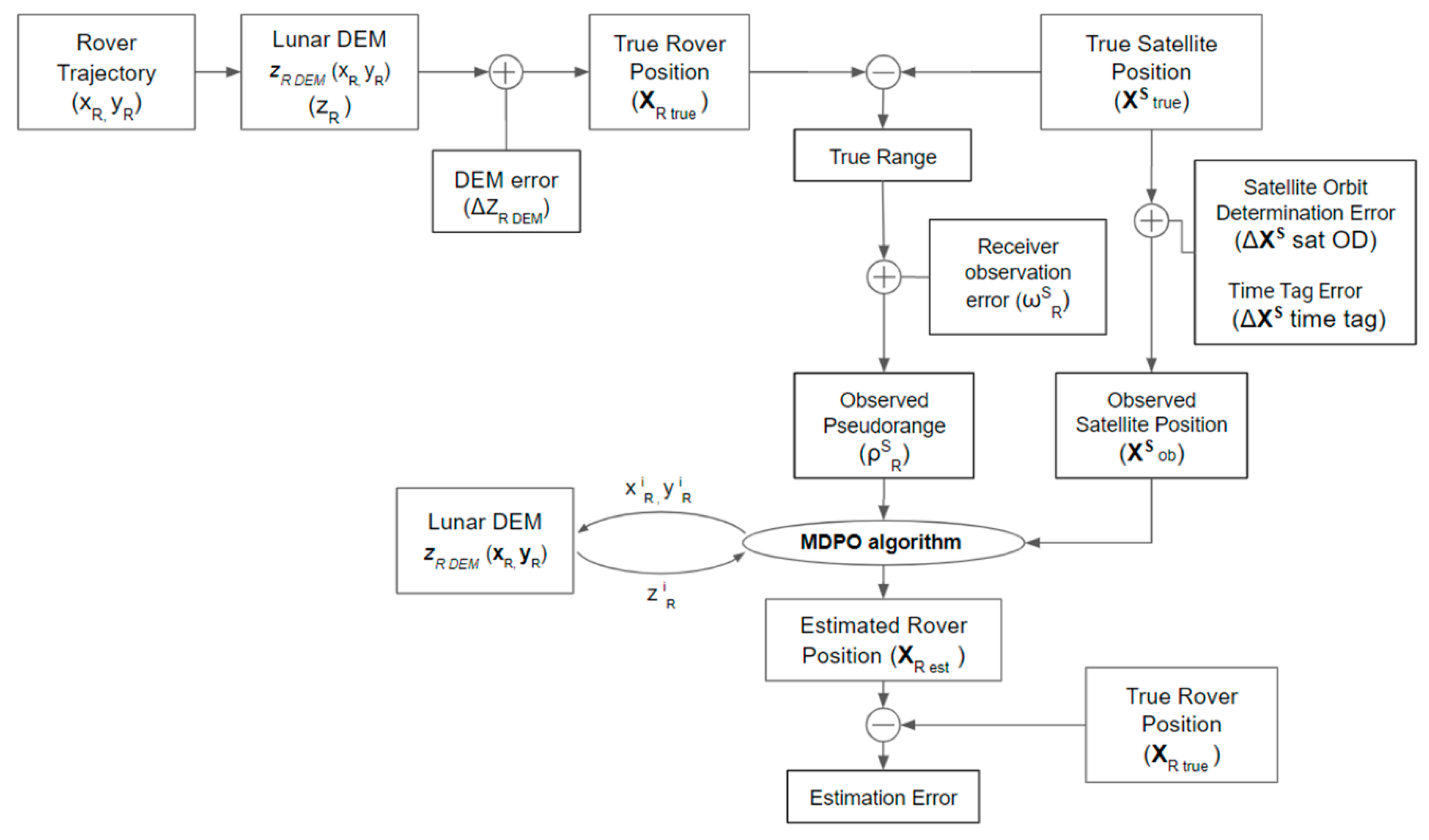
3.1. Simulation Overview
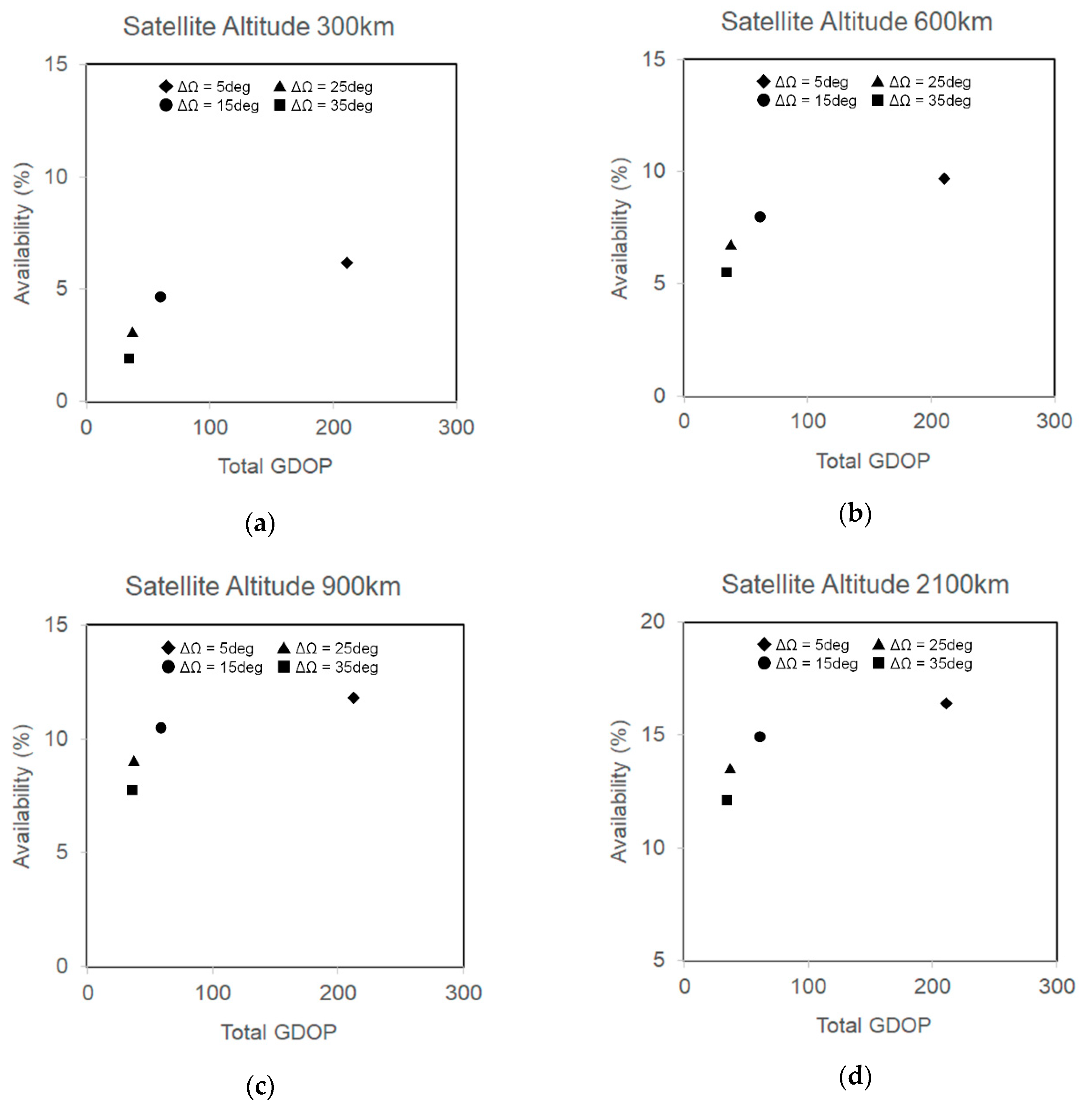
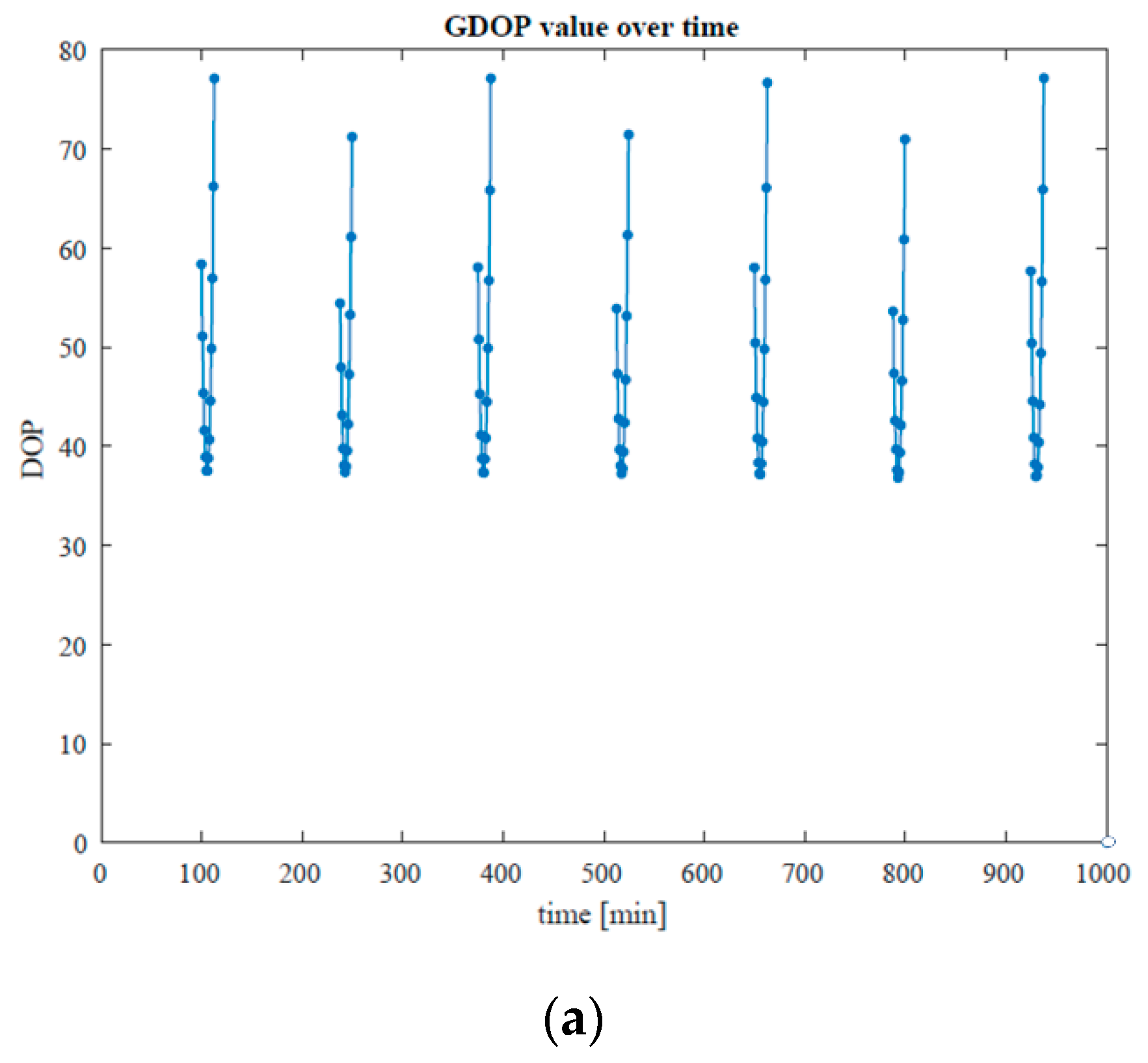
3.2. Simulation Results
3.3. Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paul, D.S. The Value of the Moon: How to Explore, Live, and Prosper in Space Using the Moon’s Resources; Smithsonian Books: Washington, DC, USA, 2016. [Google Scholar]
- Mickael, L.; Kazuya, Y. Multi-Rover Exploration Strategies: Coverage Path Planning with Myopic Sensing. Ph.D. Thesis, Tohoku University, Sendai, Japan, 2019. [Google Scholar]
- Liam, P.; Chin, S.H.; Michael, V. Dark Navigation: Sensing and Rover Navigation in Permanently Shadowed Lunar Craters. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS), Los Angeles, CA, USA, 26–29 February 2008. [Google Scholar]
- Kyle, H.; Liam, P. Strobe lit high dynamic range stereo imagery for dark navigation. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS), Los Angeles, CA, USA, 26–29 February 2008. [Google Scholar]
- Paul, F.; Tim, B. Stereo Mapping and Localization for Long-Range Path Following on Rough Terrain. In Proceedings of the IEEE International Conference on Robotics and Automation Anchorage Convention District, Anchorage, AL, USA, 3–8 May 2010. [Google Scholar]
- Xiaolin, N.; Longhua, W.; Weiren, W.; Jiancheng, F. A Celestial Assisted INS Initialization Method for Lunar Explorers. Sensors 2011, 11, 6991–7003. [Google Scholar]
- Hongru, C.; Jiangkai, L.; Long, L.; Zhenyu, X.; Yazhe, M.; Hao, Z. Lunar far side positioning enabled by a CubeSat system deployed in an Earth-Moon halo orbit. Adv. Space Res. 2019, 64, 28–41. [Google Scholar]
- Keidai, I. Optimization of Navigation Satellite Constellation and Lunar Monitoring Station Arrangement for Lunar Global Navigation Satellite System (LGNSS). In Proceedings of the 32nd International Symposium on Space Technology and Science (ISTS), Fukui, Japan, 15–21 June 2019. [Google Scholar]
- Fucheng, G.; Yun, F.; Yiyu, Z.; Caigen, X.; Qiang, L. Space Electronic Reconnaissance: Localization Theories and Methods; WILEY: New York, NY, USA, 2014. [Google Scholar]
- Chaoxin, H.; Min, Z.; Fucheng, G. Bias Compensation for AOA-Geolocation of Known Altitude Target Using Single Satellite. IEEE Access 2019, 7, 54295–54304. [Google Scholar]
- Wu, S.; Luo, J.; Gong, L. Joint FDOA and TDOA location algorithm and performance analysis of dual-satellite formations. In Proceedings of the 2010 2nd International Conference on Signal Processing Systems (ICSPS), Dalian, China, 5–7 July 2010. [Google Scholar]
- Kar-Ming, C.; Charles, L.; William, J.; Glenn, L. Single-Satellite Doppler Localization with Law of Cosines (LOC). In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 February 2019. [Google Scholar]
- William, J.; Kar-Ming, C.; Glenn, L.; Charles, L. Localizing in Urban Canyons using Joint Doppler and Ranging and the Law of Cosines Method. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; Institute of Navigation: Manassas, VA, USA, 2019; pp. 140–153. [Google Scholar]
- Margaret, M.R.; Penina, A.; Jill, S. Investigation of CSAC Driven One-Way Ranging Performance for CubeSat Navigation. In Proceedings of the Small Satellite Conference, Logan, UT, USA, 4–9 August 2018. [Google Scholar]
- Michael, M.; Lesley, N.; David, P.; Gregory, Q.; Angela, S.; Ryan, T.; Ken, A.; Erik, B.; Tyler, C.; Thomas, C.; et al. Luna POLARIS A Lunar Positioning and Communications System. Available online: https://www.researchgate.net/publication/268005025_Luna_POLARIS_A_Lunar_Positioning_and_Communications_System (accessed on 1 May 2020).
- Ho, K.C.; Chan, Y.T. Geolocation of a known altitude object from TDOA and FDOA measurements. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 770–783. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Zuber, M.T.; Haruyama, J.; Smith, D.E. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef] [Green Version]
- David, E.S.; Maria, T.Z.; Gregory, A.N.; Erwan, M.; Frank, G.L.; James, W.H.; Paul, G.L.; Oded, A.; Mark, S.R.; Xiaoli, S.; et al. Summary of the results from the lunar orbiter laser altimeter after seven years in lunar orbit. Icarus 2017, 283, 70–91. [Google Scholar]
- Ryan, P.R.; Martin, L. Long-Lifetime Lunar Repeat Ground Track Orbits. JGCD 2007, 30, 982–993. [Google Scholar]
- LRO Data Products. Available online: https://lunar.gsfc.nasa.gov/dataproducts.html (accessed on 25 July 2020).
- Mazarico, E.; Rowlands, D.D.; Neumann, G.A.; Smith, D.E.; Torrence, M.H.; Lemoine, F.G.; Zuber, M.T. Orbit determination of the Lunar Reconnaissance Orbiter. J. Geod. 2012, 86, 193–207. [Google Scholar] [CrossRef]



| Method | User (Rover) Segment Burden | Space (Satellite) Segment Burden | Ground Segment Burden |
|---|---|---|---|
| Visual Sensor-based Navigation | Visual Sensor-based navigation does not work when the lunar surface is flat with no landmarks. | - | - |
| Accelerometers and Star Tracker Navigation | Sensor alignment precision becomes outrageous to achieve high position accuracy. | - | - |
| Lunar Global Navigation Satellite Systems using TOA | Use a passive ranging receiver. | At least four satellites in view with a stable satellite clock are required. | Frequent satellite clock bias estimation by the ground segment is required. |
| Single Satellite AOA Navigation | Use a passive ranging receiver. User position accuracy is very sensitive to AOA error. | Single satellite in view with a stable satellite clock is required. | Frequent satellite clock bias estimation by the ground segment is required. |
| Dual Satellite TDOA/FDOA Navigation | Use a passive ranging and/or Doppler receiver. | Two satellites in view with a stable satellite clock and/or frequency are required. | Frequent satellite clock bias estimation by the ground segment is required. |
| Law of Cosines | Use a passive Doppler receiver with a static reference station. The frequency of the receiver must be stable. | Single satellite in view is required, with no need for a stable satellite frequency. | No need for frequent satellite clock bias estimation by the ground segment. |
| Joint Doppler and Ranging (single satellite case) | Use a passive ranging and Doppler receiver with a static reference station. The clock and frequency of the receiver must be stable or must be compensated by two-way ranging. | Single satellite in view is required, with no need for a stable satellite clock. | No need for frequent satellite clock bias estimation by the ground segment. |
| Two-way Ranging based Navigation | Active ranging between the satellite and user is required. | Two satellites in view are required, with no need for a stable satellite clock. | No need for frequent satellite clock bias estimation by the ground segment. |
| Dual Satellite MDPO Navigation (This research) | Use a passive ranging receiver with a static reference station. | Two satellites in view are required, with no need for a stable satellite clock. | No need for frequent satellite clock bias estimation by the ground segment. |
| Items | Value | Unit | Remarks |
|---|---|---|---|
| Simulation Period | 15,000 | min | Approximately two weeks in Earth time |
| Range measurement resolution of the user pseudorange receivers | 0.4 | m | Minimum observable range by the rover and lander receivers |
| Latitude of Initial Rover/Lander Position | 90 | deg | |
| Longitude of Initial Rover/Lander Position | 90 | deg | |
| Interval of pseudorange observations | 0.5 | min | Total observation period of one MDPO estimation is equivalent to 1 min when the number of multi-epoch observations is 2. |
| Rover traveling distance between MDPO observations | 3.75 | m | The rover travels at 7.5 m/min for 0.5 min between MDPO estimations |
| Rover traveling direction | Random | deg | Heading direction is selected from three values (+) randomly. |
| Items | Value | Unit | Remarks |
|---|---|---|---|
| Initial Orbital Parameters of Satellite1 | |||
| Perilune altitude | 300 | km | |
| Apolune altitude | 300 | km | |
| Inclination | 110 | deg | |
| Right Ascension of the Ascending Node | 0 | deg | |
| Argument of Perigee | 0 | deg | |
| True Anomaly | 0 | deg | |
| Initial Orbital Parameters of Satellite2 | |||
| Perilune altitude | 300 | km | |
| Apolune altitude | 300 | km | |
| Inclination | 110 | deg | |
| Right Ascension of the Ascending Node | 0 | deg | |
| Argument of Perigee | 0 | deg | |
| True Anomaly | 15 | deg | |
| Items | Type | Value | Unit | Remarks |
|---|---|---|---|---|
| Satellite Orbit Determination Error in the Along direction | = | |||
| White Gaussian noise | 100.0 | m | a random scalar drawn from the standard normal distribution. | |
| 200.0 | m | Bias is a random number that is greater than or equal to and less than | ||
| Satellite Orbit Determination Error in the Radial direction | = | |||
| White Gaussian noise | 10.0 | m | Same as above | |
| 20.0 | m | |||
| Satellite Orbit Determination Error in the Cross direction | = | |||
| White Gaussian noise | 100.0 | m | Same as above | |
| 200.0 | m | |||
| Item | Type | Value | Unit | Remarks |
|---|---|---|---|---|
| Time Tag Error | ||||
| White Gaussian noise | 100.0 | ms | a random scalar drawn from the standard normal distribution. | |
| Random walk | 0.1 | ms/min | A random walk is a time series model such that where is a discrete white noise series. Random walk noise is reset to zero periodically assuming orbit determination takes place every orbital period. | |
| Item | Type | Value | Unit | Remarks |
|---|---|---|---|---|
| DEM Error | + | |||
| White Gaussian noise | 10.0 | m | a random scalar drawn from the standard normal distribution. | |
| Bias noise | 5.0 | m | Bias is a random number that is greater than or equal to and less than | |
| Total GDOP | Total UPE (2drms) [m] | |
|---|---|---|
| 0.4 | 44.3 | 45.6 |
| 0.8 | 44.3 | 55.4 |
| 1.6 | 44.3 | 89.6 |
| 3.2 | 44.3 | 172.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanaka, T.; Ebinuma, T.; Nakasuka, S. Dual-Satellite Lunar Global Navigation System Using Multi-Epoch Double-Differenced Pseudorange Observations. Aerospace 2020, 7, 122. https://doi.org/10.3390/aerospace7090122
Tanaka T, Ebinuma T, Nakasuka S. Dual-Satellite Lunar Global Navigation System Using Multi-Epoch Double-Differenced Pseudorange Observations. Aerospace. 2020; 7(9):122. https://doi.org/10.3390/aerospace7090122
Chicago/Turabian StyleTanaka, Toshiki, Takuji Ebinuma, and Shinichi Nakasuka. 2020. "Dual-Satellite Lunar Global Navigation System Using Multi-Epoch Double-Differenced Pseudorange Observations" Aerospace 7, no. 9: 122. https://doi.org/10.3390/aerospace7090122
APA StyleTanaka, T., Ebinuma, T., & Nakasuka, S. (2020). Dual-Satellite Lunar Global Navigation System Using Multi-Epoch Double-Differenced Pseudorange Observations. Aerospace, 7(9), 122. https://doi.org/10.3390/aerospace7090122




