Unmanned Aerial Vehicle Pitch Control Using Deep Reinforcement Learning with Discrete Actions in Wind Tunnel Test
Abstract
:1. Introduction
2. Methods
2.1. Aircraft Model
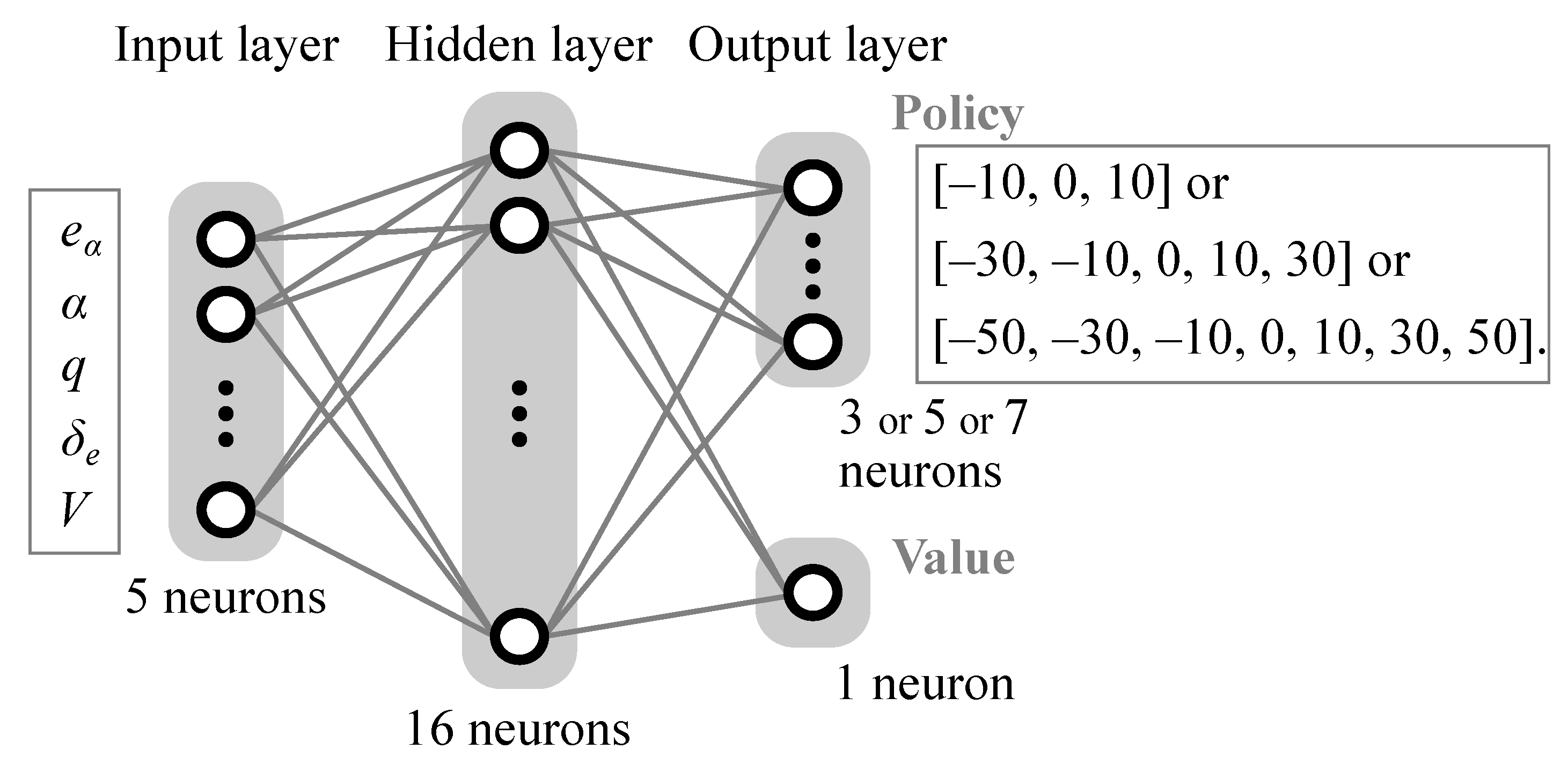
2.2. Training Algorithm
2.3. Experimental Conditions
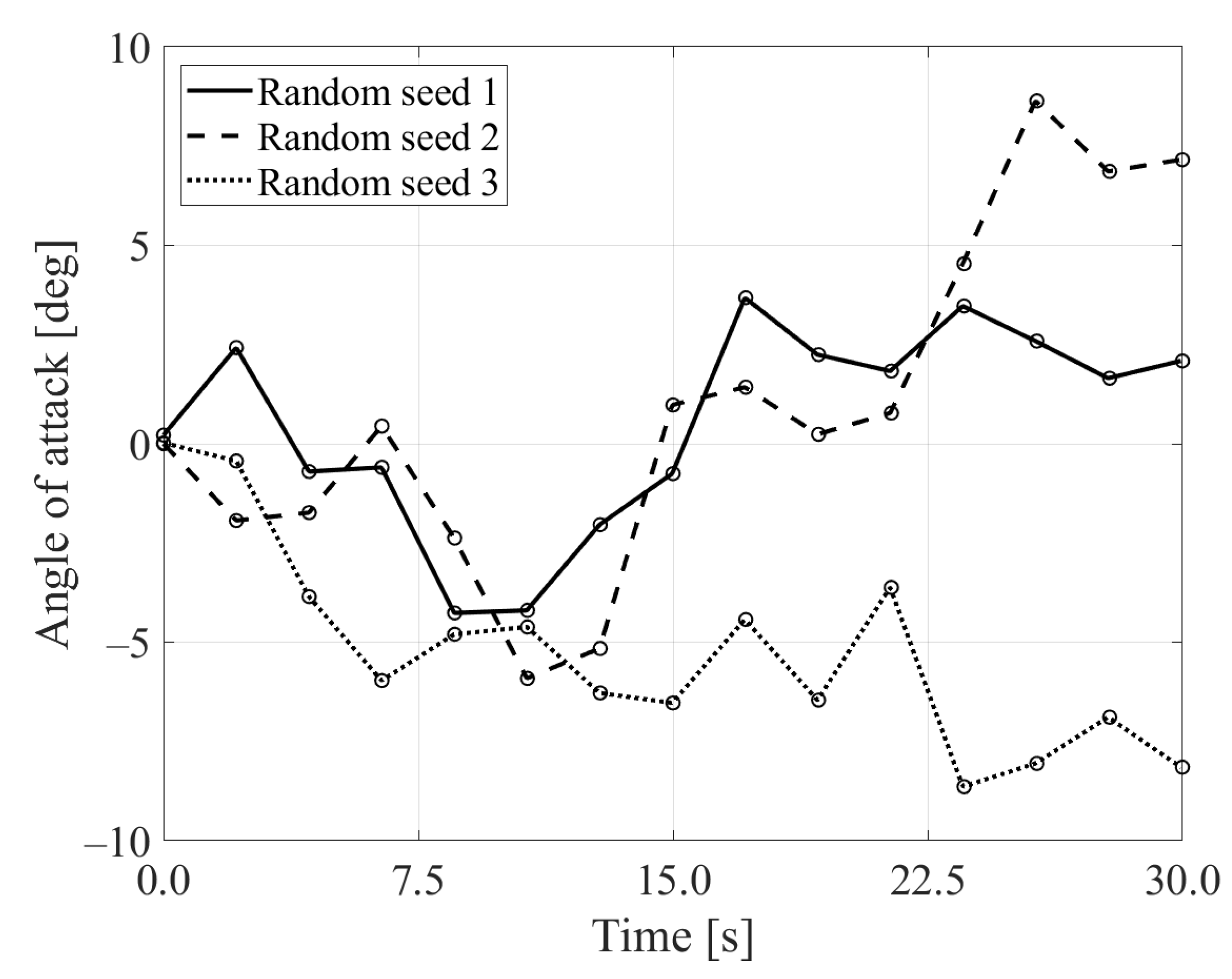
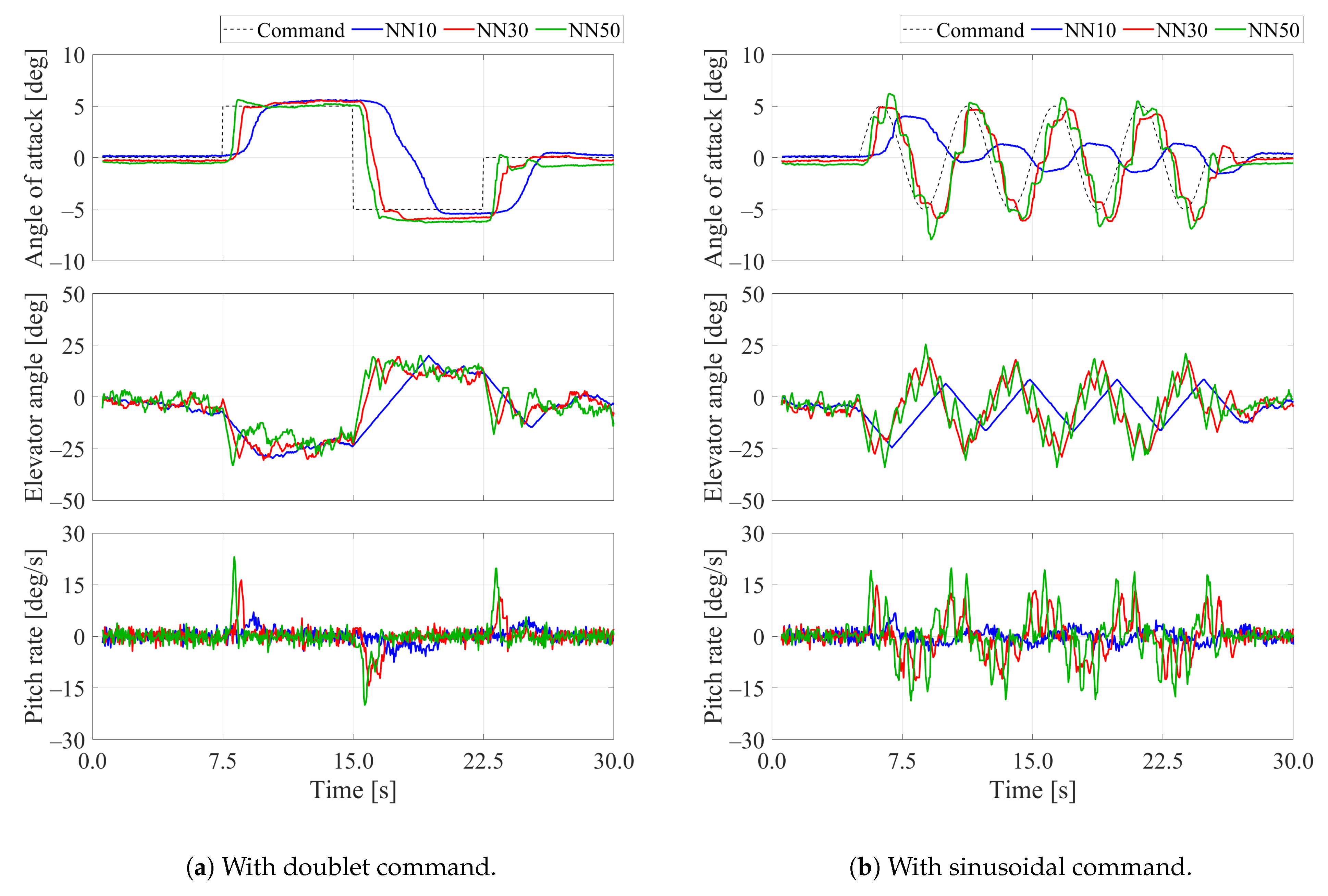
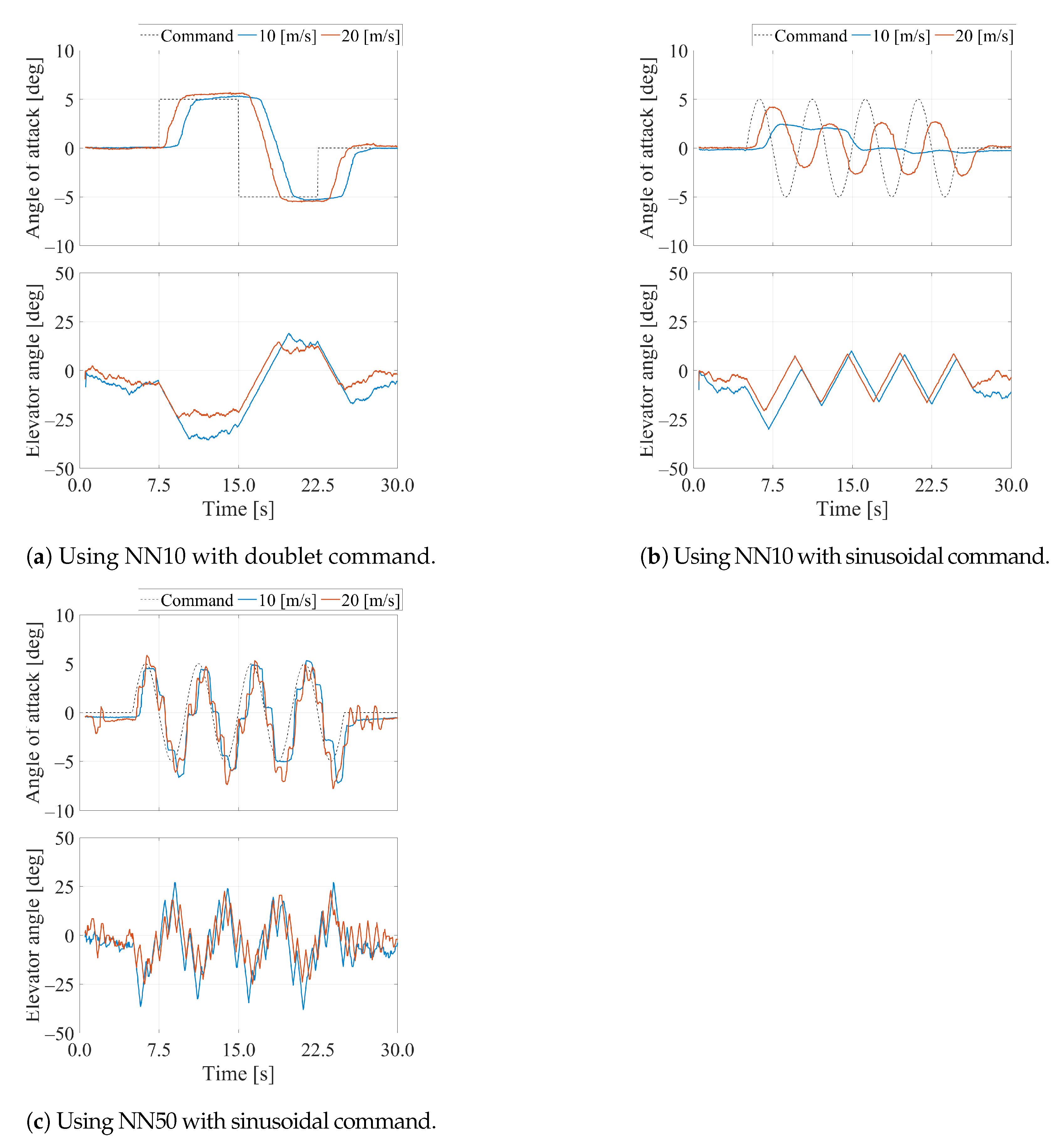
3. Results
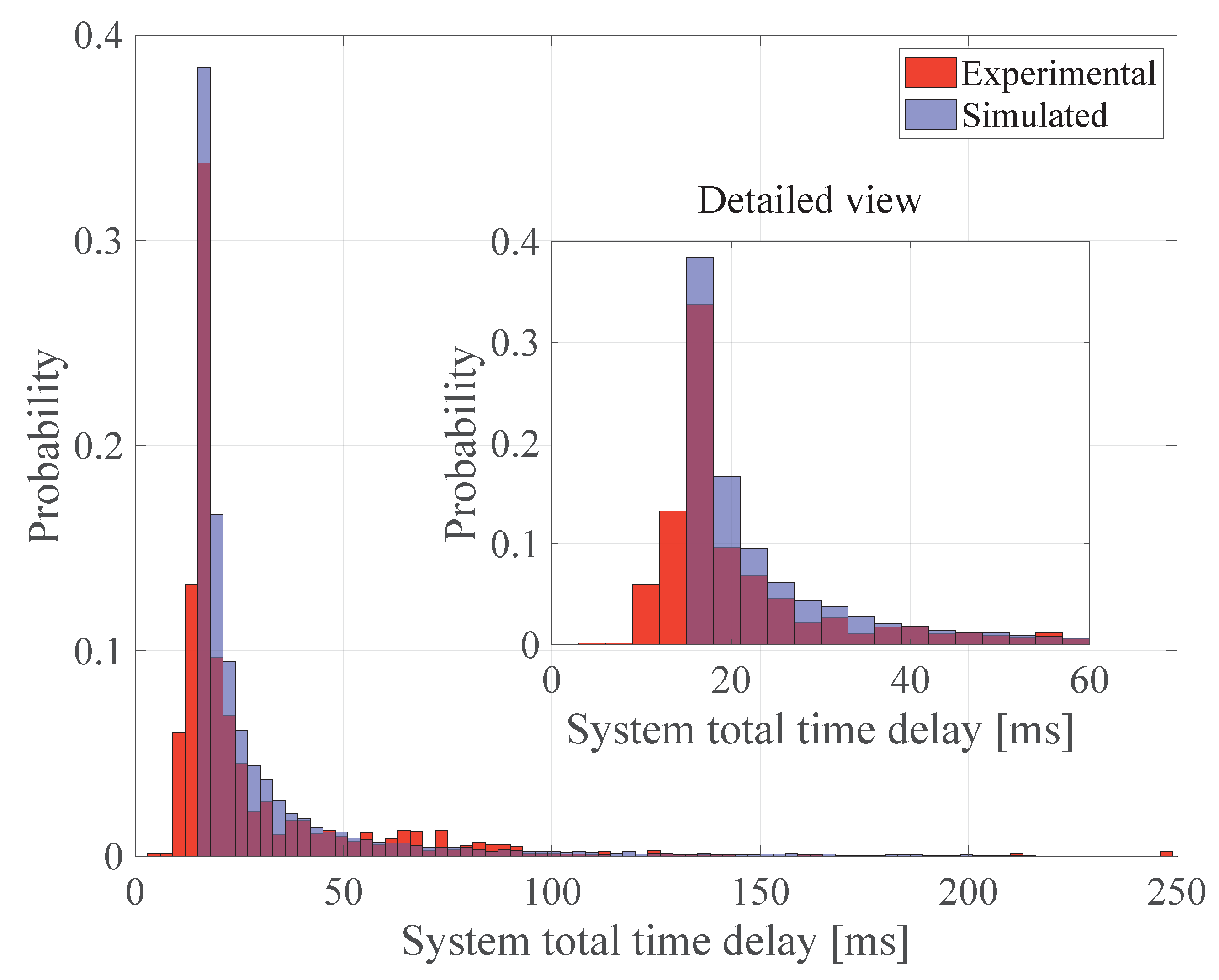
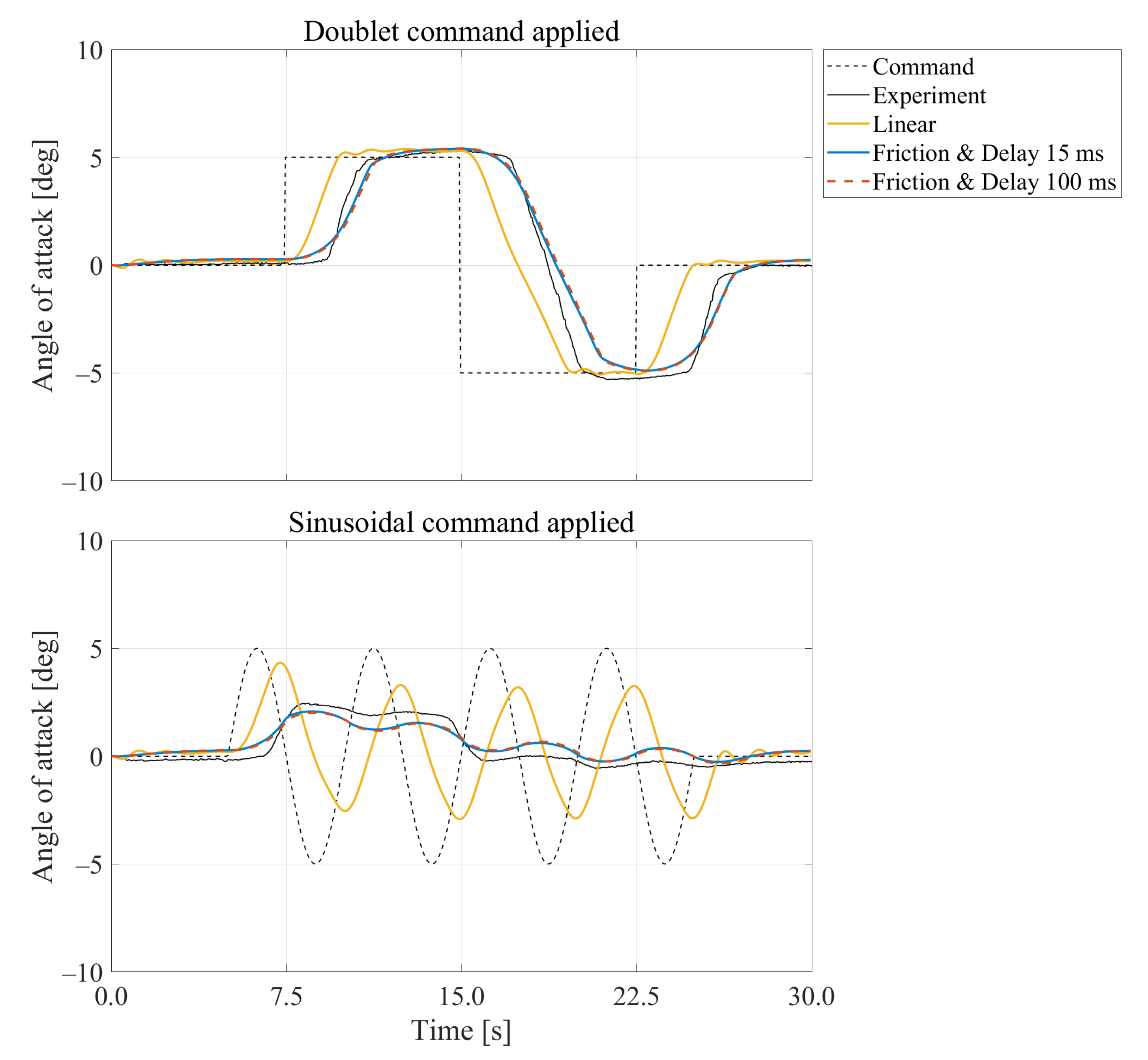
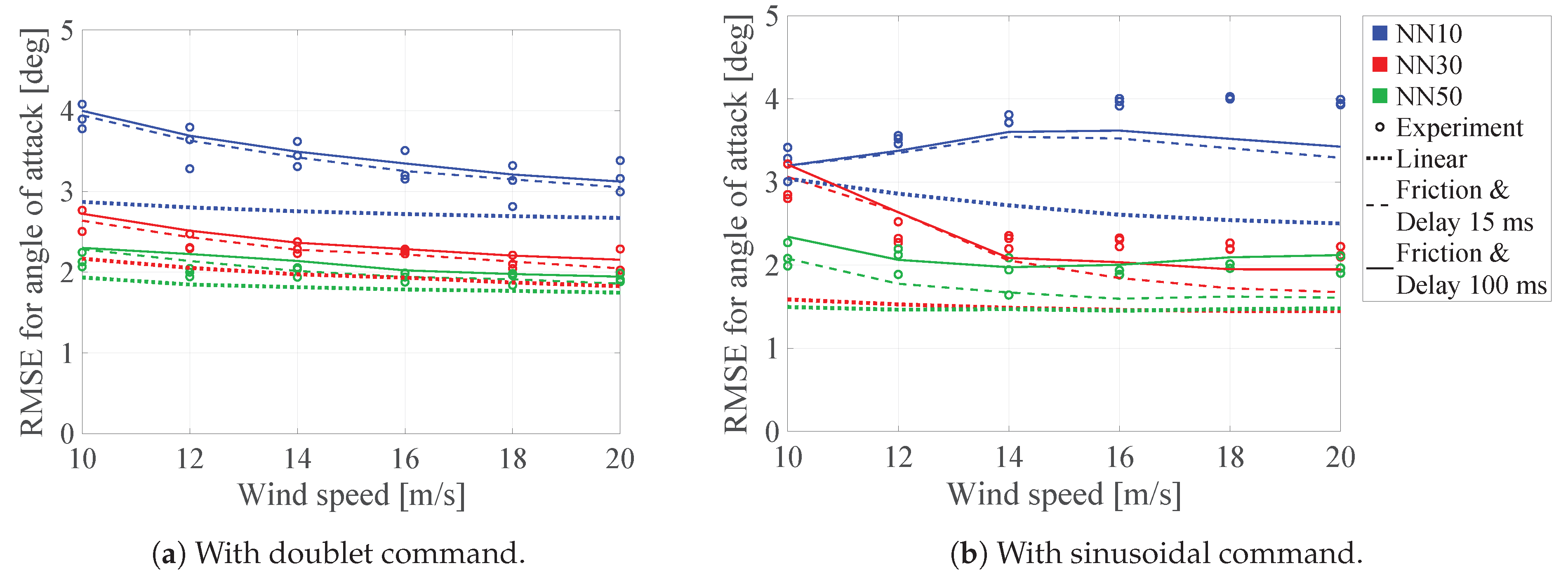
4. Effects of Friction and Delay on Pitch Control
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luca, M.D.; Mintchev, S.; Heitz, G.; Noca, F.; Floreano, D. Bioinspired Morphing Wings for Extended Flight Envelope and Roll Control of Small Drones. Interface Focus 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Chang, E.; Matloff, L.Y.; Stowers, A.K.; Lentink, D. Soft Biohybrid Morphing Wings with Feathers Underactuated by Wrist and Finger Motion. Sci. Robot. 2020, 5, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Noll, T.E.; Ishmael, S.D.; Henwood, B.; Perez-Davis, M.E.; Tiffany, G.C.; Madura, J.; Gaier, M.; Brown, J.M.; Wierzbanowski, T. Technical Findings, Lessons Learned, and Recommendations Resulting from the Helios Prototype Vehicle Mishap; NASA Technical Reports Server; NASA: Washington, DC, USA, 2007.
- Rodriguez, D.L.; Aftosmis, M.J.; Nemec, M.; Anderson, G.R. Optimization of Flexible Wings with Distributed Flaps at Off-Design Conditions. J. Aircr. 2016, 53, 1731–1745. [Google Scholar] [CrossRef] [Green Version]
- Julian, K.D.; Kochenderfer, M.J. Deep Neural Network Compression for Aircraft Collision Avoidance Systems. J. Guid. Control Dyn. 2019, 42, 598–608. [Google Scholar] [CrossRef]
- Gu, W.; Valavanis, K.P.; Rutherford, M.J.; Rizzo, A. A Survey of Artificial Neural Networks with Model-based Control Techniques for Flight Control of Unmanned Aerial Vehicles. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 362–371. [Google Scholar]
- Ferrari, S.; Stengel, R.F. Classical/Neural Synthesis of Nonlinear Control Systems. J. Guid. Control Dyn. 2002, 25, 442–448. [Google Scholar] [CrossRef]
- Dadian, O.; Bhandari, S.; Raheja, A. A Recurrent Neural Network for Nonlinear Control of a Fixed-Wing UAV. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1341–1346. [Google Scholar]
- Kim, B.S.; Calise, A.J.; Kam, M. Nonlinear Flight Control Using Neural Networks and Feedback Linearization. In Proceedings of the First IEEE Regional Conference on Aerospace Control Systems, Westlake Village, CA, USA, 25–27 May 1993; pp. 176–181. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:t1312.5602. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control Through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Gu, S.; Lillicrap, T.; Sutskever, I.; Levine, S. Continuous Deep Q-Learning with Model-based Acceleration. arXiv 2016, arXiv:1603.00748. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Reddy, G.; Wong-Ng, J.; Celani, A.; Sejnowski, T.J.; Vergassola, M. Glider soaring via reinforcement learning in the field. Nature 2018, 562, 236–239. [Google Scholar] [CrossRef] [PubMed]
- Koch, W.; Mancuso, R.; West, R.; Bestavros, A. Reinforcement Learning for UAV Attitude Control. arXiv 2018, arXiv:1804.04154. [Google Scholar] [CrossRef] [Green Version]
- Clarke, S.G.; Hwang, I. Deep Reinforcement Learning Control for Aerobatic Maneuvering of Agile Fixed-Wing Aircraft. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Bøhn, E.; Coates, E.M.; Moe, S.; Johansen, T.A. Deep Reinforcement Learning Attitude Control of Fixed-Wing UAVs Using Proximal Policy Optimization. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 523–533. [Google Scholar]
- Rabault, J.; Kuchta, M.; Jensen, A.; Réglade, U.; Cerardi, N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 2019, 865, 281–302. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Rabault, J.; Kuhnle, A.; Wang, Y.; Wang, T. Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning. Phys. Fluids 2020, 32, 053605. [Google Scholar] [CrossRef]
- Makkar, C.; Dixon, W.E.; Sawyer, W.G.; Hu, G. A New Continuously Differentiable Friction Model for Control Systems Design. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 600–605. [Google Scholar]
- Nguyen, D.; Widrow, B. Improving the Learning Speed of 2-layer Neural Networks by Choosing Initial Values of the Adaptive Weights. Int. Join Conf. Neural Netw. 1990, 3, 21–26. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the Theory of the Brownian Motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. ADAM: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-Real Transfer of Robotic Control with Dynamics Randomization. In Proceedings of the Proceedings—IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 3803–3810. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Units | Value |
|---|---|---|
| 1.90 × 10−1 | ||
| 1.23 | ||
| V | 14.0 | |
| S | 3.06 × 10−1 | |
| c | 2.54 × 10−1 | |
| – | −3.00 × 10−3 | |
| – | −2.25 × 10−1 | |
| – | −5.46 | |
| – | −5.35 × 10−2 |
| Doublet | Sinusoidal | |||||
|---|---|---|---|---|---|---|
| Method | NN10 | NN30 | NN50 | NN10 | NN30 | NN50 |
| Experiment | 3.42 | 2.29 | 1.99 | 3.74 | 2.38 | 1.99 |
| Simulation with linear model | 2.75 | 1.97 | 1.82 | 2.71 | 1.49 | 1.47 |
| Simulation with friction and delay 15 ms | 3.41 | 2.29 | 2.02 | 3.39 | 2.17 | 1.73 |
| Simulation with friction and delay 100 ms | 3.48 | 2.37 | 2.10 | 3.46 | 2.31 | 2.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wada, D.; Araujo-Estrada, S.A.; Windsor, S. Unmanned Aerial Vehicle Pitch Control Using Deep Reinforcement Learning with Discrete Actions in Wind Tunnel Test. Aerospace 2021, 8, 18. https://doi.org/10.3390/aerospace8010018
Wada D, Araujo-Estrada SA, Windsor S. Unmanned Aerial Vehicle Pitch Control Using Deep Reinforcement Learning with Discrete Actions in Wind Tunnel Test. Aerospace. 2021; 8(1):18. https://doi.org/10.3390/aerospace8010018
Chicago/Turabian StyleWada, Daichi, Sergio A. Araujo-Estrada, and Shane Windsor. 2021. "Unmanned Aerial Vehicle Pitch Control Using Deep Reinforcement Learning with Discrete Actions in Wind Tunnel Test" Aerospace 8, no. 1: 18. https://doi.org/10.3390/aerospace8010018
APA StyleWada, D., Araujo-Estrada, S. A., & Windsor, S. (2021). Unmanned Aerial Vehicle Pitch Control Using Deep Reinforcement Learning with Discrete Actions in Wind Tunnel Test. Aerospace, 8(1), 18. https://doi.org/10.3390/aerospace8010018





