Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours
Abstract
:1. Introduction
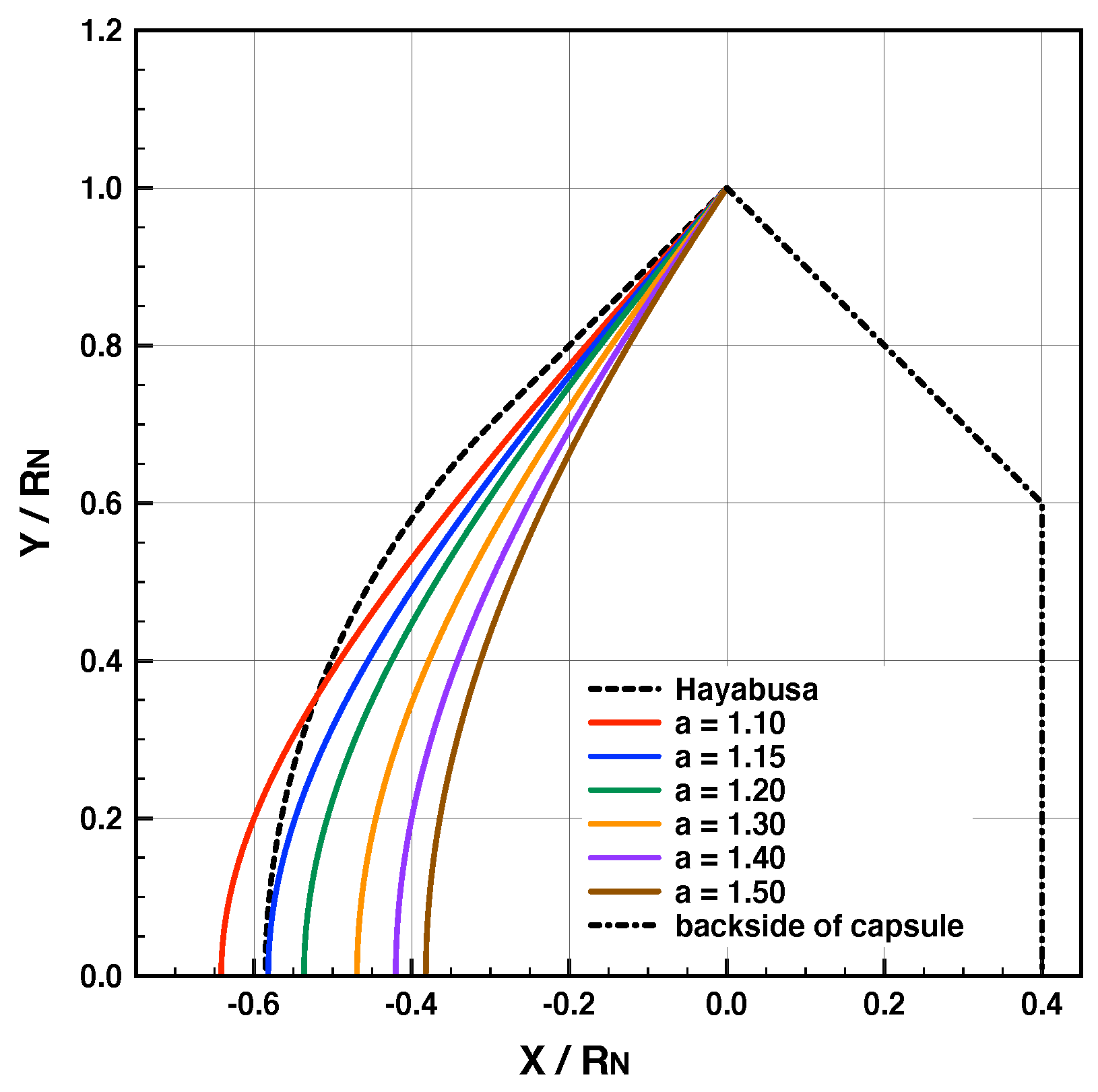
2. Design of Re-Entry Capsule Shape Using Hyperbolic Contours
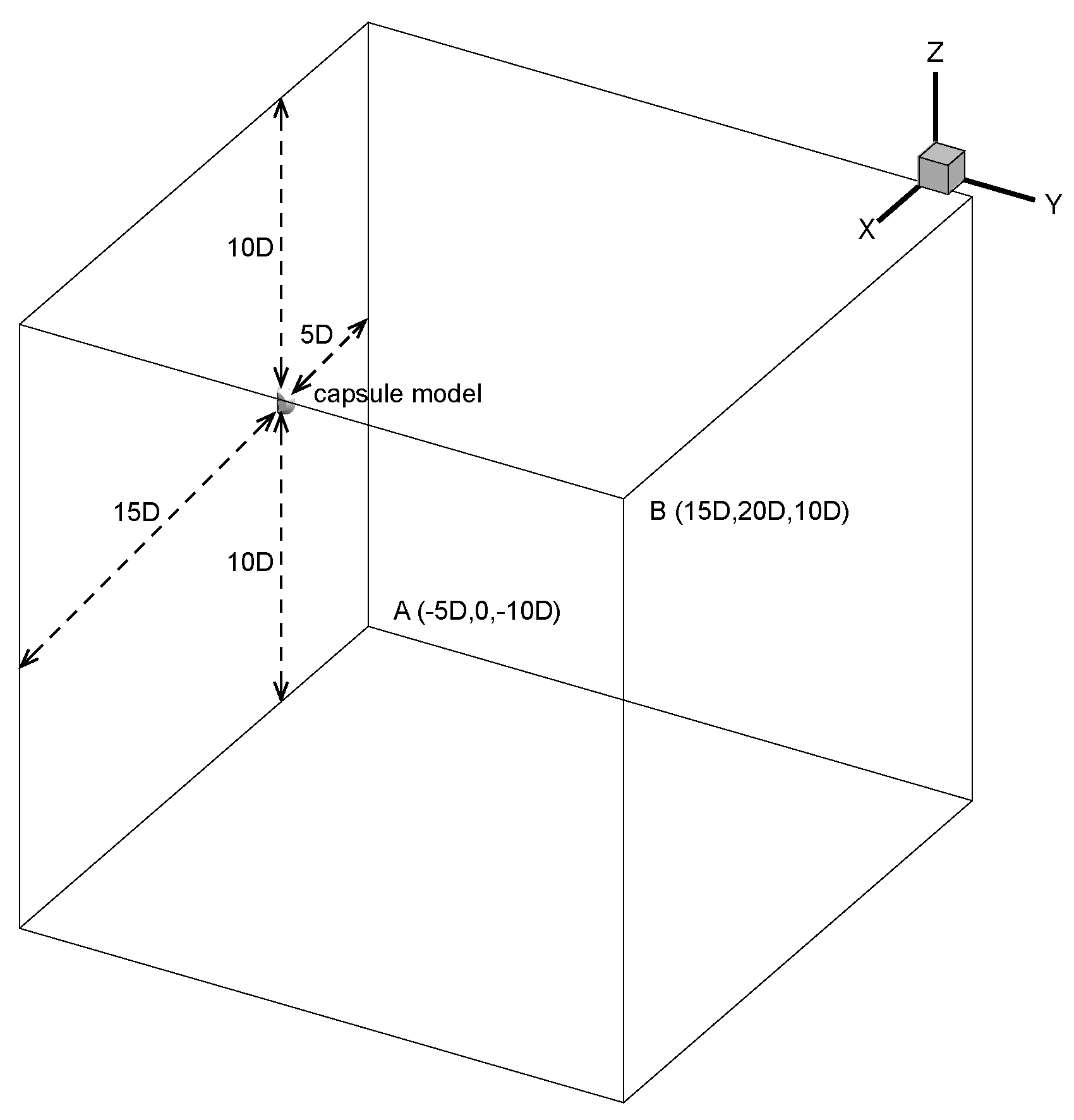
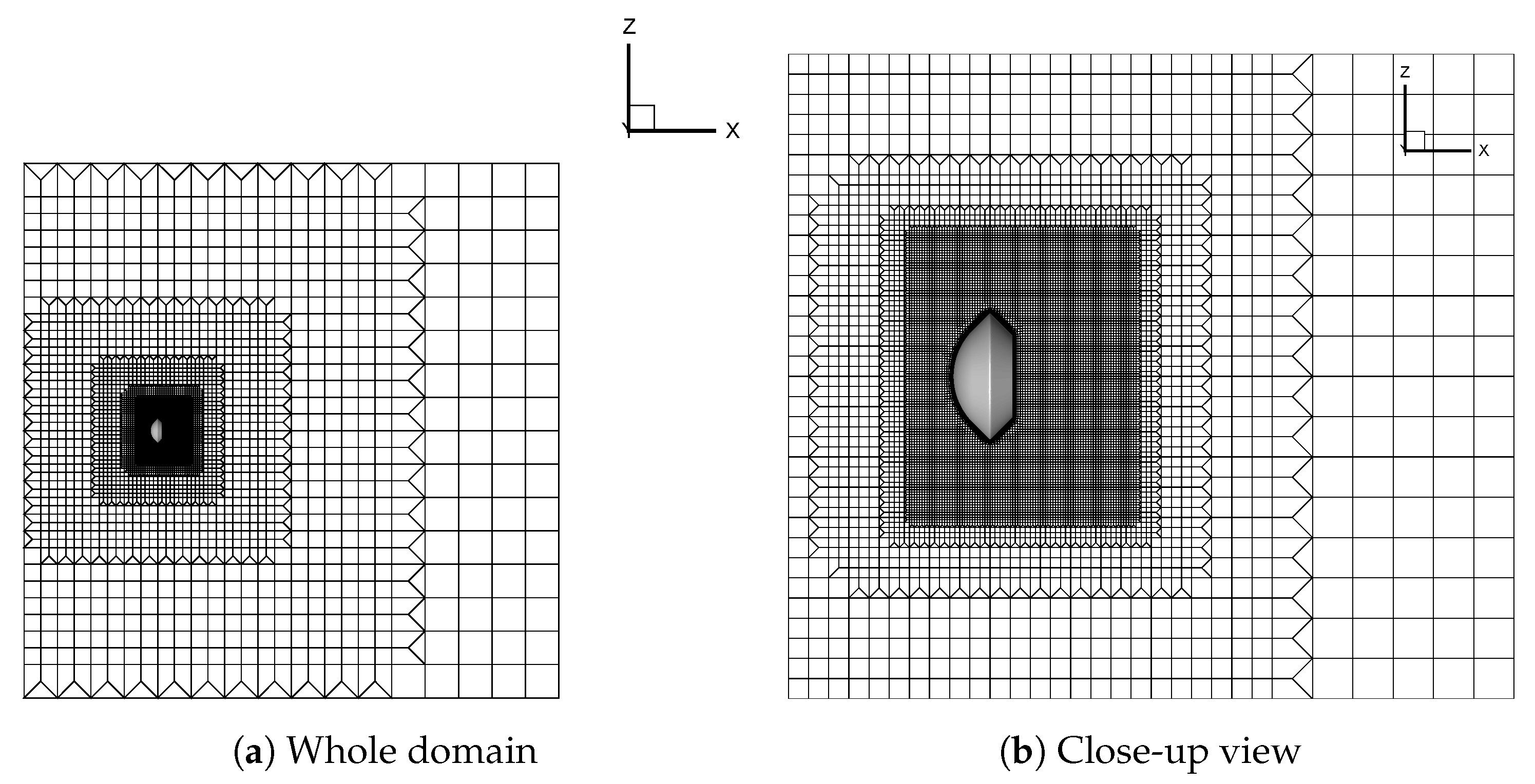
3. Numerical Methods and Computational Grid
4. Results and Discussions
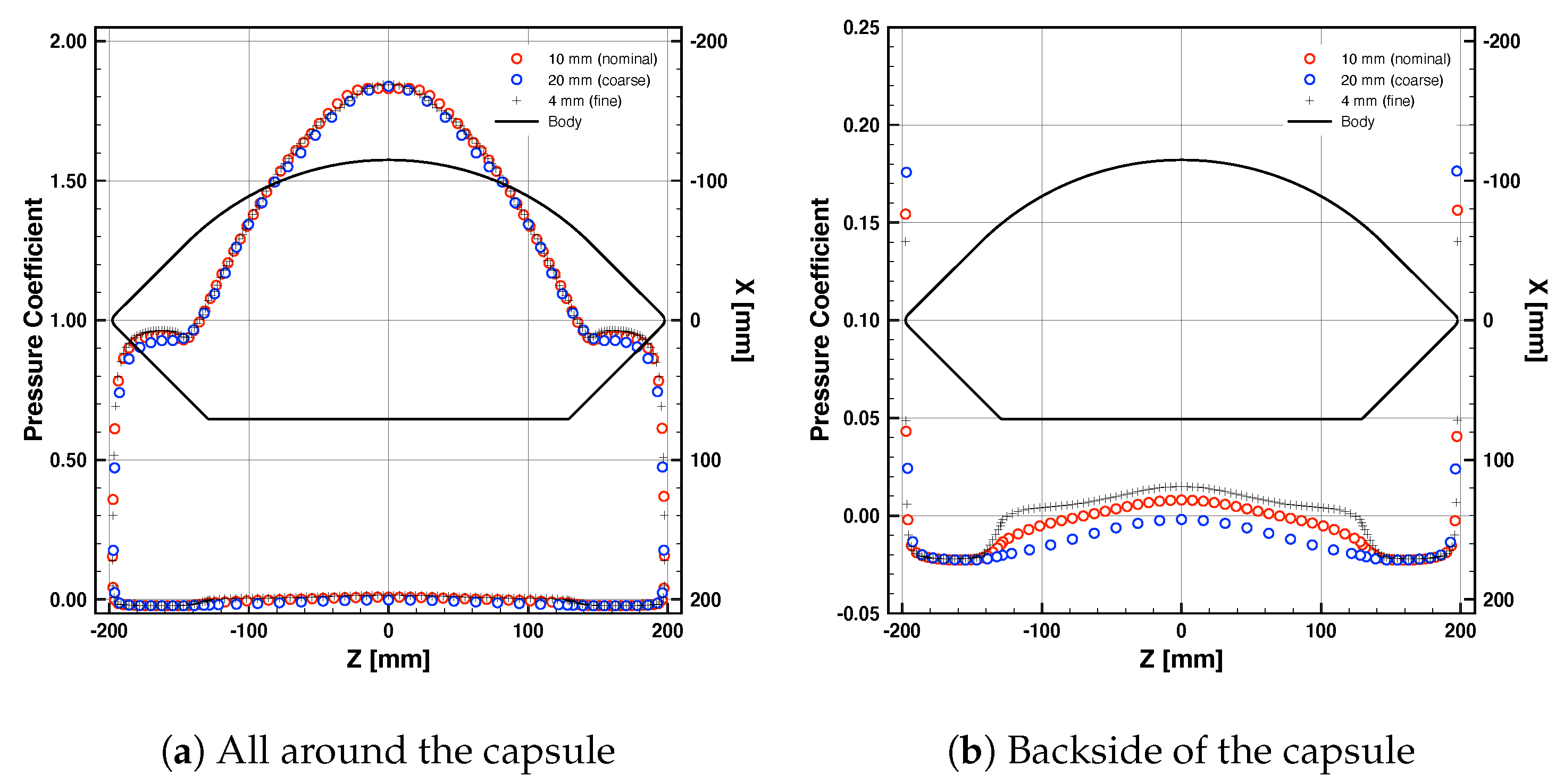
4.1. Grid Study
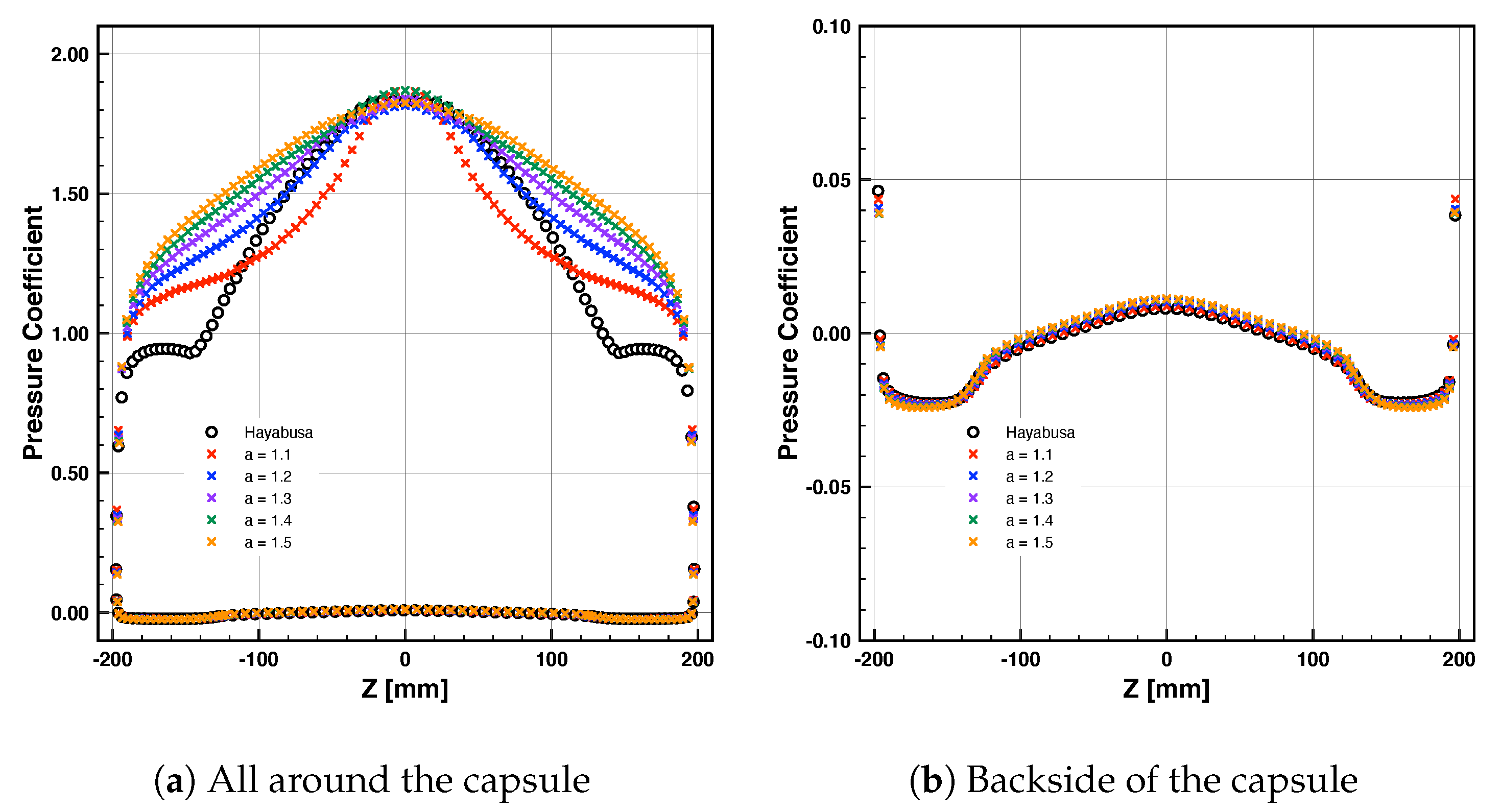
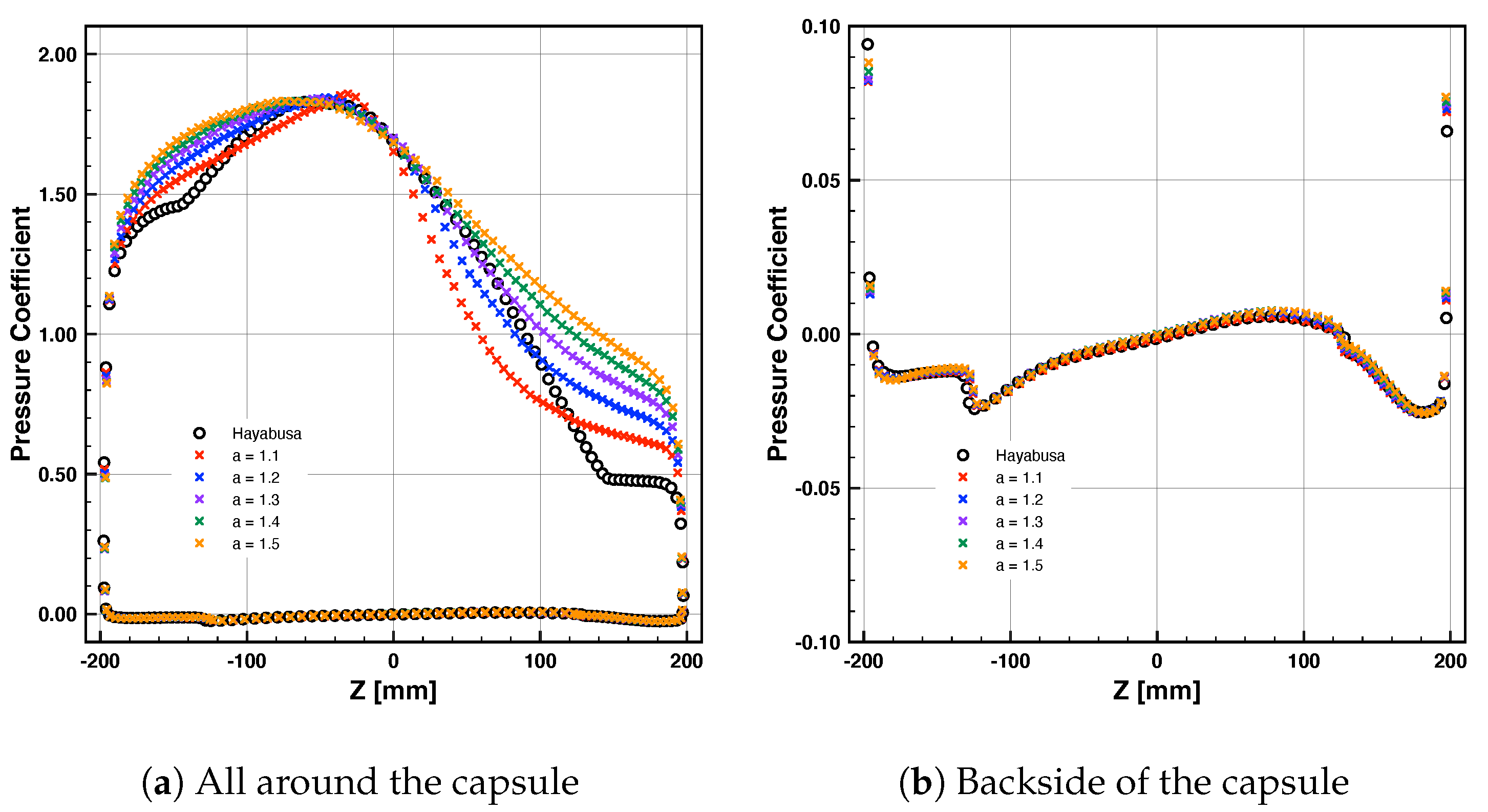
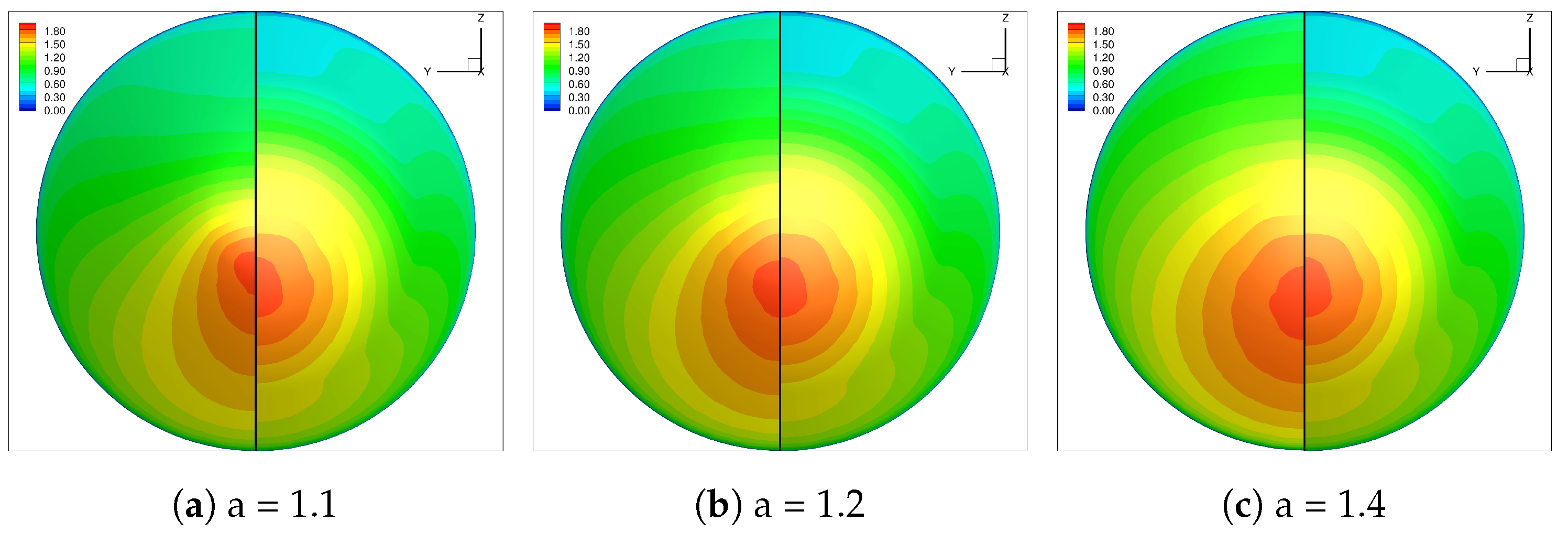
4.2. Pressure Distribution
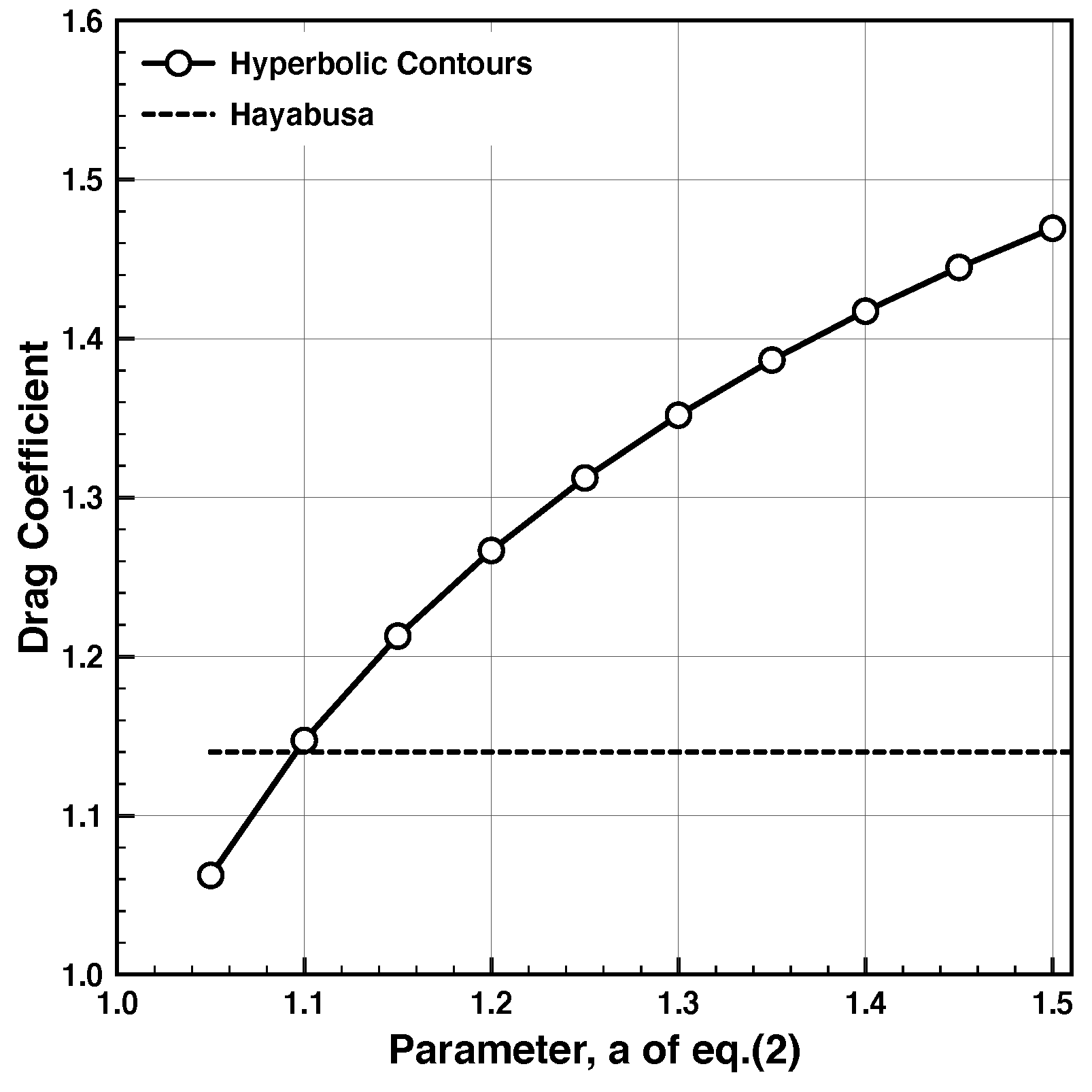
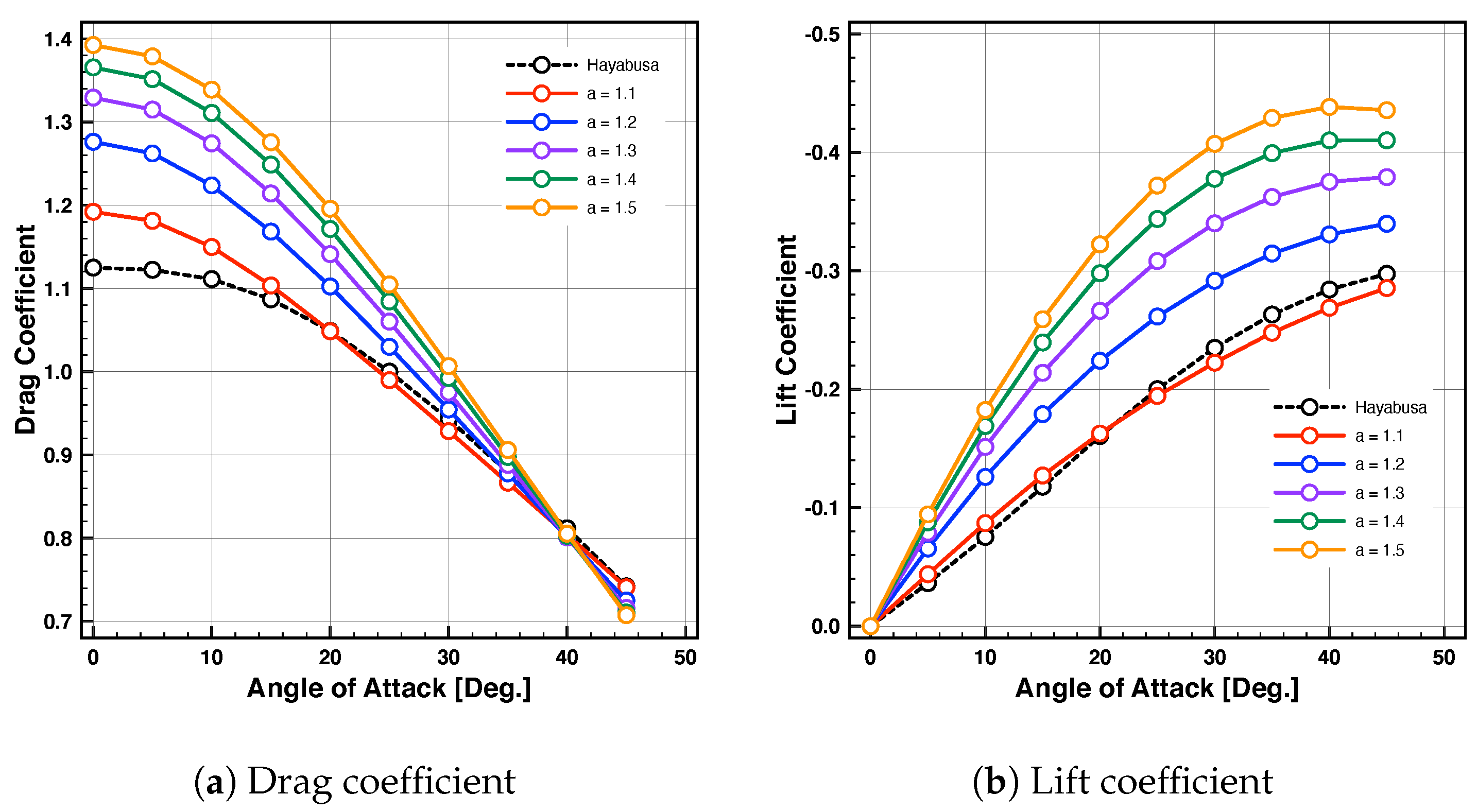
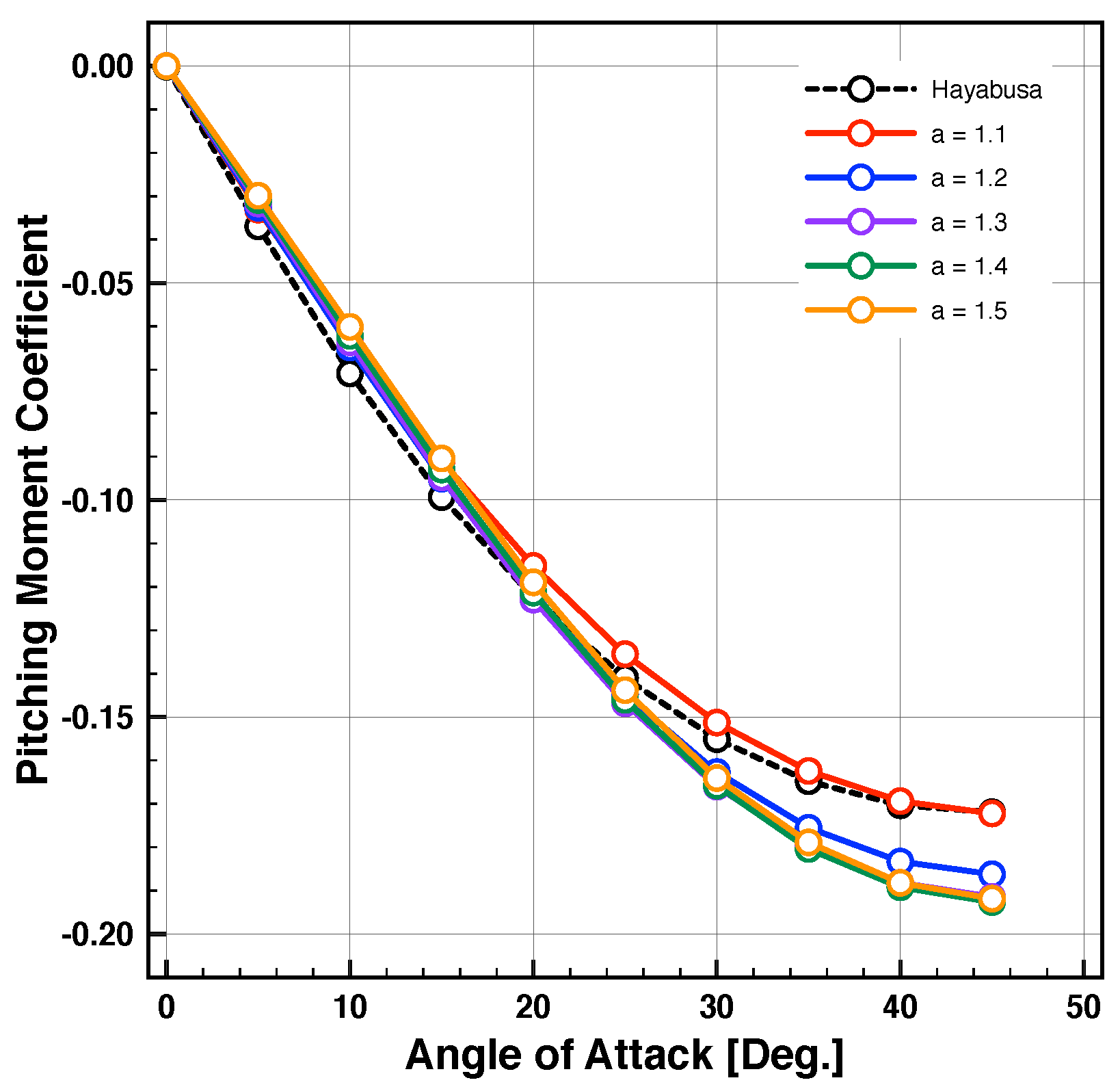
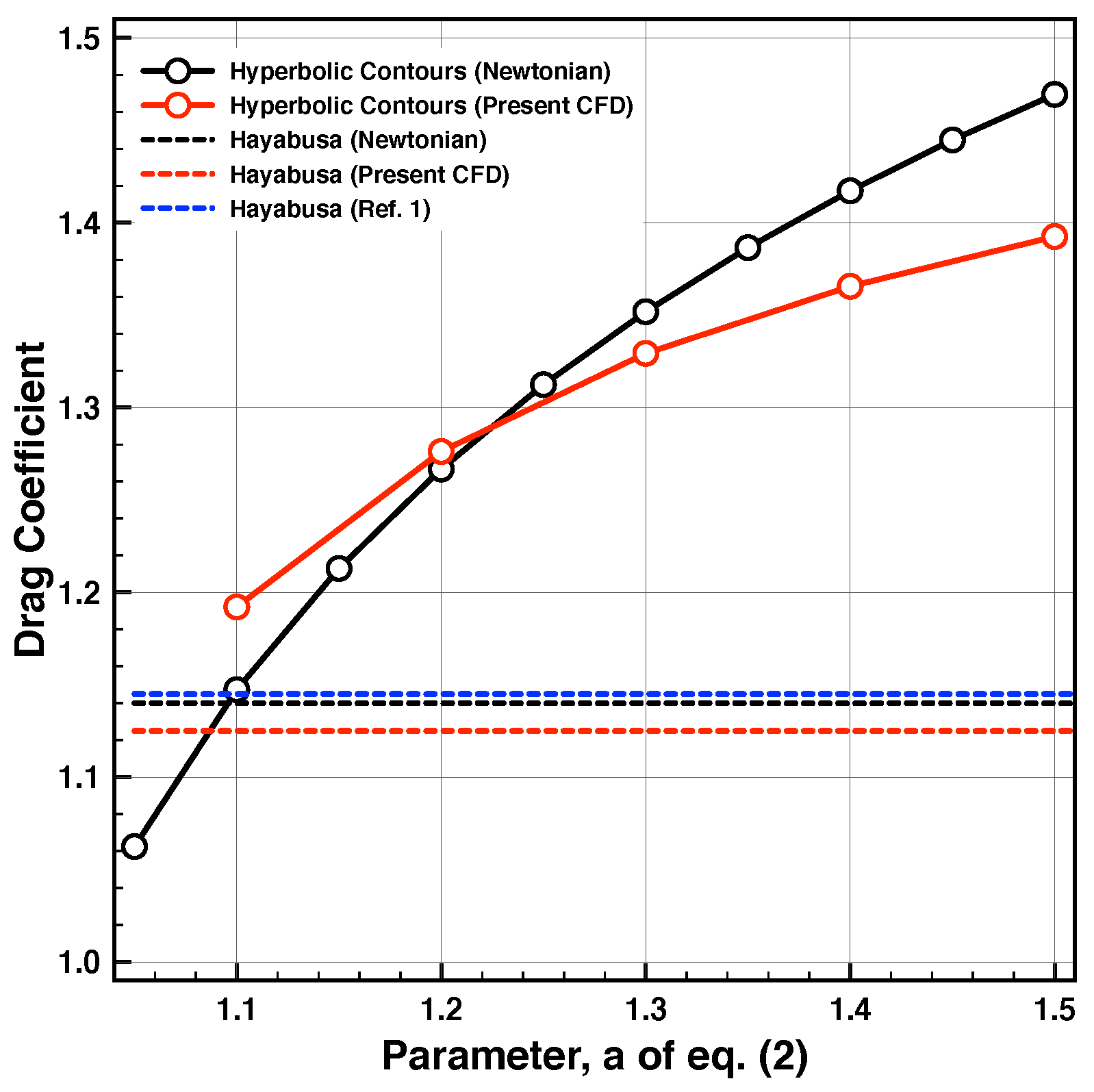
4.3. Aerodynamic Characteristics
4.4. Comparison of Volume and Stagnation Point Heat Flux
5. Conclusions
- The drag and lift coefficients can be increased when compared to the Hayabusa capsule.
- The static longitudinal stability was not affected significantly.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Detra, R.W.; Kemp, N.H.; Riddell, F.R. Addendum to Heat Transfer to Satellite Vehicles Reentering the Atmosphere. Jet Propuls. 1957, 27, 1256–1257. [Google Scholar]
- Anderson, J.D., Jr. Hypersonic and High-Temperature Gas Dynamics, 3rd ed.; AIAA Education Series; AIAA: Reston, VA, USA, 2019. [Google Scholar]
- Suzuki, K.; Abe, T. Transonic, Supersonic, and Hypersonic Wind-Tunnel Tests on Aerodynamic Chracteristics of Reentry Body with Blunted Cone Configuration; ISAS Report No. 658; Institute of Space and Astronautical Science: Sagamihara, Japan, 1995. [Google Scholar]
- Neville, A.G.; Candler, G.V. Computational-Fluid-Dynamics-Based Axisymmetric Aeroshell Shape Optimization in Hypersonic Entry Conditions. J. Spacecr. Rocket. 2015, 52, 76–88. [Google Scholar] [CrossRef]
- Seager, C.; Agarwal, R.K. Hypersonic Blunt-Body Shape Optimization for Reducing Drag and Heat Transfer. J. Thermophys. Heat Transf. 2017, 31, 48–55. [Google Scholar] [CrossRef]
- Theisinger, J.E.; Braun, R.D. Multi-Objective Hypersonic Entry Aeroshell Shape Optimization. J. Spacecr. Rocket. 2009, 46, 957–966. [Google Scholar] [CrossRef]
- Ishii, N.; Yamada, T.; Hiraki, K.; Inatani, Y. Reentry Motion and Aerodynamics of the MUSES-C Sample Return Capsule. Trans. Jpn. Soc. Aeronaut. Space Sci. 2008, 51, 65–70. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, A.; Murakami, K.; Aoyama, T.; Ishiko, K.; Hishida, M.; Sakashita, M.; Lahur, P. Toward the Fastest Unstructured CFD Code ‘FaSTAR’; 2012-1075; AIAA: Reston, VA, USA, 2012. [Google Scholar]
- Ito, Y.; Murayama, M.; Hashimoto, A.; Ishida, T.; Yamamoto, K.; Aoyama, T.; Tanaka, K.; Hayashi, K.; Ueshima, K.; Nagata, T.; et al. TAS Code, FaSTAR, and Cflow Results for the Sixth Drag Prediction Workshop. J. Aircr. 2018, 55, 1420–1432. [Google Scholar] [CrossRef]
- Kitamura, K.; Nonaka, S.; Kuzuu, K.; Aono, J.; Fujimoto, K.; Shima, E. Numerical and Experimental Investigations of Epsilon Launch Vehicle Aerodynamics at Mach 1.5. J. Spacecr. Rocket. 2013, 50, 896–916. [Google Scholar] [CrossRef]
- Takahashi, Y.; Ha, D.; Oshima, N.; Yamada, K.; Abe, T.; Suzuki, K. Aerodecelerator Performance of Flare-Type Membrane Inflatable Vehicle in Suborbital Reentry. J. Spacecr. Rocket. 2017, 54, 993–1004. [Google Scholar] [CrossRef] [Green Version]
- Teramoto, S.; Hiraki, K.; Fujii, K. Numerical Analysis of Dynamic Stability of a Reentry Capsule at Transonic Speeds. Aiaa J. 2001, 39, 646–653. [Google Scholar] [CrossRef]

| Fine | Nominal | Coarse | |
|---|---|---|---|
| Drag coefficient | 1.12986 | 1.12501 | 1.11057 |
| Normalized drag coefficient | 1.0000 | 0.9957 | 0.9829 |
| Number of cells | 5,032,000 | 963,596 | 265,743 |
| Number of faces | 14,648,152 | 2,748,156 | 740,877 |
| Number of nodes | 4,538,027 | 806,003 | 203,326 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otsu, H. Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours. Aerospace 2021, 8, 287. https://doi.org/10.3390/aerospace8100287
Otsu H. Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours. Aerospace. 2021; 8(10):287. https://doi.org/10.3390/aerospace8100287
Chicago/Turabian StyleOtsu, Hirotaka. 2021. "Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours" Aerospace 8, no. 10: 287. https://doi.org/10.3390/aerospace8100287
APA StyleOtsu, H. (2021). Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours. Aerospace, 8(10), 287. https://doi.org/10.3390/aerospace8100287






