An Evaluation Method for Dry Friction Damping of Ring Damper in Gas Turbine Engines under Axial Vibration
Abstract
:1. Introduction
2. Equivalent Damping Analysis of Dry Friction
2.1. Equation of Motion
2.2. Energy Dissipation
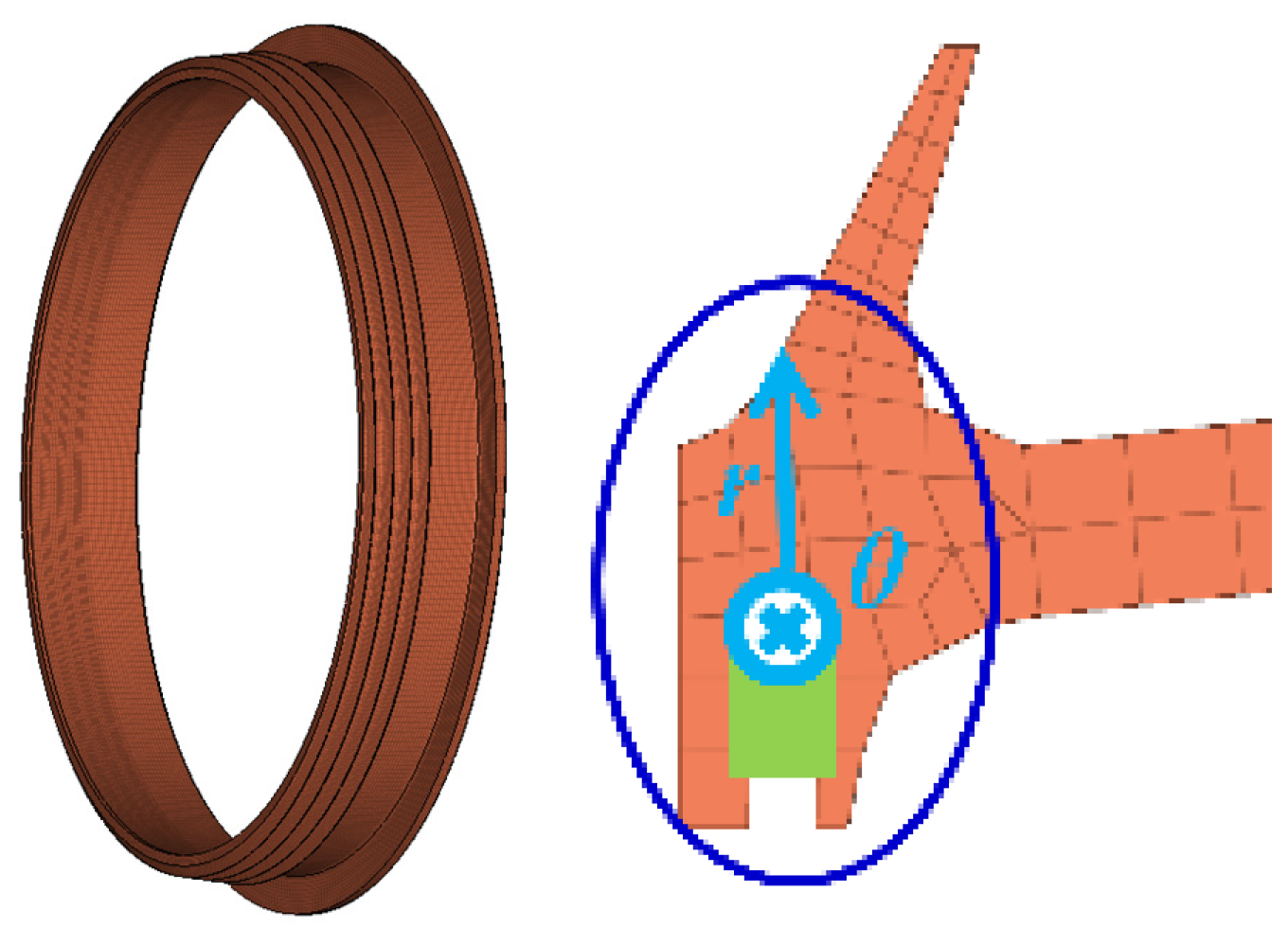
2.2.1. Relative Motion Analysis
2.2.2. Motion of Ring
Stick−Slip State
- (1)
- Stick phase
- (2)
- Transition from stick phase to slip phase
- (3)
- Slip phase
- (4)
- Transition from slip phase to stick phase
Full-Slip State
Critical State between Full-Slip and Stick-Slip
2.2.3. Relative Displacement at the Contact Surface
2.2.4. Energy Dissipated by Friction
2.3. Equivalent Damping Ratio
3. Case Study
3.1. Damping Characteristics of Ring for Blisk
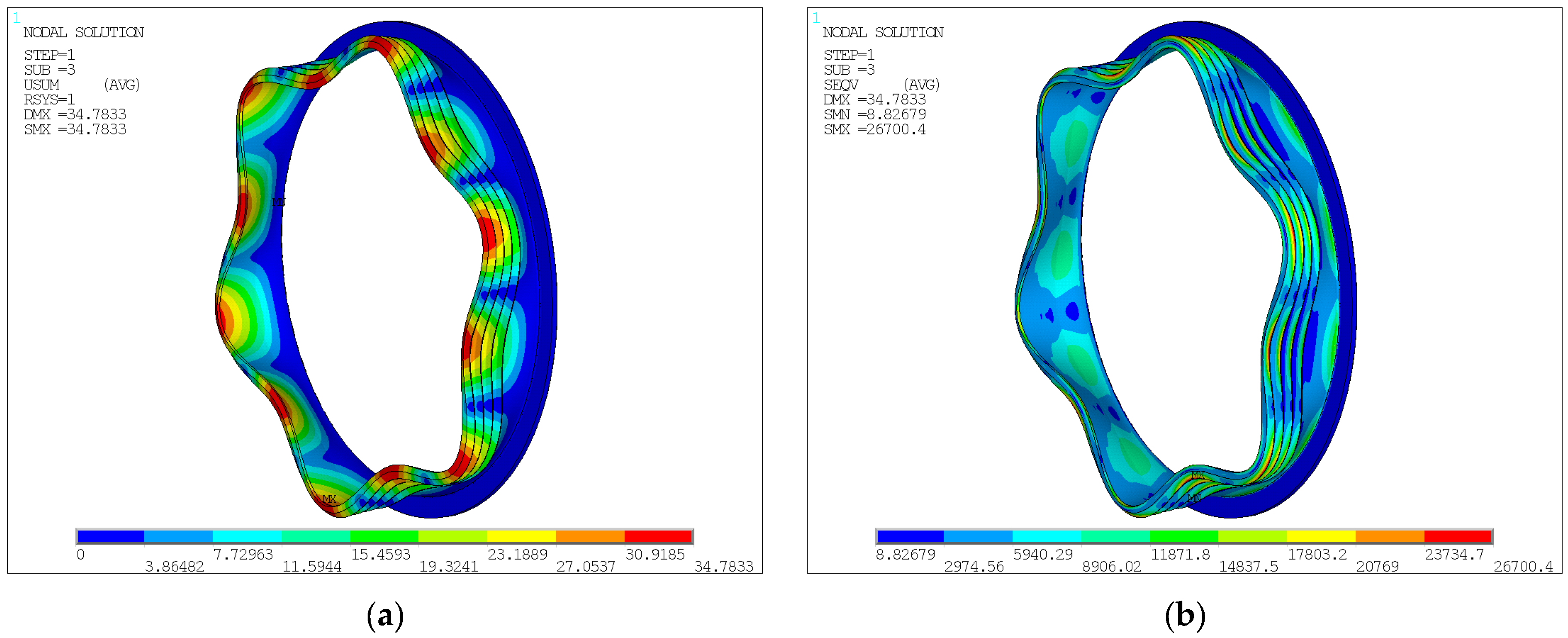
3.2. Damping Characteristics of Ring for Labyrinth Seal
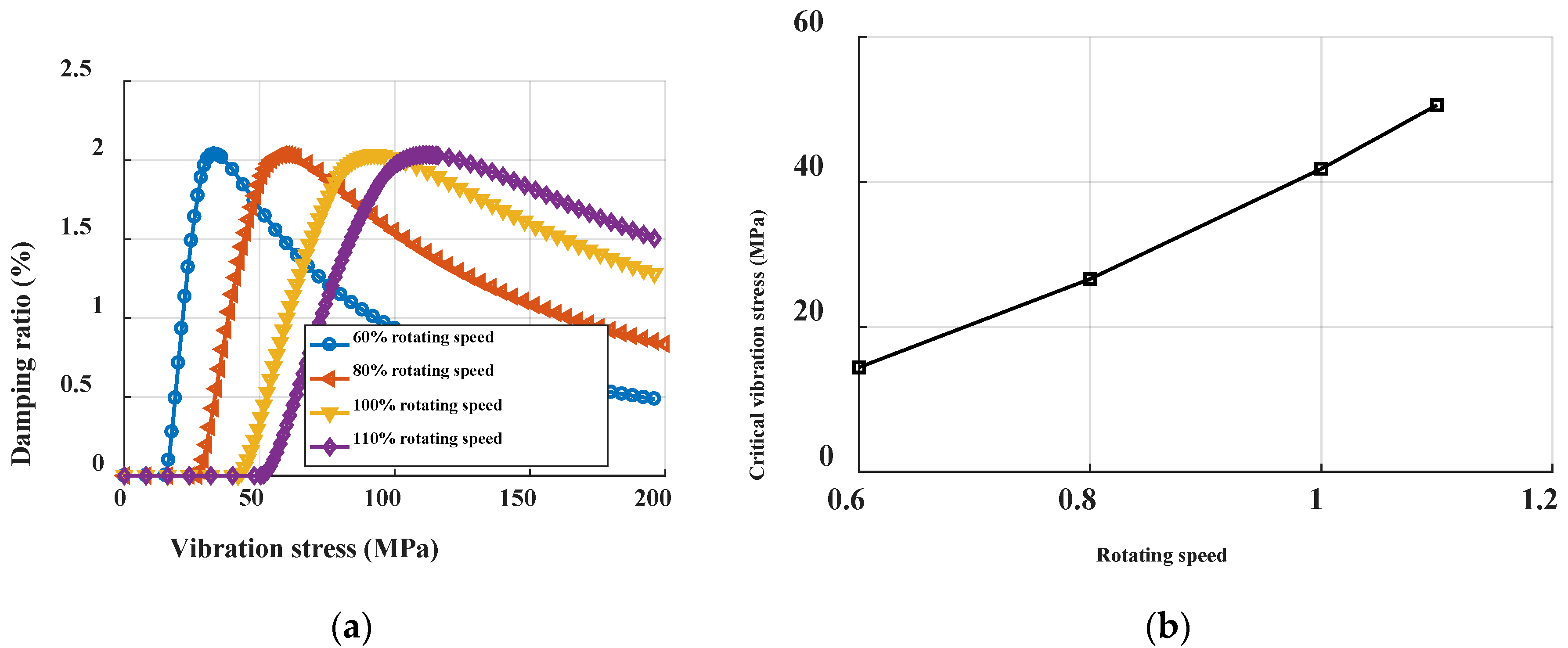
3.2.1. Rotating Speed
3.2.2. Friction Coefficient
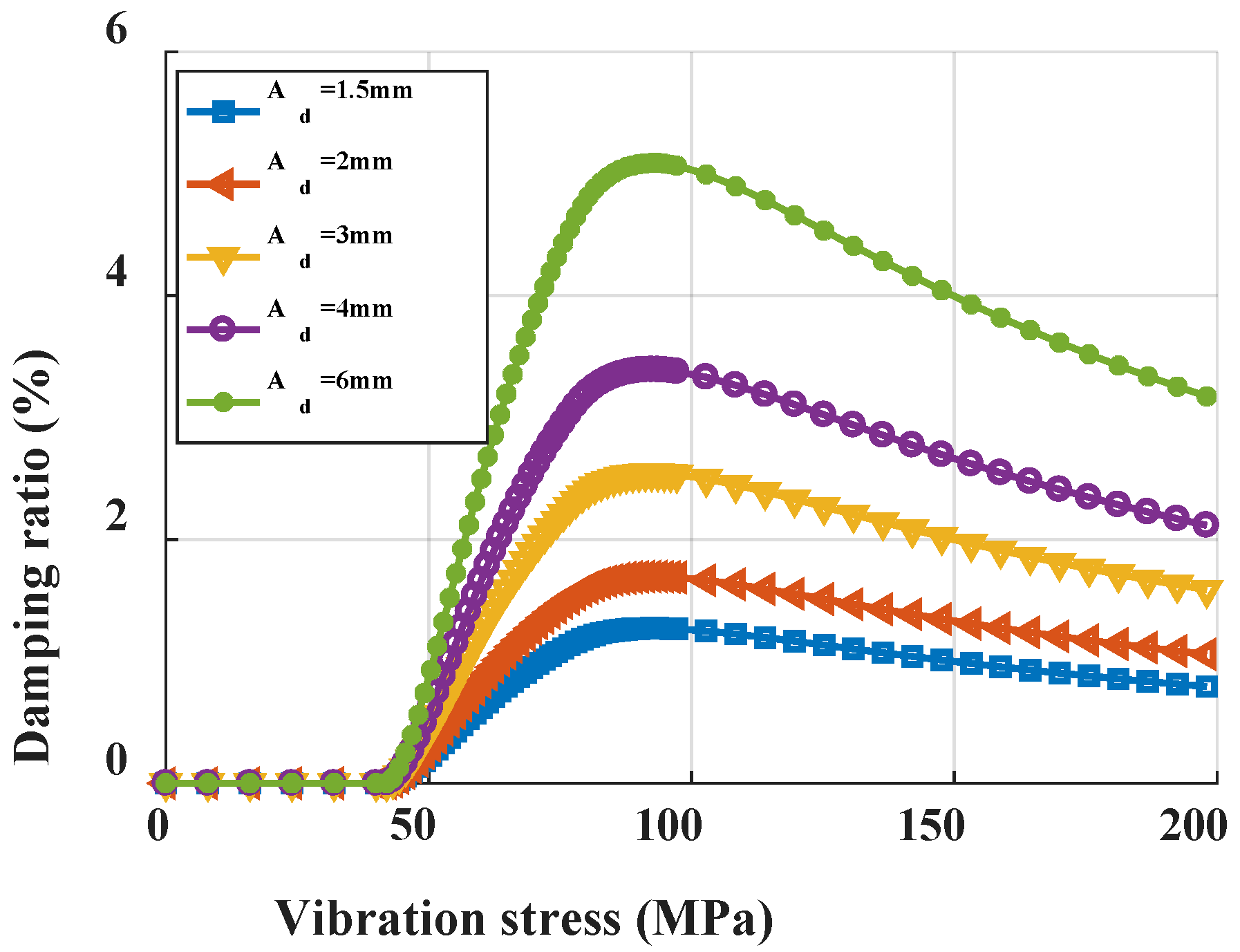
3.2.3. Cross-Section Area of the Ring
3.2.4. Density of Ring
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Srinivasan, A.V. Flutter and resonant vibration characteristics of engine blades. J. Eng. Gas Turbines Power 1997, 119, 742–775. [Google Scholar] [CrossRef]
- Ewins, D. Control of vibration and resonance in aero engines and rotating machinery—An overview. Int. J. Press. Vessel. Pip. 2010, 87, 504–510. [Google Scholar] [CrossRef]
- Afzal, M.; Arteaga, I.L.; Kari, L. Numerical analysis of multiple friction contacts in bladed disks. Int. J. Mech. Sci. 2018, 137, 224–237. [Google Scholar] [CrossRef]
- Krack, M.; Salles, L.; Thouverez, F. Vibration prediction of bladed disks coupled by friction joints. Arch. Comput. Methods Eng. 2016, 24, 589–636. [Google Scholar] [CrossRef] [Green Version]
- Bograd, S.; Reuss, P.; Schmidt, A.; Gaul, L.; Mayer, M. Modeling the dynamics of mechanical joints. Mech. Syst. Signal Process. 2011, 25, 2801–2826. [Google Scholar] [CrossRef]
- Phadke, R.; Berger, E.J. Friction damping analysis in turbine blades using a user-programmed function in ansys. In Proceedings of the 12th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 17–22 February 2008. [Google Scholar]
- Cardona, A.; Lerusse, A.; Géradin, M. Fast Fourier nonlinear vibration analysis. Comput. Mech. 1998, 22, 128–142. [Google Scholar] [CrossRef]
- Cameron, T.M.; Griffin, J.H. An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic systems. J. Appl. Mech. 1989, 56, 149–154. [Google Scholar] [CrossRef] [Green Version]
- Laxalde, D.; Sinou, J.J.; Thouverez, F.; Lombard, J.P. Modeling and analysis of friction rim dampers for blisks. In Proceedings of the ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005. [Google Scholar]
- Laxalde, D.; Thouverez, F. Non-linear vibrations of multi-stage bladed disks systems with friction ring dampers. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007. [Google Scholar]
- Laxalde, D.; Thouverez, F.; Lombard, J.-P. Vibration control for integrally bladed disks using friction ring dampers. In Proceedings of the GT2007 ASME Turbo Expo 2007: Power for Land, Sea and Air, Montreal, QC, Canada, 14–17 May 2007; pp. 255–265. [Google Scholar] [CrossRef]
- Laxalde, D.; Gibert, C.; Thouverez, F. Experimental and numerical investigations of friction rings damping of blisks. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008; pp. 469–479. [Google Scholar] [CrossRef] [Green Version]
- Laxalde, D.; Thouverez, F.; Lombard, J.-P. Forced response analysis of integrally bladed disks with friction ring dampers. J. Vib. Acoust. 2010, 132, 011013. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.; Epureanu, B.I. Reduced-order modeling of bladed disks with friction ring dampers. J. Vib. Acoust. 2017, 139, 061011. [Google Scholar] [CrossRef]
- Tang, W.; Epureanu, B.I. Nonlinear dynamics of mistuned bladed disks with ring dampers. Int. J. Non-Linear Mech. 2017, 97, 30–40. [Google Scholar] [CrossRef]
- Tang, W.; Baek, S.; Epureanu, B.I. Reduced-order models for blisks with small and large mistuning and friction dampers. J. Eng. Gas Turbines Power 2016, 139, 012507. [Google Scholar] [CrossRef]
- Tang, W.; Epureanu, B.I. Geometric optimization of dry friction ring dampers. Int. J. Non-Linear Mech. 2018, 109, 40–49. [Google Scholar] [CrossRef]
- Alford, J.S. Protection of labyrinth seals from flexural vibration. J. Eng. Power 1964, 86, 141–147. [Google Scholar] [CrossRef]
- Alford, J.S. Nature, causes, and prevention of labyrinth air seal failures. J. Aircraft 1975, 12, 313–318. [Google Scholar] [CrossRef]
- Niemotka, M.A.; Ziegert, J.C. Optimal design of split ring dampers for gas turbine engines. J. Eng. Gas Turbines Power 1995, 117, 569–575. [Google Scholar] [CrossRef]
- Buyukataman, K. A theoretical study on the vibration damping of aircraft gearbox gears. In Proceedings of the 27th Joint Propulsion Conference, Sacramento, CA, USA, 24–26 June 1991. [Google Scholar] [CrossRef]
- Buyukataman, K.; Kazerounian, K. Vibration damping of aircraft gearbox gears part II. In Proceedings of the AIAA/SAE/ASME/ASEE 31st Joint Propulsion Conference, San Diego, CA, USA, 10–12 July 1995. [Google Scholar]
- Lopez, I.; Nijmeijer, H. Prediction and validation of the energy dissipation of a friction damper. J. Sound Vib. 2009, 328, 396–410. [Google Scholar] [CrossRef]
- López, I.; Busturia, J.; Nijmeijer, H. Energy dissipation of a friction damper. J. Sound Vib. 2004, 278, 539–561. [Google Scholar] [CrossRef]
- Krack, M.; Scheidt, L.P.-V.; Wallaschek, J. A method for nonlinear modal analysis and synthesis: Application to harmonically forced and self-excited mechanical systems. J. Sound Vib. 2013, 332, 6798–6814. [Google Scholar] [CrossRef]
- Krack, M. Nonlinear modal analysis of nonconservative systems: Extension of the periodic motion concept. Comput. Struct. 2015, 154, 59–71. [Google Scholar] [CrossRef]
- Thomas, D.L. Dynamics of rotationally periodic structures. Int. J. Numer. Methods Eng. 1979, 14, 81–102. [Google Scholar] [CrossRef] [Green Version]
- Petrov, E.P. A Method for use of cyclic symmetry properties in analysis of nonlinear multiharmonic vibrations of bladed disks. J. Turbomach. 2004, 126, 175–183. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zucca, S.; Firrone, C.M.; Facchini, M. A method for the design of ring dampers for gears in aeronautical applications. J. Mech. Des. 2012, 134, 091003-1-10. [Google Scholar] [CrossRef]





















| Parameter | Value |
|---|---|
| Order | 3 ND first Bend |
| Frequency/Hz | 461.50 |
| Axial amplitude Aref/mm | 0.193 |
| Max equivalent stress σref/MPa | 1661 |
| Max kinetic energy Ek,ref/J | 4204 |
| Parameter | Value |
|---|---|
| Friction coefficient μ | 0.3 |
| Rotating speed Ω/(r/min) | 11,723 |
| Radius of contact surface Rf/mm | 184.2 |
| Young’s modulus of ring E/GPa | 210 |
| Radius of free split ring Rd,fr/mm | 188.7 |
| Radius of assembled split ring Rd/mm | 181.2 |
| Height of section of ring h/mm | 6 |
| Width of section of ring b/mm | 1.5 |
| Parameter | Value |
|---|---|
| Order | 6 ND first |
| Frequency/Hz | 1446.10 |
| Axial amplitude Aref/mm | 31.000 |
| Max equivalent stress σref/MPa | 26,700 |
| Max kinetic energy Ek,ref/J | 41,895 |
| Parameter | Value |
|---|---|
| Friction coefficient μ | 0.3 |
| Rotating speed Ω/(r/min) | 2227 |
| Radius of contact surface Rf/mm | 245.7 |
| Young’s modulus of ring E/GPa | 210 |
| Radius of free split ring Rd,fr/mm | 250.7 |
| Radius of assembled split ring Rd/mm | 243.7 |
| Height of section of ring h/mm | 2 |
| Width of section of ring b/mm | 1.2 |
| Order | Labyrinth with Ring | Labyrinth without Ring | Frequency Difference | ||
|---|---|---|---|---|---|
| Frequency | ND | Frequency | ND | ||
| 1 | 1365.90 | 5 | 1374.90 | 5 | −0.65% |
| 2 | 1390.20 | 5 | 1399.10 | 5 | −0.64% |
| 3 | 1446.10 | 6 | 1442.60 | 6 | 0.24% |
| 4 | 1467.70 | 6 | 1464.10 | 6 | 0.25% |
| 5 | 1471.00 | 4 | 1486.50 | 4 | −1.04% |
| 6 | 1498.40 | 4 | 1513.80 | 4 | −1.02% |
| 7 | 1689.30 | 7 | 1670.80 | 7 | 1.11% |
| 8 | 1708.60 | 7 | 1690.00 | 7 | 1.10% |
| 9 | 1748.20 | 3 | 1764.20 | 3 | −0.91% |
| 10 | 1778.80 | 3 | 1794.50 | 3 | −0.87% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Wang, Y. An Evaluation Method for Dry Friction Damping of Ring Damper in Gas Turbine Engines under Axial Vibration. Aerospace 2021, 8, 302. https://doi.org/10.3390/aerospace8100302
Gao S, Wang Y. An Evaluation Method for Dry Friction Damping of Ring Damper in Gas Turbine Engines under Axial Vibration. Aerospace. 2021; 8(10):302. https://doi.org/10.3390/aerospace8100302
Chicago/Turabian StyleGao, Shimin, and Yanrong Wang. 2021. "An Evaluation Method for Dry Friction Damping of Ring Damper in Gas Turbine Engines under Axial Vibration" Aerospace 8, no. 10: 302. https://doi.org/10.3390/aerospace8100302
APA StyleGao, S., & Wang, Y. (2021). An Evaluation Method for Dry Friction Damping of Ring Damper in Gas Turbine Engines under Axial Vibration. Aerospace, 8(10), 302. https://doi.org/10.3390/aerospace8100302






