A Control Method of Space Manipulator for Peg-in-Hole Assembly Task Considering Equivalent Stiffness Optimization
Abstract
:1. Introduction
- By combining the structure and control characteristics of the space manipulator, the controller parameters and configuration are introduced into the equivalent stiffness optimization process of the manipulator.
- By combining the advantages of the sliding mode control method, an impedance control law based on the result of equivalent stiffness optimization is deigned, and the zero-sum game is introduced to compensate for the interference caused by contact collision.
2. Stiffness Modeling of Space Manipulator
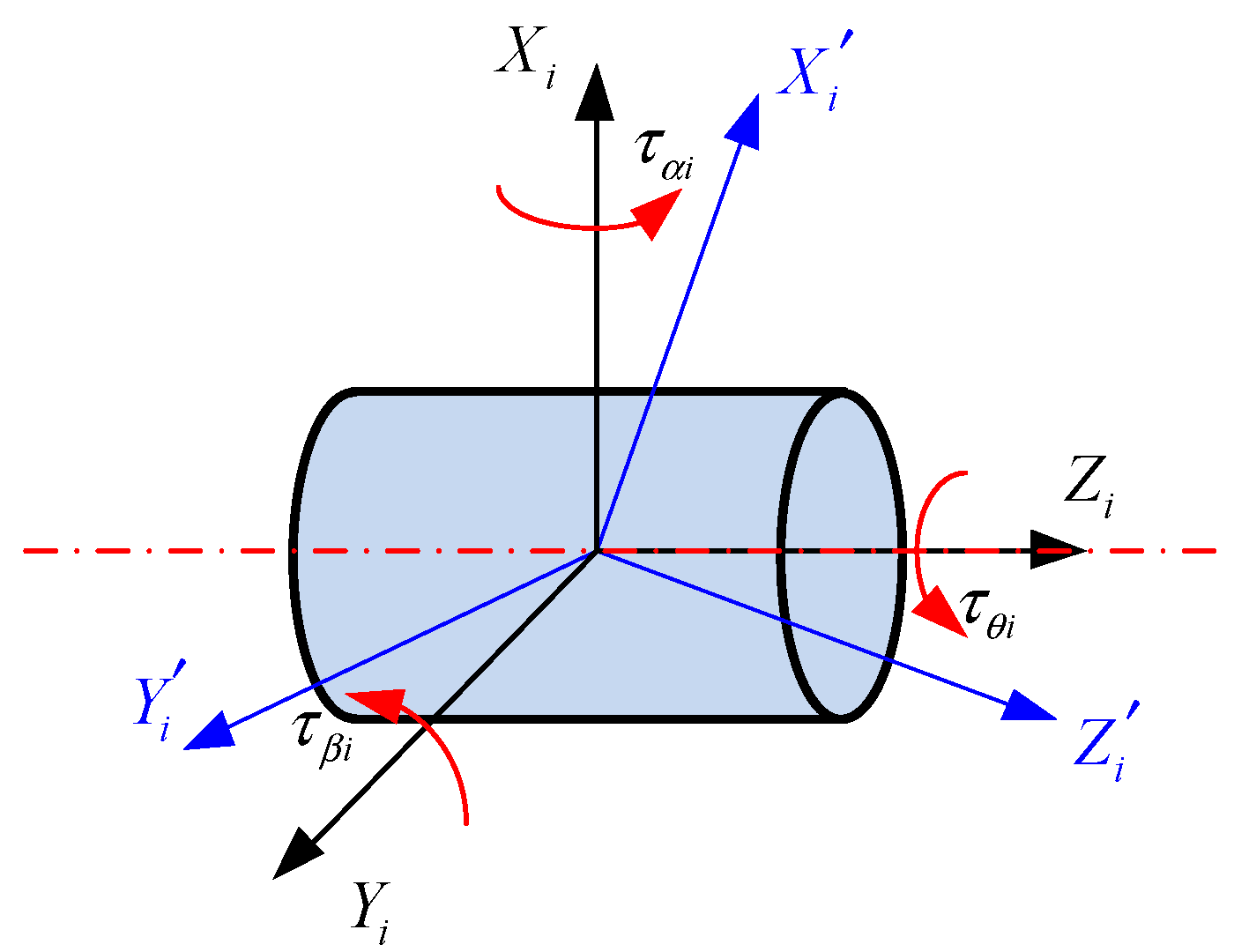
2.1. Kinematics and Dynamics Model
2.2. Equivalent Stiffness Model
2.2.1. Joint Flexibility
2.2.2. Link Flexibility
2.2.3. Control Flexibility
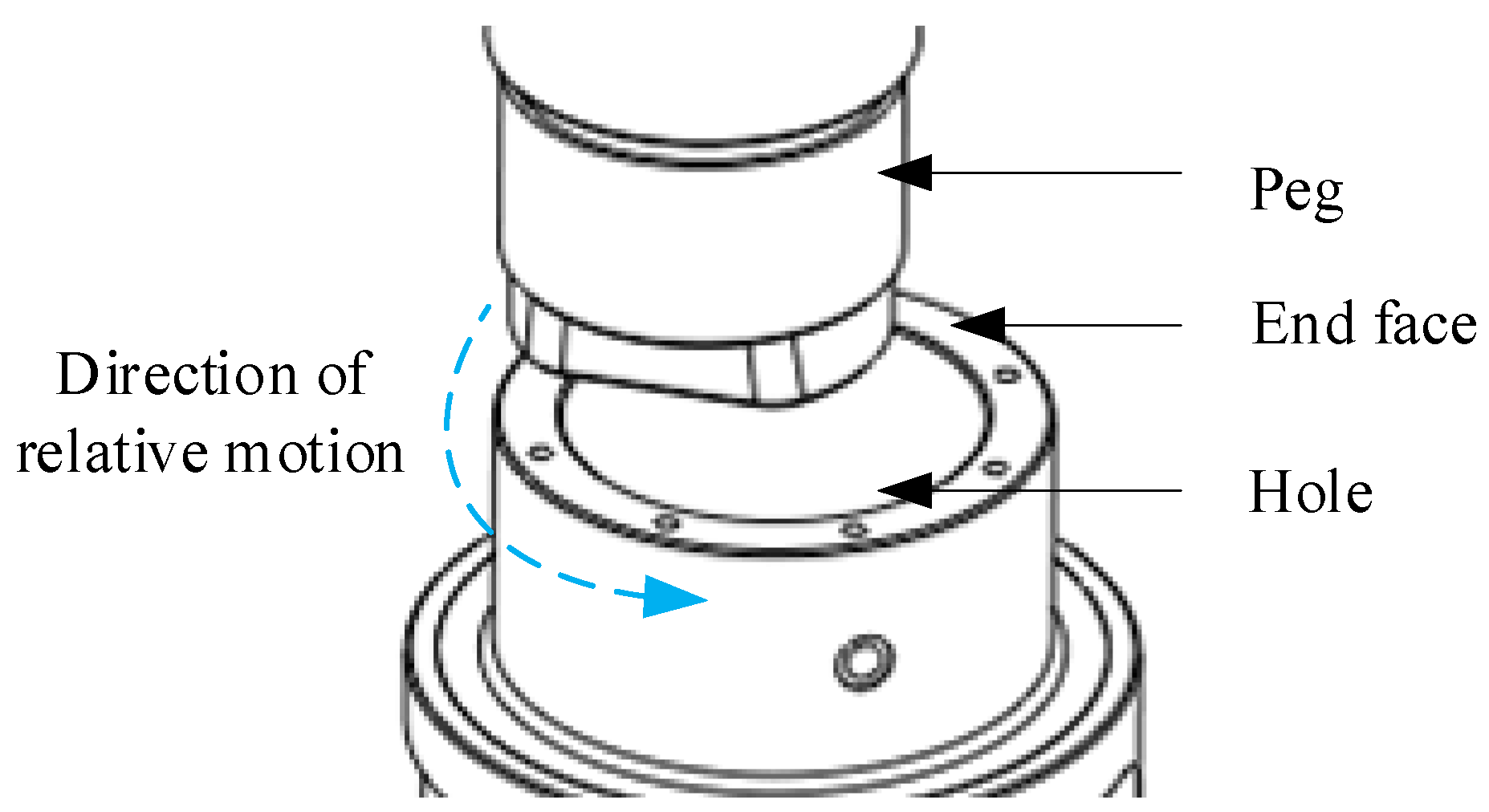
3. Stiffness Optimization Method for Peg-in-Hole Assembly
3.1. Task Direction Flexibility
3.2. Optimization
4. Sliding Mode Impedance Control Based on Disturbance Compensation
4.1. Sliding Mode Impedance Control
4.2. Disturbance Compensation
5. Test and Analysis
5.1. Subject
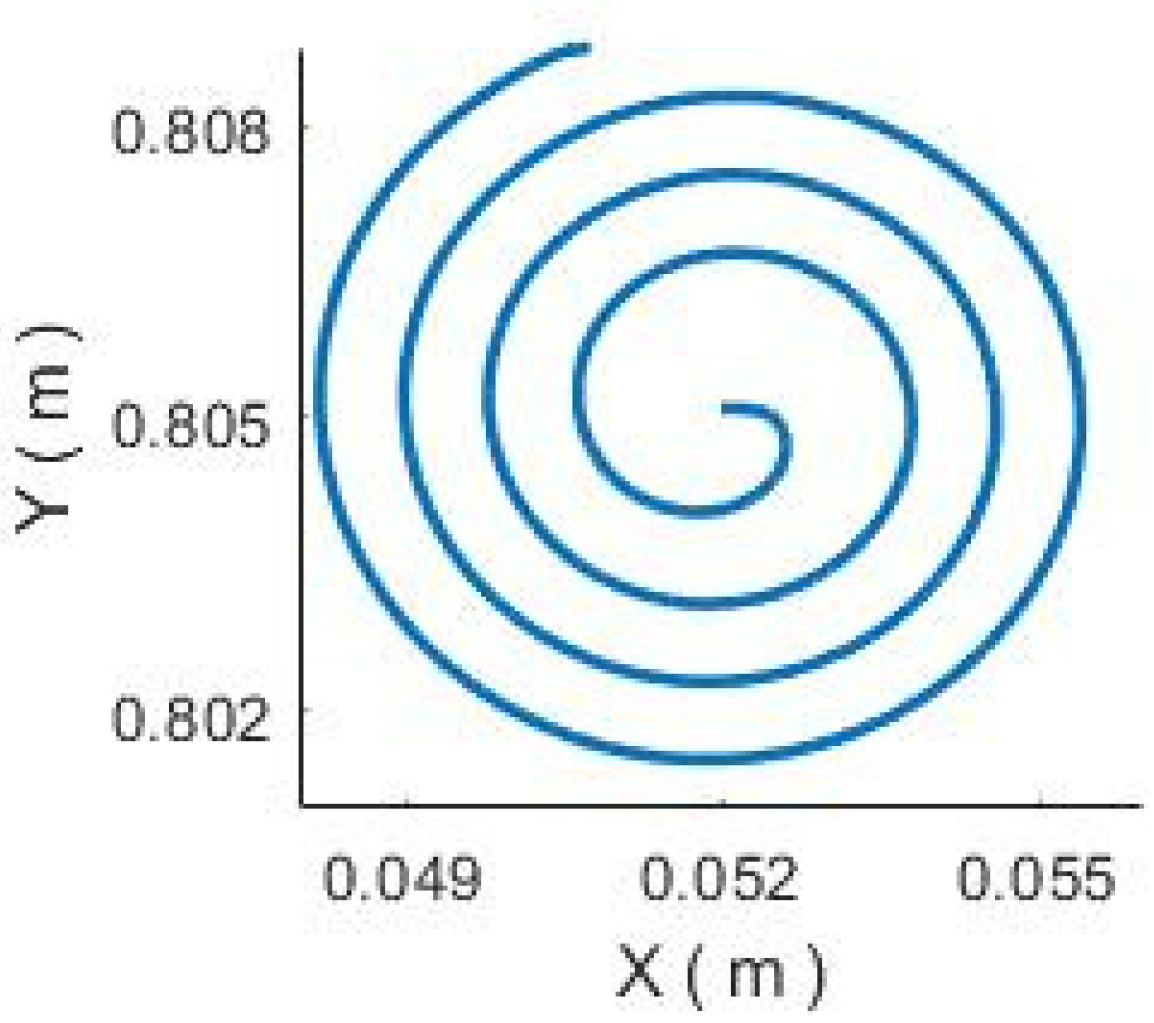
5.2. Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, Y.; Hou, X.; Rao, X.; Li, L.; Chen, T. Research on the Key Technology of Crawler Robot Orbiting on Space Solar Power Station. Space Electron. Technol. 2018, 15, 106–112. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, T.; Zhang, X. Flat-field calibration method for large diameter survey mirror aperture splicing. Chin. Opt. 2020, 13, 1094–1102. [Google Scholar] [CrossRef]
- Hao, Z.; Jiang, Z.; Li, C.; Yang, F. Assembly Trajectory Planning of Space Telescope Sub-mirror Module Based on Time Optimal Control. IOP Conf. Ser. Mater. Sci. Eng. 2018, 439, 032077. [Google Scholar] [CrossRef]
- CIOMP. The Key Special Project of Strategic International Scientific and Technological Innovation Cooperation between CIOMP and the University of Surrey Was Officially Launched. Available online: http://www.ciomp.ac.cn/xwdt/zhxw/201711/t20171101_4882749.html (accessed on 28 May 2021).
- Pei, Z.; Liu, J.; Wang, Q.; Kang, Y.; Zou, Y.; Zhang, H.; Zhang, Y.; He, H.; Wang, Q.; Yang, R.; et al. Overview of lunar exploration and International Lunar Research Station. Chin. Sci. Bull. 2020, 65, 2577–2586. (In Chinese) [Google Scholar] [CrossRef]
- Feng, P.; Bao, C.; Zhang, D.; Yue, Q.; Qi, J.; Zuo, Y. Construction technology for lunar bases using lunar in-situ resources. Ind. Constr. 2021, 51, 169–178. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Zhang, X. Kinematic Calibration and Vision-Based Object Grasping for Baxter Robot. In Proceedings of the International Conference on Intelligent Robotics and Applications, ICIRA 2016, Tokyo, Japan, 22–24 August 2016; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9834. [Google Scholar] [CrossRef]
- Shah, G.A.; Polette, A.; Pernot, J.P.; Giannini, F.; Giannini, M. Simulated annealing-based fitting of CAD models to point clouds of mechanical parts’ assemblies. In Engineering with Computers; Springer: Cham, Switzertland, 2020. [Google Scholar] [CrossRef]
- Calanca, A.; Muradore, R.; Fiorini, P. A Review of Algorithms for Compliant Control of Stiff and Fixed-Compliance Robots. IEEE/ASME Trans. Mechatron. 2016, 21, 613–624. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Jia, Q.; Sun, H.; Zhang, X. Hybrid Force and Position Control Strategy of Robonaut Performing Peg-in-Hole Assembly Task. J. Astronaut. 2017, 4, 410–419. [Google Scholar] [CrossRef]
- Wu, B.; Qu, D.; Xu, F. Industrial robot high precision peg in-hole assembly based on hybrid force/position control. J. Zhejiang Univ. Eng. Sci. 2018, 52, 379–386. [Google Scholar] [CrossRef]
- Hogan, N. Impedance control an approach to manipulation: Part I-theory, Part II-implementation, Part III-Application. J. Dyn. Syst. Meas. Control. 1985, 107, 1. [Google Scholar] [CrossRef]
- Roveda, L.; Piga, D. Robust state dependent riccati equation variable impedance control for robotic force-tracking tasks. Int. J. Intell. Robot. Appl. 2020, 4, 507–519. [Google Scholar] [CrossRef]
- Yang, C.; Ganesh, G.; Haddadin, S.; Parusel, S.; Albu-Schaeffer, A.; Burdet, E. Human-like adaptation of force and impedance in stable and unstable interactions. IEEE Trans. Robot. 2011, 27, 918–930. [Google Scholar] [CrossRef] [Green Version]
- Qu, M.; Wang, H.; Rong, Y. Static Stiffness Modeling and Experiments of Polishing Manipulator Arm. China Mech. Eng. 2017, 28, 2395–2401. [Google Scholar] [CrossRef]
- Hui, Z.; Wang, J.; Zhang, G.; Gan, Z.; Zhu, Z. Machining with flexible manipulator: Toward improving robotic machining performance. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 1127–1132. [Google Scholar] [CrossRef]
- Jiao, J.; Liao, W.; Tian, W.; Zhang, L.; Liu, S. A configuration optimizing method in robotic machining. Int. Robot. Autom. J. 2017, 3, 287–288. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Posture optimization methodology of 6R industrial robots for machining using performance evaluation indexes. Robot. Comput. Integr. Manuf. 2017, 48, 59–72. [Google Scholar] [CrossRef]
- Qu, W.; Hou, P.; Yang, G.; Huang, G.; Yin, F.; Shi, X. Research on the stiffness performance for robot machining systems. Acta Aeronaut. Astronaut. Sin. 2013, 34, 2823–2832. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, B.; Liu, J.; Chen, F.; Yang, S.; Wang, W.; Li, L. Research on layout and operational pose optimization of robot grinding system based on optimal stiffness performance. J. Adv. Mech. Des. Syst. Manuf. 2017, 11, M22. [Google Scholar] [CrossRef] [Green Version]
- Ott, C.; Mukherjee, R.; Nakamura, Y. Unified impedance and admittance control. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–8 May 2010. [Google Scholar] [CrossRef]
- Ott, C.; Mukherjee, R.; Nakamura, Y. A hybrid system framework for unified impedance and admittance control. J. Intell. Robot. Syst. 2015, 78, 359–375. [Google Scholar] [CrossRef]
- Beyer, A.; Grunwald, G.; Heumos, M.; Scheld, M.; Bayer, R.; Bertleff., W.; Brunner, B.; Burger, R.; Butterfaß, J.; Gruber, R.; et al. Caesar: Space robotics technology for assembly, maintenance, and repair. In Proceedings of the International Astronautical Congress, IAC, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Li, E.C.; Li, Z.M. The Robotic Force Tracking Based on Single Input Fuzzy Adaptive Controller. Adv. Mater. Res. 2011, 328–330, 2117–2120. [Google Scholar]
- Xiao, W. Research on Path Planning and Force Control of Peg-Hole Assembly Robot. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2018. [Google Scholar]
- Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Robot Auton. Syst. 2018, 102, 54–65. [Google Scholar] [CrossRef]
- Roveda, L.; Iannacci, N.; Molinari Tosatti, L. Discrete-time formulation for optimal impact control in interaction tasks. J. Intell. Robot. Syst. 2018, 90, 407–417. [Google Scholar] [CrossRef]
- Sadeghian, H.; Villani, L.; Keshmiri, M.; Siciliano, B. Task-Space Control of Robot Manipulators with Null-Space Compliance. IEEE Trans. Robot. 2014, 30, 493–506. [Google Scholar] [CrossRef]
- Jia, Q.; Xu, T.; Chen, G.; Sun, H.; Wang, Y. Coordinated Impedance Control of Robonaut Based on Disturbance Observer. Robot 2018, 6, 860–869. [Google Scholar] [CrossRef]
- Dong, B.; An, T.; Zhou, F.; Liu, K.; Li, Y. Decentralized robust zero-sum neuro-optimal control for modular robot manipulators in contact with uncertain environments: Theory and experimental verification. Nonlinear Dynam. 2019, 97, 503–524. [Google Scholar] [CrossRef]
- Aliyu, M.D.S. An approach for solving the Hamilton-Jacobi-Isaacs equation (HJIE) in nonlinear H∞ control. Automatica 2003, 39, 877–884. [Google Scholar] [CrossRef]
- Chen, G.; Liu, D.; Wang, Y.; Jia, Q.; Liu, X. Contact Force Minimization for Space Flexible Manipulators Based on Effective Mass. J. Guid. Control Dyn. 2019, 42, 1870–1877. [Google Scholar] [CrossRef]

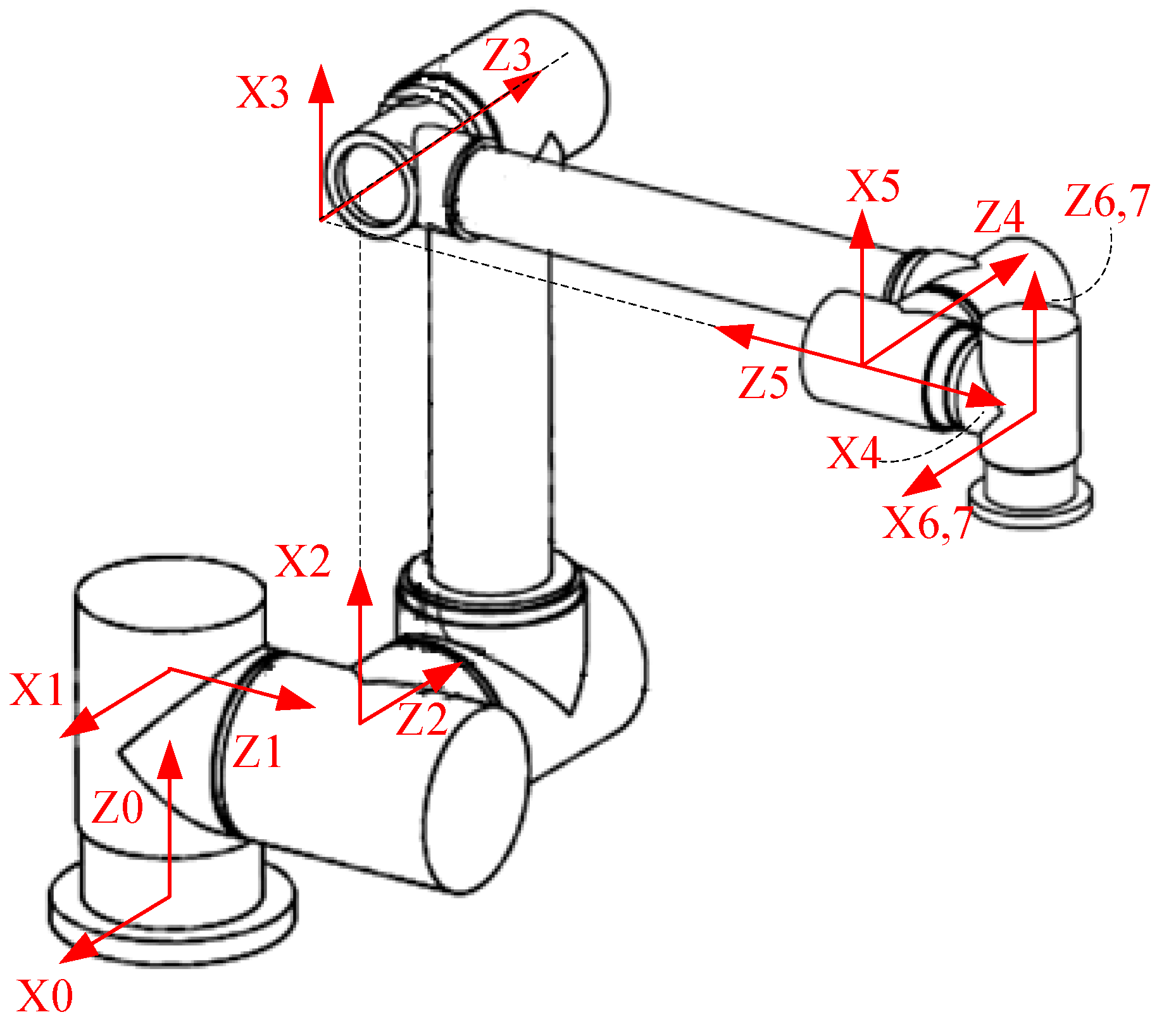



| i | (°) | (mm) | (°) | (mm) |
|---|---|---|---|---|
| 1 | −90 | 0 | 0 | 166.8 |
| 2 | 90 | 0 | −90 | 183.1 |
| 3 | 0 | 544.9 | 0 | −52 |
| 4 | 0 | 500.9 | 90 | 0 |
| 5 | 90 | 0 | −90 | 0 |
| 6 | −90 | 0 | −90 | −121.1 |
| 7 | 0 | 0 | 0 | 0 |
| Link | Center of Mass X (m) | Center of Mass Y (m) | Center of Mass Z (m) | Mass (kg) |
|---|---|---|---|---|
| Base | 0 | 0 | 0.032161 | 1.82 |
| Link1 | 0 | −0.00754 | 0.00864 | 8.5 |
| Link2 | 0 | 0.00754 | 0.00864 | 8.5 |
| Link3 | −0.45495 | 0 | 0.24168 | 10.8 |
| Link4 | −0.5013 | 0.00475 | 0.32914 | 6.3 |
| Link5 | 0 | 0.11454 | 0.00521 | 2.13 |
| Link6 | −0.00451 | −0.12413 | 0 | 2.3 |
| Link7 | 0 | −0.00354 | −0.00771 | 1.9 |
| Experiment 1 | Experiment 2 | Experiment 3 | |
|---|---|---|---|
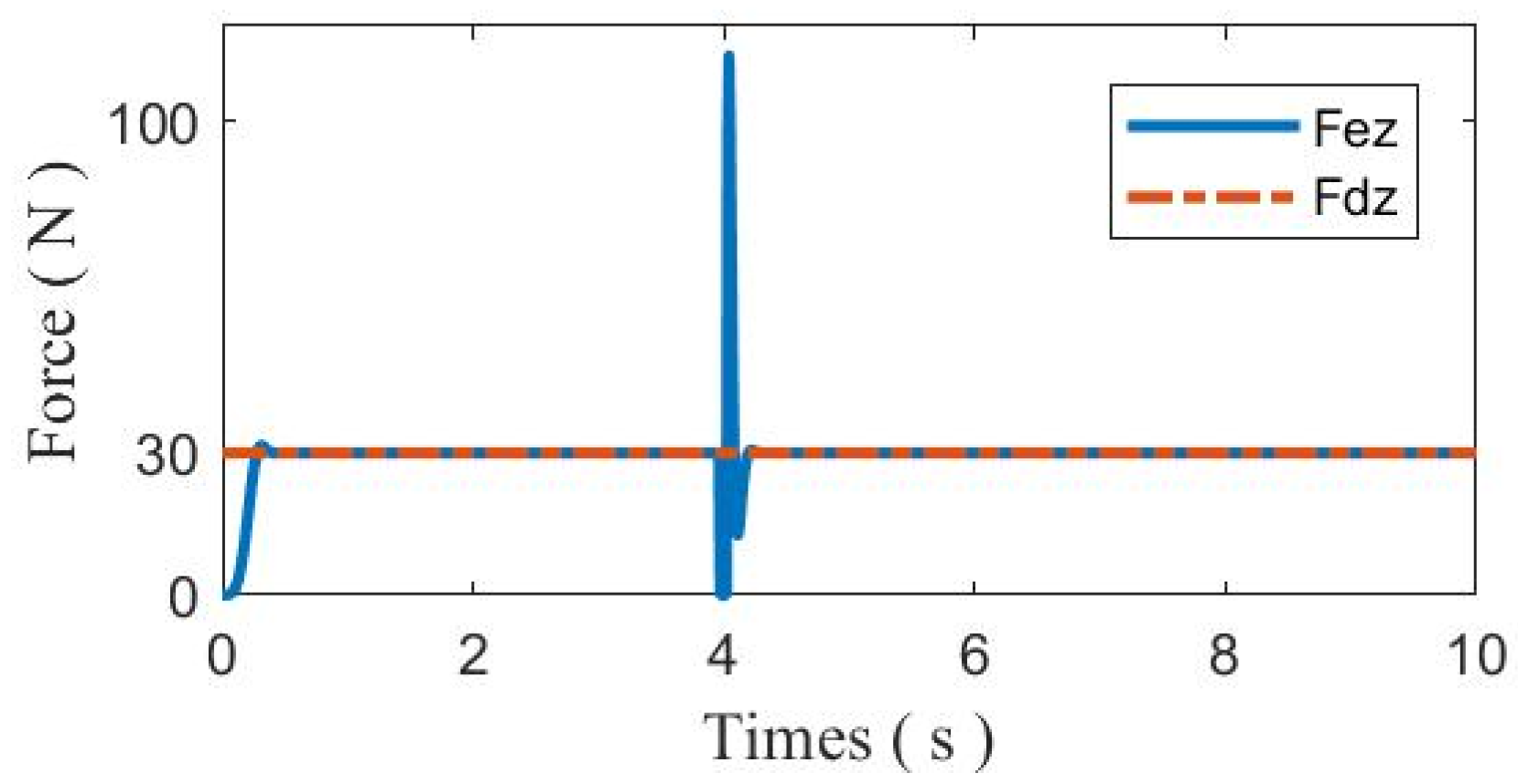
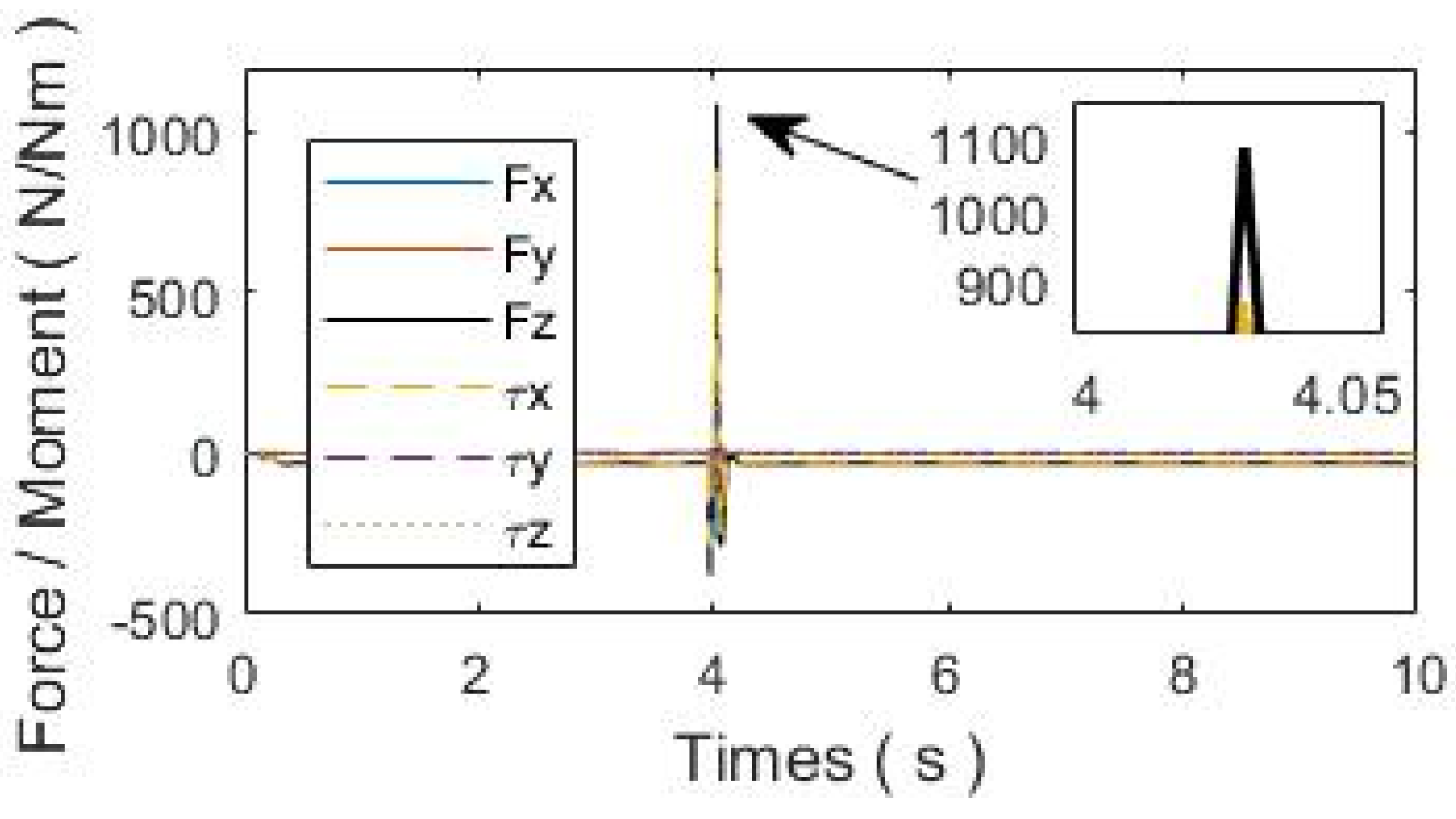
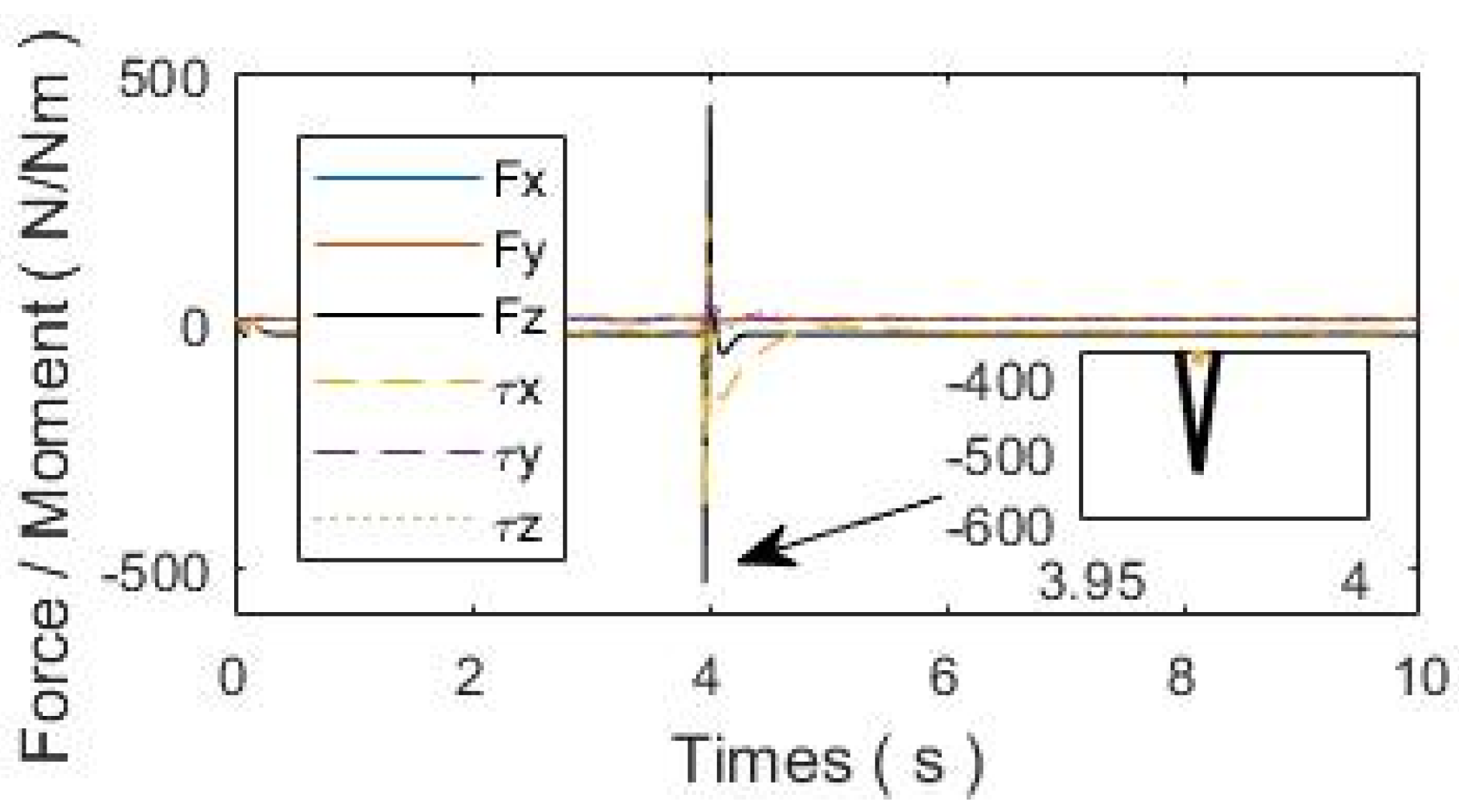
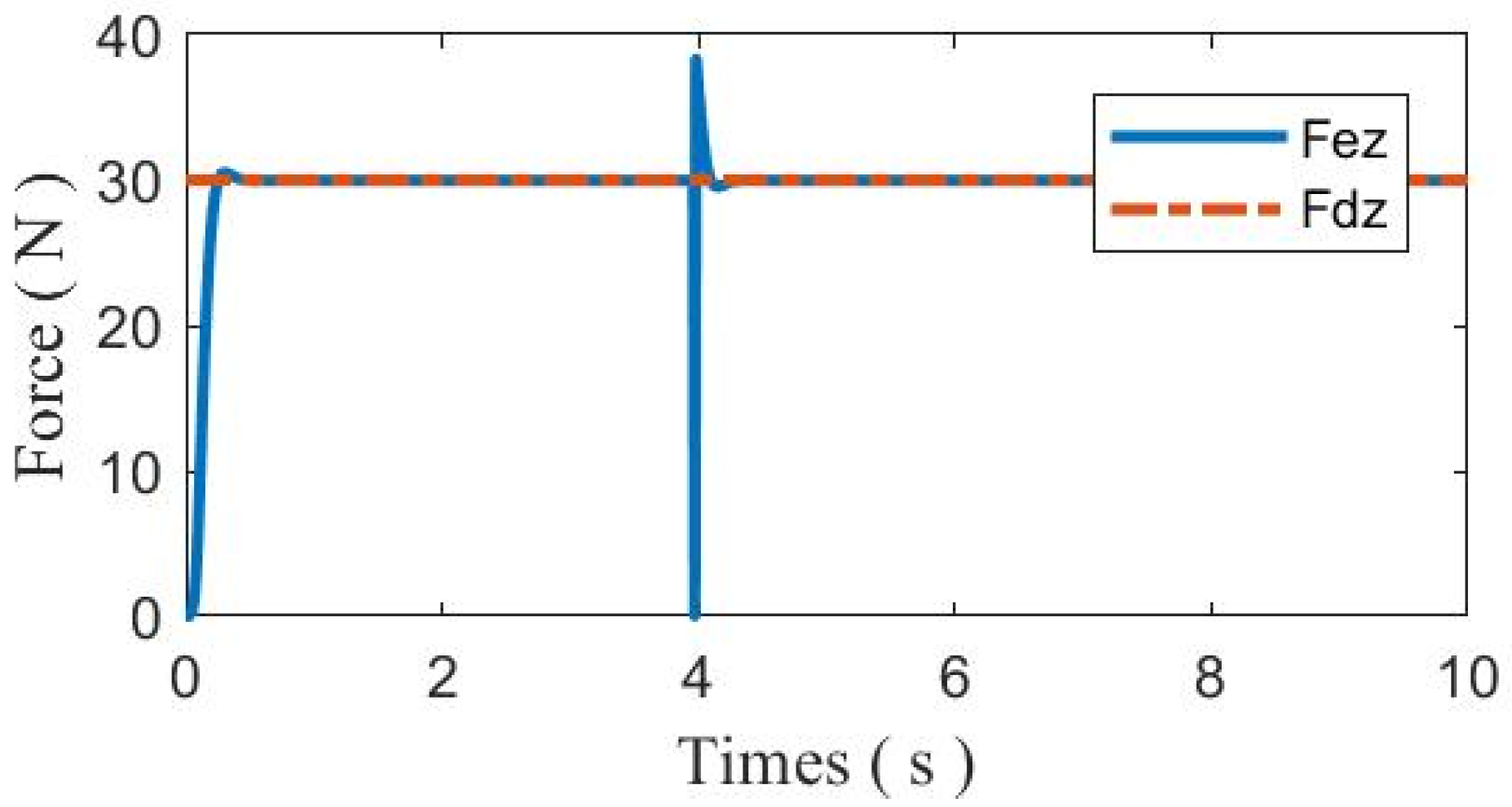
| Sudden change in contact force | 114 N | 77 N | 38 N |
| lower than experiment 1 | / | 47% | 90% |
| Peak disturbance force of the base | 1086 N | 534 N | 500 N |
| lower than experiment 1 | / | 51% | 54% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, G.; Jia, Q.; Chen, G.; Li, T.; Liu, C. A Control Method of Space Manipulator for Peg-in-Hole Assembly Task Considering Equivalent Stiffness Optimization. Aerospace 2021, 8, 310. https://doi.org/10.3390/aerospace8100310
Pan G, Jia Q, Chen G, Li T, Liu C. A Control Method of Space Manipulator for Peg-in-Hole Assembly Task Considering Equivalent Stiffness Optimization. Aerospace. 2021; 8(10):310. https://doi.org/10.3390/aerospace8100310
Chicago/Turabian StylePan, Guangtang, Qingxuan Jia, Gang Chen, Tong Li, and Chuankai Liu. 2021. "A Control Method of Space Manipulator for Peg-in-Hole Assembly Task Considering Equivalent Stiffness Optimization" Aerospace 8, no. 10: 310. https://doi.org/10.3390/aerospace8100310






