Abstract
Resonant response of turbomachinery blades can lead to high cycle fatigue (HCF) if the vibration amplitudes are significant. Therefore, the dangerousness assessment of the resonance crossing is important. It requires accurate predictions of the aerodynamic excitation, damping, and response, which will consume immense computational costs. The novel aspect of this study is the development of an efficient approach, which incorporates the time transformation (TT) method to predict the aerodynamic excitations and the harmonic forced response method to obtain the response levels. The efficiency and accuracy of this method were evaluated by comparing with traditional methods for the resonance crossing excited by upstream wake in a 1.5 multistage compressor. For the aerodynamic excitation, discrepancies of ±2% at the mean pressure and ±25% at the harmonic pressure in most areas expect for the blade root were observed, but the calculation time required by the TT method was only 5% of that by the time-marching method. Moreover, response levels with the same aerodynamic forces were compared between the harmonic forced-response and transient dynamic methods. Small differences in the displacement and stress variables were observed; the relative deviation was smaller than 2% with only 1% computing time compared with the transient method, indicating the high accuracy and efficiency of the efficient approach.
1. Introduction
Forced vibration is an important aero-elastic phenomenon in turbomachines caused by aerodynamic or mechanical excitations, which can lead to high cycle fatigue (HCF) damage. It can be divided into two types according to the excitation sources [1]. One is the classical forced vibration with the excitation from the wake and potential disturbances of the adjacent blade rows. The excitation frequencies, which are the blade passing frequency (BPF) and its harmonics, are relatively high and thus excite vibrations of higher order modes [2,3]. The other is caused by a loss of symmetry, such as the inlet distortion or non-uniform temperature field [4,5]. The excitation frequencies are usually lower and called low engine order (LEO) excitations.
In the forced response analysis, a Campbell diagram is commonly used to identify possible resonance crossings so as to avoid aero-engines working at these points as much as possible. Unfortunately, it is impossible to remove all resonance crossings, and consequently the assessment of the response levels is important. The numerical approaches to predict the response levels are mainly strong coupling and weak coupling approaches [6]. The latter is widely used in the engineering design due to its lower computational effort. In this approach, the aerodynamic forces and structure vibration are computed separately without considering the impact of vibration on the flow field.
For the weak coupling approach, the determination of aerodynamic forces is the core. It is generally achieved by CFD simulations of the transient flow. Traditional methods usually need multi-blade models or even the whole annulus to ensure the equal pitch of adjacent blade rows, which is computationally demanding and difficult to operate in practice. In order to reduce the computational effort, various methods have been developed over the past few years. These methods attempt to solve the unsteady flow by only one or a few blade passages based on the frequency-integration and time-integration approaches [7]. Due to the different assumptions, each method has its advantages and disadvantages.
The representative frequency-integration methods are the nonlinear harmonic (NLH) method [8] and the harmonic balance (HB) method [9]. The basic principle of these methods is to transfer the governing equations and boundary conditions from the time to frequency domain through the Fourier series. However, when the flow has strong nonlinear characteristics, these methods will incur large errors due to the linearization assumption.
For the time-integration methods, they consist of the time-shifted methods and the scaling methods. The former is mainly the Fourier transformation (FT) method, which is based on the time shift and phase shift [10], and it is improved by introducing the Fourier series decomposition at the rotor/stator and periodic interfaces [11,12]. This makes the significant data compression and efficiency improvement with two blade passages modeled per row, but it usually needs more calculation periods to reach convergence [13].
In terms of the scaling methods, it mainly includes the following three methods: the geometry scaling (GS) method [14], the profile transformation (PT) method [15], and the time transformation (TT) method [16]. The first one requires an adjustment of the blade numbers to reduce the blade passages in the modeling. The PT method scales the flow profiles at the rotor/stator interface (stretches or compresses) to meet the pitch requirement. However, due to the variation of blade numbers and the scaling treatment of the interface profile, the predictions of the BPF are both inaccurate in the above two methods.
The TT method is an attractive method, which is developed based on the PT method and the time-inclining method [17]. In addition to the circumferential profile scaling at the interface, time correction is also applied at the rotor/stator interface. Thus, it not only retains the advantages of the PT method, but it also can accurately predict the disturbance frequency. Compared with the FT method, this method can quickly predict the unsteady flow field, but it is not suitable to all pitch ratios. Fortunately, the pitch ratio of most compressor and turbine blades is within the scope of this method (0.75–1.4). Moreover, two or more blade passages per row can be modeled to meet the requirement.
The TT method was validated on several test cases [12,18,19,20]. However, the discussion of this method in the open literature was more concerned about the total performance parameters (mass flow, efficiency, and total pressure ratio) and time-averaged variables. Few comparisons of pressure disturbance at the blade surface were reported, which are important to the forced response analysis. In this article, the results of pressure disturbance by the TT method and the traditional method (time-marching method) are compared in detail, and the relative error of TT method is clarified.
After the determination of the aerodynamic excitation, another important task for the weak coupling approach is to calculate the structure vibration. In general, transient dynamic analysis is used to determine the dynamic response of a structure under the time-dependent loads. The equations of the motion are solved as a set of static equilibrium equations by the Newmark time-integration method at different instantaneous times to calculate the dynamic response [21]. It enables consideration of all types of nonlinearities but with intensive computational effort. In this study, a new method was proposed to predict the response levels, and it is called the harmonic forced-response method. It converts the aerodynamic excitation from the time domain to the frequency domain, which significantly improves the computational efficiency. Compared with the traditional method (transient dynamic method), the accuracy and computational efficiency of this method are clarified.
The purpose of this study was twofold: (i) to ensure the applicability and accuracy of the TT method in the prediction of the unsteady flow and (ii) to investigate the accuracy and efficiency of the new method—the harmonic forced response method. The article is organized as follows. In the first part, theoretical equations regarding the prediction of aerodynamic excitation, damping, and response are discussed. Then, the test case and resonance crossing excited by the upstream wake are presented. In Section 4, the predictions of aerodynamic excitations are investigated using the time-marching (TM) method with the full-annulus model and the TT method with a reduced model to evaluate the effectiveness and accuracy of the TT method. In addition, the aerodynamic damping is presented and regarded as the input of the response analysis. At the end, blade vibration stresses from the harmonic method and the transient dynamic method are compared based on the same excitation to validate the accuracy of the efficient harmonic method.
2. Investigation Methodology
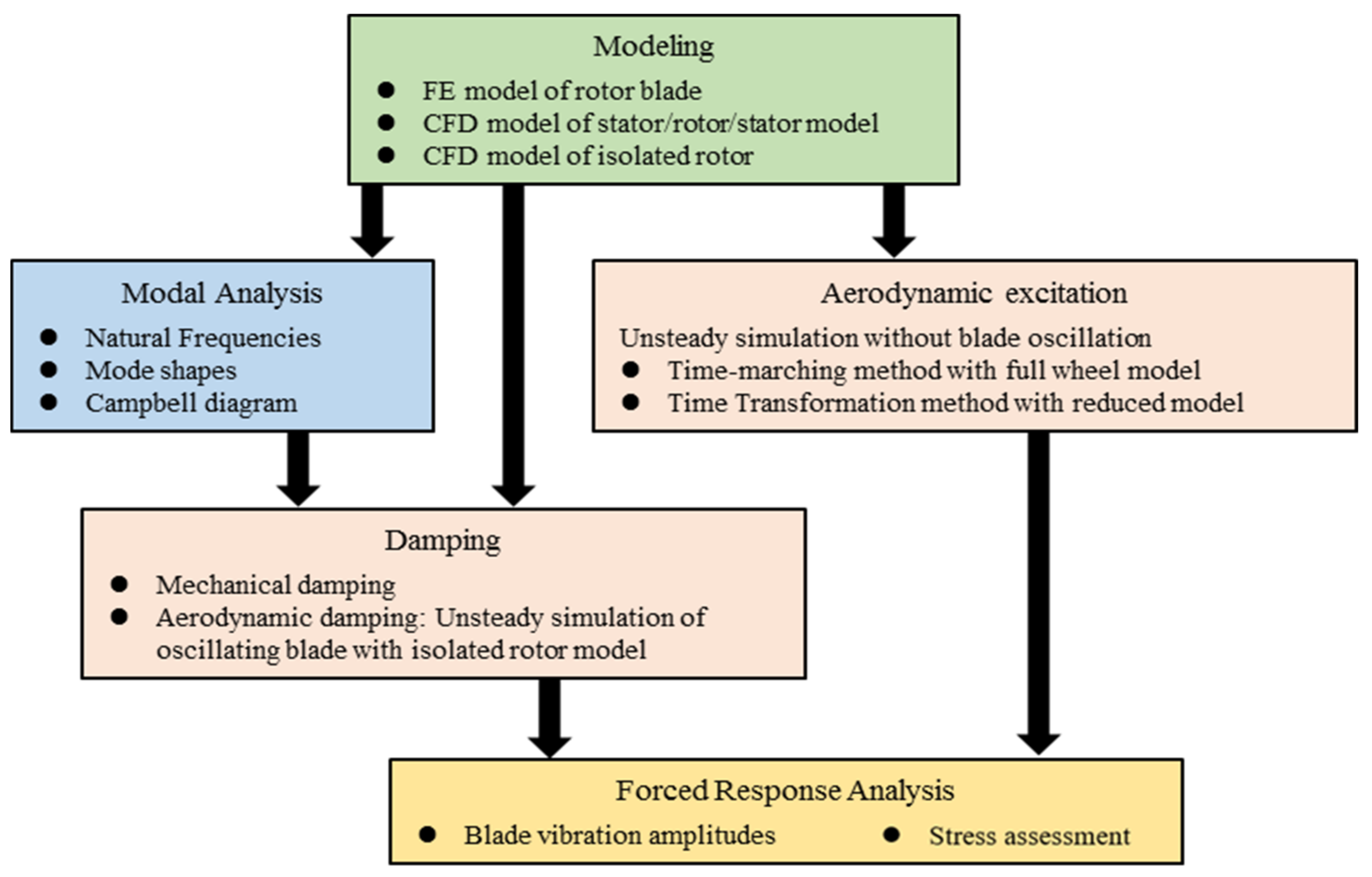
For the prediction of the response levels, a weak coupling approach was applied. It involves CFD simulations to determine the aerodynamic excitation and damping, as well as the FE structural simulations to determine the response levels. The CFD computations were conducted using ANSYS CFX and the structural analyses with the ANSYS mechanical solver. The flow chart of the investigation methodology is depicted in Figure 1.
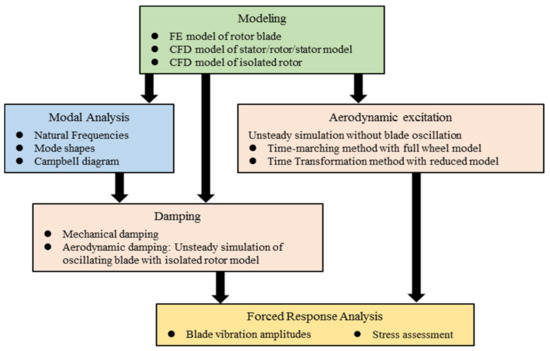
Figure 1.
Flow chart of the investigation methodology.
The first step was to create an FE model, which was utilized to predict the natural frequencies and mode shapes by means of modal analysis. Based on the modal results, a Campbell diagram can be depicted to determine the possible resonance crossings and subsequent investigated conditions. Next, two CFD simulations, the aerodynamic excitation and damping, were required to carry out at the investigated condition based on the CFD models. Then, the predicted excitation and damping were applied to the FE model for the forced response analysis, which provides the information of the vibration amplitude and stress levels. Details about the prediction of the aerodynamic excitation, damping, and response levels are provided in the following part.
2.1. Prediction of the Aerodynamic Excitation
For the transient flow simulation, there are two crucial challenges. One is the treatment of the unequal pitch between blade rows. It can be solved by the full wheel model, but the computational effort is unacceptable for most designers. The second is the pitch-wise periodic boundary condition, which is important for the application of the reduced model. For the unequal pitch challenge, the rotor/stator interface treatment in the TT method is the same as PT method, which stretches or compresses the flow profiles at the interface via flux scaling. However, this leads to a frequency error proportional to the pitch ratio. In the TT method, it is handled by transforming the time coordinates into the transformed time, which also solves the second challenge in an effective phase-shifted form. Details about the treatment are introduced as follows.
The unsteady, two-dimensional Euler equations are used to present the principle of the TT method. The Euler equation in vector form is shown as Equations (1) and (2).
where is the density, and are the velocity components, is the pressure, and and refer to the total energy and enthalpy, respectively.
For an ideal gas with a constant specific heat ratio, the pressure and enthalpy can be expressed as Equations (3) and (4):
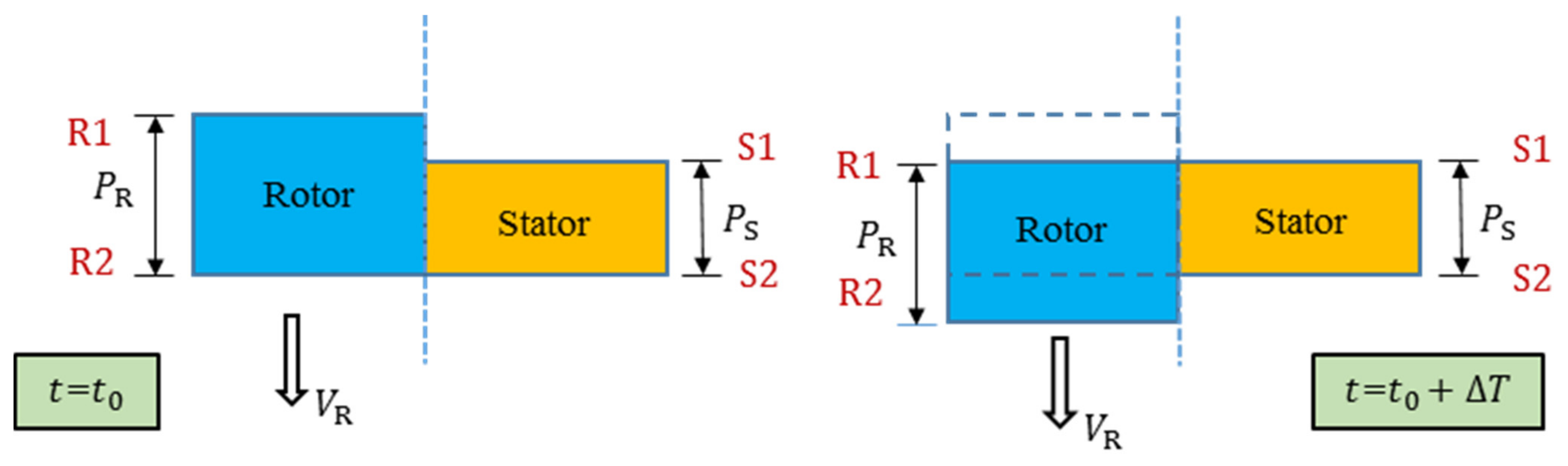
When the stator and rotor pitches are inconsistent, the phase-shifted periodic conditions is applied. It means that the pitch-wise boundaries R1/R2 and S1/S2 are periodic to each other at different times. Figure 2 shows that the relative positions of R1 and S1 at a certain time are the same as those of R2 and S2 at the time . Thus, the flow conditions on rotor and stator boundaries can be given as:
where and are the rotor and stator pitches, respectively, and is the velocity of the rotor.
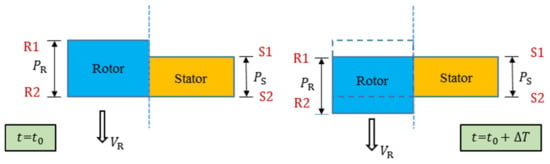
Figure 2.
Phase-shifted periodic boundary conditions.
Then, the set of space–time transformations in Equation (8) was applied to the new coordinate system. It is sloped in time such that if a node at is at time , then the periodic node at is at time . Thus, one can achieve the spatial periodicity simply in this new computational plane with a fixed computational time, as shown in Equations (10) and (11).
where () are the physical spatial coordinates, is the physical time. () are the transformed spatial coordinates, is the transformed time or computational time.
The Euler equations were solved in the transformed space–time domain, which can be written as Equation (12).
The rotor and stator passages have the different period and time-step size , as shown in Equations (13) and (14).
The frequency error then can be resolved by the combination of time transformation applied in the governing equations and the time-step difference at the interface.
2.2. Prediction of the Damping
The damping consists of the mechanical damping and aerodynamic damping. The former mainly includes the material damping and the dry friction damping related to the junction at the structure parts interface. For the blisks, the mechanical damping was very small and can be neglected compared with the aerodynamic damping.
Aerodynamic damping is related to the coupled action between the unsteady forces and blade motion. The unsteady forces are generated by the motion of the blade itself. The aerodynamic damping is calculated by the energy method [22] with the isolated CFD model in this study. It assumes that the blade vibrates at the interested natural frequency, mode shape, and nodal diameter. Then, the unsteady flow and mesh deformation due to the blade vibration can be predicted. Finally, the aerodynamic work in one vibration period was calculated by Equation (15).
where is the vibration period, is the blade surface area, is the pressure on the blade surface, is the velocity, and is the surface unit normal vector.
The aerodynamic damping ratio based on the concept of equivalent viscous damping proposed by Moffatt [23] can be calculated by Equation (16)
where refers to the vibration amplitude in the CFD simulation, and refers to the vibration angular frequency.
2.3. Prediction of the Vibration Response
The basic equation of motion solved by the transient dynamic analysis is:
where , , and are mass, damping, and stiffness matrixes, respectively. , , and are the nodal acceleration vector, the velocity vector, and the displacement vector, respectively. refers to the load vector.
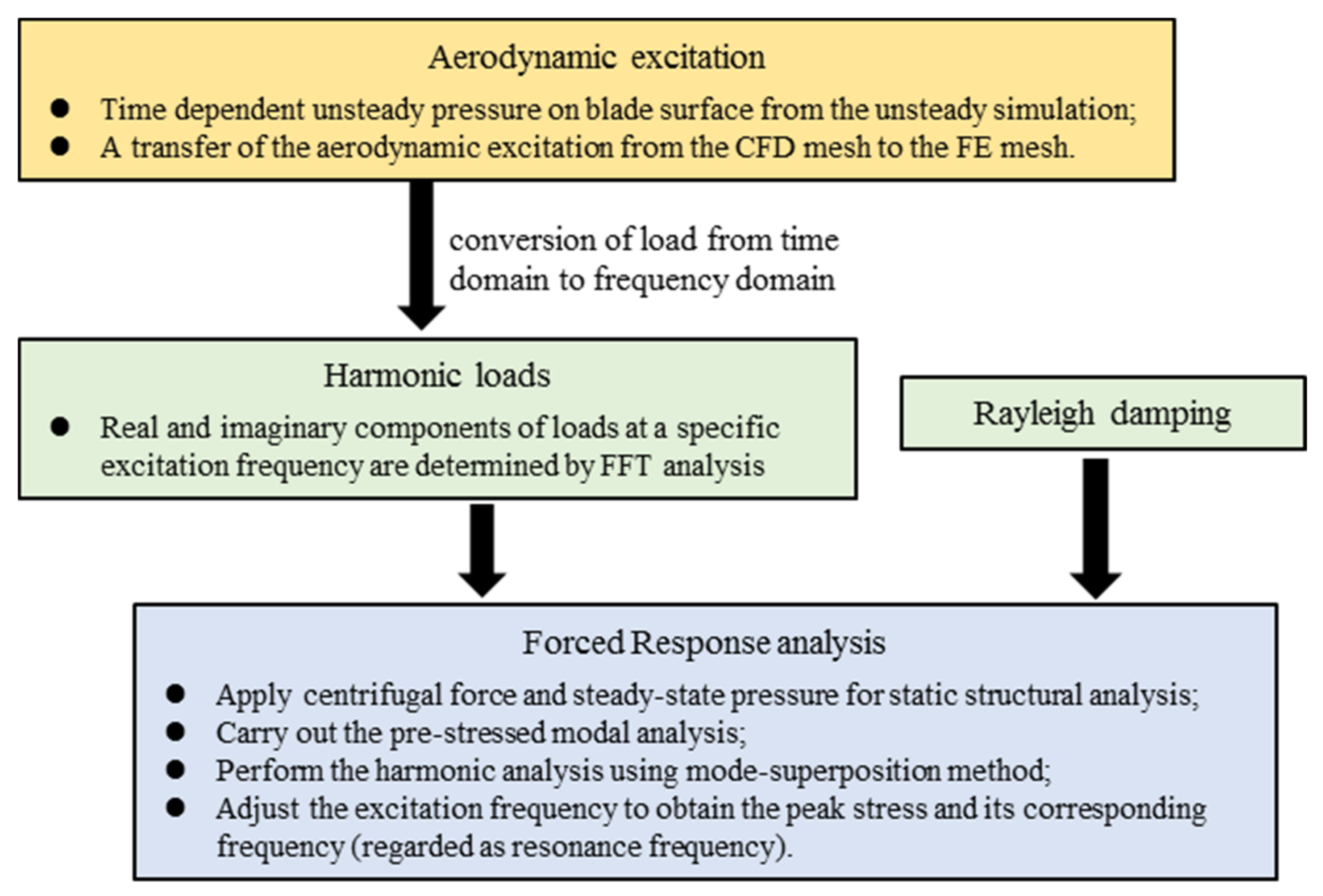
According to the characteristics of the aerodynamic excitations in the forced vibration, nodal forces and displacements can be expressed as multi-harmonics, as shown in Equation (18). This makes it possible to obtain the response level by harmonic analysis, which requires the loads to vary harmonically with time. The harmonic forced-response method solves the response in the frequency domain with harmonic forces from the unsteady simulations; the flow chart of this method is shown in Figure 3.
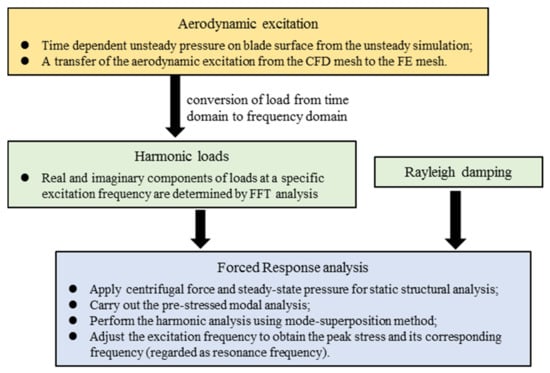
Figure 3.
Flow chart of the harmonic forced-response method.
For the harmonic loads, the information of amplitude, phase angle, and forcing frequency is required. In most cases, only the excitation corresponding to the resonance crossing, such as the first harmonic of the upstream wake excitation here, has attracted much attention. The amplitude and phase angle of the loads are determined by fast Fourier transform (FFT) analysis. The out-of-phase loads are specified in real and imaginary components, as shown in Equation (19). Then, the Equation (17) can be rewritten in Equation (21), which calculates only the steady-state vibration response of the structure.
where:
- and are the amplitude and the phase angle of the loads;
- and are the real and imaginary parts of the loads;
- and are the amplitude and the phase angle of the displacements;
- and are the real and imaginary parts of the displacements.
Besides, the mode-superposition method is used to solve the Equation (21). This projection on the modal space in Equation (22) allows to solve the problem by few modal degrees of freedom.
where is the mode shape matrix and has the form as . refers to the participation of the individual mode shape in the response.
Then, the vibration equation in the modal coordinate can finally be derived as Equation (24):
where , , , and are mass, damping, stiffness, and aerodynamic force matrixes in modal space, respectively.
The damping is modeled as the Rayleigh damping, expressed as Equations (25)–(27).
where is the damping ratio, is the vibration angular frequency, and and refer to the modal orders.
3. Test Case
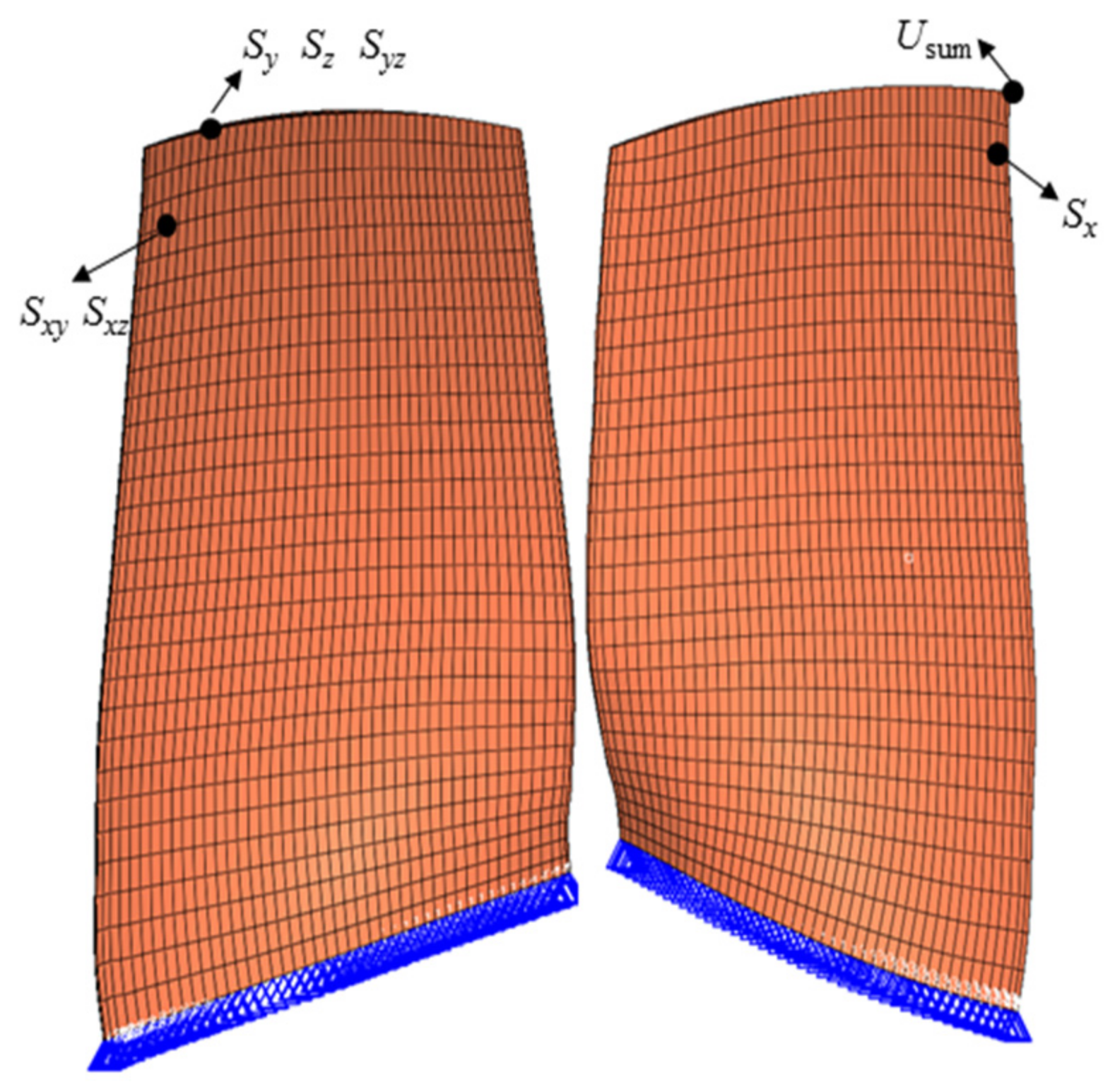
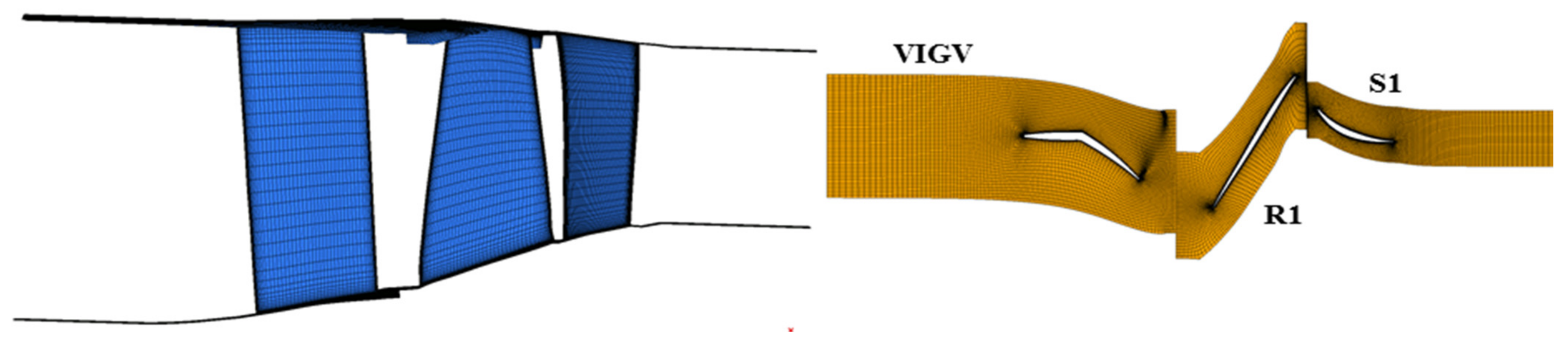
The transonic compressor geometry studied here was a 1.5-stage low-pressure compressor (LPC) with 19 adjustable variable inlet guide vanes (VIGV), 22 rotor blades, and 42 stator blades, as shown in Figure 4. The density of the rotor blade was 4680 kg/m3; the elastic modulus was 112 GPa; and the Poisson’s ratio was 0.313. The FE model of the rotor blade is shown in Figure 5, which was composed of eight-node hexahedral elements. Figure 5 shows the positions of the maximum value of each physical quantity in the response analysis. Fixed boundary conditions were imposed on the blade root. The static structural analysis was performed under the consideration of the centrifugal force. Then, the pre-stressed modal analysis was carried out for various rotational speeds to determine the mode shapes and vibration frequencies.

Figure 4.
Model of the multistage compressor.
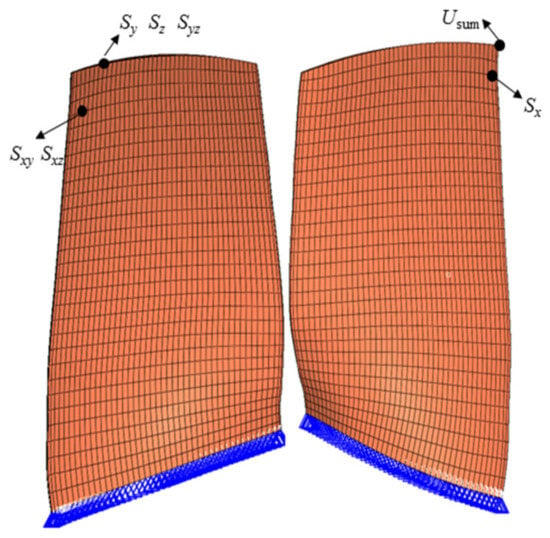
Figure 5.
FE model of the rotor blade.
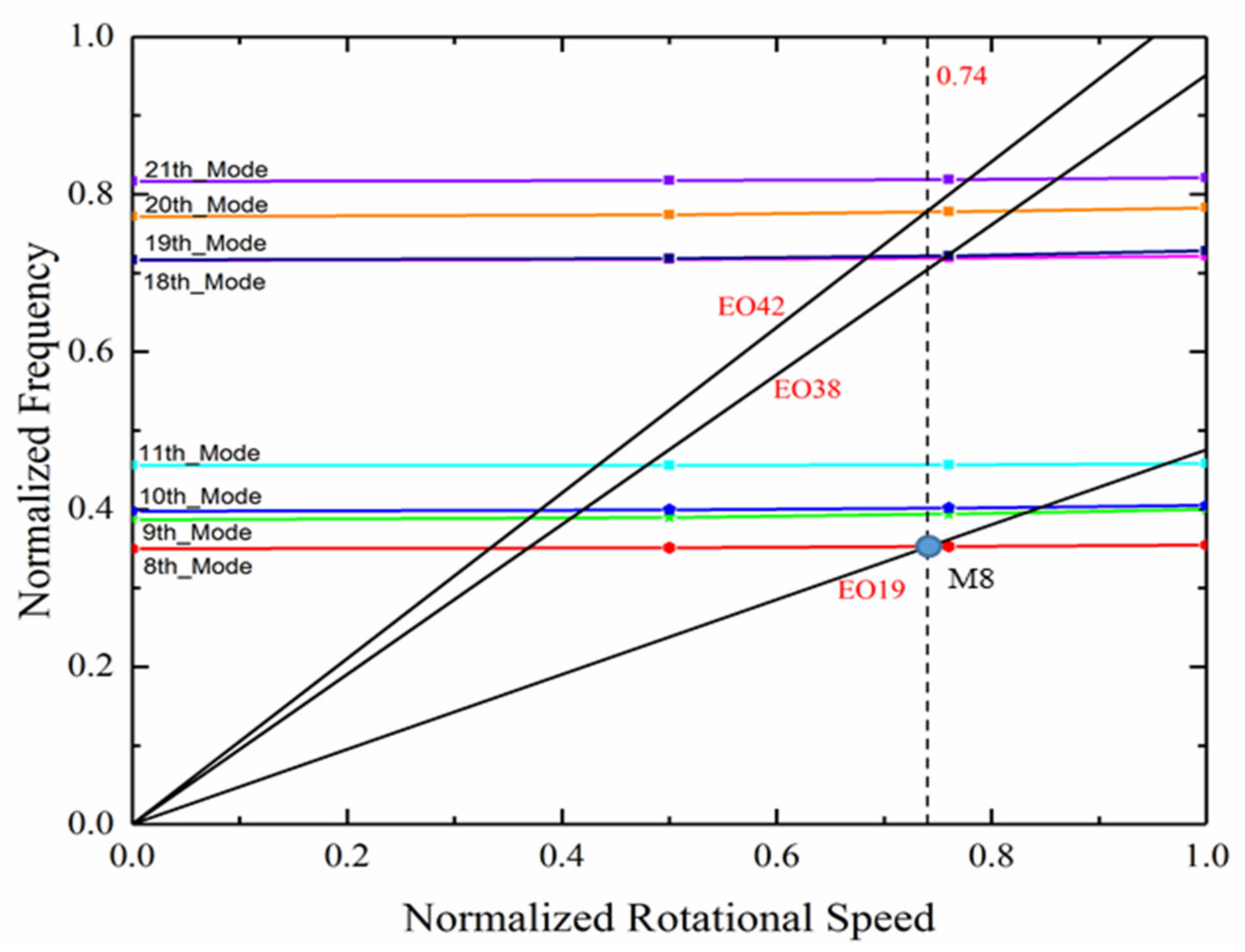
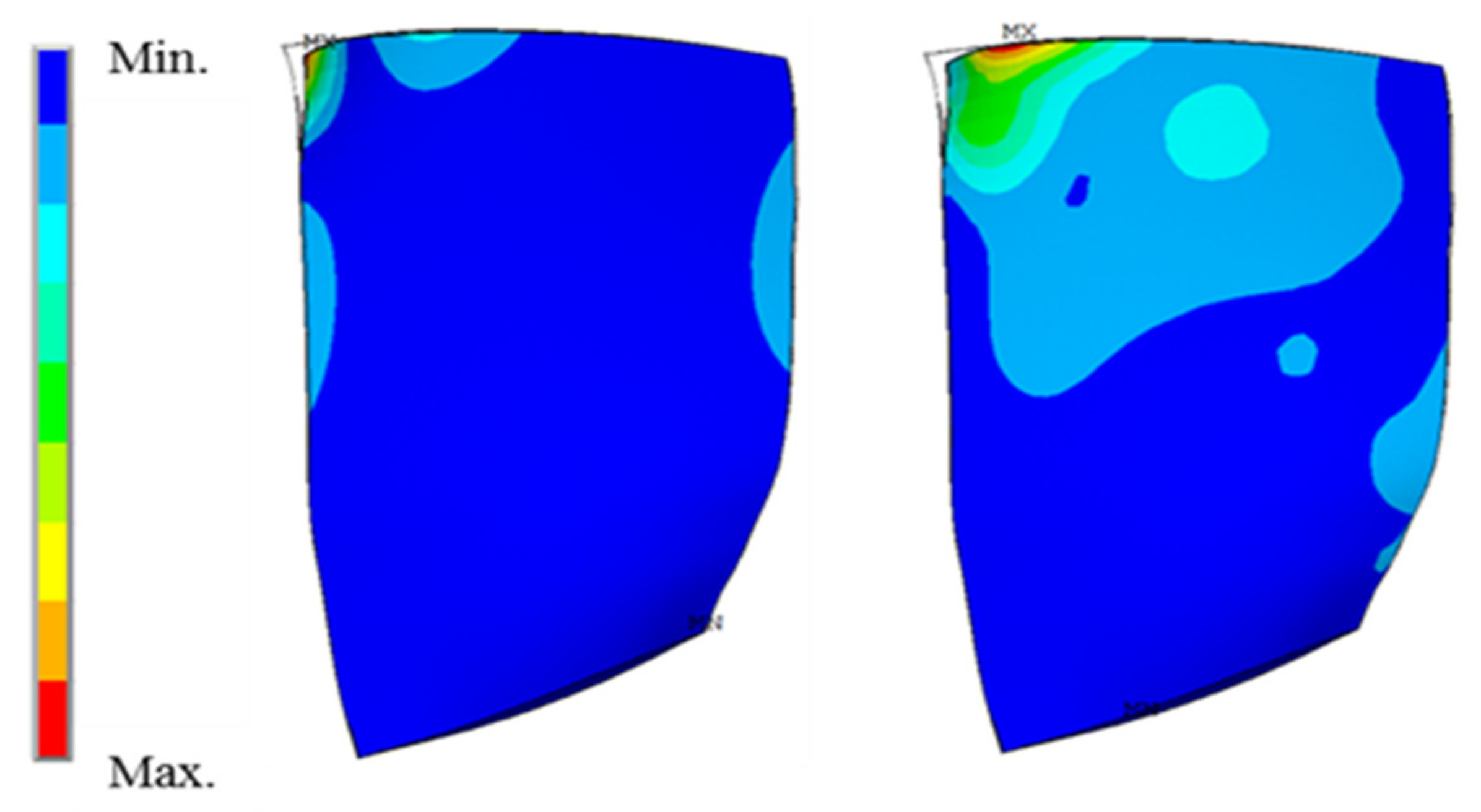
From the results of the modal analysis, the Campbell diagram is illustrated in Figure 6 to determine the operating points for further investigation, in which the rotational speed was normalized by the design rotation frequency and the frequency by an arbitrary value. The possible resonance crossings with the BPF (EO19, EO42) and its multiples (EO38) can be identified within the operating speed range of the compressor. According to the vibration test, the vibration stress was significant at a 74% rotational speed. Thus, it was chosen for the investigation, where the vibration mode M8 occurs due to the upstream wake excitation. The predicted mode shape of the M8 is depicted in Figure 7, which is a high-order mode with a large vibration amplitude near the leading edge at the blade tip region. The comparisons of the different methods were also limited to the resonance rotational speed of 74% rotational speed and the M8 mode.
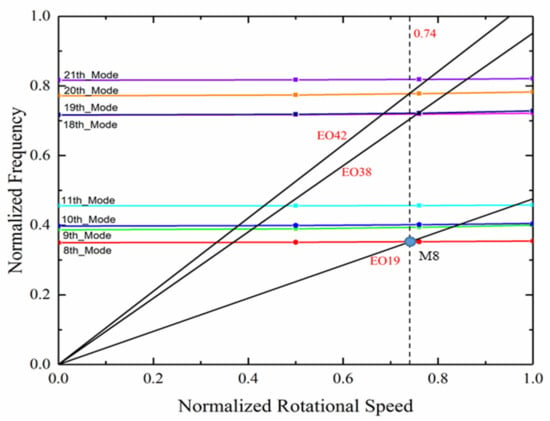
Figure 6.
Campbell diagram for the BPF and multiples.
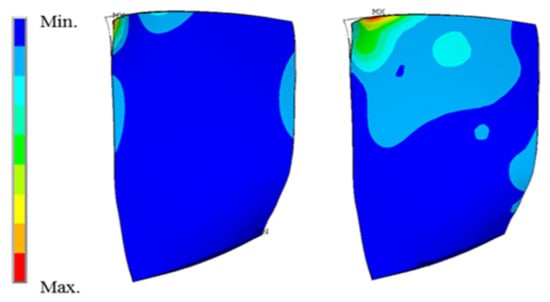
Figure 7.
Rotor blade M8 mode shape (left: total displacement, right: von Mises stress).
4. Results and Discussion
This section follows the presented workflow in Figure 1, whereby the comparison of the two simulation approaches, the TM and the TT method, prediction of the aerodynamic damping, and sections on the validation of the harmonic forced response method are included.
4.1. Aerodynamic Excitation
4.1.1. Steady Simulation
The multi-block hexahedral grids were generated using ANSYS Turbogrid software. A constant tip clearance of 0.63% of the rotor tip chord was modeled in the rotor blade. The inlet and outlet domains were extended away from the stator blades to about 1.5 times the blade chord length. After an additional mesh dependency study, the mesh was illustrated in Figure 8. It contains approximately 450,000 nodes for each passage, with a suitable near wall thickness for the turbulence model. All CFD computations were simulated as an ideal gas with the second-order spatial and temporal discretization. A mixing-plane interface was used for the rotor/stator connection in the steady simulation. A non-slip and adiabatic wall condition was set for all walls. The inlet boundary conditions were specified with constant total pressure, total temperature (101325 Pa, 288.15 K), and axial inflow. The average static pressure boundary was used to traverse the speedline from choke to near stall.
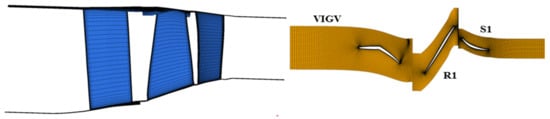
Figure 8.
Computation mesh for the CFD simulation.
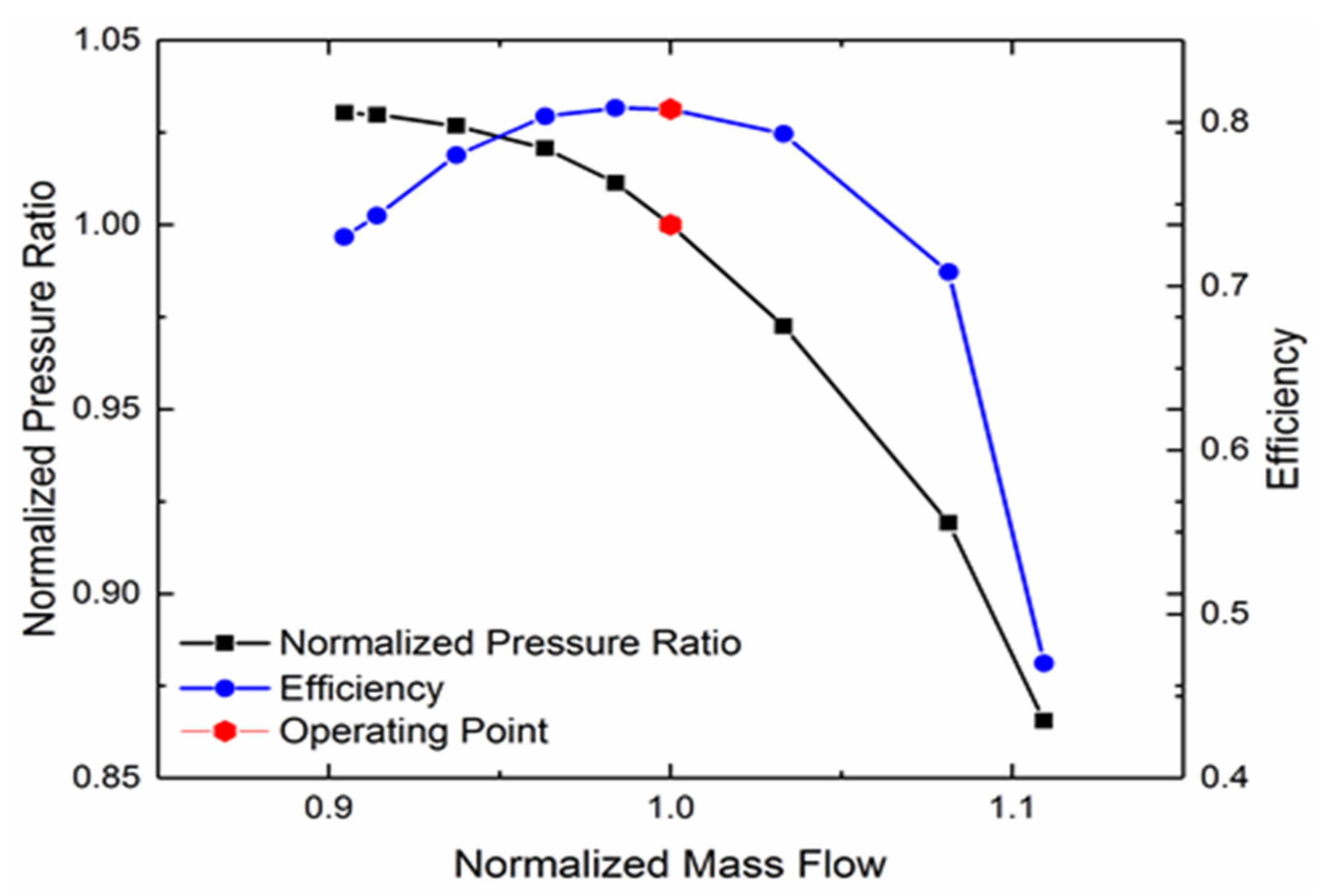
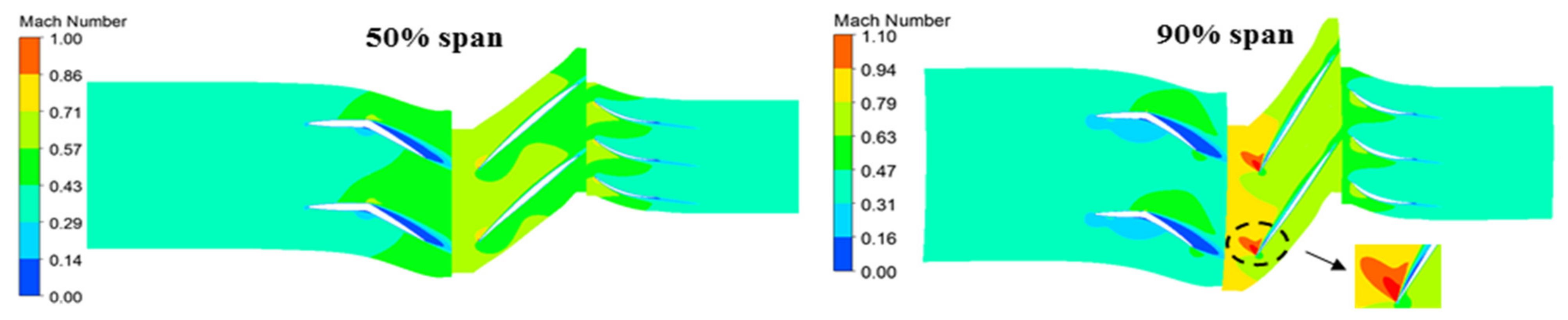
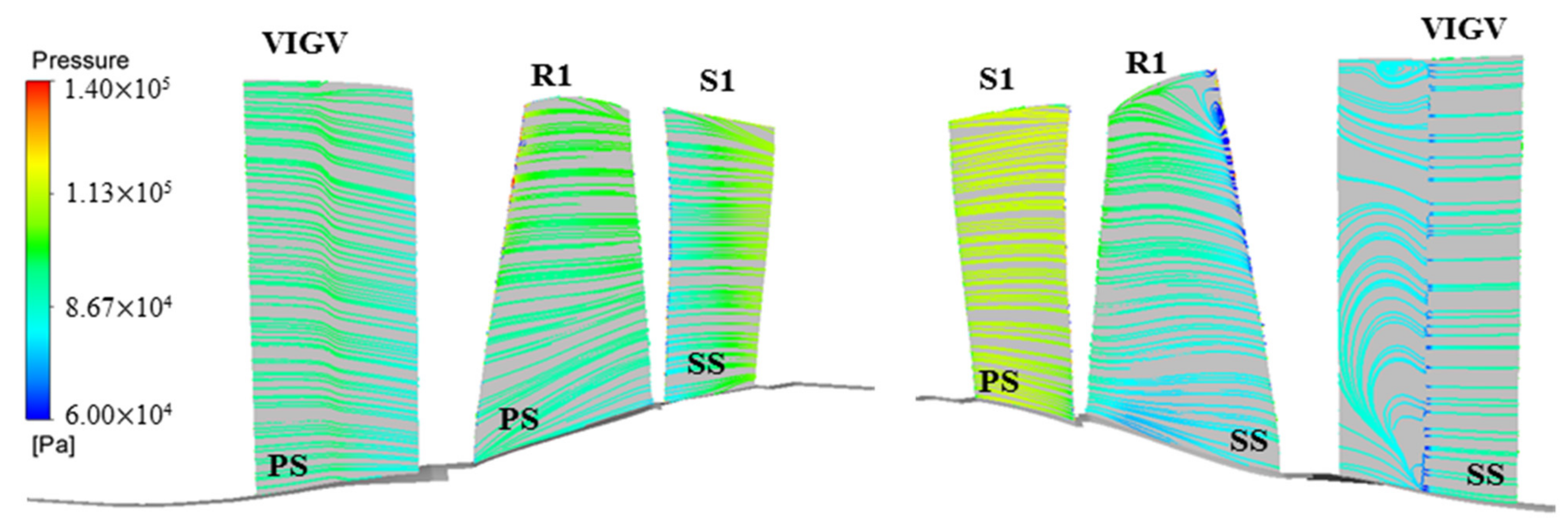
The performance map for the 1.5 multistage compressor at the 74% rotational speed was computed, and the operating point was determined based on the experimental data, as shown in Figure 9. It was normalized by the mass flow and pressure ratio at the operating point. It can be seen that the efficiency of the operating point was almost the highest. For a better understating of the flow properties at the operating point, the Mach number and surface streamline distributions are given in Figure 10 and Figure 11. It can be observed that due to the low rotational speed, there was no shock wave in the passage, and most areas were subsonic flow. In addition, obvious low-speed regions existed after the rotating axis of the VIGV and the leading edge of the R1 at the suction surface. The range of the low-speed region became larger with the increase in the blade span. From the streamline distribution, it can be intuitively seen that large-scale separation occurs at the suction surface of the VIGV and the leading edge of the R1 in the tip region, which was accompanied by the intense three-dimensional radial flow.
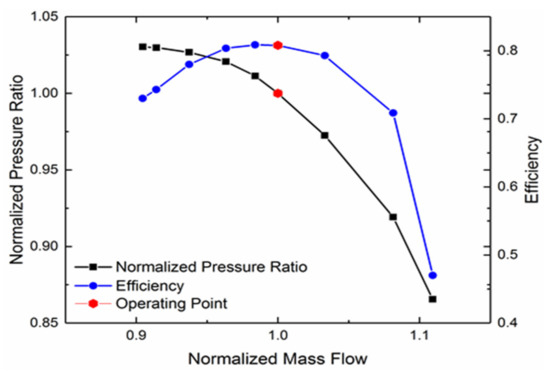
Figure 9.
Performance map for the multistage compressor.
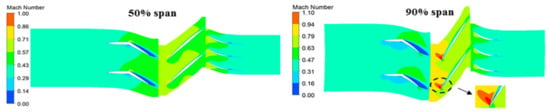
Figure 10.
Mach number distribution of the operating point.
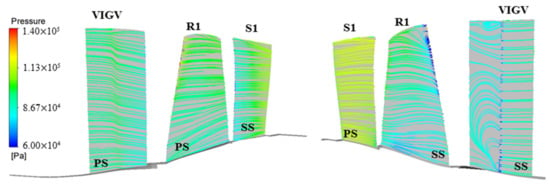
Figure 11.
Streamline and pressure distribution of the operating point.
4.1.2. Unsteady Simulation
For the unsteady simulation, two models of the 1.5 multistage compressor were created depending on the TM and TT methods. One was a 360 deg full-annulus model for the TM method, consisting of 19, 22, and 42 passages per row. A sliding interface was used for the rotor/stator connection. The other contains only a single flow passage both for the VIGV and R1, as well as two passages for the S1 for the TT method. The time transformation treatment was used for the rotor/stator interface. In order to capture the dominant blade passing frequencies from the VIGV and S1 on the rotor blade, the temporal discretization of 1596 timesteps per revolution was defined for the unsteady simulations, which corresponds to a resolution of 84 timesteps per VIGV pitch and 38 timesteps per S1 pitch. All simulations were performed for four revolutions to ensure the convergence of the solution. They used identical conditions except for the rotor/stator interface treatment.
The relative computational effort for the TT and TM methods are listed in Table 1. The TT method led to a significant reduction in mesh nodes by a factor of 20.7. The memory consumption refers to the memory required to store the computing solutions in one common period (one revolution). Obviously, the TT method was much faster than the TM method considering solely the mesh nodes reduction, as listed in Table 1. In fact, the computational efficiency of the TT method was higher, because the TT method converged faster.

Table 1.
Comparison of computational effort.
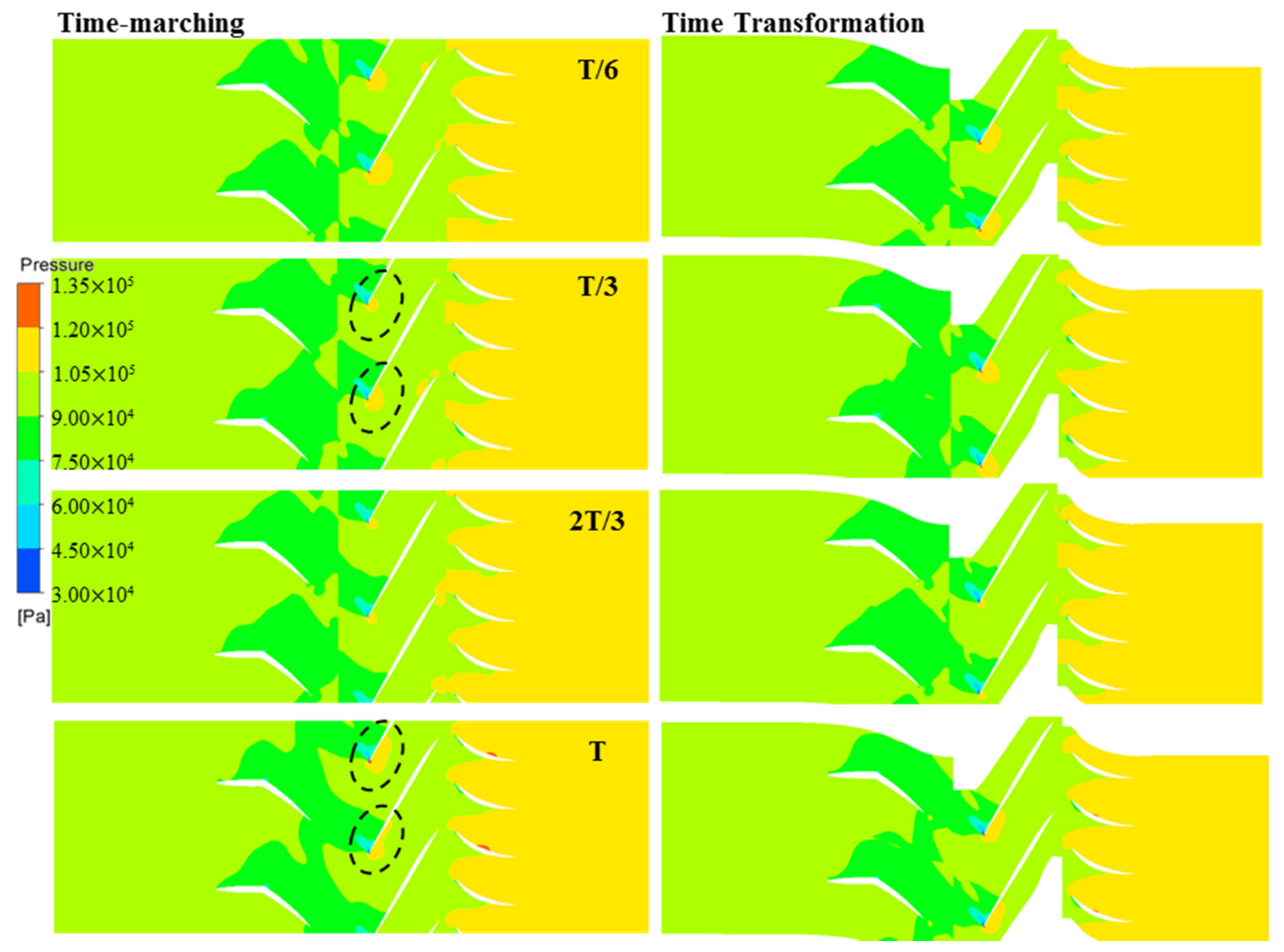
For the forced response analysis, it was important to validate the predict accuracy of the unsteady pressure and the dominant BPF from the VIGV and S1 on the rotor blade. An accurate prediction at the tip region was crucial for the evaluation of the aerodynamic excitation because most vibration modes showed significant amplitudes at this location. Four characteristic time steps were selected to compare the pressure distributions at the 95% span from the TM and TT methods, as shown in Figure 12. The transient interaction of the stator wake with the rotor at the interface showed a good agreement. The largest difference between the two methods is that the TM method presented non-uniformity along the circumferential direction (as shown in the dotted circle); however, the TT method cannot simulate this phenomenon. While there are some differences in detail, the predicted flow properties were very similar.
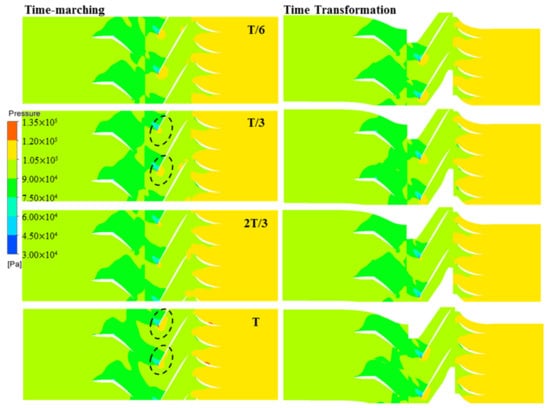
Figure 12.
Comparison of instantaneous pressure distributions at the 95% span.
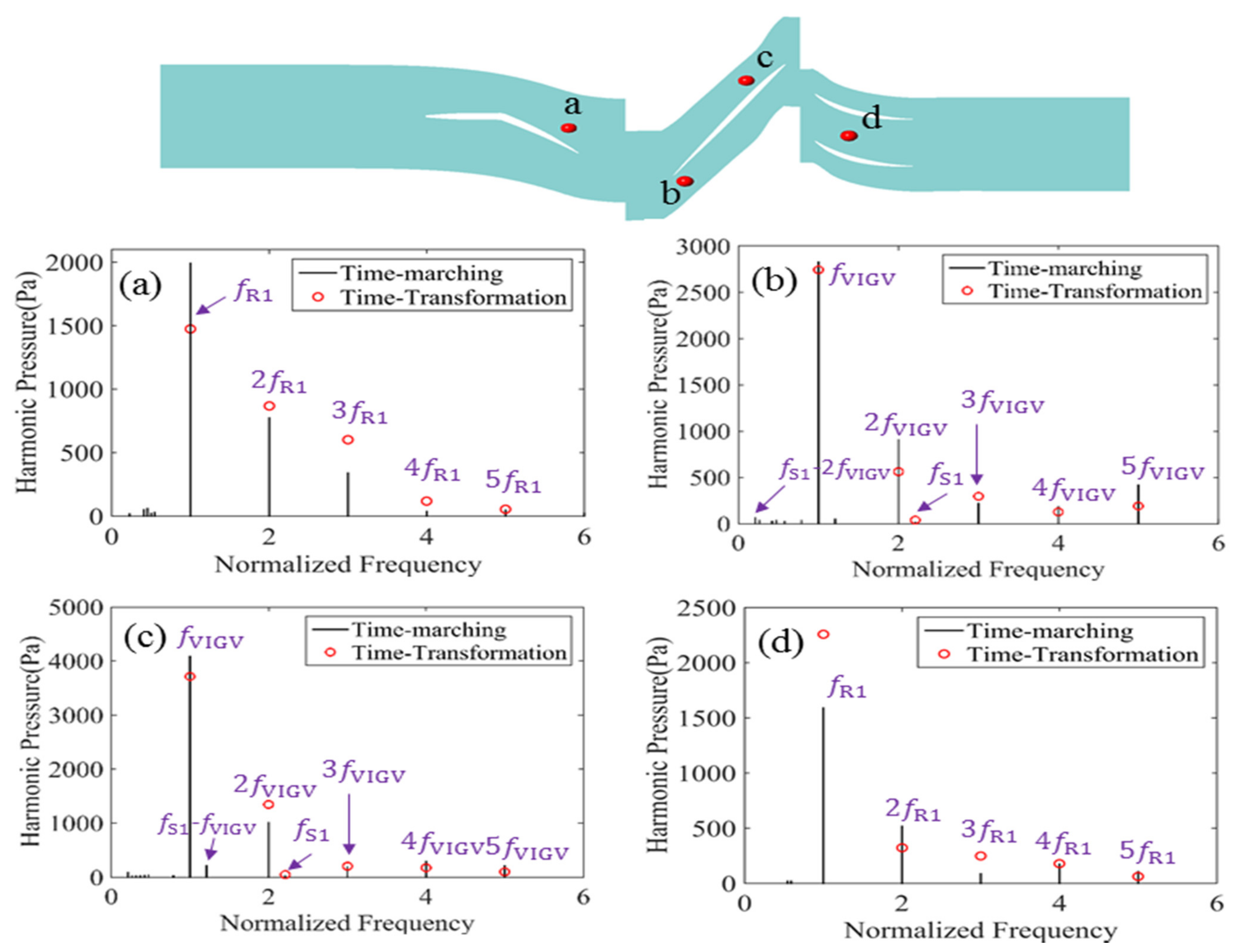
After the comparison of the flow field simulation, closer attention to the frequency capture ability was also required. The time-resolved pressure data for a single revolution were transferred into the frequency domain by an FFT analysis, as shown in Figure 13. Based on the results in Figure 12, four monitors placed at the 95% span were selected. One monitor was placed at the VIGV passage at an approximately 85% axial location, while the others were placed in the rotor passage at the 35%, 70%, and, in the S1 passage, at the 15% axial locations. Again, comparisons between the TM and TT methods were made. The spectrum of the pressure had a good agreement and showed the influence of the corresponding BPF as well as its harmonics, as expected. At the stator monitors (a and d), the rotor passing frequency and higher harmonics were captured in both the TM and the TT methods. At the rotor monitors (b and c), the signals were much more complex from both the interaction of the VIGV and S1. The TT predictions were close to the TM solution but had a loss of some harmonics, such as the linear combination of and .
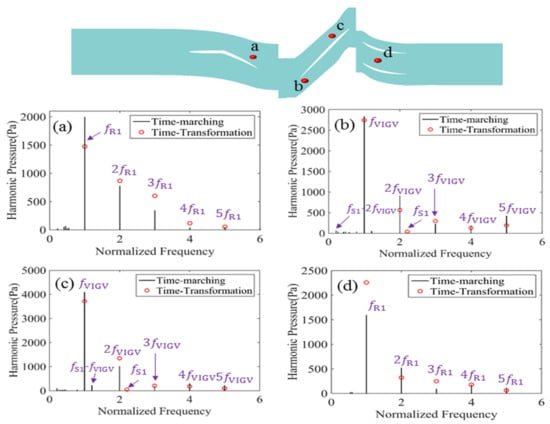
Figure 13.
Comparison of the pressure spectrum for the four monitors.
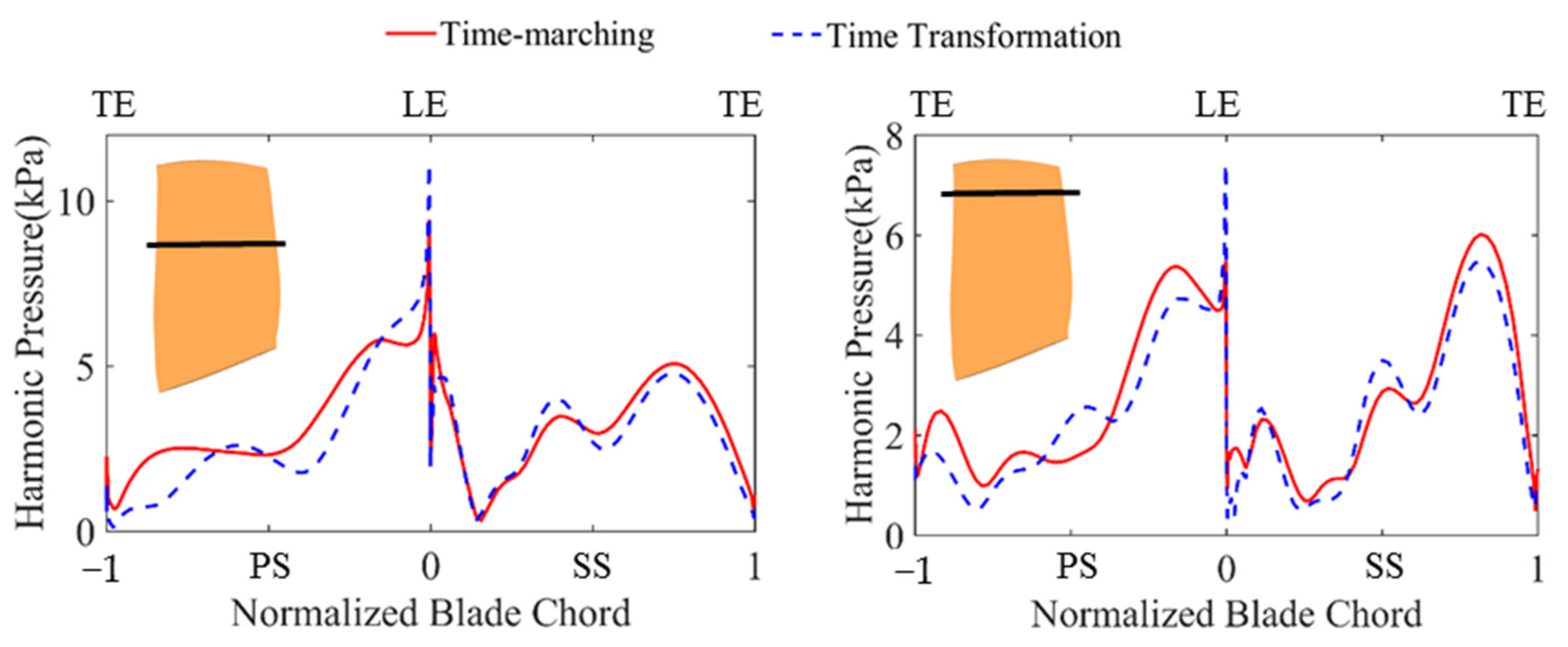
The harmonic pressure amplitude from the VIGV wake, which was responsible for the blade excitation for the M8 mode, was compared by the two methods at 65% and 90% spans, as shown in Figure 14. A better accordance with the TM method can be observed at the suction surface. Though, the amplitude showed relevant differences at the pressure surface, the comparison showed qualitatively the same distribution along the blade chord.
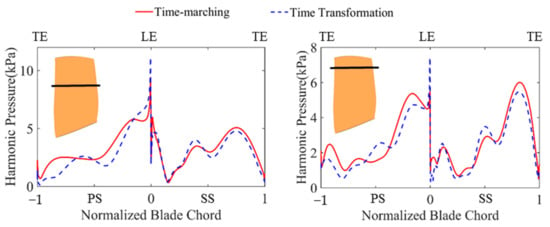
Figure 14.
Harmonic pressure amplitude at 65% span (left) and 90% span (right).
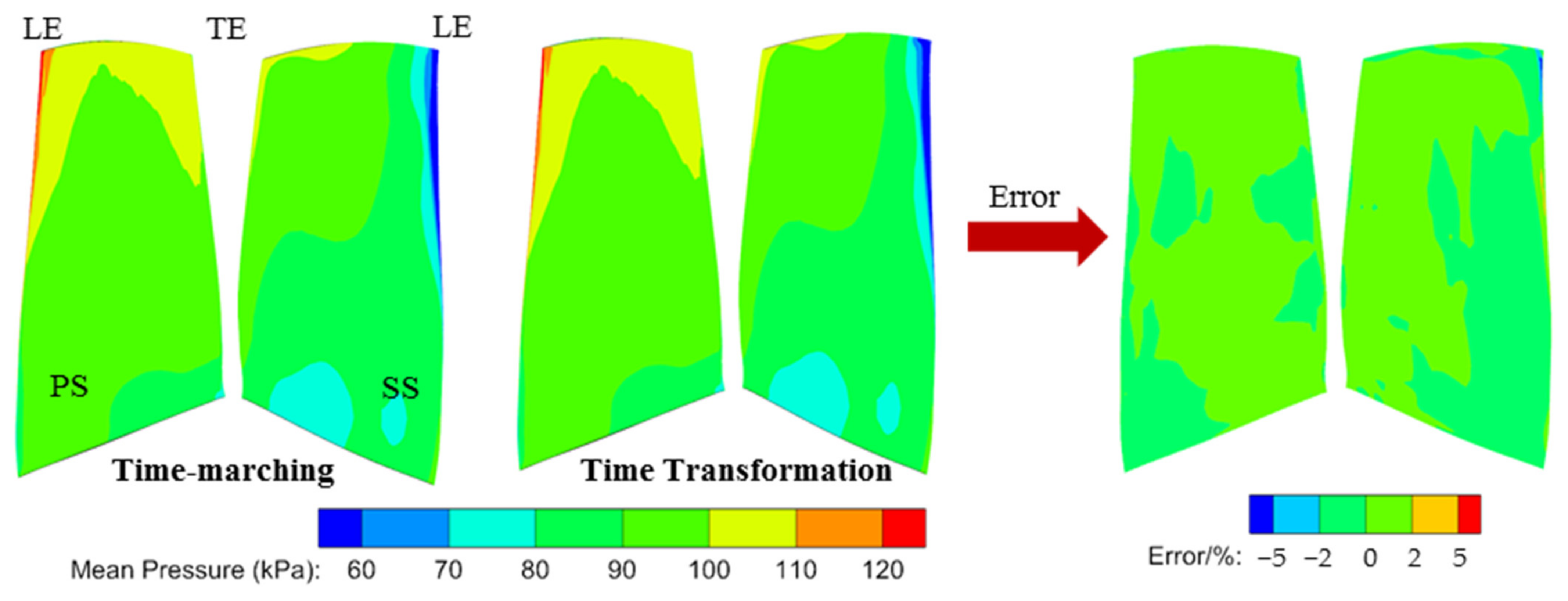
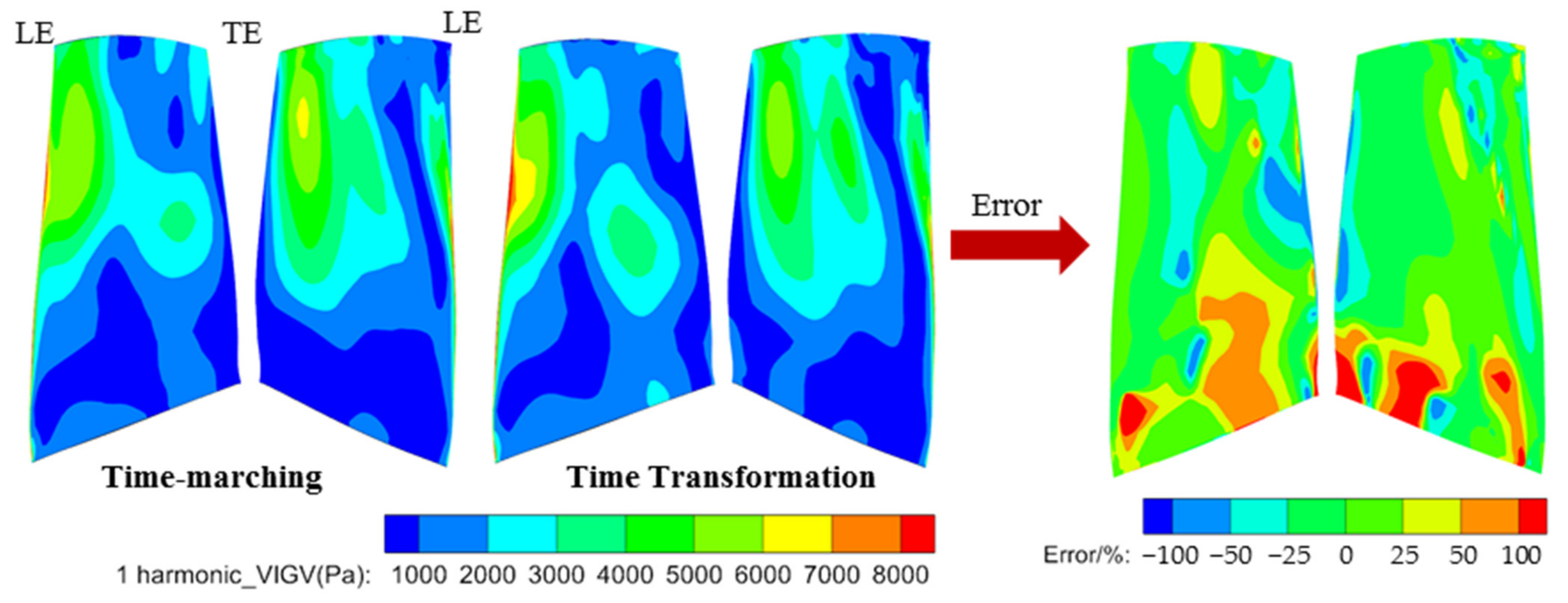
For further comparison, the distributions of the mean pressure and harmonic pressure from the VIGV wake on the whole rotor blade surface are given in Figure 15 and Figure 16. It showed an excellent agreement at the mean pressure distribution, and the error in most areas was in the range of −2% to 2%. In terms of the harmonic pressure, it could be observed that the TT method delivered some deviations compared with the TM method. In the critical area for the M8 mode, the tip region near the leading edge, the TT method delivered a similar prediction on the blade surface with the TM method. There was a discrepancy of 25% at most positions expect for the blade root. Fortunately, the harmonic pressure amplitude was small and the vibration amplitude close to zero at these locations, which would not affect the vibration at the tip region.
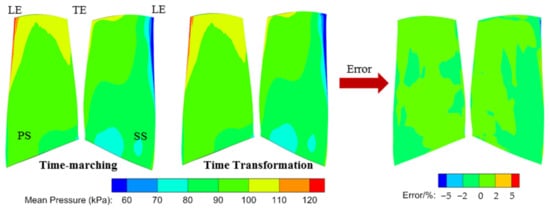
Figure 15.
Mean pressure amplitude distribution of rotor blade, error = (.
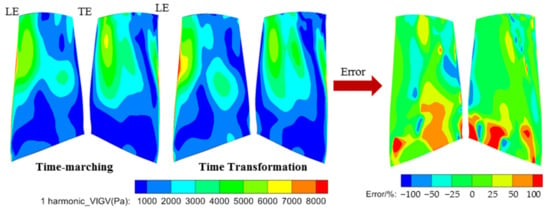
Figure 16.
Harmonic pressure amplitude distribution of rotor blade, error = (.
This was a highly encouraging result, since the TT method consists of only 4 passages, whereas the TM method requires 83 passages. Given the acceptable relative deviation of the harmonic pressure and the highly reduced computational time, the TT method can be utilized to predict the aerodynamic excitation for the forced response analysis.
4.2. Aerodynamic Damping
An isolated rotor model with two passages was created for the aerodynamic damping calculation. The boundary conditions, including the total pressure, total temperature, flow velocity for the inlet boundary, and the static pressure for the outlet boundary, were extracted from the steady simulation at the operating point. The global maximum vibration amplitude of the blade was imposed at approximately 0.3% of the tip chord length.
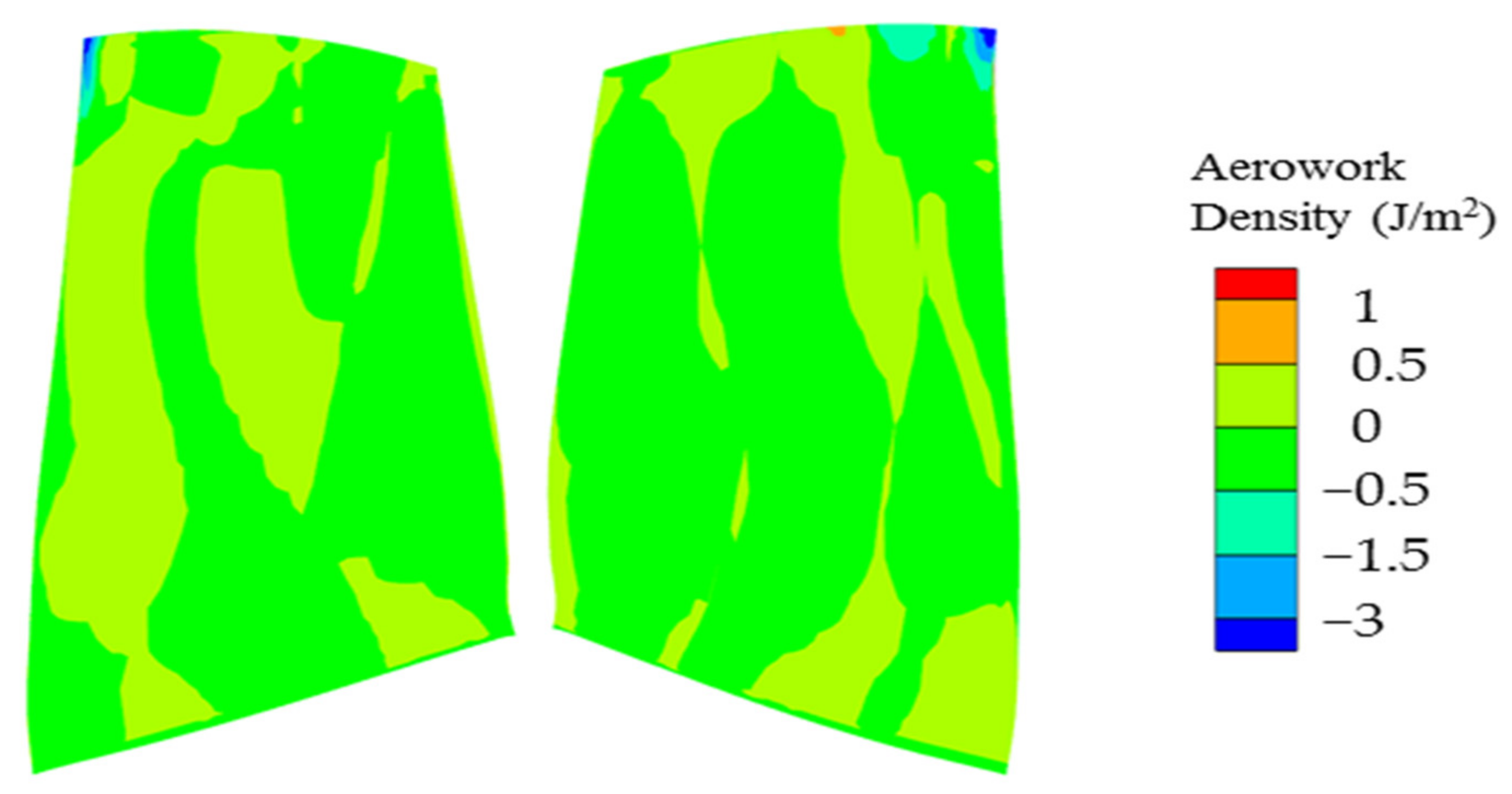
It was set to resolve only one frequency and mode shape by the energy method presented in Section 2.2, corresponding to the investigated resonance crossing M8 mode. Furthermore, according to the resonance theory [24], only a nodal diameter of three can be excited for the resonance crossings with the EO19, and the wave type was a forward-traveling wave (FTW). Figure 17 represents the aerowork density distribution for the nodal diameter of three. It is clear that the aerowork density at most areas was close to zero, except that there was a large negative aerowork density at the leading edge in the tip region, which corresponds to the position with large vibration amplitude of the M8 mode. This led to a positive damping ratio of 0.3%.
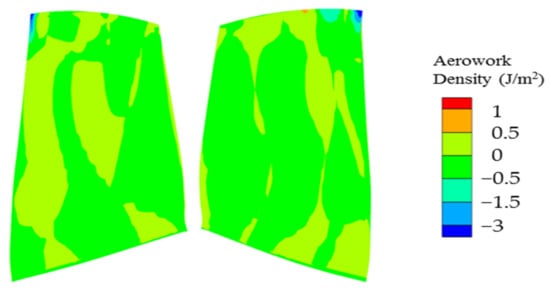
Figure 17.
Aerowork density distribution on blade surface for ND = 3 (FTW).
4.3. Harmonic Forced Response
In this study, the normal component of forces resulting from the static pressure was taken into account for the aerodynamic excitation. For the forced response analysis, a transfer of the aerodynamic excitation from the CFD mesh to the FE mesh was required. In the Ansys mechanical software, the X, Y, and Z components needed to be given for the force loading. In the process of interpolation, the nearest neighbor approach can ensure that the value of the variable is credible. However, the deviations of the force directions might occur. Thus, the pressure interpolation was applied, which can automatically load along the normal direction of the blade surface in the software.
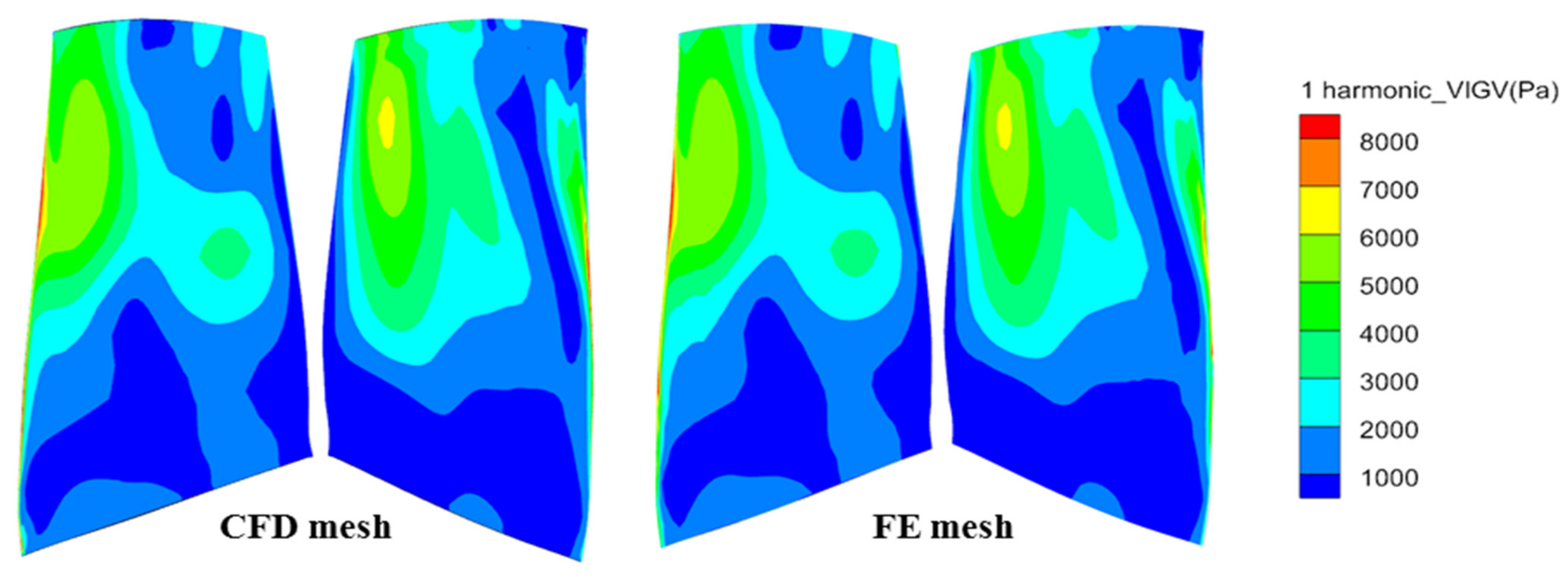
A transfer of the harmonic pressure of the EO19 from the CFD simulation to the FE mesh is depicted in Figure 18. The comparison shows excellent agreement between the CFD and FE mesh with the pressure interpolation.
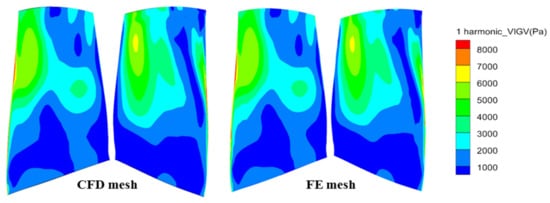
Figure 18.
Comparison of the pressure interpolation.
According to the results of the aerodynamic damping ratio, the Rayleigh damping coefficients and in Equation (25) were calculated by giving the damping ratio of the M8 and M9 modes as 0.3%. Due to the effect of damping and aerodynamic forces, the vibration frequency of the structure will change compared with Figure 6, resulting in the offset of the resonance point. In order to obtain the peak stress concerned in response analysis, several calculations were carried out near the predetermined resonance frequency. In the calculation, assuming that the aerodynamic excitation and damping remained unchanged, the excitation frequency was changed at an interval of 0.5 Hz, and finally the peak stress as well as its corresponding frequency (regarded as resonance frequency) could be obtained.
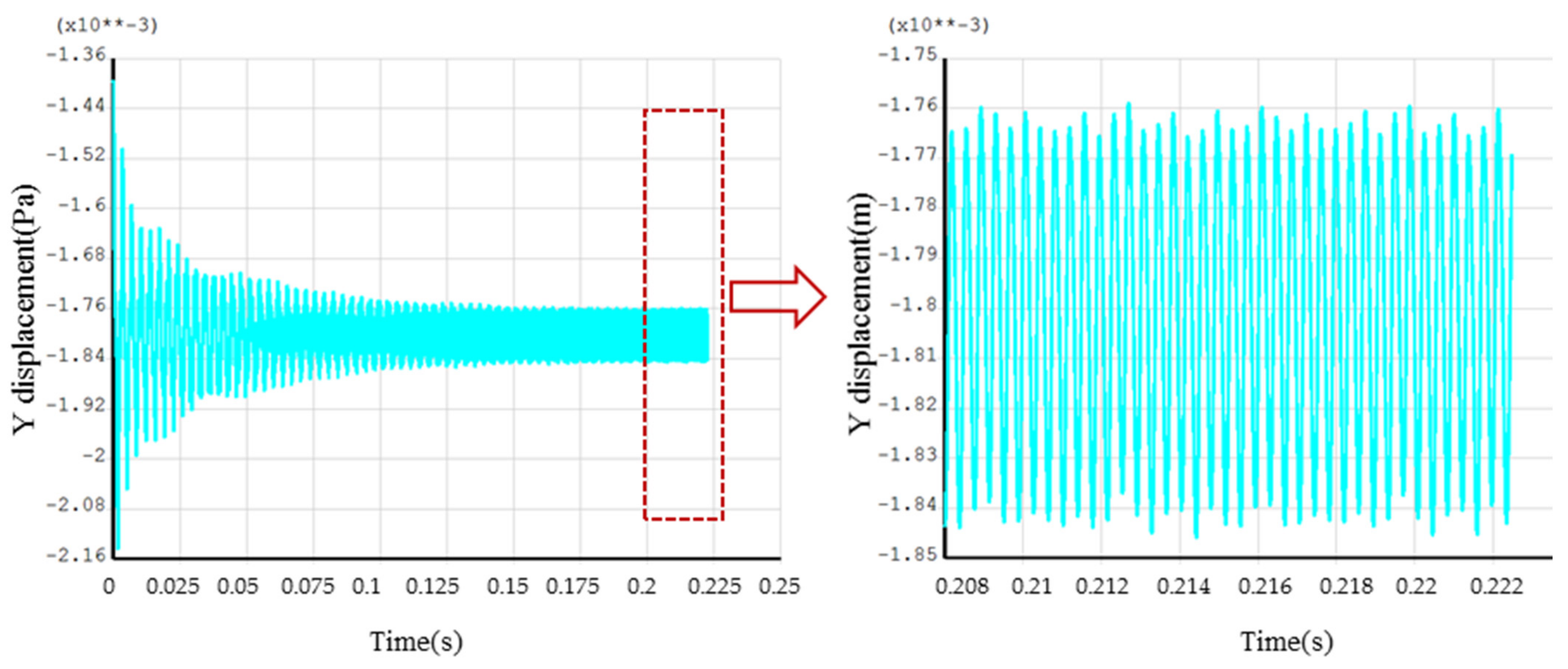
For the transient dynamic method, the aerodynamic excitation was determined as 1596 time-steps per revolution, corresponding to 84 steps in one period for EO19 excitation, which can ensure the accuracy of the calculation results. In order to ensure the convergence of the simulation, a total of 30 cycles were applied. Figure 19 shows the convergence history of the monitor in Figure 5. It can be seen that the results are convergent, indicating that the choice of calculation cycle was appropriate. The subsequent spectrum analysis extracted the stable results for the FFT analysis.
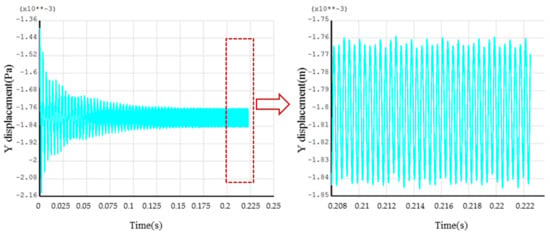
Figure 19.
Convergence of transient dynamic calculation.
For the harmonic forced response method, the result did not depend on the time-steps but on the selected modes. All modes need to be considered in theory to obtain accurate response results, but this is unrealistic. For the M8 mode resonance concerned in this study, the 10, 20, and 50 modes were selected to describe the response characteristics of the blade. The results showed that the stress difference between the 10 and the 50 modes was about 5%, and the difference between the 20 and the 50 modes was less than 1%. Therefore, the subsequent analysis used the 20 modes for calculation.
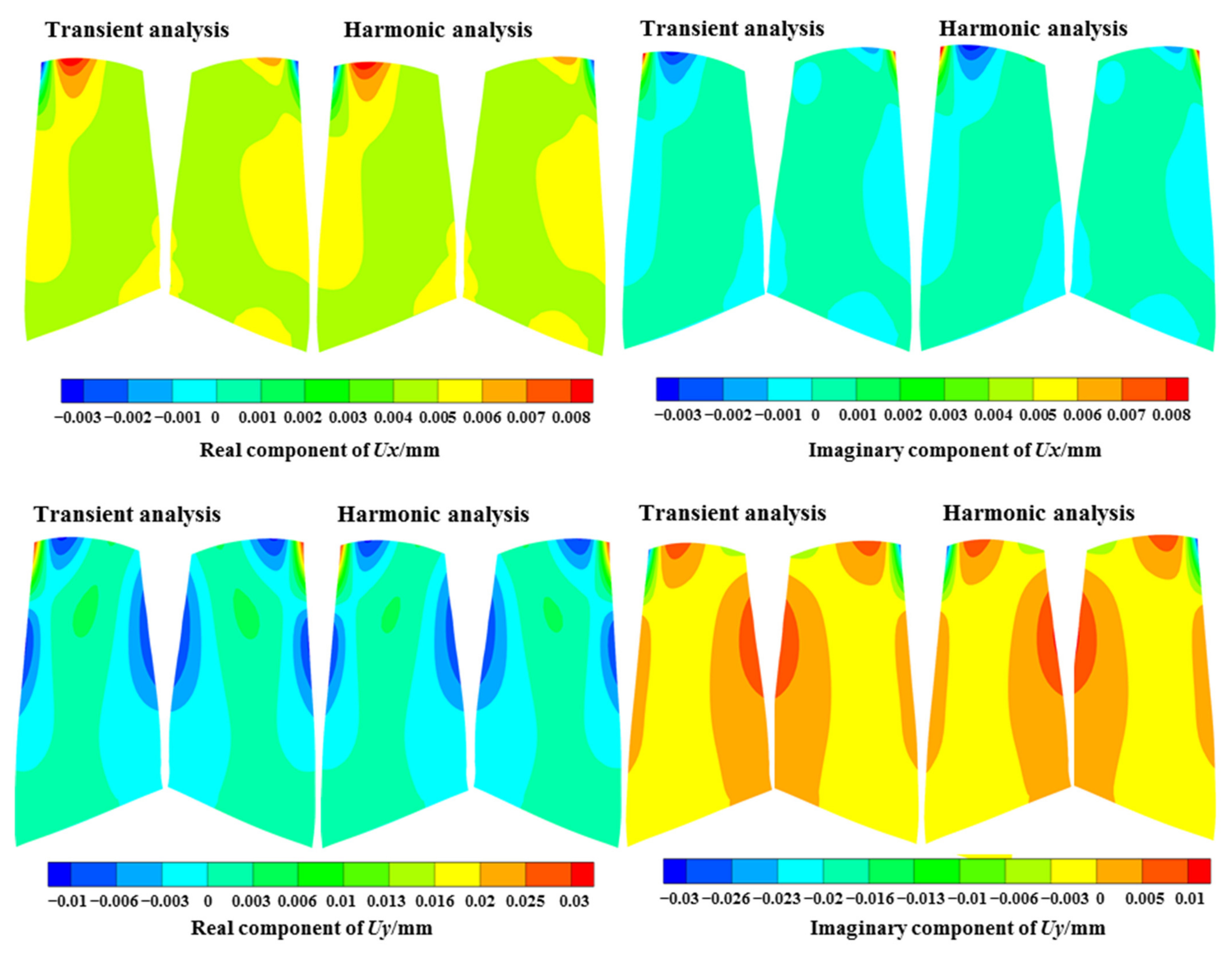
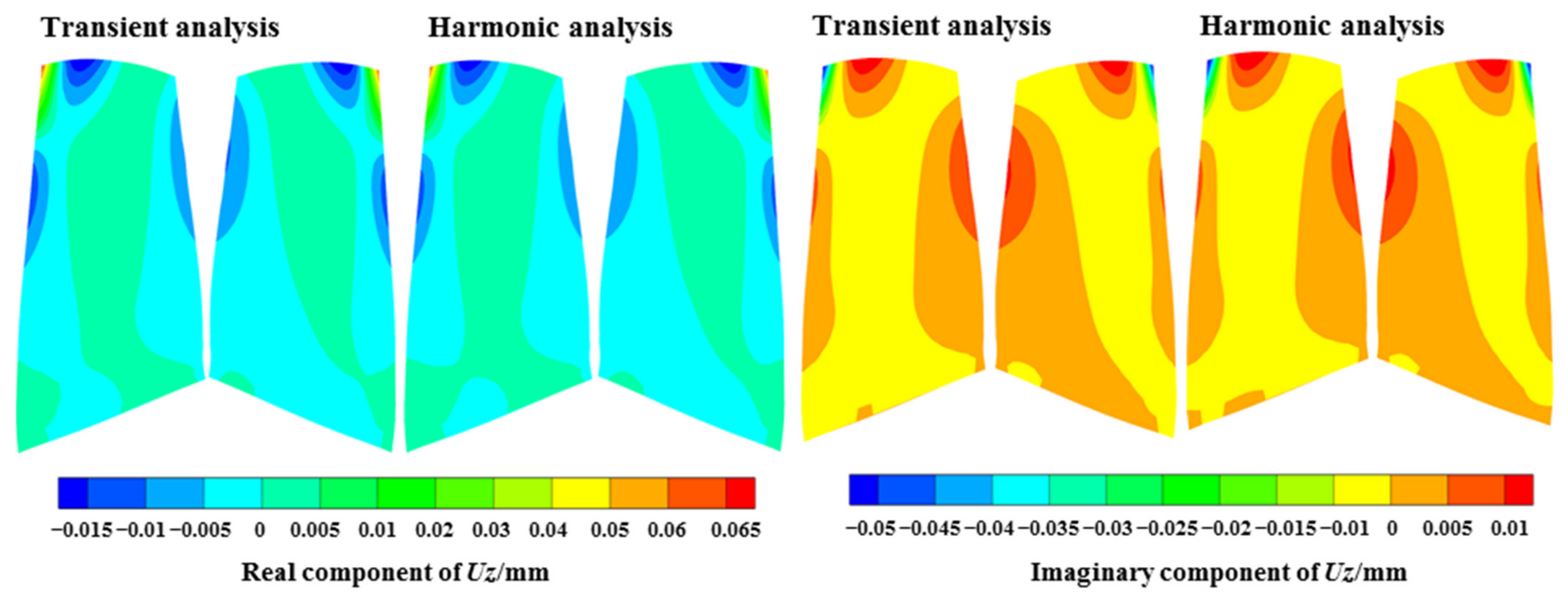
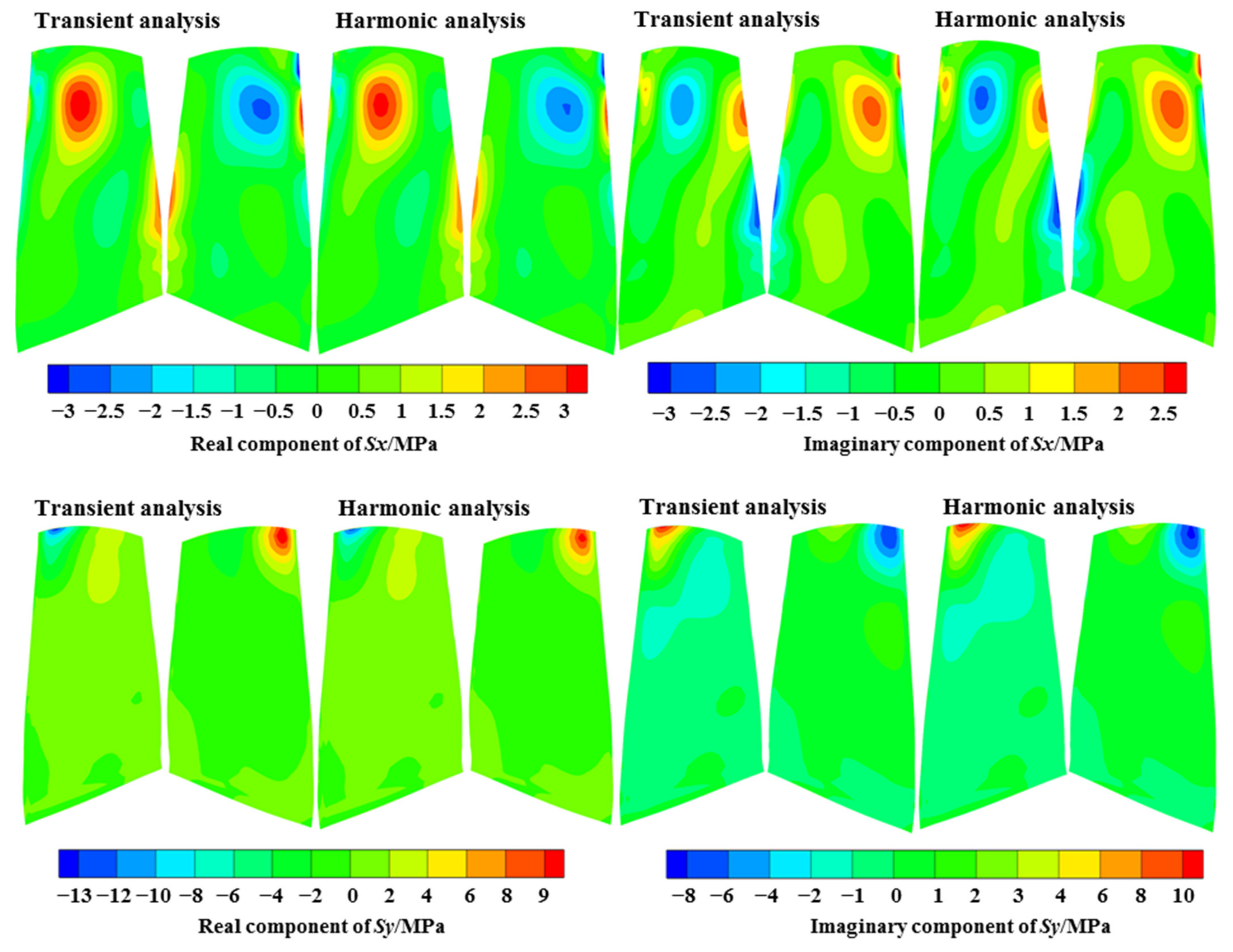
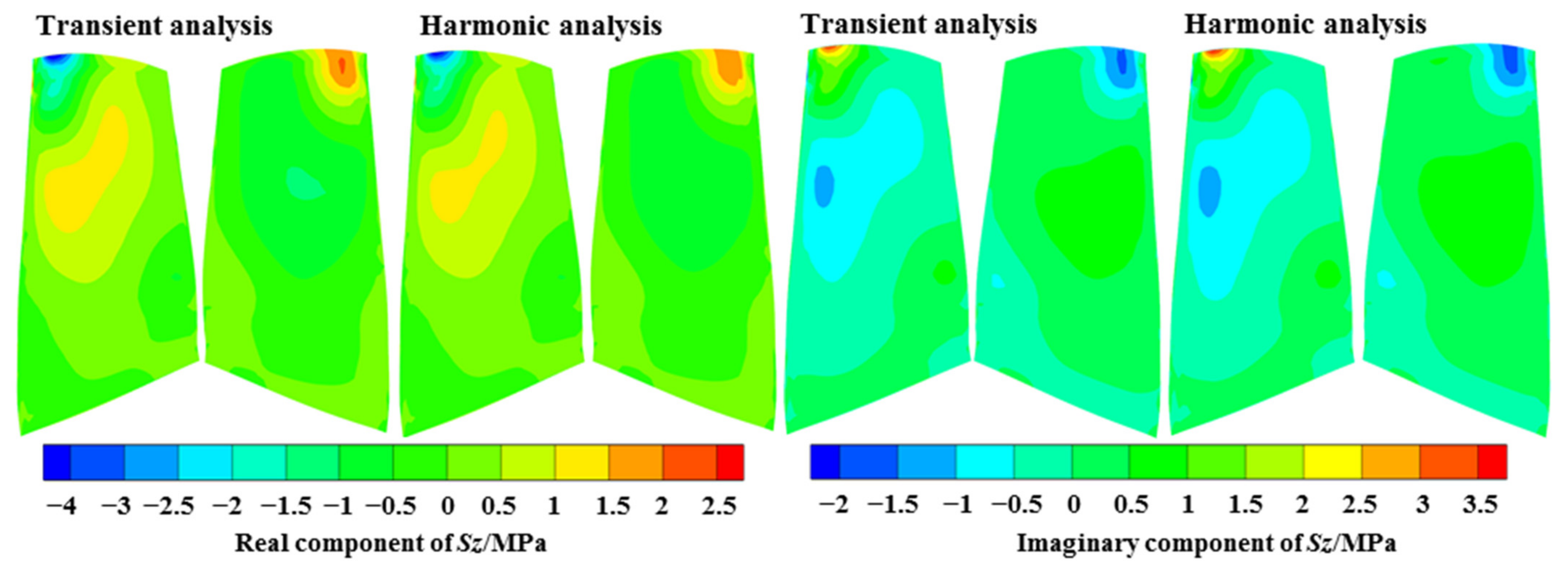
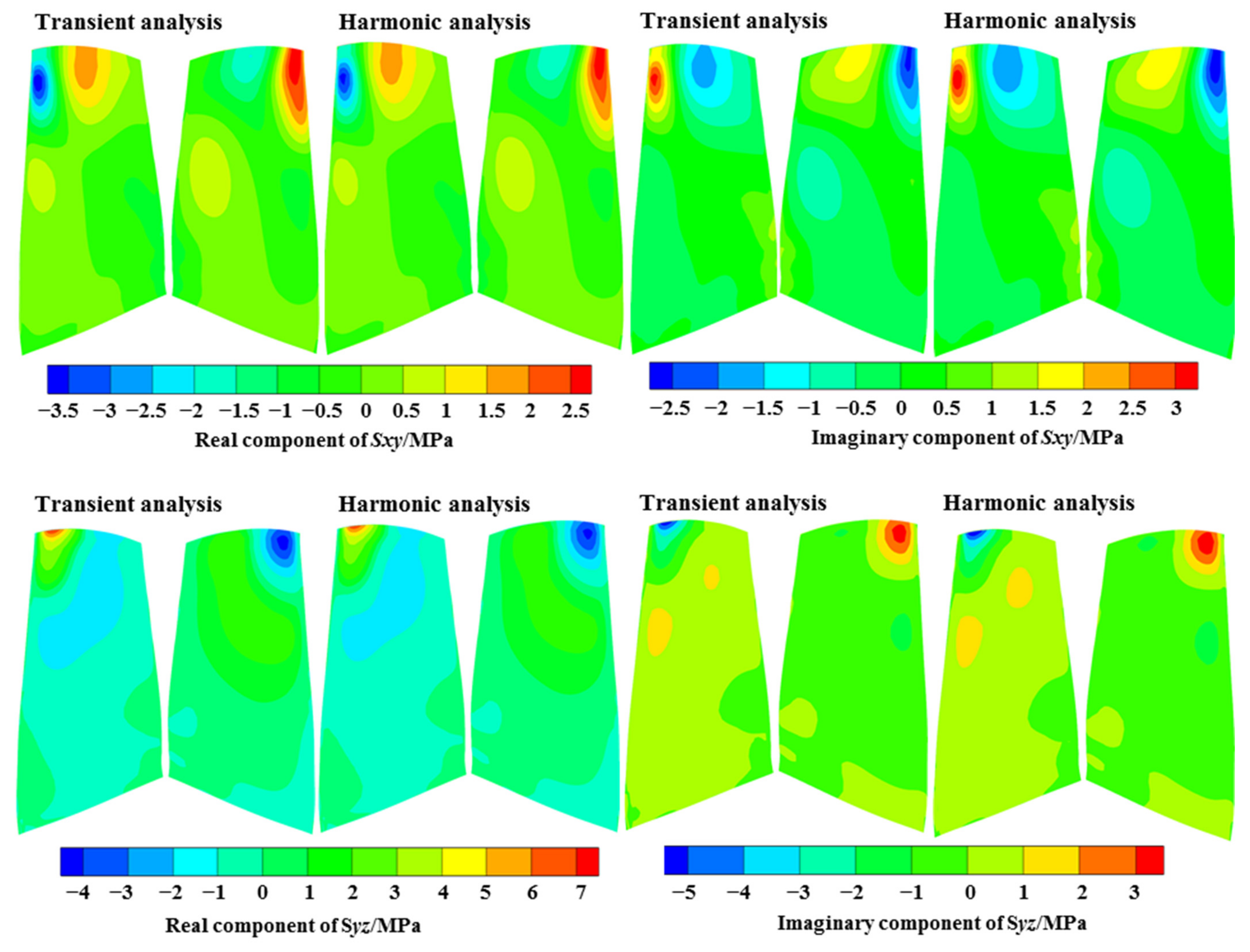
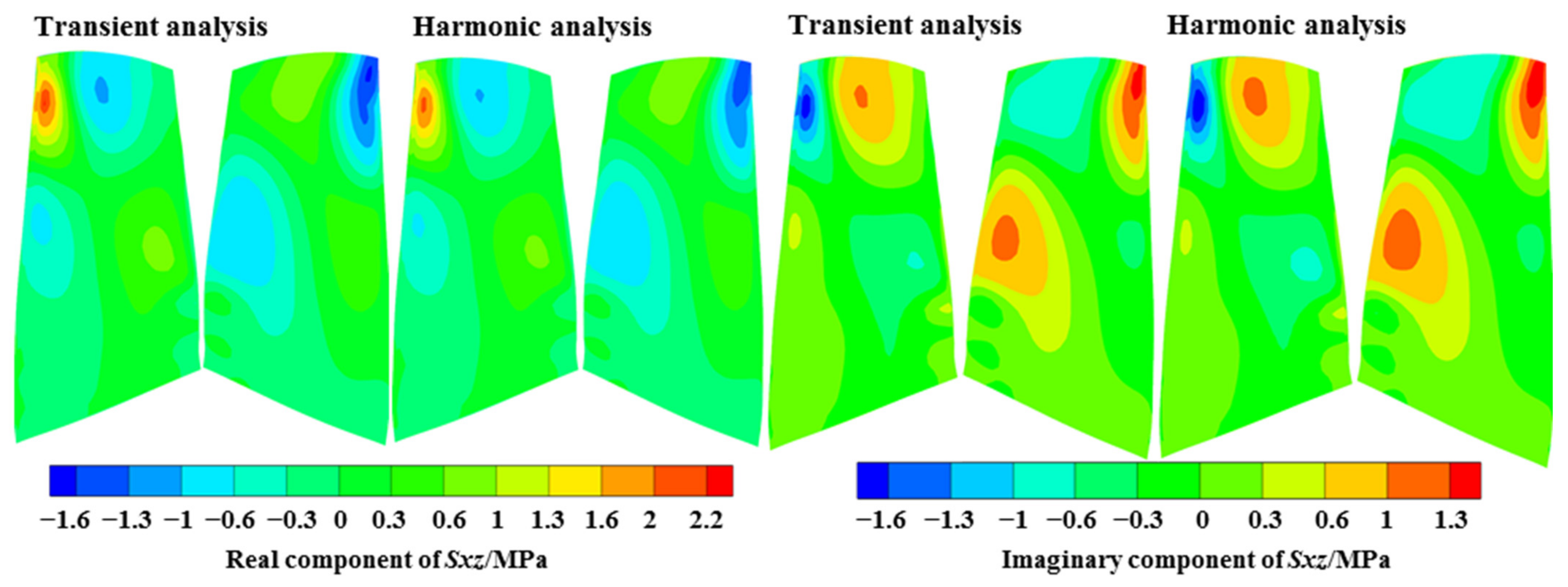
The harmonic analysis was compared with the transient analysis regarding the predicted results under the EO19 aerodynamic excitation at the resonance frequency, as shown in Figure 20, Figure 21, Figure 22. The distributions of the fundamental physical quantities at the blade surface, including three displacement variables , , and three normal stress variables , , and ; and three shear stress variables , , and showed an excellent agreement by the two methods, both at the real component and the imaginary component.
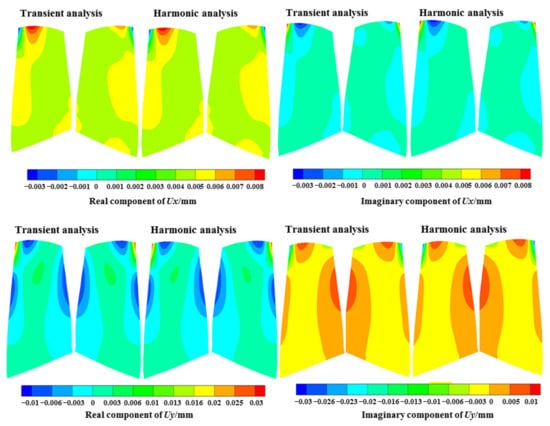
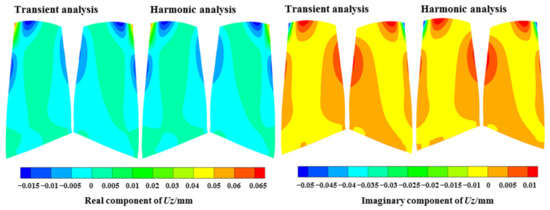
Figure 20.
Comparison of the displacement variables.
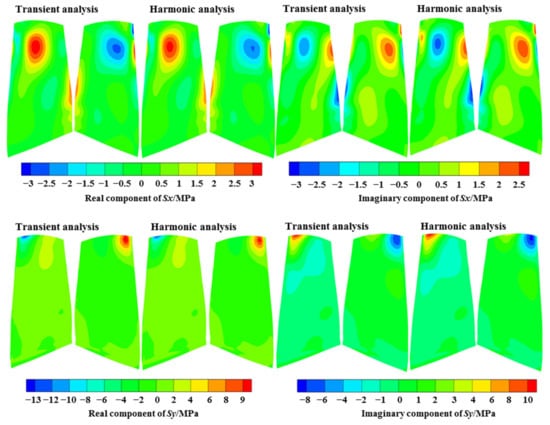
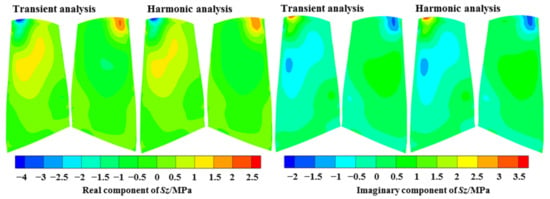
Figure 21.
Comparison of the normal stress variables.
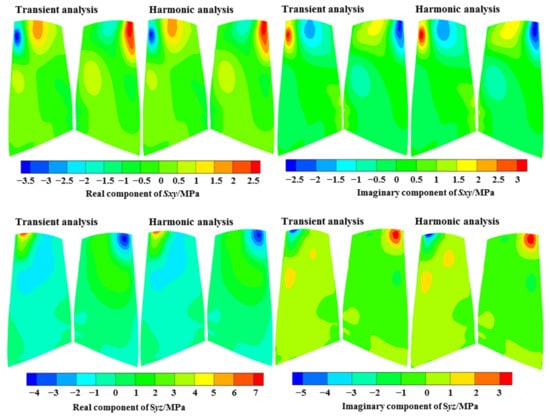
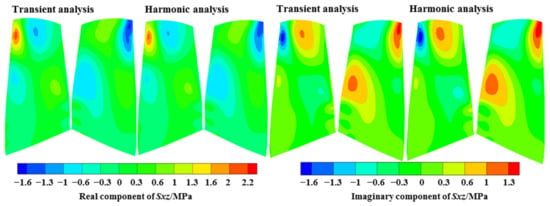
Figure 22.
Comparison of the shear stress variables.
The above variables are the results in cylindrical coordinates. It can be observed that for the displacement results, the circumferential and axial components are larger, and the positions with large displacement were at the leading edge in the tip region, which is consistent with the M8 mode. For the stress results, the circumferential normal stress and shear stress were larger, and the larger position was near 20% of the chord length in the blade tip region.
The relative deviations of the and six stress variables at the positions with the largest values (shown in Figure 5) were taken as the representative parameters to compare the differences between the two methods, as listed in Table 2. All errors were in the range of −2 to 1%, evidencing a great prediction accuracy of the harmonic forced response method. Due to the transfer to the frequency domain and the steady-state solution, the harmonic method significantly reduced the computational time by nearly 99% compared with the transient dynamic analysis. Given the low relative deviations of the fundamental physical quantities and the highly reduced computational time, the harmonic forced response method can be utilized for evaluating the resonance response levels.

Table 2.
Relative deviation of the harmonic analysis to the transient analysis.
The new method needed to convert the aerodynamic excitation from the time domain to the frequency domain and express it in the form of amplitude, phase, and frequency. Therefore, it is only suitable for harmonic loads and cannot simulate random vibration. However, for the classical forced response caused by the excitation from the wake and potential disturbances discussed in this study, this method can obtain accurate results. In addition, although this method cannot obtain the response at all frequencies through one calculation like the transient dynamic method, it can capture the main response quickly by determining the significant excitation component in advance through a Campbell diagram.
5. Conclusions
In this study, a weak coupling approach was utilized to assess the blade vibration response levels caused by the wake excitation in a 1.5 multistage compressor. Forced response analyses with the FE model were carried out for the resonance crossing of the M8 mode. The required aerodynamic excitation and damping were calculated by the CFD simulations. In terms of the aerodynamic excitation, the commonly used unsteady time-marching method was taken as the reference to validate the prediction accuracy of the time transformation method. The two methods were compared regarding the aerodynamic loads for M8 by the mean pressure and the harmonic pressure of BPF from VIGV. The comparison between the TM and the TT methods showed a discrepancy of 2% at the mean pressure distribution and 25% at the harmonic pressure amplitude in most areas expect for the blade root. Further investigations need to be done to point out the possible reasons. Fortunately, the harmonic pressure amplitude was small, and the vibration amplitude was close to zero at the blade root, which would not affect the vibration at the tip region. It should be noted that the calculation time required by the TT method was only 5% of that by TM method.
Moreover, the harmonic forced response method was compared to the commonly used transient dynamic analysis at the investigated resonance crossing. Small differences in the distributions of the fundamental physical quantities were observed, including three displacement variables , , and ; three normal stress variables , , and ; and three shear stress variables , , and . A comparison of the response results by the two methods at the positions with the maximum values showed that relative deviations were smaller than 2% with a 1% computing time with respect to the transient analysis, indicating the high accuracy and efficiency of the harmonic forced response method.
The investigations led to the conclusion that the acceptable relative deviation of the aerodynamic excitation and accurate predictions of the resonance frequency and response levels of the blade can be achieved by incorporating the TT method and harmonic analysis in the weak coupling approach with a nearly 95% reduction in the computing time.
Author Contributions
Conceptualization, X.Z. and Y.W.; methodology, X.Z. and Y.W.; validation, X.Z.; formal analysis, X.Z.; investigation, X.Z.; resources, Y.W. and X.J.; data curation, Y.W.; writing—original draft preparation, X.Z.; writing—review and editing, X.J.; supervision, Y.W.; project administration, X.J.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was co-supported by the National Science and Technology Major Project (No. 2017-Ⅳ-0002-0039) and the National Natural Science Foundation of China (No. 51475022).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this study.
References
- Kovachev, N.; Waldherr, C.U.; Mayer, J.F.; Vogt, D.M. Prediction of Aerodynamically Induced Blade Vibrations in a Radial Turbine Rotor Using the Nonlinear Harmonic Approach. ASME J. Eng. Gas Turb. Power 2018, 141, 021007. [Google Scholar] [CrossRef]
- Canepa, E.; Formosa, P.; Lengani, D.; Simoni, D.; Ubaldi, M.; Zunino, P. Influence of Aerodynamic Loading on Rotor-Stator Aerodynamic Interaction in a Two-Stage Low Pressure Research Turbine. J. Turbomach. 2007, 129, 765–772. [Google Scholar] [CrossRef]
- Efstathios, K.; Chunlei, L. Dynamic Response of a Turbulent Cylinder Wake to Forced Excitation. In Proceedings of the ASME 2009 Pressure Vessels and Piping Conference, Prague, Czech Republic, 26–30 July 2009; pp. 349–357. [Google Scholar]
- Nikola, K.; Tobias, R.M.; Christian, U.W.; Damian, M.V. Prediction of Low-Engine-Order Excitation Due to a Nonsymmetrical Nozzle Ring in a Radial Turbine by Means of the Nonlinear Harmonic Approach. J. Eng. Gas Turbines Power 2019, 141, 121004. [Google Scholar]
- Breard, C.; Green, J.; Imregun, M. Low-Engine-Order Excitation Mechanisms in Axial-Flow Turbomachinery. J. Propul. Power 2003, 19, 704–712. [Google Scholar] [CrossRef]
- Seinturier, E. Forced Response Computation for Bladed Disks Industrial Practices and Advanced Methods. In Proceedings of the 12th IFToMM World Congress, Besancon, France, 18–21 June 2007; pp. 1–17. [Google Scholar]
- He, L. Fourier Methods for Turbomachinery Applications. Prog. Aerosp. Sci. 2010, 46, 329–341. [Google Scholar] [CrossRef]
- Ning, W.; He, L. Computation of unsteady flows around oscillating blades using linear and non-linear harmonic Euler methods. J. Turbomach. 1998, 120, 508–514. [Google Scholar] [CrossRef]
- Hall, K.; Thomas, J.; Clark, W.S. Computation of Unsteady Nonlinear Flows in Cascades Using a Harmonic Balance Technique. AIAA J. 2002, 40, 879–886. [Google Scholar] [CrossRef] [Green Version]
- Erdos, J.; Alzner, E. Numerical Solution of Periodic Transonic Flow through a Fan Stage. AIAA J. 1977, 15, 1559–1568. [Google Scholar] [CrossRef]
- He, L. An Euler Solution for Unsteady Flows around Oscillating Blades. J. Turbomach. 1990, 112, 714–722. [Google Scholar] [CrossRef]
- Connell, S.; Hutchinson, B.; Galpin, P.; Campregher, R.; Godin, P. The Efficient Computation of Transient Flow in Turbine Blade Rows Using Transformation Methods. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 2631–2640. [Google Scholar]
- Sharma, G.; Zori, L.; Connell, S.; Godin, P. Efficient Computation of Large Pitch Ratio Transonic Flow in a Fan with Inlet Distortion. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; pp. 1–11. [Google Scholar]
- Rai, M.M. Navier-Stokes Simulations of Rotor-Stator Interactions Using Patched and Overlaid Grids. J. Propul. Power 1987, 3, 387–396. [Google Scholar] [CrossRef]
- Galpin, P.F.; Broberg, R.B.; Hutchinson, B.R. Three-Dimensional Navier Stokes Predictions of Steady State Rotor/Stator Interaction with Pitch Change. In Proceedings of the Third Annual Conference of the CFD Society of Canada, Banff, AB, Canada, 25–27 June 1995. [Google Scholar]
- Gerolymos, G.; Michon, G.; Neubauer, J. Analysis and Application of Chorochronic Periodicity in Turbomachinery Rotor/Stator Interaction Computations. J. Propul. Power 2002, 18, 1139–1152. [Google Scholar] [CrossRef]
- Giles, M. Calculation of Unsteady Wake/Rotor Interaction. J. Propul. Power 1988, 4, 356–362. [Google Scholar] [CrossRef]
- Zori1, L.; Galpin, P.; Campregher, R.; Morales, J.C. Time-Transformation Simulation of a 1.5 Stage Transonic Compressor. J. Turbomach. 2017, 139, 071001.1–071001.11. [Google Scholar] [CrossRef]
- Cornelius, C.; Biesinger, T.; Zori, L.; Campregher, R.; Galpin, P.; Braune, A. Efficient Time Resolved Multistage CFD Analysis Applied to Axial Compressors. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; pp. 1–14. [Google Scholar]
- Cornelius, C.; Biesinger, T.; Galpin, P.; Braune, A. Experimental and Computational Analysis of a Multistage Axial Compressor Including Stall Prediction by Steady and Transient CFD Methods. J. Turbomach. 2014, 136, 061013.1–061013.12. [Google Scholar] [CrossRef]
- Ansys CFX Version 19.2 Documentation; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Carta, F.O. Coupled Blade-Disk-Shroud Flutter Instabilities in Turbojet Engine Rotors. ASME J. Eng. Gas Turb. Power 1967, 89, 419–426. [Google Scholar] [CrossRef]
- Moffatt, S.; He, L. Blade Forced Response Prediction for Industrial Gas Turbines: Part 1—Methodologies. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003; pp. 407–414. [Google Scholar]
- Brian, J.O.; Steven, W.S.; Chengzhi, S.; Christophe, P.; Robert, G.P. Circulant Matrices and Their Application to Vibration Analysis. Appl. Mech. Rev. 2014, 66, 040803. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).