Impact of Chinese and European Airspace Constraints on Trajectory Optimization
Abstract
:1. Introduction
State of the Art
2. Operational Constraints in China and Europe
2.1. Chinese Constraints
2.2. European Constraints
3. Weather Impact on Air Traffic in China and Europe
3.1. Chinese Weather Impact on Air Traffic
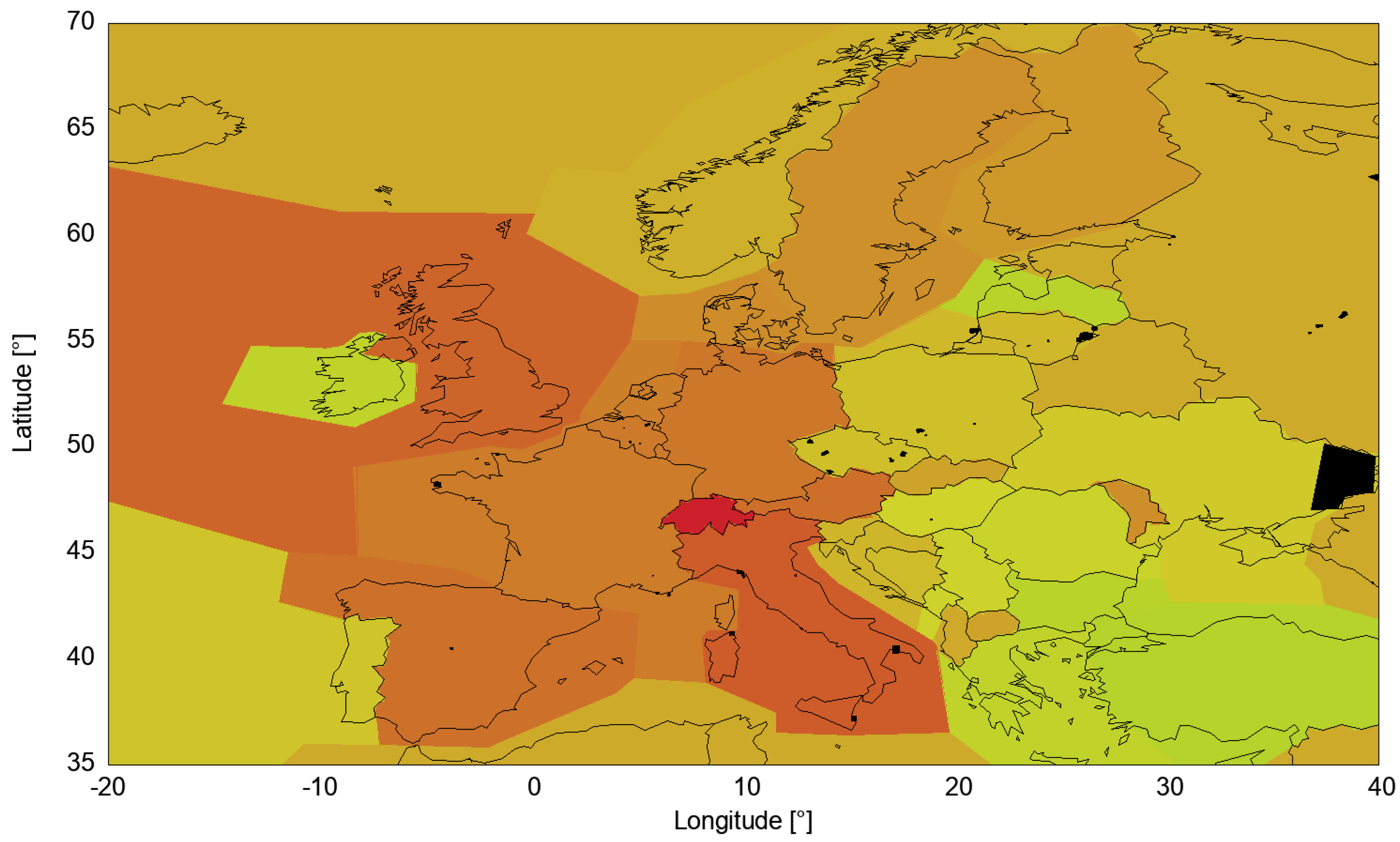
3.2. European Weather Impact on Air Traffic
4. Data Analysis
4.1. Automatic Dependent Surveillance Broadcast
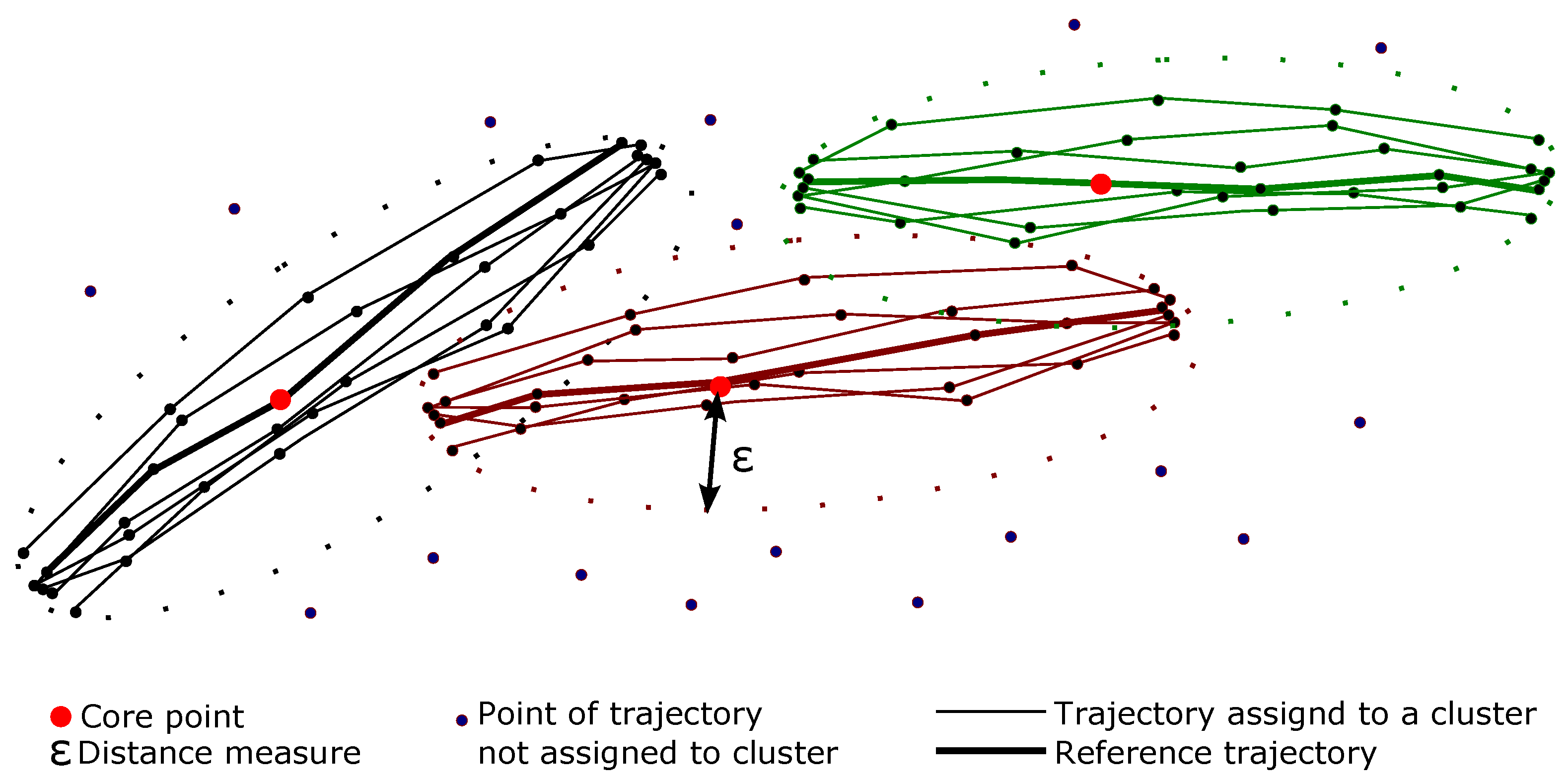
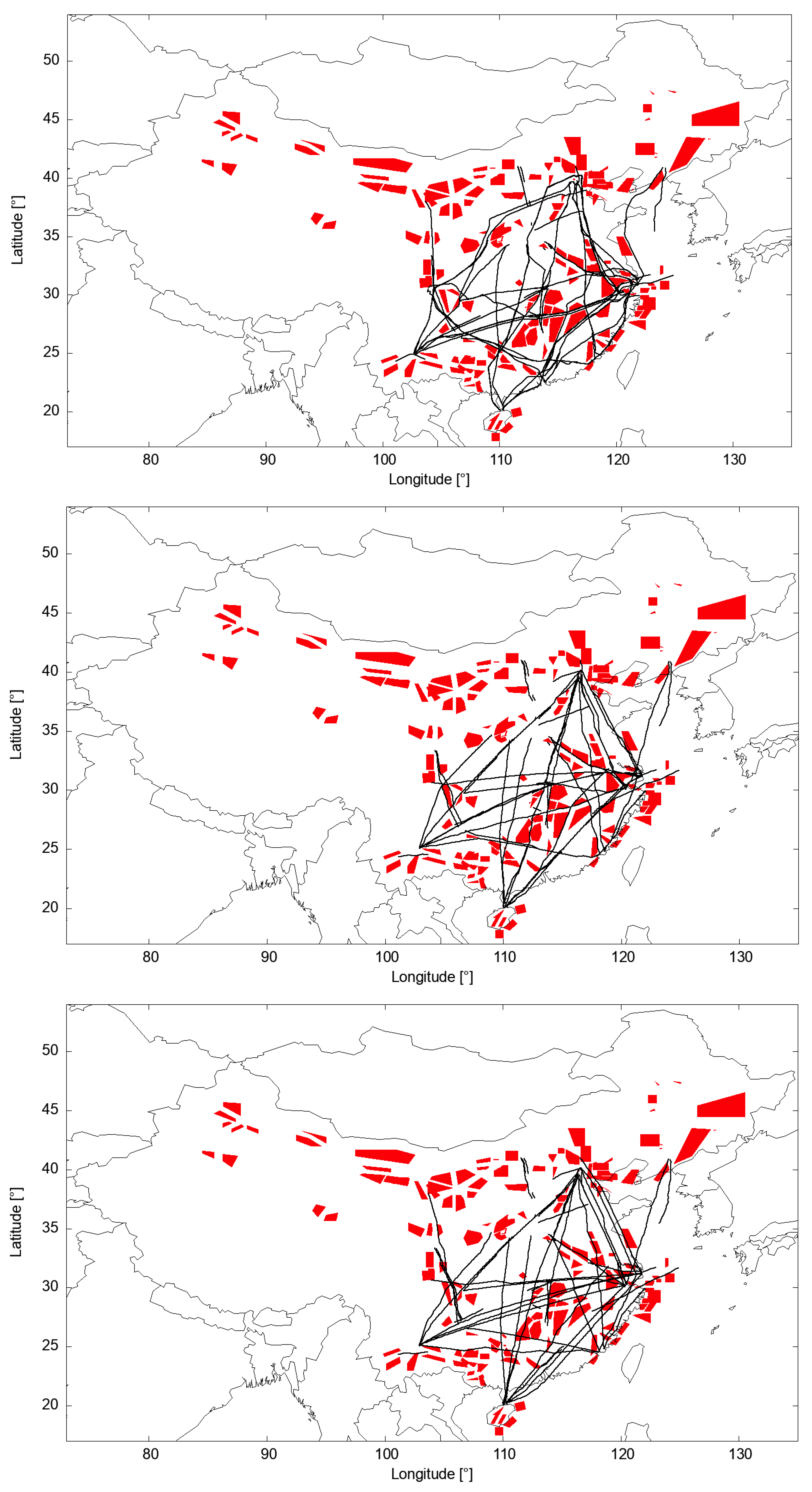
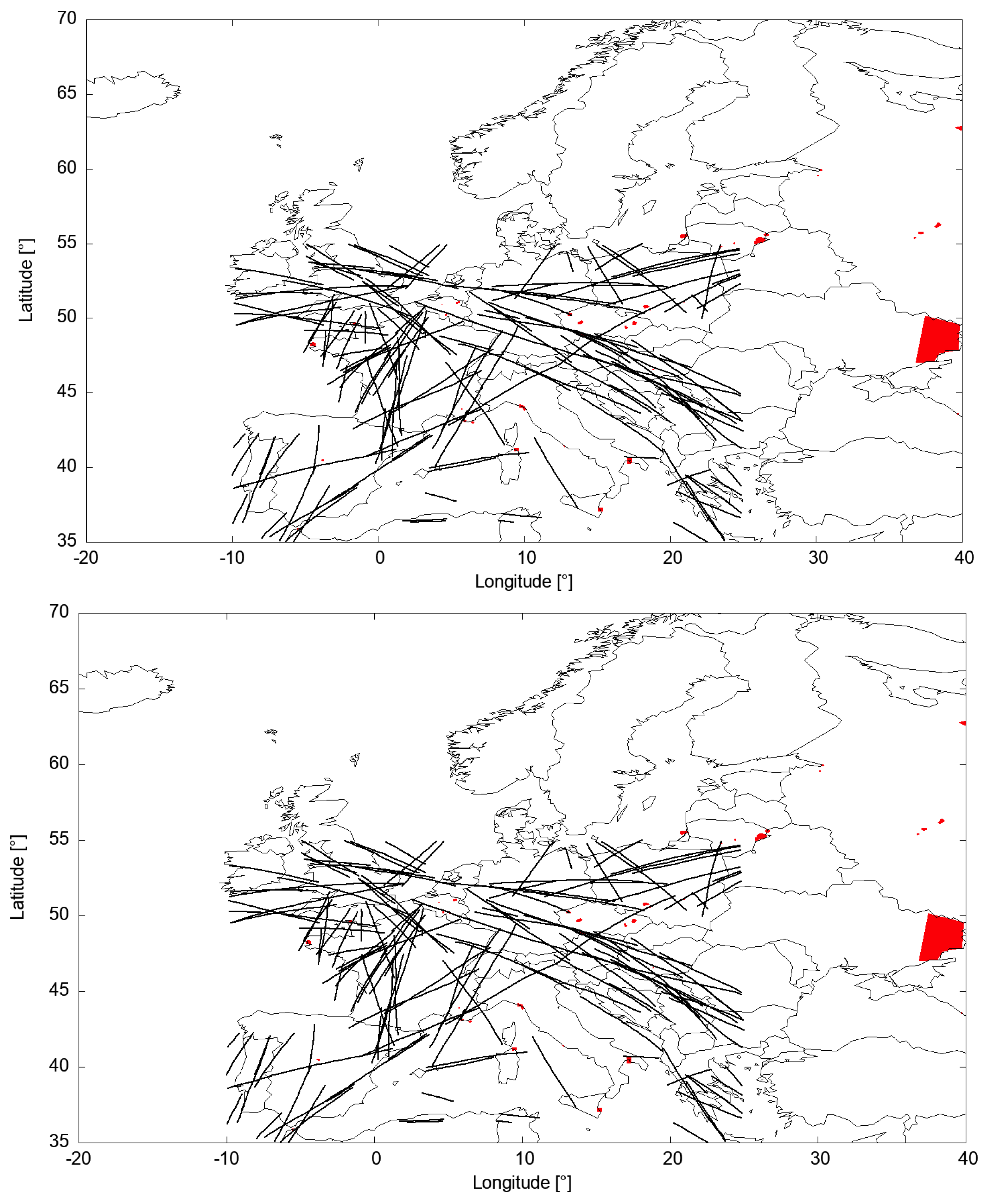
4.2. Clustering Flight Track Data
4.3. Extraction of Reference Trajectories
4.4. Multi-Criteria Trajectory Optimization
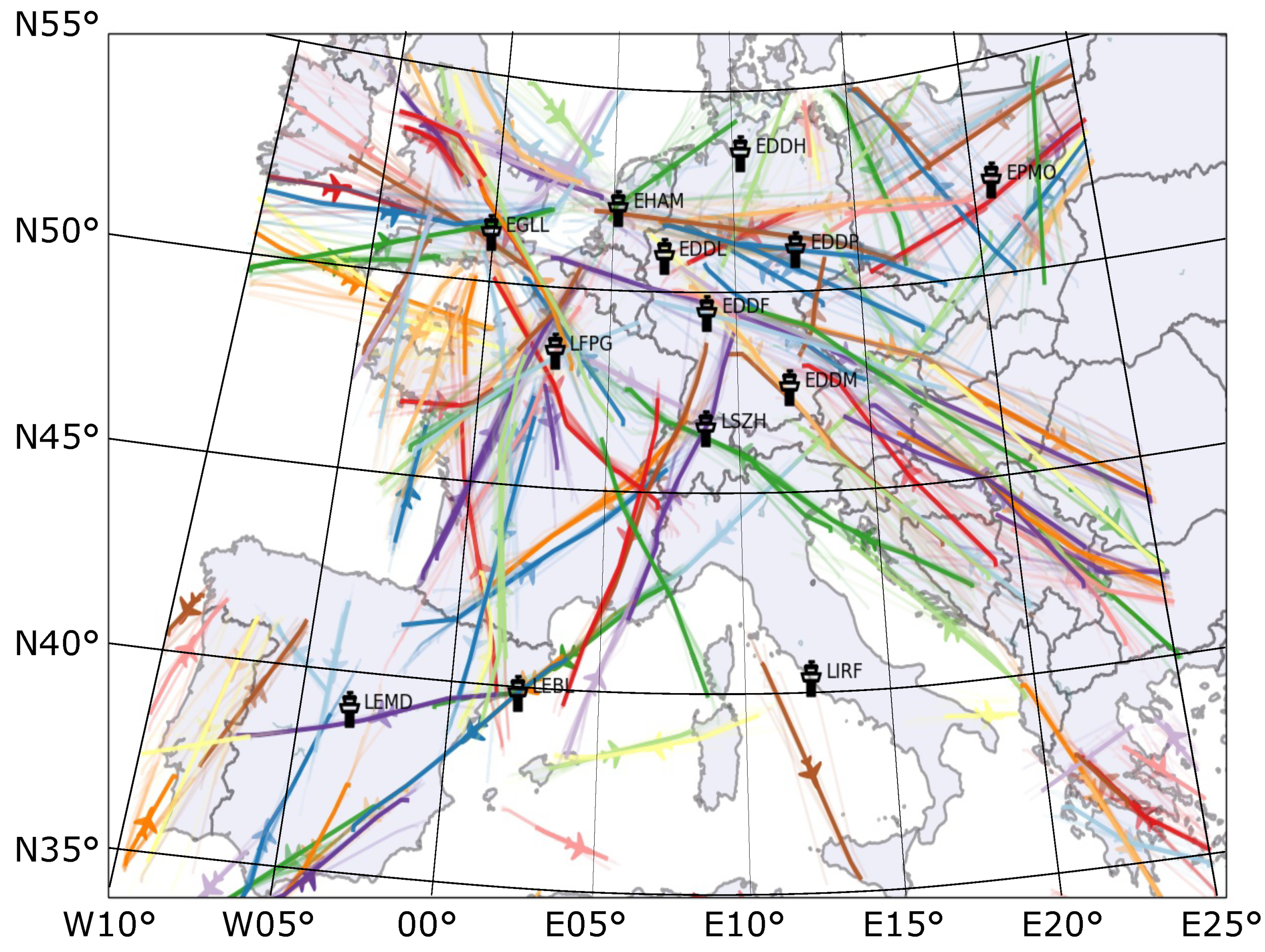
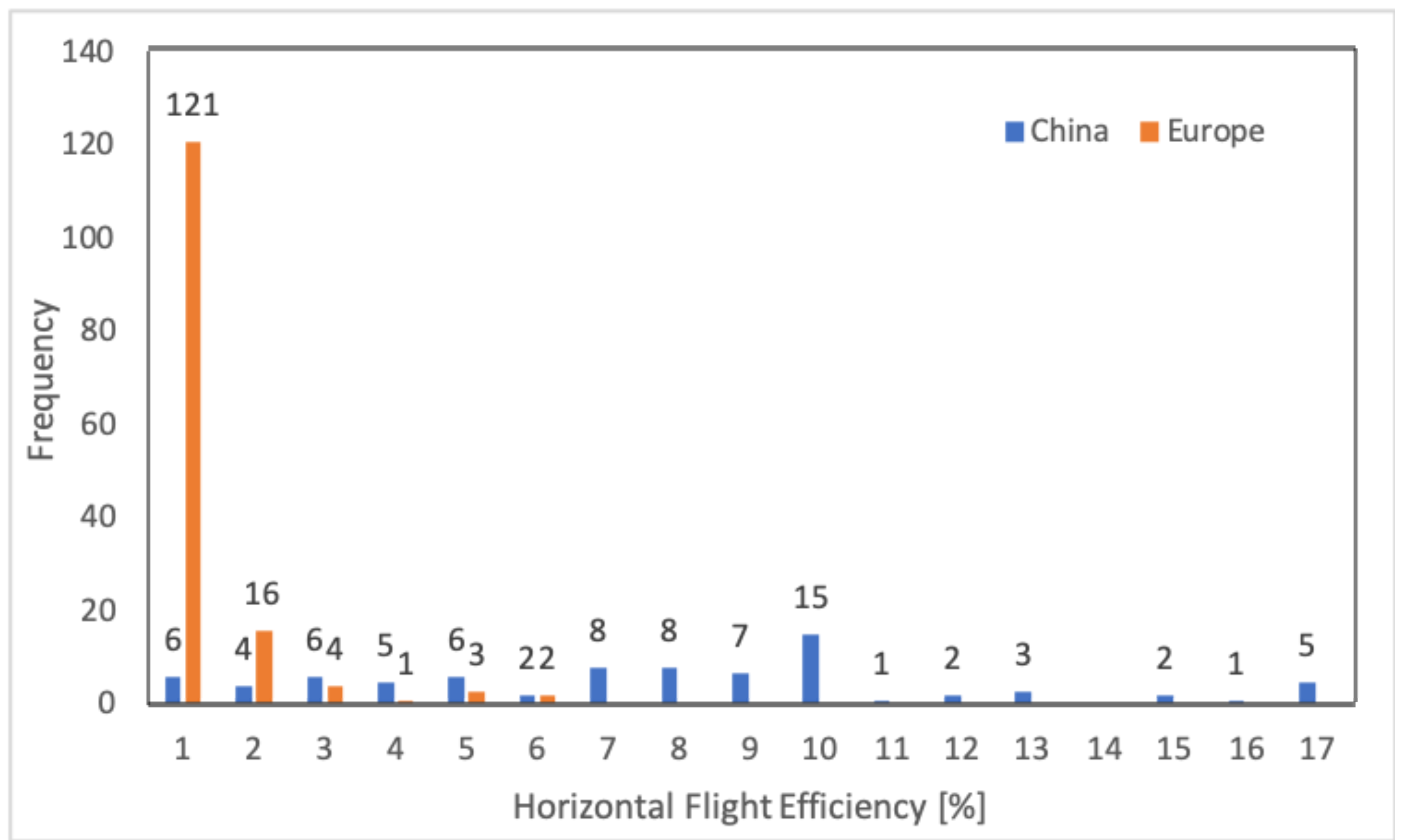
5. Chinese and European Representative Reference Trajectories
6. Differences between Real and Optimized Reference Trajectories
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Civil Air Navigation Services Organisation. Implementing Air Traffic Flow Management and Collaborative Decision Making. Available online: https://canso.fra1.digitaloceanspaces.com/uploads/2020/02/Implementating-Air-Traffic-Fow-Management-and-Airport-Collaborative-Decision-Making.pdf (accessed on 3 January 2021).
- SESAR Joint Undertaking. European ATM Master Plan Edition 2; SESAR Joint Undertaking: Brussels, Belgium, 2015. [Google Scholar]
- European Commission. Regulation (EU) No 965/2012. Off. J. Eur. Communities 2012, L 296, 1–148. [Google Scholar]
- European Commission. Commission Implementing Regulation (EU) No 2019/123. Off. J. Eur. Union 2019, L 28, 1–49. [Google Scholar]
- International Civil Aviation Organization. Aeronautical Information Services (AIS) Aeronautical Information Regulation and Control (AIRAC); Annex 15; International Civil Aviation Organization: Montreal, QC, Canada, 2005. [Google Scholar]
- International Civil Aviation Organization. Procedures of Air Navigation Services, Air Traffic Management. Doc. 4444 PANS-ATM; International Civil Aviation Organization: Montreal, QC, Canada, 2016. [Google Scholar]
- European Commission. Flight Level Orientation Scheme—FLOS; Official Journal of the European Union: Brussels, Belgium, 2016. [Google Scholar]
- Whitley, A.; Park, K. China Air Traffic Congestion Worsened by Military Control. China’s Airlines Renew the Call for Airspace Reform. Bloomberg, 17 May 2013. [Google Scholar]
- European Defence Agency. The Military in the Single European Sky. Facts and Figures; European Defence Agency: Brussels, Belgium, 2018. [Google Scholar]
- Rosenow, J.; Förster, S.; Lindner, M.; Fricke, H. Multicriteria-Optimized Trajectories Impacting Today’s Air Traffic Density, Efficiency, and Environmental Compatibility. J. Air Transp. 2018, 27, 8–15. [Google Scholar] [CrossRef]
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104. [Google Scholar] [CrossRef]
- Everitt, B.; Landau, S.; Stahl, D.; Leese, M. Cluster Analysis; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Ester, M.; Sander, J. Knowledge Discovery in Databases—Techniken und Anwendungen; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Driver, H.; Kroeber, A. Quantitative Expression of Cultural Relationships; University of California Publications in American Archaeology and Ethnology: Berkeley, CA, USA, 1932; pp. 211–256. [Google Scholar]
- Zubin, J. A technique for measuring like-mindedness. J. Abnorm. Soc. Psychol. 1938, 33, 508–516. [Google Scholar] [CrossRef]
- Tryon, R. Cluster Analysis; Correlation Profile and Orthometric (Factor) Analysis for the Isolation of Unities in Mind and Personality; Edwards Brother, Inc., Lithoprinters and Publishers: Ann Arbor, MI, USA, 1939. [Google Scholar]
- Cattell, R. The description of personality: Basic traits resolved into clusters. J. Abnorm. Soc. Psychol. 1943, 38, 476–506. [Google Scholar] [CrossRef]
- Olive, X. Traffic, a toolbox for processing and analysing air traffic data. J. Open Source Softw. 2019, 4, 1518. [Google Scholar] [CrossRef] [Green Version]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. Berkeley Symp. Math. Stat. Probab. 1967, 5.1, 281–297. [Google Scholar]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Defays, D. An efficient algorithm for a complete link method. Comput. J. 1977, 20, 364–366. [Google Scholar] [CrossRef] [Green Version]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; AAAI Press: Palo Alto, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.; Kriegel, H.; Sander, J. OPTICS: Ordering Points to Identify the Clustering Structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 31 May–3 June 1999; AAAI Press: Palo Alto, CA, USA, 1999; pp. 49–60. [Google Scholar]
- Xu, L.; Neufeld, J.; Larson, B.; Schuurmans, D. Maximum Margin Clustering. Adv. Neural Inf. Process. Syst. 2004, 17, 1537–1544. [Google Scholar]
- Li, L.; Das, S.; John Hansman, R.; Palacios, R.; Srivastava, A.N. Analysis of Flight Data Using Clustering Techniques for Detecting Abnormal Operations. J. Aerosp. Inf. Syst. 2015, 12, 587–598. [Google Scholar] [CrossRef] [Green Version]
- Campbell, A.; Zaal, P.; Schroeder, J.; Shah, S. Development of Possible Go-Around Criteria for Transport Aircraft. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Sheridan, K.; Puranik, T.; Mangortey, E.; Pinon, O.; Kirby, M.; Mavris, D. An Application of DBSCAN Clustering for Flight Anomaly Detection during the Approach Phase. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Verdonk, C.; Gomez Comendador, V.; Nieto, F.; García, M. Discussion On Density-Based Clustering Methods Applied for Automated Identification of Airspace Flows. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Ling-Ling, B.; Yo-Beng, Z.; Chao, X. Application of Kernel DBSCAN Algorithm in Civil Aviation Customer Segmentation. Comput. Eng. 2012, 38, 70–73. [Google Scholar] [CrossRef]
- Lee, C.H.; Shin, H.S.; Tsourdos, A.; Skaf, Z. Anomaly detection of aircraft engine in FDR (flight data recorder) data. In Proceedings of the IET 3rd International Conference on Intelligent Signal Processing (ISP 2017), London, UK, 4–5 December 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, S.; Vela, A.E. Clustering Aircraft Trajectories According to Air Traffic Controllers’ Decisions. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), Virtual Conference, 11–15 October 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Saez, R.; Khaledian, H.; Prats, X. Generation of emergency trajectories based on aircraft trajectory prediction. In Proceedings of the 2021 AIAA/IEEE 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 28–30 September 2021; pp. 1–10. [Google Scholar]
- Olive, X.; Sun, J.; Murça, M.; Krauth, T. A Framework to Evaluate Aircraft Trajectory Generation Methods. In Proceedings of the 14th USA/Europe Air Traffic Management Research and Development Seminar, Saclay, France, 17–19 June 2021. [Google Scholar]
- Delahaye, D.; Puechmorel, S.; Alam, S.; Fero, E. Trajectory mathematical distance applied to airspace major flows extraction. In Proceedings of the 5th ENRI International Workshop on ATM/CNS, Nakano, Japan, 29–31 October 2017; pp. 51–66. [Google Scholar]
- Olive, X.; Morio, J. Trajectory Clustering of Air Traffic Flows around Airports. Aerosp. Sci. Technol. 2019, 84, 776–781. [Google Scholar] [CrossRef] [Green Version]
- Zeng, W.; Xu, Z.; Cai, Z.; Chu, X.; Lu, X. Aircraft Trajectory Clustering in Terminal Airspace Based on Deep Autoencoder and Gaussian Mixture Model. Aerospace 2021, 8, 266. [Google Scholar] [CrossRef]
- Performance Review Comission. Performance Review Report—An Assessment of Air Traffic Management in Europe during the Calender Year 2014, 2015, 2016; Eurocontrol: Brussels, Belgium, 2017. [Google Scholar]
- International Civil Aviation Organization. Second Meeting/Workshop of Air Traffic Management (ATM) Authorities and Planners; Working Paper, CAR/SAM/3 RAN Meeting Report; International Civil Aviation Organization: Montreal, QC, Canada, 2001. [Google Scholar]
- Civil Aviation Administration of China. China. 2020. Electronic Aeronautic Information Publication. Available online: http://www.eaipchina.cn/ (accessed on 28 March 2021).
- Civil Aviation Administration of China. Civil Aviation Law of the People’s Republic of China; Standing Committee of the National People’s Congress: Beijing, China, 2007. [Google Scholar]
- Yonggang, L. Flexible Use of Airspace in China. In Proceedings of the APAC Civil/Military Cooperation Lecture/Seminar, Beijing, China, 19–21 November 2014. [Google Scholar]
- Bergman, J. This Is Why China’s Airports Are a Nightmare. Available online: https://www.bbc.com/worklife/article/20160420-this-is-why-chinas-airports-are-a-nightmare (accessed on 25 March 2021).
- Eurocontrol. Free Route Airspace (FRA) Implementation Projections—2021. Available online: https://www.eurocontrol.int/publication/free-routeairspace-fra-implementation-projection-charts (accessed on 28 February 2021).
- Available online: http://www.eurocontrol.int/services/monthly-adjusted-unit-rates (accessed on 22 February 2021).
- Eurocontrol. Customer Guide to Charges; Central Route Charges Office: Brussels, Belgium, 2020. [Google Scholar]
- Spichtinger, P.; Gierens, K.M.; Read, W. Initial Information to EU, Other Member States and Other Interested Parties on the Establishment of FABEC; (EC) 550/2004 Service Provision Regulation as Amended by (EC) 1070/2009, Art. 9a 3. and 9a 4.; FABEC: Malchina, Italy, 2003. [Google Scholar]
- Ballesteros, J.A.; Hitchens, N.M. Meteorological Factors Affecting Airport Operations during the Winter Season in the Midwest. Weather Clim. Soc. 2018, 10, 307–322. [Google Scholar] [CrossRef]
- Gultepe, I.; Sharman, R.; Williams, P.D.; Zhou, B.; Ellrod, G.; Minnis, P.; Trier, S.; Griffin, S.; Yum, S.S.; Gharabaghi, B.; et al. A Review of High Impact Weather for Aviation Meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.B.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping Annual Precipitation across Mainland China in the Period 2001–2010 from TRMM3B43 Product Using Spatial Downscaling Approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef] [Green Version]
- Ueno, Y.; Hyodo, M.; Yang, T.; Katoh, S. Intensified East Asian winter monsoon during the last geomagnetic reversal transition. Sci. Rep. 2019, 9, 9389. [Google Scholar] [CrossRef] [PubMed]
- European Centre for Medium-Range Weather Forecasts. Forecasts. Available online: https://www.ecmwf.int/ (accessed on 25 March 2021).
- Tafferner, A.; Forster, C.; Hagen, M.; Hauf, T.; Lunnon, B.; Mirza, A.; Gouillou, Y.; Zinner, T. Improved thunderstorm weather information for pilots through ground and satellite based observing systems. In Proceedings of the 14th Conference on ARAM, 90th AMS Annual Meeting 2010, Atlanta, GA, USA, 17–21 January 2010; pp. 1–12. [Google Scholar]
- Gerz, T.; Forster, C.; Tafferner, A. Mitigating the Impact of Adverse Weather on Aviation. In Atmospheric Physics. Research Topics in Aerospace; Schumann, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Taszarek, M.; Kendzierski, S.; Pilguj, N. Hazardous weather affecting European airports: Climatological estimates of situations with limited visibility, thunderstorm, low-level wind shear and snowfall from ERA5. Weather Clim. Extrem. 2020, 28, 100243. [Google Scholar] [CrossRef]
- Reiber, M. Moderne Flugmeteorologie für Ballonfahrer und Flieger: Die Theorie und ihre praktische Anwendung; Reiber; Antiquariat Fuchseck: Gammelshausen, Germany, 2002. [Google Scholar]
- Garcia, M.; Dolan, J.; Haber, B.; Hoag, A.; Diekelman, D. A Compilation of Measured ADS-B Performance Characteristics from Aiereon’s Orbit Test Program. In Proceedings of the 2018 Enhanced Solutions for Aircraft and Vehicle Surveillance (ESAVS) Applications Conference, Berlin, Germany, 18–19 October 2018. [Google Scholar]
- Rohde, R. Germany Trade and Invest—Gesellschaft für Außenwirtschaft und Standortmarketing mbH. Available online: https://www.gtai.de/gtaie/trade/branchen/branchenbericht/china/innerchinesischer-flugverkehr-und-tourismus-erholen-sich-569326 (accessed on 26 March 2021).
- European Commission. Commission Implementing Regulation (EU) No 1207/2011 of 22 November 2011 Laying down Requirements for the Performance and the Interoperability of Surveillance for the Single European Sky. Off. J. Eur. Union 2011, L 305, 35–52. [Google Scholar]
- Ali, B.S. Aircraft Surveillance Systems: Radar Limitations and the Advent of the Automatic Dependent Surveillance Broadcast; Routledge: London, UK; Taylor & Francis Group: New York, NY, USA, 2018. [Google Scholar]
- Kakubari, Y.; Kosuge, Y.; Koga, T. ADS-B Latency Estimation Technique for Surveillance Performance Assessment. In Air Traffic Management and Systems III. EIWAC 2017, Lecture Notes in Electrical Engineering; Electronic Navigation Research Institute, Ed.; Springer: Singapore, 2019; Volume 555. [Google Scholar]
- Douglas, D.; Peucker, T. Algorithms for the reduction of the number of points required to represent a line or its caricature. Can. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Förster, S.; Rosenow, J.; Lindner, M.; Fricke, H. A Toolchain for Optimizing Trajectories under Real Weather Conditions and Realistic Flight Performance; Greener Aviation: Brussels, Belgium, 2016. [Google Scholar]
- Rosenow, J.; Fricke, H.; Schultz, M. Air Traffic Simulation with 4D Multi-Criteria Optimized trajectories. In Proceedings of the 2017 Winter Simulation Conference, Las Vegas, NV, USA, 3–6 December 2017. [Google Scholar]
- Rosenow, J.; Michling, P.; Schultz, M.; Schönberger, J. Evaluation of Strategies to Reduce the Cost Impacts of Flight Delays on Total Network Costs. Aerospace 2020, 7, 165. [Google Scholar] [CrossRef]
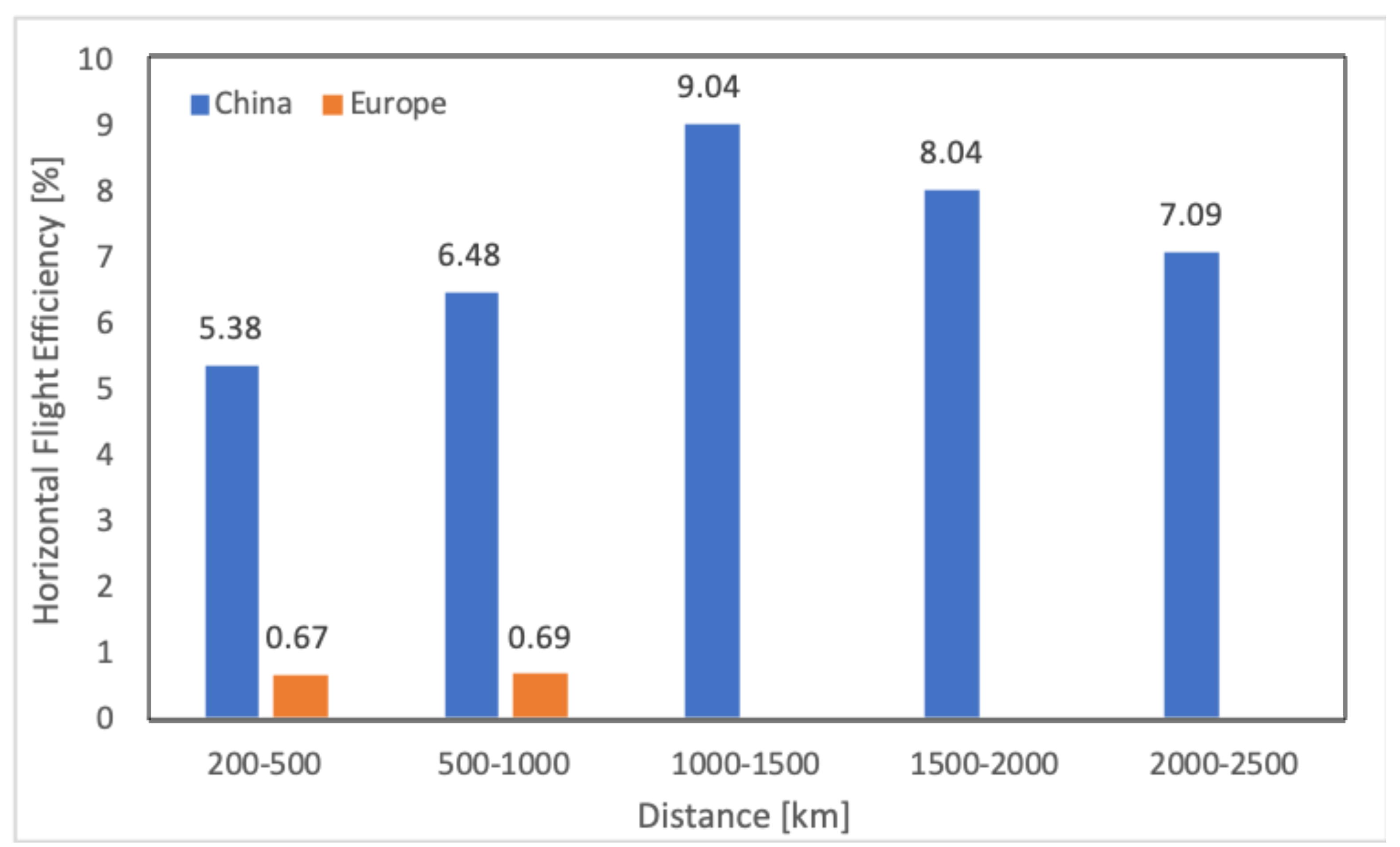
- Eurocontrol Performance Review Unit. Eurocontrol Performance Review Unit. Performance Indicator—Horizontal Flight Efficiency. Available online: https://ansperformance.eu/methodology/horizontalflight-efficiency-pi/ (accessed on 12 February 2021).
- Standfuß, T.; Rosenow, J. Applicability of Current Complexity Metrics in ATM Performance Benchmarking and Potential Benefits of Considering Weather Conditions. In Proceedings of the Digital Avionics Systems Conference, San Antonio, TX, USA, 11–15 October 2020. [Google Scholar]
- Fricke, H.; Vogel, M.; Standfuß, T. Reducing Europe’s Aviation Impact on Climate Change using enriched Air traffic Forecasts and improved efficiency benchmarks. In Proceedings of the FABEC Research Workshop “Climate Change and Role of Air Traffic Control” 2021, Vilnius, Lithuania, 22–23 September 2021. [Google Scholar]
- Performance Review Comission. Performance Review Report 2019—An Assessment of Air Traffic Management in Europe during the Calendar Year 2019; Eurocontrol: Brussels, Belgium, 2020. [Google Scholar]
- Brain, D.; Voorbach, N. ICAO’s Global Horizontal Flight Efficiency Analysis; Environmental Report 2019 Chapter 4 Climate Change Mitigation: Technology and Operations; ICAO: Montreal, QC, USA, 2019; pp. 138–144. [Google Scholar]
- SES Single European Sky. SES Single European Sky. Commission Implementing Regulation (EU) 2019/317 of 11 February 2019 laying down a performance and charging scheme in the single European sky and repealing Implementing Regulations (EU) No 390/2013 and (EU) No 391/2013. Off. J. Eur. Union 2019, L 56, 1–67. [Google Scholar]


| China | Europe | |
|---|---|---|
| Coordinates | ||
| longitude [°] | [101–125] | [−10–25] |
| latitude [°] | [20–41] | [35–55] |
| Area size | km | km |
| Inhabitants | ||
| Mean number of movements per year | ||
| Number of investigated trajectories | 12,721 | 18,264 |
| parameters of DBCSAN | ||
| [a.u.] | ||
| [a.u.] | 10 | 10 |
| Number of clusters | 99 | 160 |
| Mean number of trajectories per cluster | ||
| Number of outliers | 87% | 53% |
| China | Europe | |
|---|---|---|
| Number of reference trajectories | 99 | 160 |
| Mean HFE [%] | ||
| Mean distance [km] | 1185 | 508 |
| China | Europe | |
|---|---|---|
| Number of reference trajectories | 99 | |
| Mean distance reduction [km] | ||
| …considering restricted areas | ||
| …ignoring restricted areas | ||
| Max. distance reduction [km] | ||
| …considering restricted areas | ||
| …ignoring restricted areas | ||
| Mean HFE [%] | ||
| …considering restricted areas | ||
| …ignoring restricted areas |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosenow, J.; Chen, G.; Fricke, H.; Sun, X.; Wang, Y. Impact of Chinese and European Airspace Constraints on Trajectory Optimization. Aerospace 2021, 8, 338. https://doi.org/10.3390/aerospace8110338
Rosenow J, Chen G, Fricke H, Sun X, Wang Y. Impact of Chinese and European Airspace Constraints on Trajectory Optimization. Aerospace. 2021; 8(11):338. https://doi.org/10.3390/aerospace8110338
Chicago/Turabian StyleRosenow, Judith, Gong Chen, Hartmut Fricke, Xiaoqian Sun, and Yanjun Wang. 2021. "Impact of Chinese and European Airspace Constraints on Trajectory Optimization" Aerospace 8, no. 11: 338. https://doi.org/10.3390/aerospace8110338
APA StyleRosenow, J., Chen, G., Fricke, H., Sun, X., & Wang, Y. (2021). Impact of Chinese and European Airspace Constraints on Trajectory Optimization. Aerospace, 8(11), 338. https://doi.org/10.3390/aerospace8110338









