On a Novel Approximate Solution to the Inhomogeneous Euler–Bernoulli Equation with an Application to Aeroelastics
Abstract
1. Introduction
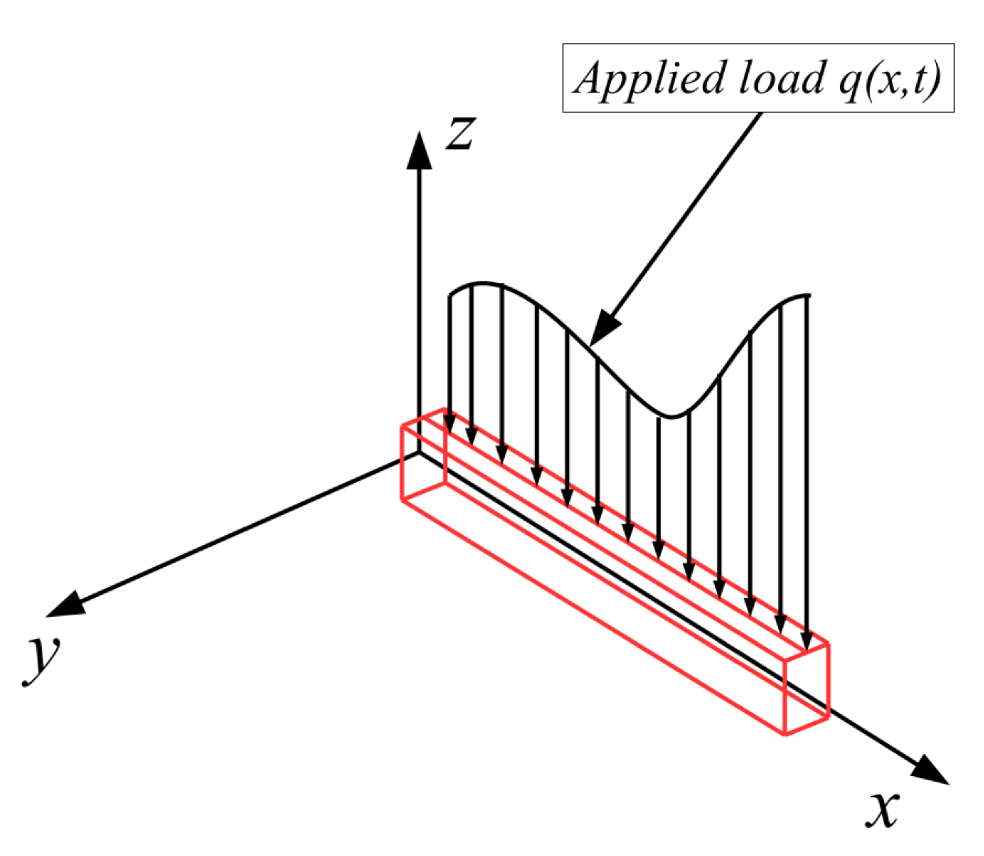
2. Governing Equations and Solution Methodology
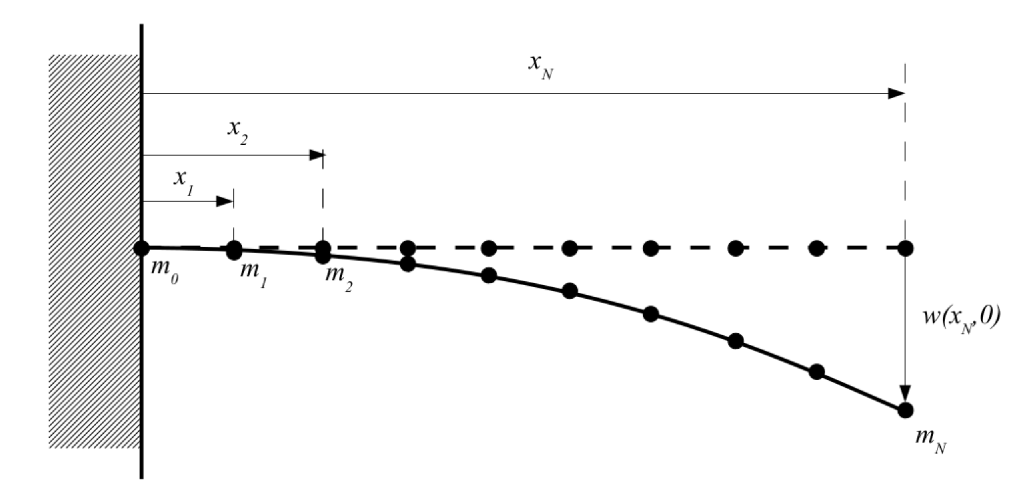
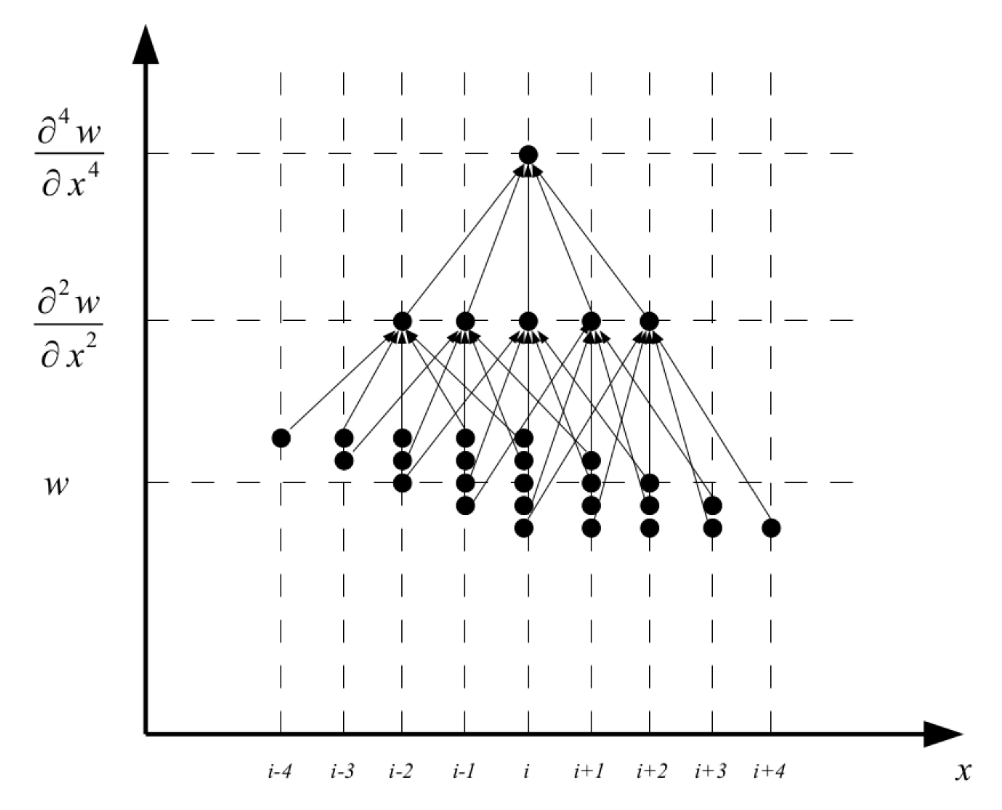
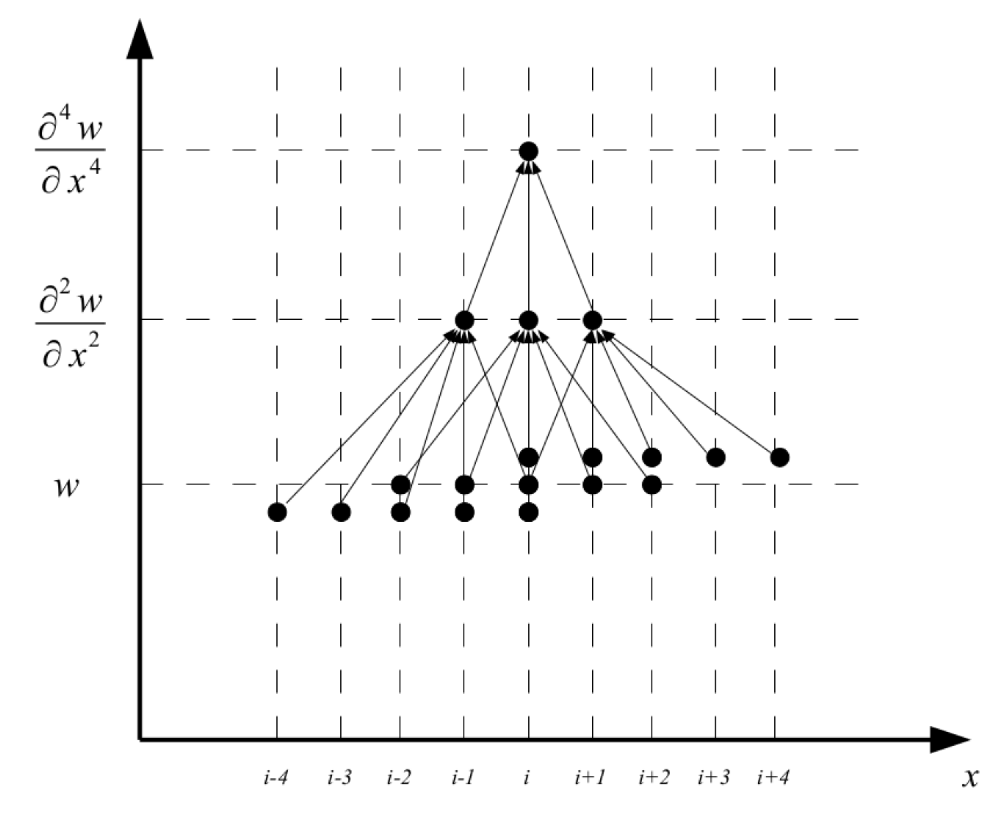
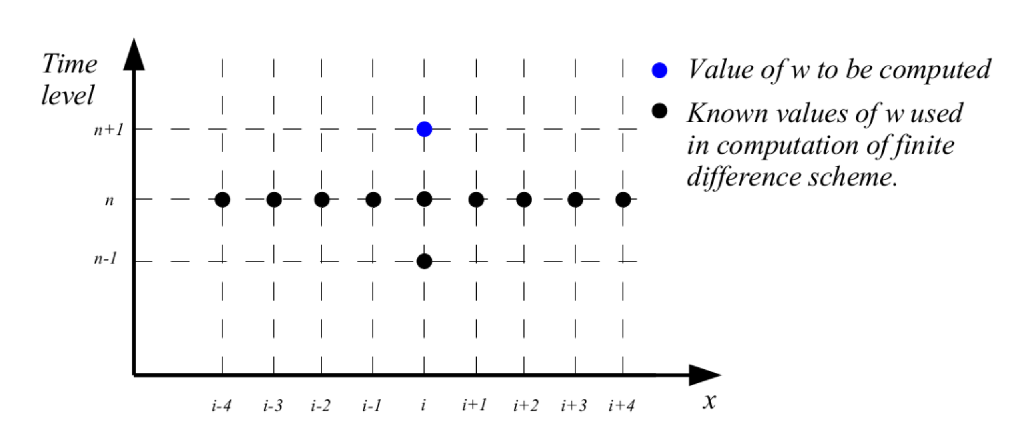
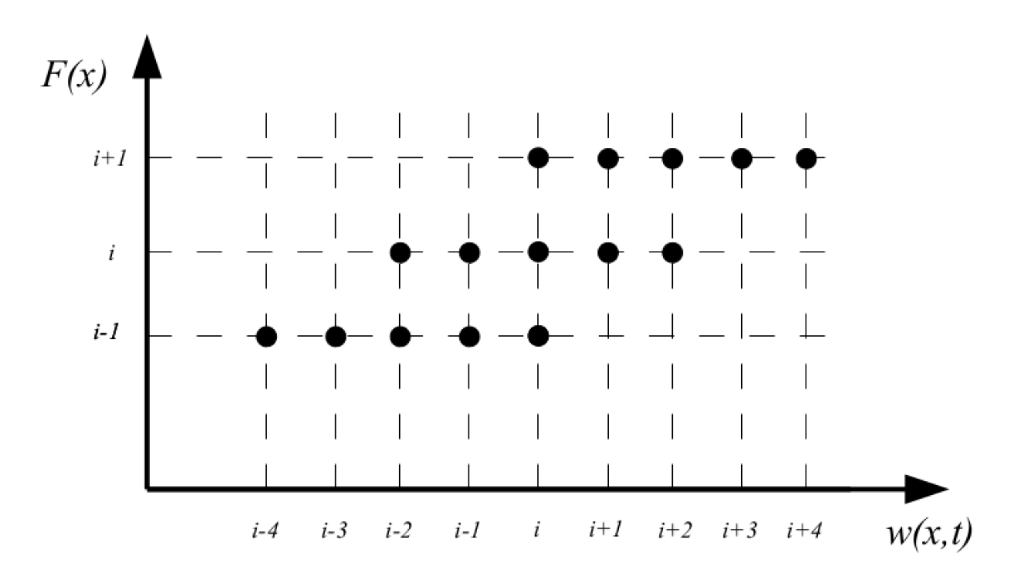
2.1. Development of a Numerical Approach for Solving the Inhomogeneous Euler–Bernoulli Equation
2.2. Extension of the Lax–Richtmyer Stability Criteria to the Fourth-Order Euler–Bernoulli Equation
2.3. Specification of Boundary Conditions and Values of Functions F and W at the Ghost Nodes
3. Results and Discussions
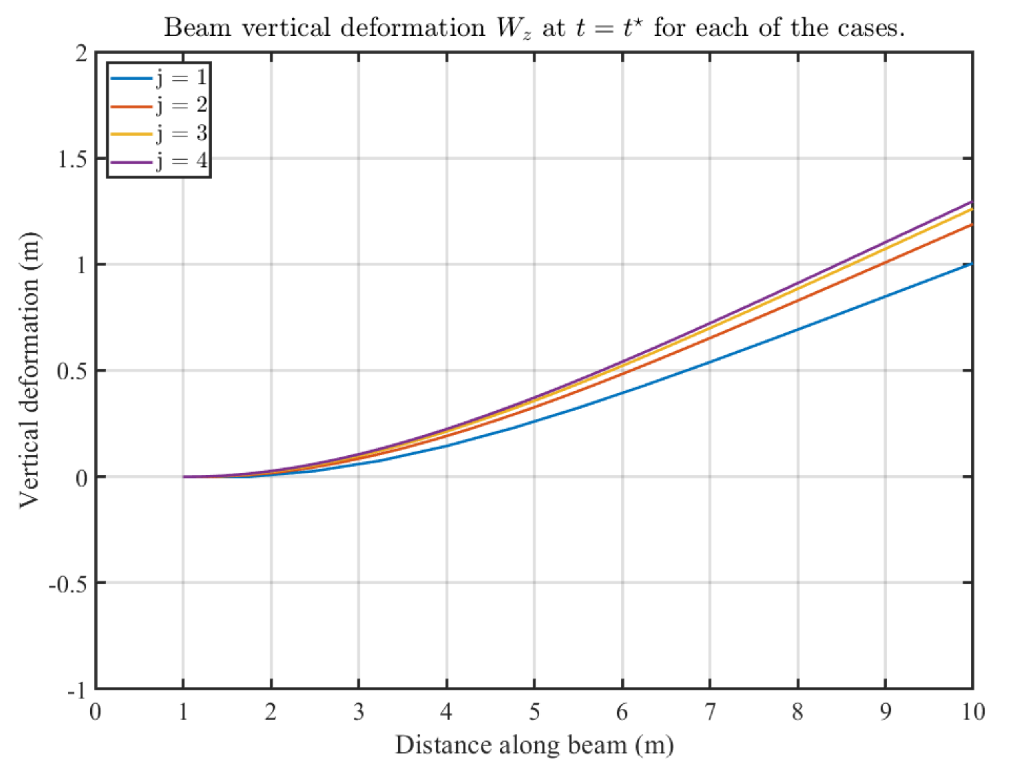
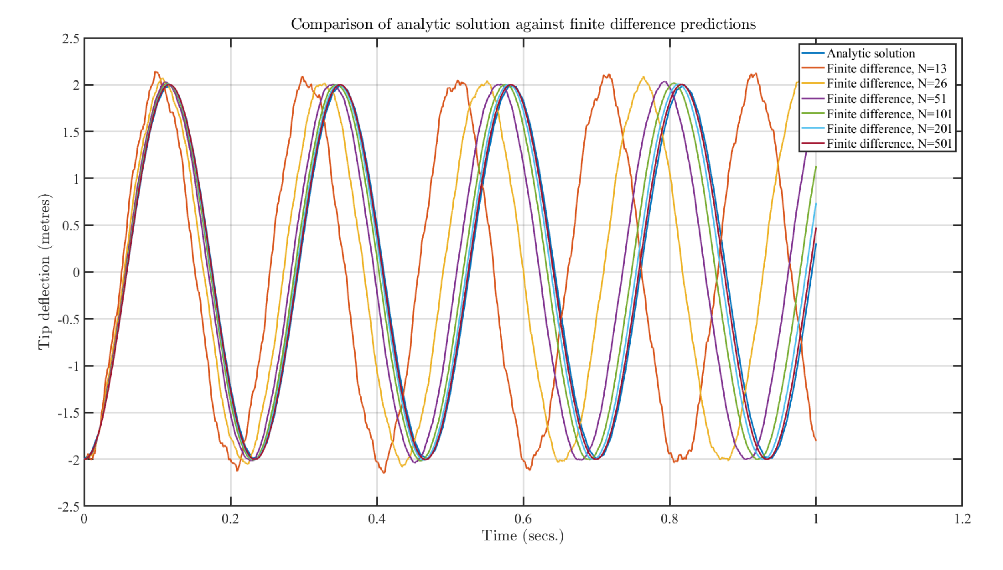
3.1. Grid Sensitivity Study for the Fourth-Order Euler–Bernoulli Equation
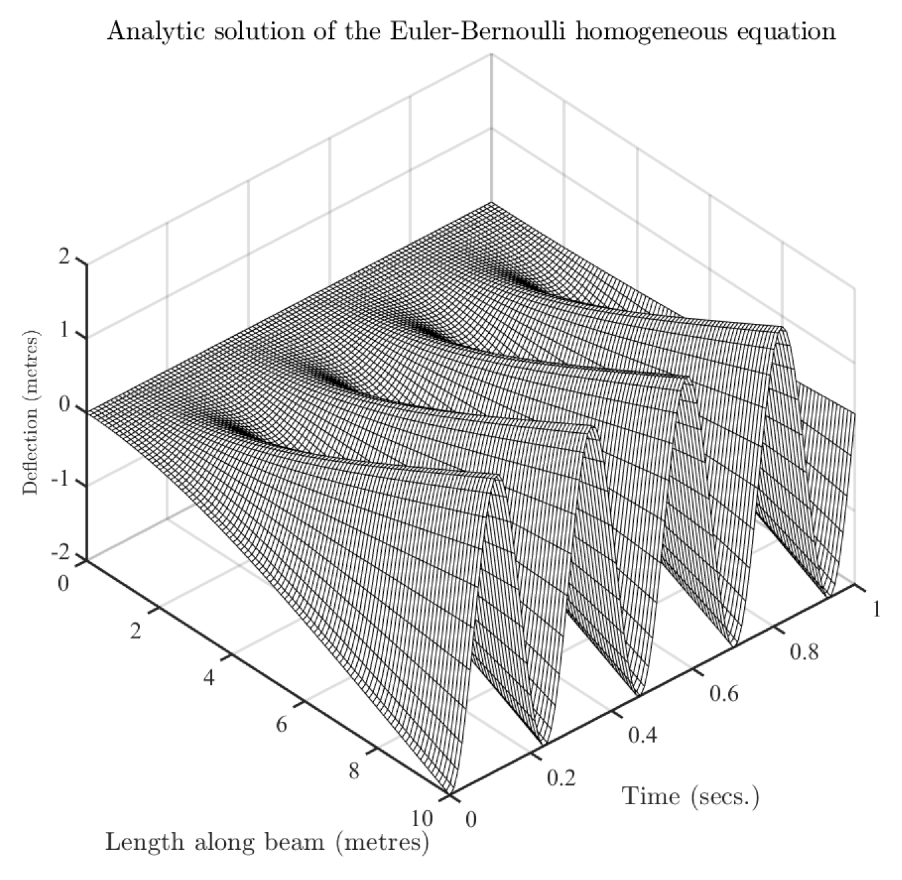
3.2. Comparison of the Simulation Results with an Analytical Solution
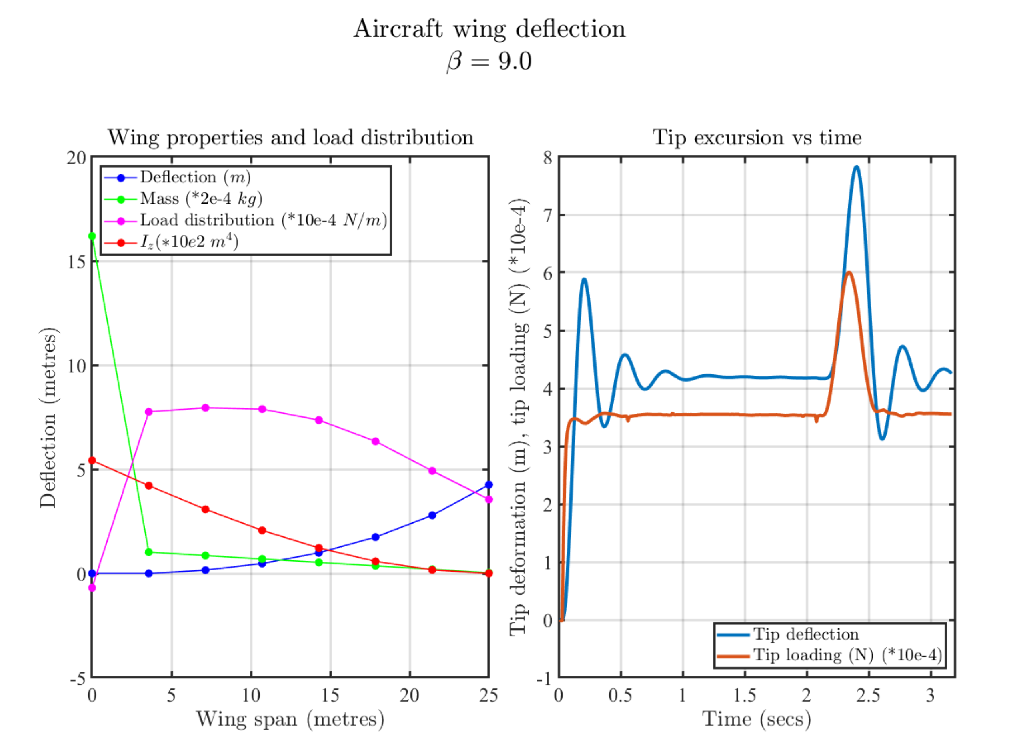
3.3. Application of the Finite Difference Scheme to a Realistic Case of a Commercial Aircraft Wing in a Gust Encounter
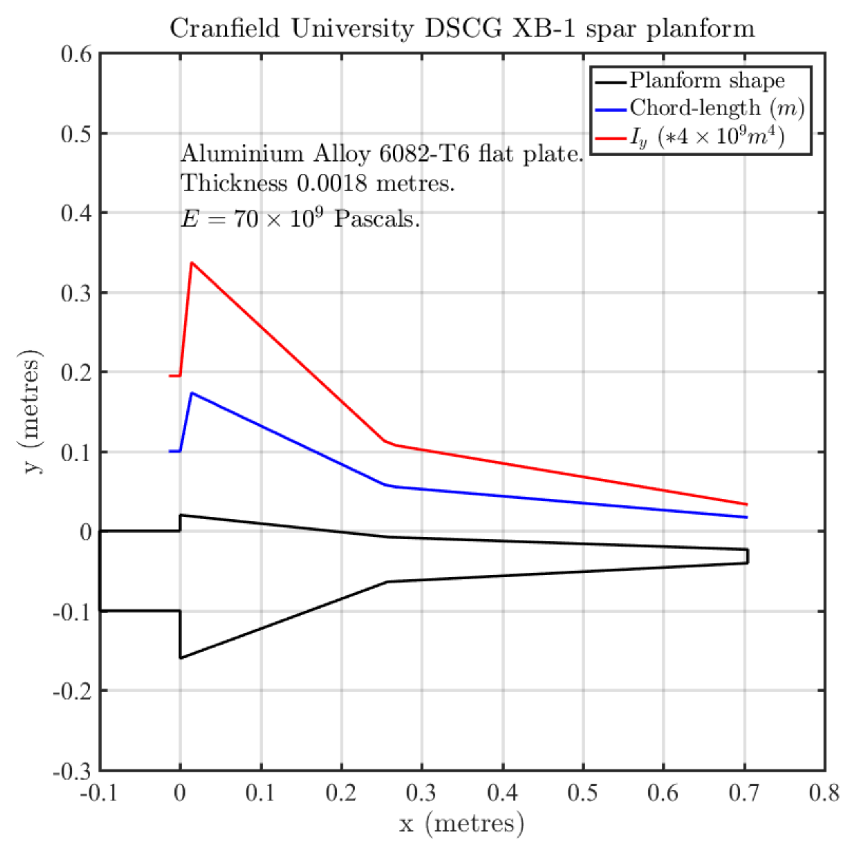
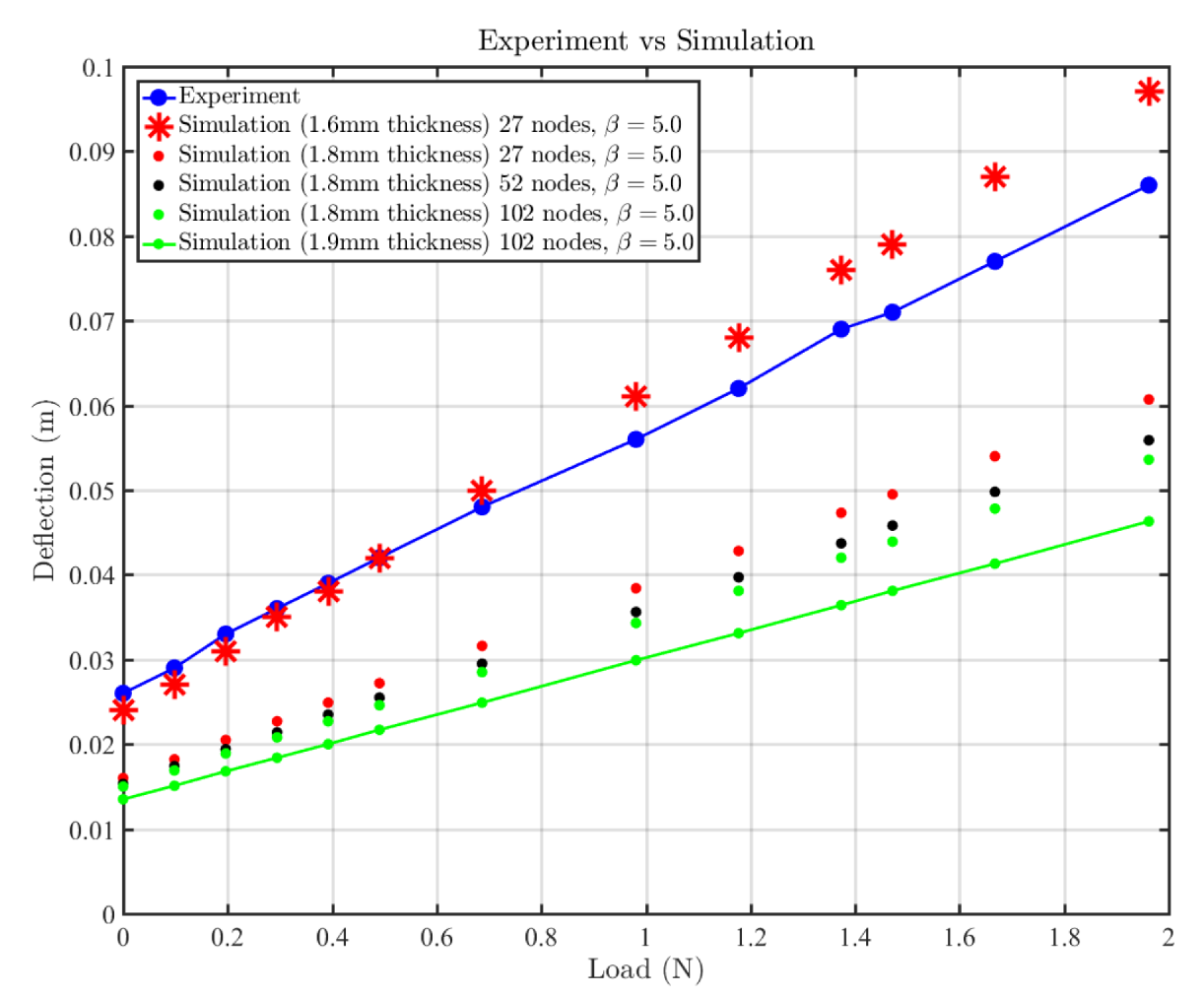
3.4. Validation of the Finite Difference Approximation for the Euler–Bernoulli Equation against Experimental Data
3.4.1. Damping Coefficient
3.4.2. Comparison of Static Deflection Experiment with Finite Difference Simulation
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GCI | Grid Convergence Index |
| MEMS | Micro-Electronic Mechanical System |
| PDE | Partial Differential Equation |
| Latin Nomenclature | |
| A | Beam Cross-Section Area () |
| A | Constant in Analytical Solution (-) |
| B | Constant in Analytical Solution (-) |
| C | Constant in Analytical Solution (-) |
| C | Fraction of Beam Span Used in Richardson Analysis (−) |
| D | Constant in Analytical Solution (-) |
| Young’s Modulus () | |
| The Product of E and I () | |
| Sequence of Constants in Analytical Solution (-) | |
| Sequence of Constants in Analytical Solution (-) | |
| Richardson Grid Convergent Index (−) | |
| G | Beam Shear Modulus () |
| Sequence of Constants in Analytical Solution (-) | |
| Second Moment of Area () | |
| i | Beam Node Index (-) |
| Beam Node Index Used for GCI (-) | |
| L | Total Beam Length (m) |
| M | The Total Mass of the Beam () |
| M | Gust Constant () |
| Beam Node Mass of Richardson Simulation () | |
| Mass of Node () | |
| N | The Number of Finite Difference Nodes along the Beam (-) |
| Number of Beam Nodes Of Richardson Simulation (-) | |
| n | Time Step Index (-) |
| Auxiliary Quantity (−) | |
| Beam External Loading Function () | |
| S | Gust Constant (-) |
| S | Auxiliary Quantity in Finite Difference () |
| T | Analytic Deflection Function Dependent Only on Time (m) |
| t | Time (s) |
| Time at which Richardson Criteria Are Applied (s) | |
| Finite Difference Time Step Size (s) | |
| Gust Velocity Vector Field () | |
| Beam Deflection Distance Function (m) | |
| Analytic Deflection Function (m) | |
| X | Analytic Deflection Function Dependent Only on Distance Along Beam (m) |
| x | Distance along the beam (m) |
| Distance Along Beam of Node (m) | |
| Distance Between Adjacent Nodes (m) | |
| z | Distance Perpendicular to Beam (m) |
| Greek Symbols | |
| Auxiliary Constants in the Analytical Solution (-) | |
| Velocity-Dependent Damping Coefficient (-) | |
| Timoshenko Shear Modulus Coefficient (-) | |
| Rayleigh Stiffness Damping Coefficient (-) | |
| Beam Mass per Unit Length () | |
| Rayleigh Mass Damping Coefficient (-) | |
| Auxiliary Constant in the Analytical Solution (-) | |
| Angular Rotation of Beam Cross-Section () |
Appendix A. An Analytical Solution of the Homogeneous Euler–Bernoulli Equation for Validation Purposes

Appendix B. Algorithm for Deriving the Coefficients of a Finite Difference of a Given Degree and Order of Accuracy
Appendix C. Accounting for Centrifugal Force in the Euler–Bernoulli Equation
Appendix D. Apply the Finite Difference Methods to Other PDEs Relevant to the Subject of This Paper
Appendix E. Description of Matlab® Supplementary Files
- constructCoefficients.m: This file contains a Matlab® script that generates the coefficients of a finite difference approximation of given order q, degree p, and bias b using the methods described in [65]. The order, degree and bias are provided by the user at the Matlab command line, and the coefficients are displayed in the Matlab command window in rational number format. The algorithm is only valid for p and q, chosen such that , that is, is even.
- EBFiniteDifference.m: This file contains a Matlab® script that performs calculations for the finite difference approximation to the inhomogeneous dynamical Euler–Bernoulli equation discussed in this paper. The script implements boundary conditions for a cantilevered beam with non-constant material properties and mass distribution that represents the scale model of the aircraft wing used in the experiments described in Section 3.4.2 of the paper. A “one minus cosine” time-dependent external load distribution is considered. In the interest of simplicity, just eight equally spaced beam nodes with lumped masses are considered. This simulation discretises the smoothly varying external load distribution into 317 time slices, each one lasting for seconds in duration. The time step used in the finite difference calculation was computed using the Lax–Richtmyer criteria.
- massR.mat: This file contains the masses (in kg) of each of the eight nodes used in the simulation.
- IyRnew.mat: This file contains the distribution of the second moment of area perpendicular to the bending axis of the wing beam cross-section. The values are sampled at the locations of the eight nodes along the length of the beam.
- IyRnew.mat: This file contains the values of the externally applied loads (the “one minus cosine” distribution) at each node at each of the 317 time slices.
- calcDt.m: This file contains a Matlab® function that is called by EBFiniteDifference.m and computes the maximum time step. For some runs of the simulation, the Lax–Richtmyer time steps are over-ridden and smaller time step values are used.
Appendix F. Coupling between Bending and Twisting
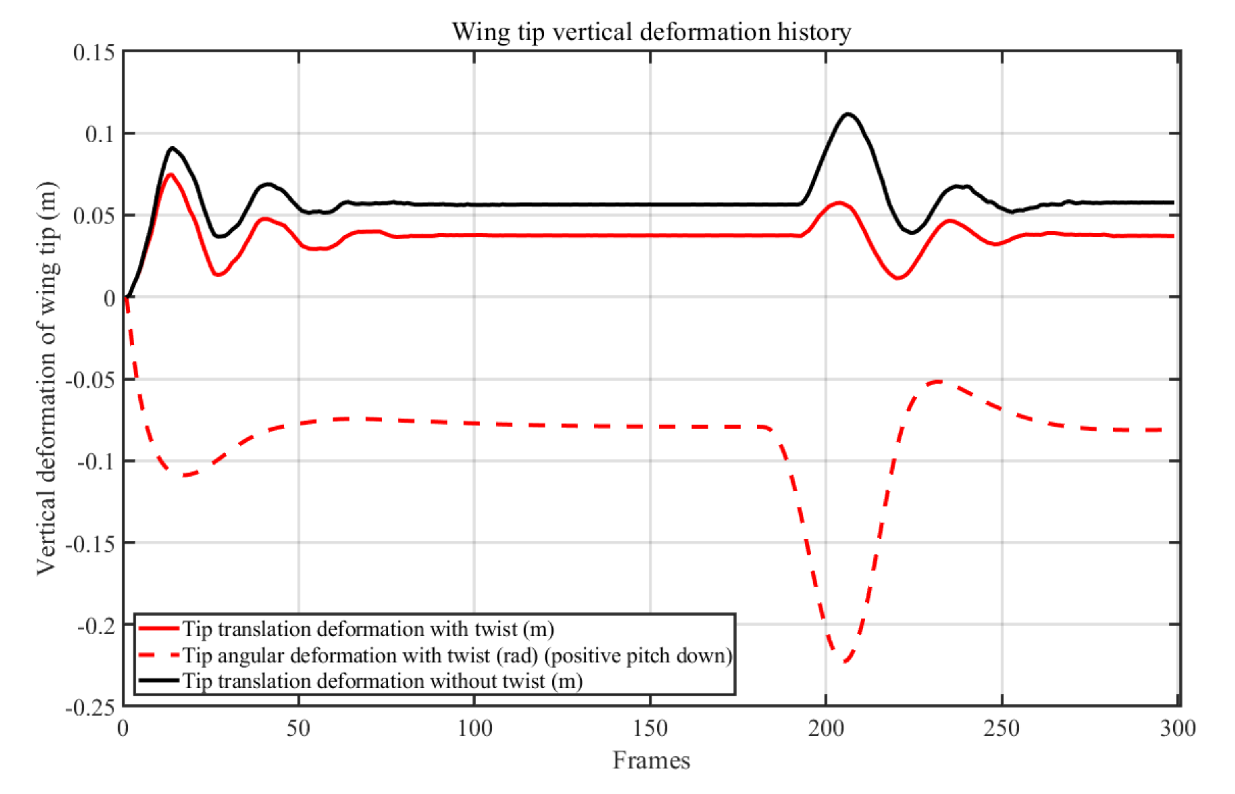
References
- Gao, S.; Liu, J. Adaptive neural network vibration control of a flexible aircraft wing system with input signal quantization. Aerosp. Sci. Technol. 2020, 96, 105593. [Google Scholar] [CrossRef]
- Azimi, M.; Farzaneh Joubaneh, E. Dynamic modeling and vibration control of a coupled rigid-flexible high-order structural system: A comparative study. Aerosp. Sci. Technol. 2020, 102, 105875. [Google Scholar] [CrossRef]
- Bekemeyer, P.; Timme, S. Flexible aircraft gust encounter simulation using subspace projection model reduction. Aerosp. Sci. Technol. 2019, 86, 805–817. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; He, W. Dynamic modeling and vibration control of a flexible aerial refueling hose. Aerosp. Sci. Technol. 2016, 55, 92–102. [Google Scholar] [CrossRef]
- Amoozgar, M.; Fazelzadeh, S.; Haddad Khodaparast, H.; Friswell, M.; Cooper, J. Aeroelastic stability analysis of aircraft wings with initial curvature. Aerosp. Sci. Technol. 2020, 107, 106241. [Google Scholar] [CrossRef]
- Vazhayil Thomas, P.; ElSayed, M.S.; Walch, D. Development of high fidelity reduced order hybrid stick model for aircraft dynamic aeroelasticity analysis. Aerosp. Sci. Technol. 2019, 87, 404–416. [Google Scholar] [CrossRef]
- Rajpal, D.; Gillebaart, E.; De Breuker, R. Preliminary aeroelastic design of composite wings subjected to critical gust loads. Aerosp. Sci. Technol. 2019, 85, 96–112. [Google Scholar] [CrossRef]
- Tsushima, N.; Yokozeki, T.; Su, W.; Arizono, H. Geometrically nonlinear static aeroelastic analysis of composite morphing wing with corrugated structures. Aerosp. Sci. Technol. 2019, 88, 244–257. [Google Scholar] [CrossRef]
- Rong, Z.; Cao, B.; Hu, J. Stability analysis on an aeroelastic system for design of a flutter energy harvester. Aerosp. Sci. Technol. 2017, 60, 203–209. [Google Scholar] [CrossRef]
- Sommerwerk, K.; Michels, B.; Lindhorst, K.; Haupt, M.; Horst, P. Application of efficient surrogate modeling to aeroelastic analyses of an aircraft wing. Aerosp. Sci. Technol. 2016, 55, 314–323. [Google Scholar] [CrossRef]
- Qin, Z.; Marzocca, P.; Librescu, L. Aeroelastic instability and response of advanced aircraft wings at subsonic flight speeds. Aerosp. Sci. Technol. 2002, 6, 195–208. [Google Scholar] [CrossRef]
- Timoshenko, S.P. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Dover Publications, Inc.: New York, NY, USA, 1983. [Google Scholar]
- Murua, J.; Palacios, R.; Graham, J.M.R. Applications of the Unsteady Vortex-Lattice Method in Aircraft Aeroelasticity and Flight Dynamics. Prog. Aerosp. Sci. 2012, 55, 46–72. [Google Scholar] [CrossRef]
- Hodges, D.H.; Pierce, G.A. Introduction to Structural Dynamics and Aeroelasticity; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Wright, J.R.; Cooper, J.E. Introduction to Aircraft Aeroelasticity and Loads; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bisplinghoff, R.L.; Ashley, H. Principles of Aeroelasticity; Dover Publications Inc.: New York, NY, USA, 2002. [Google Scholar]
- Bisplinghoff, R.L.; Ashley, H.; Halfman, R.L. Aeroelasticity; Dover Publications, Inc.: Mineola, NY, USA, 1996. [Google Scholar]
- Fernández-Sáeza, J.; Zaeraa, R.; Loyaa, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2015, 99, 107–116. [Google Scholar] [CrossRef]
- Tari, H.; Kinzel, G.L.; Mendelsohn, D.A. Cartesian and piecewise parametric large deflection solutions of tip point loaded Euler–Bernoulli cantilever beams. Int. J. Mech. Sci. 2015, 100, 216–225. [Google Scholar] [CrossRef]
- Scuciato, R.; Carrer, J.; Mansur, W. The time-dependent boundary element method formulation applied to dynamic analysis of Euler–Bernoulli beams: The linear theta method. Eng. Anal. Bound. Elem. 2017, 79, 98–109. [Google Scholar] [CrossRef]
- Scuciato, R.; Carrer, J.; Mansur, W. Dynamic analysis of Euler–Bernoulli beams by the time-dependent boundary element method formulation. Eng. Anal. Bound. Elem. 2016, 63, 134–153. [Google Scholar] [CrossRef]
- Li, F.L.; Sun, Z.Z. A finite difference scheme for solving the Timoshenko beam equations with boundary feedback. J. Comput. Appl. Math. 2007, 200, 606–627. [Google Scholar] [CrossRef][Green Version]
- Kundu, B.; Ganguli, R. Analysis of weak solution of Euler–Bernoulli beam with axial force. Appl. Math. Comput. 2017, 298, 247–260. [Google Scholar] [CrossRef]
- Fleischmann, D.; Lone, M.; Weber, S.; Sharma, A. Fast Computational Aeroelastic Analysis of Helicopter Rotor Blades. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Li, S.R.; Cao, D.F.; Wan, Z.Q. Bending solutions of FGM Timoshenko beams from those of the homogenous Euler–Bernoulli beams. Appl. Math. Model. 2013, 37, 7077–7085. [Google Scholar] [CrossRef]
- Yuan, G. Determination of two unknowns simultaneously for stochastic Euler–Bernoulli beam equations. J. Math. Anal. Appl. 2017, 450, 137–151. [Google Scholar] [CrossRef]
- Miao, Y.; Shi, Y.; Luo, H.; Gao, R. Closed-form solution considering the tangential effect under harmonic line load for an infinite Euler–Bernoulli beam on elastic foundation. Appl. Math. Model. 2018, 54, 21–33. [Google Scholar] [CrossRef]
- Xu, X.J.; Zheng, M.L.; Wang, X.C. On vibrations of nonlocal rods: Boundary conditions, exact solutions and their asymptotics. Int. J. Eng. Sci. 2017, 119, 217–231. [Google Scholar] [CrossRef]
- Sumelka, W.; Blaszczyk, T.; Liebold, C. Fractional Euler–Bernoulli beams: Theory, numerical study and experimental validation. Eur. J. Mech. Solids 2015, 54, 243–251. [Google Scholar] [CrossRef]
- Baghani, M.; Mohammadi, H.; Haghdabadi, R. An analytical solution for shape-memory-polymer Euler–Bernoulli beams under bending. Int. J. Eng. Sci. 2014, 84, 84–90. [Google Scholar] [CrossRef]
- Ma, R.; Gao, C. Nodal solutions of a nonlinear eigenvalue problem of the Euler–Bernoulli equation. J. Math. Anal. Appl. 2012, 387, 1160–1166. [Google Scholar] [CrossRef][Green Version]
- Wei, D.; Liu, Y. Analytic and finite element solutions of the power-law Euler–Bernoulli beams. Finite Elem. Anal. Des. 2012, 52, 31–40. [Google Scholar] [CrossRef][Green Version]
- Ndogmo, J. Equivalence transformations of the Euler–Bernoulli equation. Nonlinear Anal. Real World Appl. 2012, 13, 2172–2177. [Google Scholar] [CrossRef]
- Djondjorov, P.A. Invariant Properties of Timoshenko Beam Equations. Int. J. Eng. Sci. 1995, 33, 2103–2114. [Google Scholar] [CrossRef]
- Elishakoff, I.; Livshits, D. Some Closed-Form Solutions in Random Vibration of Bernoulli–Euler Beams. Int. J. Eng. Sci. 1984, 22, 1291–1302. [Google Scholar] [CrossRef]
- Reddy, J.; El-Borgi, S. Eringen’s nonlocal theories of beams accounting for moderate rotations. Int. J. Eng. Sci. 2014, 82, 159–177. [Google Scholar] [CrossRef]
- Sarkar, S.; Reddy, J. Exploring the source of non-locality in the Euler–Bernoulli and Timoshenko beam models. Int. J. Eng. Sci. 2016, 104, 110–115. [Google Scholar] [CrossRef]
- Khodabakhshi, P.; Reddy, J. A unified integro-differential nonlocal model. Int. J. Eng. Sci. 2015, 95, 60–75. [Google Scholar] [CrossRef]
- Roque, C.; Ferreira, A.; Reddy, J. Analysis of Timoshenko nanobeams with a nonlocal formulation and meshless method. Int. J. Eng. Sci. 2011, 49, 976–984. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A. Oscillations of functionally graded microbeams. Int. J. Eng. Sci. 2017, 110, 35–53. [Google Scholar] [CrossRef]
- Demir, Ç.; Civalek, Ö. On the analysis of microbeams. Int. J. Eng. Sci. 2017, 121, 14–33. [Google Scholar] [CrossRef]
- Rahaeifard, M. Static behavior of bilayer microcantilevers under thermal actuation. Int. J. Eng. Sci. 2016, 107, 28–35. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Mostafaei, H.; Nikkhah-Bahrami, M. Free flexural vibration of geometrically imperfect functionally graded microbeams. Int. J. Eng. Sci. 2016, 105, 56–79. [Google Scholar] [CrossRef]
- Shafiei, N.; Kazemi, M.; Ghadiri, M. Comparison of modeling of the rotating tapered axially functionally graded Timoshenko and Euler–Bernoulli microbeams. Phys. E 2016, 83, 74–87. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A. Non-local analysis of free vibration of bi-directional functionally graded Euler–Bernoulli nano-beams. Int. J. Eng. Sci. 2016, 105, 1–11. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A.; Rastgoo, A. Buckling analysis of arbitrary two-directional functionally graded Euler–Bernoulli nano-beams based on nonlocal elasticity theory. Int. J. Eng. Sci. 2016, 103, 1–10. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnaini, A.M.; Nikkhah-Bahrami, M. A discussion on incorporating the Poisson effect in microbeam models based on modified couple stress theory. Int. J. Eng. Sci. 2014, 86, 20–25. [Google Scholar] [CrossRef]
- Abadi, M.M.; Daneshmehr, A. An investigation of modified couple stress theory in buckling analysis of micro composite laminated Euler–Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 2014, 75, 40–53. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnaini, A.M. A discussion on different non-classical constitutive models of microbeam. Int. J. Eng. Sci. 2014, 85, 66–73. [Google Scholar] [CrossRef]
- Eltaher, M.; Alshorbagy, A.E.; Mahmoud, F. Vibration analysis of Euler–Bernoulli nanobeams by using finite element method. Appl. Math. Model. 2013, 37, 4787–4797. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. Static and dynamic analysis of micro beams based on strain gradient elasticity theory. Int. J. Eng. Sci. 2009, 47, 487–498. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. The size-dependent natural frequency of Bernoulli–Euler micro-beams. Int. J. Eng. Sci. 2008, 46, 427–437. [Google Scholar] [CrossRef]
- Khajeansari, A.; Baradaran, G.; Yvonnet, J. An explicit solution for bending of nanowires lying on Winkler-Pasternak elastic substrate medium based on the Euler–Bernoulli beam theory. Int. J. Eng. Sci. 2012, 52, 115–128. [Google Scholar] [CrossRef]
- Giunta, F.; Muscolino, G.; Sofic, A.; Elishakoff, I. Dynamic analysis of Bernoulli–Euler beams with interval uncertainties under moving loads. Procedia Eng. 2017, 199, 2591–2596. [Google Scholar] [CrossRef]
- Prasad, B. On the Response of a Timoshenko Beam Under Initial Stress to a Moving Load. Int. J. Eng. Sci. 1981, 19, 615–628. [Google Scholar] [CrossRef]
- Shang, H.; Machado, R.; Filho, J.A. Dynamic analysis of Euler–Bernoulli beam problems using the Generalized Finite Element Method. Comput. Struct. 2016, 173, 109–122. [Google Scholar] [CrossRef]
- Lerma, A.; Hinestroza, D. Coefficient identification in the Euler–Bernoulli equation using regularization methods. Appl. Math. Model. 2017, 41, 223–235. [Google Scholar] [CrossRef]
- Kawano, A. Uniqueness in the determination of unknown coefficients of an Euler–Bernoulli beam equation with observation in an arbitrary small interval of time. J. Math. Anal. Appl. 2017, 452, 351–360. [Google Scholar] [CrossRef]
- Marinov, T.T.; Vatsala, A.S. Inverse problem for coefficient identification in the Euler–Bernoulli equation. Comput. Math. Appl. 2008, 56, 400–410. [Google Scholar] [CrossRef]
- Marinova, T.T.; Marinova, R.S. Coefficient identification in Euler–Bernoulli equation from over-posed data. J. Comput. Appl. Math. 2010, 235, 450–459. [Google Scholar] [CrossRef]
- Ajaj, R.M. Flight dynamics of transport aircraft equipped with flared-hinge folding wingtips. J. Aicraft 2020, 58, 98–110. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Saavedra Flores, E.I.; Amoozgar, M.; Cooper, J.E. A Parametric Study on the Aeroelasticity of Flared Hinge Folding Wingtips. Aerospace 2021, 8, 221. [Google Scholar] [CrossRef]
- Castrichini, A.; Siddaramaiah, V.; Calderon, D.; Cooper, J.; Wilson, T.; Lemmens, Y. Preliminary investigation of use of flexible folding wing tips for static and dynamic load alleviation. Aeronaut. J. 2017, 121, 73–94. [Google Scholar] [CrossRef]
- Balatti, D.; Khodaparast, H.H.; Friswell, M.I.; Manolesos, M.; Amoozgar, M. The effect of folding wingtips on the worst-case gust loads of a simplified aircraft model. J. Aerosp. Eng. Inst. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Iskandarani, D.M. Finite Difference Approximation of Derivatives; Technical Report; Rosenstiel School of Marine Atmospheric Science University of Miami: Miami, FL, USA, 2015. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Sciences and Engineering; Hermosa Publishers: Socorro, NM, USA, 1998. [Google Scholar]
- Richtmyer, R.D.; Morton, K.W. Difference Methods for Initial-Value Problems; Krieger Publishing Company: Malabar, FL, USA, 1957. [Google Scholar]
- ANM-115. Dynamic Gust Loads; Number 25.341-1 in Advisory Circulars; Federal Aviation Administration: Washington, DC, USA, 2014. [Google Scholar]
- Katz, J.; Plotkin, A. Low Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Belendez, T.; Neipp, C.; Belendez, A. Numerical and Experimental Analysis of a Cantilever Beam: A Laboratory Project to Introduce Geometric Nonlinearity in Mechanics of Materials. Int. J. Eng. Educ. 2003, 19, 885–892. [Google Scholar]

| Symbol | Name | Vaue | Units | Notes |
|---|---|---|---|---|
| - | 1.0 | s | ||
| E | Young’s modulus | N/m2 | Aluminium | |
| I | Second moment of area | m4 | Rectangular section, height 0.2 m, breadth 0.1 m | |
| M | Total mass | 80 | kg | Mass evenly distributed over the nodes |
| Damping coefficient | 10 | − | ||
| q | External load | 4940 | N/m | |
| C | Fraction of span | 0.5 | − | |
| L | Beam length | 10 | m |
| j | No. of Iterations | No. of Nodes | ||||
|---|---|---|---|---|---|---|
| 1 | 0.833 | 13 | 1.0043 | 13 | ||
| 2 | 0.4 | 26 | 1.1881 | 26 | ||
| 3 | 0.2 | 51 | 1.2609 | 51 | ||
| 4 | 0.1 | 101 | 1.2957 | 101 |
| j | No. of Iterations | No. of Nodes | No. of Oscillations | ||||
|---|---|---|---|---|---|---|---|
| 1 | 0.8 | 13 | −0.7165 | 13 | 5 | ||
| 2 | 0.4 | 26 | 3.1390 | 26 | 4.6 | ||
| 3 | 0.2 | 51 | 3.2071 | 51 | 4.5 | ||
| 4 | 0.1 | 101 | 2.5763 | 101 | 4.4 |
| Station | Chord Length (m) | Element Mass (kg) | |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | |||
| 12 | |||
| 13 | |||
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | |||
| 18 | |||
| 19 | |||
| 20 | |||
| 21 | |||
| 22 | |||
| 23 | |||
| 24 | |||
| 25 | |||
| 26 | |||
| 27 | |||
| 28 | |||
| 29 | |||
| 30 | |||
| 31 | |||
| 32 | |||
| 33 | |||
| 34 | |||
| 35 | |||
| 36 | |||
| 37 | |||
| 38 | |||
| 39 | |||
| 40 | |||
| 41 | |||
| 42 | |||
| 43 | |||
| 44 | |||
| 45 | |||
| 46 | |||
| 47 | |||
| 48 | |||
| 49 | |||
| 50 | |||
| 51 | |||
| 52 | - |
| Case | Tip Load (N) | Measured Deflection (m) | Simulated Deflection. Thickness 1.9 mm | Simulated Deflection. Thickness 1.8 mm | Simulated Deflection. Thickness 1.6 mm |
|---|---|---|---|---|---|
| 0 | 0.000 | 0.026 | 0.0135 | 0.0150 | 0.024 |
| 1 | 0.098 | 0.029 | 0.0151 | 0.0169 | 0.027 |
| 2 | 0.196 | 0.033 | 0.0168 | 0.0189 | 0.031 |
| 3 | 0.294 | 0.036 | 0.0184 | 0.0208 | 0.035 |
| 4 | 0.392 | 0.039 | 0.0200 | 0.0227 | 0.038 |
| 5 | 0.490 | 0.042 | 0.0217 | 0.0246 | 0.042 |
| 6 | 0.687 | 0.048 | 0.0249 | 0.0285 | 0.050 |
| 7 | 0.981 | 0.056 | 0.0299 | 0.0343 | 0.061 |
| 8 | 1.177 | 0.062 | 0.0331 | 0.0381 | 0.068 |
| 9 | 1.373 | 0.069 | 0.0364 | 0.0420 | 0.076 |
| 10 | 1.471 | 0.071 | 0.0381 | 0.0439 | 0.079 |
| 11 | 1.668 | 0.076 | 0.0413 | 0.0478 | 0.087 |
| 12 | 1.962 | 0.086 | 0.0463 | 0.0536 | 0.097 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fleischmann, D.; Könözsy, L. On a Novel Approximate Solution to the Inhomogeneous Euler–Bernoulli Equation with an Application to Aeroelastics. Aerospace 2021, 8, 356. https://doi.org/10.3390/aerospace8110356
Fleischmann D, Könözsy L. On a Novel Approximate Solution to the Inhomogeneous Euler–Bernoulli Equation with an Application to Aeroelastics. Aerospace. 2021; 8(11):356. https://doi.org/10.3390/aerospace8110356
Chicago/Turabian StyleFleischmann, Dominique, and László Könözsy. 2021. "On a Novel Approximate Solution to the Inhomogeneous Euler–Bernoulli Equation with an Application to Aeroelastics" Aerospace 8, no. 11: 356. https://doi.org/10.3390/aerospace8110356
APA StyleFleischmann, D., & Könözsy, L. (2021). On a Novel Approximate Solution to the Inhomogeneous Euler–Bernoulli Equation with an Application to Aeroelastics. Aerospace, 8(11), 356. https://doi.org/10.3390/aerospace8110356







