Physics Guided Deep Learning for Data-Driven Aircraft Fuel Consumption Modeling
Abstract
:1. Introduction
2. Problem Formulation
3. Preliminaries
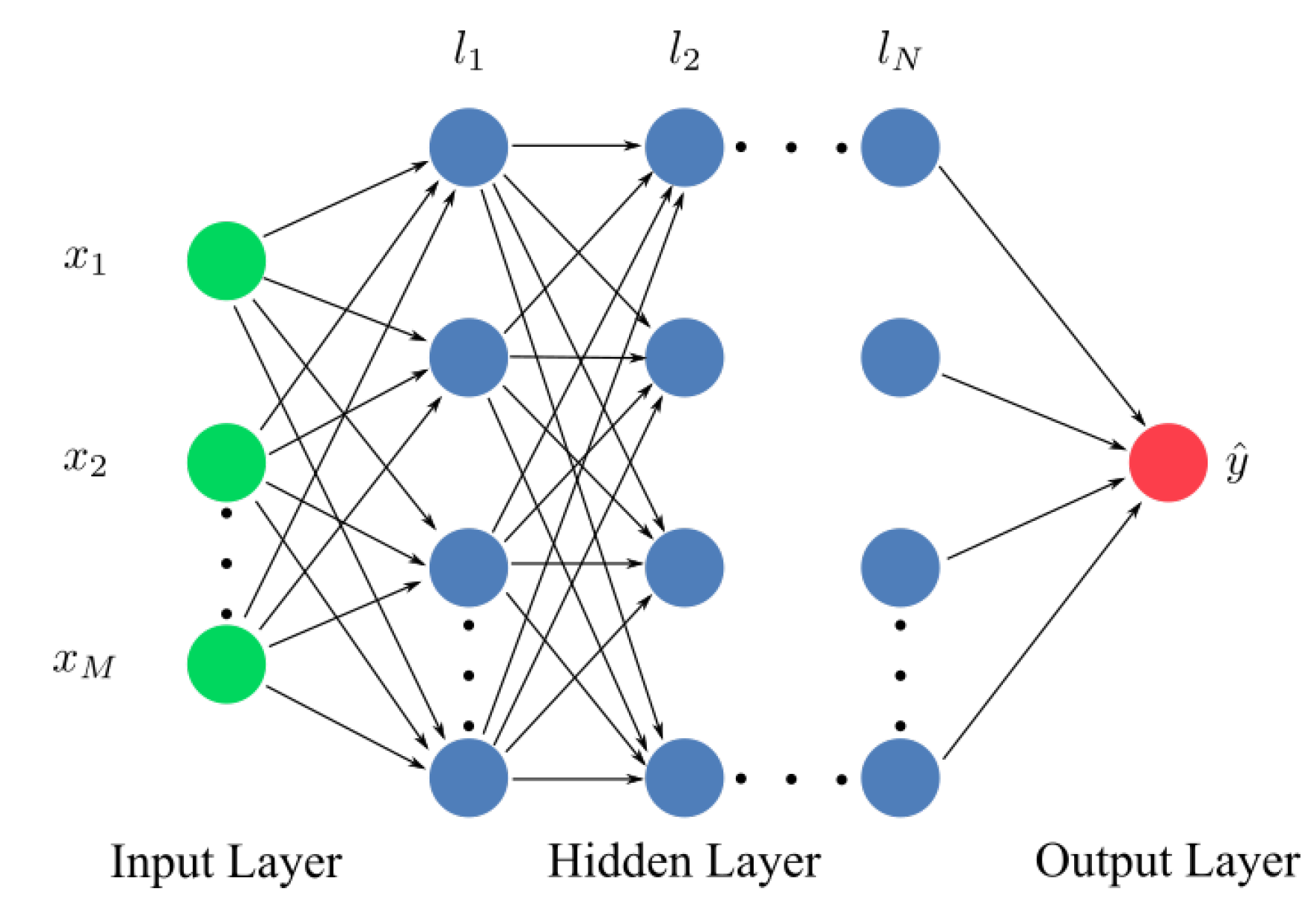
3.1. Neural Networks with Multi-Layer Perceptrons (MLP)
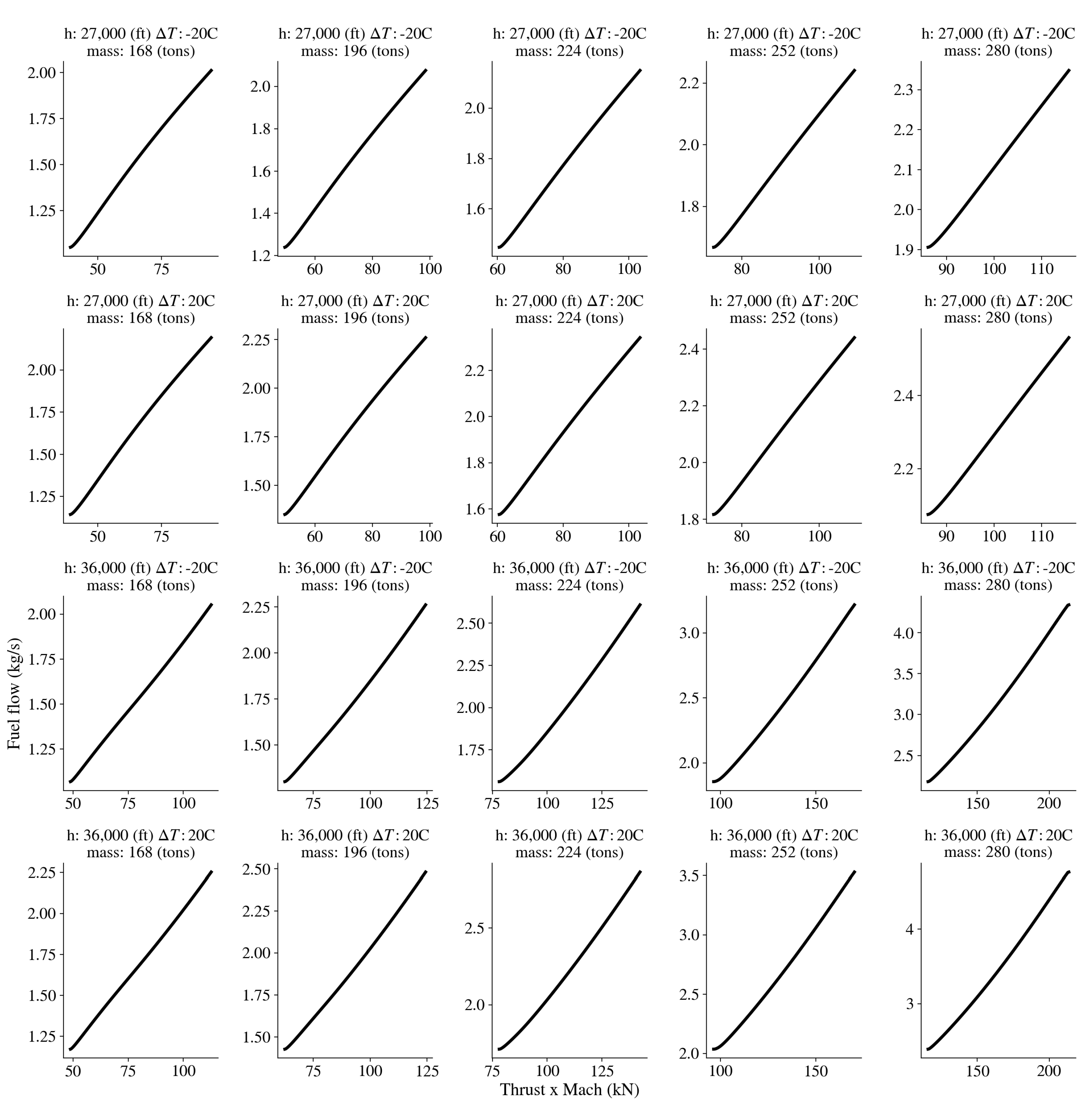
3.2. Cruise Fuel Consumption Dynamics
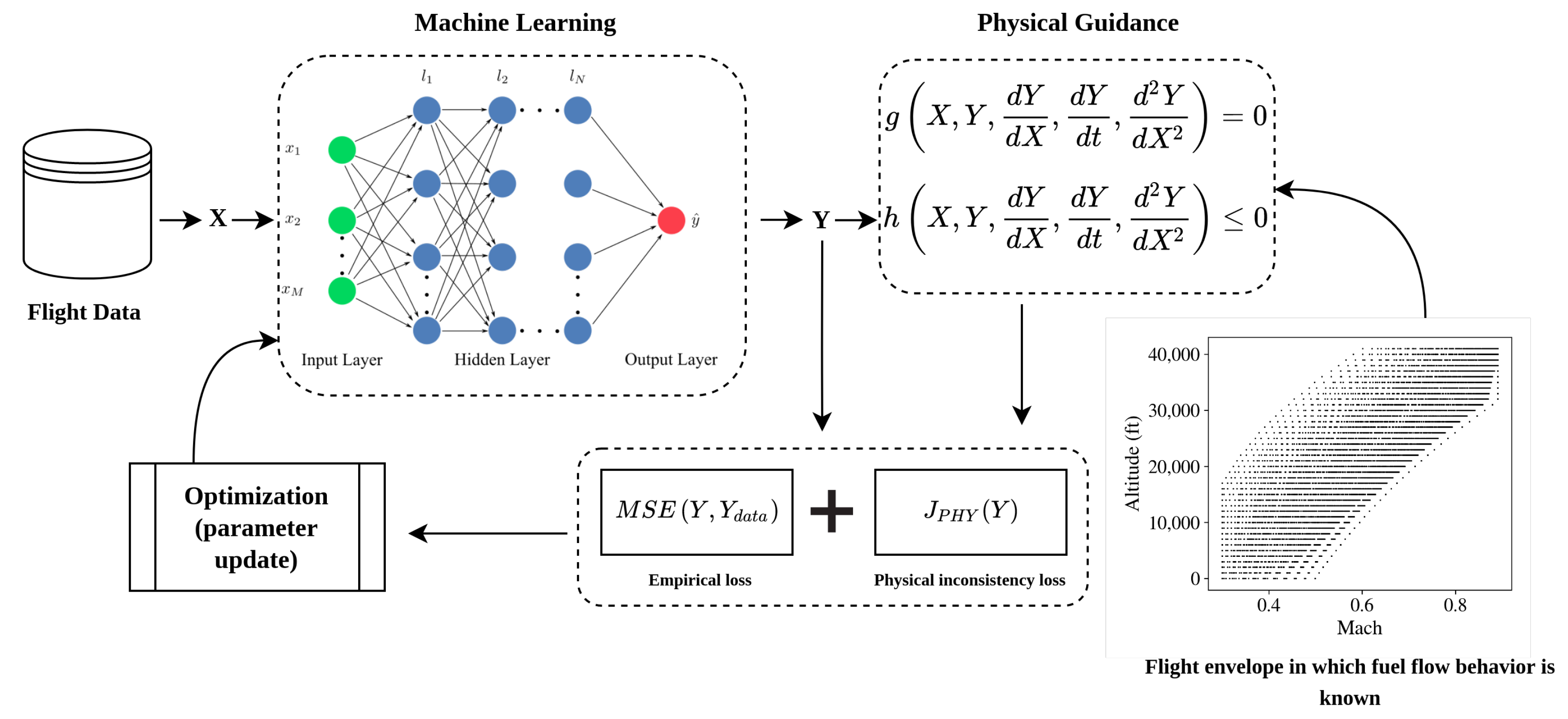
4. Methodology
4.1. Physics-Based Loss Function Design for Fuel Consumption
4.2. Implementation of the Physics Guided Loss Function
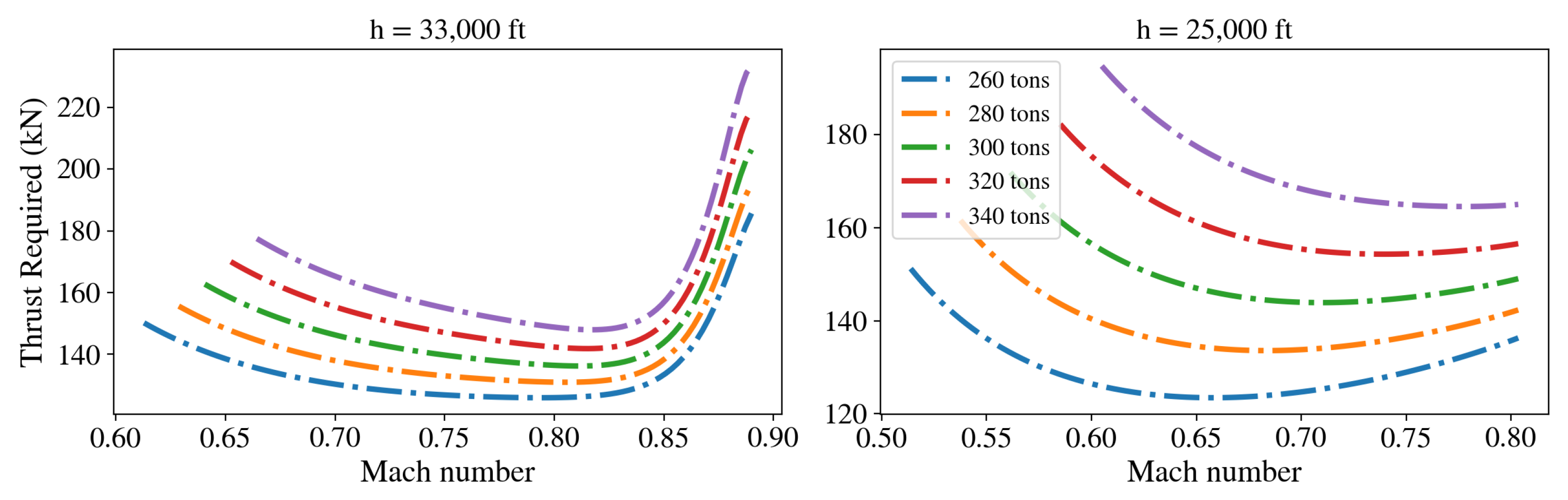
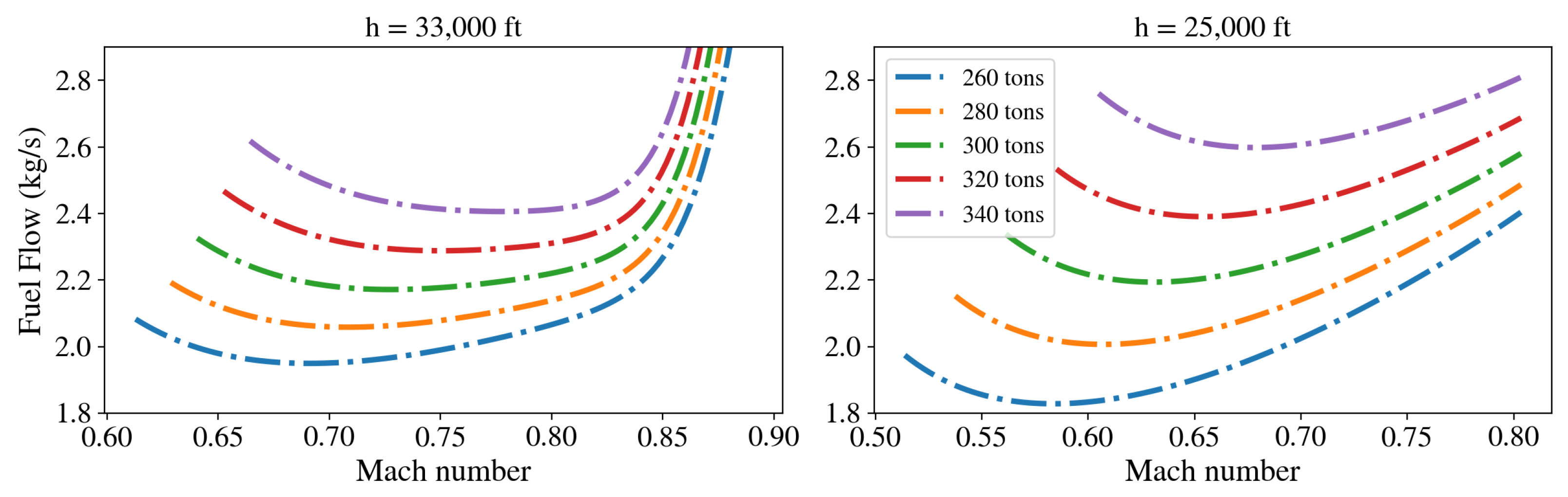
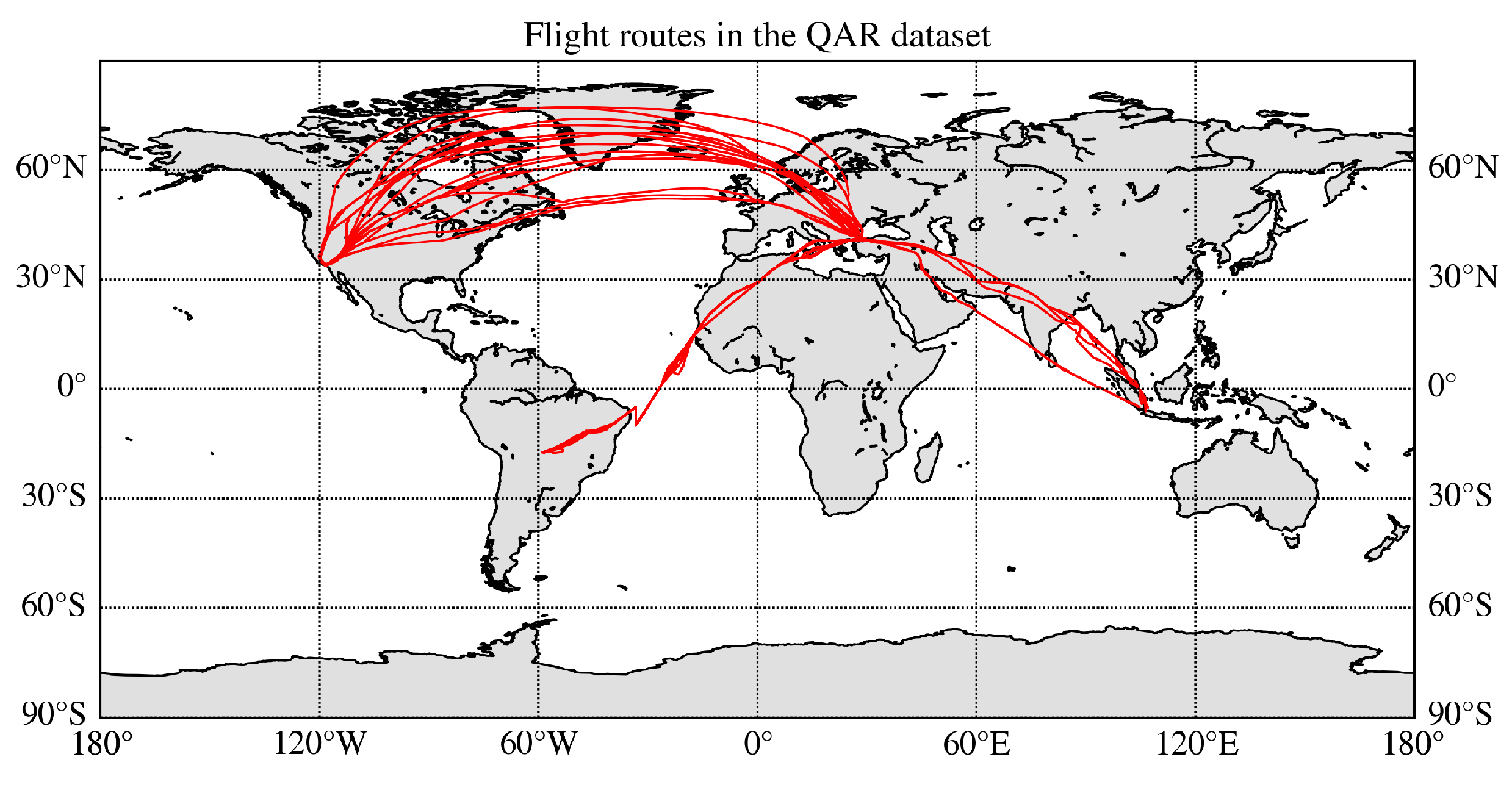
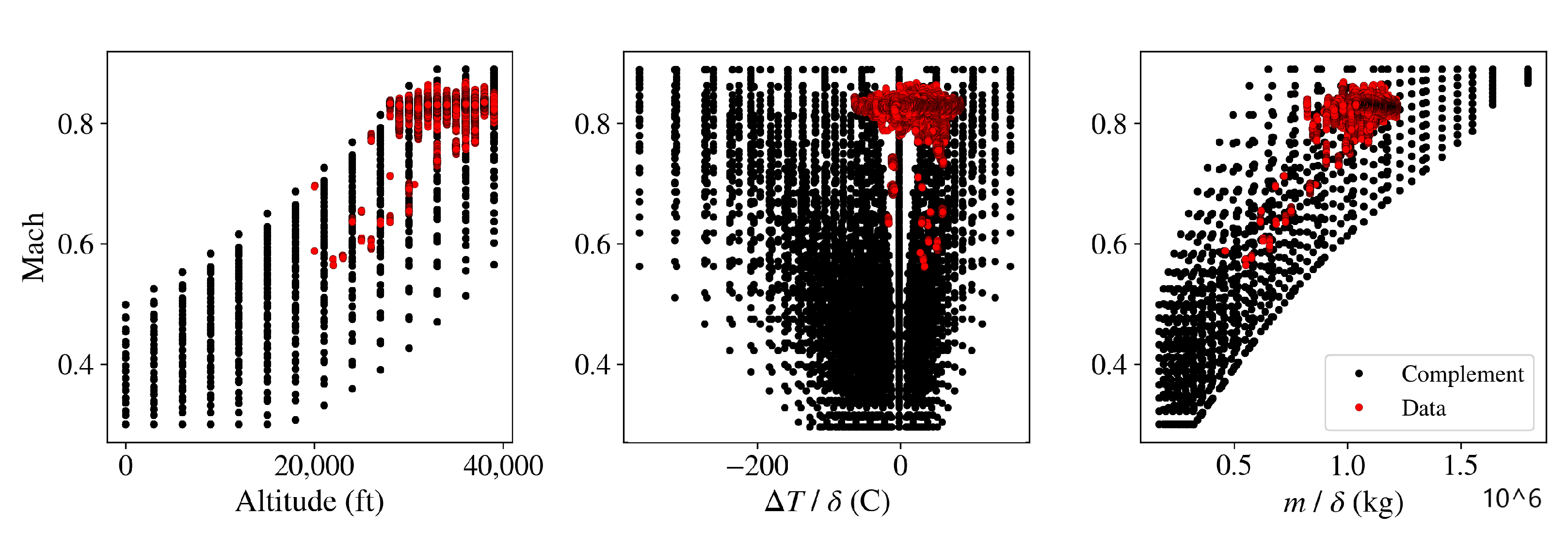
5. Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QAR | Quick Access Recorder |
| MLP | Multi-layer Perceptron |
| OEM | Original Equipment Manufacturer |
| BADA | Base of Aircraft Data |
| ML | Machine Learning |
| DL | Deep Learning |
| NN | Neural Networks |
| DNN | Deep Neural Networks |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
References
- Gallo, E.; Lopez-Leones, J.; Vilaplana, M.A.; Navarro, F.A.; Nuic, A. Trajectory computation infrastructure based on BADA aircraft performance model. In Proceedings of the 2007 IEEE/AIAA 26th Digital Avionics Systems Conference, Dallas, TX, USA, 21–25 October 2007; pp. 1.C.4-1–1.C.4-13. [Google Scholar]
- Jensen, L.; Hansman, R.J.; Venuti, J.C.; Reynolds, T. Commercial airline speed optimization strategies for reduced cruise fuel consumption. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; p. 4289. [Google Scholar]
- Malaek, S.; Alaeddini, A.; Gerren, D. Optimal maneuvers for aircraft conflict resolution based on efficient genetic webs. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2457–2472. [Google Scholar] [CrossRef]
- Rodrigues, L. A unified optimal control approach for maximum endurance and maximum range. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 385–391. [Google Scholar] [CrossRef]
- Brown, A.; Anderson, D. Trajectory optimization for high-altitude long endurance UAV maritime radar surveillance. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2406–2421. [Google Scholar] [CrossRef] [Green Version]
- Wasiuk, D.; Lowenberg, M.; Shallcross, D. An aircraft performance model implementation for the estimation of global and regional commercial aviation fuel burn and emissions. Transp. Res. Part D Transp. Environ. 2015, 35, 142–159. [Google Scholar] [CrossRef] [Green Version]
- Uzun, M.; Demirezen, M.U.; Koyuncu, E.; Inalhan, G. Design of a Hybrid Digital-Twin Flight Performance Model through Machine Learning. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; pp. 1–14. [Google Scholar]
- Uzun, M.; Demirezen, M.U.; Koyuncu, E.; Inalhan, G.; Lopez, J.; Vilaplana, M. Deep Learning Techniques for Improving Estimations of Key Parameters for Efficient Flight Planning. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–8. [Google Scholar]
- Sun, J.; Hoekstra, J.M.; Ellerbroek, J. OpenAP: An Open-Source Aircraft Performance Model for Air Transportation Studies and Simulations. Aerospace 2020, 7, 104. [Google Scholar] [CrossRef]
- Baumann, S.; Klingauf, U. Modeling of aircraft fuel consumption using machine learning algorithms. CEAS Aeronaut. J. 2020, 11, 277–287. [Google Scholar] [CrossRef]
- Swischuk, R.C.; Allaire, D.L. A Machine Learning Approach to Aircraft Sensor Error Detection and Correction. J. Comput. Inf. Sci. Eng. 2019, 19, 041009. [Google Scholar] [CrossRef]
- Behjat, A.; Zeng, C.; Rai, R.; Matei, I.; Doermann, D.; Chowdhury, S. A physics-aware learning architecture with input transfer networks for predictive modeling. Appl. Soft Comput. 2020, 96, 106665. [Google Scholar] [CrossRef]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Rad, K.R.; Zhou, W.; Maleki, A. Error bounds in estimating the out-of-sample prediction error using leave-one-out cross validation in high-dimensions. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics; Chiappa, S., Calandra, R., Eds.; Proceedings of Machine Learning Research (PMLR), 2020; Volume 108, pp. 4067–4077. Available online: https://arxiv.org/pdf/2003.01770v1.pdf (accessed on 2 November 2020).
- Wu, Z.; Li, X.; Du, J. Fuel Consumption Model of Aircraft in Descent Stage Based on DBN. IOP Conf. Ser. Mater. Sci. Eng. 2019, 569, 032005. [Google Scholar] [CrossRef]
- Chati, Y.S.; Balakrishnan, H. Data-Driven Modeling of Aircraft Engine Fuel Burn in Climb Out and Approach. Transp. Res. Rec. 2018, 2672, 1–11. [Google Scholar] [CrossRef]
- Muralidhar, N.; Bu, J.; Cao, Z.; He, L.; Ramakrishnan, N.; Tafti, D.; Karpatne, A. Physics-Guided Deep Learning for Drag Force Prediction in Dense Fluid-Particulate Systems. Big Data 2020, 8, 431–449. [Google Scholar] [CrossRef] [PubMed]
- Muralidhar, N.; Islam, M.R.; Marwah, M.; Karpatne, A.; Ramakrishnan, N. Incorporating prior domain knowledge into deep neural networks. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 36–45. [Google Scholar]
- Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-informed neural networks for power systems. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Yucesan, Y.A.; Viana, F.A. A physics-informed neural network for wind turbine main bearing fatigue. Int. J. Progn. Health Manag. 2020, 11, 17. [Google Scholar]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.; Hanson, P.C.; Watkins, W.; et al. Process-guided deep learning predictions of lake water temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef] [Green Version]
- Rai, R.; Sahu, C.K. Driven by Data or Derived Through Physics? A Review of Hybrid Physics Guided Machine Learning Techniques With Cyber-Physical System (CPS) Focus. IEEE Access 2020, 8, 71050–71073. [Google Scholar] [CrossRef]
- Shukla, K.; Di Leoni, P.C.; Blackshire, J.; Sparkman, D.; Karniadakis, G.E. Physics-Informed Neural Network for Ultrasound Nondestructive Quantification of Surface Breaking Cracks. J. Nondestruct. Eval. 2020, 39, 61. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Sidiropoulos, N.D. Physics-aware neural networks for distribution system state estimation. IEEE Trans. Power Syst. 2020, 35, 4347–4356. [Google Scholar] [CrossRef] [Green Version]
- Todd, J.C. Flight Data Recorder System. U.S. Patent 6,397,128, 28 May 2002. [Google Scholar]
- Wang, L.; Wu, C.; Sun, R. An analysis of flight Quick Access Recorder (QAR) data and its applications in preventing landing incidents. Reliab. Eng. Syst. Saf. 2014, 127, 86–96. [Google Scholar] [CrossRef]
- Sembiring, J.; Drees, L.; Holzapfel, F. Extracting unmeasured parameters based on quick access recorder data using parameter-estimation method. In Proceedings of the AIAA Atmospheric Flight Mechanics (AFM) Conference, Boston, MA, USA, 19–22 August 2013; p. 4848. [Google Scholar]
- Luo, H.; Zhong, S. Gas turbine engine gas path anomaly detection using deep learning with Gaussian distribution. In Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Chati, Y.S.; Balakrishnan, H. Aircraft engine performance study using flight data recorder archives. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; p. 4414. [Google Scholar]
- Chati, Y.S.; Balakrishnan, H. Statistical modeling of aircraft engine fuel flow rate. In Proceedings of the 30th Congress of the International Council of the Aeronautical Science, Daejeon, Korea, 25–30 September 2016. [Google Scholar]
- Chati, Y.S.; Balakrishnan, H. A Gaussian process regression approach to model aircraft engine fuel flow rate. In Proceedings of the 2017 ACM/IEEE 8th International Conference on Cyber-Physical Systems (ICCPS), Pittsburgh, PA, USA, 18–21 April 2017; pp. 131–140. [Google Scholar]
- Baklacioglu, T. Modeling the fuel flow-rate of transport aircraft during flight phases using genetic algorithm-optimized neural networks. Aerosp. Sci. Technol. 2016, 49, 52–62. [Google Scholar] [CrossRef]
- Huang, C.; Xu, Y.; Johnson, M.E. Statistical modeling of the fuel flow rate of GA piston engine aircraft using flight operational data. Transp. Res. Part D Transp. Environ. 2017, 53, 50–62. [Google Scholar] [CrossRef]
- Khadilkar, H.; Balakrishnan, H. Estimation of aircraft taxi fuel burn using flight data recorder archives. Transp. Res. Part D Transp. Environ. 2012, 17, 532–537. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Roberson, B. Fuel Conservation Strategies: Cost index explained. Boeing Aero Q. 2007, 2, 26–28. [Google Scholar]
- Abu-Mostafa, Y.S. Learning from hints in neural networks. J. Complex. 1990, 6, 192–198. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, F.; Lawson, K.; Ouyang, W.; Appling, A.; Oliver, S.; Shen, C. Exploring the exceptional performance of a deep learning stream temperature model and the value of streamflow data. Environ. Res. Lett. 2020, 16, 024025. [Google Scholar]
- Ramadhan, A.; Marshall, J.; Souza, A.; Wagner, G.L.; Ponnapati, M.; Rackauckas, C. Capturing missing physics in climate model parameterizations using neural differential equations. arXiv 2020, arXiv:2010.12559. [Google Scholar]
- Winkler, D.A.; Le, T.C. Performance of deep and shallow neural networks, the universal approximation theorem, activity cliffs, and QSAR. Mol. Inform. 2017, 36, 1600118. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Chen, H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 911–917. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Nuic, A.; Poinsot, C.; Iagaru, M.G.; Gallo, E.; Navarro, F.A.; Querejeta, C. Advanced aircraft performance modeling for ATM: Enhancements to the BADA model. In Proceedings of the 24th Digital Avionics System Conference, AIAA/IEEE, Washington, DC, USA, 30 October–3 November 2005; pp. 1–14. [Google Scholar]
- Airbus Customer Services. Getting to Grips with Aircraft Performance; Technical Report; Airbus Customer Services: Blagnac, France, 2002. [Google Scholar]
- Anderson, D. Cruise Performance Monitoring. Boeing Aero Magazine. 2006, pp. 5–11. Available online: http://www.boeing.com/commercial/aeromagazine/articles/qtr_4_06/AERO_Q406_article2.pdf (accessed on 2 November 2020).
- Mouillet, V.; Nuić, A.; Casado, E.; Leonés, J.L. Evaluation of the Applicability of a Modern Aircraft Performance Model to Trajectory Optimization. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–9. [Google Scholar]
- Yechout, T.R. Introduction to Aircraft Flight Mechanics; Aiaa: Blacksburg, VA, USA, 2003; pp. 68–75. [Google Scholar]
- Center, E.E. User Manual for the Base of Aircraft Data (BADA) Revison 3.11; Eurocontrol: Brussels, Belgium, 2013. [Google Scholar]
- Blake, W. Jet Transport Performance Methods; Boeing Commercial Airplanes: Seattle, WA, USA, 2009; Volume 6-1420. [Google Scholar]
- Sudolsky, M. ARINC 573/717, 767 and 647A: The Logical Choice for Maintenance Recording And IVHM Interface Control or Frame Updates. In Proceedings of the Prognostics and Health Management Society, San Diego, CA, USA, 27 September–1 October 2009. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Luo, L.; Xiong, Y.; Liu, Y. Adaptive Gradient Methods with Dynamic Bound of Learning Rate. arXiv 2019, arXiv:1902.09843.8024. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BA, Canada, 8–14 December 2019; pp. 8024–8035. [Google Scholar]
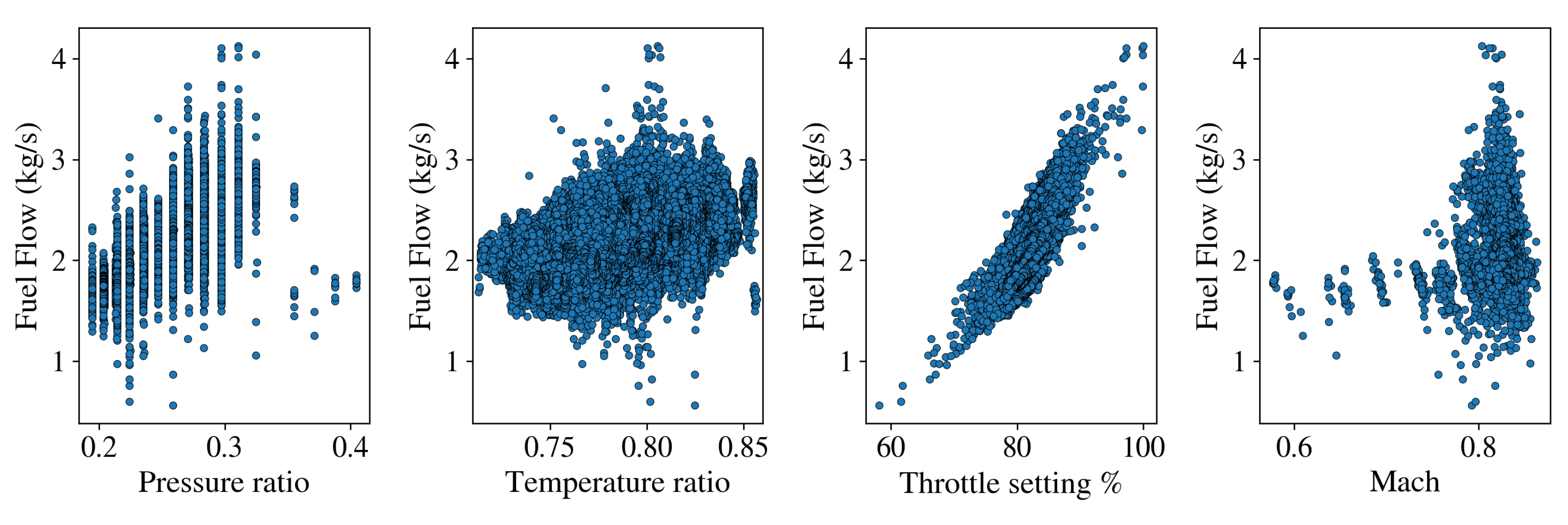

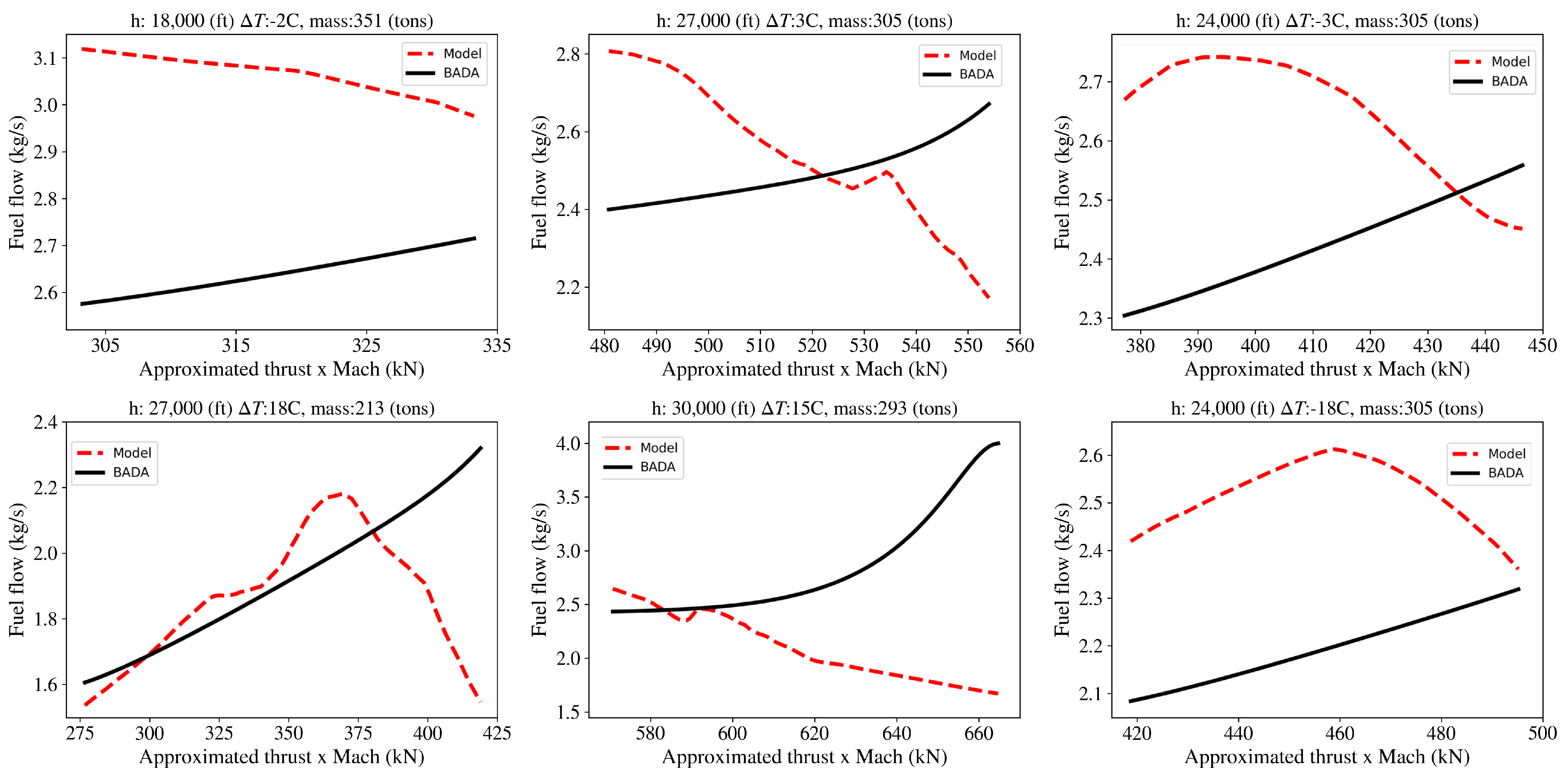
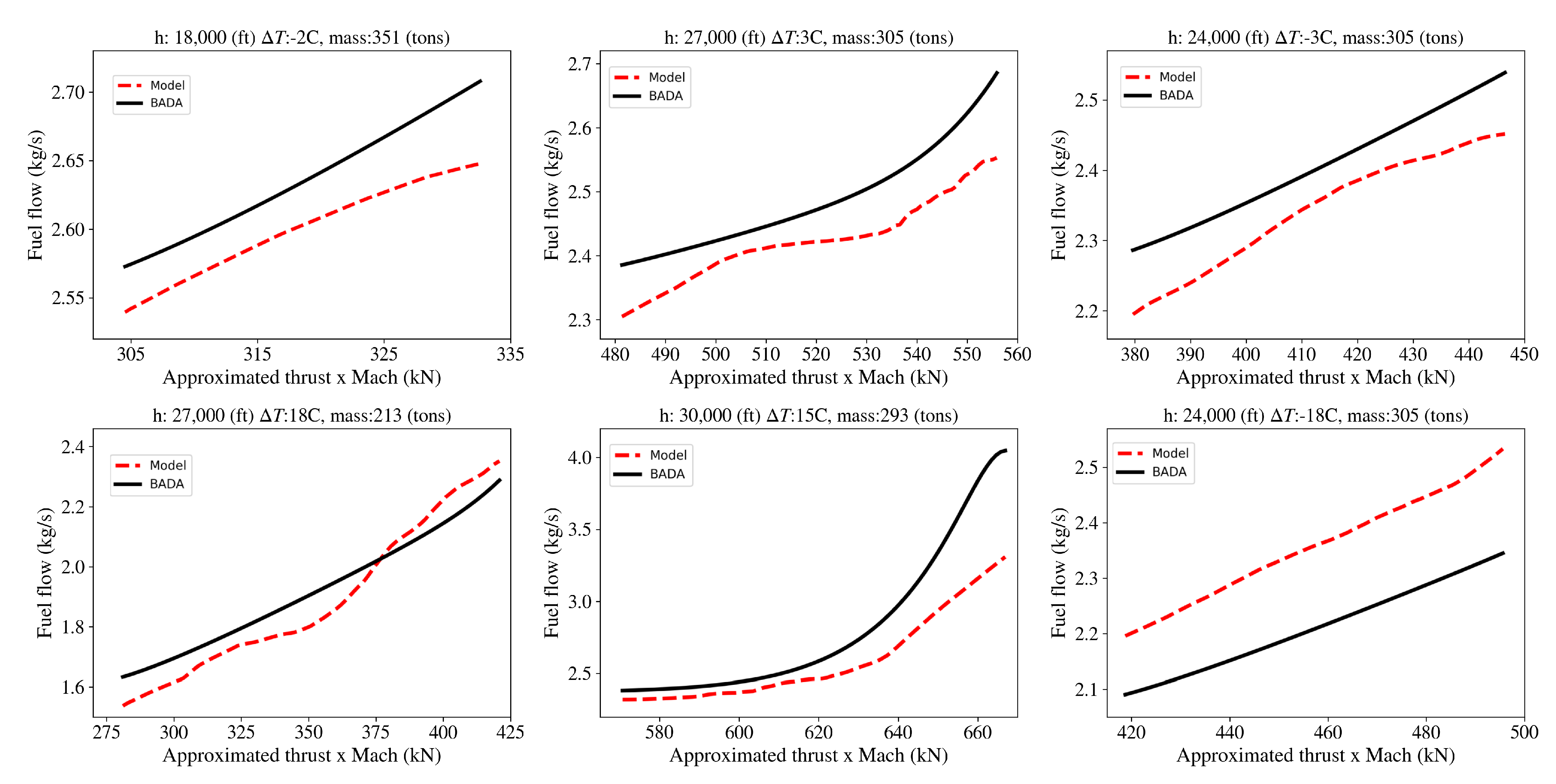
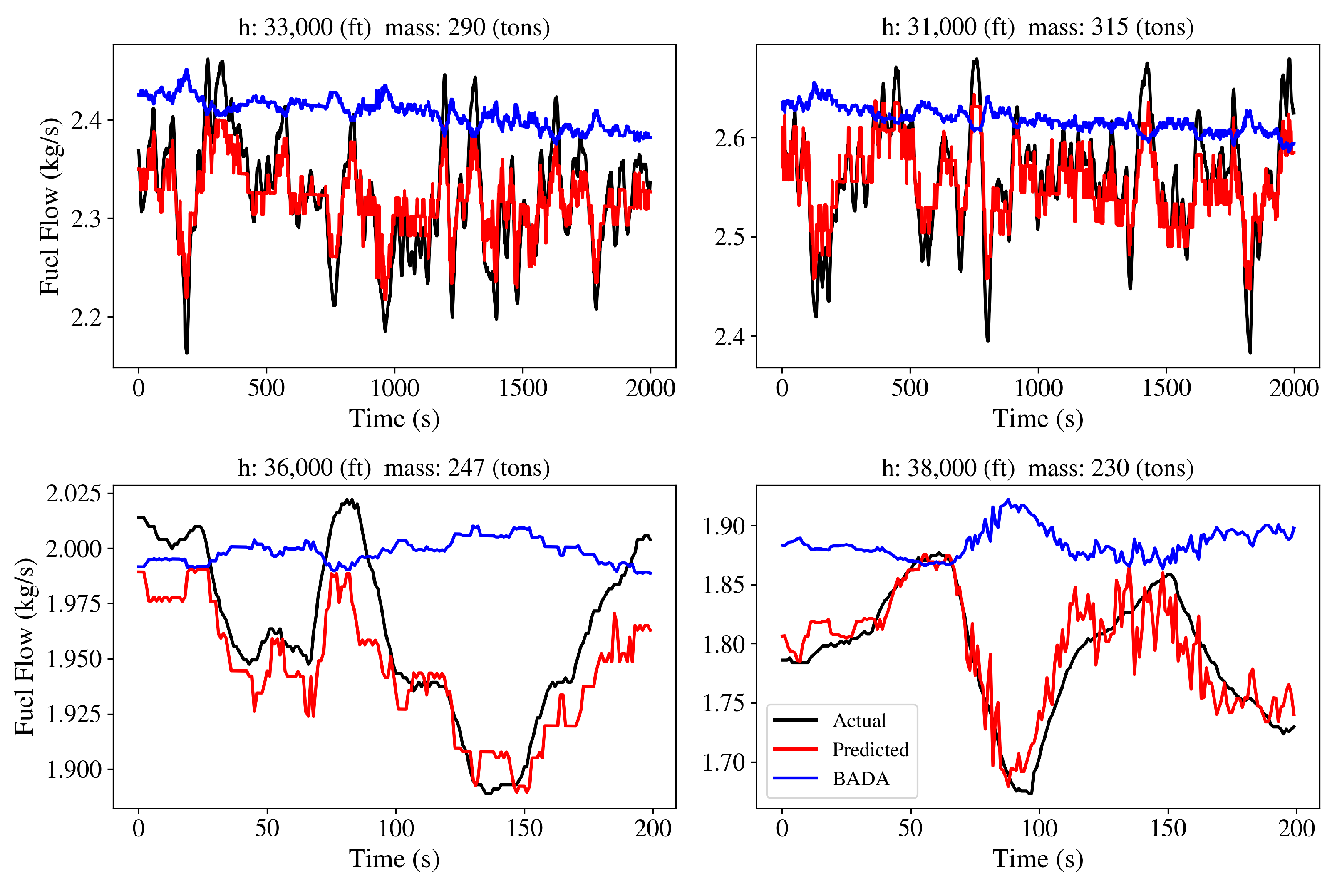
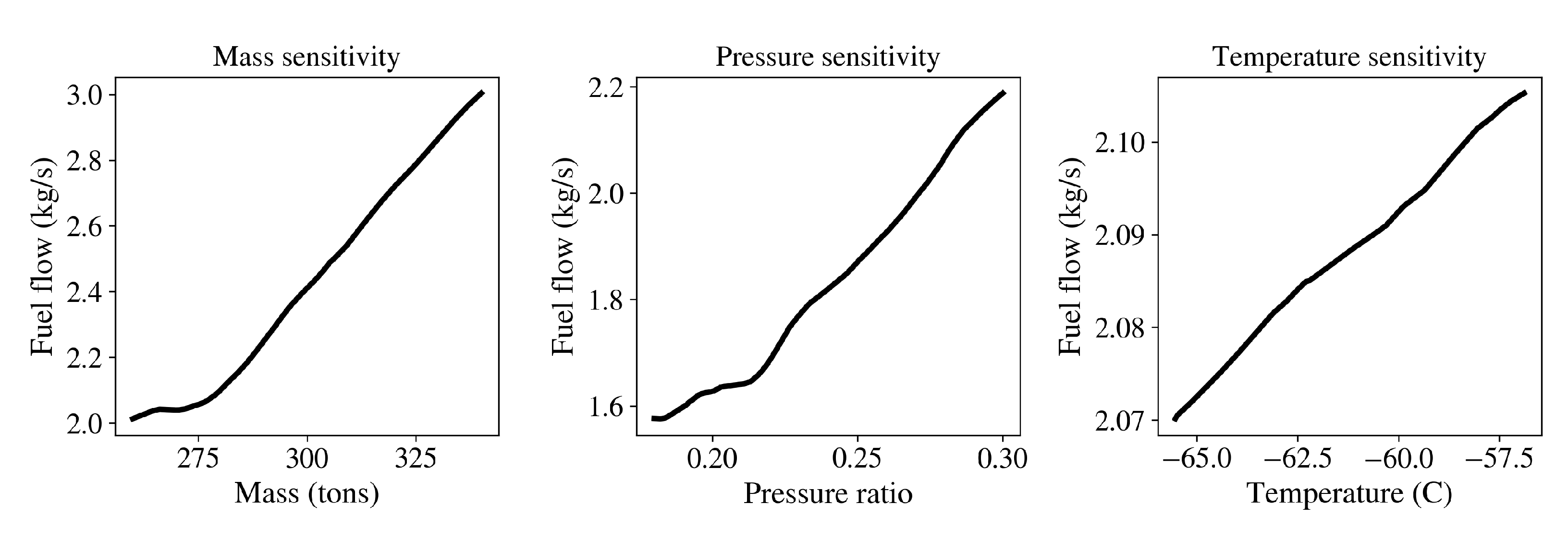
| Approach | Parameters That Affect Fuel Consumption |
|---|---|
| Model-based | Pressure ratio , temperature ratio , throttle , Mach number M |
| Data-driven | Pressure ratio , temperature ratio , throttle , mass , true airspeed |
| h | Barometric altitude [ft] |
| Static air temperature [C] | |
| Calibrated airspeed [kt] | |
| M | Mach speed |
| Aircraft mass [kg] | |
| Fuel flow from engines [lb/hr] | |
| Throttle positions of engines 1 and 2 | |
| Wind speed [kt] | |
| Wind direction [deg] | |
| True heading [deg] | |
| Flap deflection [deg] | |
| Landing gear status | |
| Speed break deflection [deg] | |
| APU fuel consumption [lb/hr] |
| Parameter | Min | Max |
|---|---|---|
| Altitude h (ft) | 0 | 41,000 |
| ISA deviation (C) | −77 | 50 |
| Mass (kg) | 167,000 | 353,000 |
| Criteria | BADA4 | SVR | LR | NN | DNN | Proposed | |
|---|---|---|---|---|---|---|---|
| MAE [kg/h] | 291 | 215 | 195 | 201 | 172 | 127 | 133 |
| MAPE % | 3.712 | 2.632 | 2.677 | 2.695 | 1.897 | 1.521 | 1.568 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzun, M.; Demirezen, M.U.; Inalhan, G. Physics Guided Deep Learning for Data-Driven Aircraft Fuel Consumption Modeling. Aerospace 2021, 8, 44. https://doi.org/10.3390/aerospace8020044
Uzun M, Demirezen MU, Inalhan G. Physics Guided Deep Learning for Data-Driven Aircraft Fuel Consumption Modeling. Aerospace. 2021; 8(2):44. https://doi.org/10.3390/aerospace8020044
Chicago/Turabian StyleUzun, Mevlut, Mustafa Umut Demirezen, and Gokhan Inalhan. 2021. "Physics Guided Deep Learning for Data-Driven Aircraft Fuel Consumption Modeling" Aerospace 8, no. 2: 44. https://doi.org/10.3390/aerospace8020044
APA StyleUzun, M., Demirezen, M. U., & Inalhan, G. (2021). Physics Guided Deep Learning for Data-Driven Aircraft Fuel Consumption Modeling. Aerospace, 8(2), 44. https://doi.org/10.3390/aerospace8020044







