Climate Impact Mitigation Potential of European Air Traffic in a Weather Situation with Strong Contrail Formation †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Algorithmic Climate Change Functions
2.2. Trajectory Optimization
2.2.1. General Optimal Control Problem Formulation
2.2.2. Choice of State, Control, and Path Vectors
2.2.3. Objective Function
2.2.4. Dynamic Constraints
3. Results
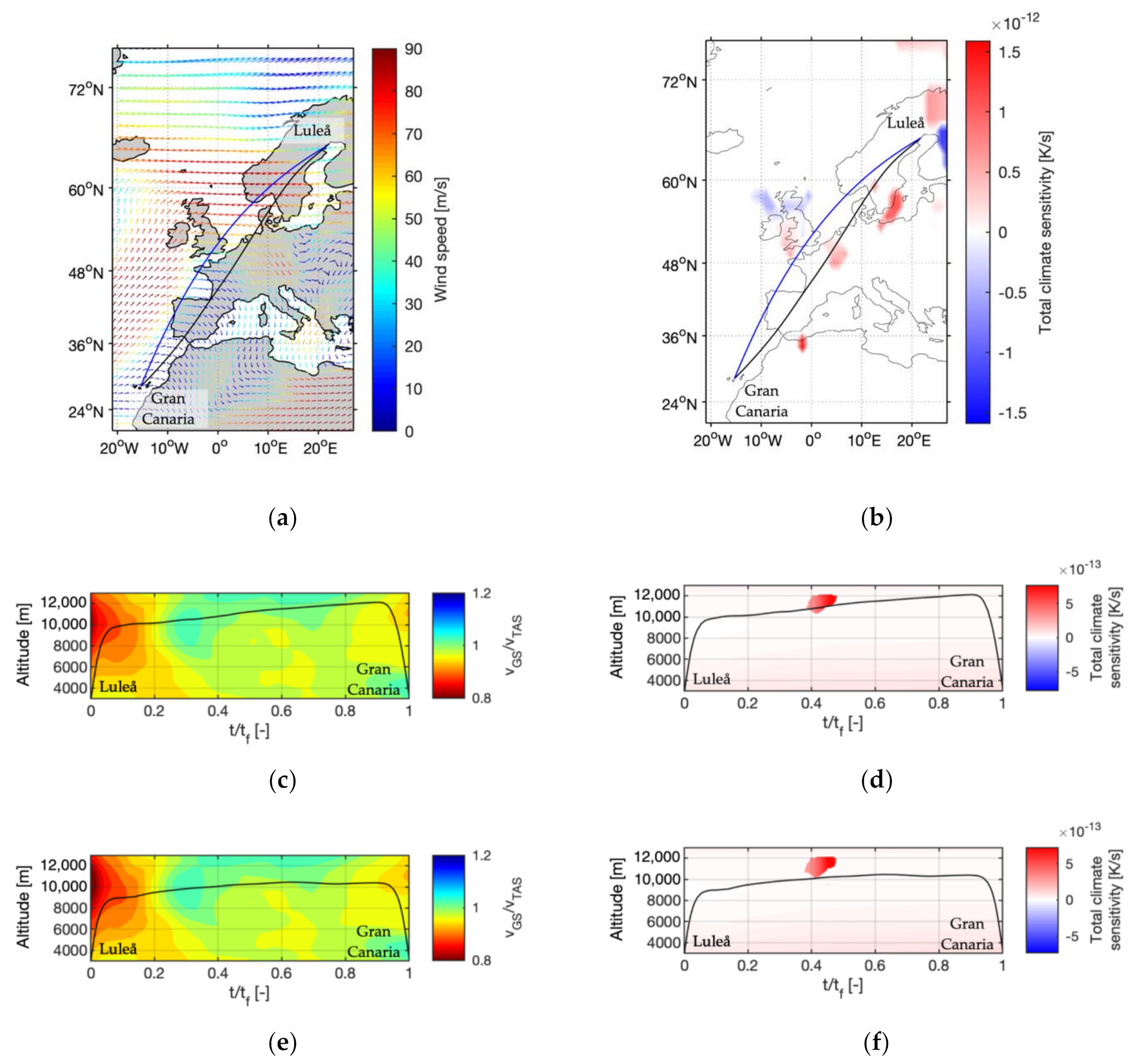
3.1. One-Day Case Study of European Air Traffic
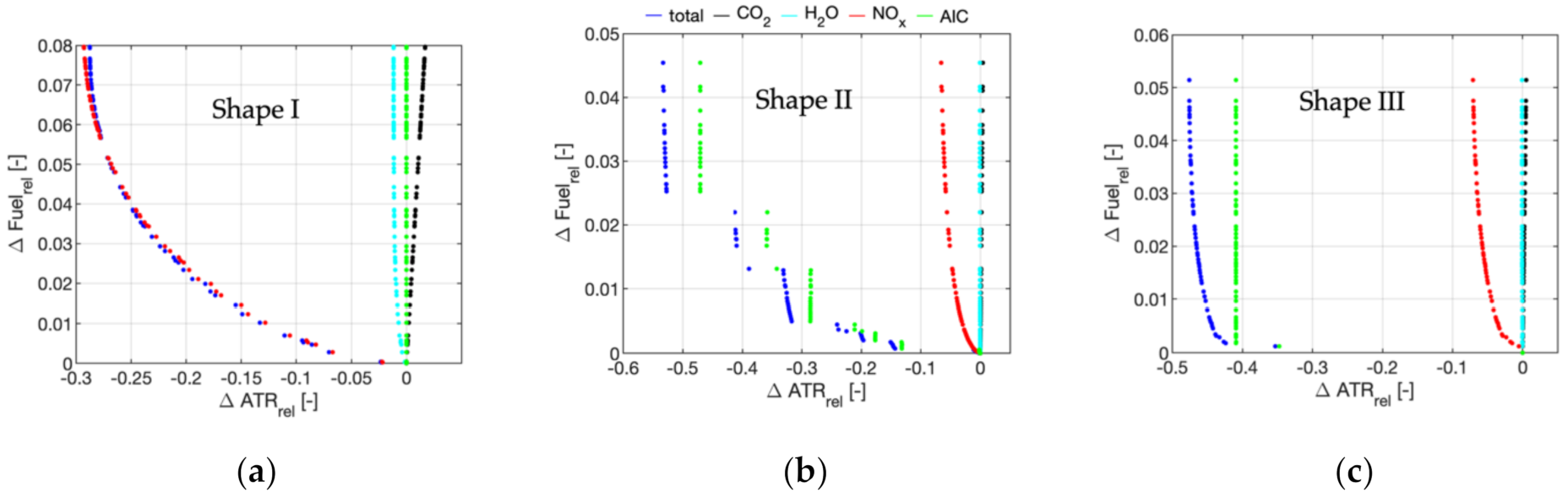
3.2. Results for Individual Routes
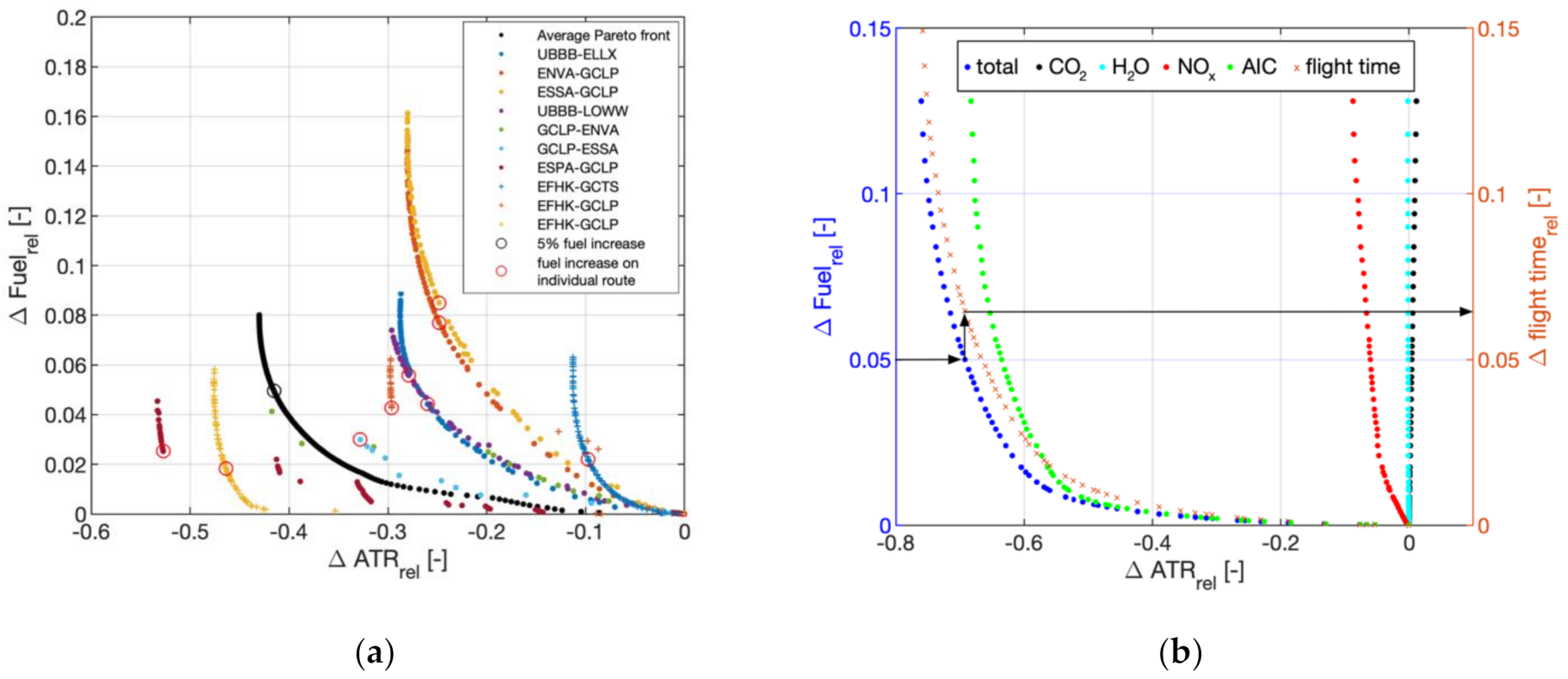
3.3. Consolidated Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| aCCF | Algorithmic Climate Change Function |
| ATC | Air Traffic Control |
| ATM4E | Air Traffic Management for Environment |
| ATR | Average Temperature Response |
| BADA | Base of Aircraft Data |
| CCF | Climate Change Function |
| DDR | Demand Data Repository |
| DLR | Deutsches Zentrum für Luft- und Raumfahrt (German Aerospace Center) |
| ECAC | European Civil Aviation Conference |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| Eco2Fly ERA | Ecological and Economical Flying ECMWF Reanalysis |
| EU | European Union |
| REACT4C | Reducing Emissions from Aviation by Changing Trajectories for the benefit of Climate |
| TOM | Trajectory Optimization Module |
References
- Lee, D.S. Aviation and global climate change in the 21st century. Atmos. Environ. 2009, 43, 352020133537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schumann, U.; Graf, K.; Mannstein, H. Potential to reduce the climate impact of aviation by flight level changes. In Proceedings of the 3rd AIAA Atmospheric Space Environments Conference, Honululu, HI, USA, 27–30 June 2011. [Google Scholar]
- Sridhar, B.; Chen, N.Y.; Ng, H.K. Energy efficient contrail mitigation strategies for reducing the environmental impact of aviation. In Proceedings of the 10th USA/Europe Air Traffic Management Research and Development Seminar, Chicago, IL, USA, 10–13 June 2013. [Google Scholar]
- Hartjes, S.; Hendriks, T.; Visser, H.G. Contrail mitigation through 3D aircraft trajectory optimization. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- Zou, B.; Buxi, G.S.; Hansen, M. Optimal 4-D aircraft trajectories in a Contrail-sensitive Environment. Netw. Spat. Econ. 2016, 16, 415–446. [Google Scholar] [CrossRef]
- Matthes, S. Climate-optimised flight planning–REACT4C. In Innovation for a Sustainable Aviation in a Global Environment, Proceedings of the Sixth European Aeronautics Days 2011, Madrid, Spain, 30 March--1 April 2011; IOS Press & European Union: Madrid, Spain, 2012; ISBN 978-92-79-22968-8. [Google Scholar]
- Grewe, V.; Frömming, C.; Matthes, S.; Brinkop, S.; Ponater, M.; Dietmüller, S.; Jöckel, P.; Garny, H.; Tsati, E.; Dahlmann, K.; et al. Aircraft routing with minimal climate impact: The REACT4C climate cost function modelling approach (V1.0). Geosci. Model Dev. 2014, 7, 175–201. [Google Scholar] [CrossRef] [Green Version]
- Irvine, E.A.; Hoskins, B.J.; Shine, K.P.; Lunnon, R.W.; Frömming, C. Characterizing North Atlantic weather patterns for climate-optimal aircraft routing. Meteorol. Appl. 2013, 20, 80–93. [Google Scholar] [CrossRef] [Green Version]
- Grewe, V.; Champougny, T.; Matthes, S.; Frömming, C.; Brinkop, S.; Søvde, O.; Irvine, E.A.; Halscheidt, L. Reduction of the air traffic’s contribution to climate change: A REACT4C case study. Atmos. Environ. 2014, 94, 616–625. [Google Scholar] [CrossRef] [Green Version]
- Grewe, V.; Matthes, S.; Frömming, C.; Brinkop, S.; Jöckel, P.; Gierens, K.; Champougny, T.; Fuglestvedt, J.; Haslerud, A.; Irvine, E.A.; et al. Feasibility of climate-optimized air traffic routing for trans-atlantic flights. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Lührs, B.; Niklaß, M.; Frömming, C.; Grewe, V.; Gollnick, V. Cost-Benefit Assessment of Climate and Weather Optimized Trajectories for different North Atlantic Weather Patterns. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences (ICAS), Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Matthes, S.; Grewe, V.; Dahlmann, K.; Frömming, C.; Irvine, E.; Lim, L.; Linke, F.; Lührs, B.; Owen, B.; Shine, K.P.; et al. A Concept for Multi-Criteria Environmental Assessment of Aircraft Trajectories. Aerospace 2017, 4, 42. [Google Scholar] [CrossRef] [Green Version]
- Frömming, C.; Grewe, V.; Brinkop, S.; Jöckel, P.; Haslerud, A.S.; Rosanka, S.; van Manen, J.; Matthes, S. Influence of the actual weather situation on non-CO2 aviation climate effects: The REACT4C Climate Change Functions. Atmos. Chem. Phys. Discuss. 2020. under review. [Google Scholar] [CrossRef]
- Van Manen, J.; Grewe, V. Algorithmic climate change functions for the use in eco-efficient flight planning. Trans. Res. Part D Trans. Environ. 2019, 67, 388–405. [Google Scholar] [CrossRef]
- Yin, F.; Grewe, V.; van Manen, J.; Matthes, S.; Yamashita, H.; Irvine, E.A.; Shine, K.P.; Lührs, B.; Linke, F. Verification of the ozone algorithmic climate change functions for predicting the short-term NOx effects from aviation en-route. In Proceedings of the 8th International Conference on Air Transportation (ICRAT), Barcelona, Spain, 26–29 June 2018. [Google Scholar]
- Yin, F.; Grewe, V.; Matthes, S.; Yamashita, H.; Irvine, E.A.; Shine, K.P.; Lührs, B.; Linke, F. Predicting the climate impact of aviation for en-route emissions: The algorithmic climate change function sub model ACCF 1.0 of EMAC 2.53. Geosci. Model Dev. Discuss. 2020. in preparation. [Google Scholar]
- Yamashita, H.; Yin, F.; Grewe, V.; Jöckel, P.; Matthes, S.; Kern, B.; Dahlmann, K.; Frömming, C. Various aircraft routing options for air traffic simulation in the chemistry-climate model EMAC 2.53: AirTraf 2.0. Geosci. Model Dev. Discuss. 2020. under review. [Google Scholar] [CrossRef]
- Appleman, H. The Formation of Exhaust Condensation Trails by Jet Aircraft. Bull. Am. Meteorol. Soc. 1953, 34, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Lührs, B.; Niklaß, M.; Frömming, C.; Grewe, V.; Gollnick, V. Cost-Benefit Assessment of 2D- and 3D Climate and Weather Optimized Trajectories. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB Software for Solving Multiple-Phase Optimal Control Problems Using hp-Adaptive Gaussian Quadrature Collocation Methods and Sparse Nonlinear Programming. ACM Trans. Math. Softw. 2014, 41, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Progr. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Nuic, A.; Mouillet, V. User Manual for the Base of Aircraft Data (BADA) Family 4; ECC Technical/Scientific Report No. 12/11/22-58; Eurocontrol: Brussels, Belgium, 2012. [Google Scholar]
- DuBois, D.; Paynter, G. ‘Fuel Flow Method 2’ for Estimating Aircraft Emissions. SAE Trans. 2006, 115, 1–14. [Google Scholar]
- Jelinek, F. Advanced Emission Model (AEM3) v1.5-Validation Report; EEC Report EEC/SEE/2004/004; Eurocontrol: Brussels, Belgium, 2004. [Google Scholar]
- Dee, D.P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Matthes, S.; Lührs, B.; Dahlmann, K.; Linke, F.; Grewe, V.; Yin, F.; Shine, K.P. Climate-Optimized Trajectories and Robust Mitigation Potential: Flying ATM4E. Aerospace 2020, 7, 156. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lührs, B.; Linke, F.; Matthes, S.; Grewe, V.; Yin, F. Climate Impact Mitigation Potential of European Air Traffic in a Weather Situation with Strong Contrail Formation. Aerospace 2021, 8, 50. https://doi.org/10.3390/aerospace8020050
Lührs B, Linke F, Matthes S, Grewe V, Yin F. Climate Impact Mitigation Potential of European Air Traffic in a Weather Situation with Strong Contrail Formation. Aerospace. 2021; 8(2):50. https://doi.org/10.3390/aerospace8020050
Chicago/Turabian StyleLührs, Benjamin, Florian Linke, Sigrun Matthes, Volker Grewe, and Feijia Yin. 2021. "Climate Impact Mitigation Potential of European Air Traffic in a Weather Situation with Strong Contrail Formation" Aerospace 8, no. 2: 50. https://doi.org/10.3390/aerospace8020050
APA StyleLührs, B., Linke, F., Matthes, S., Grewe, V., & Yin, F. (2021). Climate Impact Mitigation Potential of European Air Traffic in a Weather Situation with Strong Contrail Formation. Aerospace, 8(2), 50. https://doi.org/10.3390/aerospace8020050







