Three different methods to design the phasing maneuver are proposed in this section. The main differences are the computation of initial conditions necessary to compute the invariant manifolds. The first method is based on the Lambert’s problem initial guess followed by a differential correction, the second method uses a Hohmann solution as initial guess and then the differential correction, the third method, instead, is based on an optimization approach that may lead to residual errors.
In this work we assume a two-impulse maneuver, so phasing can be computed in two steps:
The positions are then normalized to the Earth–Moon distance, and the velocities are normalized to the orbit semimajor axis times the mean motion of the CR3BP model orbit, for better numerical conditioning.
3.1. Phasing Using Lambert’s Initial Conditions
A classical procedure for determining an initial transfer velocity is given by the solution of the problem proposed by Lambert in the 18th century. It requires finding all possible trajectories (or the optimal trajectory)
that connect an initial point
at time
, with a final point
at time
, under a gravitational field, and with the time of flight specified by the difference
. For the two-body case, the solution is known to provide two unique trajectories (long TOF and short TOF), which satisfy the boundaries [
16,
17]. In the case of CR3BP or of a gravitational field generated by three or more masses, the problem has many possible numerical solutions for any specified initial data set (such as the terminal transfer positions, transfer time, and number of complete orbits around the attracting center). This is the main reason for using Lambert’s problem in the two-body setting.
The computation of a first guess on the initial velocity is crucial, and can be done using the procedure in [
1], with final position and final velocity written in terms of initial position, initial velocity for a given time of flight. The required initial conditions in position and velocity can be found using the
f and
g Lagrange coefficients formulation.
The Lagrange coefficients, which are functions of true anomaly, and time, and their time derivatives are computed as in [
17,
18], although more recent algorithms could also be used, such as those in [
10,
19,
20,
21].
Once a set of initial conditions is obtained, we fix a time of flight, and the trajectory is propagated using differential correction on the linearized dynamics to reach the final state. This procedure provides the system’s transition matrix. The error on final position and the inverse of the transition matrix are then used to correct the initial velocity value, and this procedure continues until the position at the final time is below the constraints specified above.
An example is shown in
Figure 5. In the figure, the blue line corresponds to the trajectory evolution based on Lambert’s theorem in the two-body problem. The black line is the result of the differential correction propagation using the CR3BP model. The final position corresponds to an eccentric anomaly of 180 degrees. The time of flight is obtained from Lambert’s theorem application from [
17], or from [
1], and results in a value of 15.72 h.
The plots on the left in
Figure 6 shows the evolution of the trajectory propagated for different (longer) times of flight. 9 different time intervals were used from 15.72 to 78.6 h (0.655–3.275 days). Transfer trajectories propagated to the aposelene region as final point, with different TOF are shown in the same figure on the right plots. The out-of-plane nature of the transfer orbits is evident from the simulations.
Figure 7 shows a summary of the tests carried out for the direct transfer using Lambert’s first guess and the propagation via differential correction. The figure presents the results as function of different TOF and different final positions in the vicinity of the target orbit, combining what is described in the previous figures. The transfer trajectories were computed according to
Table 3, where
T is the target orbit period. The table shows propagation time versus the achieved final true anomaly.
The computation of the
V for the transfers shown above is performed assuming the following vector relationship:
The fuel expenditure depends on many factors. In this paper, we relate the
to the stable manifold propagation time, and the time of flight, in order to obtain a general picture of the phasing requirements. The results are summarized in
Figure 8.
In the figure, the x-axis represents the propagation time (in hours) of the stable manifold from LLO to the final position location; the nine points show selected locations of the manifold starting from the aposelene. The y-axis represents the selected duration (in hours) of the phasing maneuver, and the z-axis shows the associated
consumption computed according to Equation (
5). A total of 81 runs were performed, in order to create the grid in the figure. The total propagation time was selected to be about 62 h.
Consider, for instance, the two-dimensional projections of
Figure 8 shown in
Figure 9. The point in the figure indicates the amount of
used for a direct phasing of 78.6 h, with a manifold propagated at time 180.8 h. From the same figure we can also determine the minimum
, which is about 660.6 m/s. Combining the results in
Figure 7 and
Figure 8, we obtain the phasing trajectory, which produces the least expenditure in
. This is shown in
Figure 10.
3.3. Numerical Optimization
This section describes the design of a phasing sequence via numerical optimization. A phasing trajectory is designed under the CR3BP dynamic model, based on critical parameters such as position error, , TOF, and number of impulses.
The main objective of this procedure is to evaluate the relative influence between final state error and fuel consumption. Therefore, a soft constraint optimization on the state was selected, which provides useful trade-off at the preliminary stage. This approach allowed information on the variation of fuel consumption as weights are changed in the cost function.
Consider the reference equations for the CR3BP model described by Equation (
1) or Equation (
2). The approach used is the selection of an appropriate cost function, whose minimization will produce a set of optimal (or sub-optimal) maneuvers. The optimization uses a nonlinear programming technique taken from [
22]. The general problem can be formulated as that of minimizing a cost function
with respect to the state vector
with constraints given by:
The function uses a gradient-based method that is designed to work with problems that are continuous, with at least continuous first derivatives. A sequential quadratic programming algorithm is used with updates of an estimate of the Hessian matrix at each iteration [
23,
24]. In our problem, we selected a quadratic cost function given by a weighted sum of the position error and the
. Its analytical expression is given by:
The vector
e is the error between final state and desired state,
and
are the fuel consumption expenditures at each impulse. The weighting coefficients
and
are selectable by the designer according to the relative importance of the cost components. In the paper we report the tests obtained using the numerical values in
Table 5.
In the optimization, the number of impulses (thruster firings) is fixed, and simulations were performed assuming the number of impulses equal to 2, 3, 4, and 5. Spacing of the firings as well as fuel expenditure between odd/even firings were a result of the optimization and its trade-off between position error and . The starting initial position was the LLO, the arrival point was the aposelene of the target orbit and the selected stable manifold was maintained the same as in the previous sections, in order to compare the errors.
The simulation results are summarized in
Table 6.
The graphical representation of the phasing trajectories in the case of 2 impulses and 4 impulses are shown in
Figure 12.
The two-impulse case, although requires a smaller , has a very large position vector error.
Based on the above results, a four-impulse maneuver was selected, since it provided a lower position error than a two-impulse case. To evaluate the influence of the selected manifold, the stable arrival manifold was then changed by varying the value of the initial perturbation in the propagation (80 km in norm) along the direction of the eigenvector associated with the eigenvalue less than 1 of the Monodromy matrix, and used for the propagation of the manifold itself. The results are shown in
Table 7.
Figure 13 shows the trajectory corresponding to a four-impulse with the original initial perturbation (the same as the plot on the right in
Figure 12) and the one resulting from a 200 km perturbation. A change in manifold selection does not appreciatively change the fuel consumption.
To verify potential
reduction as a function of time of flight, the phasing maneuver was propagated for five times the target orbital period. The selected trajectory was the one corresponding to the stable manifold generated with an initial perturbation of 100 km (see third row in
Table 7). The longer propagation yields an arrival point closer to the target orbit. The simulation results are summarized in
Table 8.
Table 9 gives the results in terms of perturbation amount.
In the previous tables, the bold values indicate the occurrence of the minimum
. The resulting best scenario corresponds to a five-period manifold propagation, with four impulses and a total expenditure of
= 671 m/s. The phasing maneuver is shown in
Figure 14. The total
divided into the impulse occurrence is shown in
Table 10. As in all cases tested, the largest
occurs at the departure from LLO.
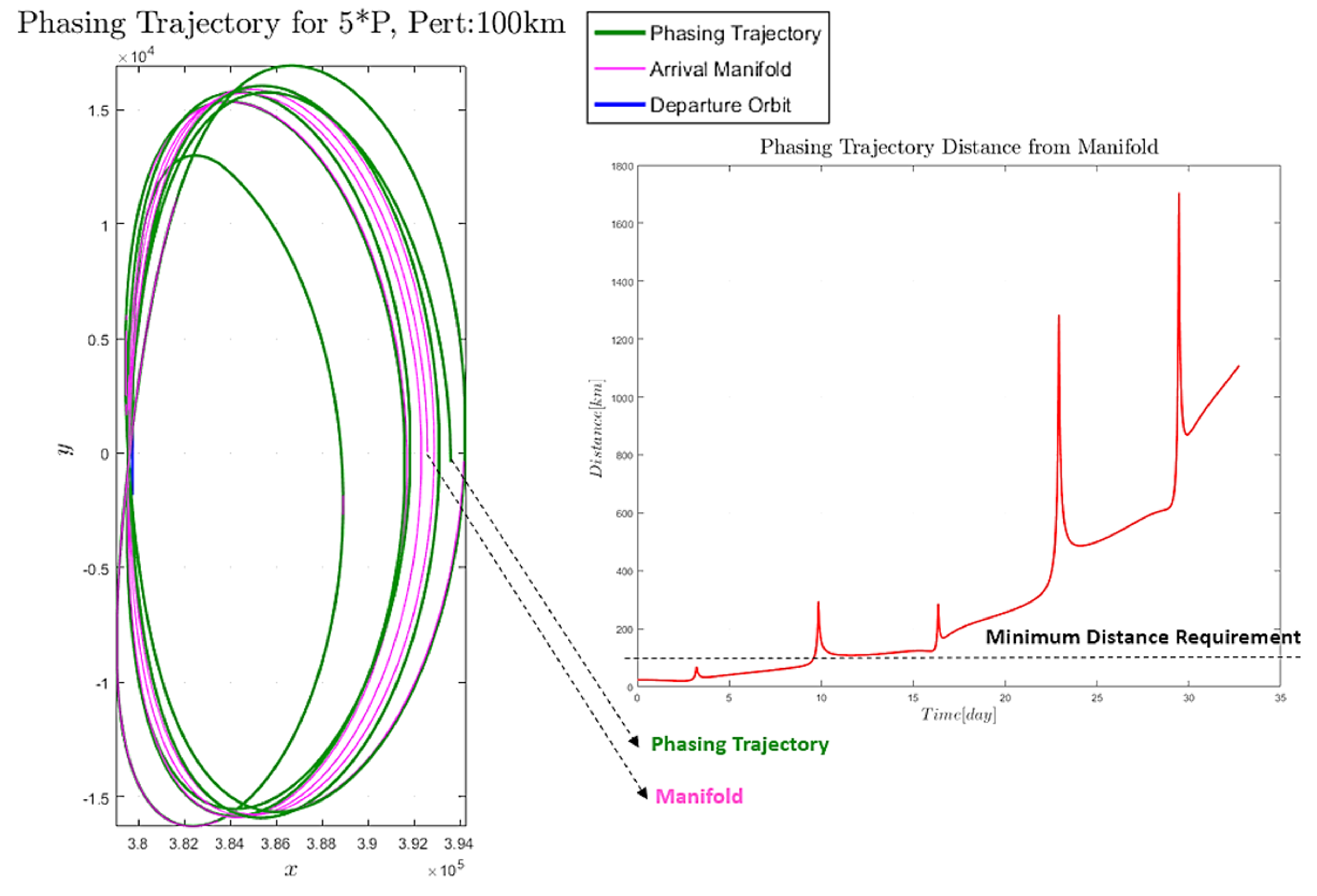
If we also propagate the phasing trajectory over a five-period time, however, the distance to the manifold increases to values that do not satisfy the specifications imposed by the boundary conditions defined at the beginning in
Table 2.
An example is shown in
Figure 15 for a manifold computed with a 100 km initial perturbation (projection on the
plane). The time evolution of manifold and phasing trajectories are shown on the left. On the right, we have the relative position mismatch during the orbital propagation. The increase in distance is evident already after 2 time periods. Please note that similar results were obtained for the case of 80 km perturbation.
To reduce the error between phasing and manifold, the optimization was performed by changing weighting more the error component in the cost function (
= 9 ×
). The simulation best results are shown in
Figure 16 for an initial manifold perturbation of 80 km (the 100 km case is not reported here). The 80 km selection was a requirement for the initial rendezvous and proximity operations. The final position error between the phasing trajectory and the desired final position is lower than the one shown in
Figure 15, at the expense of a slight increase on the total
.
In summary, the phasing trajectory that appears more promising is the one that reaches the target stable manifold generated with an initial perturbation of 80 km, and a propagation time of five time the target orbit period. The
consumption, and the impulse timing are shown in
Table 11. Even if it is obtained with a four-impulse strategy, the main
is used in the first two impulses, thus comparable with the previous approaches.
Based on the above results, some comments can be made on the results shown in
Figure 16 and
Table 11. First the 80 km perturbation target manifold satisfies the requirements after a time of four orbital periods, without additional maneuvers, which are necessary for a 100 km initial perturbation. This result produces the lowest position error with negligible increase in
.
The propagation to five orbital periods yields a phasing maneuver duration of about 701 h before satisfying the insertion requirements. However, if we remove the CR3BP restriction and perform the targeting with the real LOP-G orbit, the final position on the manifold is much closer to the orbit, than the one period case.
The real target orbit considered in the paper was obtained using the public domain “Free-Flyer” code with propagation dates 9 January 2020 to 7 February 2020. This results in a more stable phasing compared to the one using the manifold obtained with a 100 km initial perturbation.
Finally, direct targeting to the real orbit was not performed, since it would not provide any guaranteed stable drift to the target, unlike the stable manifold.