Monte Carlo Predictions of Aero-Engine Performance Degradation Due to Particle Ingestion
Abstract
:1. Introduction
2. Materials and Methods
2.1. Background
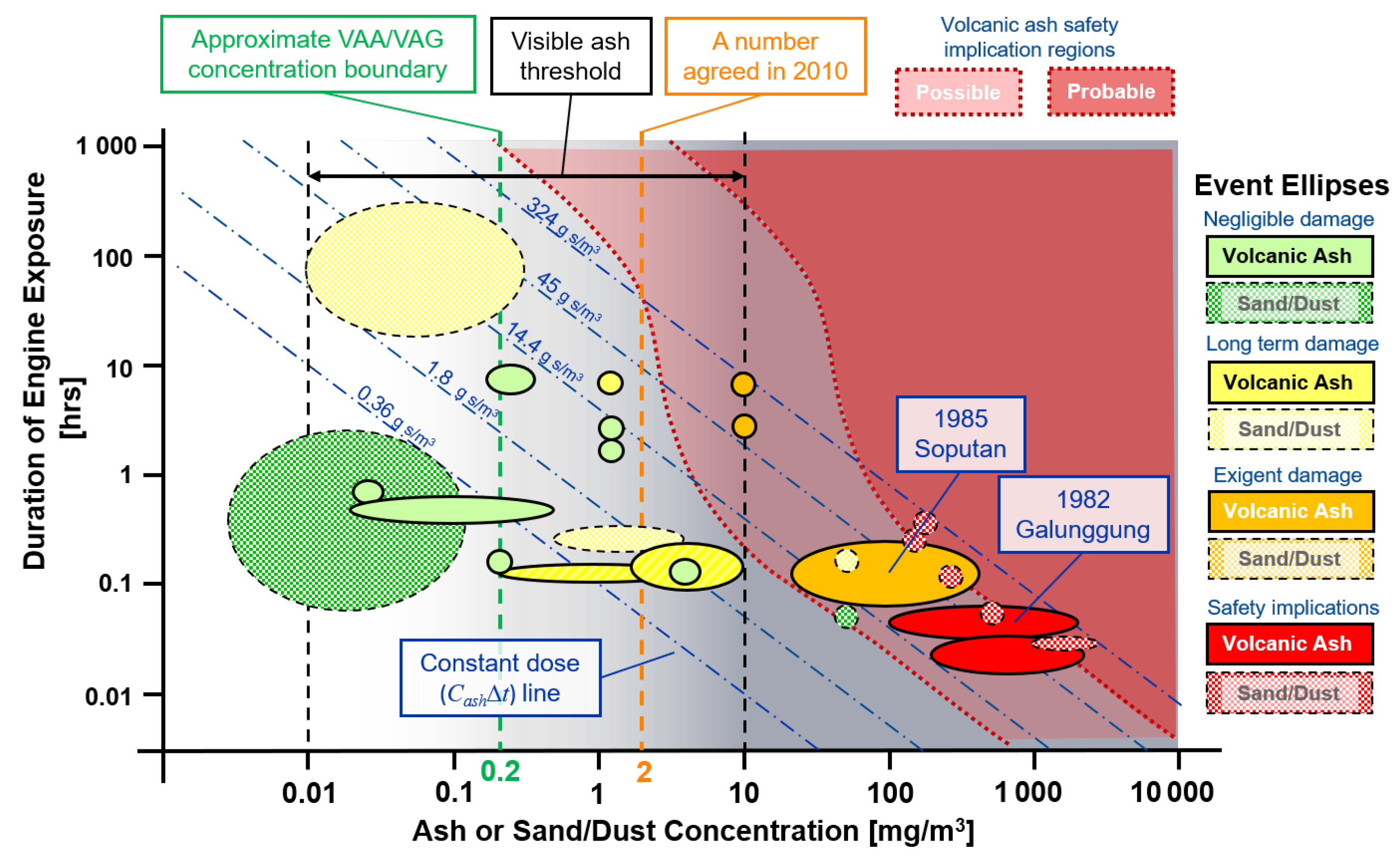
2.1.1. Historical Encounter Events
2.1.2. 1982 Mount Galunggung Event
2.1.3. 1985 Mount Soputan Event
2.1.4. Engine Dose
2.1.5. Nozzle Guide Vane Deposition
2.1.6. The Accumulation Factor
2.2. Methodology
2.2.1. Engine Performance Model
2.2.2. Reduced-Order Accumulation Factor Model
2.2.3. Interaction Probability
2.2.4. Retention Probability
2.2.5. Accumulation Factor
2.2.6. NGV Throat Area Reduction
2.2.7. Deposit Distribution Severity
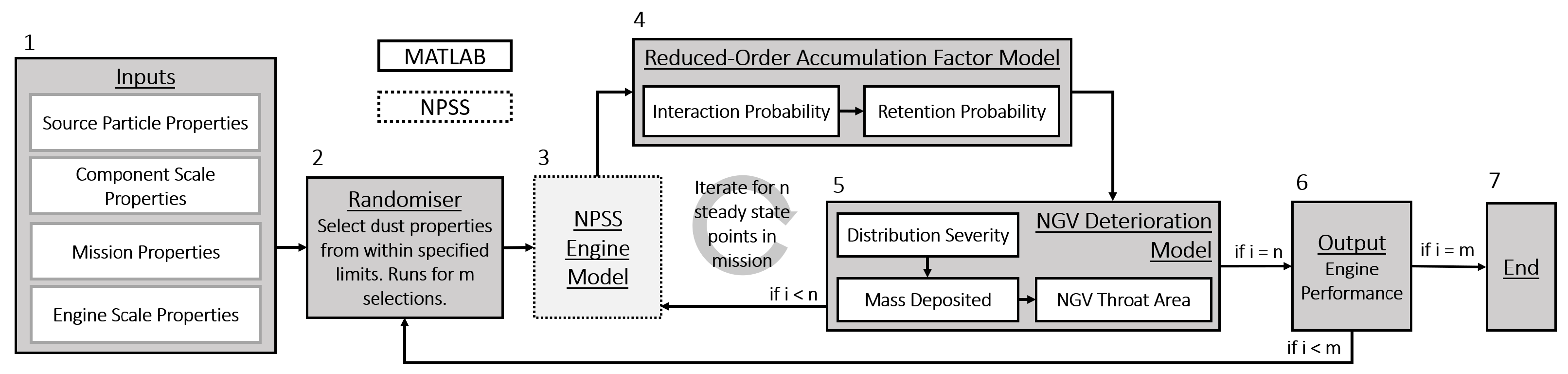
2.2.8. Coupled Degradation Model
2.2.9. Model Inputs
2.2.10. Coupled Algorithm
2.2.11. Input Variable Randomisation
2.2.12. Damage Assessment of Historic Encounter Events
2.2.13. Independence of Outcomes
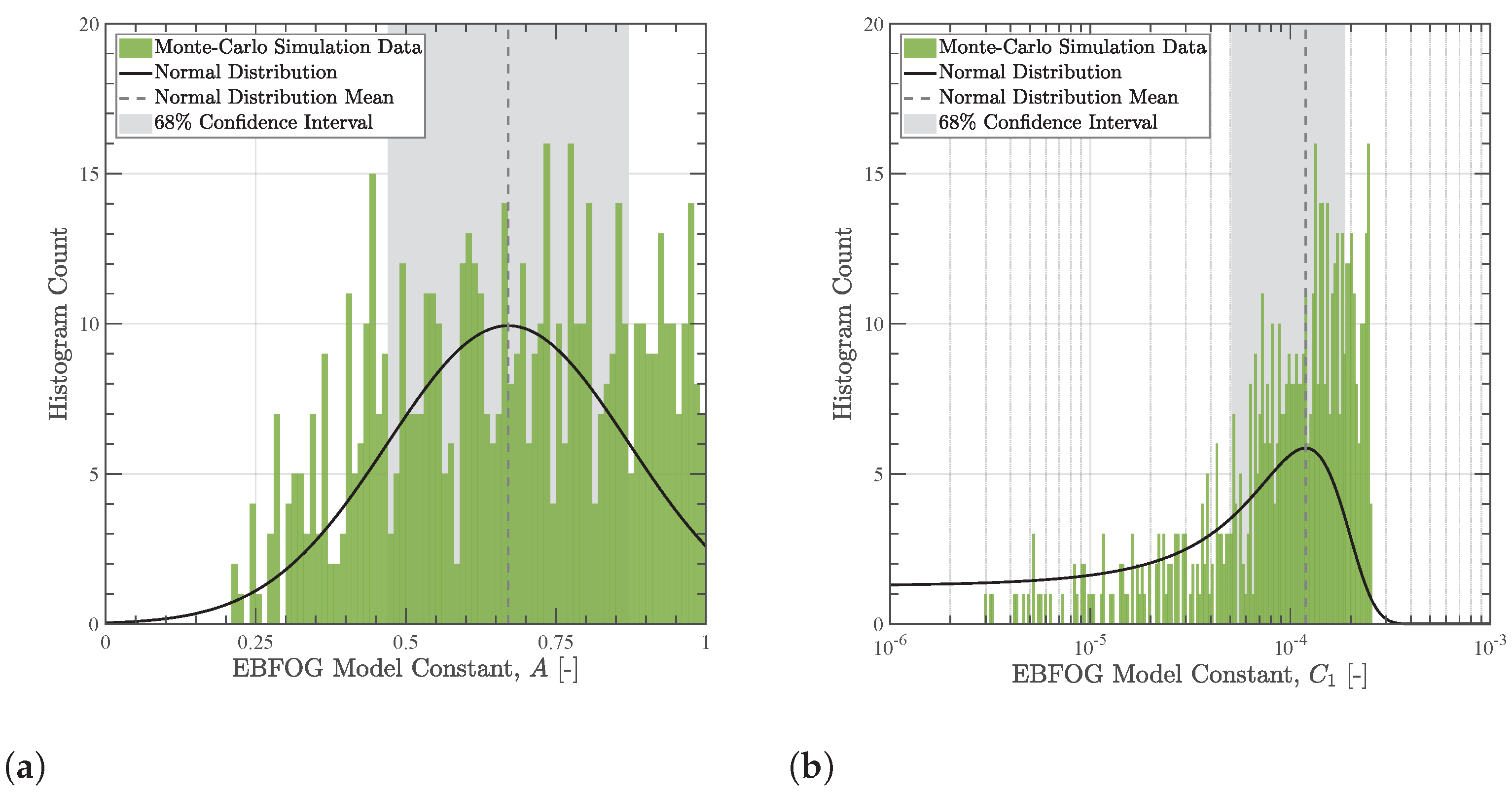
2.2.14. Predicting Empirical Constants
3. Results
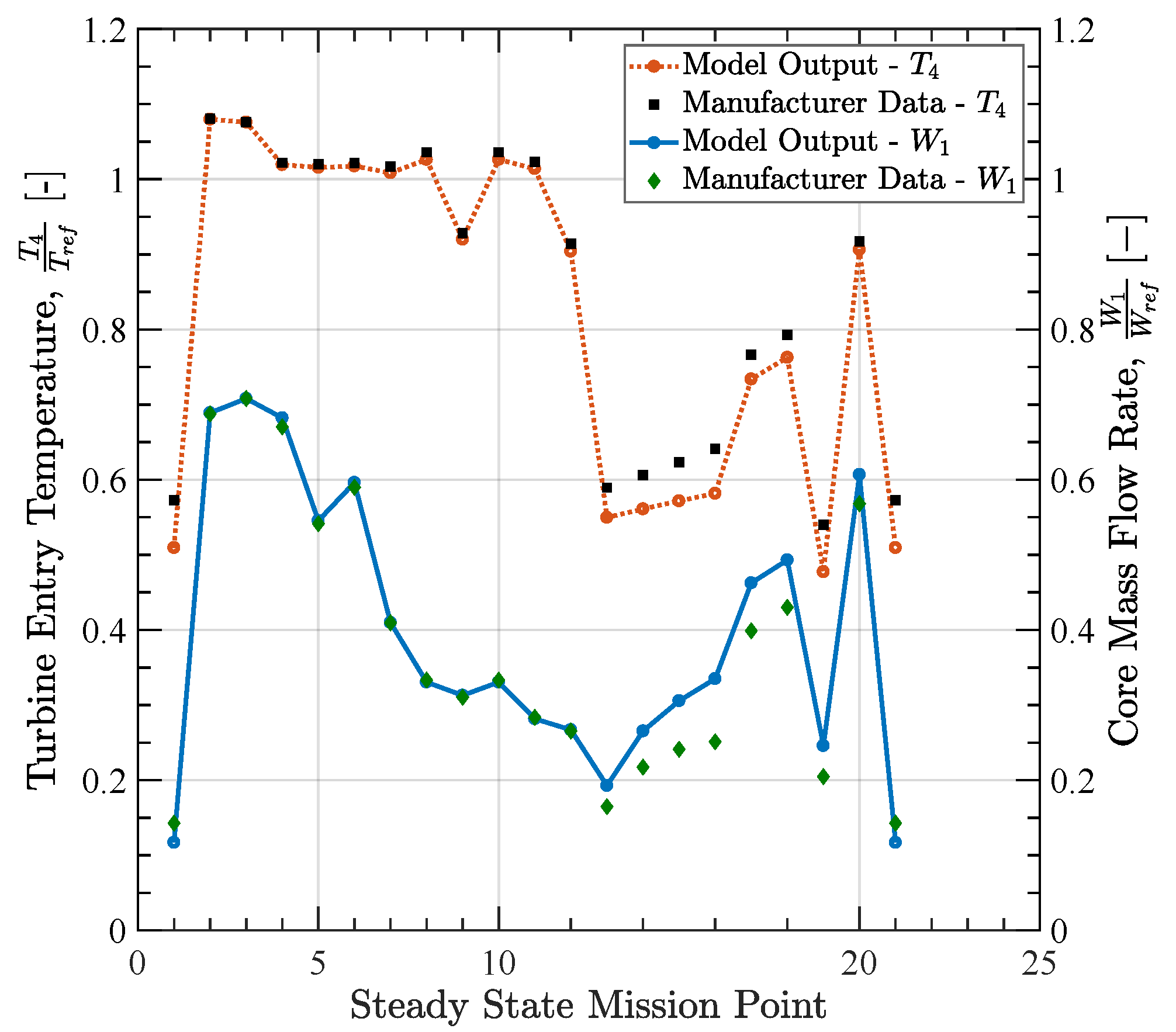
3.1. Accumulation Factor Model Validation
3.2. Coupled Algorithm Validation
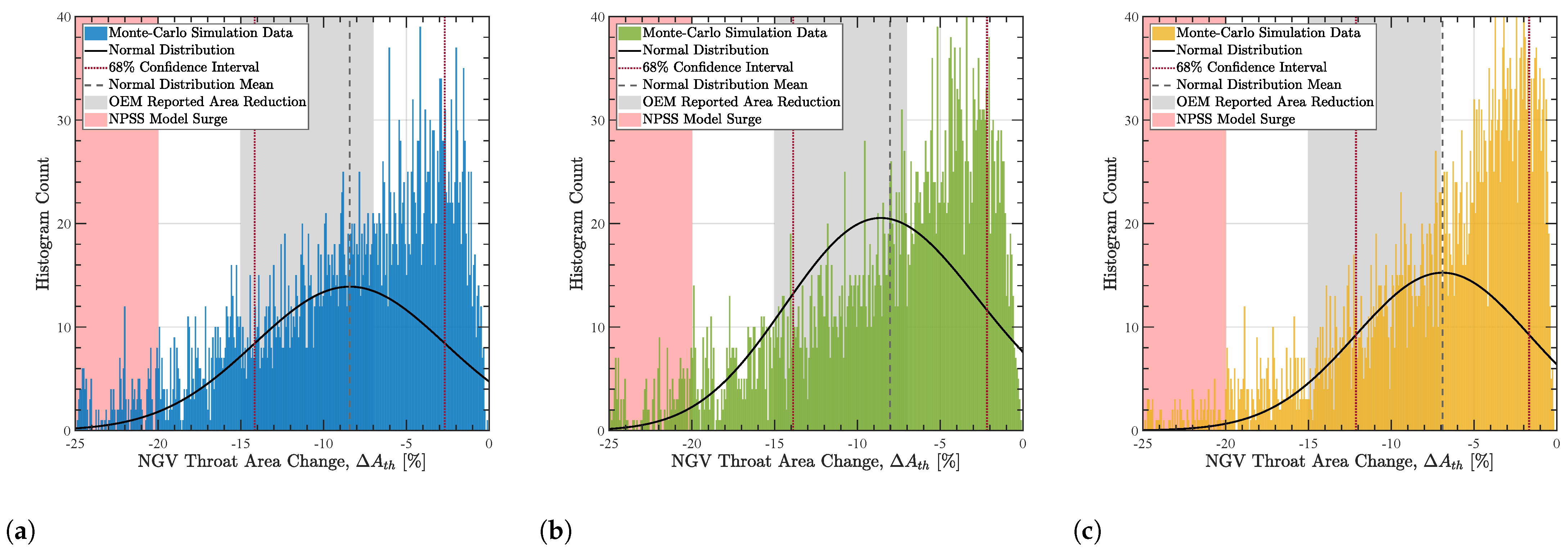
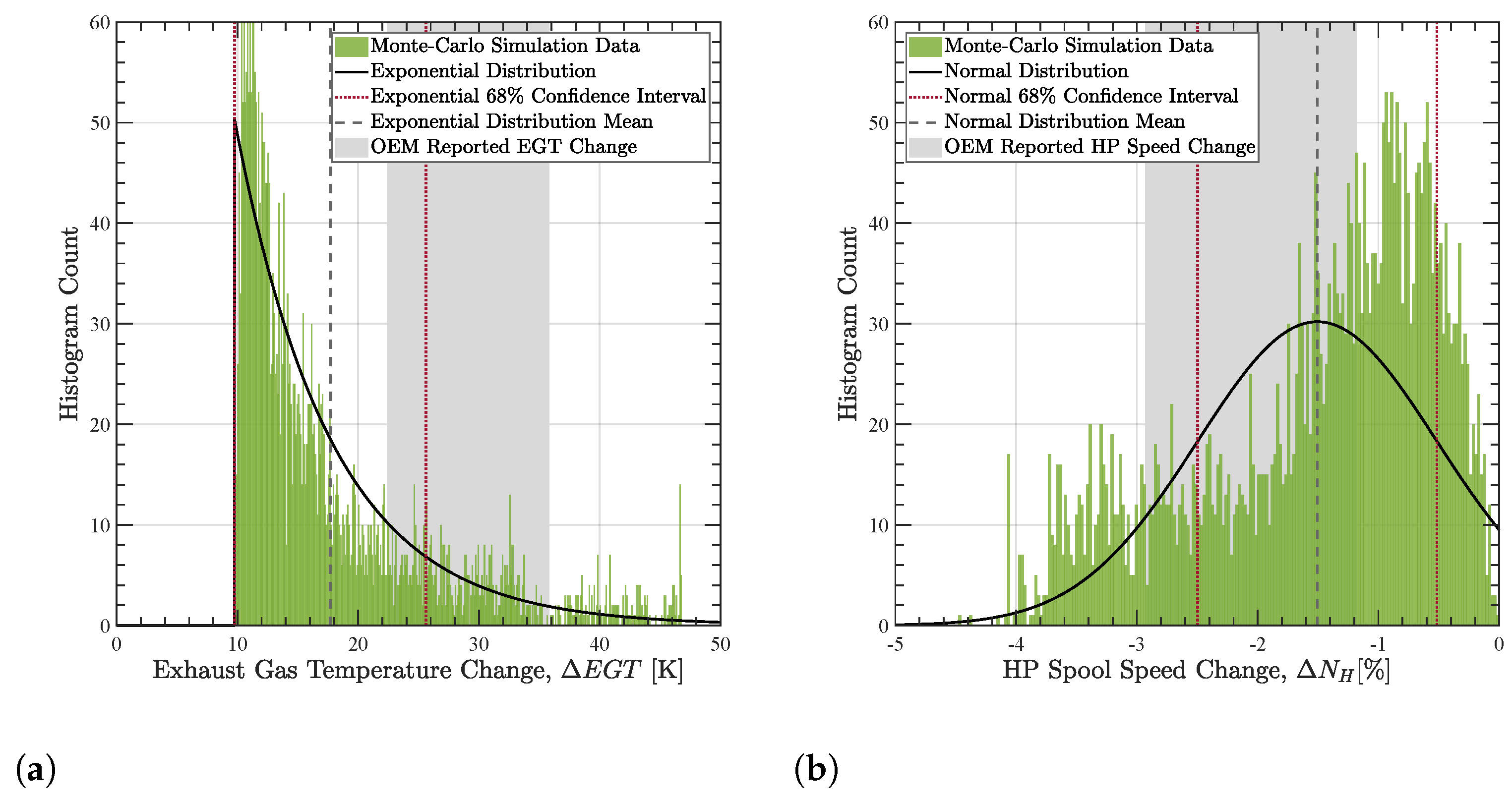
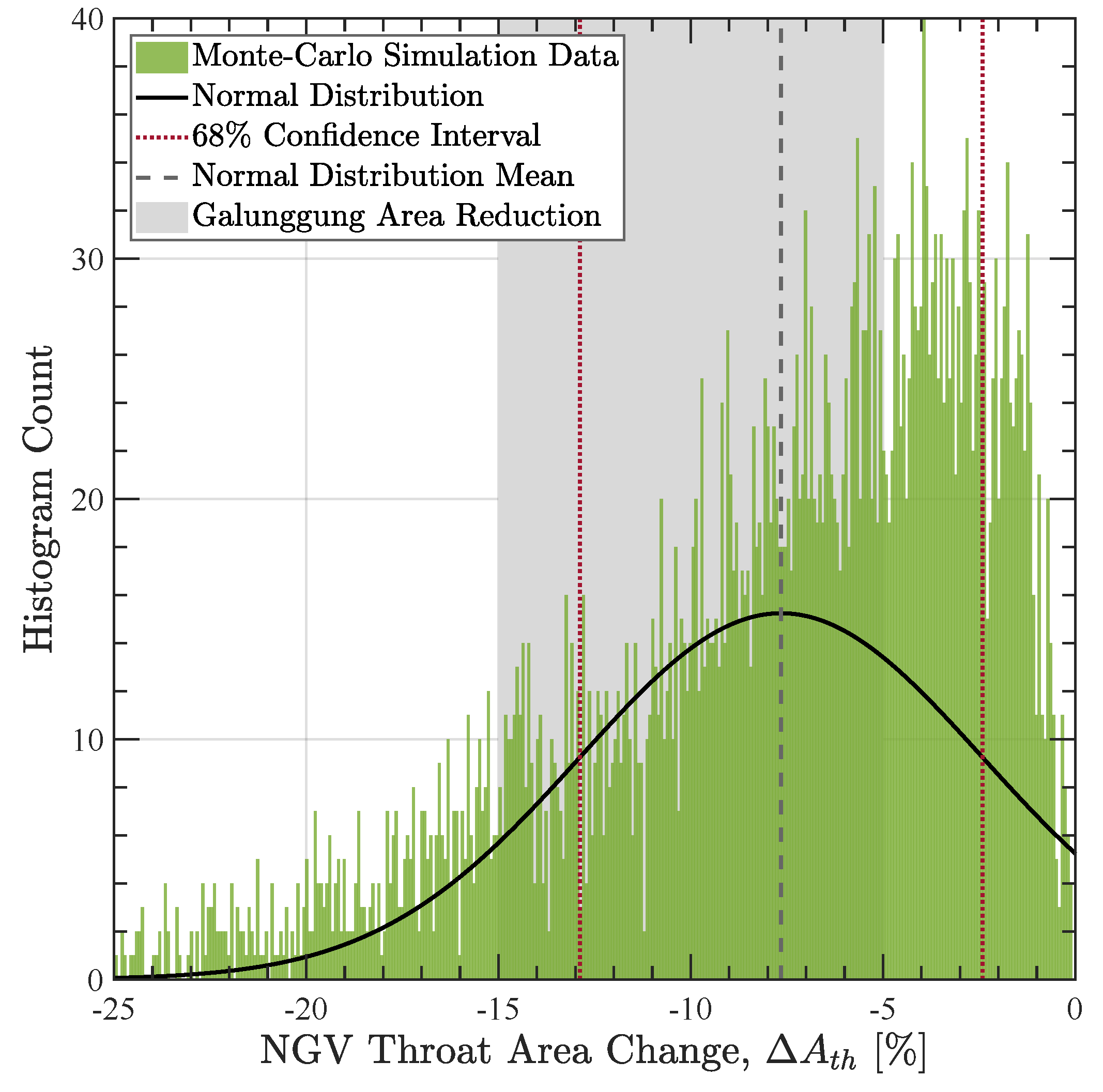
3.2.1. 1982 Galunggung Encounter
3.2.2. 1985 Soputan Encounter
3.3. Empirical Constant Prediction
- Case 1—the 1982 Galunggung event, as defined in Table 1.
- Case 2—hypothetical scenario where the constants A and are the only unknowns.
- Case 3—hypothetical scenario where the constant A is the only unknown.
4. Discussion
4.1. Improving Data Quality
4.2. Model Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CI | Confidence Interval |
| EGT | Exhaust Gas Temperature |
| HP | High Pressure |
| HPT | High-Pressure Turbine |
| NPSS | Numerical Propulsion System Simulation |
| NGV | Nozzle Guide Vane |
| OEM | Original Equipment Manufacturer |
| PSD | Particle Size Distribution |
References
- Clarkson, R.J.; Majewicz, E.J.; Mack, P. A Re-Evaluation of the 2010 Quantitative Understanding of the Effects Volcanic Ash Has on Gas Turbine Engines. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 2274–2291. [Google Scholar] [CrossRef]
- Prata, F.; Rose, B. Volcanic Ash Hazards to Aviation. In The Encyclopedia of Volcanoes, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 911–934. [Google Scholar] [CrossRef]
- Bojdo, N.; Filippone, A.; Parkes, B.; Clarkson, R. Aircraft Engine Dust Ingestion Following Sand Storms. Aerosp. Sci. Technol. 2020, 106, 106072. [Google Scholar] [CrossRef]
- Li, R.; Verhagen, W.; Curran, R. Toward a Methodology of Requirements Definition for Prognostics and Health Management System to Support Aircraft Predictive Maintenance. Aerosp. Sci. Technol. 2020, 102, 105877. [Google Scholar] [CrossRef]
- Clarkson, R.; Simpson, H. Maximising Airspace Use during Volcanic Eruptions: Matching Engine Durability against Ash Cloud Occurrence; Technical Report STO-MP-AVT-272; NATO STO: Porton Down, UK, 2017.
- Döring, F.; Staudacher, S.; Koch, C.; Weißschuh, M. Modeling Particle Deposition Effects in Aircraft Engine Compressors. J. Turbomach. 2017, 139, 051003. [Google Scholar] [CrossRef]
- Al-Zyoud, S. Thermo-Physical and Mechanical Properties of Al Hashimiyya Basaltic Rocks, Jordan. Int. J. Geosci. 2019, 10, 193–208. [Google Scholar] [CrossRef] [Green Version]
- Ebert, H.; Hemberger, F.; Fricke, J.; Büttner, R.; Bez, S.; Zimanowski, B. Thermophysical Properties of a Volcanic Rock Material. High Temp.-High Press. 2002, 34, 561–568. [Google Scholar] [CrossRef]
- Vogel, A.; Diplas, S.; Durant, A.J.; Azar, A.S.; Sunding, M.F.; Rose, W.I.; Sytchkova, A.; Bonadonna, C.; Krüger, K.; Stohl, A. Reference Data Set of Volcanic Ash Physicochemical and Optical Properties. J. Geophys. Res. Atmos. 2017, 122, 9485–9514. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Tafti, D. Particle Deposition Model for Particulate Flows at High Temperatures in Gas Turbine Components. Int. J. Heat Fluid Flow 2015, 52, 72–83. [Google Scholar] [CrossRef]
- Bons, J.P.; Prenter, R.; Whitaker, S. A Simple Physics-Based Model for Particle Rebound and Deposition in Turbomachinery. J. Turbomach. 2017, 139, 081009. [Google Scholar] [CrossRef]
- Bojdo, N.; Ellis, M.; Filippone, A.; Jones, M.; Pawley, A. Particle-Vane Interaction Probability in Gas Turbine Engines. J. Turbomach. 2019, 141. [Google Scholar] [CrossRef] [Green Version]
- Ellis, M.; Bojdo, N.; Covey-Crump, S.; Jones, M.; Filippone, A.; Pawley, A. Generalised Predictions of Particle-Vane Retention Probability in Gas Turbine Engines. J. Turbomach. 2021. [Google Scholar] [CrossRef]
- Grayburn, M. British Airways Boeing 747-236 Volcanic Cloud Encounter on the 24 June 1982—Investigation Report; Technical Report SPA 60332; Rolls-Royce: Westhampnett, UK, 1983. [Google Scholar]
- Guffanti, M.; Casadevall, T.; Budding, K. Encounters of Aircraft with Volcanic Ash Clouds: A Compilation of Known Incidents, 1953–2009; Technical Report U.S. Geological Survey Data Series 545; US Geological Survey: Reston, VA, USA, 2010.
- Witham, C.; Webster, H.; Hort, M.; Jones, A.; Thomson, D. Modelling Concentrations of Volcanic Ash Encountered by Aircraft in Past Eruptions. Atmos. Environ. 2012, 48, 219–229. [Google Scholar] [CrossRef]
- Martin, E.; Napier, J. Qantas Airways Boeing 747 Comb. Volcanic Cloud Encounter on 19 May 1985—Investigation Report; Technical Report; Rolls-Royce: Westhampnett, UK, 1985. [Google Scholar]
- Kristiansen, N.I.; Prata, A.J.; Stohl, A.; Carn, S.A. Stratospheric Volcanic Ash Emissions from the 13 February 2014 Kelut Eruption. Geophys. Res. Lett. 2015, 42, 588–596. [Google Scholar] [CrossRef] [Green Version]
- Cohen, H.; Rogers, G.; Saravanamuttoo, H. Gas Turbine Theory, 4th ed.; Longman: Harlow, UK, 2009. [Google Scholar]
- Kern, D.; Seaton, R. A Theoretical Analysis of Thermal Surface Fouling. Br. Chem. Eng. 1959, 4, 258–262. [Google Scholar]
- Senior, C.L.; Srinivasachar, S. Viscosity of Ash Particles in Combustion Systems for Prediction of Particle Sticking. Energy Fuels 1995, 9, 277–283. [Google Scholar] [CrossRef]
- Whitaker, S.M.; Peterson, B.; Miller, A.F.; Bons, J.P. The Effect of Particle Loading, Size, and Temperature on Deposition in a Vane Leading Edge Impingement Cooling Geometry; ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition; ASME: Seoul, Korea, 2016. [Google Scholar] [CrossRef]
- Dunn, M. Operation of Gas Turbine Engines in an Environment Contaminated with Volcanic Ash. J. Turbomach. 2012, 134, 051001. [Google Scholar] [CrossRef]
- Giehl, C.; Brooker, R.; Marxer, H.; Nowak, M. An Experimental Simulation of Volcanic Ash Deposition in Gas Turbines and Implications for Jet Engine Safety. Chem. Geol. 2017, 461, 160–170. [Google Scholar] [CrossRef]
- Dean, J.; Taltavull, C.; Clyne, T. Influence of the Composition and Viscosity of Volcanic Ashes on Their Adhesion within Gas Turbine Aeroengines. Acta Mater. 2016, 109, 8–16. [Google Scholar] [CrossRef] [Green Version]
- Ellis, M.; Bojdo, N.; Filippone, A. Influence of Turboshaft Engine Architecture on Ash Particle Deposition-Reduced Order Model Application. In ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2020; p. 12. [Google Scholar] [CrossRef]
- Lytle, J. The Numerical Propulsion Simulation: An Overview; Technical Report NASA/TM-2000-209915; NASA Glenn Research Center: Cleveland, OH, USA, 2000.
- Phillips, F. RB 211-524C2 Typical Flight Profiles; Technical Report TDR 60449; Rolls-Royce: Westhampnett, UK, 1979. [Google Scholar]
- Casari, N.; Pinelli, M.; Suman, A.; Di Mare, L.; Montomoli, F. An Energy-Based Fouling Model for Gas Turbines: EBFOG. J. Turbomach. 2017, 139, 021002. [Google Scholar] [CrossRef]
- Pearson, D.; Brooker, R. The Accumulation of Molten Volcanic Ash in Jet Engines; Simulating the Role of Magma Composition, Ash Particle Size and Thermal Barrier Coatings. J. Volcanol. Geotherm. Res. 2020, 389, 106707. [Google Scholar] [CrossRef]


| Property | Unit | Upper Limit | Lower Limit | Refs. |
|---|---|---|---|---|
| Concentration, | mgm | 1000 | 100 | [1,16] |
| Event Duration, D | min | 4 | 2 | [1] |
| Particle Heat Capacity, | JkgK | 1600 | 510 | [7,8] |
| Particle Density, | kgm | 2900 | 2590 | [7,9] |
| Particle Softening Temperature, | K | 1420 | 923 | [25] |
| Deposit Density, | kgm | 2400 | 1430 | [30] |
| Particle Size Distribution | − | Log-Normal | [9] | |
| Geometric Mean Diameter, | − | 3.25 | 1.50 | [9] |
| Geometric Standard Deviation, | − | 2.00 | 1.00 | [9] |
| EBFOG Model Constant, A | − | 1.00 | 0.10 | – |
| EBFOG Model Constant, | − | 2.51 × 10 | 2.51 × 10 | – |
| Shedding Rate Parameter, | s | 5.00 × 10 | 2.00 × 10 | – |
| Property | Unit | Upper Limit | Lower Limit | Refs. |
|---|---|---|---|---|
| Concentration, | mgm | 400 | 20 | [16] |
| Event Duration, D | min | 14 | 4 | [15,16] |
| Particle Heat Capacity, | JkgK | 1600 | 510 | [7,8] |
| Particle Density, | kgm | 2900 | 2590 | [7,9] |
| Particle Softening Temperature, | K | 1420 | 923 | [25] |
| Deposit Density, | kgm | 2400 | 1520 | [30] |
| Particle Size Distribution | − | Log-Normal | [9] | |
| Geometric Mean Diameter, | − | 3.50 | 1.50 | [9] |
| Geometric Standard Deviation, | − | 2.00 | 0.50 | [9] |
| EBFOG Model Constant, A | − | 1.00 | 0.10 | – |
| EBFOG Model Constant, | − | 2.51 × 10 | 2.51 × 10 | – |
| Shedding Rate Parameter, | s | 5.00 × 10 | 2.00 × 10 | – |
| All Engines | Engine 1 | Engine 2 | Engine 3 | Engine 4 | |
|---|---|---|---|---|---|
| Performance Parameter | Number of Cases Falling in OEM Range | ||||
| HP Spool Speed Change | 1522 | 163 | 150 | 151 | 86 |
| Exhaust Gas Temperature Change | 630 | 148 | 94 | 66 | 168 |
| Both HP and EGT Changes | 262 | 71 | 9 | 7 | 10 |
| Predicted Throat Area Change [%] | – | −12.3 | −13.1 | −16.7 | −12.0 |
| Event Failure Order | – | 3 | 2 | 4 | 1 |
| Flight Cycles | – | 1116 | 2324 | 2207 | 2605 |
| Case 1 | Case 2 | Case 3 | |||||
|---|---|---|---|---|---|---|---|
| Property | Unit | Upper Limit | Lower Limit | Upper Limit | Lower Limit | Upper Limit | Lower Limit |
| mgm | 1000 | 100 | 400 | 400 | |||
| D | min | 4 | 2 | 4 | 4 | ||
| JkgK | 1600 | 510 | 800 | 800 | |||
| kgm | 2900 | 2590 | 2680 | 2680 | |||
| K | 1420 | 923 | 1100 | 1100 | |||
| kgm | 2400 | 1430 | 1915 | 1915 | |||
| Distribution | − | Log-Normal | Log-Normal | Log-Normal | |||
| − | 3.25 | 1.50 | 1.825 | 1.825 | |||
| − | 2.00 | 1.00 | 1.50 | 1.50 | |||
| A | − | 1.00 | 0.10 | 1.00 | 0.1 | 1.00 | 0.1 |
| − | 2.51 × 10 | 2.51 × 10 | 2.51 × 10 | 2.51 × 10 | 5.00 × 10 | ||
| s | 5.00 × 10 | 2.00 × 10 | 4.00 × 10 | 4.00 × 10 | |||
| Case | Optimisation Variables | Mean | Standard Deviation | 68% Confidence Interval | |||
|---|---|---|---|---|---|---|---|
| ) | ( | ||||||
| Case 1 | 0.66 | 11.9 | 0.21 | 6.76 | 0.45–0.87 | 5.16–13.5 | |
| Case 2 | 0.82 | 7.38 | 0.13 | 3.70 | 0.95–0.70 | 3.68–7.40 | |
| Case 3 | A | 0.75 | – | 0.03 | – | 0.79–0.72 | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ellis, M.; Bojdo, N.; Filippone, A.; Clarkson, R. Monte Carlo Predictions of Aero-Engine Performance Degradation Due to Particle Ingestion. Aerospace 2021, 8, 146. https://doi.org/10.3390/aerospace8060146
Ellis M, Bojdo N, Filippone A, Clarkson R. Monte Carlo Predictions of Aero-Engine Performance Degradation Due to Particle Ingestion. Aerospace. 2021; 8(6):146. https://doi.org/10.3390/aerospace8060146
Chicago/Turabian StyleEllis, Matthew, Nicholas Bojdo, Antonio Filippone, and Rory Clarkson. 2021. "Monte Carlo Predictions of Aero-Engine Performance Degradation Due to Particle Ingestion" Aerospace 8, no. 6: 146. https://doi.org/10.3390/aerospace8060146
APA StyleEllis, M., Bojdo, N., Filippone, A., & Clarkson, R. (2021). Monte Carlo Predictions of Aero-Engine Performance Degradation Due to Particle Ingestion. Aerospace, 8(6), 146. https://doi.org/10.3390/aerospace8060146






