Propulsion Sizing Correlations for Electrical and Fuel Powered Unmanned Aerial Vehicles
Abstract
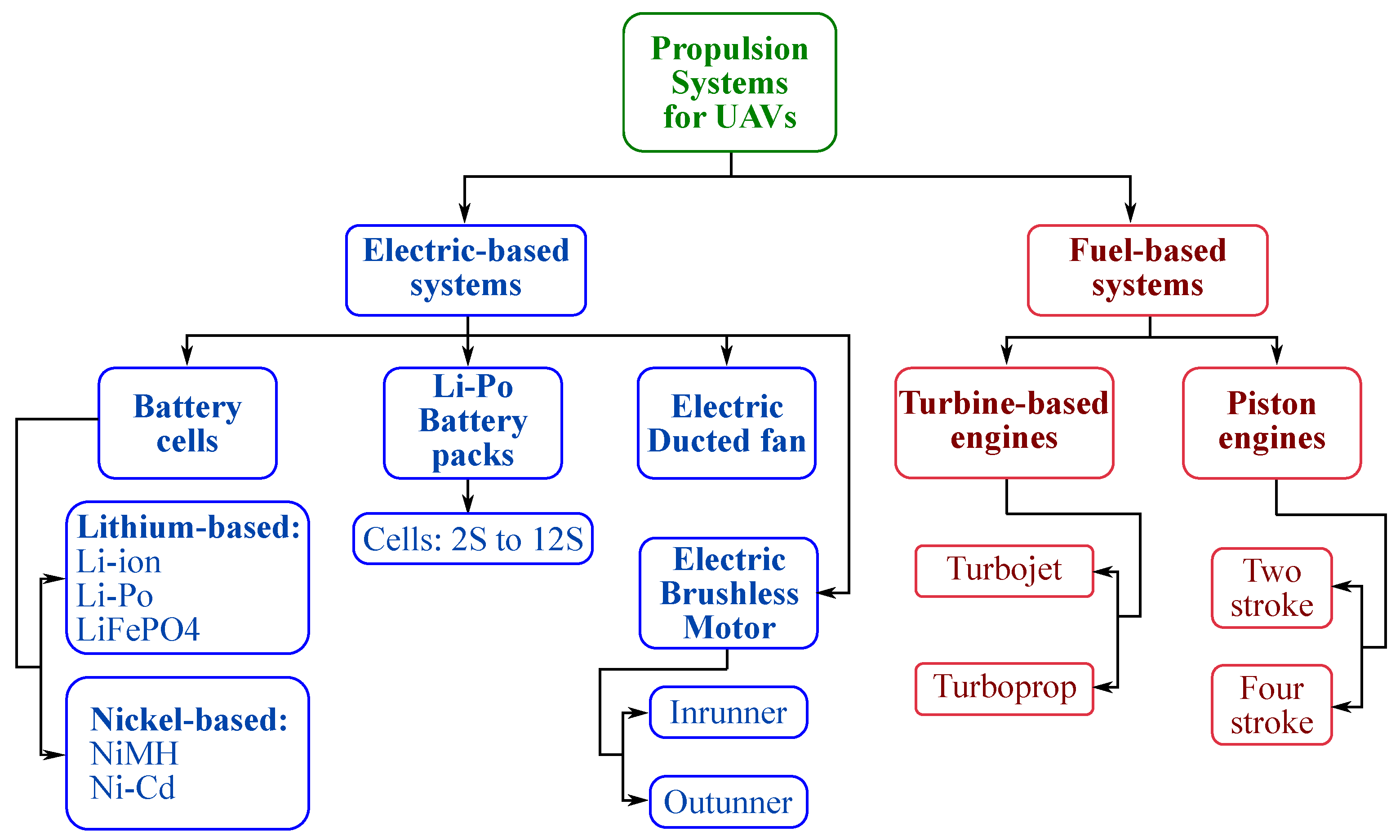
:1. Introduction
2. Mission Requirements and UAV Categories
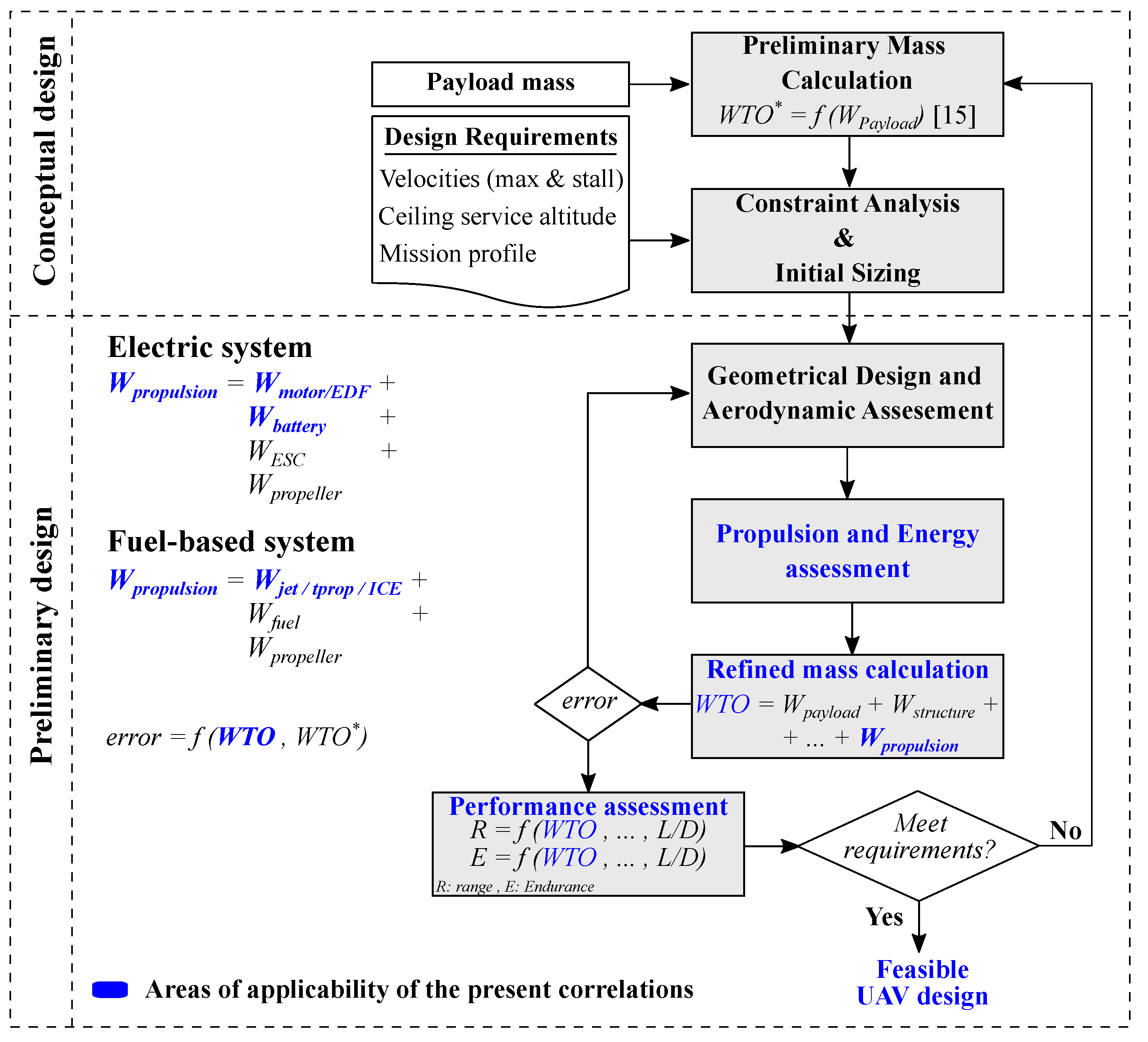
3. Methodology
4. Results and Discussion
4.1. Electric Propulsion Systems
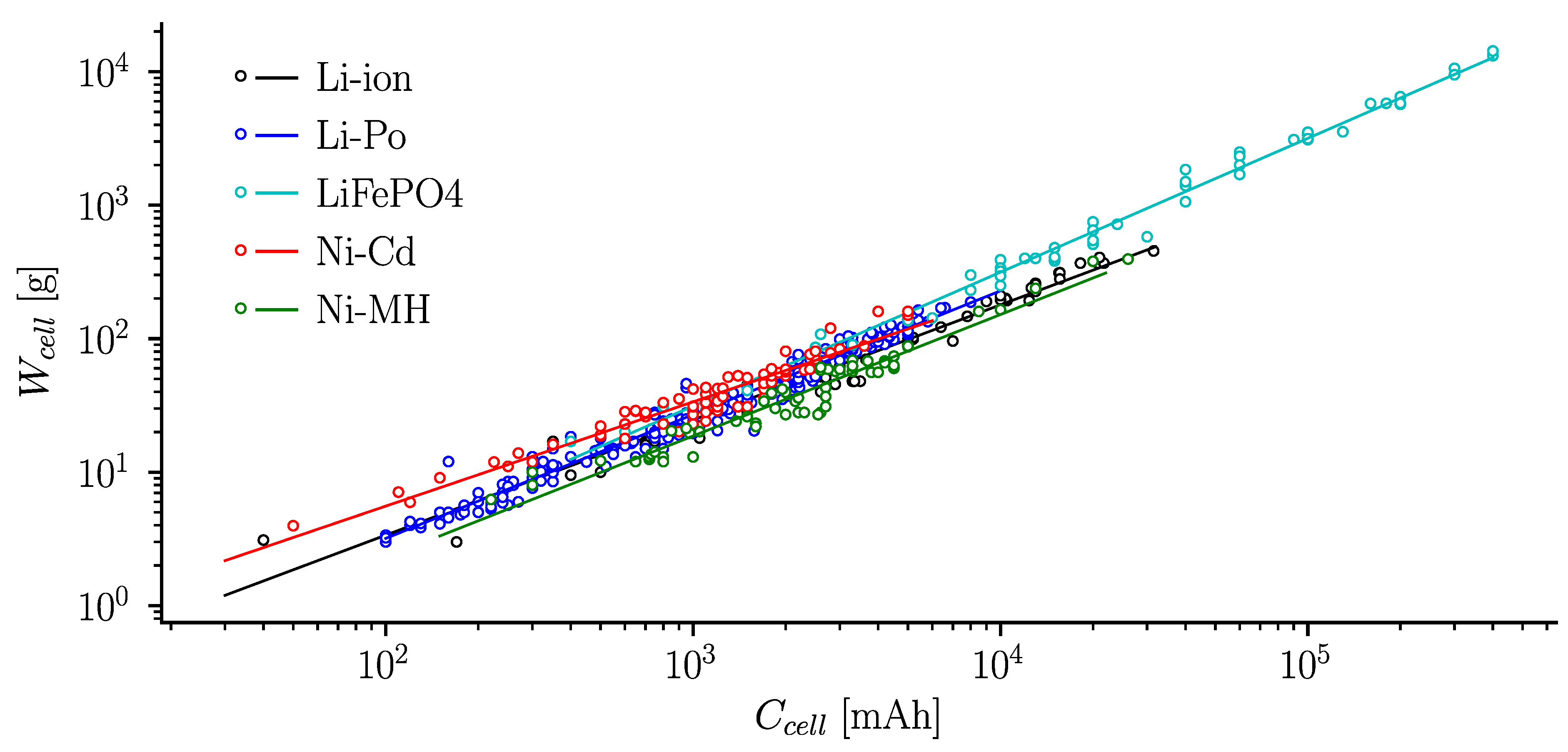
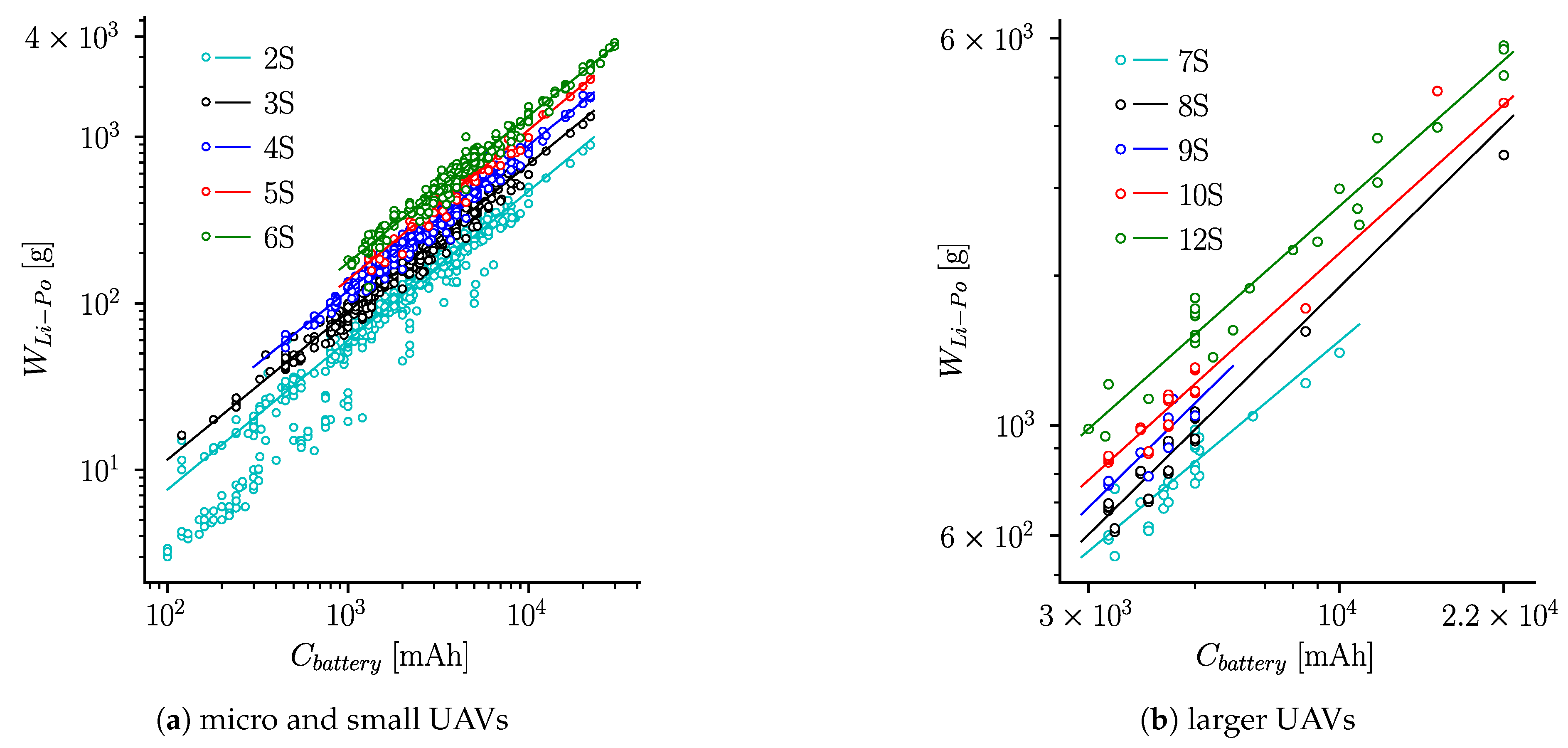
4.1.1. Cells and Batteries
4.1.2. Electric Ducted Fan (EDF)
4.1.3. Electric Brushless Motors
4.2. Fuel-Based Propulsion Systems
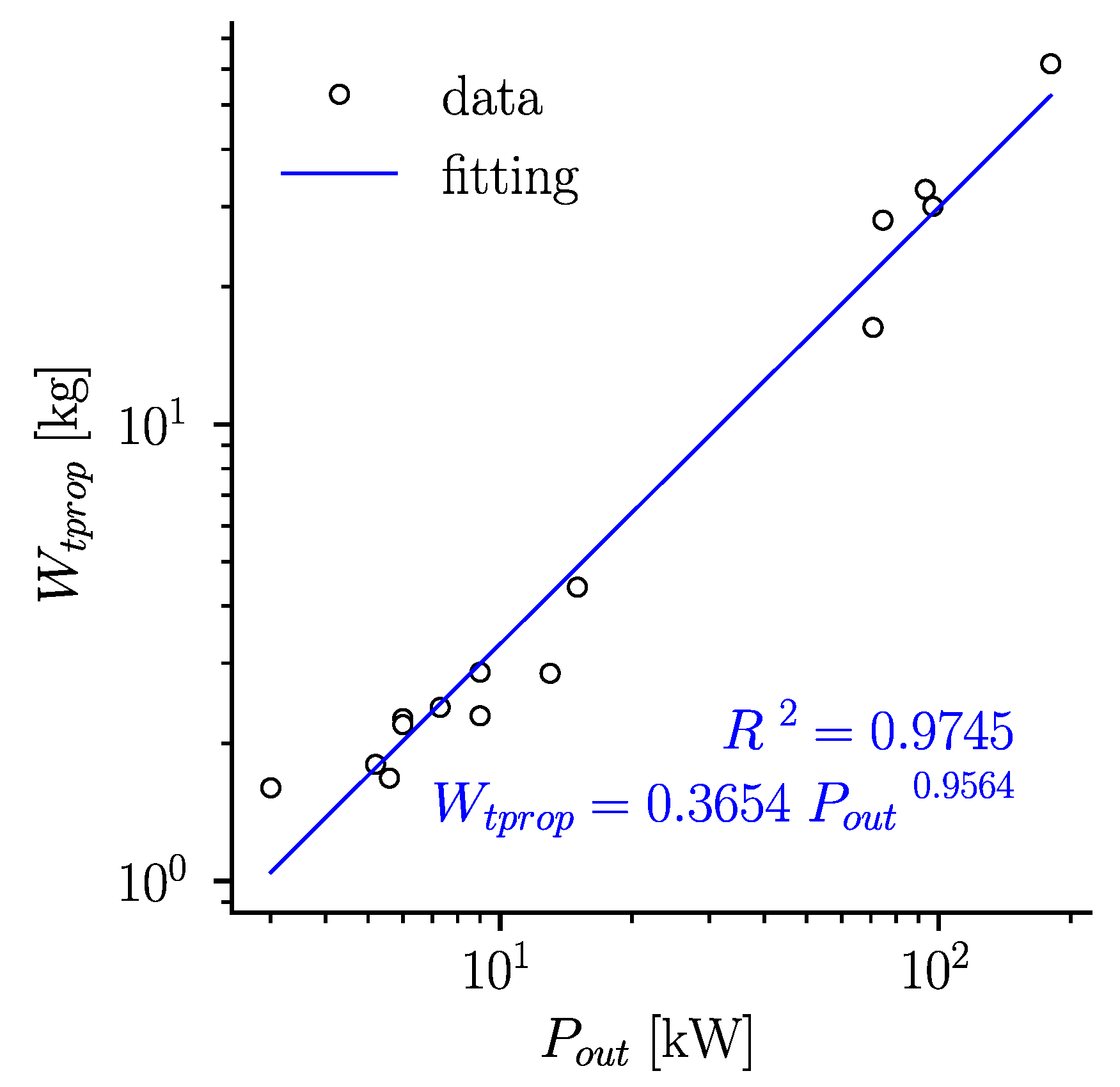
4.2.1. Turbojet and Turboprop Engines
4.2.2. Internal Combustion Engines (ICE)
5. Application Examples: Electric and Fuel-Based UAVs
5.1. Electric-Powered UAV
5.2. Fuel-Powered UAV
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Isikveren, A.T. Quasi-Analytical Modelling and Optimisation Techniques for Transport Aircraft Design. Ph.D. Thesis, Royal Institute of Technology (KTH), Stockholm, Sweden, 2002. [Google Scholar]
- Chambers, M.C.; Ardema, M.D.; Patron, A.P.; Hahn, A.S.; Miura, H.; Moore, M.D. Analytical Fuselage and Wing Weight Estimation of Transport Aircraft; Nasa Technical Memorandum 110392: Washington, DC, USA, 1996.
- Torenbeek, E. Synthesis of Subsonic Airplane Design: An Introduction to the Preliminary Design of Subsonic General Aviation and Transport Aircraft, with Emphasis on Layout, Aerodynamic Design, Propulsion and Performance; Springer Science & Business Media: New York, NY, USA, 1982. [Google Scholar]
- Roskam, J. Airplane Design; DARcorporation: Lawrence, KS, USA, 1985. [Google Scholar]
- Anderson, J.D. Aircraft Performance and Design; WCB/McGraw-Hill: Boston, MA, USA, 1999; Volume 1. [Google Scholar]
- Nield, B.N. An overview of the Boeing 777 high lift aerodynamic design. Aeronaut. J. 1995, 99, 361–371. [Google Scholar]
- Liebeck, R.; Page, M.; Rawdon, B. Blended-wing-body subsonic commercial transport. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 438. [Google Scholar]
- Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bravo-Mosquera, P.D.; Cerón-Mu noz, H.D.; Díaz-Vázquez, G.; Catalano, F.M. Conceptual design and CFD analysis of a new prototype of agricultural aircraft. Aerosp. Sci. Technol. 2018, 80, 156–176. [Google Scholar] [CrossRef]
- Panagiotou, P.; Kaparos, P.; Salpingidou, C.; Yakinthos, K. Aerodynamic design of a MALE UAV. Aerosp. Sci. Technol. 2016, 50, 127–138. [Google Scholar] [CrossRef]
- Kontogiannis, S.G.; Ekaterinaris, J.A. Design, performance evaluation and optimization of a UAV. Aerosp. Sci. Technol. 2013, 29, 339–350. [Google Scholar] [CrossRef]
- Sóbester, A.; Keane, A.; Scanlan, J.; Bressloff, N. Conceptual design of UAV airframes using a generic geometry service. In Proceedings of the Infotech@ Aerospace, Arlington, VA, USA, 26–29 September 2005; p. 7079. [Google Scholar]
- Gundlach, J. Designing Unmanned Aircraft Systems: A Comprehensive Approach; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Götten, F.; Finger, D.; Braun, C.; Havermann, M.; Bil, C.; Gómez, F. Empirical correlations for geometry build-up of fixed wing unmanned air vehicles. In Proceedings of the Asia-Pacific International Symposium on Aerospace Technology, Chengdu, China, 16–18 October 2018; Springer: Singapore, 2018; pp. 1365–1381. [Google Scholar]
- Verstraete, D.; Palmer, J.L.; Hornung, M. Preliminary Sizing Correlations for Fixed-Wing Unmanned Aerial Vehicle Characteristics. J. Aircr. 2017, 55, 715–726. [Google Scholar] [CrossRef]
- Gómez-Rodríguez, Á.; Sanchez-Carmona, A.; García-Hernández, L.; Cuerno-Rejado, C. Preliminary Correlations for Remotely Piloted Aircraft Systems Sizing. Aerospace 2018, 5, 5. [Google Scholar] [CrossRef] [Green Version]
- Gur, O.; Rosen, A. Optimizing electric propulsion systems for unmanned aerial vehicles. J. Aircr. 2009, 46, 1340–1353. [Google Scholar] [CrossRef] [Green Version]
- Bershadsky, D.; Haviland, S.; Johnson, E.N. Electric multirotor UAV propulsion system sizing for performance prediction and design optimization. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; p. 0581. [Google Scholar]
- Schoemann, J.; Hornung, M. Modeling of hybrid electric propulsion systems for small unmanned aerial vehicles. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, Indiana, 17–19 September 2012; p. 5610. [Google Scholar]
- Cirigliano, D.; Frisch, A.M.; Liu, F.; Sirignano, W.A. Diesel, spark-ignition, and turboprop engines for long-duration unmanned air flights. J. Propuls. Power 2017, 34, 878–892. [Google Scholar] [CrossRef]
- Mattingly, J.D.; Heiser, W.H.; Pratt, D.T. Aircraft Engine Design; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2002. [Google Scholar]
- Roux, Elodie. Turbofan and Turbojet Engines: Database Handbook; Elodie Roux: Blagnac, France, 2007. [Google Scholar]
- Lidor, A.; Weihs, D.; Sher, E. Novel Propulsion Systems for Micro Aerial Vehicles. J. Propuls. Power 2018, 35, 243–267. [Google Scholar] [CrossRef]
- Valencia, E.A.; Jimenez, D.; Alulema, V.H.; Roumeliotis, I.; Montalvan, J.; Pozo, M.; Cando, E. Modeling of a series hybrid propulsion UAV used for monitoring in the Galapagos Islands. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, 24–28 August 2020; p. 3960. [Google Scholar]
- Griffis, C.L.; Wilson, T.A.; Schneider, J.A.; Pierpont, P.S. Framework for the conceptual decomposition of unmanned aircraft propulsion systems. In Proceedings of the 2018 IEEE, Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–10. [Google Scholar]
- Griffis, C.; Wilson, T.; Schneider, J.; Pierpont, P. Unmanned Aircraft System Propulsion Systems Technology Survey; Embry Riddle Scholarly Commons: Daytona Beach, FL, USA, 2009. [Google Scholar]
- Gupta, S.G.; Ghonge, M.M.; Jawandhiya, P. Review of unmanned aircraft system (UAS). Int. J. Adv. Res. Comput. Eng. Technol. (IJARCET) 2013, 2, 1646. [Google Scholar] [CrossRef]
- Adamski, M. Analysis of propulsion systems of unmanned aerial vehicles. J. Mar. Eng. Technol. 2017, 16, 291–297. [Google Scholar] [CrossRef]
- Cwojdziński, L.; Adamski, M. Power units and power supply systems in UAV. Aviation 2014, 18, 1–8. [Google Scholar] [CrossRef]
- Huitema, B. The Analysis of Covariance and Alternatives: Statistical Methods for Experiments, Quasi-Experiments, and Single-Case Studies; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 608. [Google Scholar]
- Alulema, V.H.; Valencia, E.A.; Cando, E.; Rodriguez, D. Preliminary sizing correlations for UAVs’ propulsion system. In Proceedings of the AIAAPropulsion and Energy Forum 2019, Indianapolis, IN, USA, 19–22 August 2019; p. 10. [Google Scholar]
- Logan, M.; Chu, J.; Motter, M.; Carter, D.; Ol, M.; Zeune, C. Small UAV research and evolution in long endurance electric powered vehicles. In Proceedings of the AIAA Infotech@ Aerospace 2007 Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007; p. 2730. [Google Scholar]
- Gong, A.; Verstraete, D. Role of battery in a hybrid electrical fuel cell UAV propulsion system. In Proceedings of the 52nd AIAA Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Traub, L.W. Range and endurance estimates for battery-powered aircraft. J. Aircr. 2011, 48, 703–707. [Google Scholar] [CrossRef]
- Karunarathne, L.; Economou, J.T.; Knowles, K. Model Based Power and Energy Management System for PEM Fuel Cell/Li-Ion Battery Driven Propulsion System. In Proceedings of the 5th IET International Conference on Power Electronics, Machines and Drives (PEMD 2010), Brighton, UK, 19–21 April 2010. [Google Scholar]
- Jung, S.; Jeong, H. Extended kalman filter-based state of charge and state of power estimation algorithm for unmanned aerial vehicle Li-Po battery packs. Energies 2017, 10, 1237. [Google Scholar] [CrossRef] [Green Version]
- Crompton, T.P. Battery Reference Book; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, E.; Forgez, C.; Lagonotte, P.; Friedrich, G. Modelling Ni-mH battery using Cauer and Foster structures. J. Power Sources 2006, 158, 1490–1497. [Google Scholar] [CrossRef]
- Piolenc, M.; Wright, G. Ducted Fan Design: Volume 1; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2015. [Google Scholar]
- Xia, C.l. Permanent Magnet Brushless DC Motor Drives and Controls; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Sforza, P.M. Commercial Airplane Design Principles; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Mair, W.A.; Birdsall, D.L. Aircraft Performance; Cambridge University Press: Cambridge, UK, 1996; Volume 5. [Google Scholar]
- Gudmundsson, S. General Aviation Aircraft Design: Applied Methods and Procedures; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Zeraoulia, M.; Benbouzid, M.E.H.; Diallo, D. Electric motor drive selection issues for HEV propulsion systems: A comparative study. IEEE Trans. Veh. Technol. 2006, 55, 1756–1764. [Google Scholar] [CrossRef] [Green Version]
- Hendershot, J.R.; Miller, T.J.E. Design of Brushless Permanent-Magnet Machines; Motor Design Books: Venice, FL, USA, 2010. [Google Scholar]
- Guzzella, L.; Onder, C. Introduction to Modeling and Control of Internal Combustion Engine Systems; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Taylor, C.F. The Internal-Combustion Engine in Theory and Practice: Combustion, Fuels, Materials, Design; MIT Press: Cambridge, MA, USA, 1985; Volume 2. [Google Scholar]
- Valencia, E.A.; Changoluisa, D.; Alulema, V.H.; Rodriguez, D.A.; Valencia, D.; Nandar, J.; Hernandez, J.; Pozo, M.; Cruz, P.; Cando, E. Power Management Strategies for Small Electric Fixed WingUAVs Employed in Natural Resources Mapping. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, 24–28 August 2020; p. 3963. [Google Scholar]





| Type | A | B | n | ||
|---|---|---|---|---|---|
| Li-ion | 0.0635 | 0.8627 | 0.9644 | 77 | 3.7 |
| Li-Po | 0.0446 | 0.9273 | 0.9696 | 241 | 3.7 |
| LiFePo4 | 0.0306 | 1.0031 | 0.9918 | 64 | 3.3 |
| Ni-Cd | 0.1524 | 0.7813 | 0.9237 | 73 | 1.2 |
| Ni-MH | 0.0349 | 0.9095 | 0.9439 | 66 | 1.2 |
| 2S | 3S | 4S | 5S | 6S | 7S | 8S | 9S | 10S | 12S | |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 0.1224 | 0.1931 | 0.2828 | 0.2777 | 0.3988 | 0.8657 | 0.2975 | 0.3564 | 0.7246 | 1.0378 |
| B | 0.8963 | 0.8874 | 0.8744 | 0.8993 | 0.8810 | 0.8081 | 0.9512 | 0.9443 | 0.8715 | 0.8562 |
| 0.9723 | 0.9741 | 0.9763 | 0.9509 | 0.9761 | 0.8553 | 0.9527 | 0.8423 | 0.9434 | 0.9675 | |
| n | 719 | 620 | 440 | 141 | 346 | 43 | 51 | 21 | 47 | 31 |
| Inrunner | Outrunner | |||
|---|---|---|---|---|
| Class | [g] | [g] | ||
| I | 50–100 | 1500–3000 | 50–100 | 9000–2500 |
| II | 100–500 | 500–1500 | 100–500 | 300–9000 |
| III | 500–5000 | 100–500 | 500–2000 | 50–300 |
| IV | 5000–10,000 | 30–100 | 2000–10,000 | 10–50 |
| A | B | n | ||
|---|---|---|---|---|
| Two stroke | 0.0003 | 1.0530 | 0.8959 | 114 |
| Four stroke | 0.0013 | 0.8952 | 0.9300 | 113 |
| A | B | n | ||
|---|---|---|---|---|
| Two stroke | 0.0035 | 1.1327 | 0.9353 | 114 |
| Four stroke | 0.0151 | 0.9940 | 0.9612 | 113 |
| Aerodynamics | Requirements | ||
|---|---|---|---|
| Wing area S [m] | 0.8 | Operating Altitude | 4000 |
| Max. UAV mass [kg] | 4 | Air Density, p @4000 m.a.s.l | 0.8023 |
| 0.01764 | Cruise Altitude [m] | 100 | |
| Aspect Ratio, AR | 5.51 | Rate of Climb [m/s] | 5 |
| Empty mass (fixed) [kg] | 2.5 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alulema, V.; Valencia, E.; Cando, E.; Hidalgo, V.; Rodriguez, D. Propulsion Sizing Correlations for Electrical and Fuel Powered Unmanned Aerial Vehicles. Aerospace 2021, 8, 171. https://doi.org/10.3390/aerospace8070171
Alulema V, Valencia E, Cando E, Hidalgo V, Rodriguez D. Propulsion Sizing Correlations for Electrical and Fuel Powered Unmanned Aerial Vehicles. Aerospace. 2021; 8(7):171. https://doi.org/10.3390/aerospace8070171
Chicago/Turabian StyleAlulema, Victor, Esteban Valencia, Edgar Cando, Victor Hidalgo, and Dario Rodriguez. 2021. "Propulsion Sizing Correlations for Electrical and Fuel Powered Unmanned Aerial Vehicles" Aerospace 8, no. 7: 171. https://doi.org/10.3390/aerospace8070171
APA StyleAlulema, V., Valencia, E., Cando, E., Hidalgo, V., & Rodriguez, D. (2021). Propulsion Sizing Correlations for Electrical and Fuel Powered Unmanned Aerial Vehicles. Aerospace, 8(7), 171. https://doi.org/10.3390/aerospace8070171






