PSO-Based Soft Lunar Landing with Hazard Avoidance: Analysis and Experimentation
Abstract
:1. Introduction
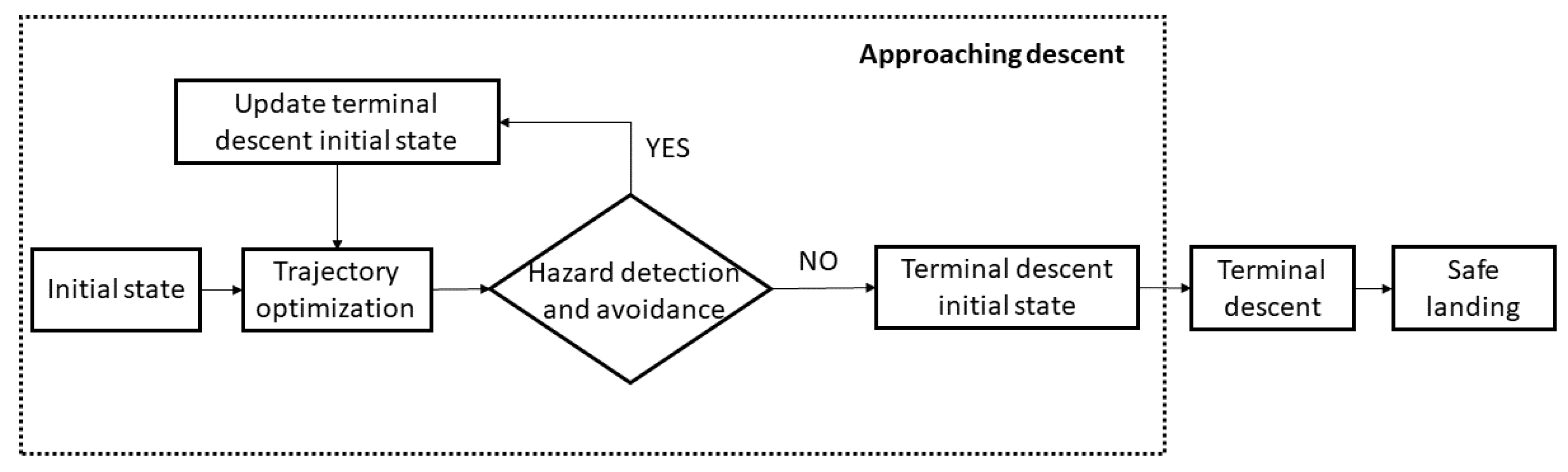
2. Autonomous Trajectory Planning Framework
2.1. Related Works
- Development and practical implementation of a sub-optimal trajectory generation algorithm that can allow for fast trajectory re-planning.
- Development of a strategy to eventually counteract possible algorithm failures and allow for a soft landing.
- Tests for the reliability and robustness analysis of the proposed approach based on a Monte Carlo campaign.
2.2. Experimental Facility
- Cartesian robot: the Cartesian robot is actuated by stepping motors (located on the principal axes of the robot) with holding bipolar torque of 820 Ncm. Due to the maximum linear speed of the robot, especially along the z-axis that is of 2 cm/s, the simulation time is about four times larger than the real landing time.
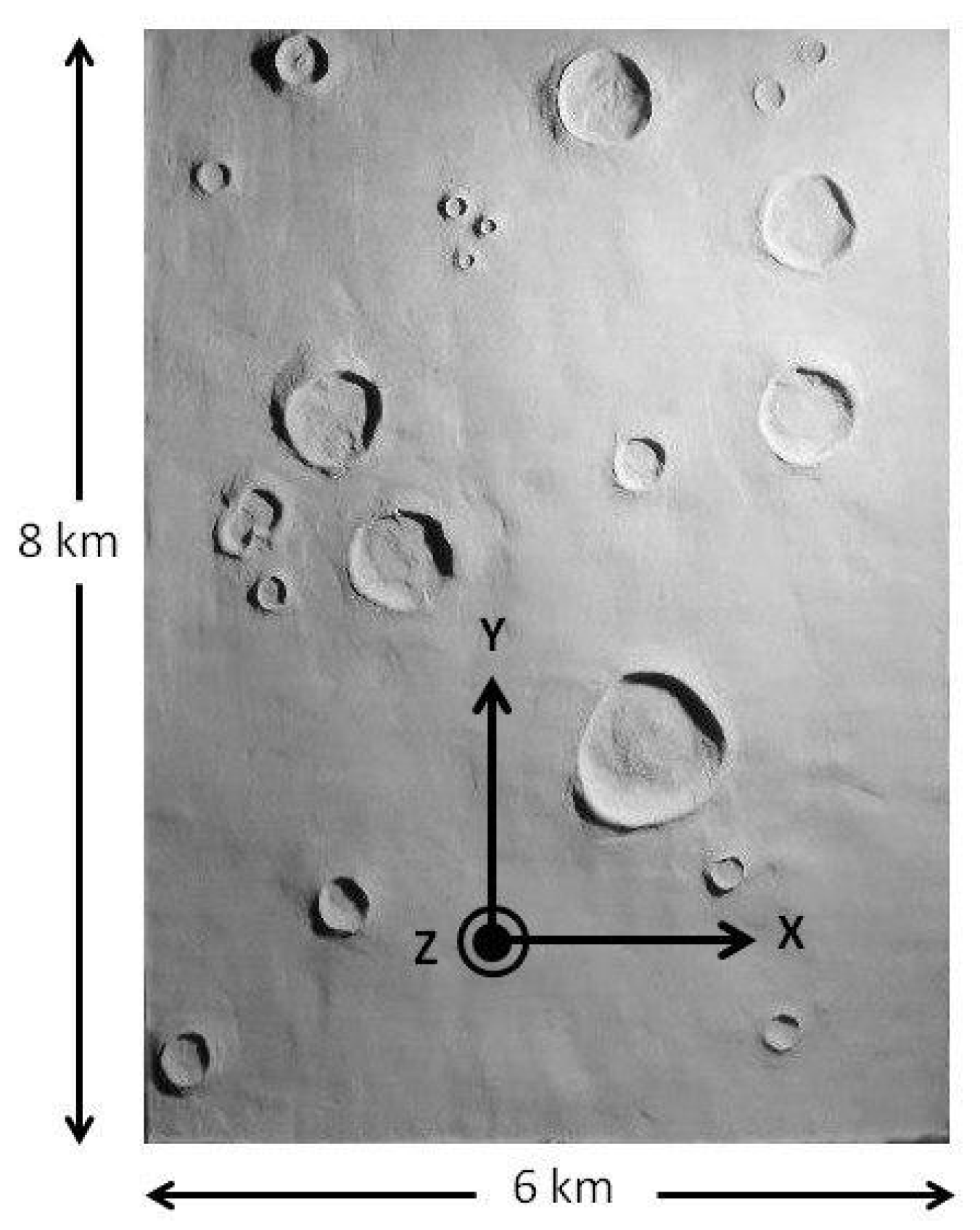
- Lunar scenario: the Cartesian manipulator is installed on a high-fidelity reproduction of the lunar equatorial zone located at the Mare Serenitatis (23° North–14° East). The lunar soil simulant is made by sifted basalt powder, while the craters are made by calk using molds with sizes and shapes according to [41]. The physical dimension of the lunar terrain in the facility is 3 m × 4 m. Since the scale of the image with respect to the real terrain is 1:2000 m, the reproduced dimensions along the x and y-axis would be in reality 6000 m and 8000 m, respectively.
3. Dynamical Model
4. Guidance Philosophy
4.1. Trajectory Optimization
4.1.1. Particle Swarm Optimization
- The first term is called the inertia term and makes the particle move in the direction through which it reached the actual position. This term is multiplied by the inertia weight (w), which is set equal to 1.2 in this work, although it can also be decreased during the loop to encourage the exploration at the beginning of the algorithm and the exploitation at the end.
- The second term is the personal best term. Each particle keeps the memory of its personal best position (), i.e., the position associated with the best fitness function. Thanks to this term, the particle always tends to return to that position. In particular, represents a real random value in the interval , whereas is another coefficient which is supposed to be constant and set equal to 1.5. The personal best is updated during the iterations as follows:where is the current fitness function.
- The third term is the local term and, for each particle, considers the position of the best particle (with the best cost function ) within a small neighborhood (). This means that the entire population is split into many subgroups, where each subgroup is composed of the current particle and its previous and successive particles (in this work, is set equal to 5). The local term allows for hopefully avoiding being trapped in local minima. Even for this term, represents a real random value in the interval , whereas is another coefficient that is supposed to be constant and set equal to 1.5. The local best is updated during the iterations as follows:
- The fourth term is the global term and takes into account the position with the best fitness function () within the entire population (). This term attracts all the particles towards the best position and thus plays a crucial role in the convergence of the algorithm. The coefficients involved in this term are , which represents a real random value in the interval , and , which is supposed to be constant and set equal to 1.5. The global best is updated as follows:
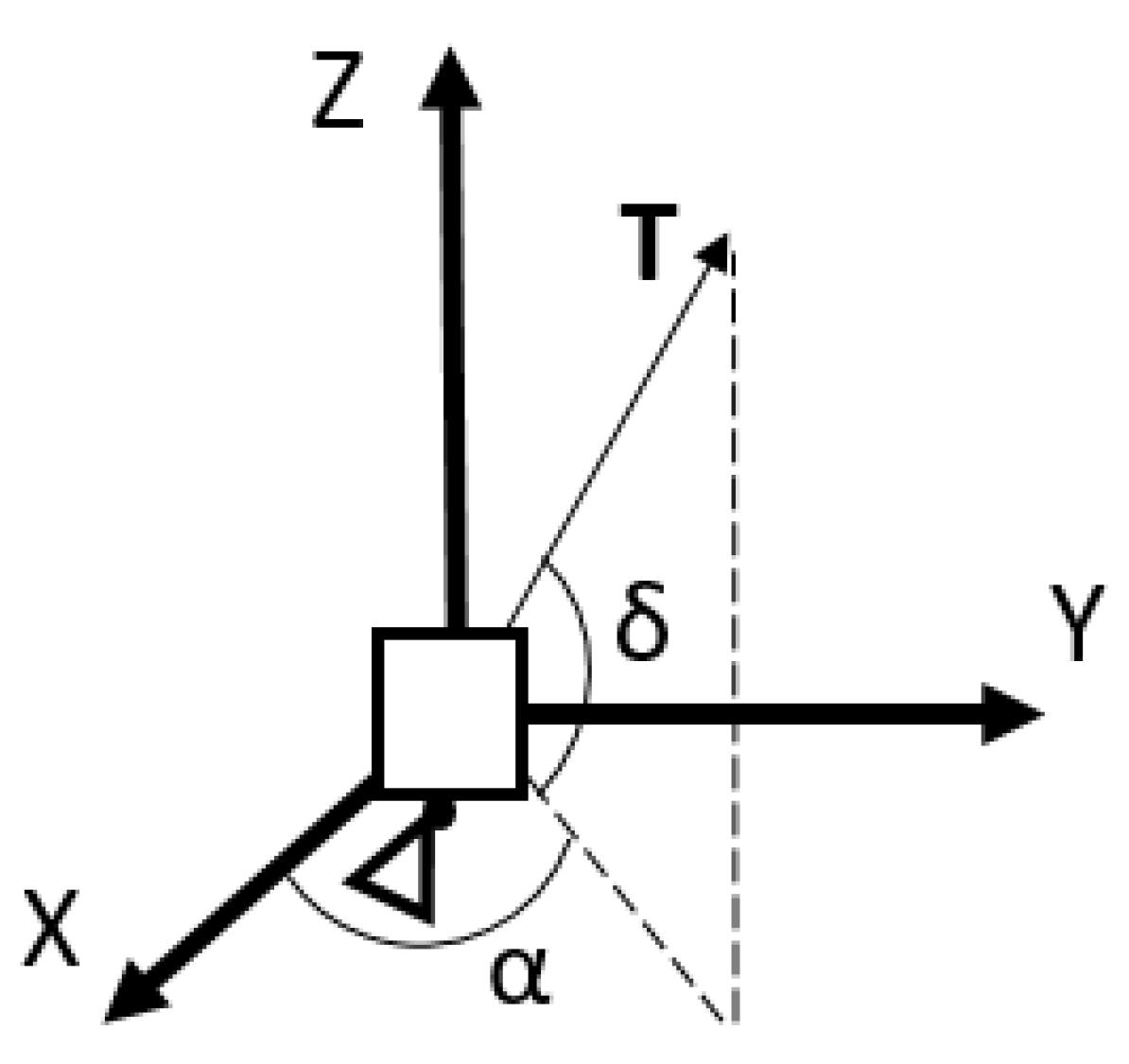
4.1.2. Guidance Concept and Inverse Dynamics Approach
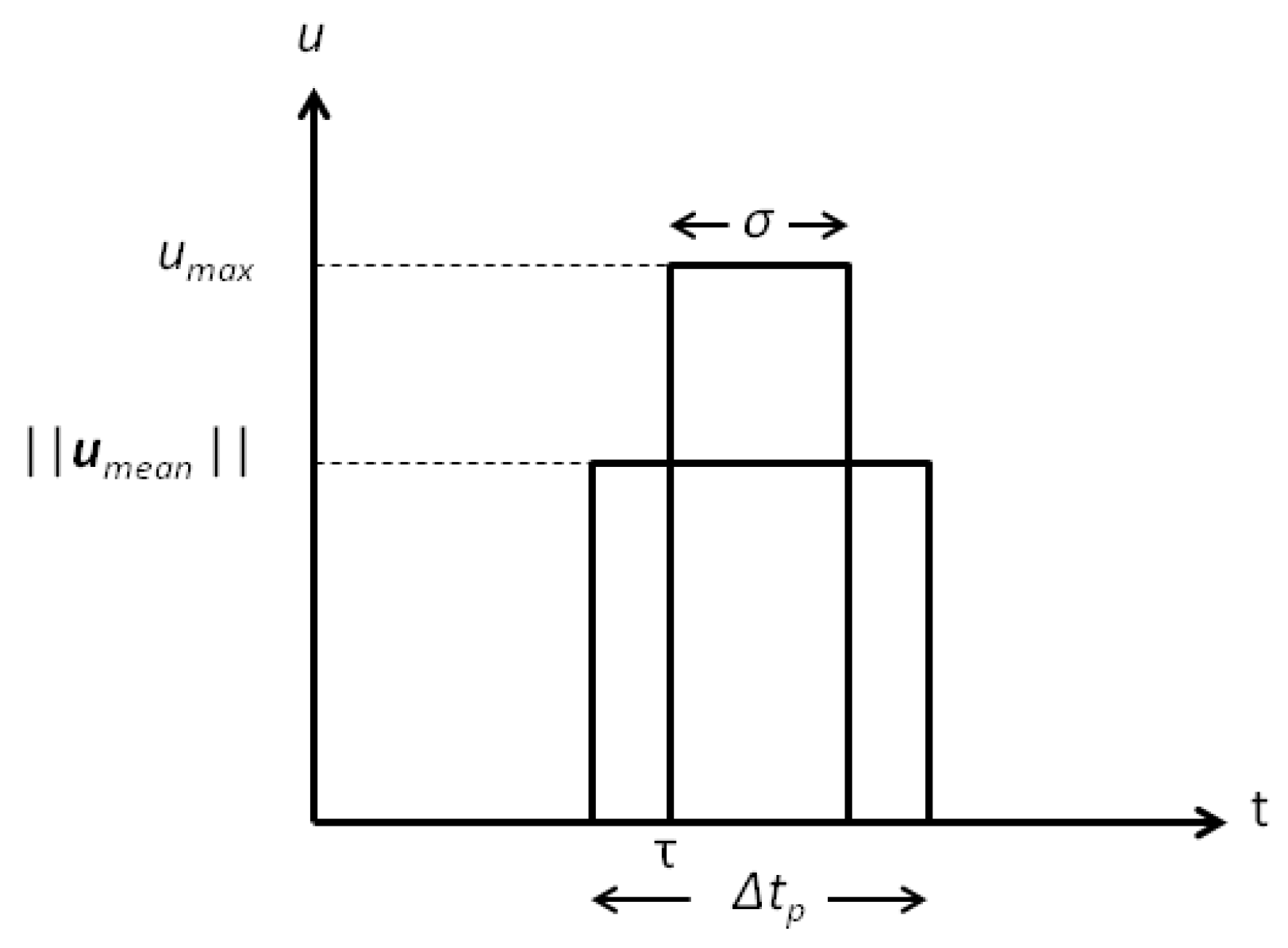
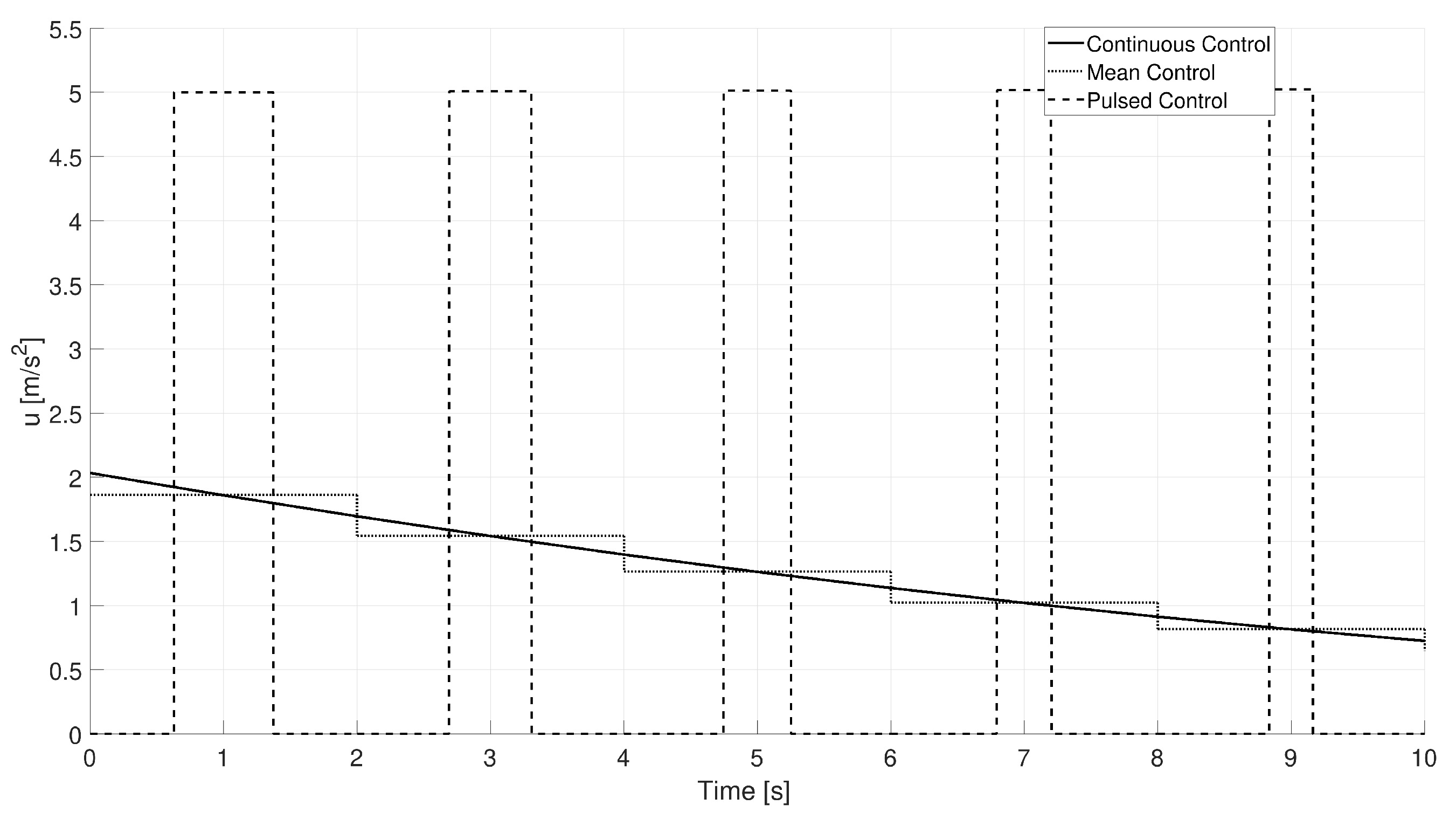
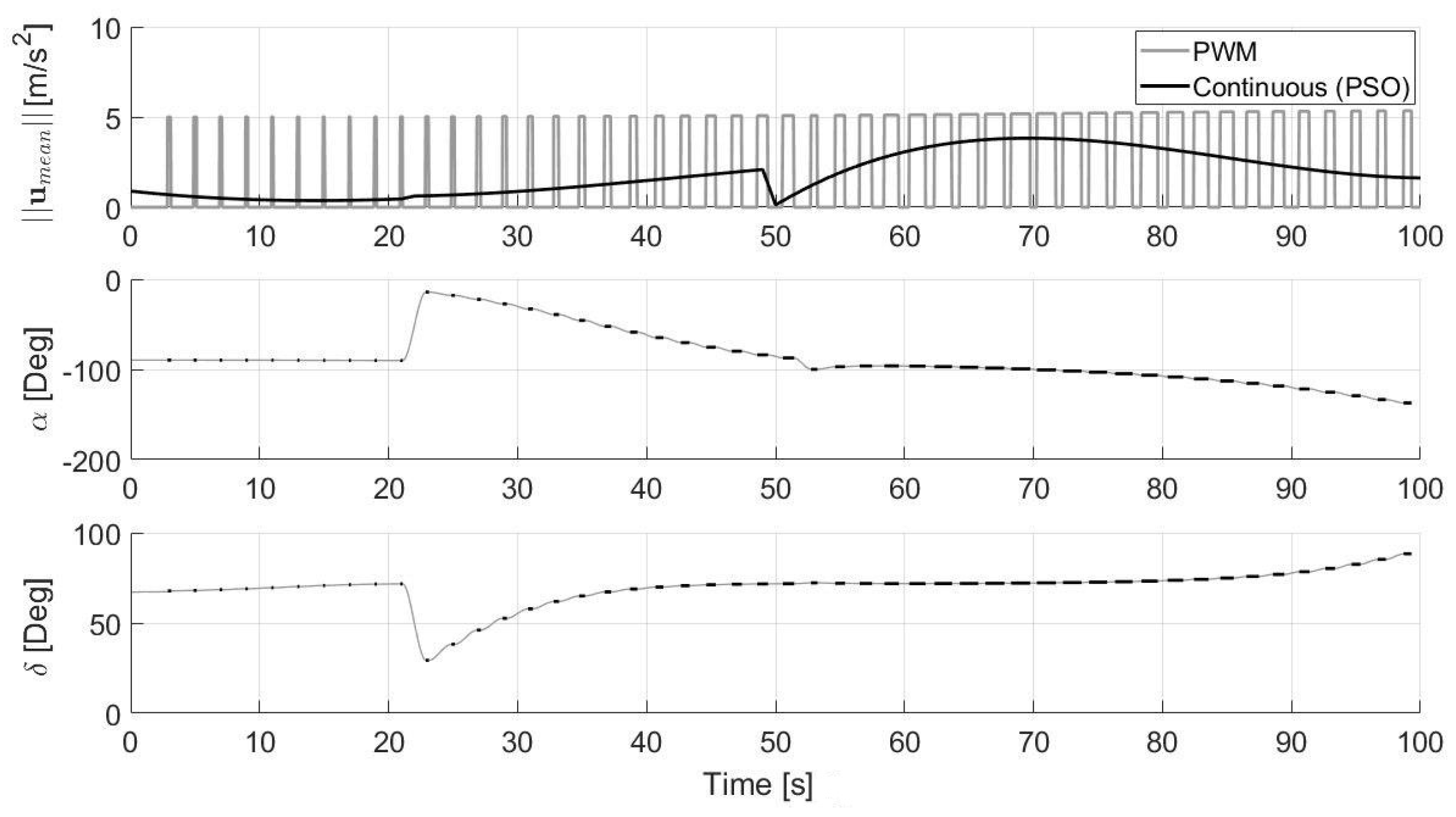
4.1.3. Continuous to Pulsed Control Acceleration
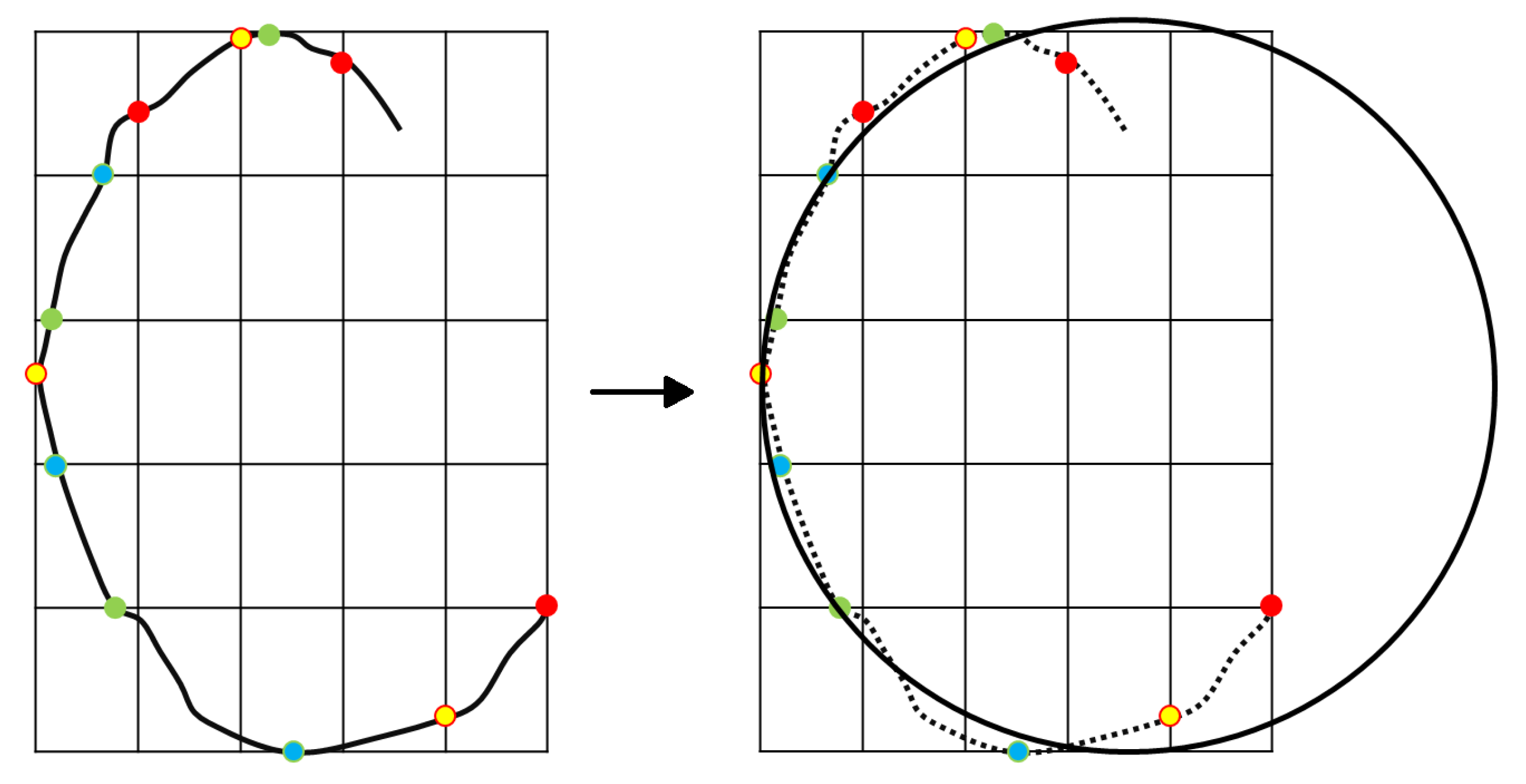
4.2. Hazard Detection and Avoidance
- Once the image of the lunar terrain is taken by the camera, the Canny algorithm is used to detect the edges.
- Thanks to the circles detection algorithm, craters are identified in the image processed via Canny algorithm.
- Compute and , where e and f correspond to the resolution of the camera ( and , as stated in Section 2.2). These parameters allow for performing the conversion between meters and pixels in the image.
- Identify the final landing position (in pixels) within the current image. In pixel coordinates, we obtain and , where and are the current X and Y components of the position vector of the lander, whereas represents the final landing position vector. Note that the origin of the matrix associated with the pixels is taken as the bottom left part of the image.
- If the landing position does not belong to the portion of the image actually seen by the camera or, if it appears to reside outside craters, the hazard avoidance is not performed and the descent continues. Instead, if the landing position pixel lies within the portion of the image seen by the camera and, at the same time, it resides within a crater, a safety distance (d), transformed into a pixel distance, is applied to the original (unsafe) final position to obtain a new safe final position () for the approaching phase. This position is then converted from a pixel in the image to a position in meters with respect to the origin of the reference frame. The new position is updated considering the closer edge of the hazard (left or right) and adding the safety distance (in this work set equal to 50 m) in the same direction. Therefore, only the X component of the original final position vector of the approaching phase is actually modified.
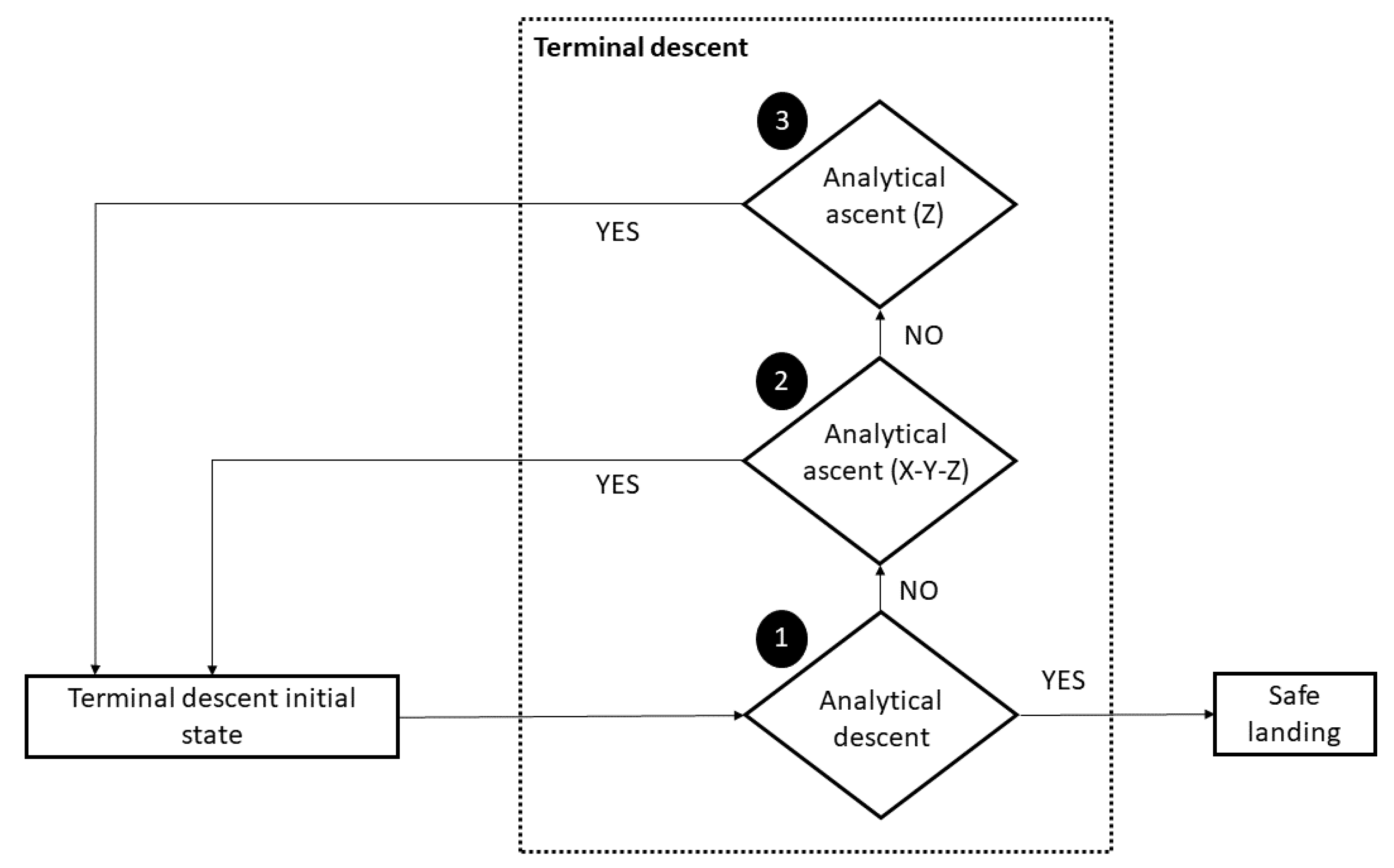
4.3. Terminal Descent
4.3.1. Analytical Descent Control
4.3.2. Analytical Ascent (X-Y-Z) Control
4.3.3. Analytical Ascent (Z) Control
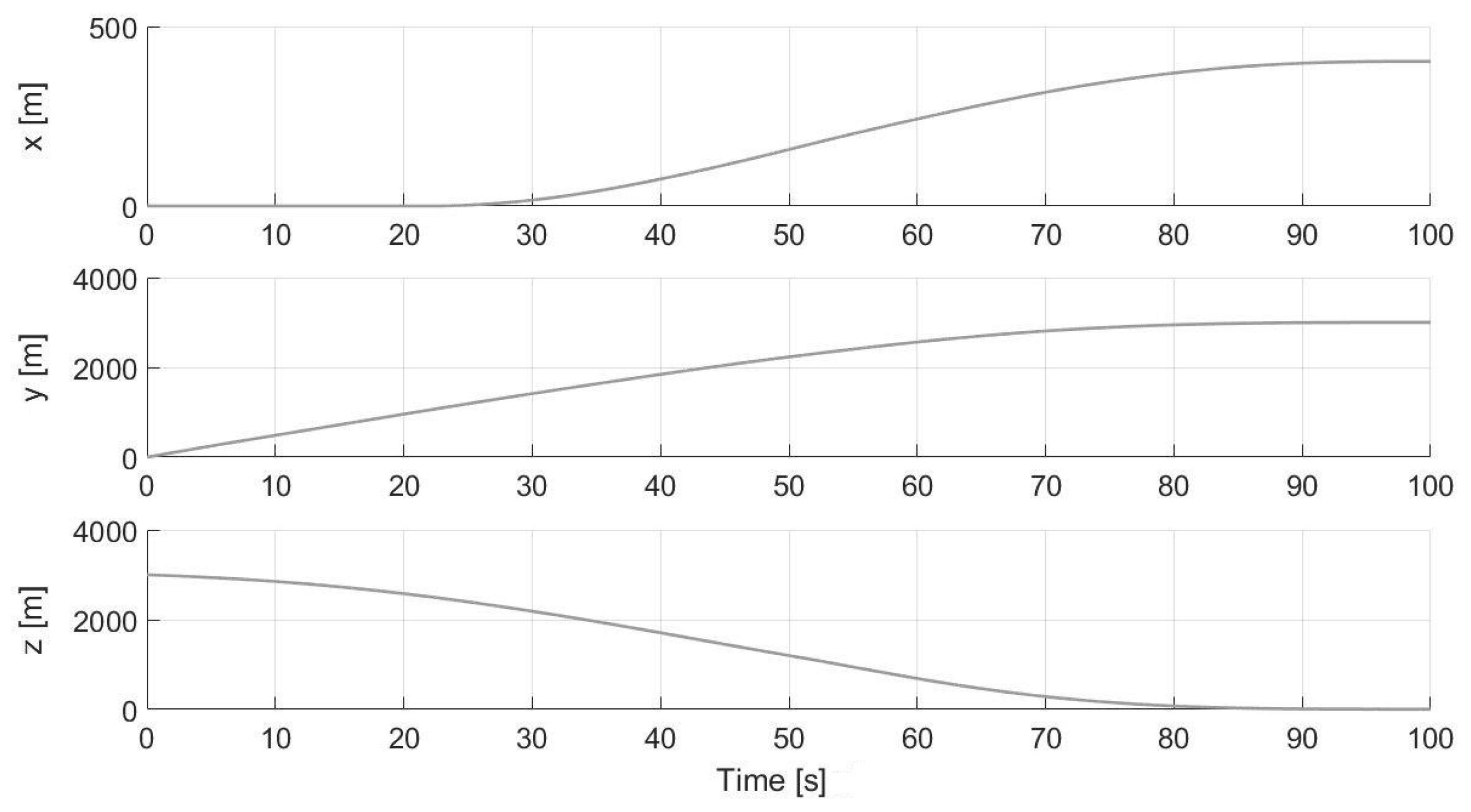
5. Simulations
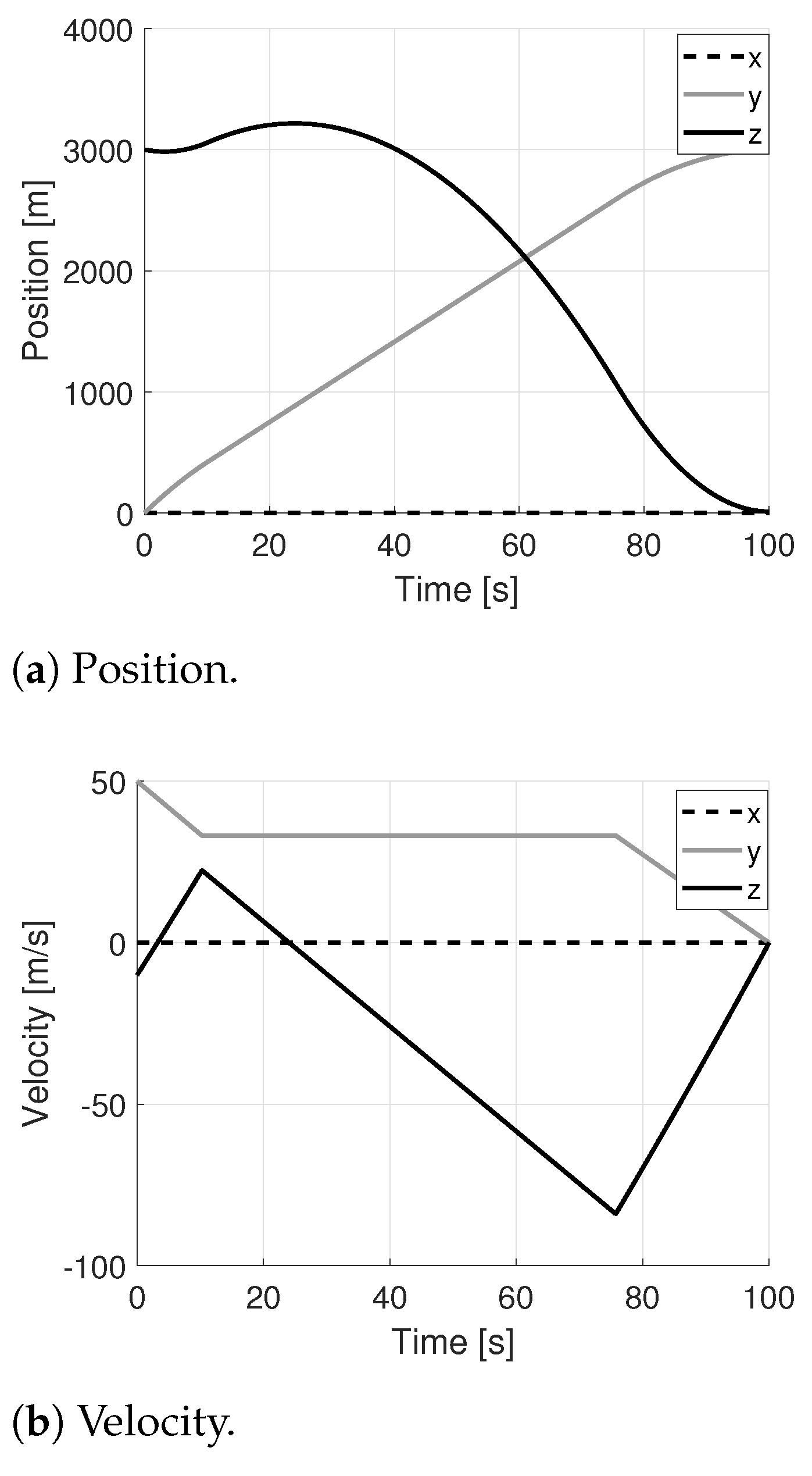
5.1. Numerical Results
Comparison with GPOPS-II
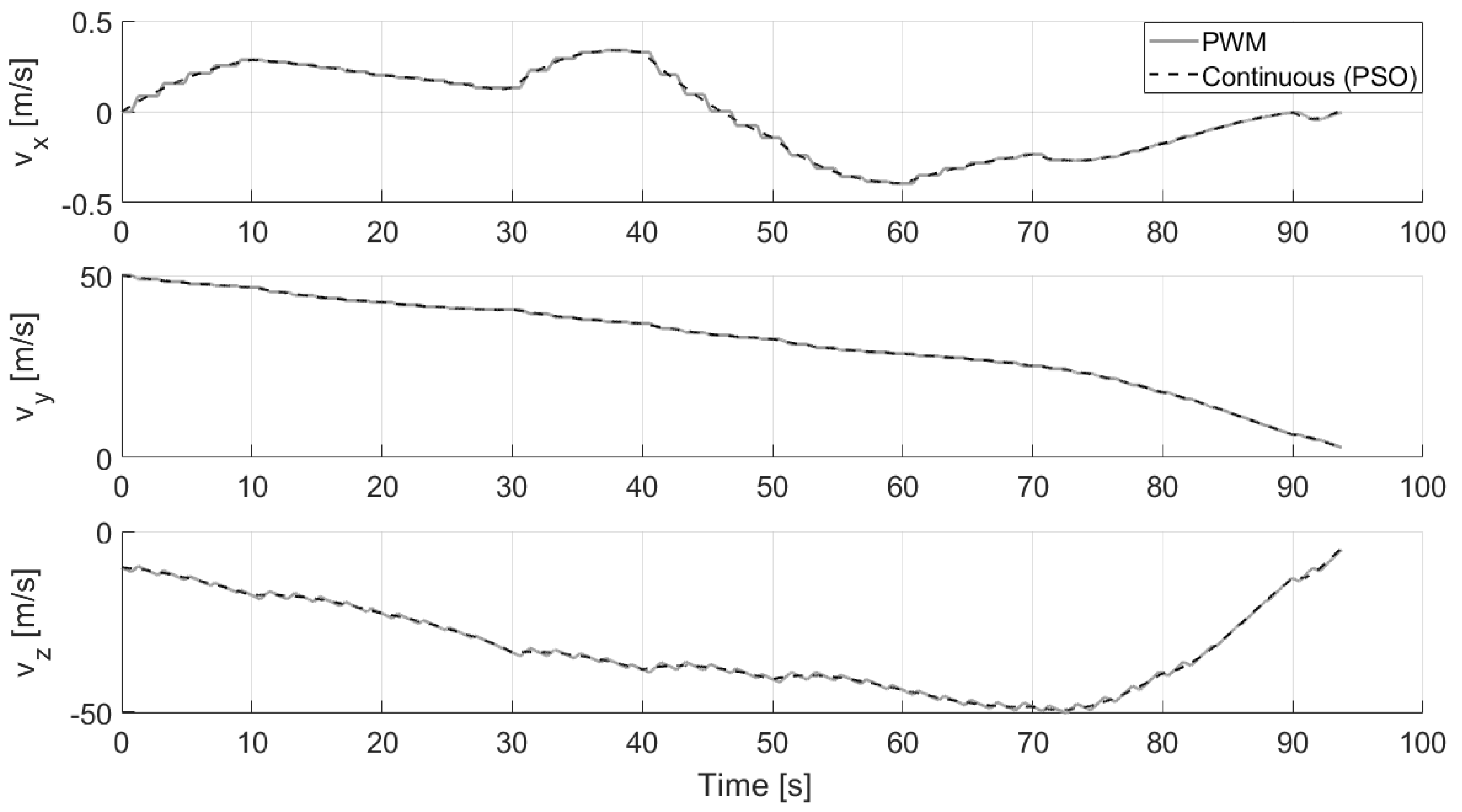
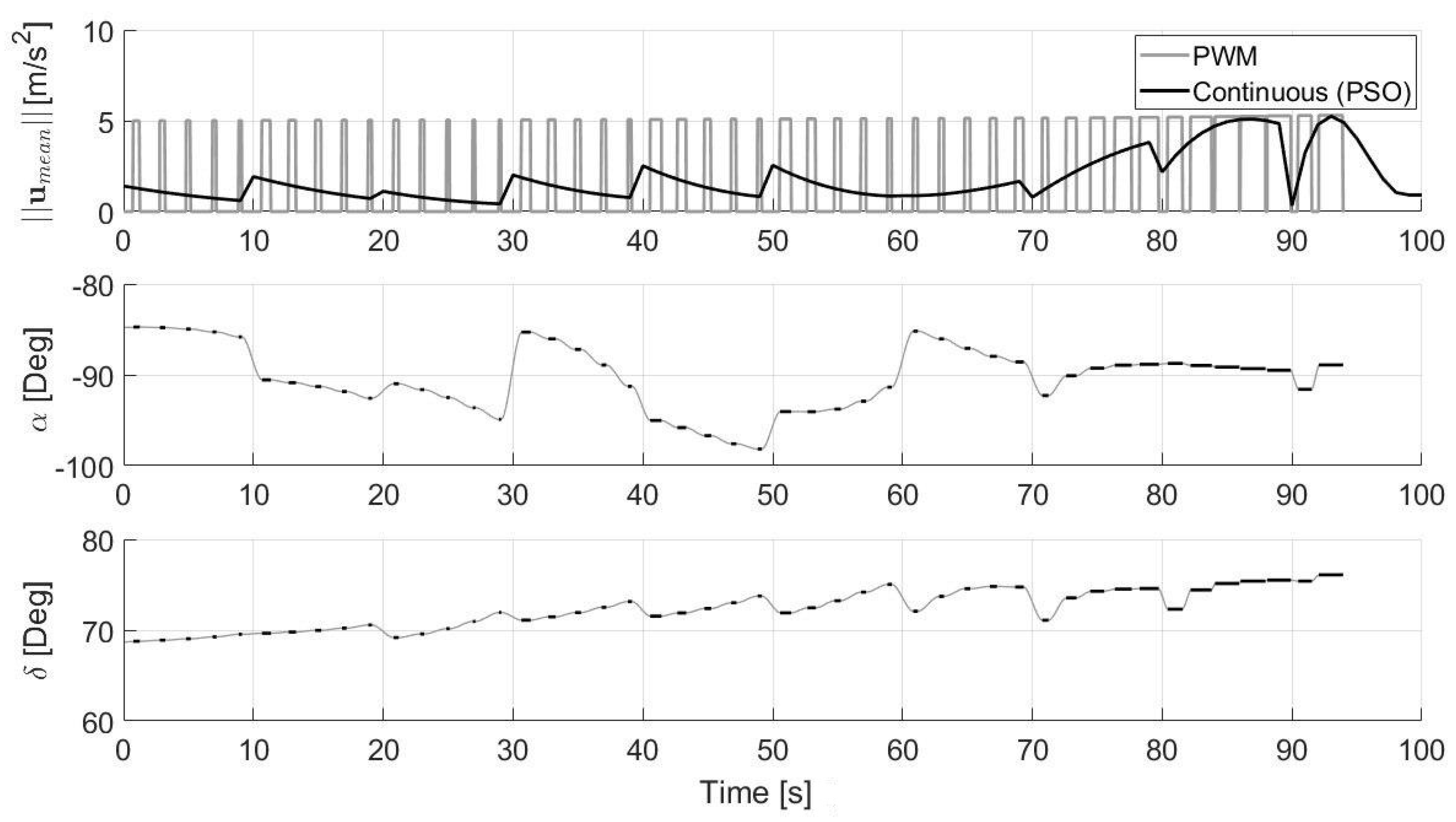
5.2. Experimental Results
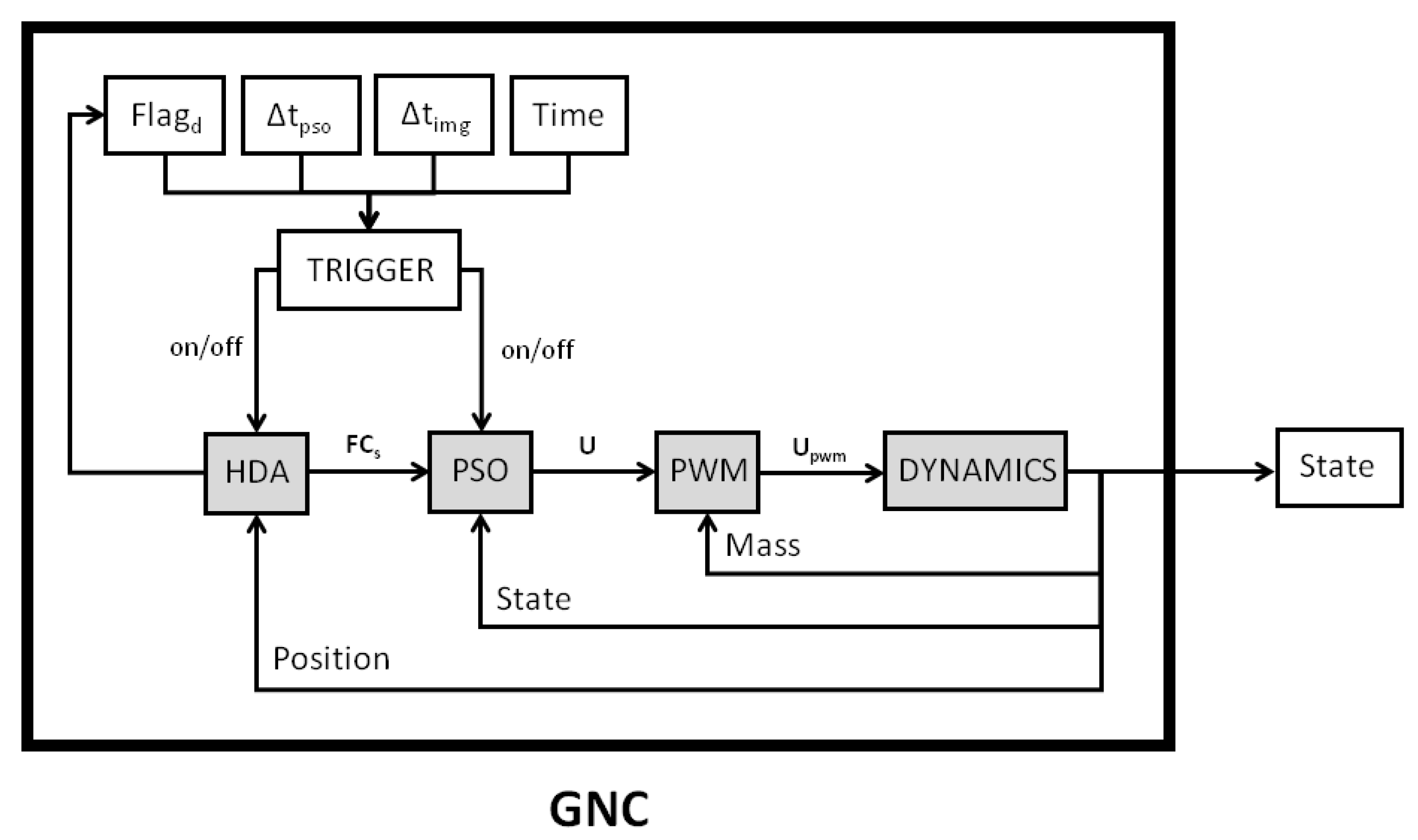
- The GNC block is the central part of the proposed algorithm previously explained. As can be seen from the lower level blocks of the GNC module shown in Figure 20, the main blocks are: the HDA, which takes the position as input each s, acquires the images from the camera, recognizes the hazards and eventually computes a new safe landing site near the nominal one; the PSO, which nominally performs the optimizations each s ( s and s) and also if the landing position is updated (based on the value of the whose value is 1 if the landing position is detected within a hazard, 0 otherwise); the PWM, which transforms the continuous control into the pulsed control; and the DYNAMICS, which integrates the equations of motion.
- The second block handles data transfer between ports operating at different rates, so that the actual transmission of the information to the hardware occurs at different times. Indeed, the GNC module has a sample time of 0.002 s, while the transmission to the hardware occurs every 0.09 s.
- This block scales down the actual computed velocities to the simulated ones to be implemented by the manipulator. Each component of the velocity is multiplied by a factor of 0.5 and the output velocities are considered in mm/s.
- Once the velocities are scaled-down, these need to be transmitted to the manipulator and be actionable by the stepping motors. For this reason, saturation values need to be considered: for x and y components of the velocity vector the range is [−200, 200] mm/s, whereas, for the z-component, the range is [−25.5, 25.5] mm/s (these values depend on the physical limitations of the manipulator).
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Li, C.; Liu, J.; Ren, X.; Zuo, W.; Tan, X.; Wen, W.; Li, H.; Mu, L.; Su, Y.; Zhang, H.; et al. The Chang’e 3 mission overview. Space Sci. Rev. 2015, 190, 85–101. [Google Scholar] [CrossRef]
- Jia, Y.; Zou, Y.; Ping, J.; Xue, C.; Yan, J.; Ning, Y. The scientific objectives and payloads of Chang’E- 4 mission. Planet. Space Sci. 2018, 162, 207–215. [Google Scholar] [CrossRef]
- Li, F.; Ye, M.; Yan, J.; Hao, W.; Barriot, J.P. A simulation of the Four-way lunar Lander–Orbiter tracking mode for the Chang’E-5 mission. Adv. Space Res. 2016, 57, 2376–2384. [Google Scholar] [CrossRef]
- Bhandari, N. Chandrayaan-1: Science goals. J. Earth Syst. Sci. 2005, 114, 701–709. [Google Scholar] [CrossRef] [Green Version]
- Sundararajan, V. Overview and Technical Architecture of India’s Chandrayaan-2 Mission to the Moon. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 2178. [Google Scholar]
- Song, Y.J.; Lee, D.; Bae, J.; Kim, Y.R.; Choi, S.J. Flight dynamics and navigation for planetary missions in Korea: Past efforts, recent status, and future preparations. J. Astron. Space Sci. 2018, 35, 119–131. [Google Scholar]
- Efanov, V.; Dolgopolov, V. The Moon: From research to exploration (To the 50th anniversary of Luna-9 and Luna-10 Spacecraft). Sol. Syst. Res. 2017, 51, 573–578. [Google Scholar] [CrossRef]
- Voosen, P. NASA to Pay Private Space Companies for Moon Rides; American Association for the Advancement of Science: Washington, DC, USA, 2018. [Google Scholar]
- Sawabe, Y.; Matsunaga, T.; Rokugawa, S. Automated detection and classification of lunar craters using multiple approaches. Adv. Space Res. 2006, 37, 21–27. [Google Scholar] [CrossRef]
- Clerc, M. Particle Swarm Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2010; Volume 93. [Google Scholar]
- Ross, I.M.; Fahroo, F. A perspective on methods for trajectory optimization. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4727. [Google Scholar]
- Rijesh, M.; Sijo, G.; Philip, N.; Natarajan, P. Geometrical guidance algorithm for soft landing on lunar surface. IFAC Proc. Vol. 2014, 47, 14–19. [Google Scholar] [CrossRef]
- Mathavaraj, S.; Pandiyan, R.; Padhi, R. Constrained optimal multi-phase lunar landing trajectory with minimum fuel consumption. Adv. Space Res. 2017, 60, 2477–2490. [Google Scholar] [CrossRef]
- Park, B.G.; Ahn, J.S.; Tahk, M.J. Two-dimensional trajectory optimization for soft lunar landing considering a landing site. Int. J. Aeronaut. Space Sci. 2011, 12, 288–295. [Google Scholar] [CrossRef]
- Wibben, D.R.; Furfaro, R.; Sanfelice, R.G. Optimal lunar landing and retargeting using a hybrid control strategy. In 23rd AAS/AIAA Space Flight Mechanics Meeting; Spaceflight Mechanics 2013; Univelt Inc.: Escondido, CA, USA, 2013; pp. 1901–1919. [Google Scholar]
- Guo, J.; Han, C. Design of guidance laws for lunar pinpoint soft landing. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Pittsburgh, PA, USA, 9–13 August 2009. [Google Scholar]
- Banerjee, A.; Padhi, R. Inverse polynomial based explicit guidance for lunar soft landing during powered braking. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015; pp. 768–773. [Google Scholar]
- Qu, M.F. Lunar soft-landing trajectory of mechanics optimization based on the improved ant colony algorithm. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2015; Volume 721, pp. 446–449. [Google Scholar]
- Pontani, M.; Conway, B.A. Particle swarm optimization applied to space trajectories. J. Guid. Control. Dyn. 2010, 33, 1429–1441. [Google Scholar] [CrossRef]
- Pontani, M.; Conway, B. Optimal Finite-Thrust Rendezvous Trajectories Found via Particle Swarm Algorithm. J. Spacecr. Rocket. 2013, 50, 1222–1234. [Google Scholar] [CrossRef]
- Spiller, D.; Curti, F.; Circi, C. Minimum-Time Reconfiguration Maneuvers of Satellite Formations Using Perturbation Forces. J. Guid. Control. Dyn. 2017, 5, 1130–1143. [Google Scholar] [CrossRef]
- Lavagna, M.; Parigini, C.; Armellin, R. PSO algorithm for planetary atmosphere entry vehicles multidisciplinary guidance design. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–26 August 2006; p. 6027. [Google Scholar]
- Gao, X.; Liang, B.; Qiu, Y. A PSO algorithm of multiple impulses guidance and control for GEO space robot. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Marina Bay Sands, Singapore, 10–12 December 2014; pp. 1560–1565. [Google Scholar]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of nonlinear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef] [Green Version]
- Louembet, C.; Cazaurang, F.; Zolghadri, A.; Charbonnel, C.; Pittet, C. Design of algorithms for satellite slew manoeuver by flatness and collocation. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 3168–3173. [Google Scholar]
- Curti, F.; Parisse, M.; Ansalone, L.; Nardi, E.; Cassiano, P.; Testi, F.; Paiano, S. Multi-purpose Experimental Test-bed For Space In addition, Planetary Exploration. In Proceedings of the 2nd IAA Conference on Dynamics and Control of Space Systems (DYCOSS), Rome, Italy, 24–26 March 2014; 2015. [Google Scholar]
- Ansalone, L.; Grava, E.; Curti, F. Experimental results of a Terrain Relative Navigation algorithm using a simulated lunar scenario. Acta Astronaut. 2015, 116, 78–92. [Google Scholar] [CrossRef]
- Julien, C.R.; LaMeres, B.J.; Weber, R.J. An FPGA-based radiation tolerant SmallSat Computer System. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–13. [Google Scholar] [CrossRef]
- Lu, P.; Liu, X. Autonomous trajectory planning for rendezvous and proximity operations by conic optimization. J. Guid. Control. Dyn. 2013, 36, 375–389. [Google Scholar] [CrossRef]
- Rea, J.; Bishop, R. Analytical dimensional reduction of a fuel optimal powered descent subproblem. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2010; p. 8026. [Google Scholar]
- Szmuk, M.; Eren, U.; Acikmese, B. Successive convexification for mars 6-dof powered descent landing guidance. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; p. 1500. [Google Scholar]
- Açıkmeşe, B.; Carson, J.M.; Blackmore, L. Lossless convexification of nonconvex control bound and pointing constraints of the soft landing optimal control problem. IEEE Trans. Control Syst. Technol. 2013, 21, 2104–2113. [Google Scholar] [CrossRef]
- Liu, X.; Lu, P.; Pan, B. Survey of convex optimization for aerospace applications. Astrodynamics 2017, 1, 23–40. [Google Scholar] [CrossRef]
- Pinson, R.M.; Lu, P. Trajectory design employing convex optimization for landing on irregularly shaped asteroids. J. Guid. Control. Dyn. 2018, 41, 1243–1256. [Google Scholar] [CrossRef]
- Yang, H.; Bai, X.; Baoyin, H. Rapid generation of time-optimal trajectories for asteroid landing via convex optimization. J. Guid. Control. Dyn. 2017, 40, 628–641. [Google Scholar] [CrossRef]
- Izzo, D.; Öztürk, E. Real-Time Optimal Guidance and Control for Interplanetary Transfers Using Deep Networks. arXiv 2020, arXiv:2002.09063. [Google Scholar]
- Li, H.; Chen, S.; Izzo, D.; Baoyin, H. Deep networks as approximators of optimal low-thrust and multi-impulse cost in multitarget missions. Acta Astronaut. 2020, 166, 469–481. [Google Scholar] [CrossRef]
- Hossain, M.A.; Madkour, A.; Dahal, K.P.; Zhang, L. A real-time dynamic optimal guidance scheme using a general regression neural network. Eng. Appl. Artif. Intell. 2013, 26, 1230–1236. [Google Scholar] [CrossRef]
- Esposito, M.; Conticello, S.; Pastena, M.; Domínguez, B.C. In-orbit demonstration of artificial intelligence applied to hyperspectral and thermal sensing from space. In CubeSats and SmallSats for Remote Sensing III; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11131, p. 111310C. [Google Scholar]
- Li, C.; Liang, B.; Xu, W. Autonomous trajectory planning of free-floating robot for capturing space target. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1008–1013. [Google Scholar]
- Heiken, G.H.; Vaniman, D.T.; French, B.M. Lunar Sourcebook, a User’s Guide to the Moon; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kennedy, J. The particle swarm: Social adaptation of knowledge. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 303–308. [Google Scholar]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A survey of historical and recent developments with hybridization perspectives. Mach. Learn. Knowl. Extr. 2019, 1, 157–191. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.X.; Cheng, H.Z.; Yan, J.Y.; Zhang, L. New discrete method for particle swarm optimization and its application in transmission network expansion planning. Electr. Power Syst. Res. 2007, 77, 227–233. [Google Scholar] [CrossRef]
- Izquierdo, J.; Montalvo, I.; Pérez, R.; Fuertes, V.S. Design optimization of wastewater collection networks by PSO. Comput. Math. Appl. 2008, 56, 777–784. [Google Scholar] [CrossRef] [Green Version]
- Lalwani, S.; Sharma, H.; Satapathy, S.C.; Deep, K.; Bansal, J.C. A Survey on Parallel Particle Swarm Optimization Algorithms. Arab. J. Sci. Eng. 2019, 44, 2899–2923. [Google Scholar] [CrossRef]
- Bernelli-Zazzera, F.; Mantegazza, P. Pulse-width equivalent to pulse-amplitude discrete control of linearsystems. J. Guid. Control. Dyn. 1992, 15, 461–467. [Google Scholar] [CrossRef]
- Mokhtarian, F.; Suomela, R. Robust image corner detection through curvature scale space. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1376–1381. [Google Scholar] [CrossRef] [Green Version]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- MATLAB. Version 9.5.0.1067069 (R2018b); The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Wang, D.; Huang, X.; Guan, Y. GNC system scheme for lunar soft landing spacecraft. Adv. Space Res. 2008, 42, 379–385. [Google Scholar] [CrossRef]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. (TOMS) 2014, 41, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Amzajerdian, F.; Pierrottet, D.; Petway, L.; Hines, G.; Roback, V. Lidar systems for precision navigation and safe landing on planetary bodies. In International Symposium on Photoelectronic Detection and Imaging 2011: Laser Sensing and Imaging; and Biological and Medical Applications of Photonics Sensing and Imaging; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8192, p. 819202. [Google Scholar]
- Ghilardi, L.; D’Ambrosio, A.; Scorsoglio, A.; Furfaro, R.; Curti, F. Image-based lunar landing hazard detection via deep learning. In Proceedings of the 31st AAS/AIAA Space Flight Mechanics Meeting, Virtual. 1–4 February 2021. [Google Scholar]
- Scorsoglio, A.; D’Ambrosio, A.; Ghilardi, L.; Furfaro, R.; Gaudet, B.; Linares, R.; Curti, F. Safe lunar landing via images: A reinforcement meta-learning application to autonomous hazard avoidance and landing. In Proceedings of the 2020 AAS/AIAA Astrodynamics Specialist Conference, Virtual. 9–12 August 2020. [Google Scholar]




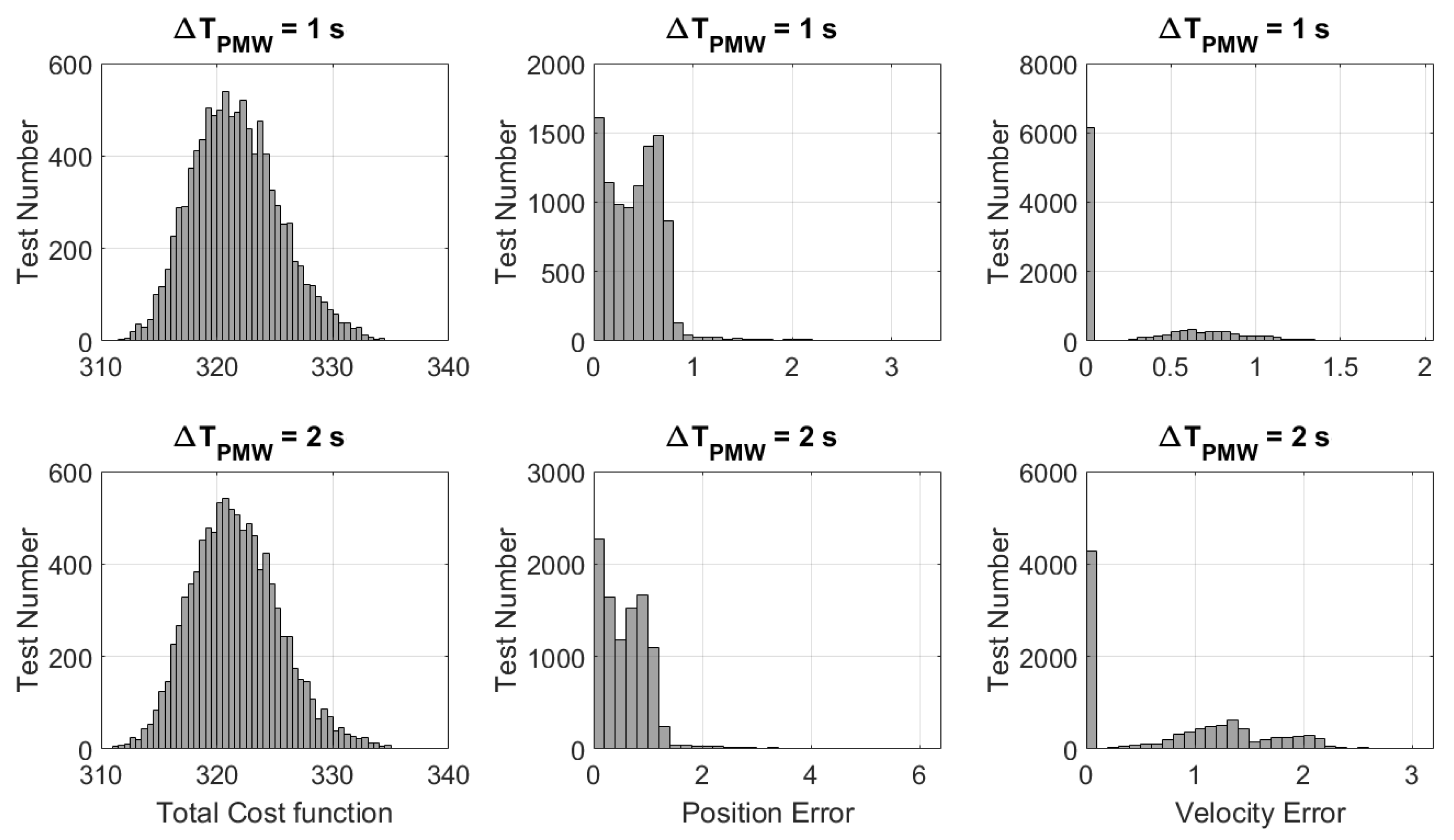








| Monte Carlo | Mean | std | min | max |
|---|---|---|---|---|
| 1 | 321.6794 | 3.7921 | 310.7846 | 337.2861 |
| 2 | 321.6643 | 3.8038 | 310.2898 | 338.6446 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ambrosio, A.; Carbone, A.; Spiller, D.; Curti, F. PSO-Based Soft Lunar Landing with Hazard Avoidance: Analysis and Experimentation. Aerospace 2021, 8, 195. https://doi.org/10.3390/aerospace8070195
D’Ambrosio A, Carbone A, Spiller D, Curti F. PSO-Based Soft Lunar Landing with Hazard Avoidance: Analysis and Experimentation. Aerospace. 2021; 8(7):195. https://doi.org/10.3390/aerospace8070195
Chicago/Turabian StyleD’Ambrosio, Andrea, Andrea Carbone, Dario Spiller, and Fabio Curti. 2021. "PSO-Based Soft Lunar Landing with Hazard Avoidance: Analysis and Experimentation" Aerospace 8, no. 7: 195. https://doi.org/10.3390/aerospace8070195
APA StyleD’Ambrosio, A., Carbone, A., Spiller, D., & Curti, F. (2021). PSO-Based Soft Lunar Landing with Hazard Avoidance: Analysis and Experimentation. Aerospace, 8(7), 195. https://doi.org/10.3390/aerospace8070195








