Unscented Kalman Filter-Aided Long Short-Term Memory Approach for Wind Nowcasting
Abstract
:1. Introduction
2. Related Work
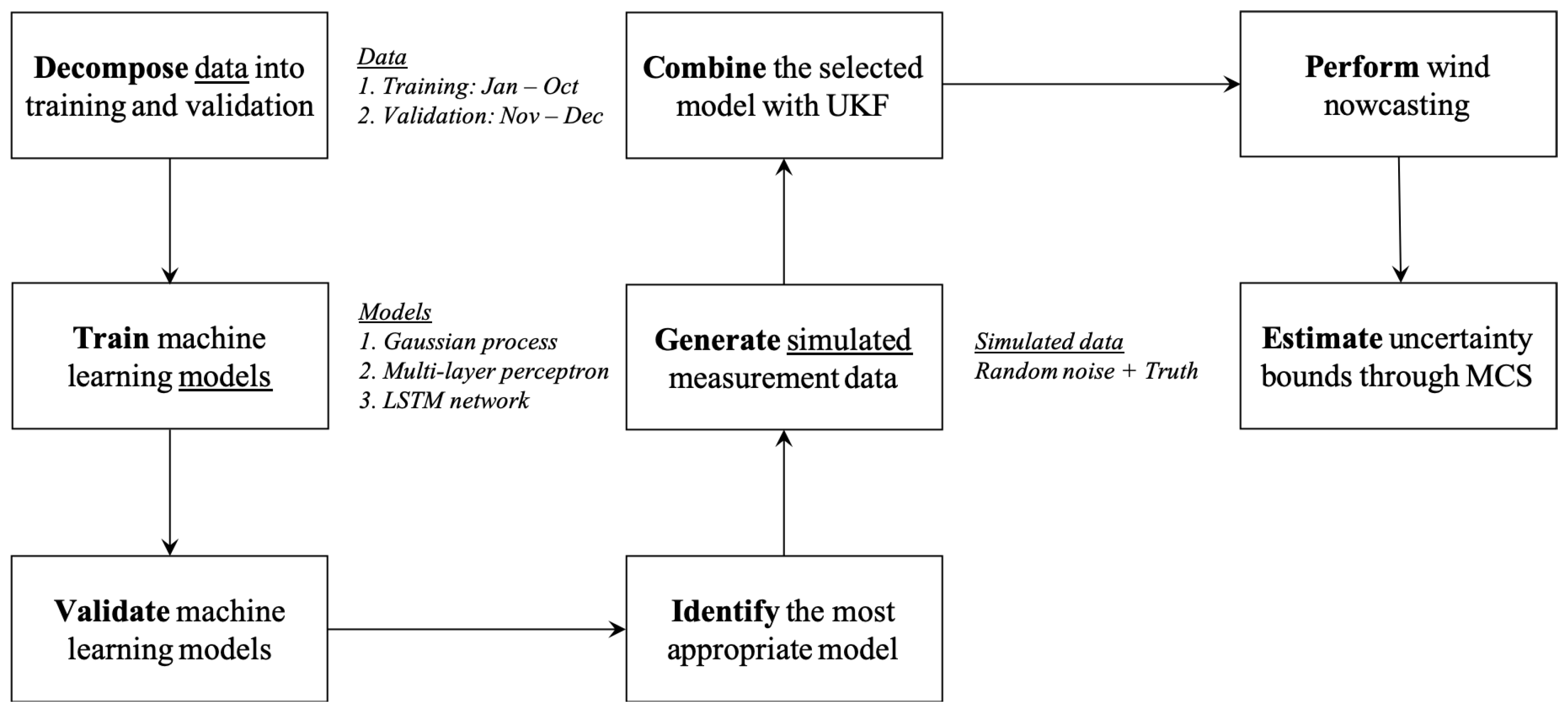
3. Methodology
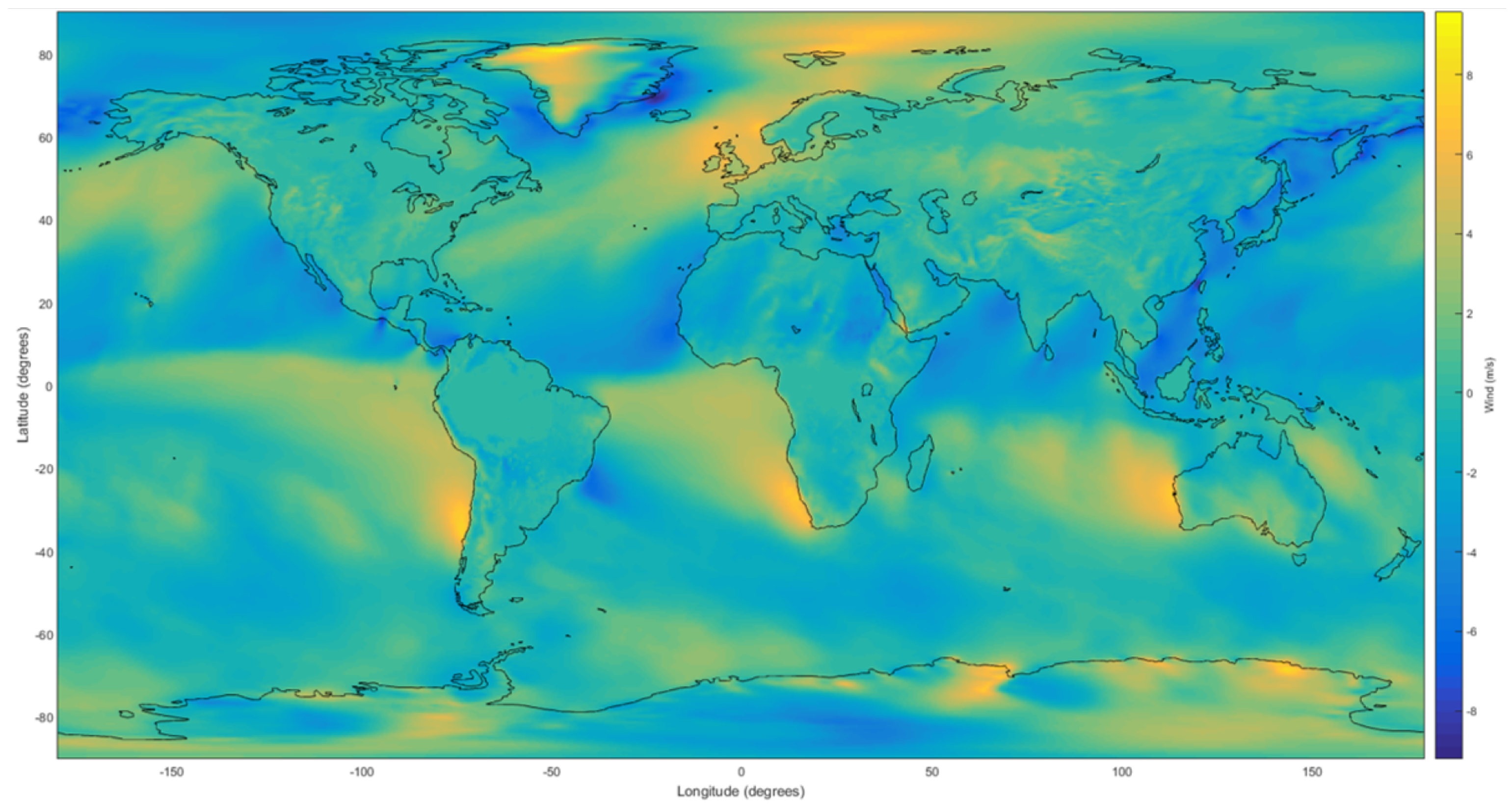
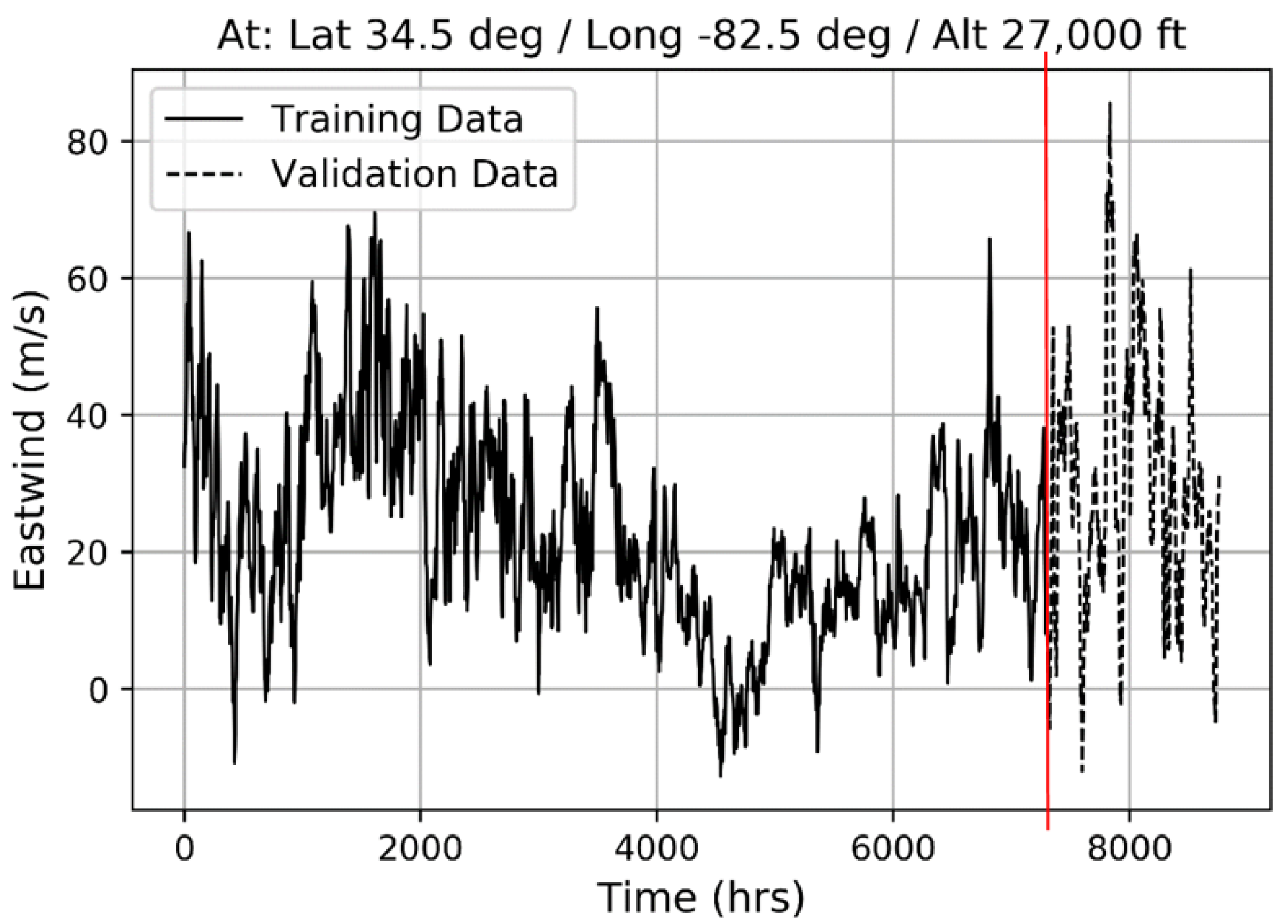
3.1. Data Preparation
3.2. Gaussian Process (GP)
3.3. Multi-Layer Perceptron (MLP)
3.4. Long Short-Term Memory (LSTM) Network
3.5. Model Evaluation and Comparison
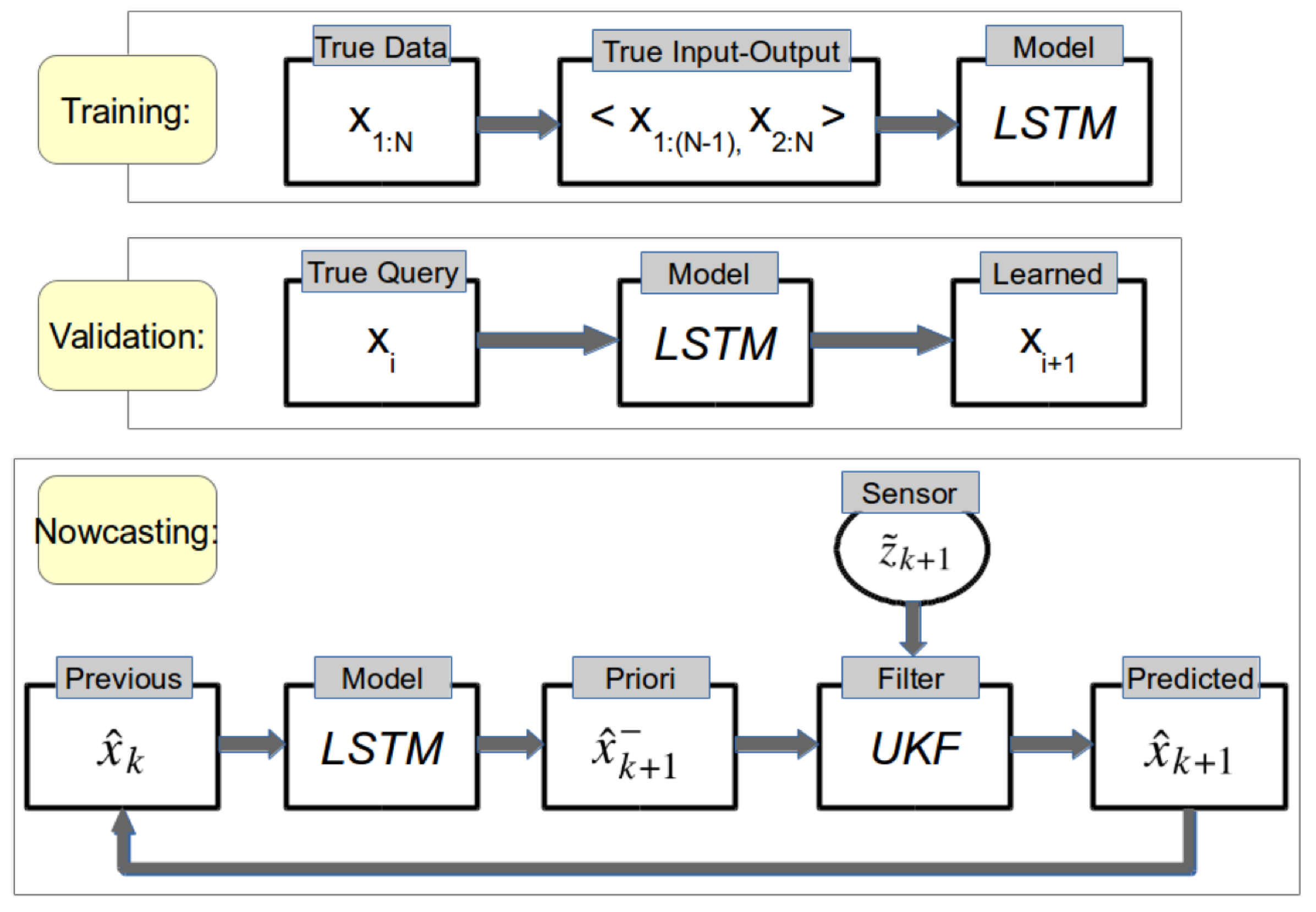
3.6. UKF-Aided LSTM (UKF-LSTM) Approach
3.7. Monte Carlo Simulation (MCS)-Based Uncertainty Quantification
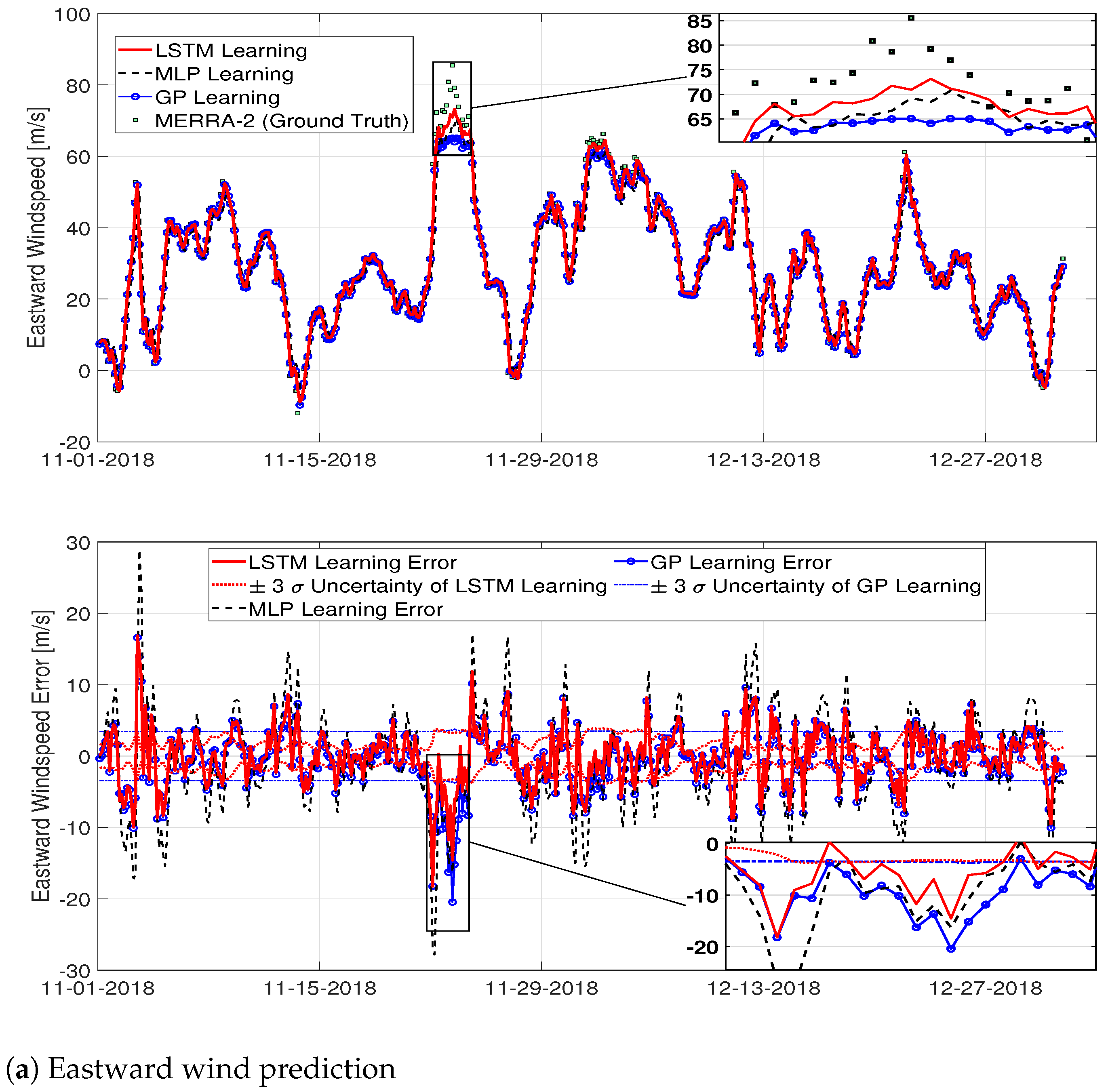
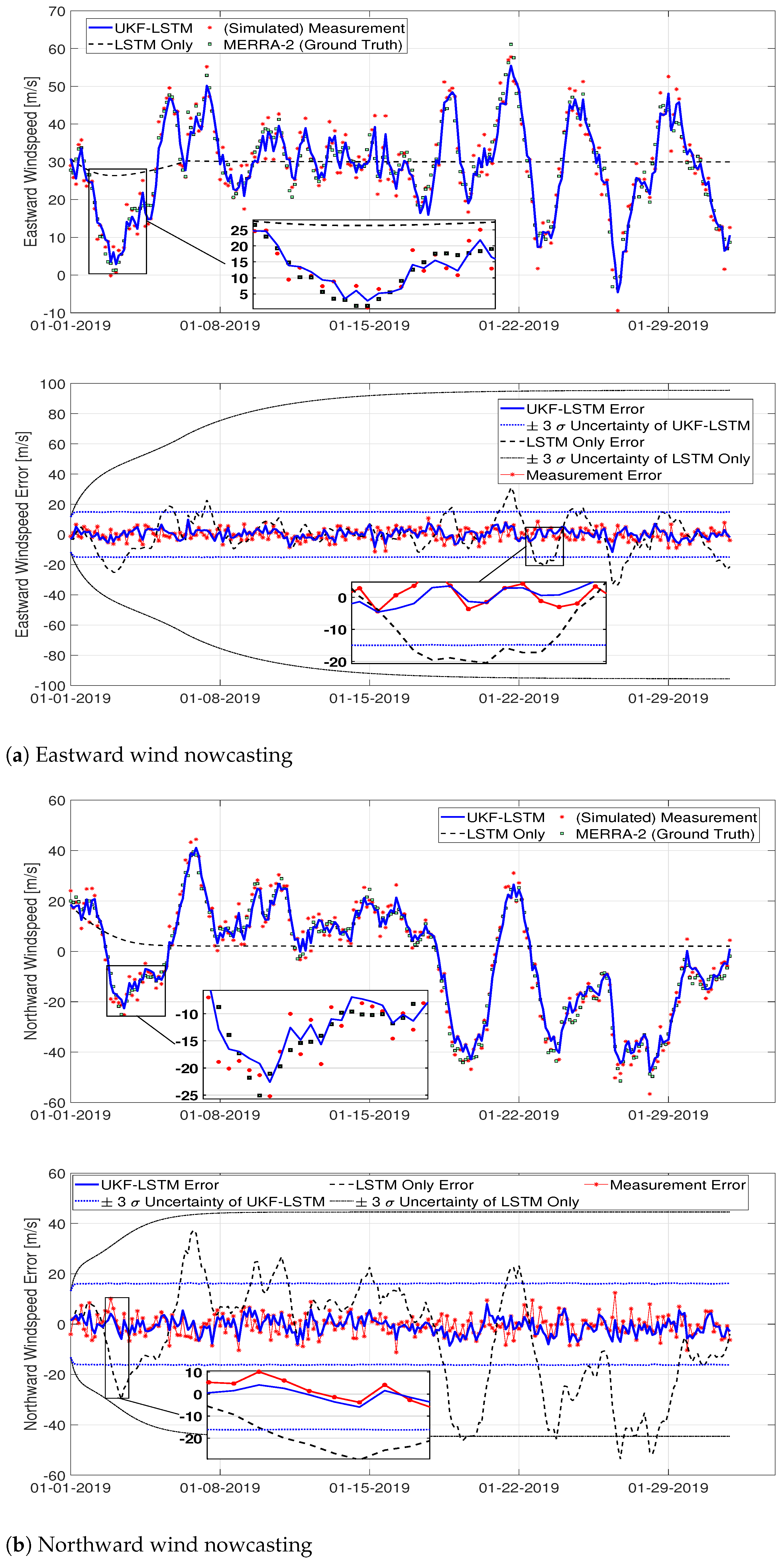
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| DL | Deep learning |
| DoE | Design of experiment |
| EKF | Extended Kalman filter |
| FAA | Federal Aviation Administration |
| GP | Gaussian process |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MCS | Monte Carlo simulation |
| MERRA-2 | Modern-Era Retrospective analysis for Research and Applications-2 |
| MLP | Multi-layer perceptron |
| NASA | National Aeronautics and Space Administration |
| NOAA | National Oceanic and Atmospheric Administration |
| RMSE | Root-mean-square error |
| RNN | Recurrent neural network |
| UKF | Unscented Kalman filter |
| U.S. | United States |
Appendix A. Gaussian Process
Appendix B. Unscented Kalman Filter
Appendix B.1. Time Update
Appendix B.2. Measurement Update
References
- Federal Aviation Administration. Air Traffic by the Numbers; U.S. Department of Transportation: Washington, DC, USA, 2019. [Google Scholar]
- Federal Aviation Administration. FAA Aerospace Forecast Fiscal Years 2019–2039; U.S. Department of Transportation: Washington, DC, USA, 2019. [Google Scholar]
- Mangortey, E.; Puranik, T.G.; Pinon-Fischer, O.J.; Mavris, D.N. Classification, Analysis, and Prediction of the Daily Operations of Airports Using Machine Learning. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1196. [Google Scholar] [CrossRef]
- Mangortey, E.; Pinon-Fischer, O.J.; Puranik, T.G.; Mavris, D.N. Predicting The Occurrence of Weather And Volume Related Ground Delay Programs. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3188. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Abbasnejad, E.; Mirjalili, S.; Tjernberg, L.B.; Garcia, D.A.; Alexander, B.; Wagner, M. A deep learning-based evolutionary model for short-term wind speed forecasting: A case study of the Lillgrund offshore wind farm. Energy Convers. Manag. 2021, 236, 114002. [Google Scholar] [CrossRef]
- Liou, C.S.; Chen, J.H.; Terng, C.T.; Wang, F.J.; Fong, C.T.; Rosmond, T.E.; Kuo, H.C.; Shiao, C.H.; Cheng, M.D. The second–generation global forecast system at the central weather bureau in Taiwan. Weather Forecast. 1997, 12, 653–663. [Google Scholar] [CrossRef] [Green Version]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI. International Society for Optics and Photonics, Orlando, FL, USA, 28 July 1997; Volume 3068, pp. 182–193. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Ahearn, M.; Boeker, E.; Gorshkov, S.; Hansen, A.; Hwang, S.; Koopmann, J.; Malwitz, A.; Noel, G.; Reherman, C.N.; Senzig, D.A. Aviation Environmental Design Tool (AEDT) Technical Manual: Version 2c; Technical Report; United States Federal Aviation Administration, Office of Environment and Energy: Washington, DC, USA, 2016. [Google Scholar]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A.A. Support vector machines for wind speed prediction. Renew. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]
- Kulkarni, M.A.; Patil, S.; Rama, G.; Sen, P. Wind speed prediction using statistical regression and neural network. J. Earth Syst. Sci. 2008, 117, 457–463. [Google Scholar] [CrossRef] [Green Version]
- Rozas-Larraondo, P.; Inza, I.; Lozano, J.A. A method for wind speed forecasting in airports based on nonparametric regression. Weather Forecast. 2014, 29, 1332–1342. [Google Scholar] [CrossRef]
- Khosravi, A.; Machado, L.; Nunes, R. Time-series prediction of wind speed using machine learning algorithms: A case study Osorio wind farm, Brazil. Appl. Energy 2018, 224, 550–566. [Google Scholar] [CrossRef]
- Xie, A.; Yang, H.; Chen, J.; Sheng, L.; Zhang, Q. A Short-Term Wind Speed Forecasting Model Based on a Multi-Variable Long Short-Term Memory Network. Atmosphere 2021, 12, 651. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. Application of Long-Short-Term-Memory Recurrent Neural Networks to Forecast Wind Speed. Appl. Sci. 2021, 11, 2387. [Google Scholar] [CrossRef]
- Geng, D.; Zhang, H.; Wu, H. Short-term wind speed prediction based on principal component analysis and lstm. Appl. Sci. 2020, 10, 4416. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Ak, R.; Fink, O.; Zio, E. Two machine learning approaches for short-term wind speed time-series prediction. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1734–1747. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, X.; Bai, Y. Short-term wind speed prediction using an extreme learning machine model with error correction. Energy Convers. Manag. 2018, 162, 239–250. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Zhang, Y.; Ye, X.; Xiong, X.; Zhang, F. A Novel Hybrid Model Based on An Improved Seagull Optimization Algorithm for Short-Term Wind Speed Forecasting. Processes 2021, 9, 387. [Google Scholar] [CrossRef]
- Nezhad, M.M.; Heydari, A.; Groppi, D.; Cumo, F.; Garcia, D.A. Wind source potential assessment using Sentinel 1 satellite and a new forecasting model based on machine learning: A case study Sardinia islands. Renew. Energy 2020, 155, 212–224. [Google Scholar] [CrossRef]
- Imani, M.; Fakour, H.; Lan, W.H.; Kao, H.C.; Lee, C.M.; Hsiao, Y.S.; Kuo, C.Y. Application of Rough and Fuzzy Set Theory for Prediction of Stochastic Wind Speed Data Using Long Short-Term Memory. Atmosphere 2021, 12, 924. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E.; Bucy, R.S. New Results in Linear Filtering and Prediction Theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Lee, K.; Johnson, E.N. State Estimation Using Gaussian Process Regression for Colored Noise Systems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Ullah, I.; Fayaz, M.; Kim, D. Improving accuracy of the kalman filter algorithm in dynamic conditions using ANN-based learning module. Symmetry 2019, 11, 94. [Google Scholar] [CrossRef] [Green Version]
- Hur, S.H. Short-term wind speed prediction using Extended Kalman filter and machine learning. Energy Rep. 2021, 7, 1046–1054. [Google Scholar] [CrossRef]
- FlightAware. Available online: https://flightaware.com/ (accessed on 14 May 2021).
- Matheron, G. Splines and kriging; their formal equivalence. Mater. Sci. 1981, 20. [Google Scholar]
- Keras LSTM ayer. Available online: https://keras.io/api/layers/recurrent_layers/lstm/ (accessed on 14 May 2021).
- Bokde, N.D.; Yaseen, Z.M.; Andersen, G.B. Forecasttb—An R package as a test-bench for time series forecasting—Application of wind speed and solar radiation modeling. Energies 2020, 13, 2578. [Google Scholar] [CrossRef]
- Ko, J.; Fox, D. GP-BayesFilters: Bayesian filtering using Gaussian process prediction and observation models. Auton. Robots 2009, 27, 75–90. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Choi, Y.; Johnson, E.N. Kernel Embedding-Based State Estimation for Colored Noise Systems. In Proceedings of the IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Anderson, B.D.; Moore, J.B. Optimal Filtering; Prentice Hall: Englewood Cliffs, NJ, USA, 1979; Chapters 2–4. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004; Chapters 2–9. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006; Chapters 2–13. [Google Scholar]
- FilterPy. Available online: https://filterpy.readthedocs.io/ (accessed on 14 May 2021).
- Leininger, T. Confidence and Prediction Intervals for Simple Linear Regression; Lecture Note of Statistics 101; The Department of Statistical Science, Duke University: Durham, NC, USA, 2013. [Google Scholar]
- El-Fouly, T.; El-Saadany, E.; Salama, M. Improved grey predictor rolling models for wind power prediction. IET Gener. Transm. Distrib. 2007, 1, 928–937. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974; Chapters 4, 6; pp. 102–155, 180–228. [Google Scholar]
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]



| Hyperparameter | Lower Bound | Upper Bound | Final Choice |
|---|---|---|---|
| Number of hidden layers | 1 | 2 | 2 |
| Number of hidden nodes | 10 | 100 | 50 |
| Learning rate | 0.01 | 0.00001 | 0.0001 |
| Regularization penalty parameter | 0.01 | 0.00001 | 0.001 |
| Batch size | 1 | 400 | 200 |
| Parameter | Value |
|---|---|
| Number of layers | 6 |
| Number of nodes | 30 |
| Number of epochs | 100 |
| Learning rate | 0.001 |
| Dropout rate (hidden layer) | 0.2 |
| Model | Eastward Wind Prediction | ||
| RMSE (m/s) | MAE (m/s) | R-Squared | |
| LSTM | 3.9193 | 2.9354 | 0.9525 |
| MLP | 6.7425 | 5.1157 | 0.8593 |
| GP | 4.2414 | 3.1051 | 0.9433 |
| Model | Northward Wind Prediction | ||
|---|---|---|---|
| RMSE (m/s) | MAE (m/s) | R-Squared | |
| LSTM | 4.4486 | 3.2335 | 0.9410 |
| MLP | 4.9947 | 3.4274 | 0.9257 |
| GP | 4.9538 | 3.4926 | 0.9269 |
| Approach | Eastward Wind Prediction | ||
| RMSE (m/s) | MAE (m/s) | R-Squared | |
| UKF-LSTM | 3.2204 | 2.5828 | 0.9267 |
| LSTM Only | 11.5524 | 8.9116 | 0.0567 |
| Approach | Northward Wind Prediction | ||
| RMSE (m/s) | MAE (m/s) | R-Squared | |
| UKF-LSTM | 3.3205 | 2.6763 | 0.9767 |
| LSTM Only | 22.4417 | 18.1376 | −0.0632 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Lee, K. Unscented Kalman Filter-Aided Long Short-Term Memory Approach for Wind Nowcasting. Aerospace 2021, 8, 236. https://doi.org/10.3390/aerospace8090236
Kim J, Lee K. Unscented Kalman Filter-Aided Long Short-Term Memory Approach for Wind Nowcasting. Aerospace. 2021; 8(9):236. https://doi.org/10.3390/aerospace8090236
Chicago/Turabian StyleKim, Junghyun, and Kyuman Lee. 2021. "Unscented Kalman Filter-Aided Long Short-Term Memory Approach for Wind Nowcasting" Aerospace 8, no. 9: 236. https://doi.org/10.3390/aerospace8090236
APA StyleKim, J., & Lee, K. (2021). Unscented Kalman Filter-Aided Long Short-Term Memory Approach for Wind Nowcasting. Aerospace, 8(9), 236. https://doi.org/10.3390/aerospace8090236







