Evaluation of Computational Models for Electron Transpiration Cooling
Abstract
1. Introduction
2. Methods and Materials
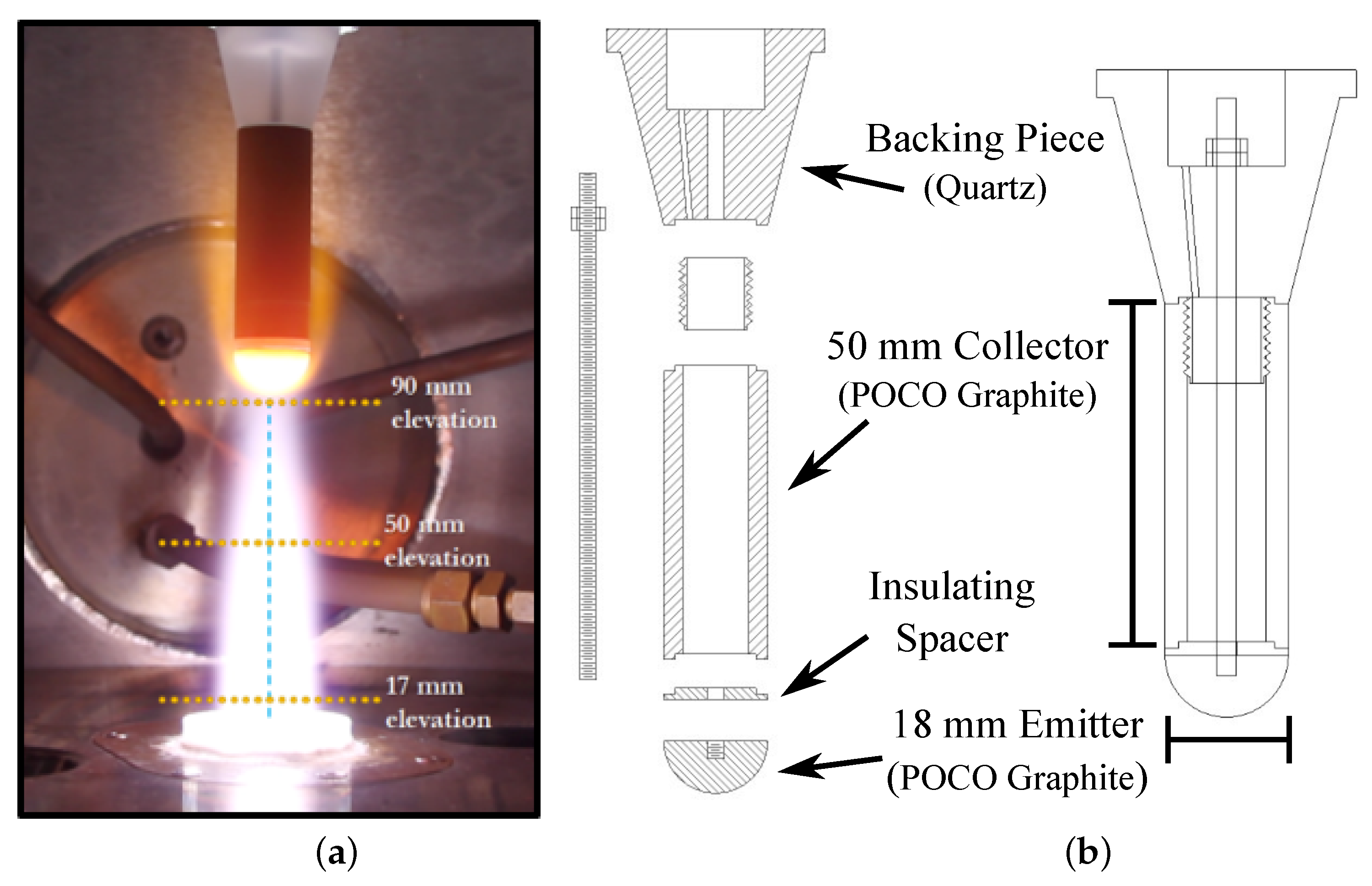
2.1. Plasma Torch Experiments
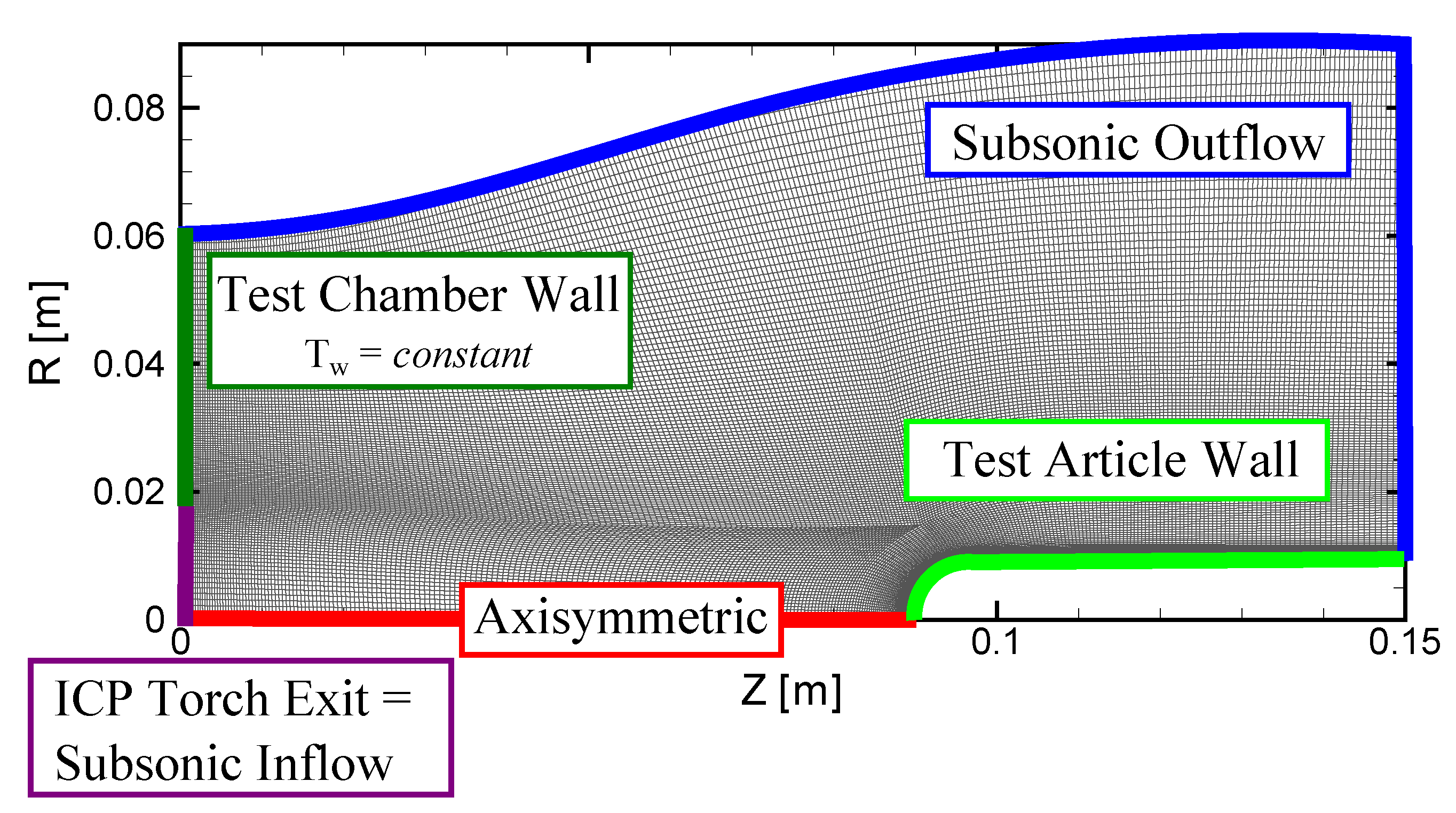
2.2. Numerical
2.3. Thermionic Emission
2.4. Space Charge Limitations
2.4.1. Floating Surface
2.4.2. Biased Surface
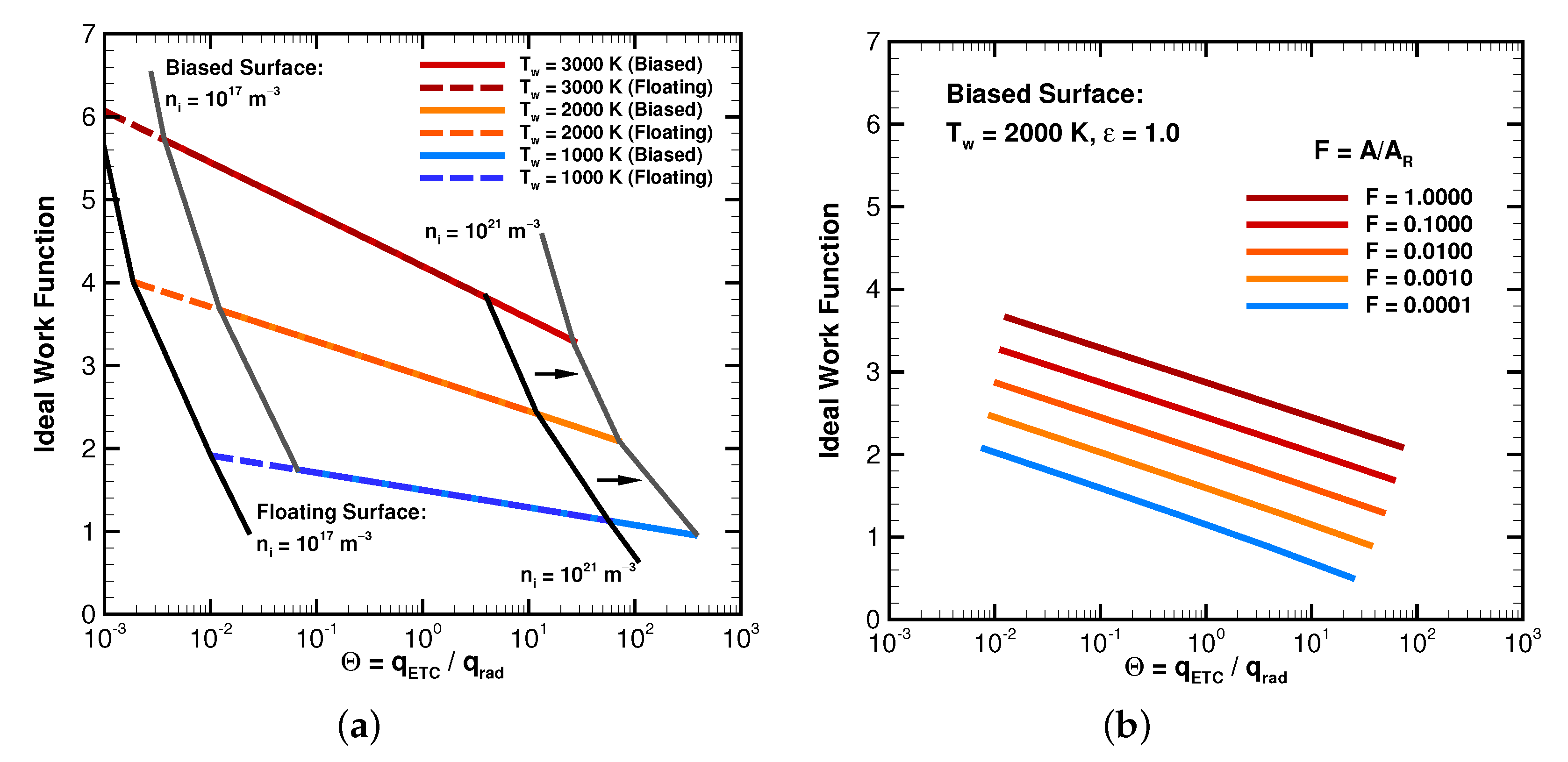
2.4.3. Ideal Work Function
3. Results
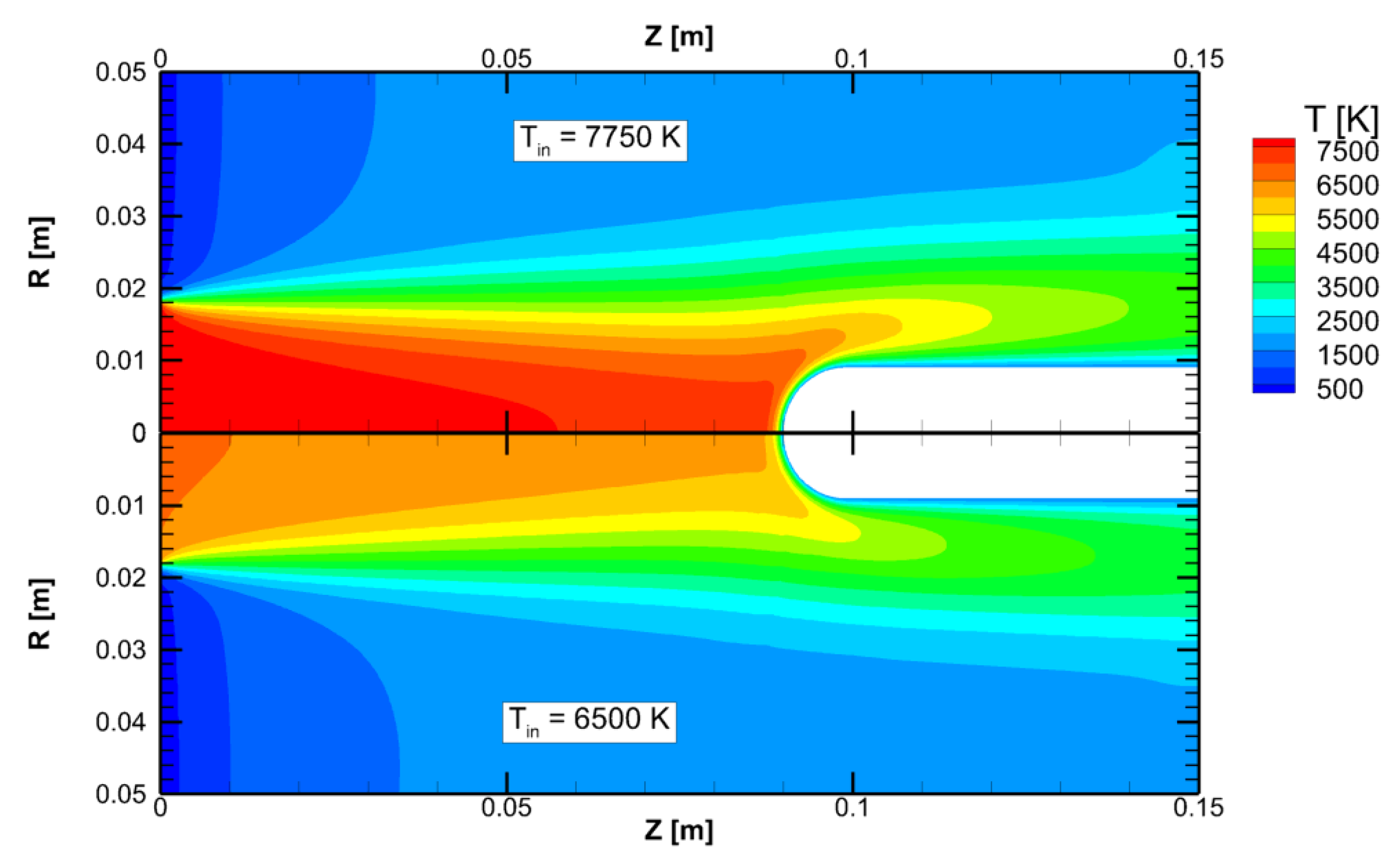
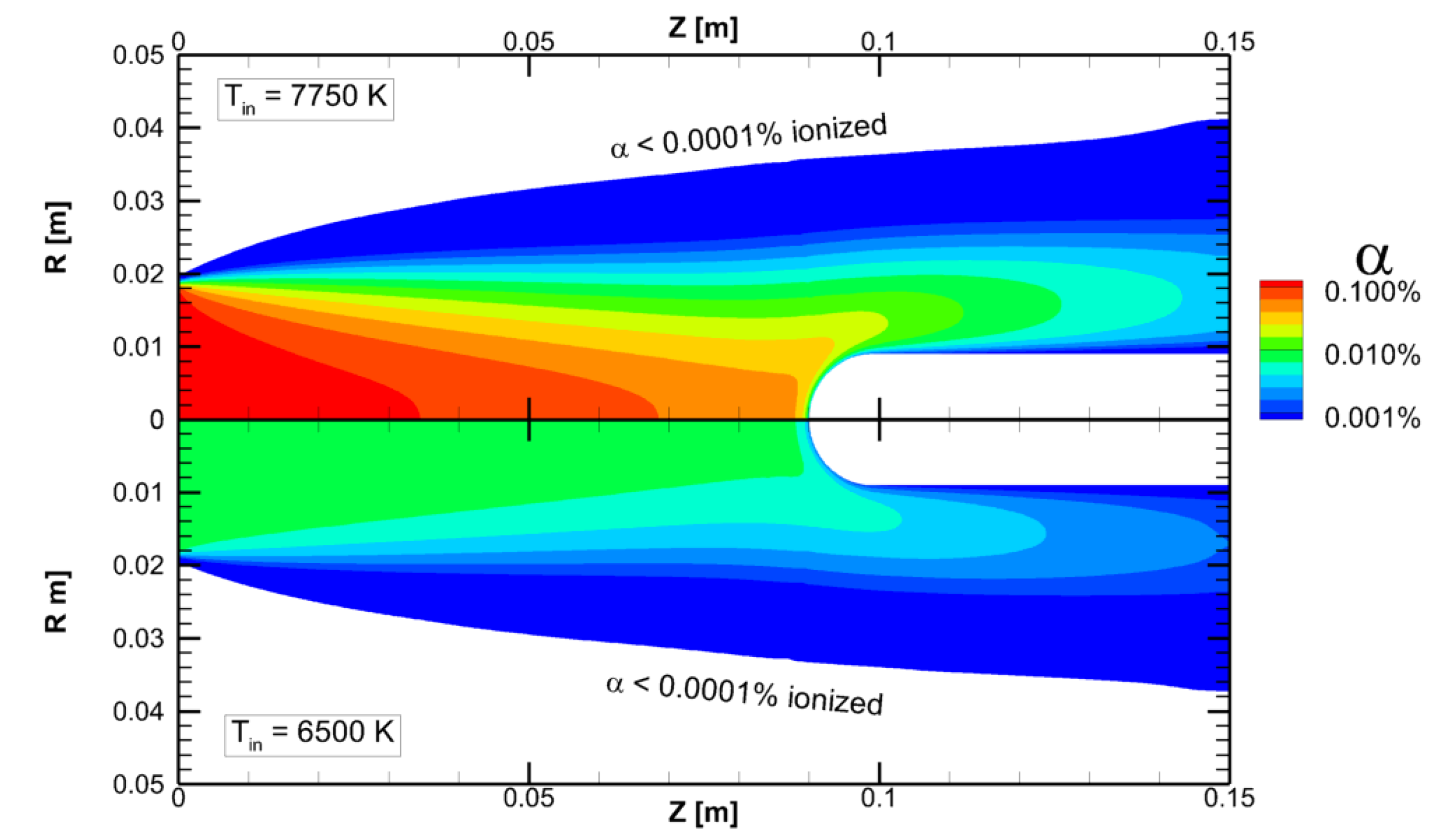
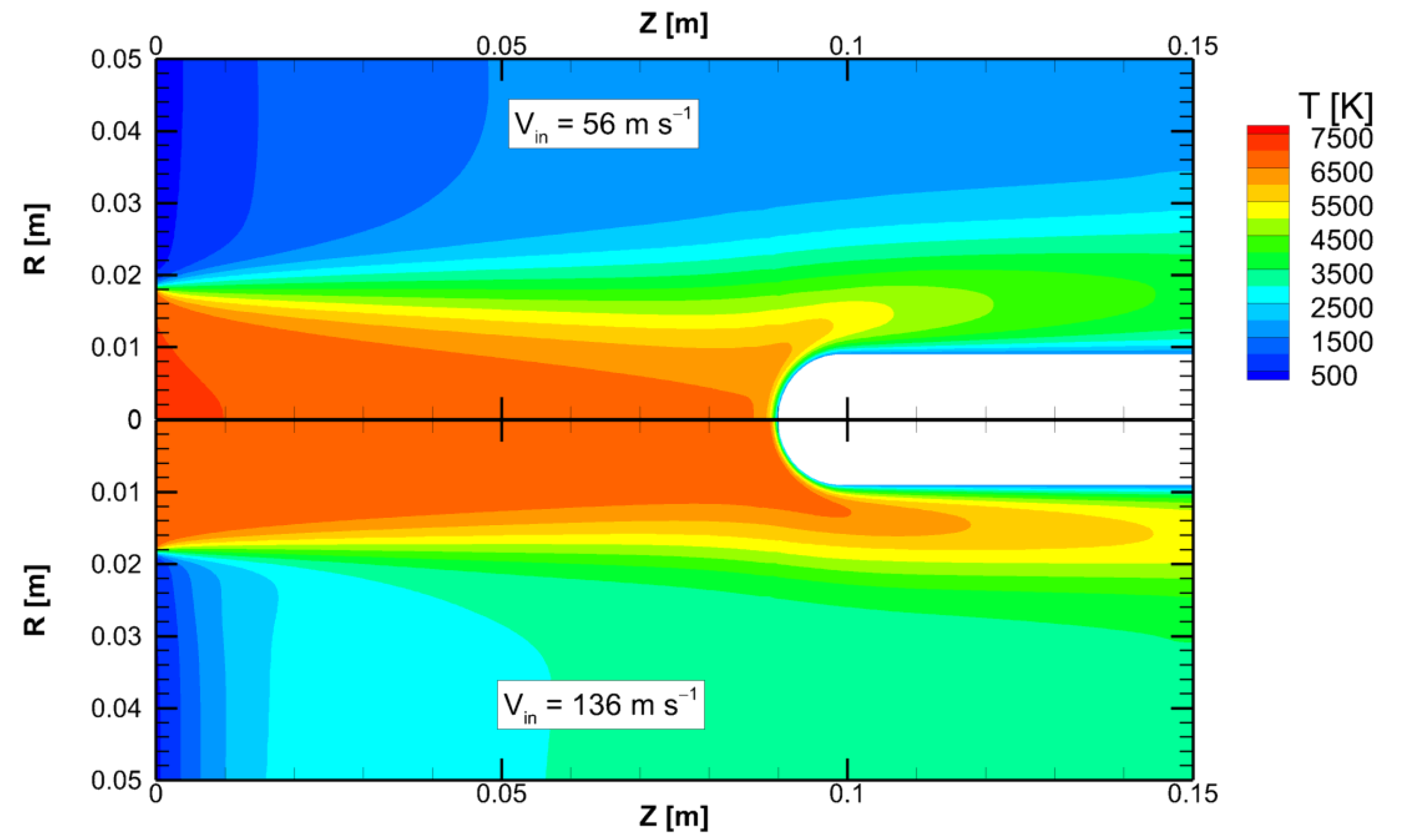
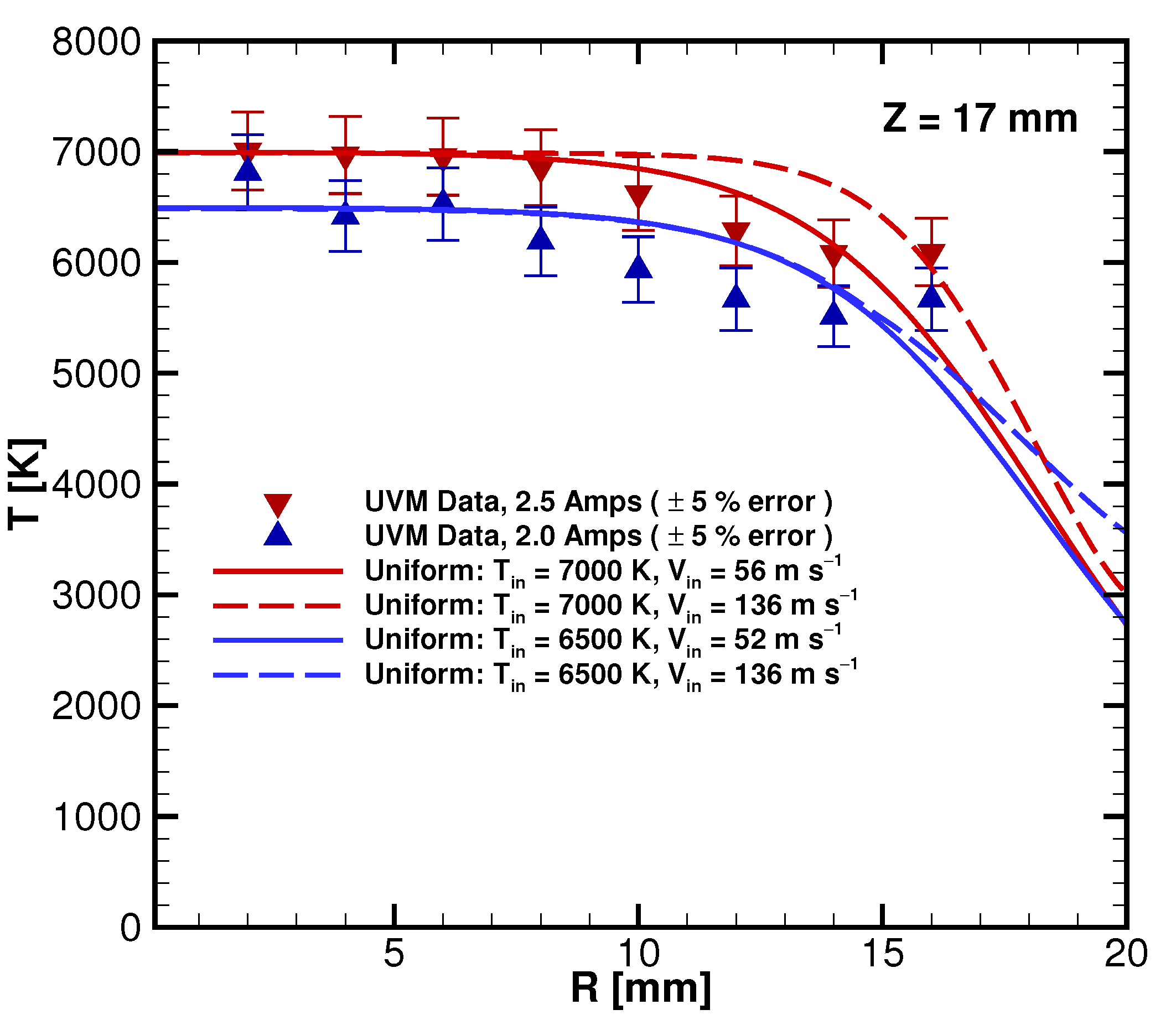
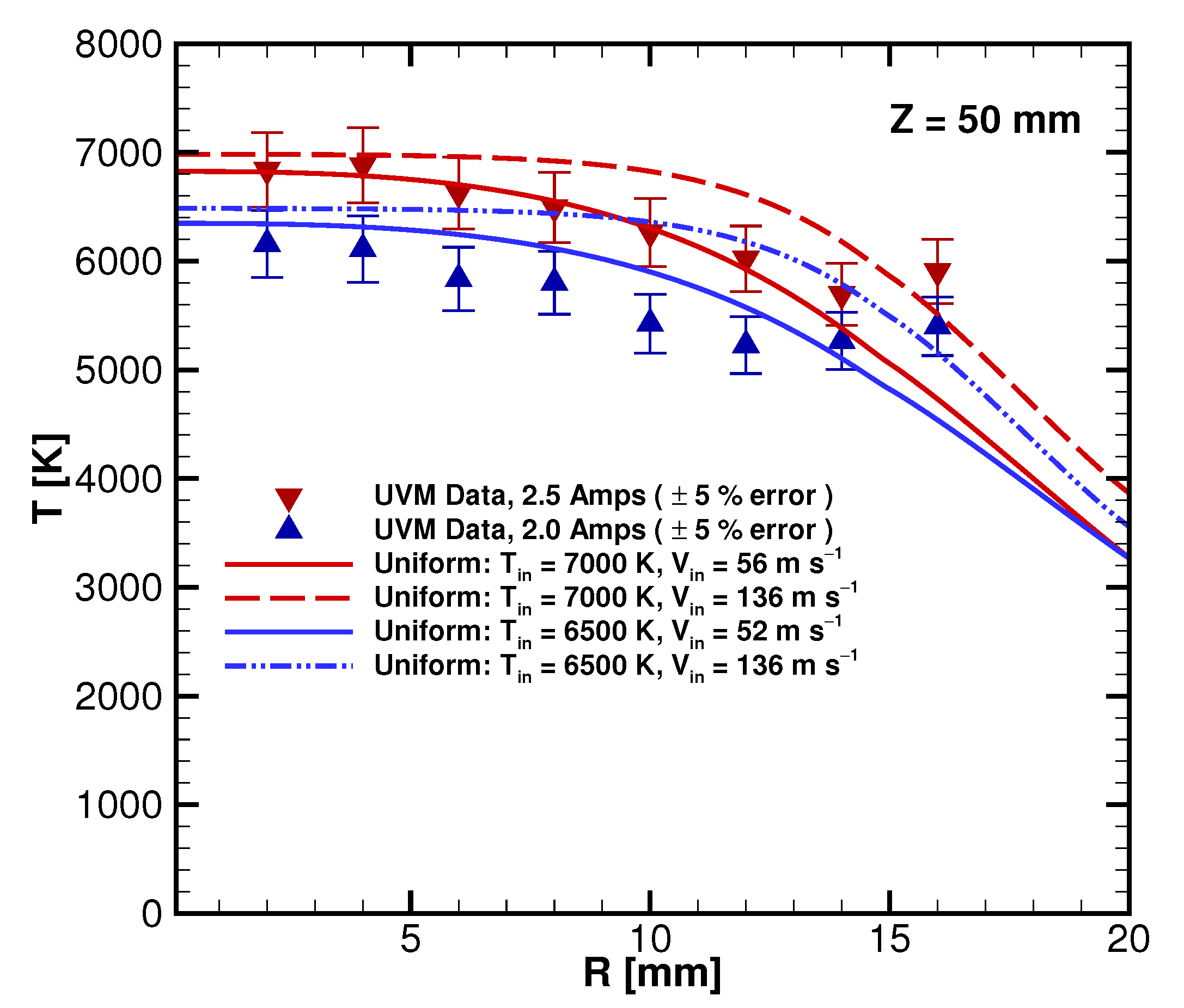
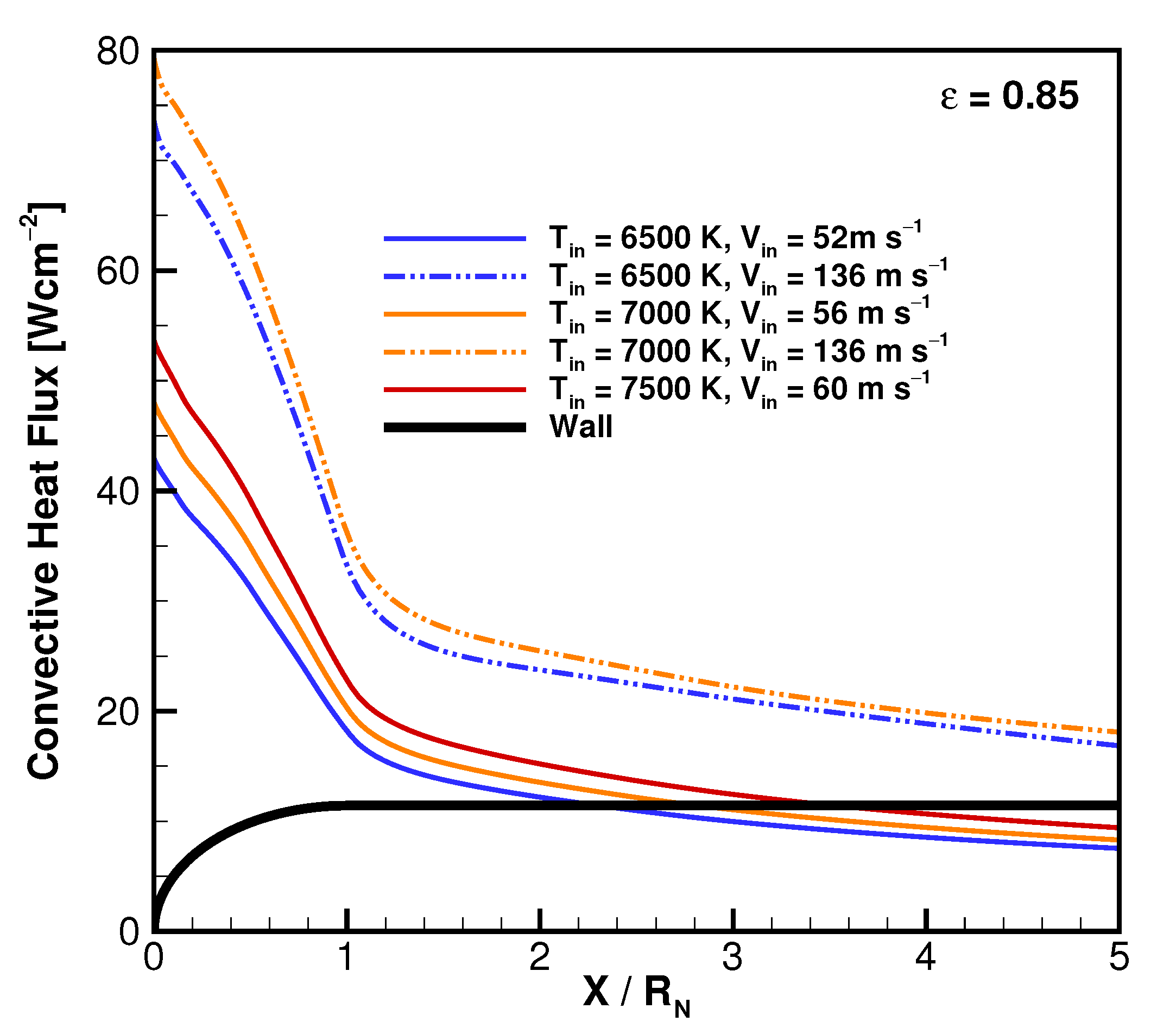
3.1. Torch Conditions
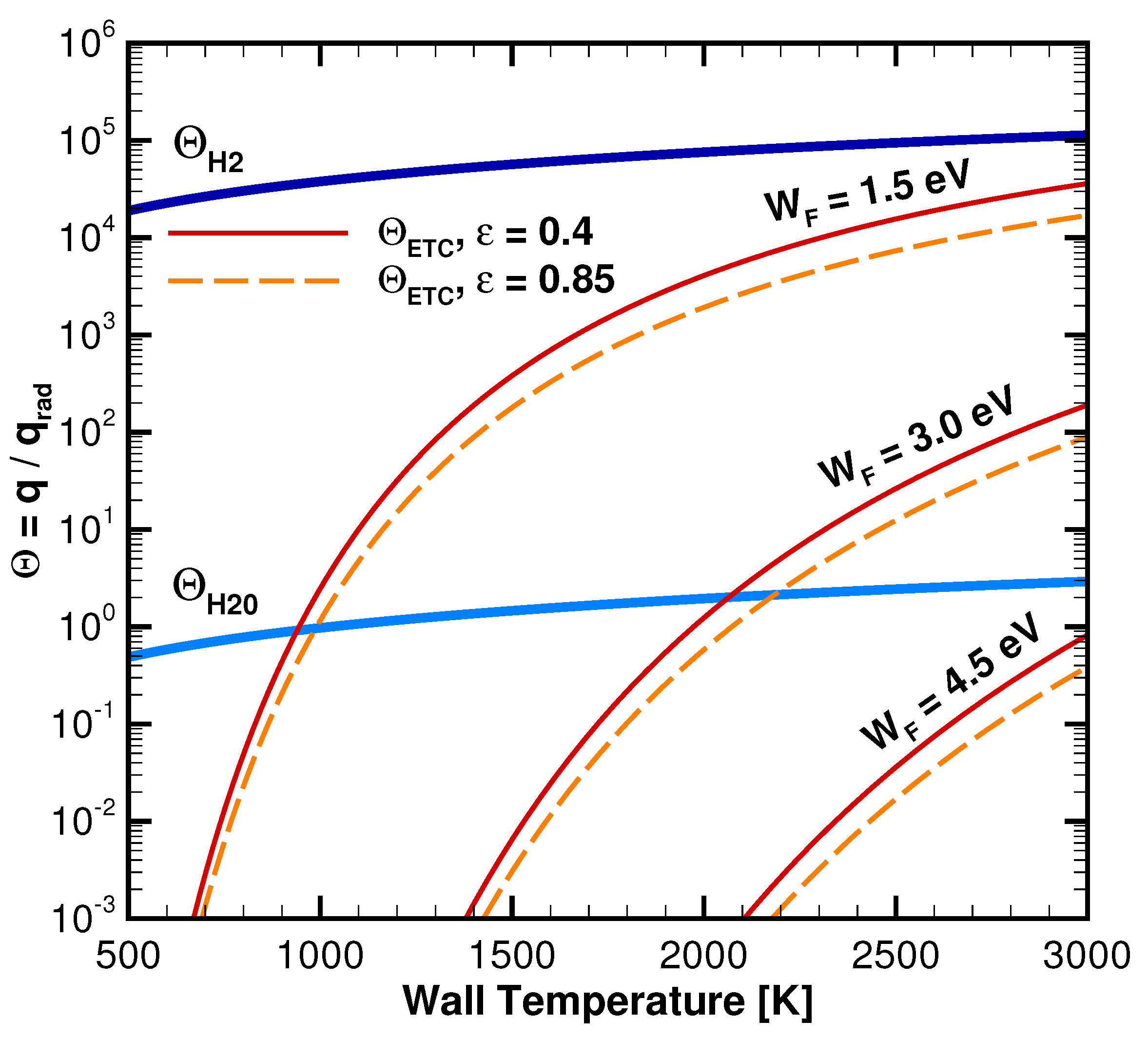
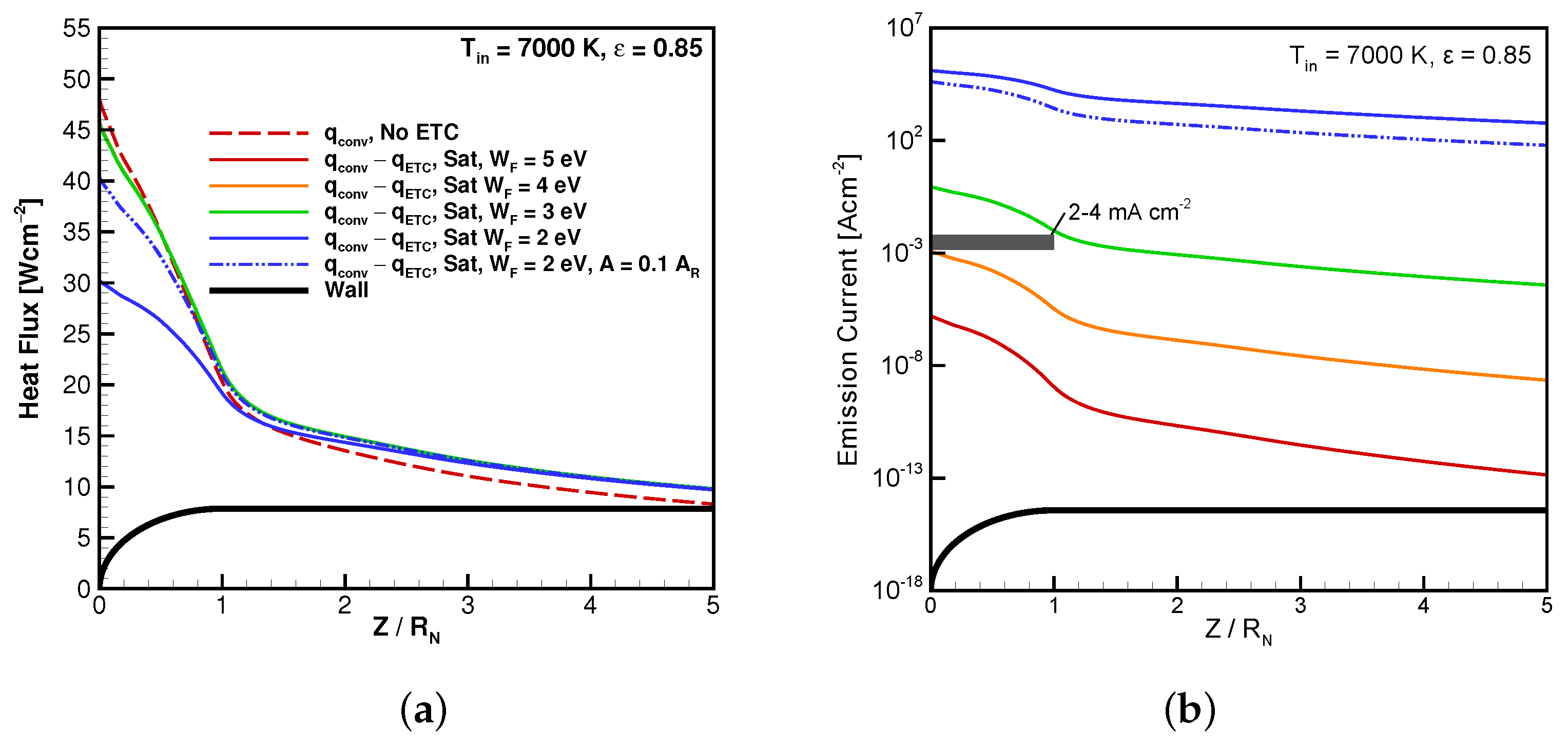
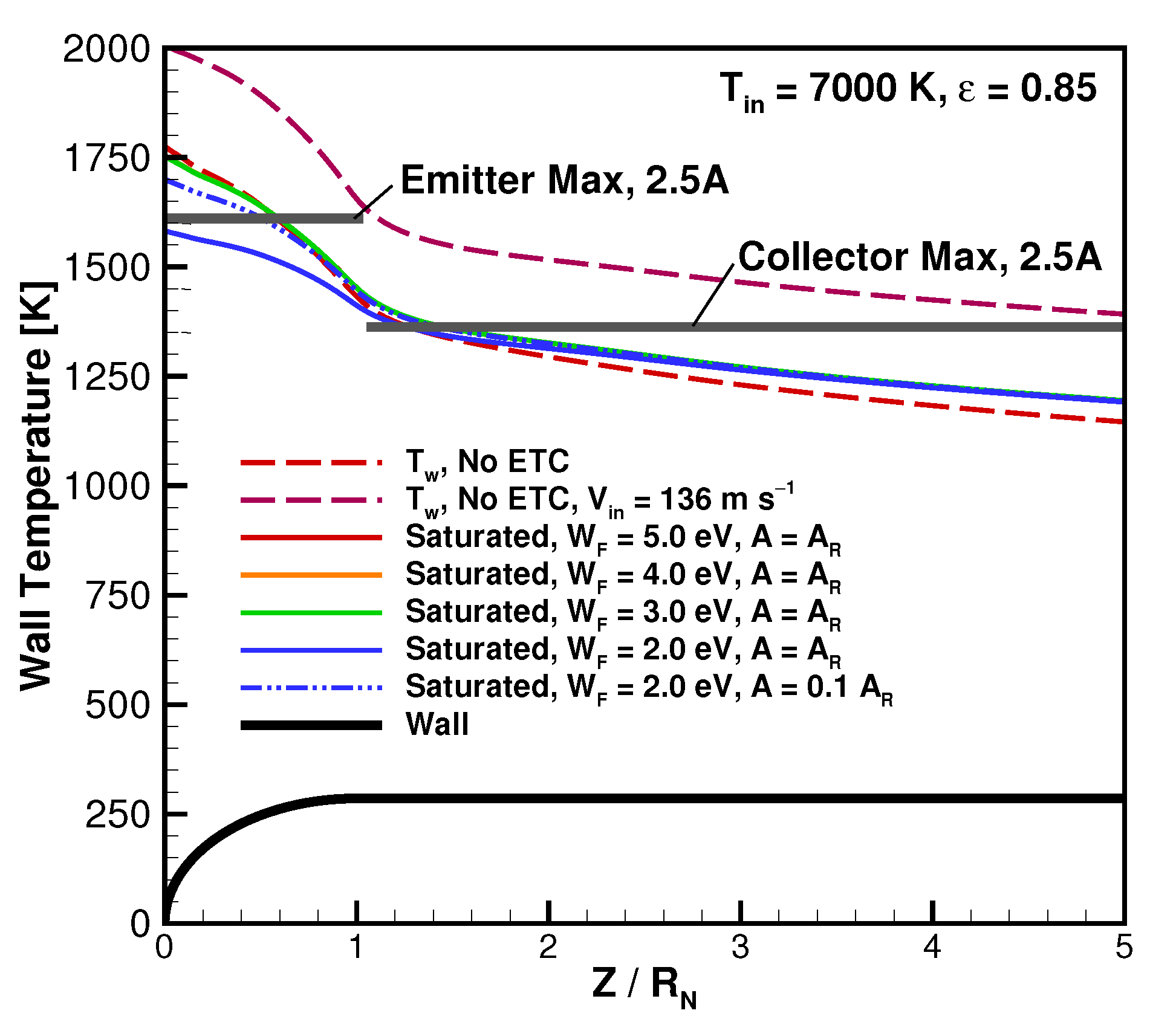
3.2. ETC Results
3.3. Considerations for Future Experiments
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anna, A. Numerical Modeling of Surface Chemistry Processes for Hypersonic Entry Environments. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2013. [Google Scholar]
- Martin, A.; Boyd, I.D. Strongly Coupled Computation of Material Response and Nonequilibrium Flow for Hypersonic Ablation. J. Spacecr. Rocket. 2015, 52, 89–104. [Google Scholar] [CrossRef]
- Wiebenga, J.E. High-Fidelity Material Response Modeling as Part of an Aerothermoelastic Framework for Hypersonic Flows. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2014. [Google Scholar]
- Jin, X.; He, R.; Zhang, X.; Hu, P. Ablation behavior of ZrB2-SiC sharp leading edges. J. Alloys Compd. 2013, 566, 125–130. [Google Scholar] [CrossRef]
- Uyanna, O.; Najafi, H. Thermal Protection Systems for Space Vehicles: A Review on Technology Development, Current Challenges and Future Prospects. Acta Astonautica 2020, 176, 341–356. [Google Scholar] [CrossRef]
- Glass, D.E. Ceramix Matrix Composite (CC) Thermal Protection Systems (TPS) and Hot Structures for Hypersonic Vehicles; AIAA Paper 2008-2682; American Institute of Aeronautics and Astronautic: Reston, VA, USA, 2008. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Hypersonic and High-Temperature Gas Dynamics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Hanquist, K.M. Modeling of Electron Transpiration Cooling for Leading Edges of Hypersonic Vehicles. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2017. [Google Scholar]
- Uribarri, L.A.; Allen, E.H. Electron Transpiration Cooling for Hot Aerospace Surfaces; AIAA Paper 2015-3674; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Richardson, O.W. The Emission of Electricity from Hot Bodies; Longmans, Green and Co.: New York, NY, USA, 1921. [Google Scholar]
- Herring, C.; Nichols, M.H. Thermionic Emission. Rev. Mod. Phys. 1949, 21, 185. [Google Scholar] [CrossRef]
- Richardson, O.W. The Electrical Conductivity Imparted to a Vacuum by Hot Conductors. Philos. Trans. R. Soc. Lond. 1903, 201, 497–549. [Google Scholar]
- Smithells, C.J. 18—Electron Emission. In Smithells Metals Reference Book; Gale, W.F., Totemeier, T.C., Eds.; Elsevier Ltd.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Touryan, K.J. The Hypersonic Plasma Converter: II; Technical Report SC RR 4960; Sandia Laboratories: Albuquerque, NM, USA, 1964. [Google Scholar]
- LeBlanc, A.R.; Grannemann, W.W. Thermionic Generator for Re-Entry Vehicles. Proc. IEEE 1964, 52, 1302–1310. [Google Scholar] [CrossRef]
- Touryan, K.J. A Hypersonic Plasma Power Generator. AIAA J. 1965, 3, 652. [Google Scholar] [CrossRef]
- Hanquist, K.M.; Boyd, I.D. Effectiveness of Thermionic Emission for Cooling Hypersonic Vehicle Surfaces; AIAA Paper 2018-1714; American Institute of Aeronautics and Astronautic: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Hanquist, K.M.; Boyd, I.D. Plasma Assisted Cooling of Hot Surfaces on Hypersonic Vehicles. Front. Phys. Plasma Aerosp. 2019, 7, 1–13. [Google Scholar] [CrossRef]
- Morin, A.; Osborn, R.; Schindler, J.; Voll, B.; Fletcher, D.; Meyers, J. Inductively Coupled Facility Qualification for Electron Transpiration Cooling Investigations. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Owens, W.; Uhl, J.; Dougherty, M.; Lutz, A.; Fletcher, D. Development of a 30 kW Inductively Coupled Plasma Torch for Aerospace Material Testing; AIAA Paper 2010-4322; American Institute of Aeronautics and Astronautic: Reston, VA, USA, 2010. [Google Scholar]
- Kolesnikov, A.F. Extrapolation from High Enthalpy Tests to Flight Based on the Concept of Local Heat Transfer Simulation; Defense Technical Information Center: Fort Belvoir, VA, USA, 1999. [Google Scholar]
- Chazot, O.; Panerai, F.; Muylaert, J.; Thoemel, J. Catalysis Phenomena Determination in Plasmatron Facility for Flight Experiment Design; AIAA Paper 2010-1248; American Institute of Aeronautics and Astronautic: Reston, VA, USA, 2010. [Google Scholar]
- Barbante, P.; Chazot, O. Flight Extrapolation of Plasma Wind Tunnel Stagnation Region Flowfield. J. Thermophys. Heat Transf. 2006, 20, 493–499. [Google Scholar] [CrossRef]
- Barbante, P. Heat Flux Duplication Between Ground Facility and Hypersonic Flight. J. Thermophys. Heat Transf. 2009, 23, 684–692. [Google Scholar] [CrossRef]
- Anna, A.; Boyd, I.D. Numerical Analysis of Surface Chemistry in High-Enthalpy Flows. J. Thermophys. Heat Transf. 2015, 29, 653–670. [Google Scholar] [CrossRef][Green Version]
- Chen, Y.S.; Boyd, I.D.; Martin, N.C.; Fletcher, D.G. Modeling of Gas-Phase Chemical Kinetics for Pyrolyzing Ablators. In Proceedings of the 2018 Joint Thermophysics and Heat Transfer Conference, Atlanta, GA, USA, 25–29 June 2018; pp. 1–15. [Google Scholar] [CrossRef]
- Fletcher, D.G.; Meyers, J.M. Surface Catalyzed Reaction Efficiencies in Oxygen Plasmas from LIF Measurements. J. Thermophys. Heat Transf. 2016, 31, 410–420. [Google Scholar] [CrossRef]
- Meyers, J.M.; Fletcher, D.G. Nitrogen Surface Catalyzed Recombination Efficiency from Two-Photon Laser Induced Fluorescence Measurements. J. Thermophys. Heat Transf. 2019, 33, 1–11. [Google Scholar] [CrossRef]
- Tillson, C.C.; Uhl, J.; Meyers, J.M.; Fletcher, D.G. Investigation of Pyrolysis Gas Chemistry in an Inductively Coupled Plasma Facility; AIAA Paper 2016-3235; American Institute of Aeronautics and Astronautic: Reston, VA, USA, 2016. [Google Scholar] [CrossRef][Green Version]
- Scalabrin, L.C. Numerical Simulation of Weakly Ionized Hypersonic Flow Over Reentry Capsules. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2007. [Google Scholar]
- Holman, T.D.; Boyd, I.D. Numerical Investigation of the Effects of Continuum Breakdown on Hypersonic Vehicle Surface Properties; AIAA Paper 2008-3928; American Institute of Aeronautics and Astronautic: Reston, VA, USA, 2008. [Google Scholar]
- Deschenes, T.R. Extension of a Modular Particle-Continuum Method for Nonequilibrium, Hypersonic Flows. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2011. [Google Scholar]
- Alkandry, H. Aerodynamic Interactions of Propulsive Deceleration and Reaction Control System Jets on Mars-Entry Aeroshells. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2012. [Google Scholar]
- Martin, A.; Scalabrin, L.C.; Boyd, I.D. High Performance Modeling of Atmospheric Re-entry Vehicles. J. Phys. Conf. Ser. 2012, 341, 1–12. [Google Scholar] [CrossRef]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.4.0. 2018. Available online: https://www.cantera.org (accessed on 15 July 2021).
- Hanquist, K.M.; Hara, K.; Boyd, I.D. Detailed modeling of electron emission for transpiration cooling of hypersonic vehicles. J. Appl. Phys. 2017, 121, 1–13. [Google Scholar] [CrossRef]
- Sheehan, J.P.; Hershkowitz, N. Emissive Probes. Plasma Sources Sci. Technol. 2011, 20, 063001. [Google Scholar] [CrossRef]
- Hobbs, G.D.; Wesson, J.A. Heat Flow Through a Langmuir Sheath in the Presence of Electron Emission. Plasma Phys. 1967, 9, 85–87. [Google Scholar] [CrossRef]
- Hara, K.; Hanquist, K. Test cases for grid-based direct kinetic modeling of plasma flows. Plasma Sources Sci. Technol. 2018, 27, 1–14. [Google Scholar] [CrossRef]
- Takamura, S.; Ohno, N.; Ye, M.; Kuwabara, T. Space-charge limited current from plasma-facing material surface. Contrib. Plasma Phys. 2004, 44, 126–137. [Google Scholar] [CrossRef]
- Hanquist, K.M.; Alkandry, H.; Boyd, I.D. Evaluation of Computational Modeling of Electron Transpiration Cooling at High Enthalpies. J. Thermophys. Heat Transf. 2017, 31, 283–293. [Google Scholar] [CrossRef]
- Bohm, D. Minimum ionic kinetic energy for a stable sheath. In The Characteristics of Electrical Discharges in Magnetic Fields; Guthrie, A., Wakerling, R.K., Eds.; McGraw-Hill: New York, NY, USA, 1949; pp. 77–86. [Google Scholar]
- Chen, S.Y.; Boyd, I.D.; Martin, N.C.; Fletcher, D.G. Modeling of Emission Spectra in Nonequilibrium Plasmas for Testing Pyrolyzing Ablators. J. Thermophys. Heat Transf. 2019, 33, 907–916. [Google Scholar] [CrossRef]
- Reiman, A.L. Thermionic Emission from Carbon. Proc. Phys. Soc. 1938, 50, 496. [Google Scholar] [CrossRef]
- Krishnan, K.S.; Jain, S.C. Thermionic Constants of Graphite. Nature 1952, 169, 702–703. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]

| Torch Current, I | 2.0, 2.2, 2.5 | [A] |
| Gas Flow Rate, | 0.838 | [g/s] |
| Chamber Pressure, | 21.3 | [kPa] |
| Case No. | [K] | [m/s] | [MJ/kg] | [m] | [m] |
|---|---|---|---|---|---|
| 1 | 6500 | 52 | 3.24 | 6.02 × 10 | 1.13 × 10 |
| 2 | 6500 | 136 | 3.24 | 6.02 × 10 | 1.13 × 10 |
| 3 | 7000 | 56 | 3.51 | 6.02 × 10 | 3.41 × 10 |
| 4 | 7000 | 136 | 3.52 | 6.02 × 10 | 3.40 × 10 |
| 5 | 7500 | 60 | 3.81 | 6.00 × 10 | 8.89 × 10 |
| 6 | 7750 | 62 | 3.98 | 5.99 × 10 | 1.37 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campbell, N.S.; Hanquist, K.; Morin, A.; Meyers, J.; Boyd, I. Evaluation of Computational Models for Electron Transpiration Cooling. Aerospace 2021, 8, 243. https://doi.org/10.3390/aerospace8090243
Campbell NS, Hanquist K, Morin A, Meyers J, Boyd I. Evaluation of Computational Models for Electron Transpiration Cooling. Aerospace. 2021; 8(9):243. https://doi.org/10.3390/aerospace8090243
Chicago/Turabian StyleCampbell, Nicholas S., Kyle Hanquist, Andrew Morin, Jason Meyers, and Iain Boyd. 2021. "Evaluation of Computational Models for Electron Transpiration Cooling" Aerospace 8, no. 9: 243. https://doi.org/10.3390/aerospace8090243
APA StyleCampbell, N. S., Hanquist, K., Morin, A., Meyers, J., & Boyd, I. (2021). Evaluation of Computational Models for Electron Transpiration Cooling. Aerospace, 8(9), 243. https://doi.org/10.3390/aerospace8090243





