Unmanned Aerial Vehicle Pitch Control under Delay Using Deep Reinforcement Learning with Continuous Action in Wind Tunnel Test
Abstract
:1. Introduction
2. Methods
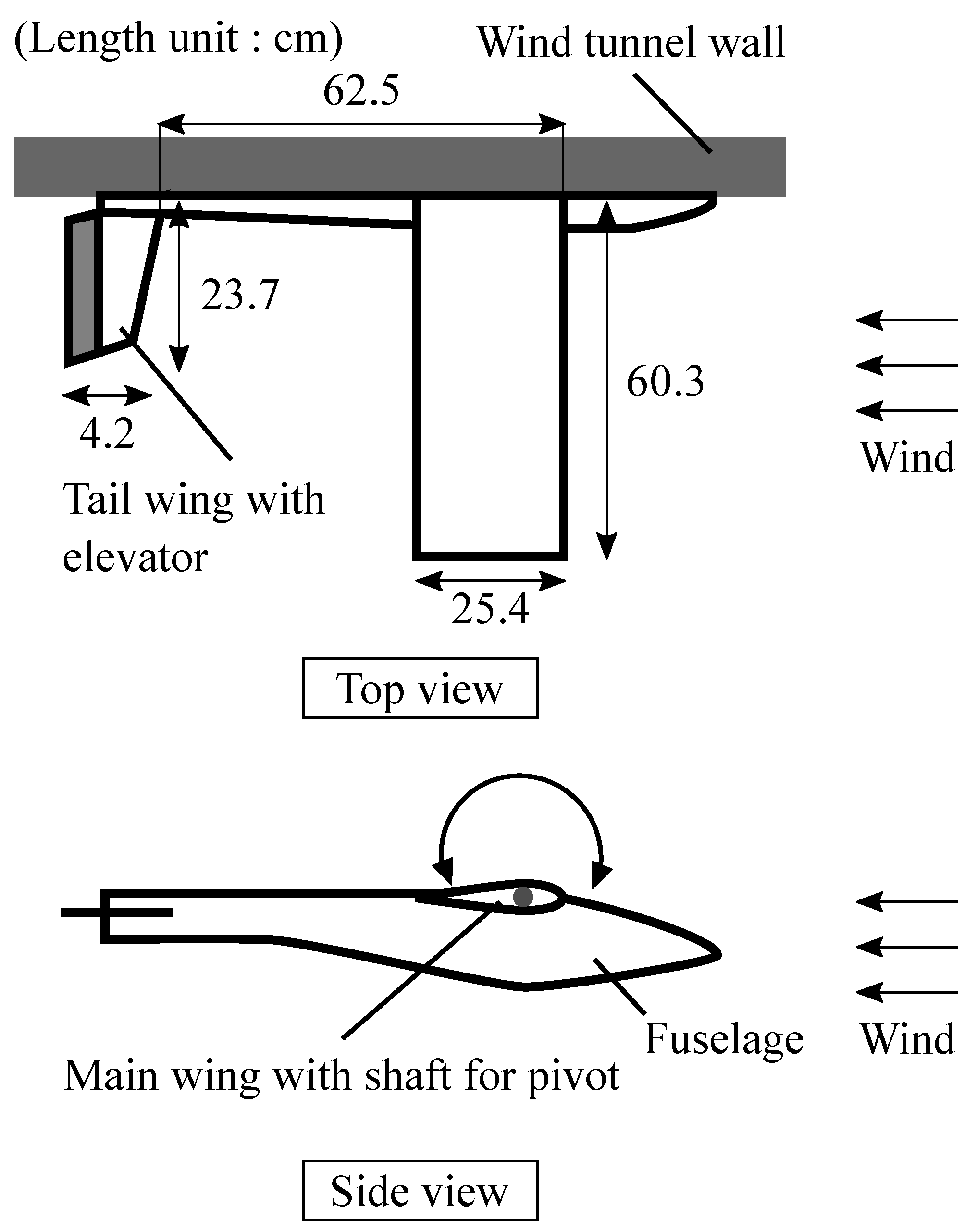
2.1. Experimental Model
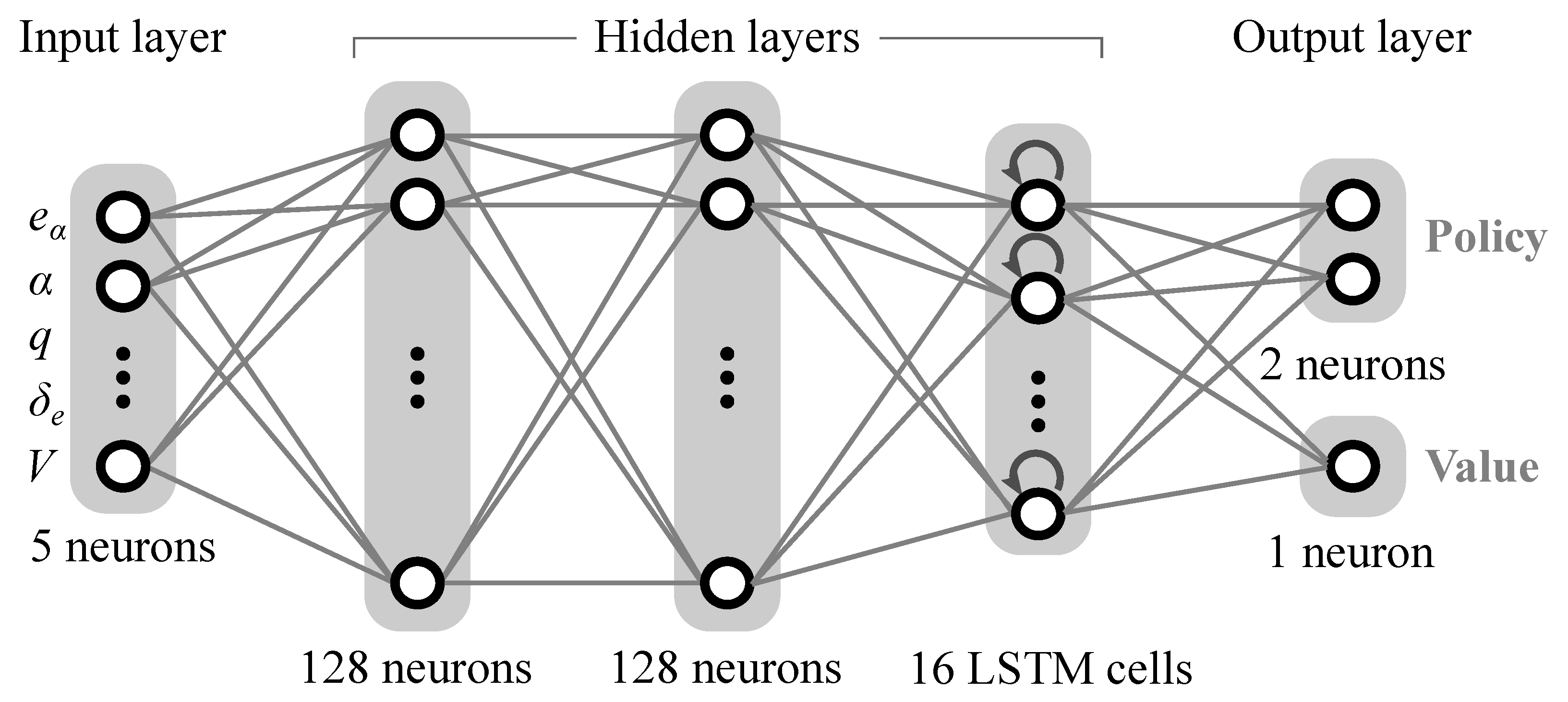
2.2. Training Algorithm
3. Results
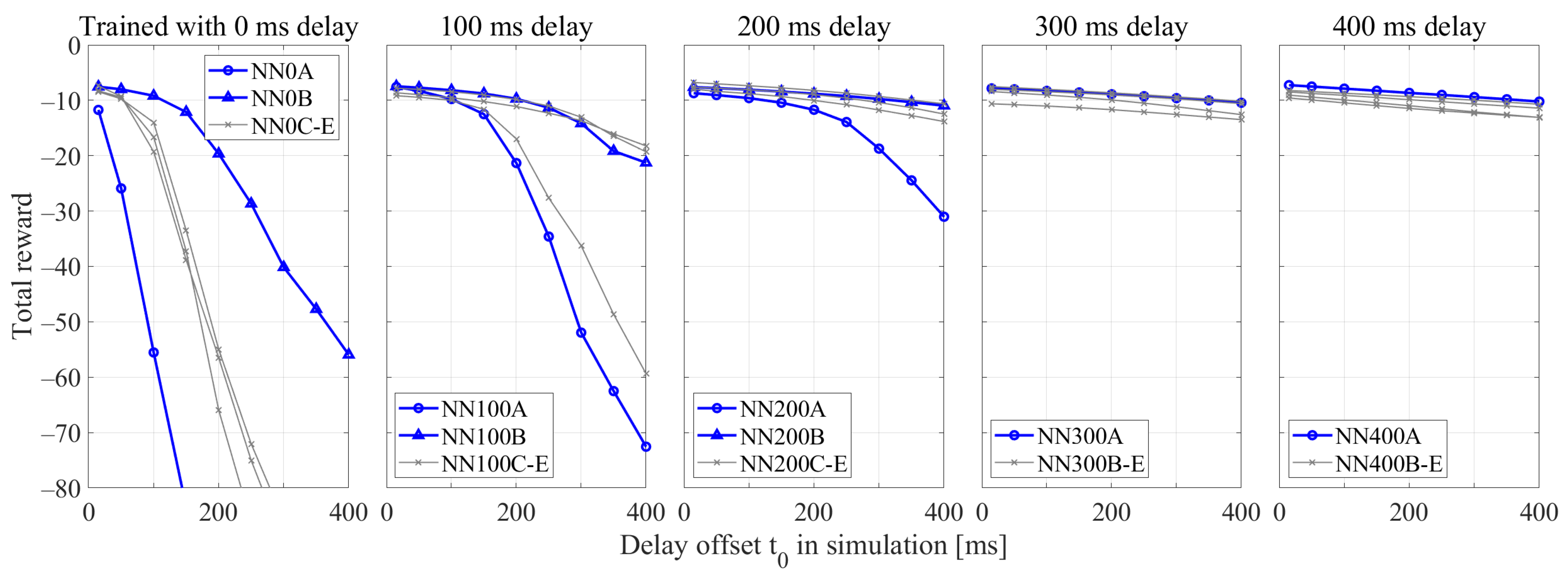
3.1. Training Results
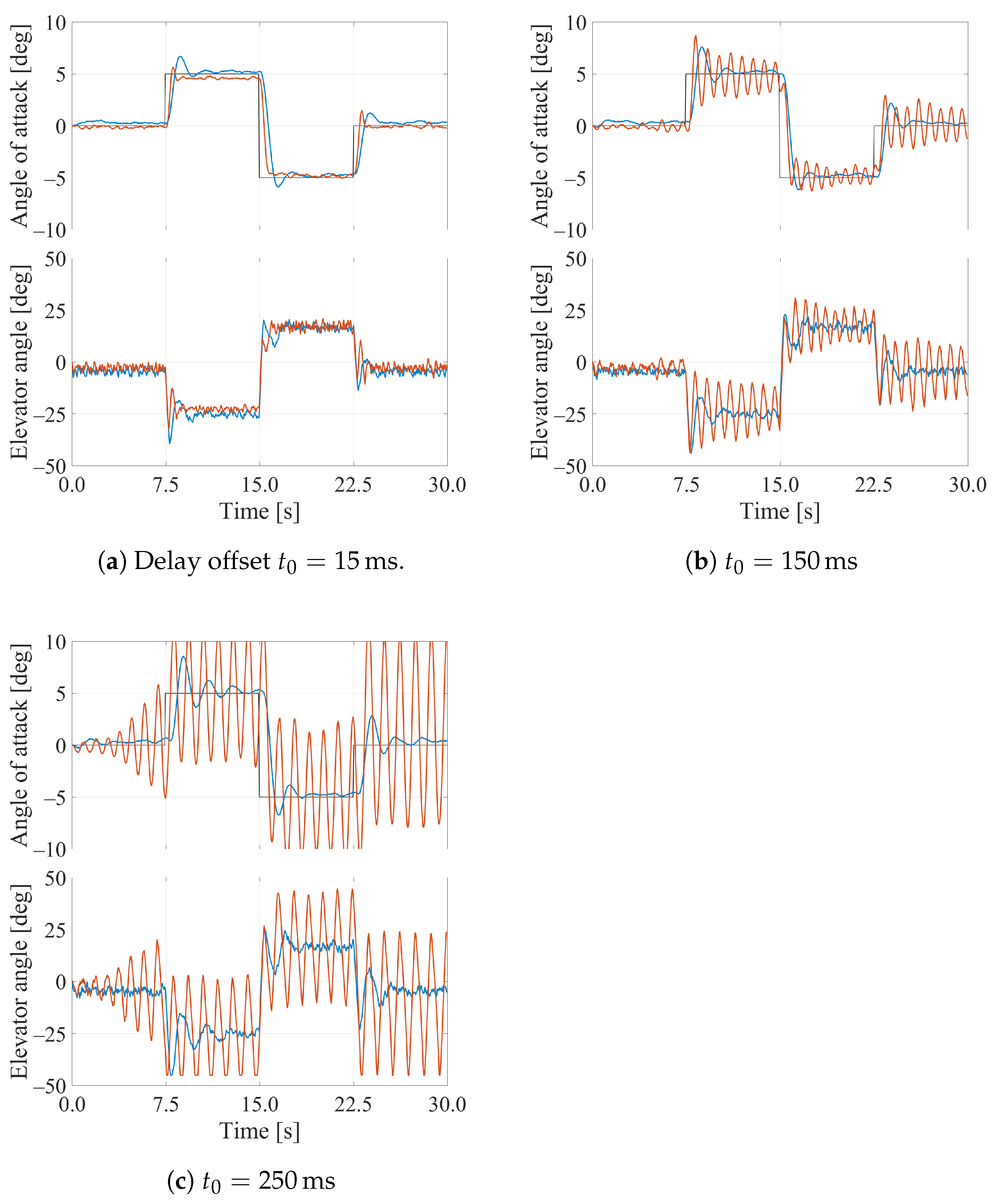
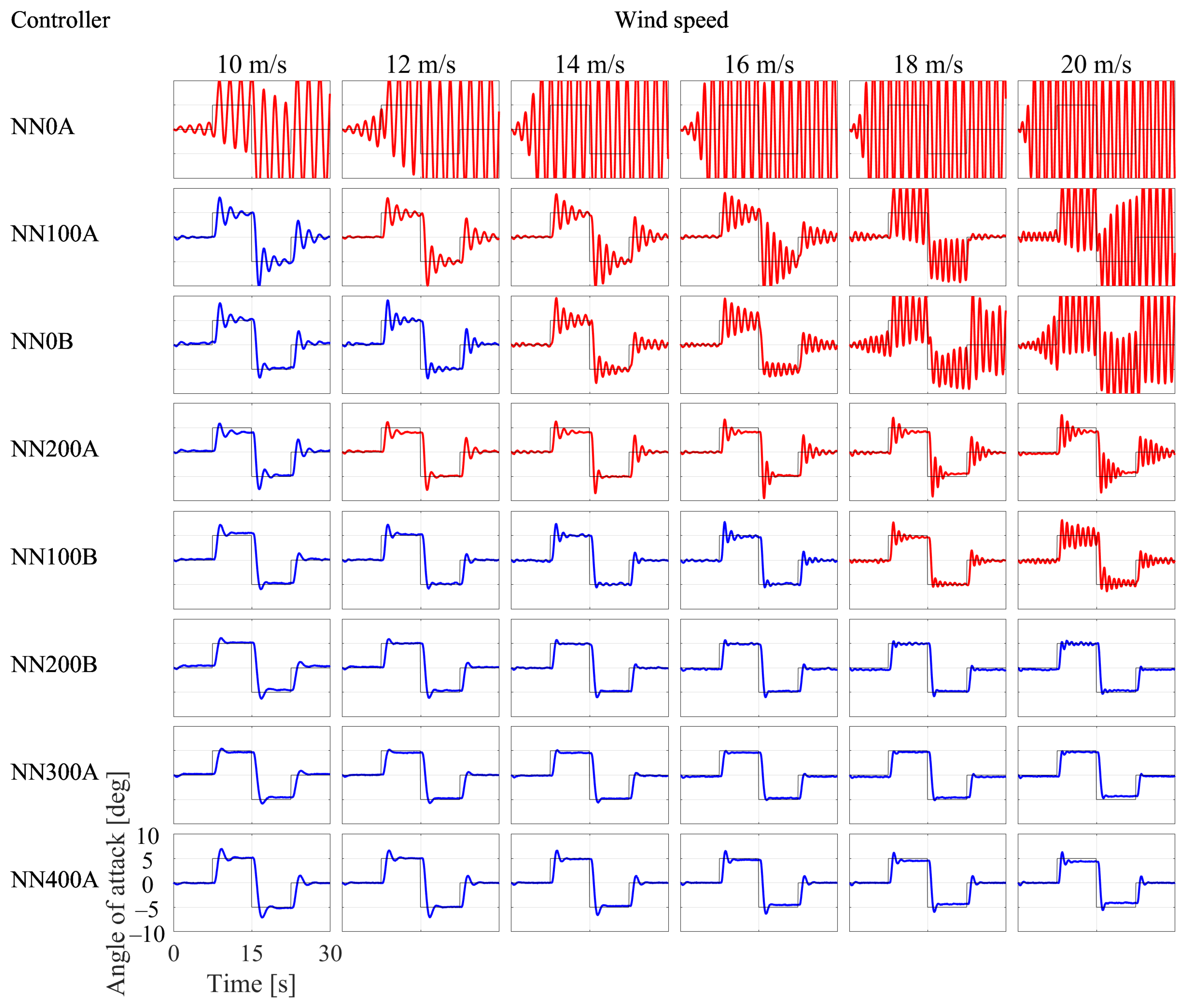
3.2. Simulation Results
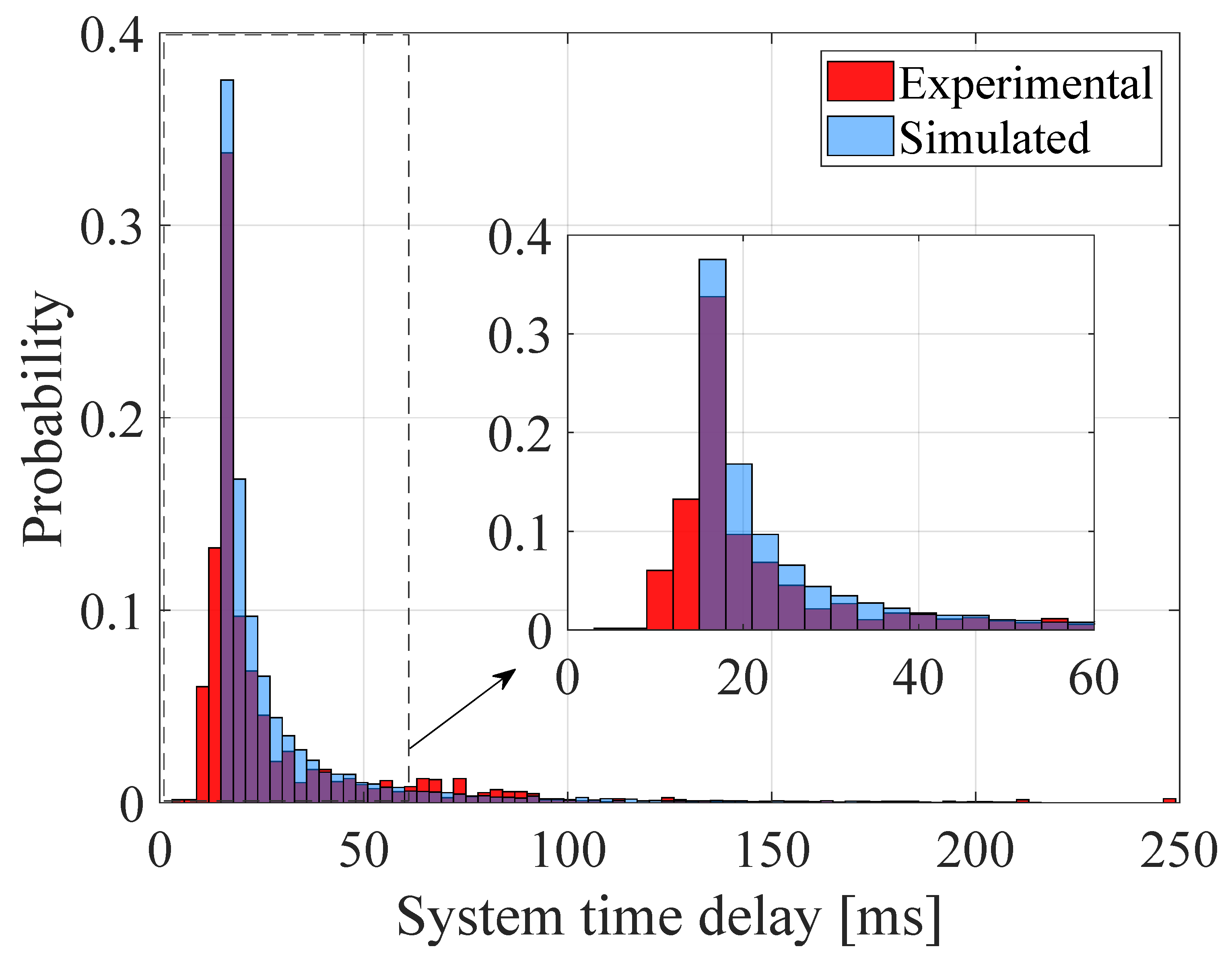
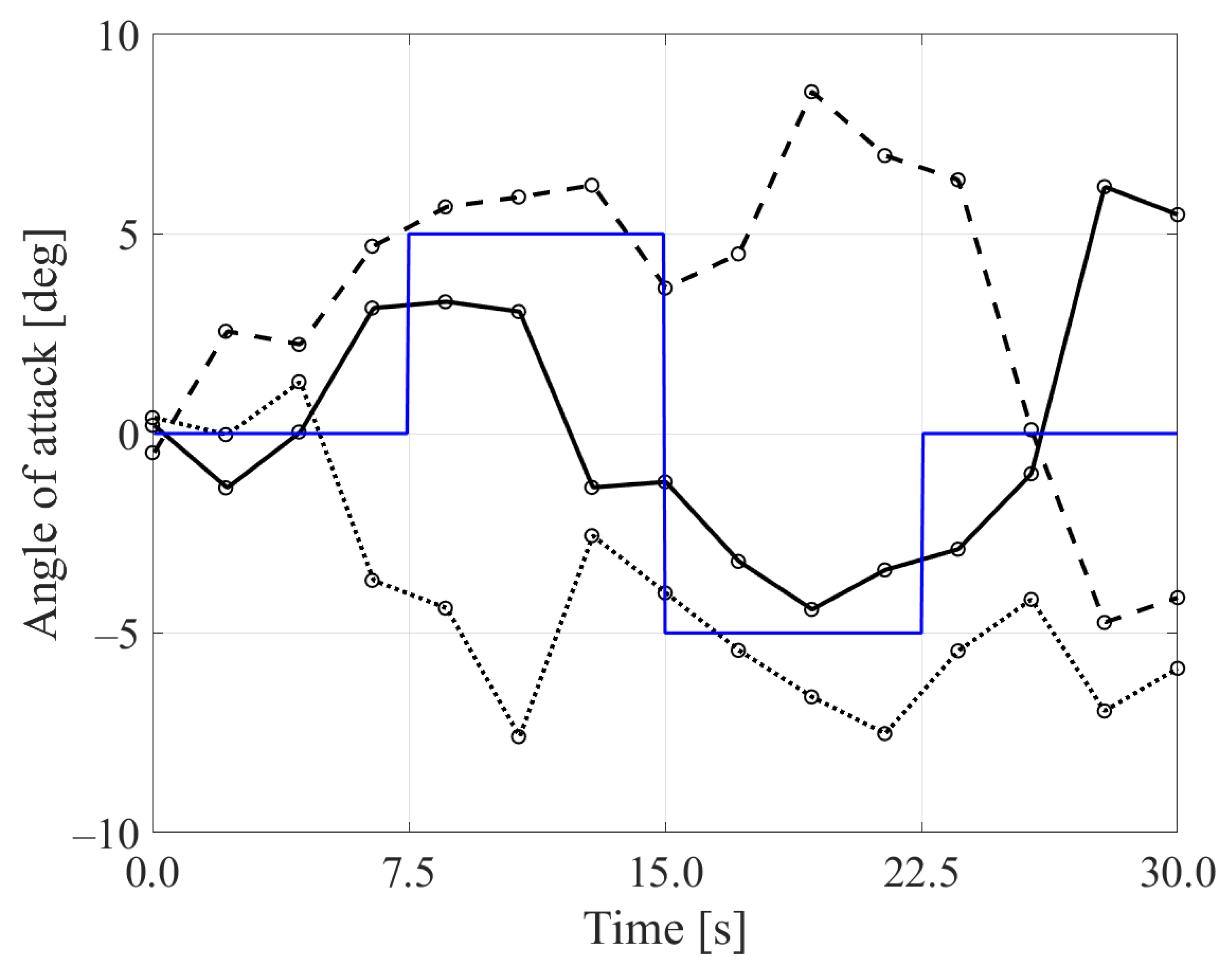
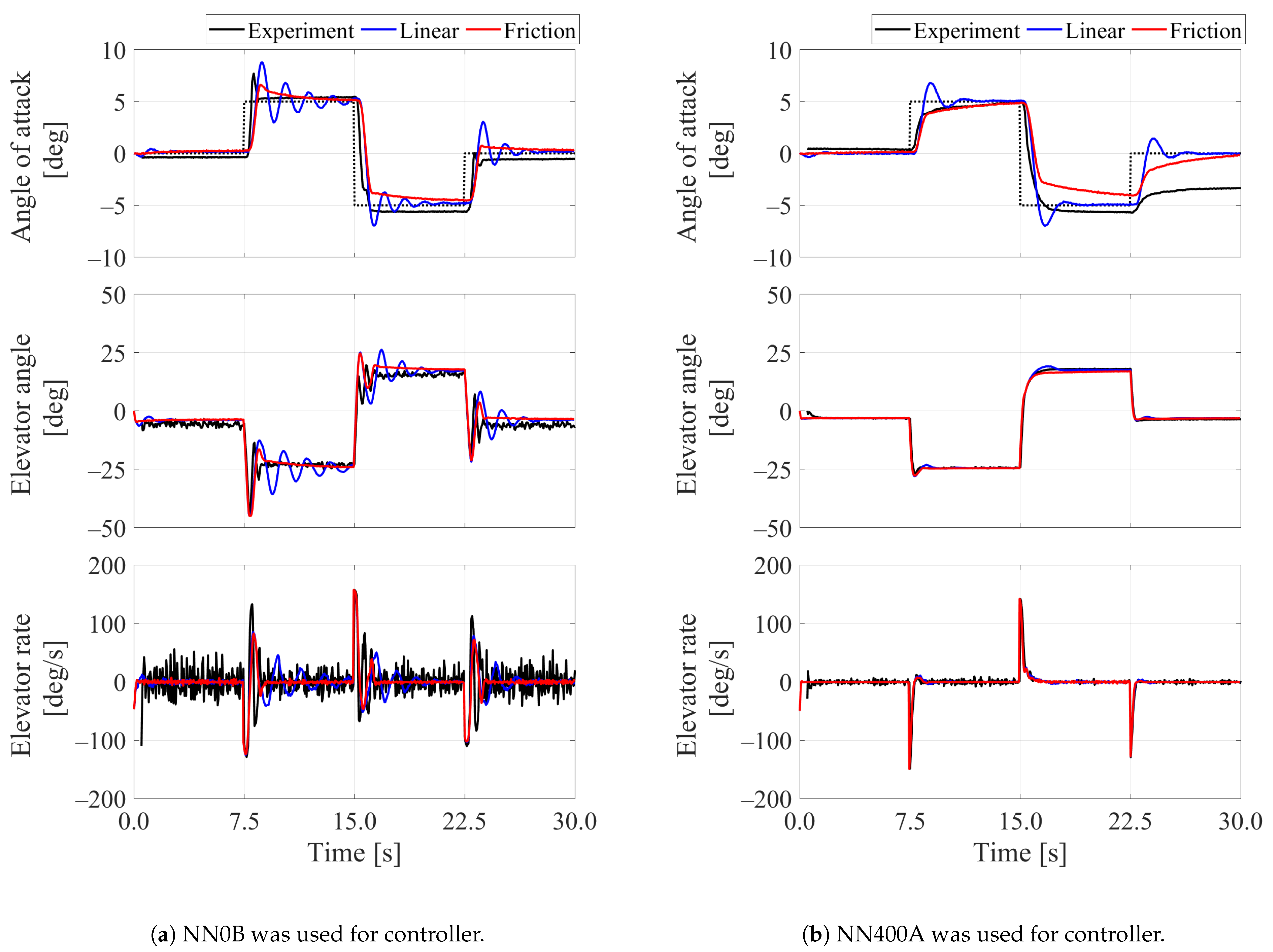
3.3. Experimental Results
4. Discussion on Friction Effect
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Julian, K.D.; Kochenderfer, M.J. Deep Neural Network Compression for Aircraft Collision Avoidance Systems. J. Guid. Control Dyn. 2019, 42, 598–608. [Google Scholar] [CrossRef]
- Gu, W.; Valavanis, K.P.; Rutherford, M.J.; Rizzo, A. A Survey of Artificial Neural Networks with Model-based Control Techniques for Flight Control of Unmanned Aerial Vehicles. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 362–371. [Google Scholar]
- Ferrari, S.; Stengel, R.F. Classical/Neural Synthesis of Nonlinear Control Systems. J. Guid. Control Dyn. 2002, 25, 442–448. [Google Scholar] [CrossRef]
- Dadian, O.; Bhandari, S.; Raheja, A. A Recurrent Neural Network for Nonlinear Control of a Fixed-Wing UAV. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1341–1346. [Google Scholar]
- Kim, B.S.; Calise, A.J.; Kam, M. Nonlinear Flight Control Using Neural Networks and Feedback Linearization. In Proceedings of the First IEEE Regional Conference on Aerospace Control Systems, Westlake Village, CA, USA, 25–27 May1993; pp. 176–181. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control Through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Xi, C.; Liu, X. Unmanned Aerial Vehicle Trajectory Planning via Staged Reinforcement Learning. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 9–12 June 2020; pp. 246–255. [Google Scholar] [CrossRef]
- Tang, C.; Lai, Y.C. Deep Reinforcement Learning Automatic Landing Control of Fixed-Wing Aircraft Using Deep Deterministic Policy Gradient. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems, ICUAS 2020, Athens, Greece, 9–12 June 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Fixed-Wing UAVs flocking in continuous spaces: A deep reinforcement learning approach. Robot. Auton. Syst. 2020, 131, 103594. [Google Scholar] [CrossRef]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Koch, W.; Mancuso, R.; West, R.; Bestavros, A. Reinforcement Learning for UAV Attitude Control. arXiv 2018, arXiv:1804.04154. [Google Scholar] [CrossRef] [Green Version]
- Gu, S.; Lillicrap, T.; Sutskever, I.; Levine, S. Continuous Deep Q-Learning with Model-based Acceleration. arXiv 2016, arXiv:1603.00748. [Google Scholar]
- Clarke, S.G.; Hwang, I. Deep Reinforcement Learning Control for Aerobatic Maneuvering of Agile Fixed-Wing Aircraft. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Bøhn, E.; Coates, E.M.; Moe, S.; Johansen, T.A. Deep Reinforcement Learning Attitude Control of Fixed-Wing UAVs Using Proximal Policy Optimization. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Cranfield, UK, 25–27 November 2019; pp. 523–533. [Google Scholar]
- Pi, C.H.; Dai, Y.W.; Hu, K.C.; Cheng, S. General Purpose Low-Level Reinforcement Learning Control for Multi-Axis Rotor Aerial Vehicles. Sensors 2021, 21, 4560. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar]
- Wada, D.; Araujo-Estrada, S.A.; Windsor, S. Unmanned Aerial Vehicle Pitch Control Using Deep Reinforcement Learning with Discrete Actions in Wind Tunnel Test. Aerospace 2021, 8, 18. [Google Scholar] [CrossRef]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-Real Transfer of Robotic Control with Dynamics Randomization. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 3803–3810. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Du, T.; Foshey, M.; Li, B.; Zhu, B.; Schulz, A.; Matusik, W. Learning to fly: Computational controller design for hybrid UAVs with reinforcement learning. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Jategaonkar, R.V. Flight Vehicle System Identification: A Time Domain Methodology; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar] [CrossRef]
- Makkar, C.; Dixon, W.E.; Sawyer, W.G.; Hu, G. A New Continuously Differentiable Friction Model for Control Systems Design. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 600–605. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the Theory of the Brownian Motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–14. [Google Scholar]
- Kingma, D.P.; Ba, J. ADAM: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]




| Parameter | Units | Value |
|---|---|---|
| 1.90 × 10−1 | ||
| 1.23 | ||
| S | 3.06 × 10−1 | |
| c | 2.54 × 10−1 | |
| – | −3.00 × 10−3 | |
| – | −2.25 × 10−1 | |
| – | −5.46 | |
| – | −5.35 × 10−2 |
| Parameter | Value |
|---|---|
| Weight for policy loss | 1 |
| Weight for value loss | 0.5 |
| Weight for regularization with policy entropy | 0.01 |
| Discount factor | 0.99 |
| Number of forward steps in advantage estimation | 20 |
| Exponential weight parameter in GAE | 1 |
| Learning rate | 0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wada, D.; Araujo-Estrada, S.A.; Windsor, S. Unmanned Aerial Vehicle Pitch Control under Delay Using Deep Reinforcement Learning with Continuous Action in Wind Tunnel Test. Aerospace 2021, 8, 258. https://doi.org/10.3390/aerospace8090258
Wada D, Araujo-Estrada SA, Windsor S. Unmanned Aerial Vehicle Pitch Control under Delay Using Deep Reinforcement Learning with Continuous Action in Wind Tunnel Test. Aerospace. 2021; 8(9):258. https://doi.org/10.3390/aerospace8090258
Chicago/Turabian StyleWada, Daichi, Sergio A. Araujo-Estrada, and Shane Windsor. 2021. "Unmanned Aerial Vehicle Pitch Control under Delay Using Deep Reinforcement Learning with Continuous Action in Wind Tunnel Test" Aerospace 8, no. 9: 258. https://doi.org/10.3390/aerospace8090258
APA StyleWada, D., Araujo-Estrada, S. A., & Windsor, S. (2021). Unmanned Aerial Vehicle Pitch Control under Delay Using Deep Reinforcement Learning with Continuous Action in Wind Tunnel Test. Aerospace, 8(9), 258. https://doi.org/10.3390/aerospace8090258






