Stress Intensity Factors for a Non-Circular Hole with Inclusion Layer Embedded in a Cracked Matrix
Abstract
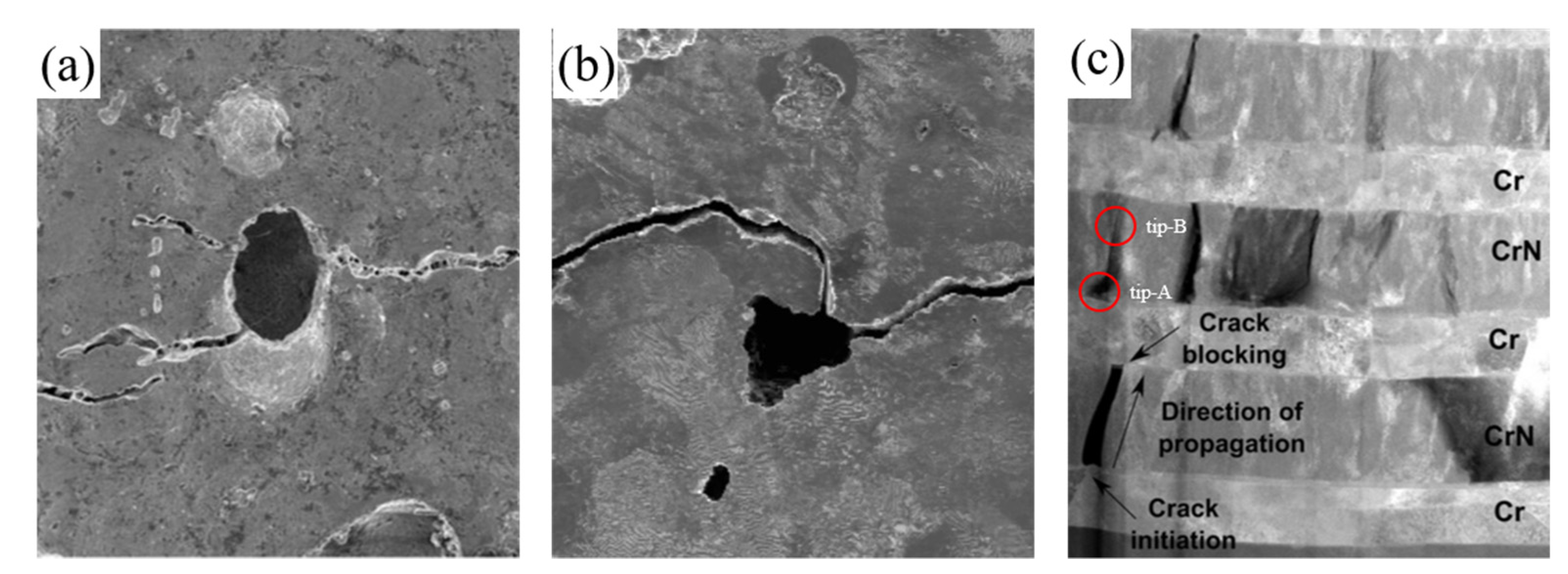
:1. Introduction
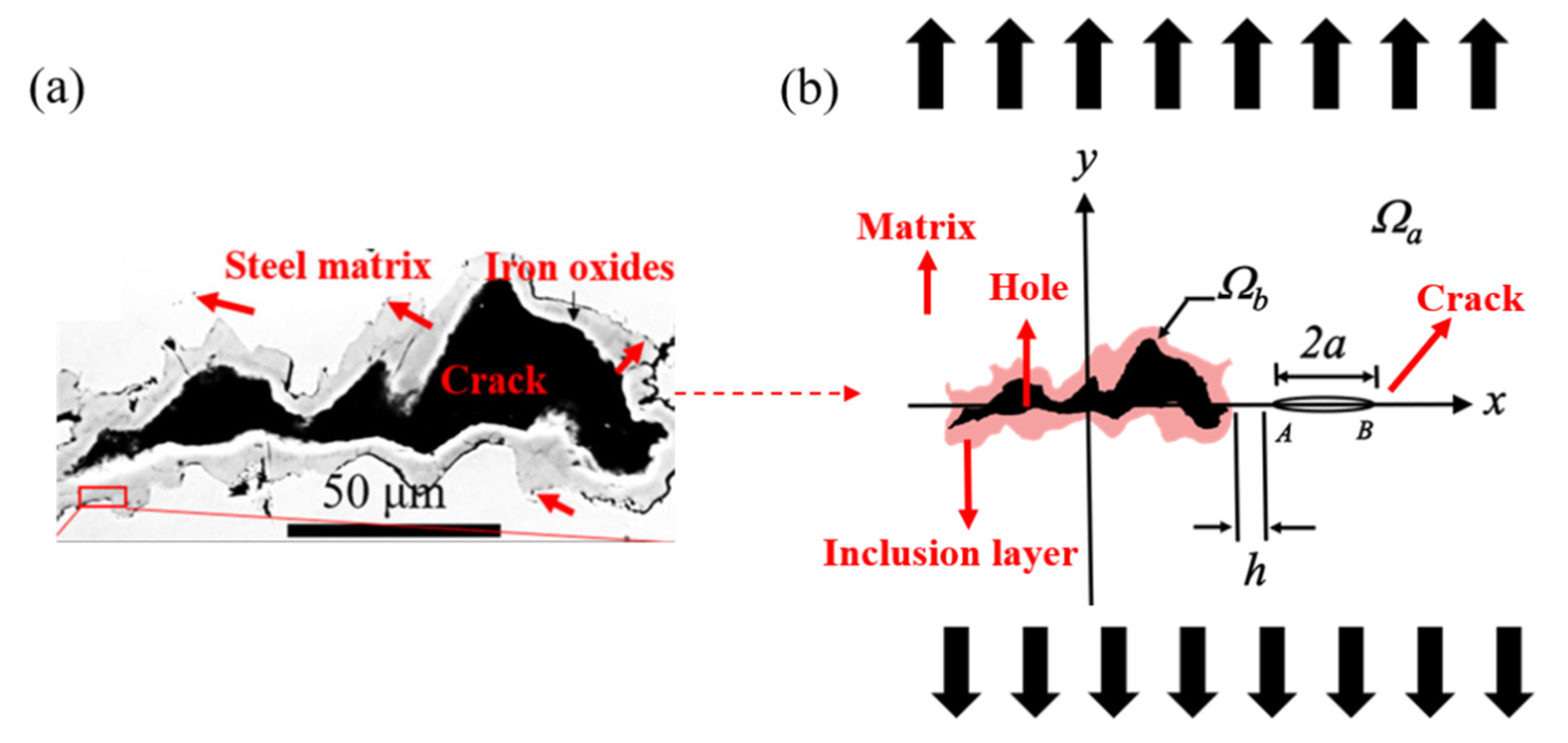
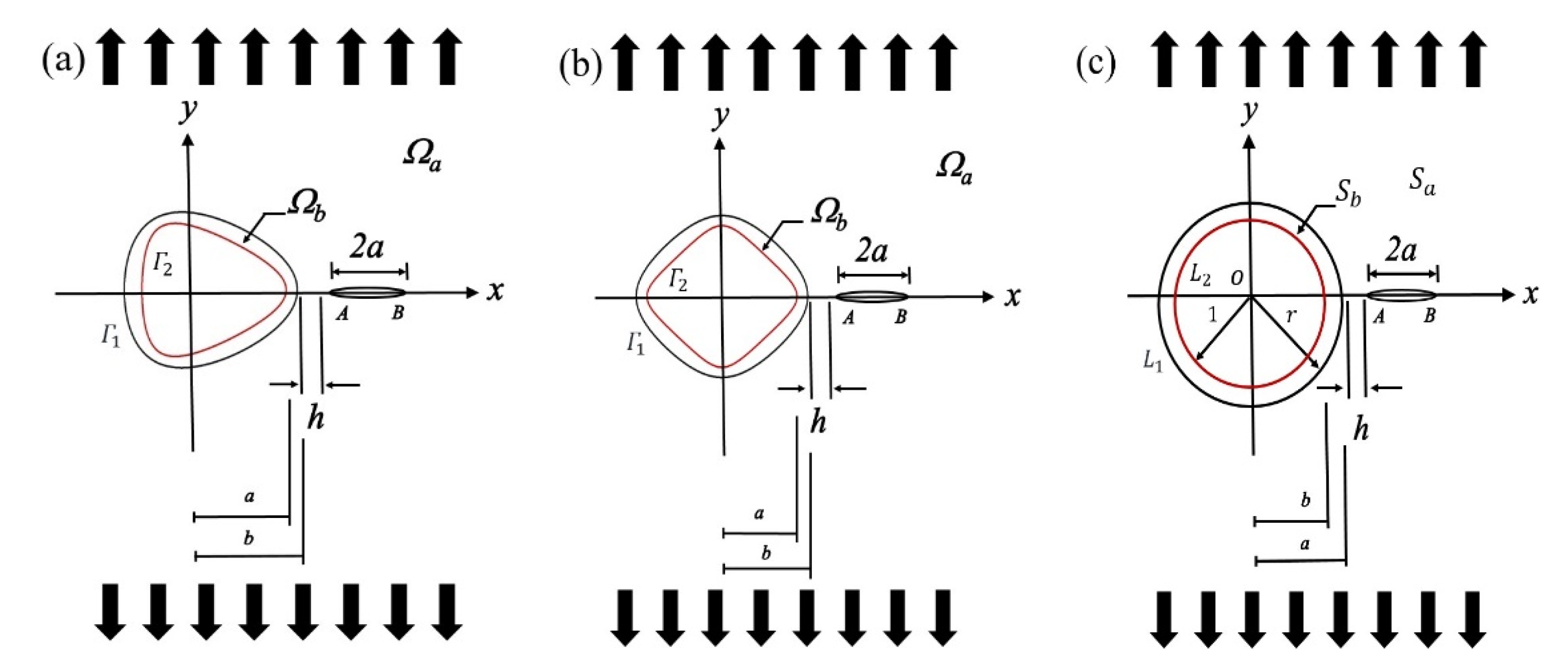
2. Problem Formulation
3. Stress Field
3.1. Homogeneous Solution
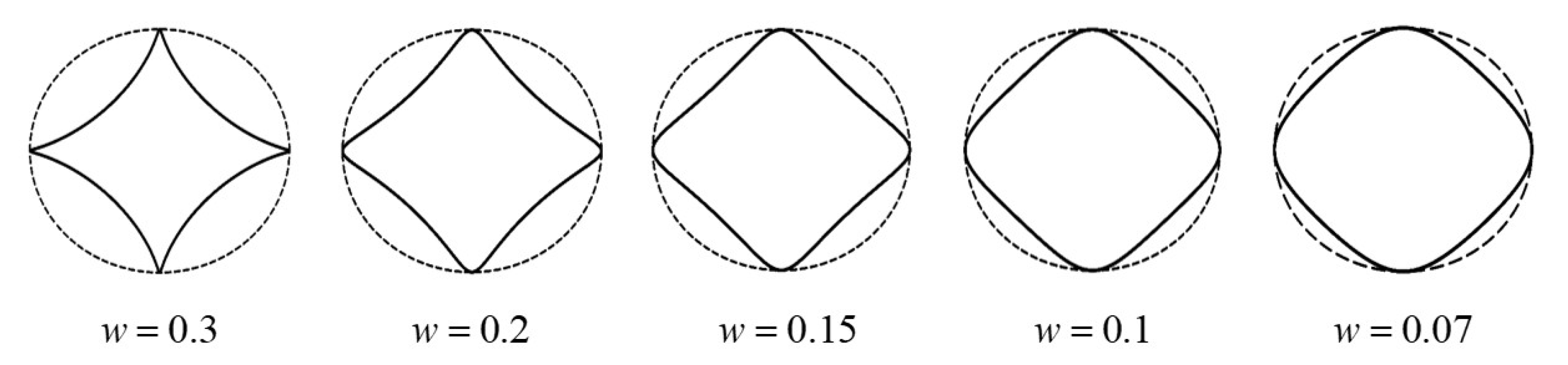
3.2. Stress Functions for the Triangular and Square Hole with Inclusion Layer
4. Singular Integral Equations
5. Stress Intensity Factors
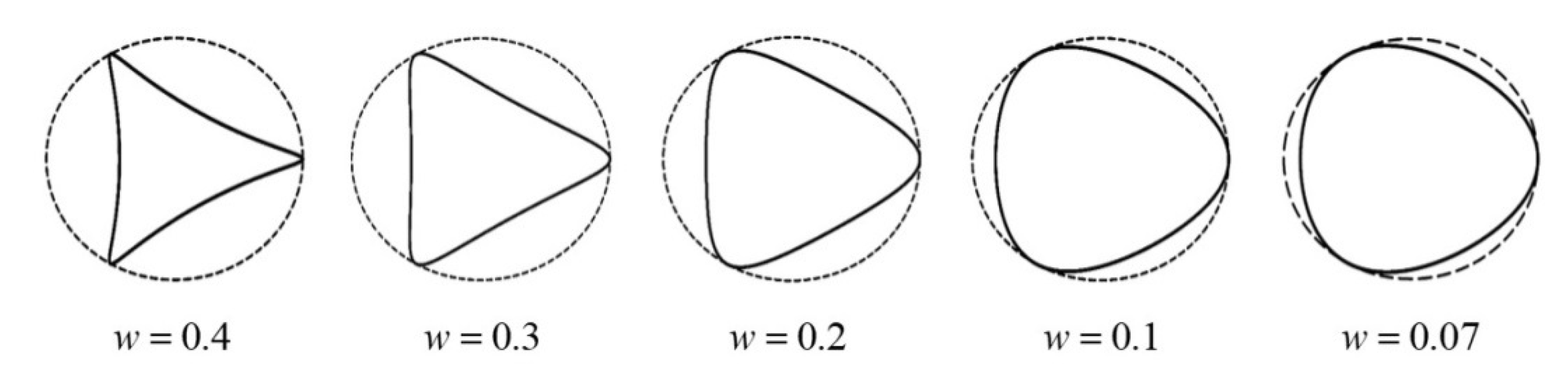
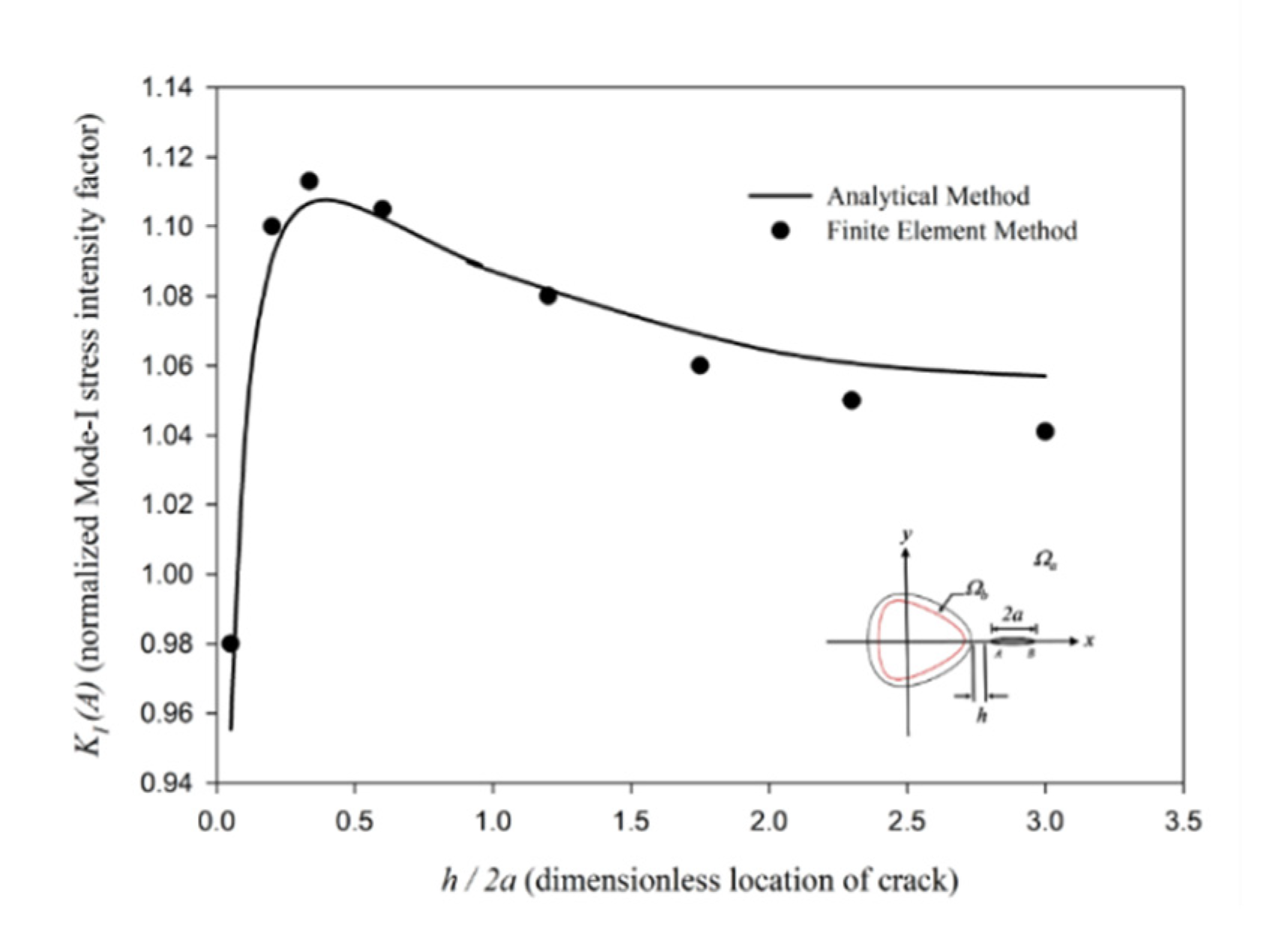
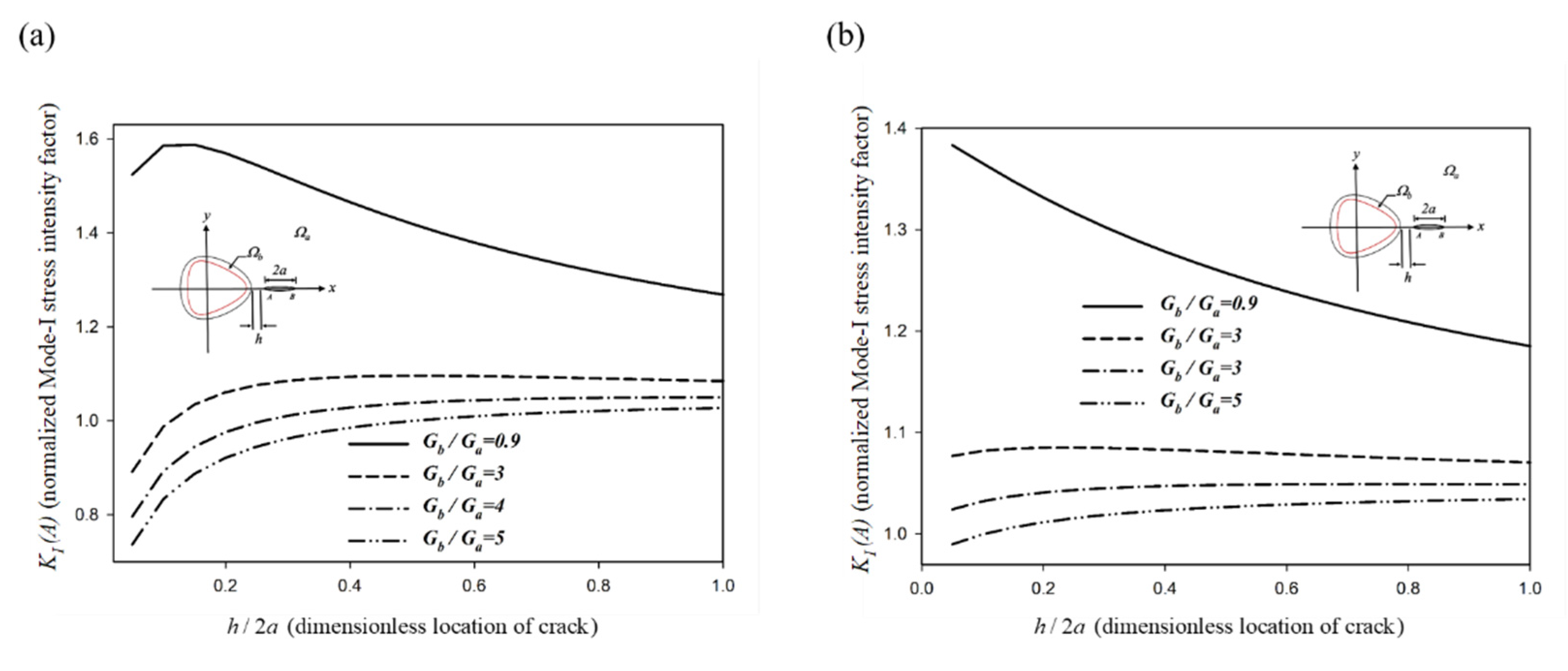
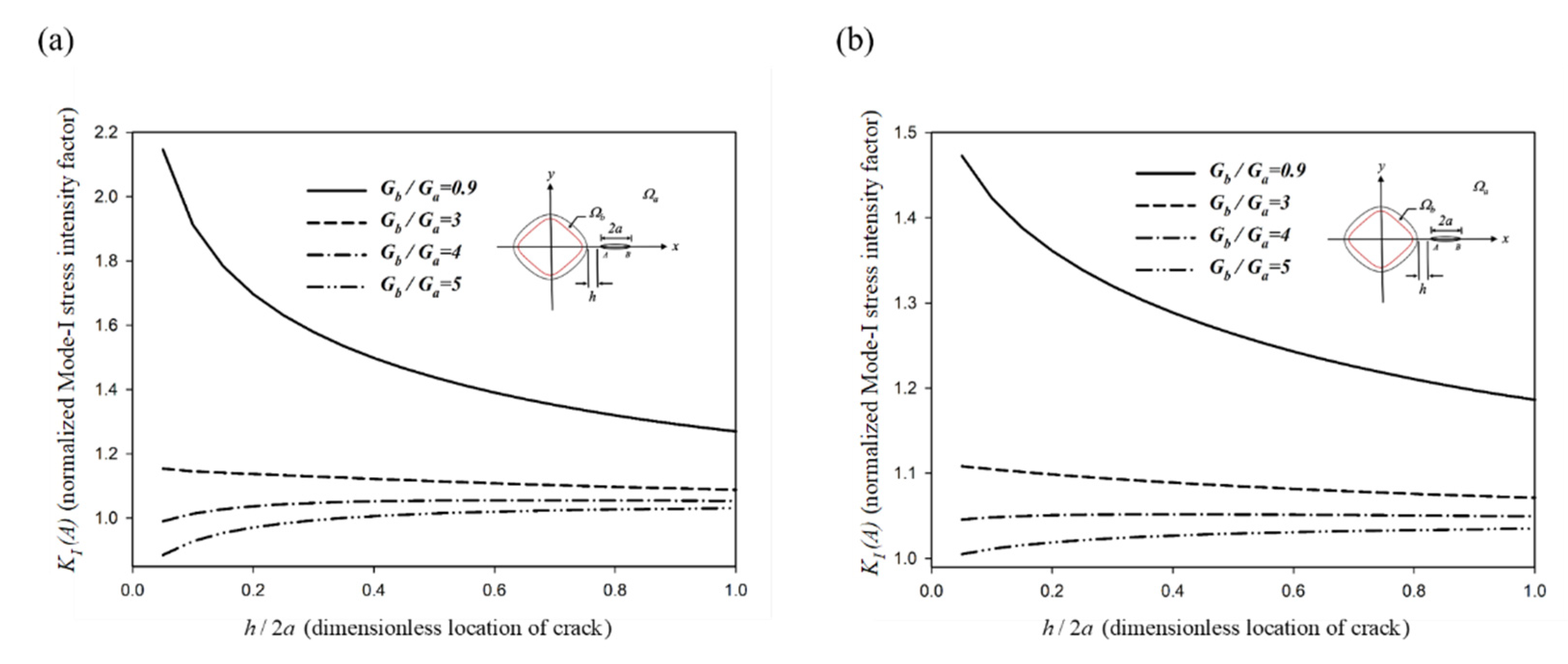
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Determination of Corrected Constants
References
- Turnbull, A. Corrosion pitting and environmentally assisted small crack growth. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140254. [Google Scholar] [CrossRef] [Green Version]
- Nový, F.; Kopas, P.; Bokůvka, O.; Jambor, M.; Trško, L. Influence of microscopic casting defects on fatigue endurance of ductile cast iron. MATEC Web Conf. 2018, 157, 05019. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Shao, Z.; Tian, F.; Hopper, C.; Jiang, J. Microstructural effects on central crack formation in hot cross-wedge-rolled high-strength steel parts. J. Mater. Sci. 2020, 55, 9608–9622. [Google Scholar] [CrossRef] [Green Version]
- Wieciński, P.; Smolik, J.; Garbacz, H.; Kurzydłowski, K. Failure and deformation mechanisms during indentation in nanostructured Cr/CrN multilayer coatings. Surf. Coat. Technol. 2014, 240, 23–31. [Google Scholar] [CrossRef]
- Mohtadi-Bonab, M.A.; Eskandari, M.; Sanayei, M.; Das, S. Microstructural aspects of intergranular and transgranular crack propagation in an API X65 steel pipeline related to fatigue failure. Eng. Fail. Anal. 2018, 94, 214–225. [Google Scholar] [CrossRef]
- Erdogan, F.; Gupta, G. The stress analysis of multi-layered composites with a flaw. Int. J. Solids Struct. 1971, 7, 39–61. [Google Scholar] [CrossRef]
- Chao, C.K.; Chen, F.M.; Shen, M.H. Circularly cylindrical layered media in plane elasticity. Int. J. Solids Struct. 2006, 43, 4739–4756. [Google Scholar] [CrossRef] [Green Version]
- Pak, Y.E.; Mishra, D.; Yoo, S.-H. Closed-form solution for a coated circular inclusion under uniaxial tension. Acta Mech. 2012, 223, 937–951. [Google Scholar] [CrossRef]
- England, A.H. Complex Variable Methods in Elasticity; Courier Corporation: Chelmsford, MA, USA, 2003. [Google Scholar]
- Tseng, S.C.; Chao, C.K.; Chen, F.M. Stress field for a coated triangle-like hole problem in plane elasticity. J. Mech. 2020, 36, 55–72. [Google Scholar] [CrossRef]
- Tseng, S.C.; Chao, C.K.; Chen, F.M. Interfacial stresses of a coated square hole induced by a remote uniform heat flow. Int. J. Appl. Mech. 2020, 12, 2050063. [Google Scholar] [CrossRef]
- Tseng, S.C.; Chao, C.K.; Chen, F.M.; Chiu, W.C. Interfacial stresses of a coated polygonal hole subject to a point heat source. J. Therm. Stresses 2020, 43, 1487–1512. [Google Scholar] [CrossRef]
- Jafari, M.; Nazari, M.B.; Taherinasab, A. Thermal stress analysis in metallic plates with a non-circular hole subjected to uniform heat flux. Eur. J. Mech.-A/Solids 2016, 59, 356–363. [Google Scholar] [CrossRef]
- Jafari, M. Thermal stress analysis of orthotropic plate containing a rectangular hole using complex variable method. Eur. J. Mech.-A/Solids 2019, 73, 212–223. [Google Scholar] [CrossRef]
- Theocaris, P.; Demakos, C. Antiplane shear crack in an infinite plate with a circular inclusion. Ing.-Arch. 1985, 55, 295–306. [Google Scholar] [CrossRef]
- Chao, C.K.; Young, C.W. On the general treatment of multiple inclusions in antiplane elastostatics. Int. J. Solids Struct. 1998, 35, 3573–3593. [Google Scholar] [CrossRef]
- Chao, C.K.; Wikarta, A.; Korsunsky, A. Anti-plane interaction of a crack and reinforced elliptic hole in an infinite matrix. Theor. Appl. Fract. Mech. 2010, 53, 205–210. [Google Scholar] [CrossRef]
- Chao, C.K.; Tseng, S.C.; Chen, F.M. Mode-III stress intensity factors for two circular inclusions subject to a remote uniform shear load. J. Chin. Inst. Eng. 2018, 41, 590–602. [Google Scholar] [CrossRef]
- Park, P.; Sudak, L. Stress intensity factor for an interphase Griffith crack interacting with two imperfect interfaces. Math. Mech. Solids 2010, 15, 353–367. [Google Scholar] [CrossRef]
- Wikarta, A. Anti-plane interaction of a coated circular inclusion with a crack located in matrix. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2016; Volume 836, pp. 26–30. [Google Scholar] [CrossRef]
- Chen, D.-H. The effect of an elliptical inclusion on a crack. Int. J. Fract. 1997, 85, 351–364. [Google Scholar] [CrossRef]
- Chao, C.K.; Chen, F.M.; Lin, T.H. Stress intensity factors for fibrous composite with a crack embedded in an infinite matrix under a remote uniform load. Eng. Fract. Mech. 2017, 179, 294–313. [Google Scholar] [CrossRef]
- Chao, C.K.; Wikarta, A. Solutions of a crack interacting with tri-material composite in plane elasticity. CMES-Comput. Model. Eng. Sci. 2013, 93, 167–186. [Google Scholar] [CrossRef]
- Chao, C.K.; Wikarta, A. Solutions of a crack interacting with a three-phase composite in plane elasticity. Appl. Math. Model. 2016, 40, 2454–2472. [Google Scholar] [CrossRef]
- Greco, F.; Leonetti, L.; Blasi, P.N. Non-linear macroscopic response of fiber-reinforced composite materials due to initiation and propagation of interface cracks. Eng. Fract. Mech. 2012, 80, 92–113. [Google Scholar] [CrossRef]
- Cheung, Y.; Chen, Y. New integral equation for plane elasticity crack problems. Theor. Appl. Fract. Mech. 1987, 7, 177–184. [Google Scholar] [CrossRef]
- Chen, H.Y.; Tsai, C.J.; Lu, F.-H. The Young’s modulus of chromium nitride films. Surf. Coat. Technol. 2004, 184, 69–73. [Google Scholar] [CrossRef]
- Kaplan, M.; Uyaner, M.; Ozgurluk, Y.; Doleker, K.M.; Karaoglanli, A.C. Evaluation of hot corrosion behavior of APS and HVOF sprayed thermal barrier coatings (TBCs) exposed to molten Na2SO4 + V2O5 salt at 1000 °C. In Engineering Design Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 441–459. [Google Scholar] [CrossRef]
- Tseng, S.C.; Chao, C.K.; Guo, J.Y. Failure analysis of a polygonal void with an oxide layer in a cracked matrix. Int. J. Appl. Mech. 2021, 13, 2150099. [Google Scholar] [CrossRef]




| Corrected Constant | Value | Contribution |
|---|---|---|
| C11 | −1.1171 | 72.7% |
| C21 | −0.2866 | 18.7% |
| C31 | −0.1327 | 8.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, C.; Tseng, S.; Chao, C.; Guo, J. Stress Intensity Factors for a Non-Circular Hole with Inclusion Layer Embedded in a Cracked Matrix. Aerospace 2022, 9, 17. https://doi.org/10.3390/aerospace9010017
Chiu C, Tseng S, Chao C, Guo J. Stress Intensity Factors for a Non-Circular Hole with Inclusion Layer Embedded in a Cracked Matrix. Aerospace. 2022; 9(1):17. https://doi.org/10.3390/aerospace9010017
Chicago/Turabian StyleChiu, Chenchun, Shaochen Tseng, Chingkong Chao, and Jheyuan Guo. 2022. "Stress Intensity Factors for a Non-Circular Hole with Inclusion Layer Embedded in a Cracked Matrix" Aerospace 9, no. 1: 17. https://doi.org/10.3390/aerospace9010017
APA StyleChiu, C., Tseng, S., Chao, C., & Guo, J. (2022). Stress Intensity Factors for a Non-Circular Hole with Inclusion Layer Embedded in a Cracked Matrix. Aerospace, 9(1), 17. https://doi.org/10.3390/aerospace9010017






