Range and Accuracy Improvement of Artillery Rocket Using Fixed Canards Trajectory Correction Fuze
Abstract
1. Introduction
2. Fixed Canards Trajectory Correction Fuze
2.1. 7-Degree of Freedom (DOF) Dynamic Model
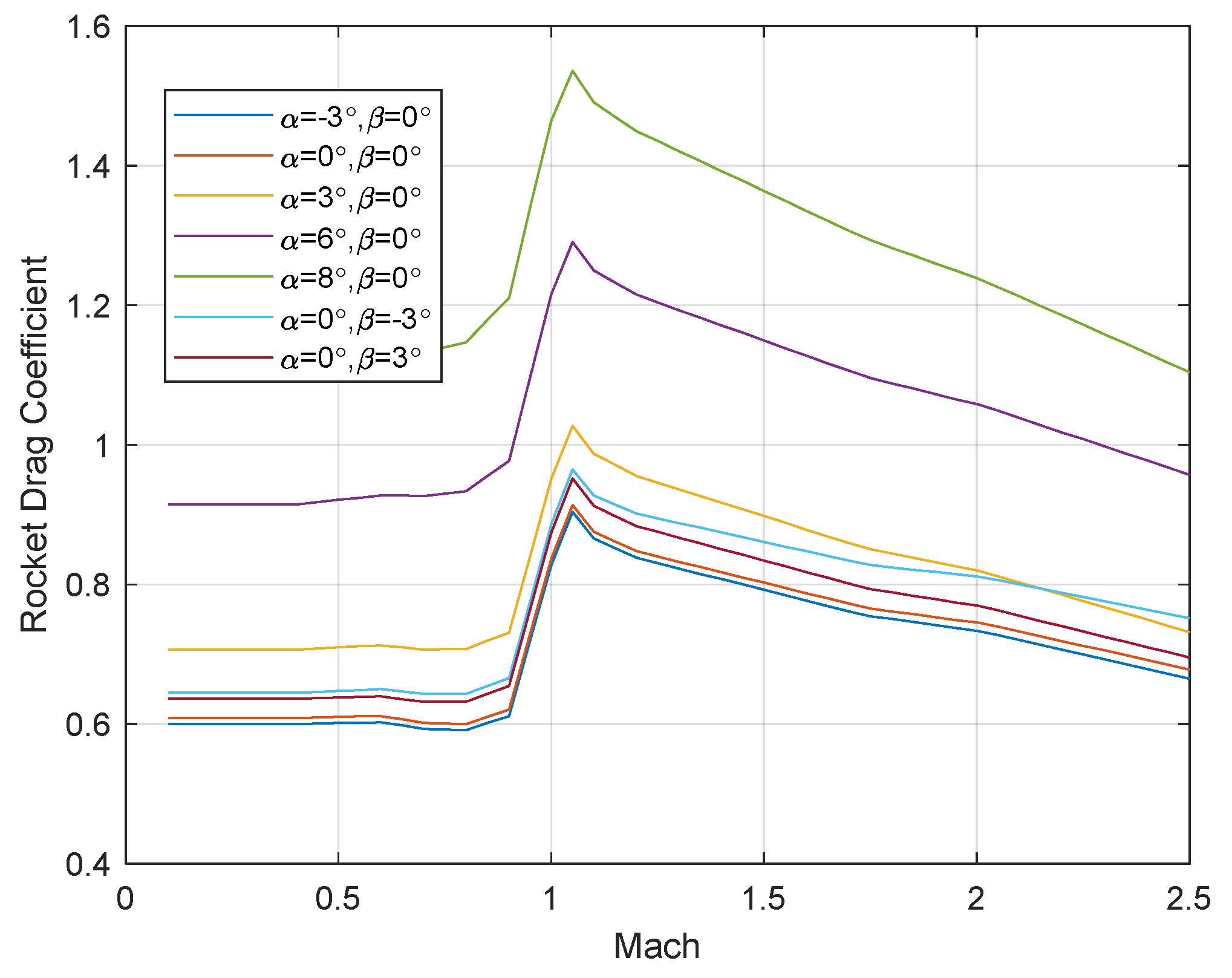
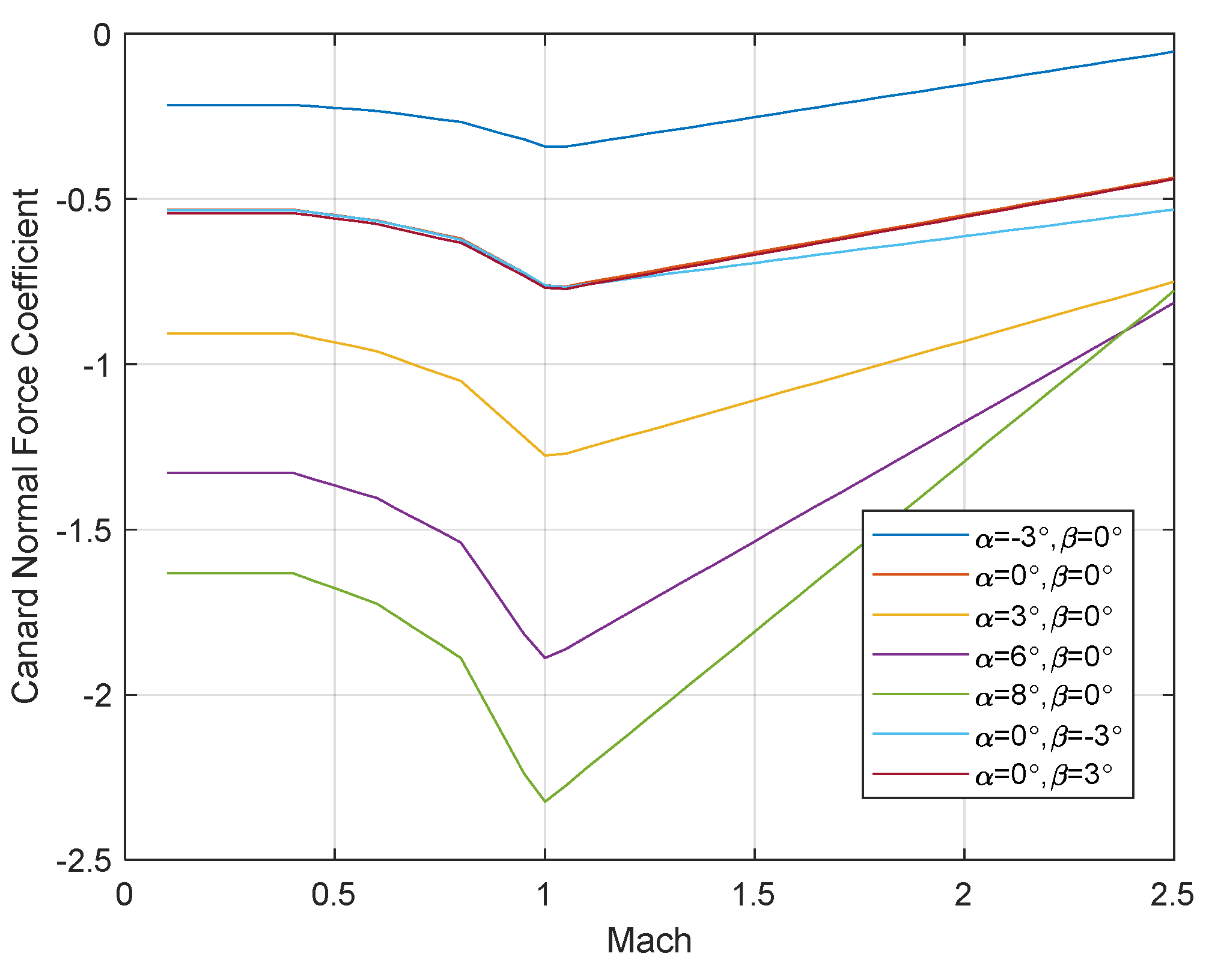
2.2. Control Authority Analysis
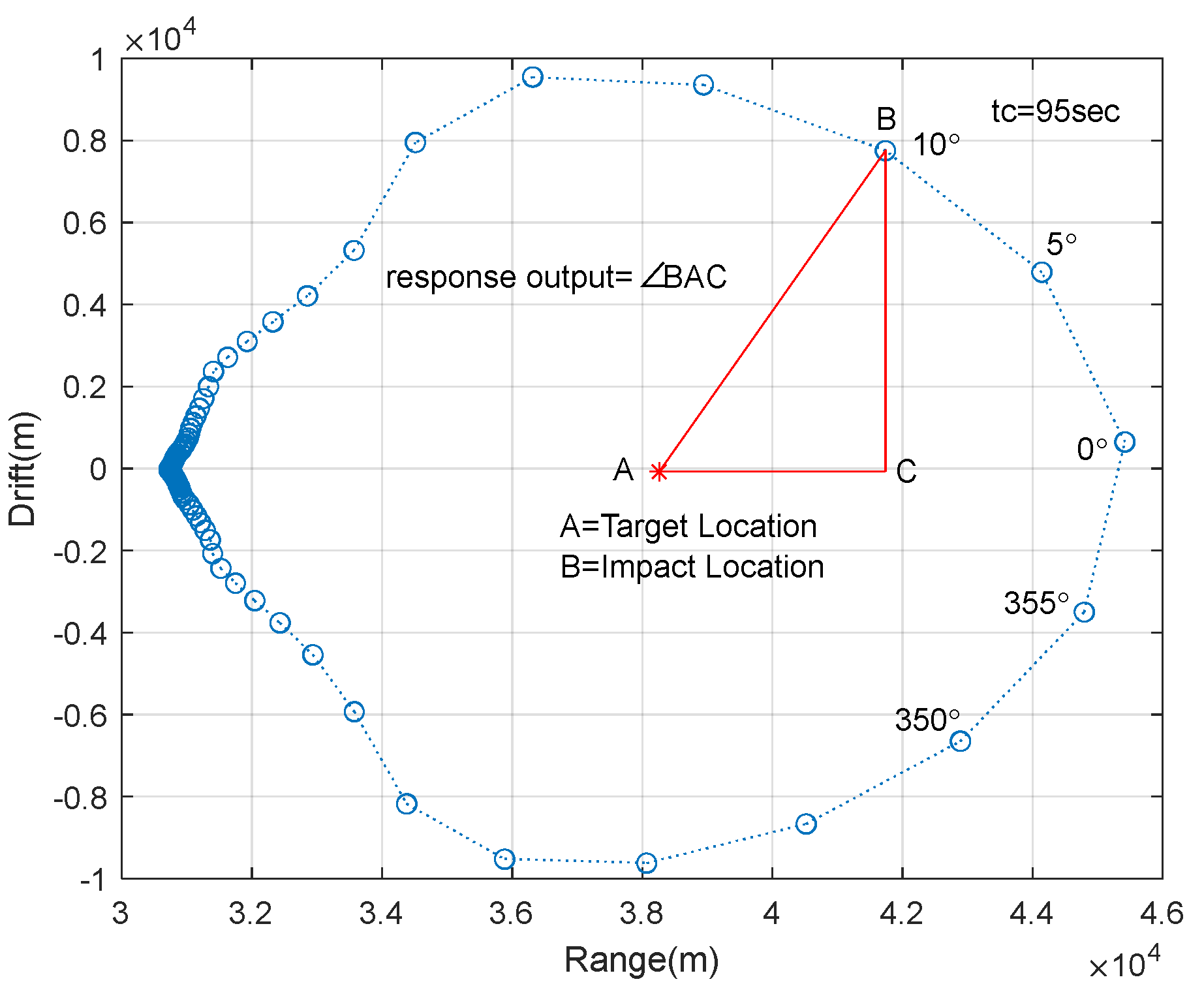
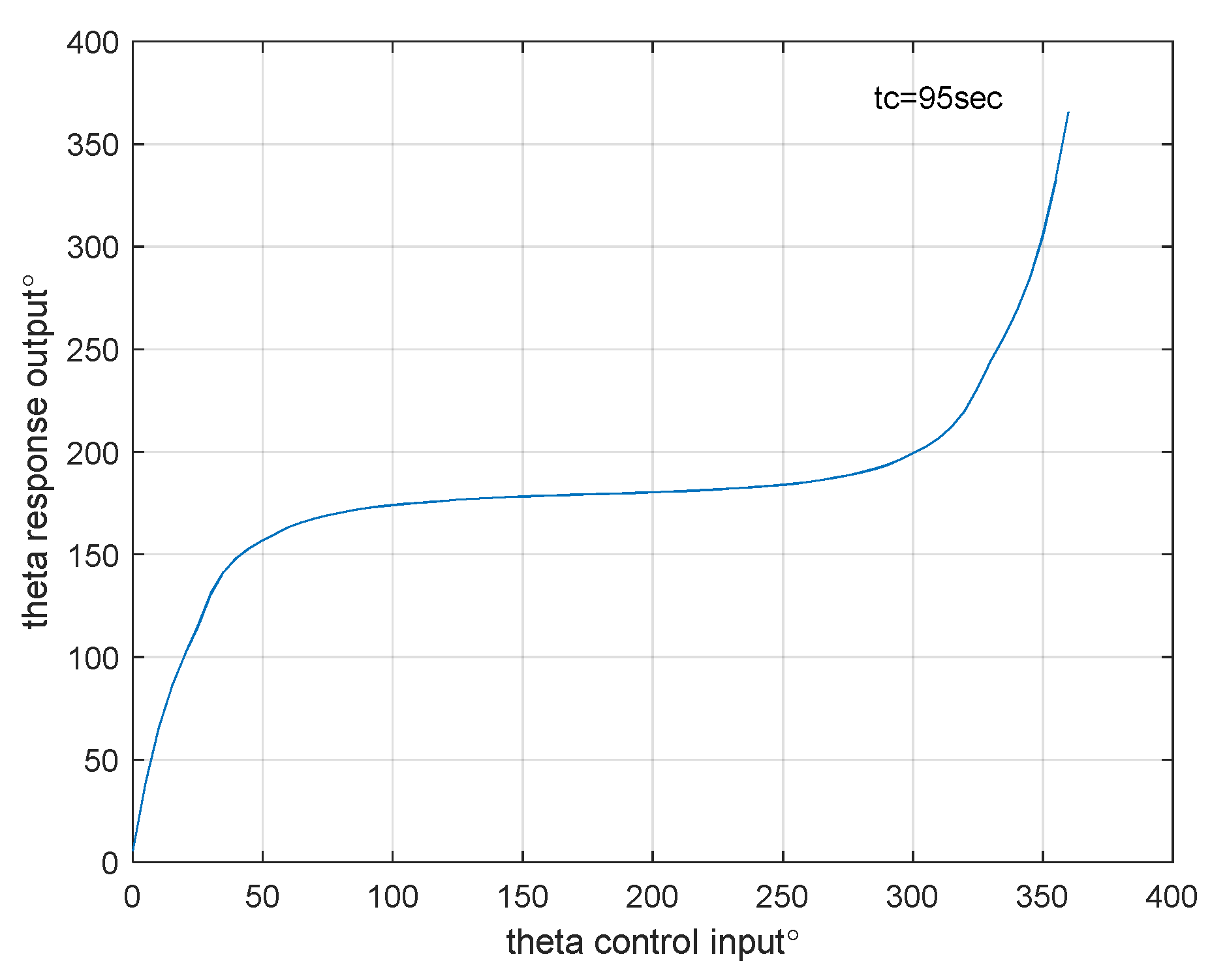
2.3. Swerve Response
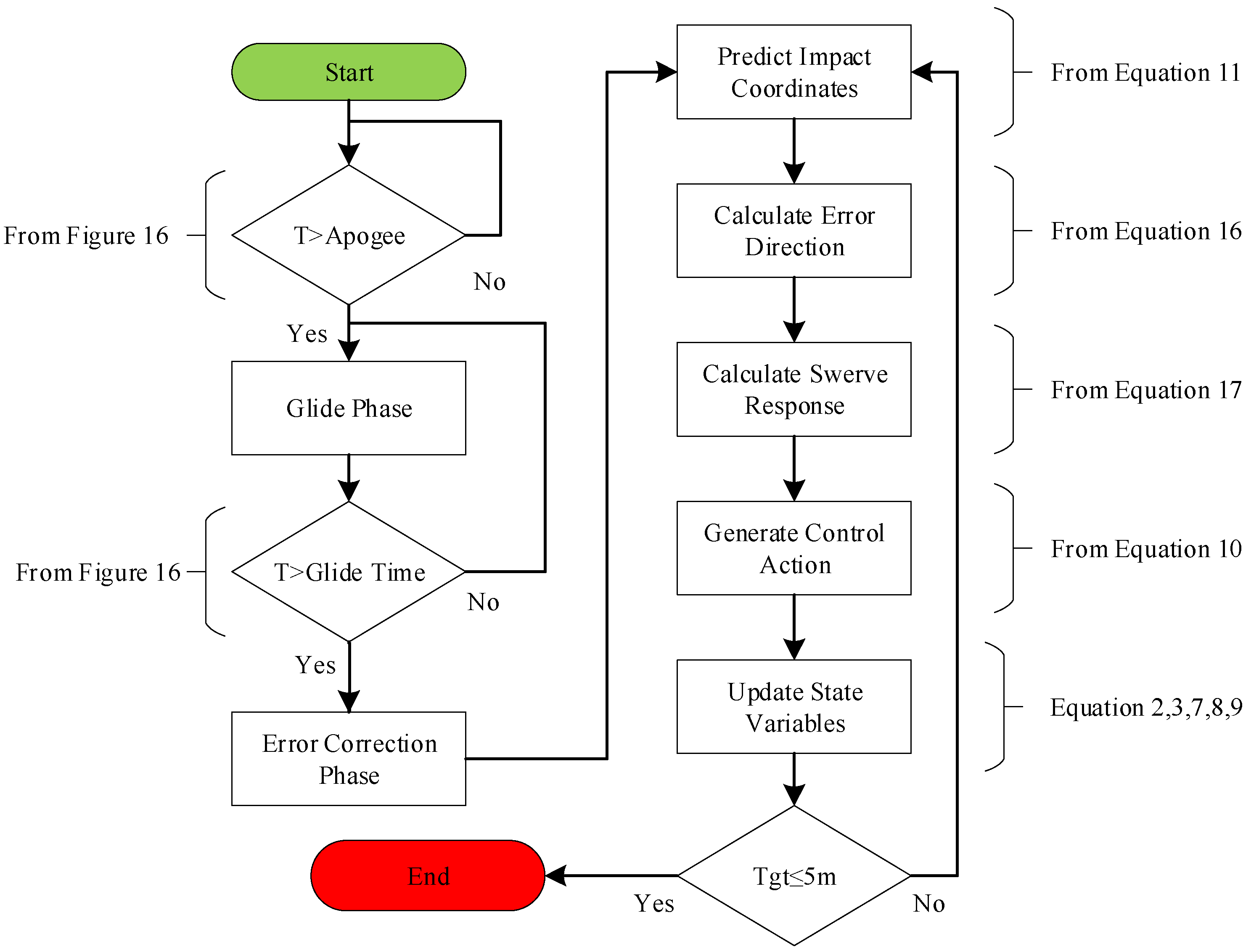
3. Guidance Scheme
3.1. Glide Phase
3.2. Error Correction Phase
3.3. Impact Point Prediction
3.4. Modified Projectile Linear Theory
4. Simulation Implementation
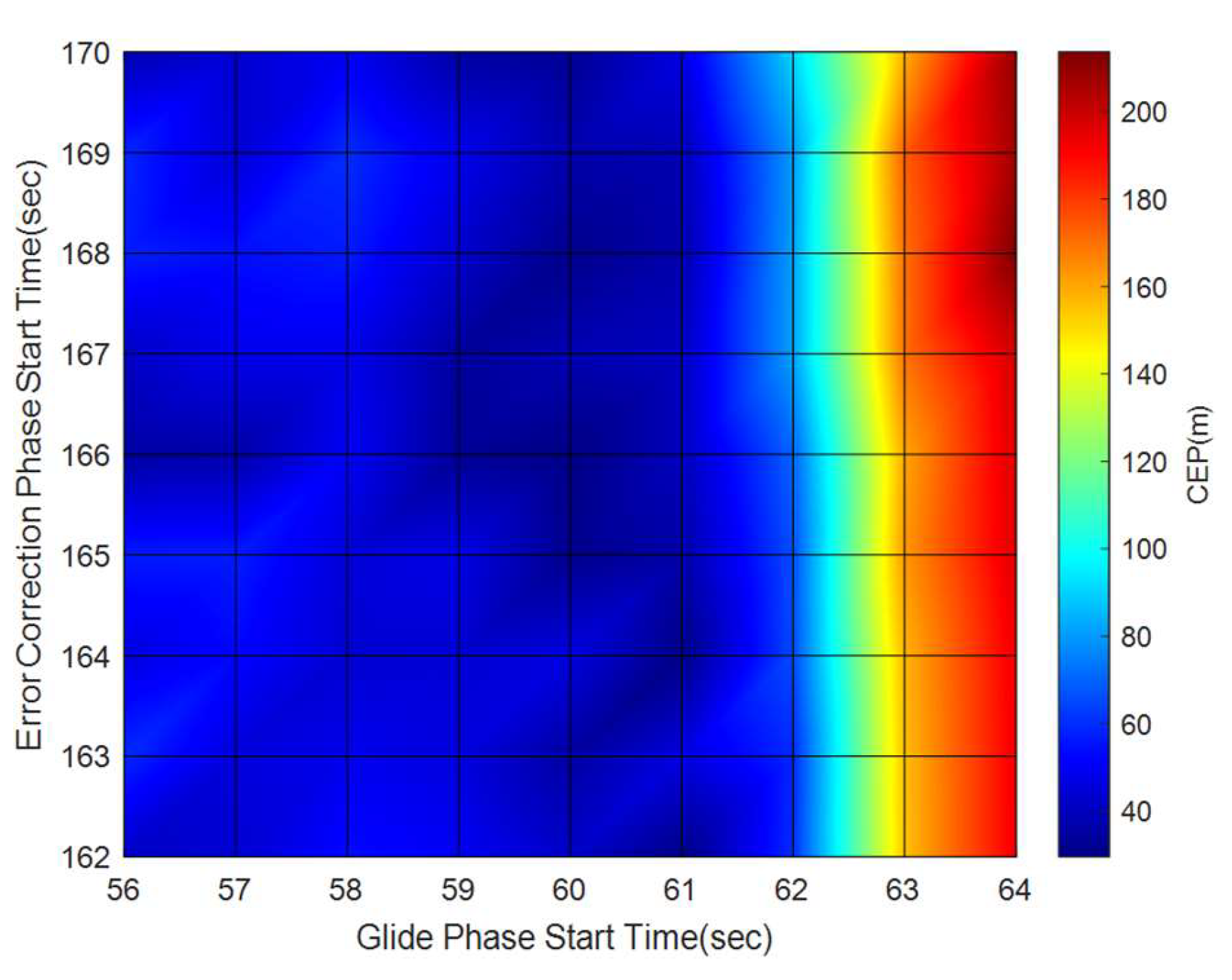
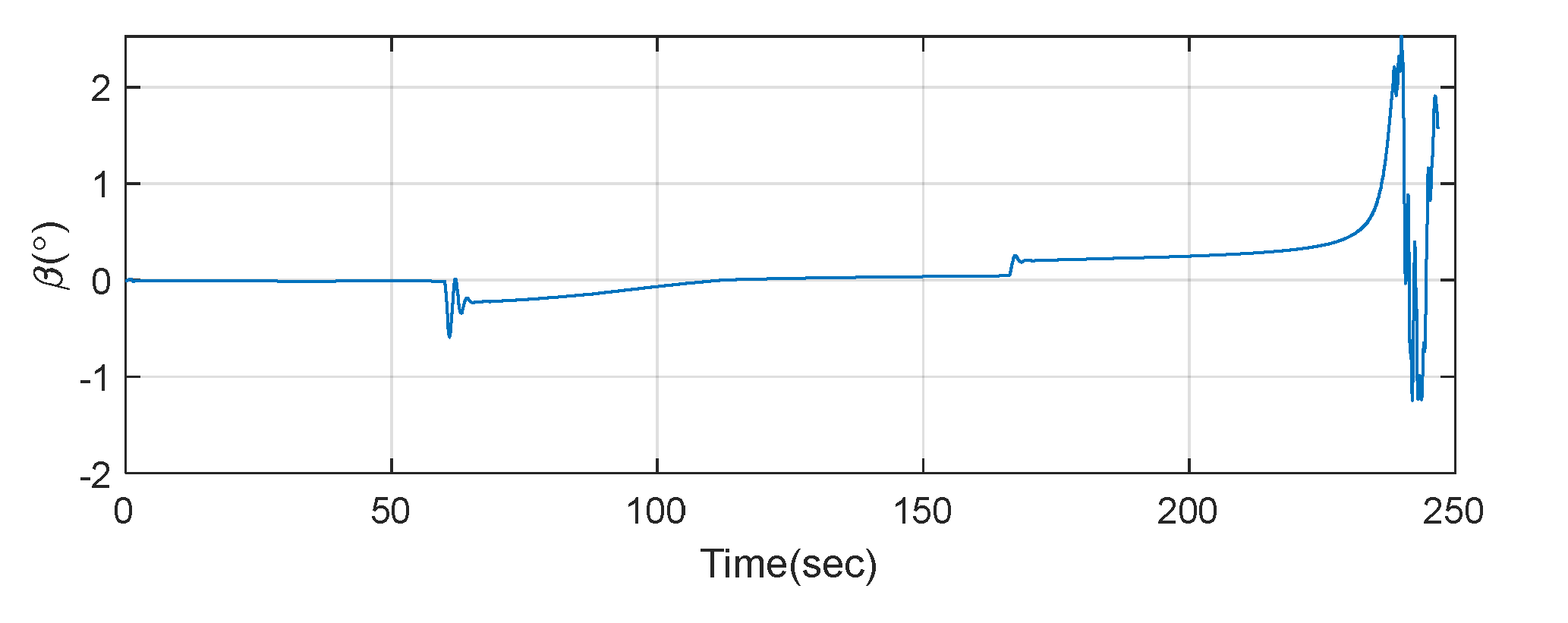
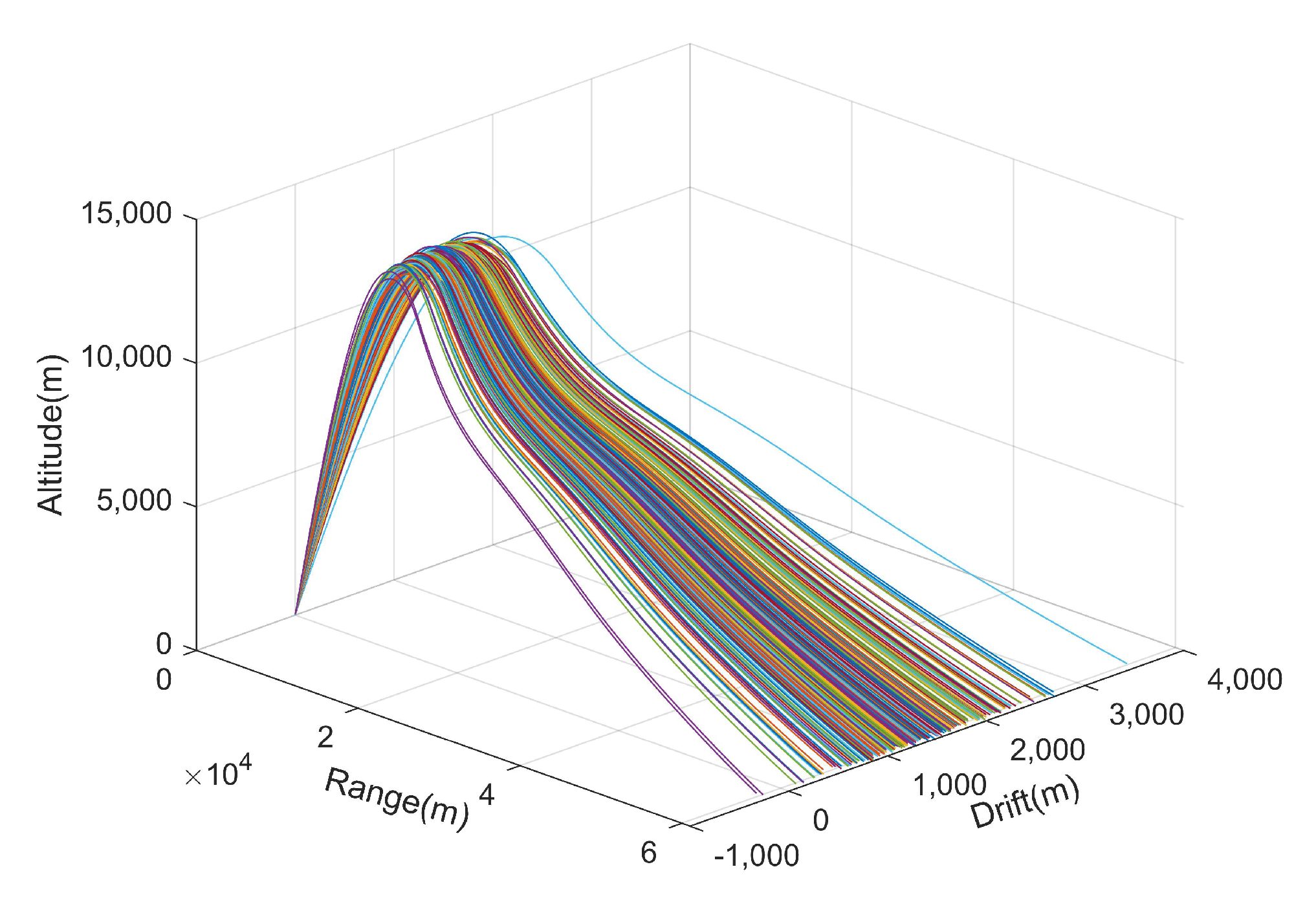
4.1. Perturbation Analysis
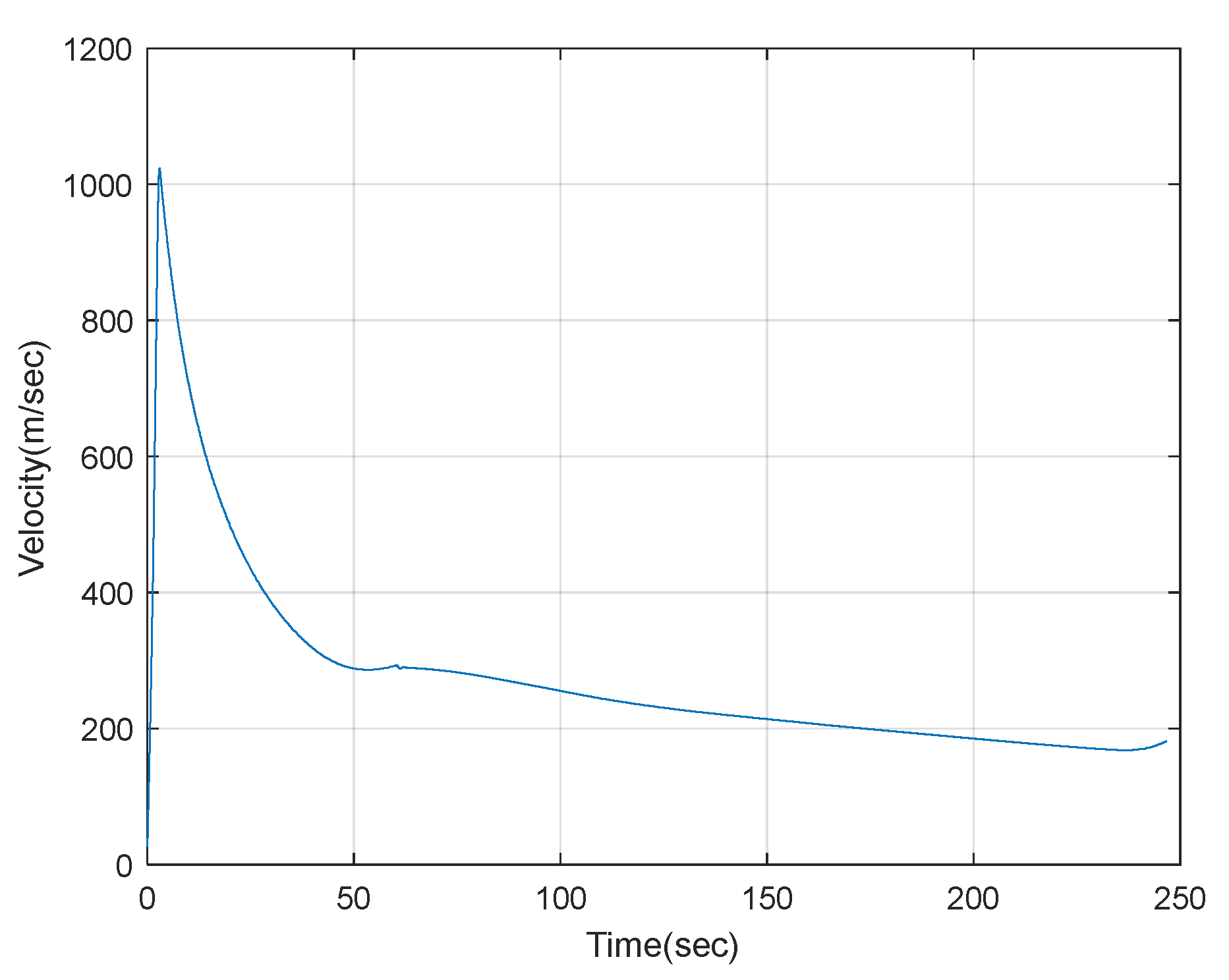
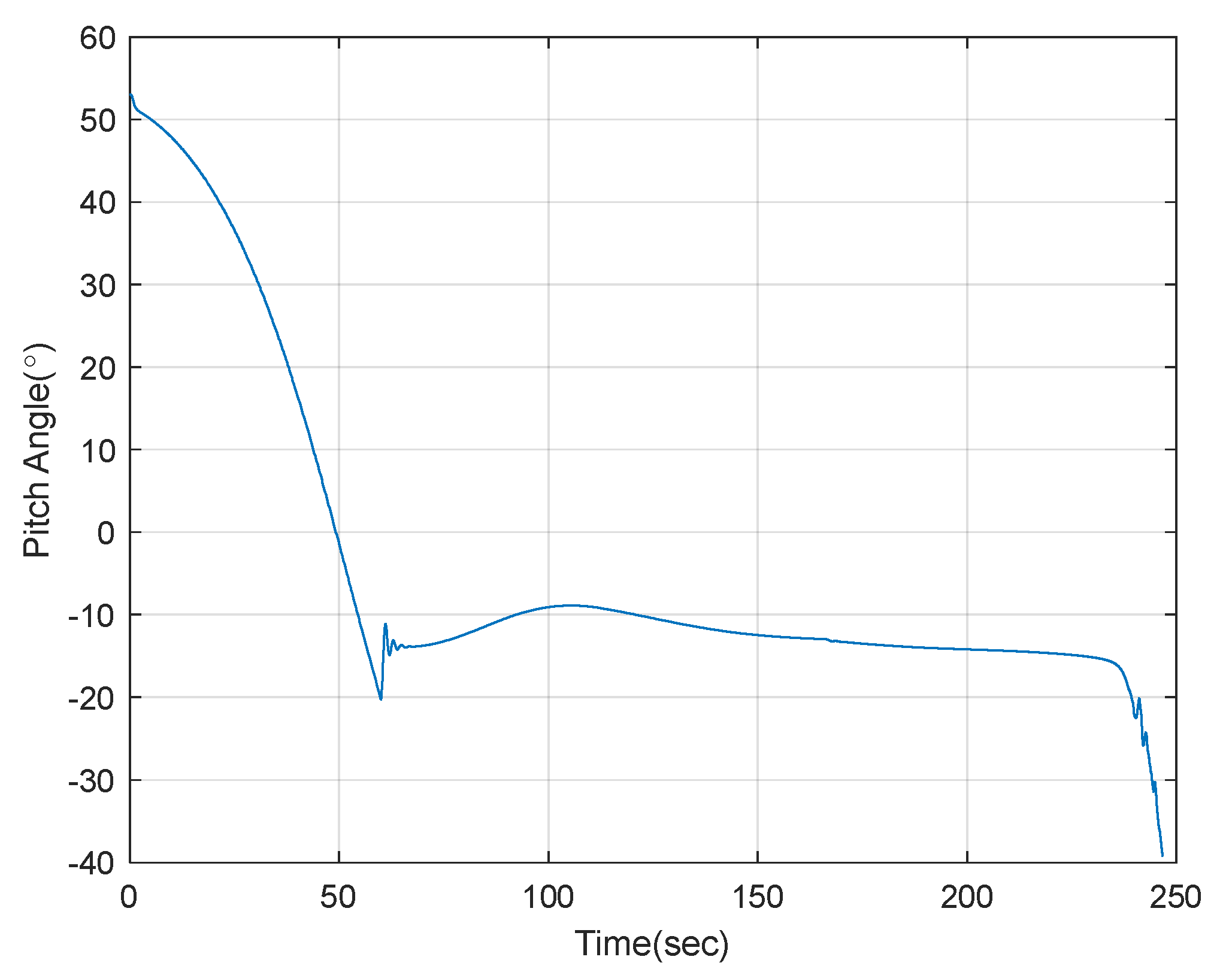
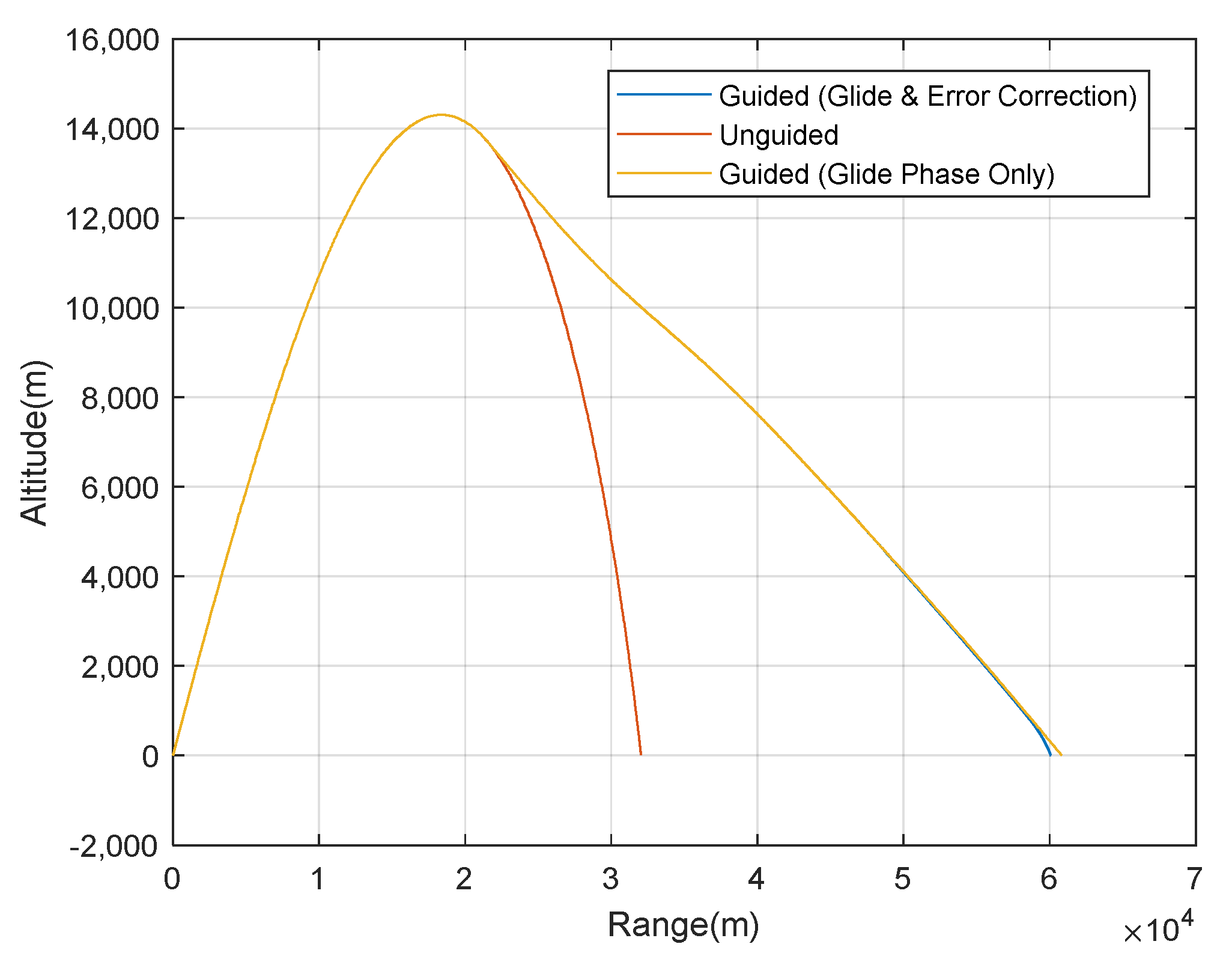
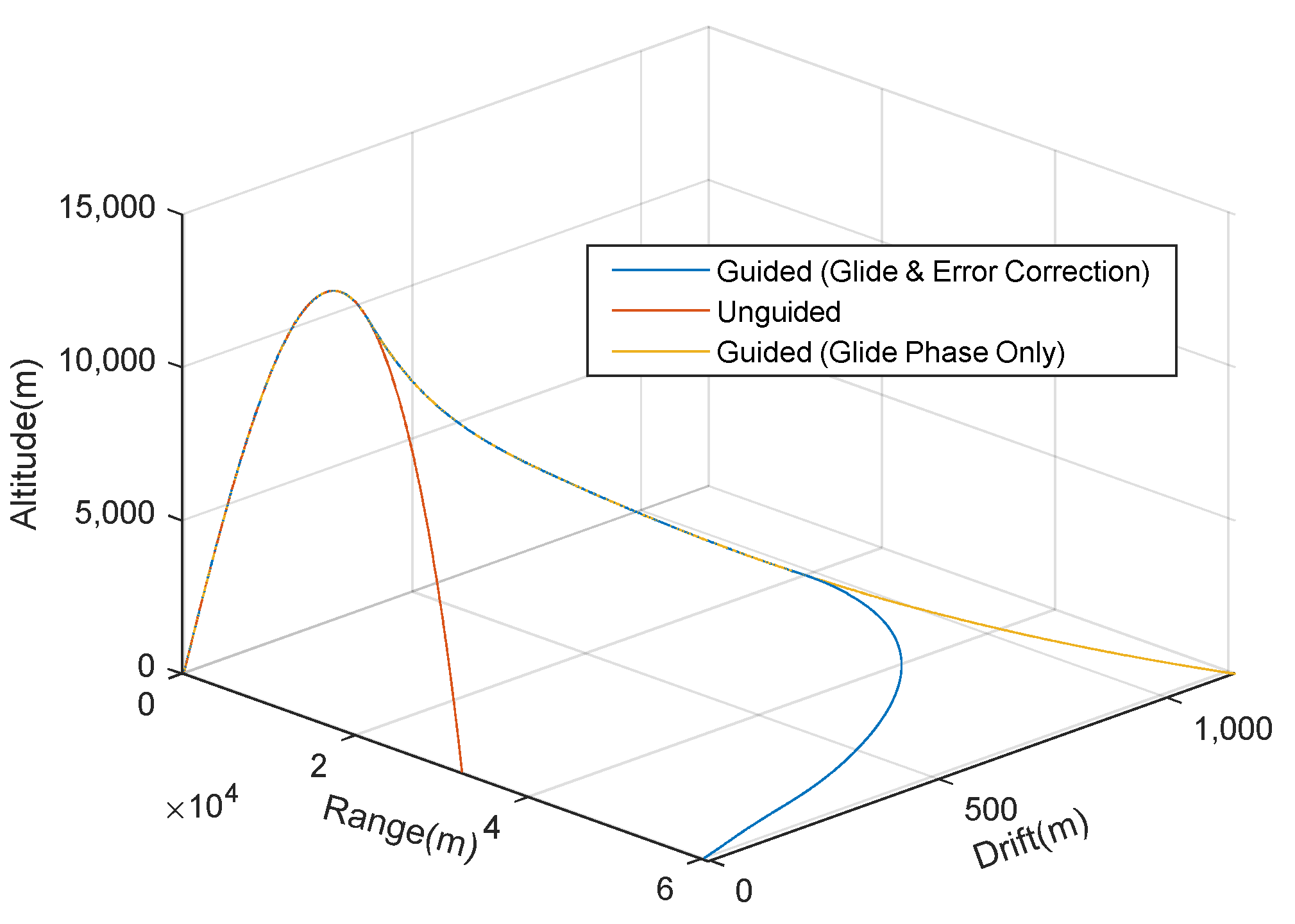
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Earth Frame | Rocket Aerodynamic Force Coefficients in Velocity Frame | ||
| Body Fixed Plane (BFP) Frame | Canard Fuze Aerodynamic Force Coefficients in Velocity Frame | ||
| Canard Frame | Rocket Aerodynamic Moment Coefficients in BFP Frame | ||
| Velocity Frame | Canard Fuze Aerodynamic Moment Coefficients in BFP Frame | ||
| Rocket Velocity in BFP Frame | Zero Drag, Spin, Spin-Damping, Side Force, Normal, and Pitch Damping Coefficients | ||
| Wind Velocities in BFP Frame | Air Density, Characteristic Length, Gravitational Constant, Thrust, Mass | ||
| Rocket Angular Rates in BFP Frame | Dynamic Pressure, Reference Area, Characteristic Length of Projectile | ||
| Quaternion Elements | Distance between Center of Mass and Magnus Center of Pressure | ||
| Euler Role, Pitch, and Yaw Angles | Distance between Center of Mass and Center of Pressure | ||
| Aero-ballistic Angle of Attack and Sideslip | Transformation Matrix from Canard to BFP Frame | ||
| Control Angle input, Orientation of Fuze, and Angular Velocity of Fuze | Transformation Matrix from Velocity to BFP Frame | ||
| Inertia Matrix, Rolling Inertia, Pitch Inertia | Transformation Matrix from Velocity to Canard Frame | ||
| Sum of All forces in BFP Frame | Sum of All Moments in BFP Frame | ||
| Mass of projectile, acceleration due to gravity | Total Velocity along the Trajectory | ||
| Rocket Motor Thrust | Trigonometric Ratio of Subscript Angle |
References
- Rogers, J.; Costello, M. Design of a Roll-Stabilized Mortar Projectile with Reciprocating Canards. J. Guid. Control. Dyn. 2010, 33, 1026–1034. [Google Scholar] [CrossRef]
- Chang, S.; Wang, Z.; Liu, T. Analysis of Spin-Rate Property for Dual-Spin-Stabilized Projectiles with Canards. J. Spacecr. Rockets 2014, 51, 958–966. [Google Scholar] [CrossRef]
- Cooper, G.; Fresconi, F.; Costello, M. Flight Stability of an Asymmetric Projectile with Activating Canards. J. Spacecr. Rockets 2012, 49, 130–135. [Google Scholar] [CrossRef]
- Spagni, J.; Theodoulis, S.; Wernert, P. Flight control for a class of 155 mm spin-stabilized projectile with reciprocating canards. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 1–10. [Google Scholar]
- Theodoulis, S.; Gassmann, V.; Wernert, P.; Dritsas, L.; Kitsios, I.; Tzes, A. Guidance and Control Design for a Class of Spin-Stabilized Fin-Controlled Projectiles. J. Guid. Control Dyn. 2013, 36, 517–531. [Google Scholar] [CrossRef]
- Elsaadany, A.; Wen-Jun, Y. Accuracy improvement capability of advanced projectile based on course correction fuze concept. Sci. World J. 2014, 2014, 273450. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, E.; Lauzon, M. Course Correction Fuze Concept Analysis for In-Service 155 mm Spin-Stabilized Gunnery Projectiles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 1–21. [Google Scholar]
- Theodoulis, S.; Sève, F.; Wernert, P. Robust gain-scheduled autopilot design for spin-stabilized projectiles with a course-correction fuze. Aerosp. Sci. Technol. 2015, 42, 477–489. [Google Scholar] [CrossRef]
- Clancy, J.A.; Bybee, T.D.; Friedrich, W.A. Fixed Canard 2-D Guidance of Artillery Projectiles. Patent 6,981,672, 3 January 2006. [Google Scholar]
- Gao, M.; Zhang, Y.; Yang, S. Firing control optimization of impulse thrusters for trajectory correction projectiles. Int. J. Aerosp. Eng. 2015, 2015, 781472. [Google Scholar] [CrossRef]
- Jacewicz, M.; Glebocki, R.; Ozog, R. Monte-Carlo Based Lateral Thruster Parameters Optimization for 122 mm Rocket. In Automation 2020: Towards Industry of the Future; Springer: Cham, Switzerland, 2020; pp. 125–134. [Google Scholar]
- Yang, S. Impact-Point-Based Guidance of a Spinning Artillery Rocket Using Canard Cyclic Control. J. Guid. Control Dyn. 2020, 43, 1975–1982. [Google Scholar] [CrossRef]
- Mingireanu, F. Trajectory Modeling of GRAD Rocket with Low—Cost Terminal Guidance Upgrade Coupled to Range Increase Through Step—Like Thrust—Curves. In Proceedings of the 15th International Conference on Aerospace Sciences & Aviation Technology, Cairo, Egypt, 28–30 May 2013; pp. 1–12. [Google Scholar]
- Costello, M. Extended Range of a Gun Launched Smart Projectile Using Controllable Canards. Shock Vib. 2001, 8, 203–213. [Google Scholar] [CrossRef]
- Costello, M.F. Potential Field Artillery Projectile Improvement Using Movable Canards; ARL-TR-1344 Report; US Army Research Laboratory: Aberdeen, MD, USA, 1997; 52p. [Google Scholar]
- Bybee, T. Precision Guidance Kit XM1156. In Proceedings of the 45th Annual NDIA Gun and Missile Systems Conference, Dallas, TX, USA, 17–20 May 2010; Volume 4. [Google Scholar]
- Liu, X.; Li, D.; Shen, Q. Swerving Orientation of Spin-Stabilized Projectile for Fixed-Cant Canard Control Input. Math. Probl. Eng. 2015, 2015, 173571. [Google Scholar] [CrossRef]
- Yin, T.; Jia, F.; Yu, J. Research on Roll Control System for Fixed Canard Rudder of the Dual-Spin Trajectory Correction Projectile. Wirel. Pers. Commun. 2018, 103, 83–98. [Google Scholar] [CrossRef]
- Cheng, J.; Shen, Q.; Deng, Z.; Deng, Z. Novel aiming method for spin-stabilized projectiles with a course correction fuze actuated by fixed canards. Electronics 2019, 8, 1135. [Google Scholar] [CrossRef]
- Zhu, D.; Tang, S.; Guo, J.; Chen, R. Flight stability of a dual-spin projectile with canards. Proc. Inst. Mech. Eng. Part. G J. Aerosp. Eng. 2015, 229, 703–716. [Google Scholar] [CrossRef]
- Fresconi, F.; Ilg, M. Model predictive control of agile projectiles. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; pp. 1–17. [Google Scholar]
- Letniak, R.; Costello, M. A Nonlinear Model Predictive Observer for Smart Projectile Applications. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; Volume 2, pp. 830–850. [Google Scholar]
- Slegers, N. Predictive Control of a Munition Using Low-Speed Linear Theory. J. Guid. Control Dyn. 2008, 31, 768–775. [Google Scholar] [CrossRef]
- Calise, A. An analysis of aerodynamic control for direct fire spinning projectiles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Calise, A.J.; El-Shirbiny, H.A.; Kim, N.; Kutay, A.T. An adaptive guidance approach for spinning projectiles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 3226–3238. [Google Scholar] [CrossRef]
- Fresconi, F. Guidance and Control of a Projectile with Reduced Sensor and Actuator Requirements. J. Guid. Control Dyn. 2011, 34, 1757–1766. [Google Scholar] [CrossRef]
- Fresconi, F.; Cooper, G.; Costello, M. Practical Assessment of Real-Time Impact Point Estimators for Smart Weapons. J. Aerosp. Eng. 2011, 24, 1–11. [Google Scholar] [CrossRef][Green Version]
- ZHANG, X.; YAO, X.; ZHENG, Q. Impact point prediction guidance based on iterative process for dual-spin projectile with fixed canards. Chin. J. Aeronaut. 2019, 32, 1967–1981. [Google Scholar] [CrossRef]
- Hainz, L.C.; Costello, M. Modified Projectile Linear Theory for Rapid Trajectory Prediction. J. Guid. Control Dyn. 2005, 28, 1006–1014. [Google Scholar] [CrossRef]
- Wernert, P.; Leopold, F.; Lehmann, L.; Baer, K.; Reindler, A.; Bidino, D.; Juncker, J. Wind Tunnel Tests and Open-Loop Trajectory Simulations for a 155 mm Canards Guided Spin Stabilized Projectile. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008; pp. 1–18. [Google Scholar]
- Zipfel, P.H. Modeling and Simulation of Aerospace Vehicle Dynamics, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007; ISBN 978-1-56347-875-8. [Google Scholar]
- Dupuis, A.; Berner, C. Wind tunnel tests of a long range artillery shell concept. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar] [CrossRef]
- Li, J.M.; He, G.L.; Guo, H.Y. A Study on the Aerodynamic Characteristics for a Two-Dimensional Trajectory Correction Fuze. Appl. Mech. Mater. 2014, 703, 370–375. [Google Scholar] [CrossRef]
- Tun, N.L.; Thuri, M.; Minnzinoo; Li, Z. Aerodynamic Coefficients Prediction for 122 mm Rocket by Using Computational Fluid Dynamics. IOP Conf. Ser. Mater. Sci. Eng. 2020, 816, 012010. [Google Scholar] [CrossRef]
- Khalil, M.; Abdalla, H.; Kamal, O. Trajectory prediction for a typical fin stabilized artillery rocket. In Proceedings of the Aerospace Sciences & Aviation Technology, Cairo, Egypt, 26–28 May 2009. [Google Scholar] [CrossRef]
- Fresconi, F.; Plostins, P. Control mechanism strategies for spin-stabilized projectiles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 979–991. [Google Scholar] [CrossRef]
- Hainz, L.; Costello, M. In flight projectile impact point prediction. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; Volume 1, pp. 87–127. [Google Scholar]
- Wang, Z.; Chang, S.-J. Impact Point Prediction and Analysis of Lateral Correction Analysis of Two-Dimensional Trajectory Correction Projectiles. Def. Technol. 2013, 9, 48–52. [Google Scholar] [CrossRef]
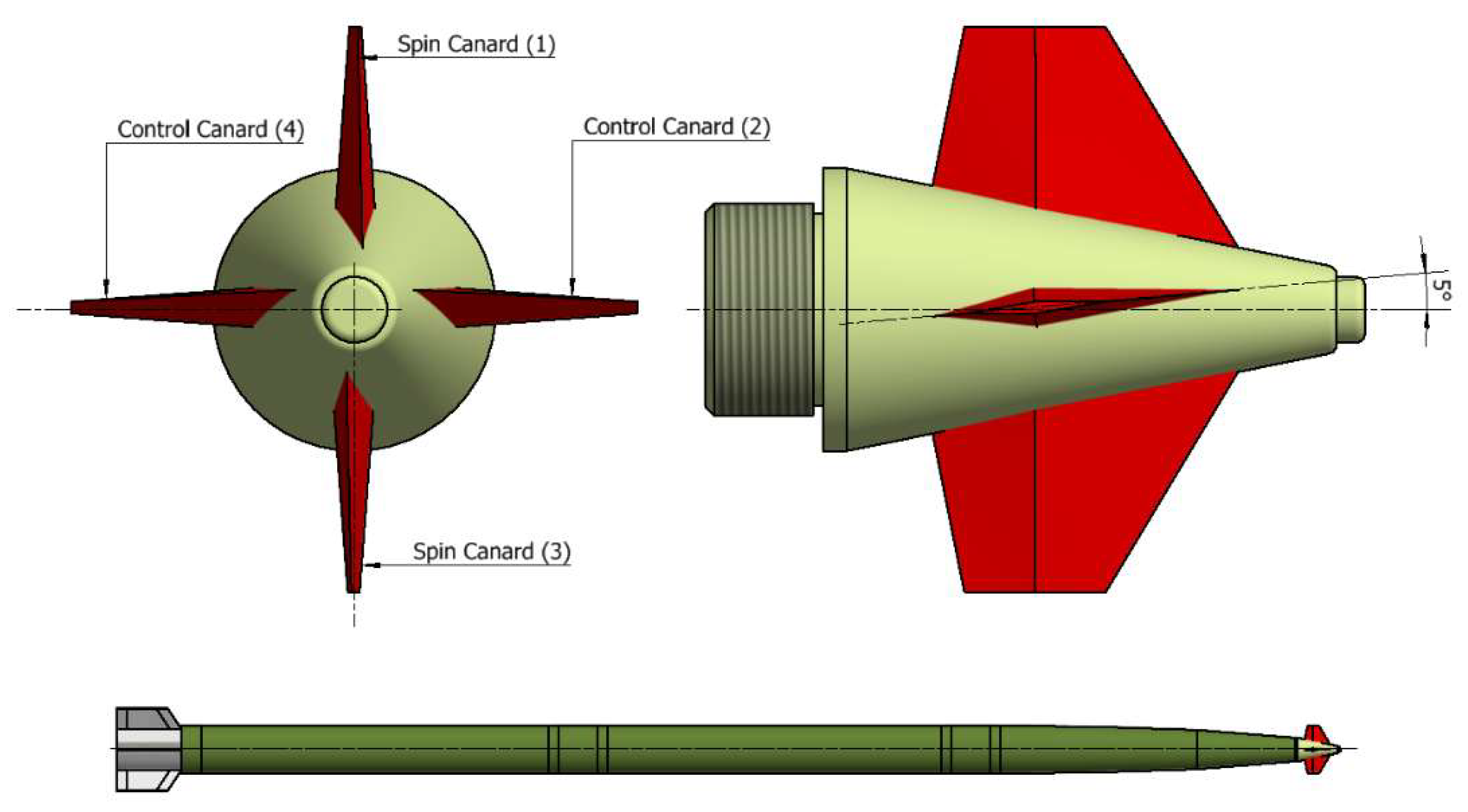
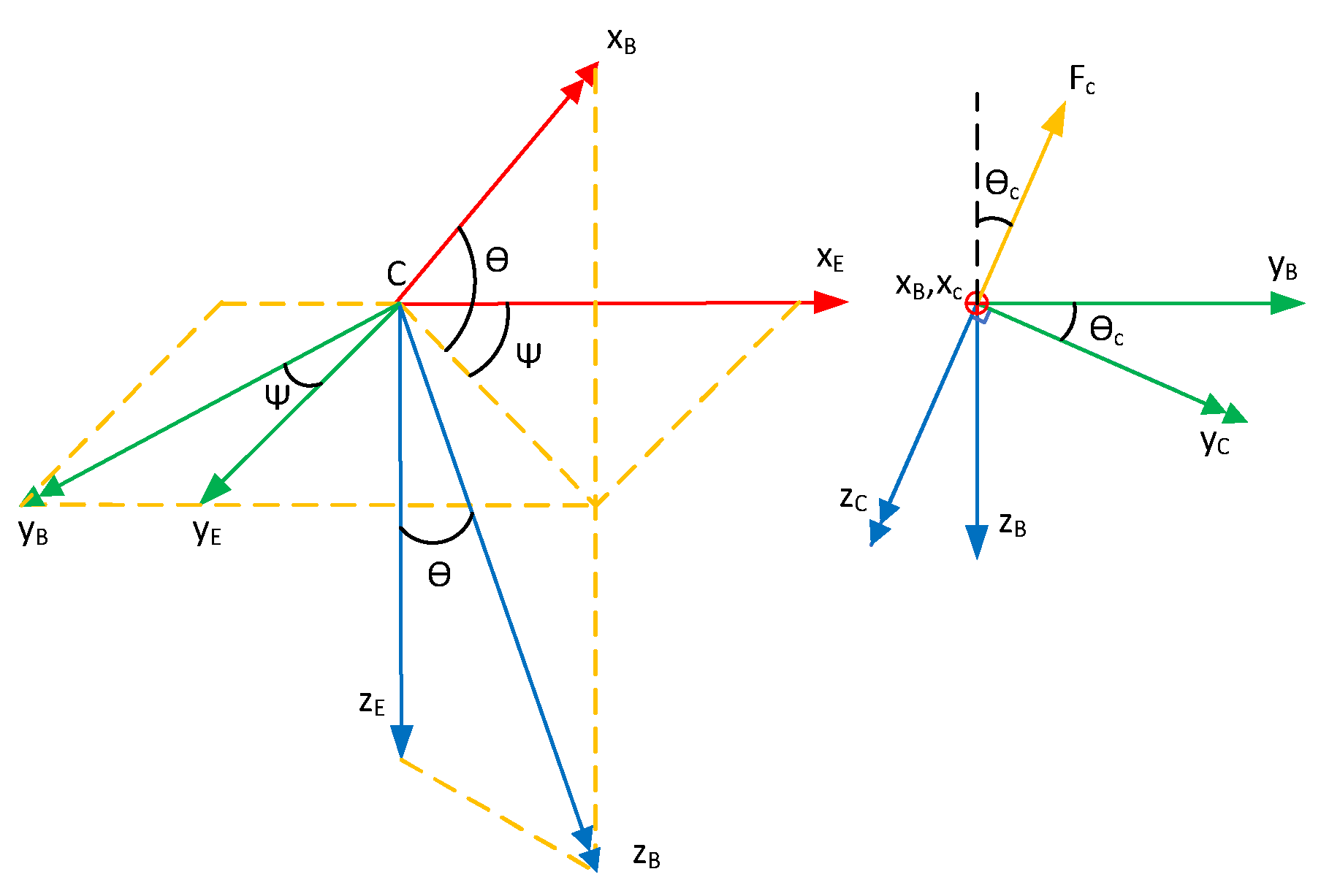
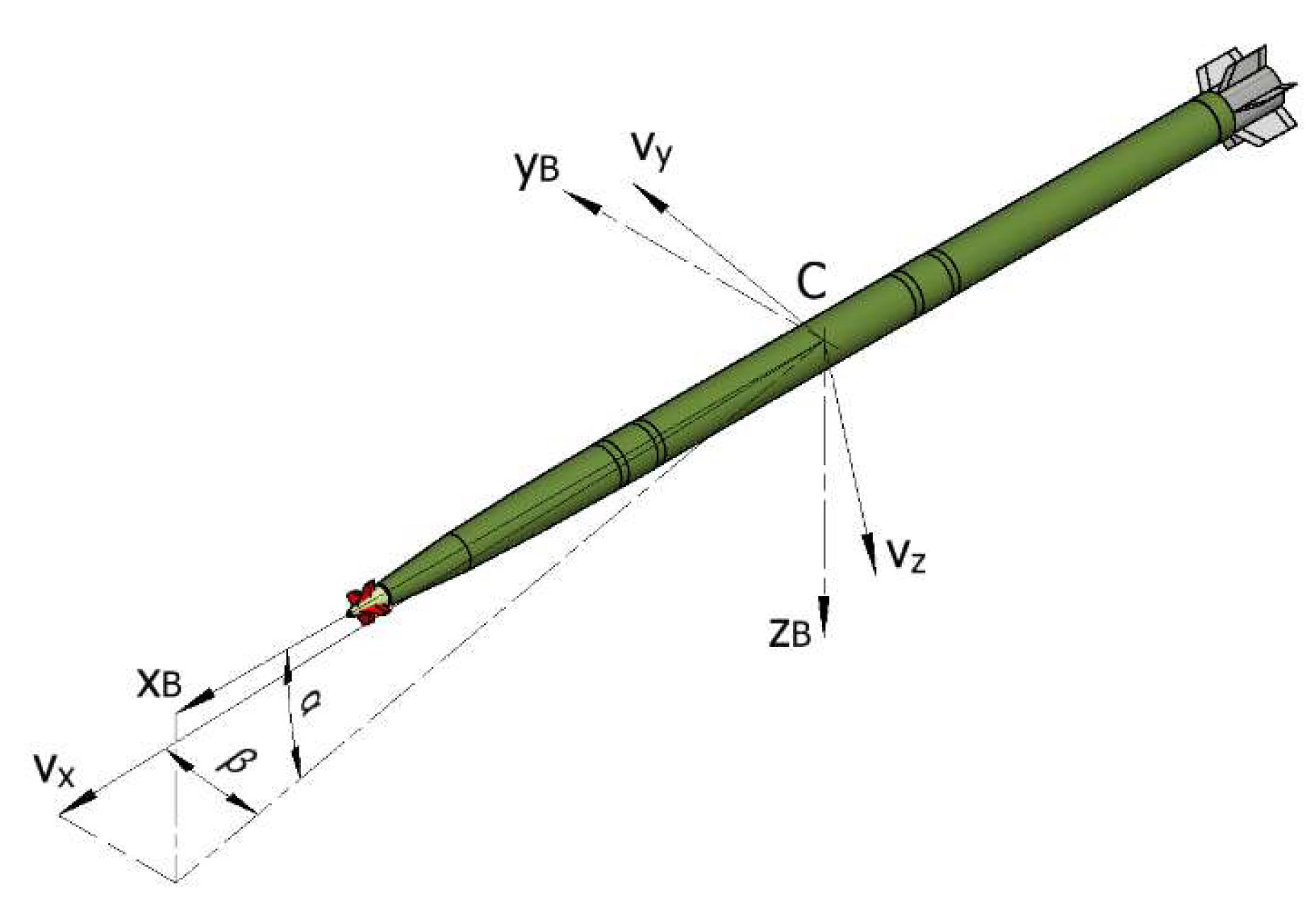

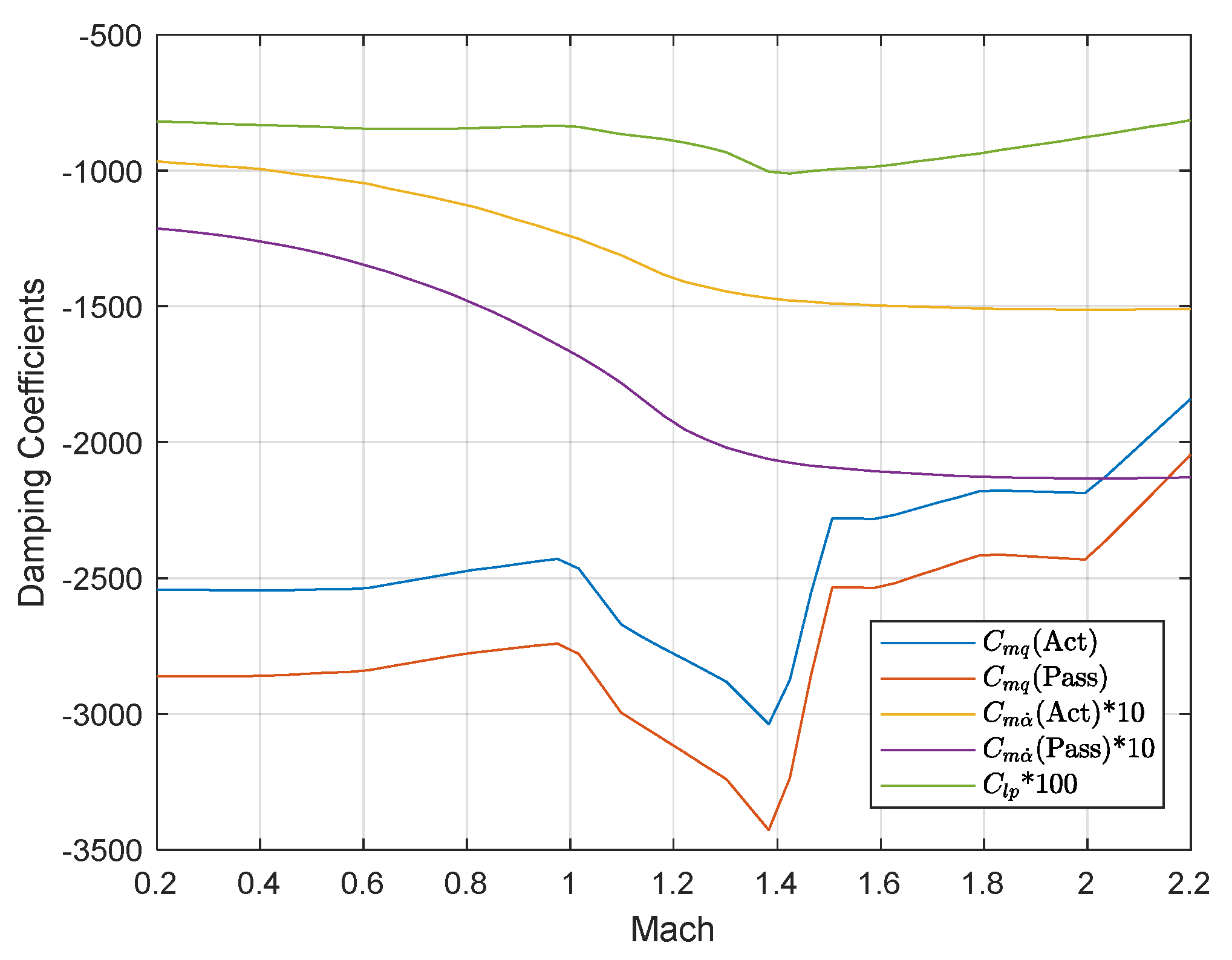






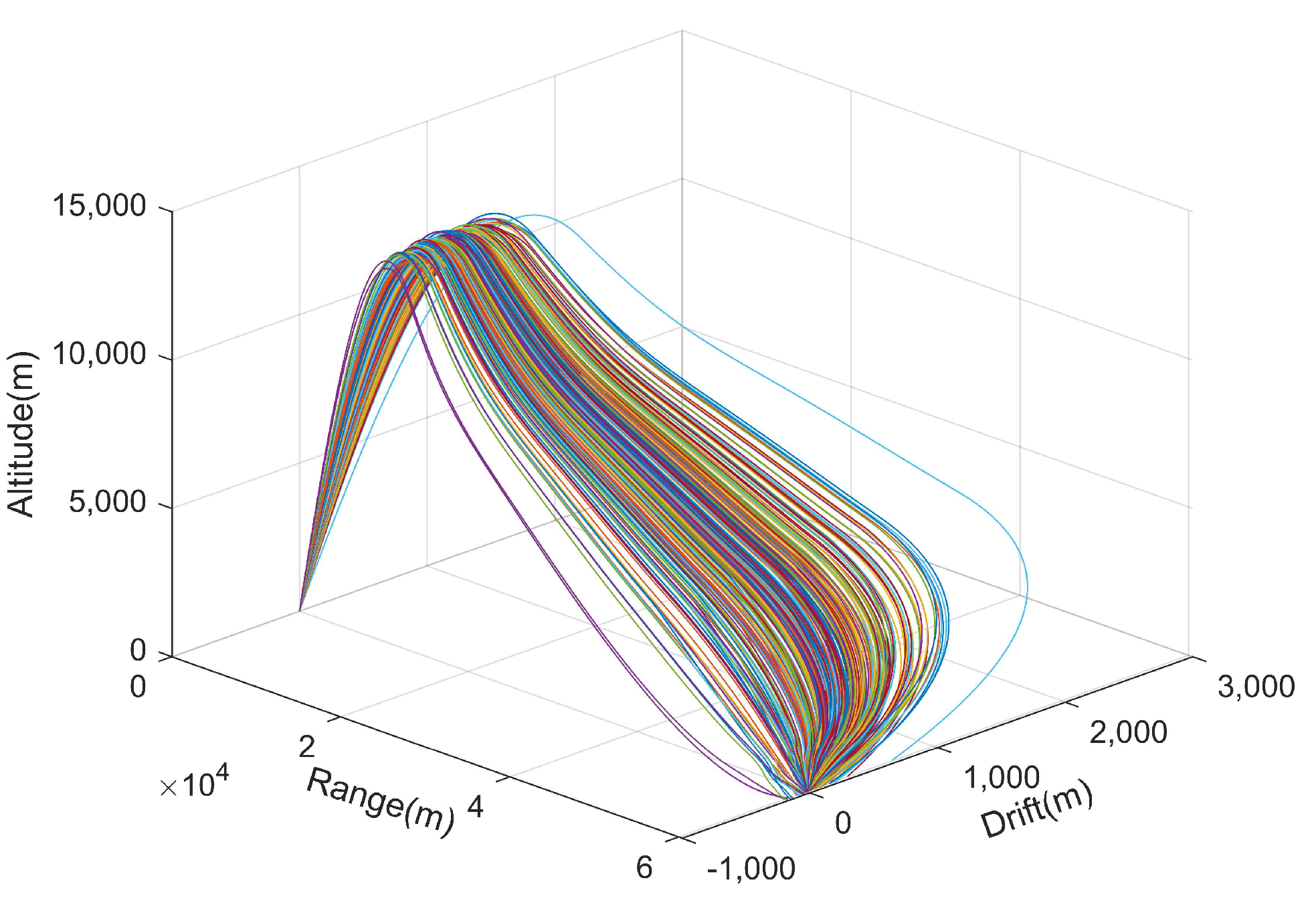

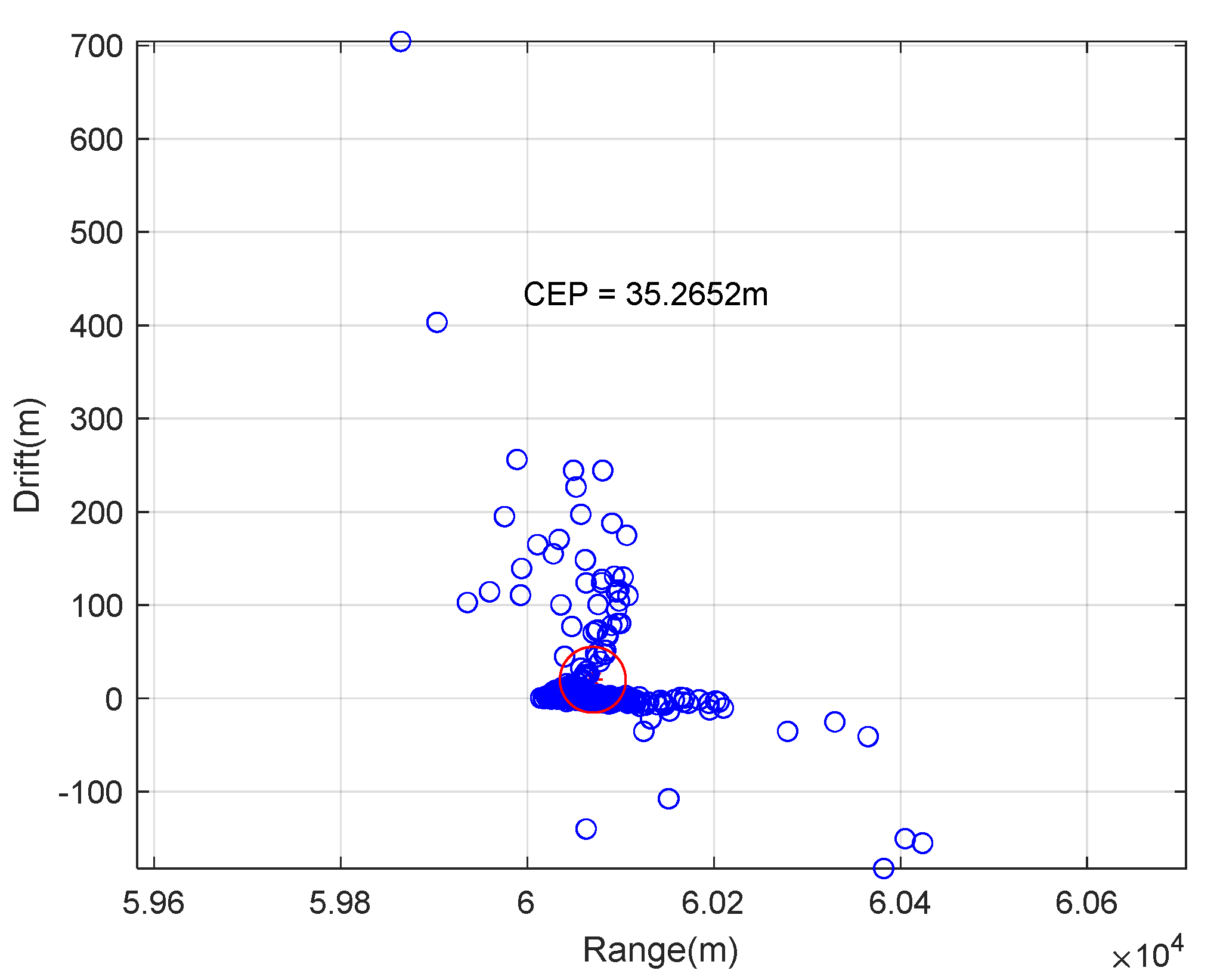

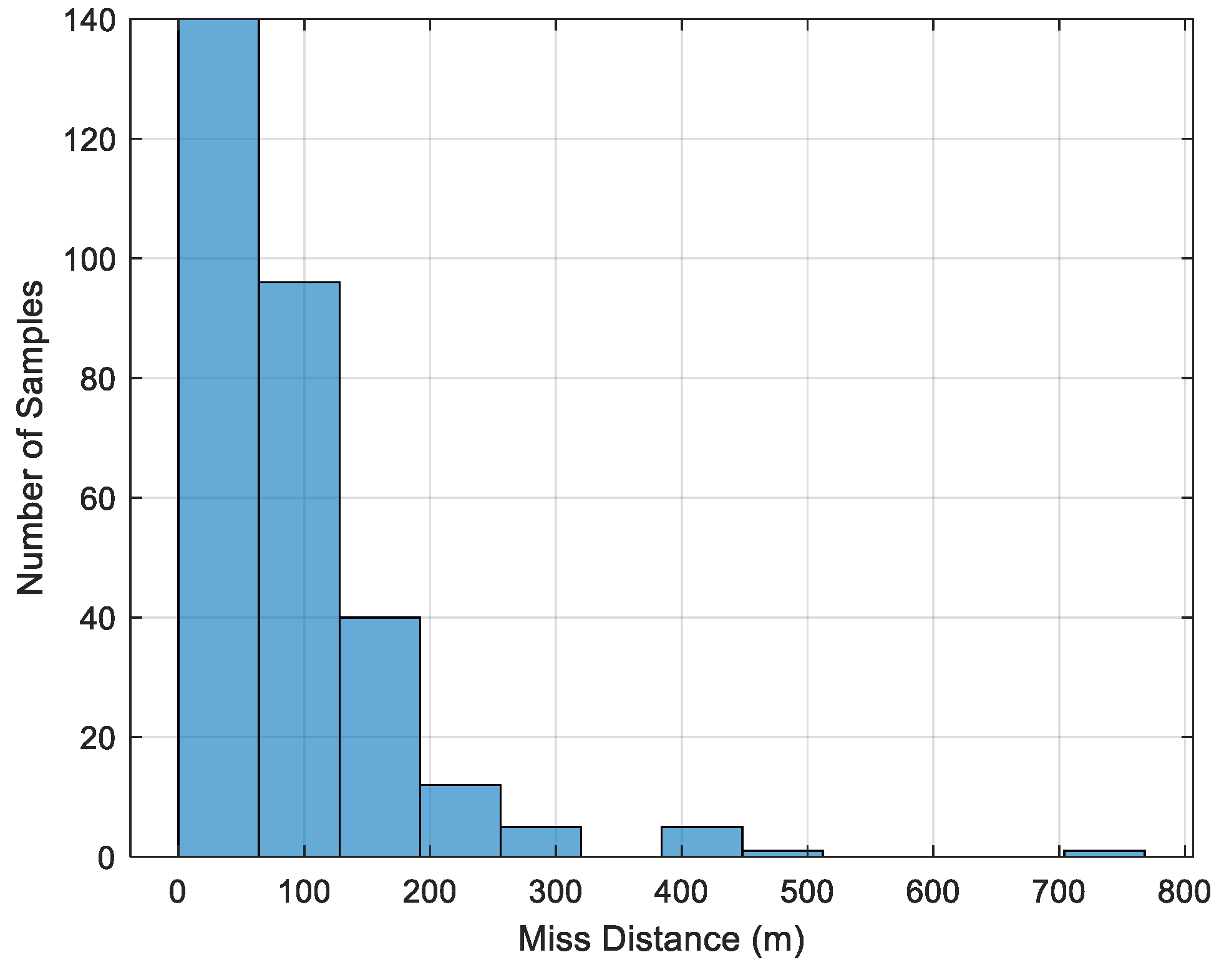
| Sr. | Parameter | Nominal Values | Std Deviation | Minimum Value | Maximum Value |
|---|---|---|---|---|---|
| a. | Initial Mass | 67.43 (Kg) | 0.1 | 67.12 | 67.78 |
| b. | Final Mass | 43.63 (Kg) | 0.1 | 43.38 | 43.90 |
| c. | Iyy Final | 85.3 (Kg.m2) | 0.5 | 84.08 | 86.66 |
| d. | Ixx Final | 85.3 (Kg.m2) | 0.005 | 0.08 | 0.11 |
| e. | Elevation Angle | 53 (deg) | 0.1 | 52.67 | 53.27 |
| f. | Azimuth Angle | 0 (deg) | 0.15 | −0.38 | 0.52 |
| g. | Roll Rate | 125.66 (rad/s) | 0.02 | 125.60 | 125.72 |
| h. | Pitch Rate | 0 | 0.02 | −0.05 | 0.05 |
| i. | Yaw Rate | 0 | 0.02 | −0.05 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Wang, H. Range and Accuracy Improvement of Artillery Rocket Using Fixed Canards Trajectory Correction Fuze. Aerospace 2022, 9, 32. https://doi.org/10.3390/aerospace9010032
Raza A, Wang H. Range and Accuracy Improvement of Artillery Rocket Using Fixed Canards Trajectory Correction Fuze. Aerospace. 2022; 9(1):32. https://doi.org/10.3390/aerospace9010032
Chicago/Turabian StyleRaza, Ali, and Hua Wang. 2022. "Range and Accuracy Improvement of Artillery Rocket Using Fixed Canards Trajectory Correction Fuze" Aerospace 9, no. 1: 32. https://doi.org/10.3390/aerospace9010032
APA StyleRaza, A., & Wang, H. (2022). Range and Accuracy Improvement of Artillery Rocket Using Fixed Canards Trajectory Correction Fuze. Aerospace, 9(1), 32. https://doi.org/10.3390/aerospace9010032






