Characterisation and Design of Direct Numerical Simulations of Turbulent Statistically Planar Flames
Abstract
:1. Introduction
2. Theoretical Background
2.1. Laminar Flame Theory
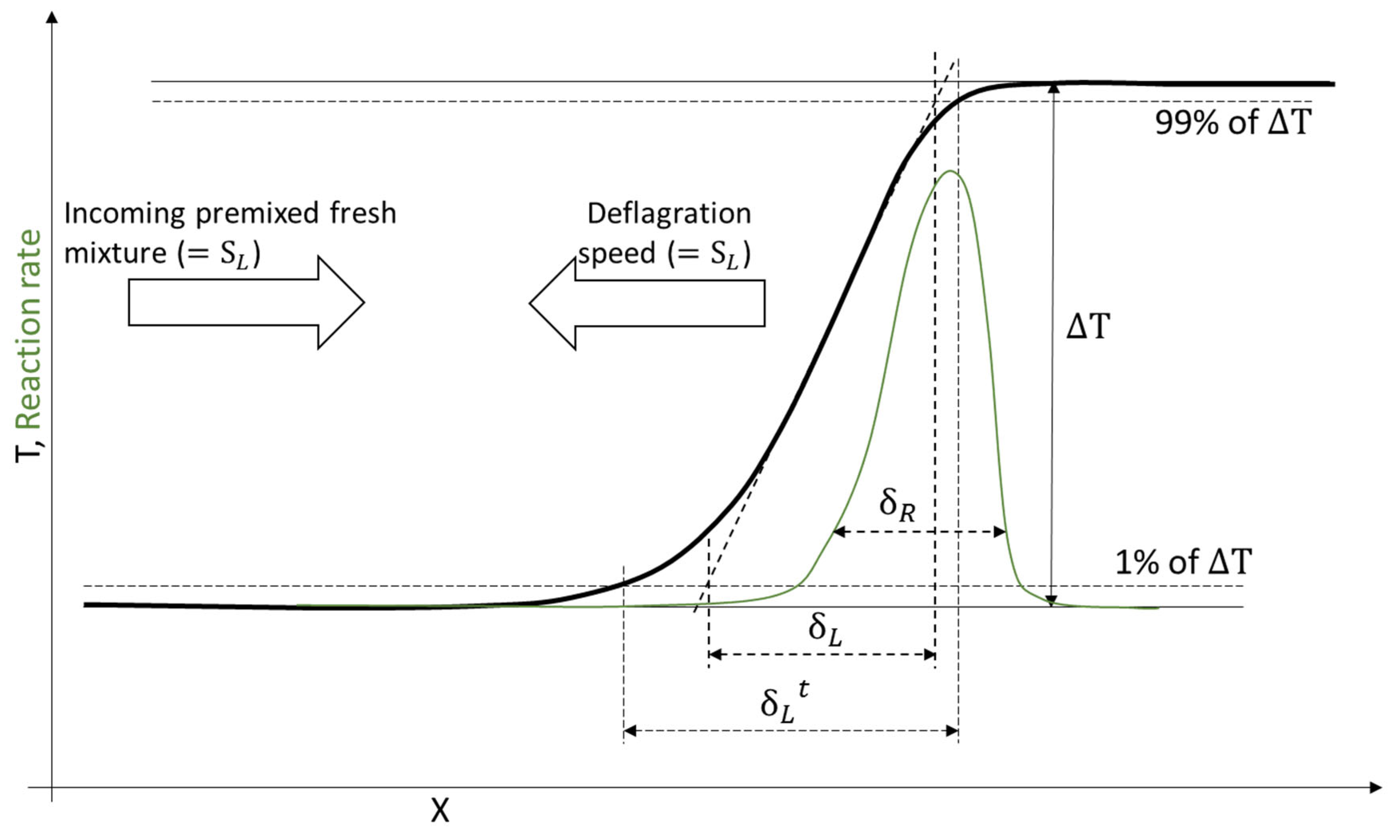
2.2. Turbulent Flame Theory
- For the function behind in Equation (13), it is sufficient to rearrange Equation (3).
- The function for is the result of Equation (8) being plugged into Equation (10), leading to . That expression can be rearranged to create Equation (14).
- The function for is derived from Equation (4), where statements from Equations (11) and (6) are plugged, in leading to . Here, Equation (10) and then Equation (8) can be plugged in, resulting in . A simple rearrangement leads to Equation (15).
- For the derivation of , Equation (5) is combined with Equation (6) to create ()/(). Here, the statement from Equation (10) is plugged in, leading to . The insertion of Equation (8) results in Now, Equation (16) can be inferred.
2.3. Simulative Setup
3. Results and Discussion
3.1. Mathematical Relations of Design Parameters
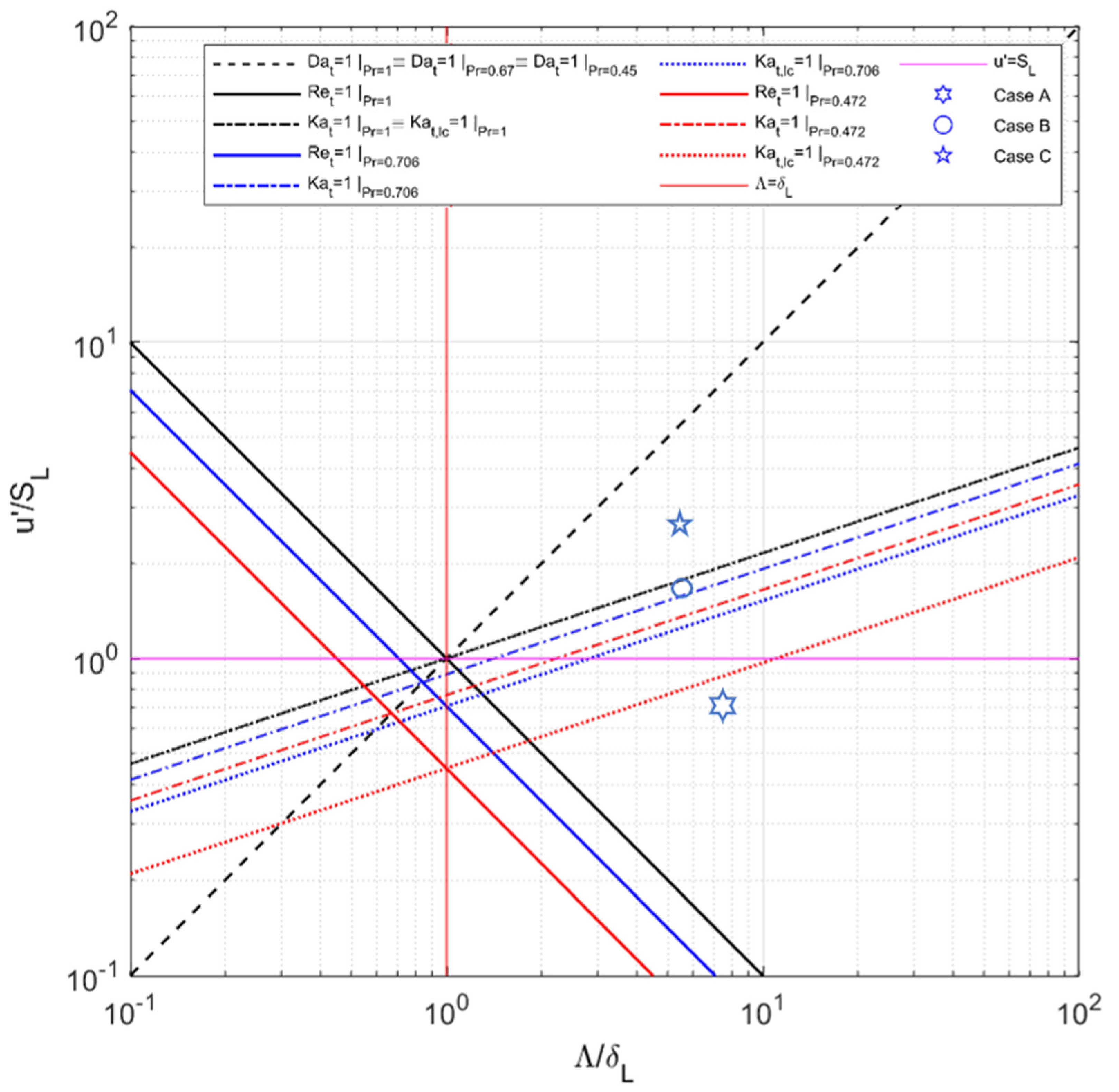
3.2. Trade-Off of Design Parameters
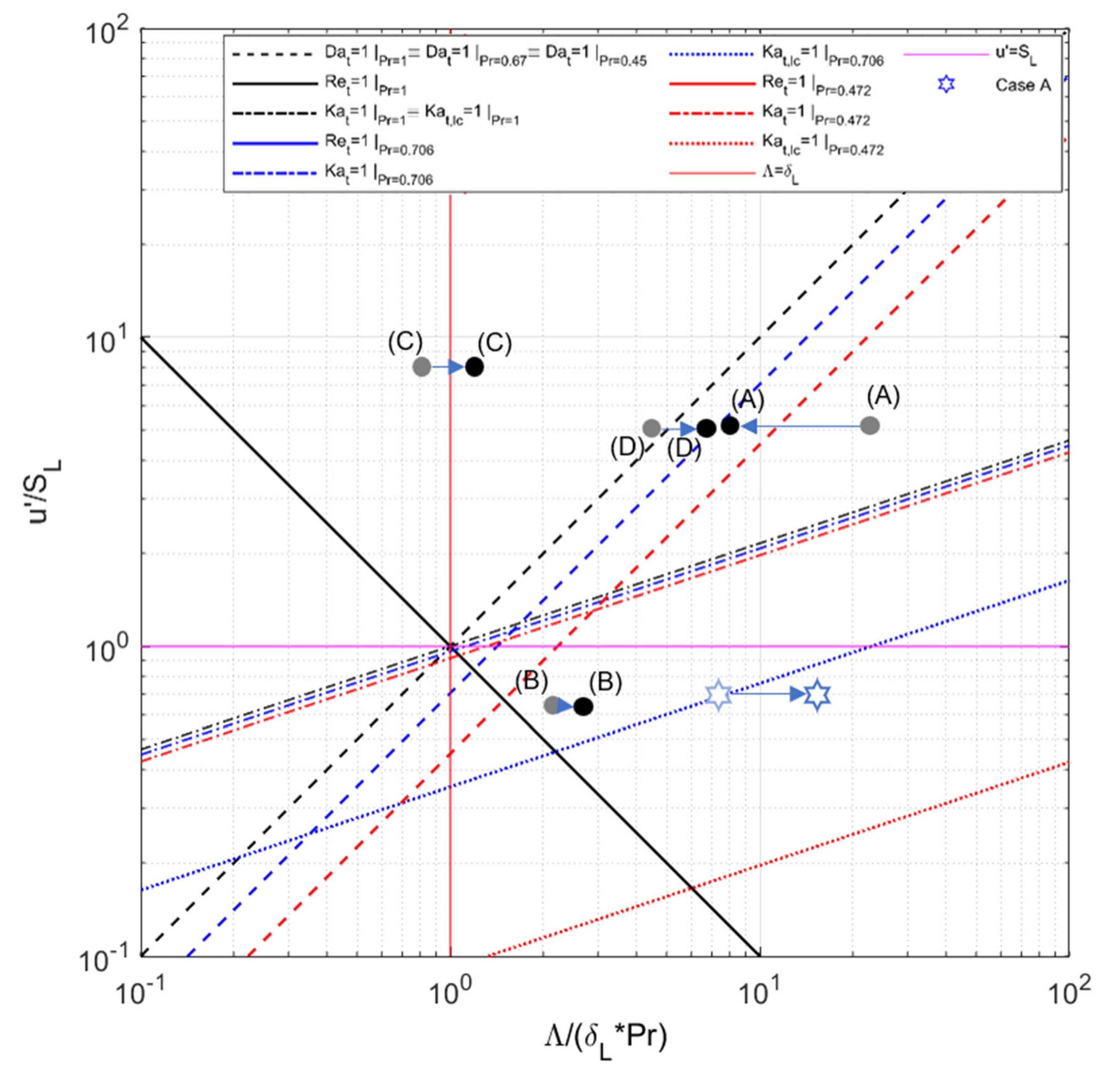
3.3. Definition of a Representative Point for Characteristic Flame Properties
3.4. Adaption of the Regime Diagram
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin: | |
| Heat capacity at constant pressure | |
| Damköhler number | |
| Karlovitz number | |
| Turbulent kinetic energy | |
| Molecular Prandtl number | |
| Pressure | |
| Reynolds number | |
| Flame front propagation velocity | |
| Temperature | |
| Time | |
| Velocity | |
| Turbulent fluctuations | |
| X | Molar Fraction |
| Indices | |
| Average between reactants and products | |
| Burned | |
| Chemical | |
| char | Characteristic |
| Initial | |
| Laminar | |
| Length-scale | |
| max | Maximum |
| Turbulence | |
| Unburned | |
| Based on the characteristic length of eddies | |
| Based on the Kolmogorov scale | |
| s | Species index |
| Greek: | |
| Thermal diffusivity | |
| Empirical constant for the Karman spectrum. Usually, it equals 2.7. | |
| Flame front thickness | |
| Flame front thickness based on the turbulence | |
| Flame front thickness based on the reaction zone | |
| Dissipation | |
| Kolmogorov scale | |
| Domain size divided by characteristic length of eddies | |
| Wave number (=1/wave length) | |
| Characteristic length of eddies | |
| Heat conductivity | |
| Molecular viscosity | |
| Density | |
| Time scale | |
| Aspect ratio | |
| ϕ | Equivalence ratio |
| Flame front resolution | |
| Mesh size (=number of cells) | |
| Abbreviations: | |
| DNS | Direct numerical simulation |
| HIT | Homogeneous isotropic turbulence |
| TCI | Turbulence–chemistry interaction |
| ML | Machine learning |
| TKE | Turbulent kinetic energy |
| RAM | Random-access memory |
References
- Chakraborty, N.; Katragadda, M.; Cant, R.S. Statistics and Modelling of Turbulent Kinetic Energy Transport in Different Regimes of Premixed Combustion. Flow Turbul. Combust. 2011, 87, 205–235. [Google Scholar] [CrossRef]
- Cao, Y.; Daskin, A.; Frankel, S.; Kais, S. Quantum Circuit Design for Solving Linear Systems of Equations. Mol. Phys. 2012, 110, 1675–1680. [Google Scholar] [CrossRef]
- Kassem, H.I.; Saqr, K.M.; Aly, H.S.; Sies, M.M.; Wahid, M.A. Implementation of the eddy dissipation model of turbulent non-premixed combustion in OpenFOAM. Int. Commun. Heat Mass Transf. 2011, 38, 363–367. [Google Scholar] [CrossRef]
- Lewandowski, M.; Pozorski, J. Assessment of turbulence-chemistry interaction models in the computation of turbulent non-premixed flames. J. Phys. Conf. Ser. 2016, 760, 012015. [Google Scholar] [CrossRef]
- Ertesvåg, I. Analysis of Some Recently Proposed Modifications to the Eddy Dissipation Concept (EDC). Mol. Phys. 2019, 192, 1108–1136. [Google Scholar] [CrossRef]
- Arndt, C.; Meier, W. Influence of Boundary Conditions on the Flame Stabilization Mechanism and on Transient Auto-Ignition in the DLR Jet-in-Hot-Coflow Burner. Flow Turbul. Combust. 2019, 102, 973–993. [Google Scholar] [CrossRef]
- Magnussen, B. On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow. In Proceedings of the 19th Aerospace Sciences Meeting, St. Louis, MO, USA, 12–15 January 1981. [Google Scholar] [CrossRef]
- Chakraborty, N. Influence of Thermal Expansion on Fluid Dynamics of Turbulent Premixed Combustion and Its Modelling Implications. Flow Turbul. Combust. 2021, 106, 753–848. [Google Scholar] [CrossRef]
- Towery, C.A.Z.; Poludenko, A.; Urzay, J.; O’Brien, J.; Ihme, M.; Hamlington, P.E. Spectral kinetic energy transfer in turbulent premixed reacting flows. Phys. Rev. 2016, 93, 053115. [Google Scholar] [CrossRef]
- Wang, Z.; Abraham, J. Effects of Karlovitz number on turbulent kinetic energy transport in turbulent lean premixed methane/air flames. Phys. Fluids 2017, 29, 085102. [Google Scholar] [CrossRef]
- Peters, N. Combustion Theory; CEFRC Summer School: Princeton, NJ, USA, 2010. [Google Scholar]
- Borghi, R.; Escudie, D. Assessment of a Theoretical Model of Turbulent Combustion by Comparison with a Simple Experiment. Combust. Flame 1984, 56, 149–164. [Google Scholar] [CrossRef]
- Peters, N. The turbulent burning velocity for large-scale and small-scale turbulence. J. Fluid Mech. 1999, 384, 107–132. [Google Scholar] [CrossRef]
- Libby, P.A.; Williams, F.A. Turbulent Reacting Flows; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; RT Edwards, Inc.: Morningside, Australia, 2001; ISBN 1-930217-10-2. [Google Scholar]
- Skiba, A.; Wabel, T.; Carter, C.; Hammack, S.; Temme, J.; Driscoll, J. Premixed flames subjected to extreme levels of turbulence part I: Flame structure and a new measured regime diagram. Combust. Flame 2017, 189, 407–432. [Google Scholar] [CrossRef]
- Drsicoll, J.; Chen, J.H.; Skiba, A.; Carter, C.D.; Hawkes, E.R.; Wang, H. Premixed Flames Subjected to Extreme Turbulence: Some Questions and Recent Answers. Prog. Energy Combust. Sci. 2020, 76, 100802. [Google Scholar] [CrossRef]
- Sabelnikov, V.; Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. Investigation of the influence of combustion-induced thermal expansion on two-point turbulence statistics using conditioned structure functions. J. Fluid Mech. 2019, 867, 45–76. [Google Scholar] [CrossRef]
- Lipatnikov, A.; Chomiak, J.; Sabelnikov, V.; Nishiki, S.; Hasegawa, T. A DNS study of the physical mechanisms associated with density ratio influence on turbulent burning velocity in premixed flames. Combust. Theory Model. 2018, 22, 131–155. [Google Scholar] [CrossRef]
- Im, H.G.; Pal, P.; Wooldridge, M.S.; Mansfield, A.B. A Regime Diagram for Autoignition of Homogeneous Reactant Mixtures with Turbulent Velocity and Temperature Fluctuations. Combust. Sci. Technol. 2015, 187, 1263–1275. [Google Scholar] [CrossRef]
- Martínez-Sanchis, D.; Sternin, A.; Tagscherer, K.; Sternin, D.; Haidn, O.; Tajmar, M. Interactions Between Flame Topology and Turbulent Transport in High-Pressure Premixed Combustion. Flow Turbul. Combust. 2022. [Google Scholar] [CrossRef]
- Martinez, D. A Flame Control Method for Direct Numerical Simulations of Reacting Flows in Rocket Engines. Master’s Thesis, Technical University of Munich, Munich, Germany, 2020. [Google Scholar]
- Zhang, F.; Bonart, H.; Zirwes, T.; Habisreuther, P.; Bockhorn, H.; Zarzalis, N. Direct Numerical Simulation of Chemically Reacting Flows with the Public Domain Code OpenFOAM. In High Performance Computing in Science and Engineering; Springer: Cham, Switzerland, 2015; Volume 14. [Google Scholar] [CrossRef]
- Weller, H.; Tabor, G.; Jasak, H.; Fureby, C. Tensorial Approach to Computational Continuum Mechanics using Object-Oriented Techniques. Comput. Phys 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Weller, H.; Tabor, G.; Jasak, H.; Fureby, C. OpenFOAM; OpenCFD: Bracknell, UK, 2017. [Google Scholar]
- Zirwes, T.; Zhang, F.; Habisreuther, P.; Hansinger, M.; Bockhorn, H.; Pfitzner, M.; Trimis, D. Quasi-DNS dataset of a piloted flame with inhomogeneous inlet conditions. Flow Turbul. Combust. 2020, 104, 997–1027. [Google Scholar] [CrossRef]
- Cantera Developers, Documentation of the Cantera Solvers. Available online: https://cantera.org/science/flames.html (accessed on 18 November 2021).
- Kee, R.; Coltrin, M.; Glarborg, P. Chemically Reacting Flow: Theory and Practice; Wiley & Sons Ltd: Hoboken, NJ, USA, 2017; ISBN 978-1-119-18487-4. [Google Scholar]
- Slavinskaya, N.; Abbasi, M.; Starcke, J.H.; Haidn, O. Methane Skeletal Mechanism for Space Propulsion Applications. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef]
- Martinez-Sanchis, D.; Sternin, A.; Sternin, D.; Haidn, O.; Tajmar, M. Analysis of periodic synthetic turbulence generation and development for direct numerical simulations applications. Phys. Fluids 2021, 33, 125130. [Google Scholar] [CrossRef]
- Von Kármán, T. Progress in the Statistical Theory of Turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef]
- Klein, M.; Herbert, A.; Kosaka, H.; Böhm, B.; Dreizler, A.; Chakraborty, N.; Papapostolou, V.; Im, H.G.; Hasslberger, J. Evaluation of Flame Area Based on Detailed Chemistry DNS of Premixed Turbulent Hydrogen-Air Flames in Different Regimes of Combustion. Flow Turbul. Combust. 2019, 104, 403–419. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Nishiki, S.; Hasegawa, T. A direct numerical simulation study of the influence of flame-generated vorticity on reaction-zone-surface area in weakly turbulent premixed combustion. Phys. Fluids 2019, 31, 055101. [Google Scholar] [CrossRef]
- Trivedi, S.; Cant, R.S. Turbulence Intensity and Length Scale Effects on Premixed Turbulent Flame Propagation. Flow Turbul. Combust 2021, 109, 101–123. [Google Scholar] [CrossRef]
- Keil, S.; Klein, N.; Chakraborty, N. Sub-grid Reaction Progress Variable Variance Closure in Turbulent Premixed Flames. Flow Turbul. Combust 2021, 106, 1195–1212. [Google Scholar] [CrossRef]
- Poludenko, A.; Oran, E.S. The interaction of high-speed turbulence with flames: Global properties and internal flame structure. Combust. Flame 2010, 157, 995–1011. [Google Scholar] [CrossRef]
- Liao, S.Y.; Jiang, D.M.; Cheng, Q. Determination of laminar burning velocities for natural gas. Fuel 2004, 83, 1247–1250. [Google Scholar] [CrossRef]
- Konnov, A.; Mohammad, A.; Kishore, V.; Kim, N.; Prathap, C.; Kumar, S. A comprehensive review of measurements and data analysis of laminar burning velocities for various fuel + air mixtures. Prog. Energy Combust. Sci. 2018, 68, 197–267. [Google Scholar] [CrossRef]
- Bobbitt, B.; Blanquart, G. Vorticity isotropy in high Karlovitz number premixed flames. Phys. Fluids 2016, 28, 105101. [Google Scholar] [CrossRef]
- Whitmann, S.; Towery, C.; Poludenko, A.; Hamlington, E. Scaling and collapse of conditional velocity structure functions in turbulent premixed flames. Proc. Combust. Inst. 2019, 37, 2527–2535. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Poludenko, A. Assessment of a transport equation for mean reaction rate using DNS data obtained from highly unsteady premixed turbulent flames. Int. J. Heat Mass Transf. 2019, 134, 398–404. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Sabelnikov, V.A.; Nikitin, N.V.; Nishiki, S.; Hasegawa, T. Analysis of synthetic turbulence generation and development for direct numerical simulations applications. Flow Turbul. Combust. 2021, 33, 125130. [Google Scholar] [CrossRef]
- Bougrine, S.; Richard, S. Fuel Composition Effects on Flame Stretch in Turbulent Premixed Combustion: Numerical Analysis of Flame-Vortex Interaction and Formulation of a New Efficiency Function. Flow Turbul. Combust 2014, 93, 259–281. [Google Scholar] [CrossRef]
- Martinez, D.; Banik, S.; Sternin, A.; Sternin, D.; Haidn, O.; Tajmar, M. Analysis of Turbulence Generation and Dissipation in Shear Layers of Methane-Oxygen Diffusion Flames using Direct Numerical Simulations. Phys. Fluids 2022, 34, 045121. [Google Scholar] [CrossRef]
- Lipatnikov, A.; Sabelnikov, V.; Hernández-Pérez, F.; Song, W.; Im, H.G. A priori DNS study of applicability of flamelet concept to predicting mean concentrations of species in turbulent premixed flames at various Karlovitz numbers. Combust. Flame 2020, 222, 370–382. [Google Scholar] [CrossRef]
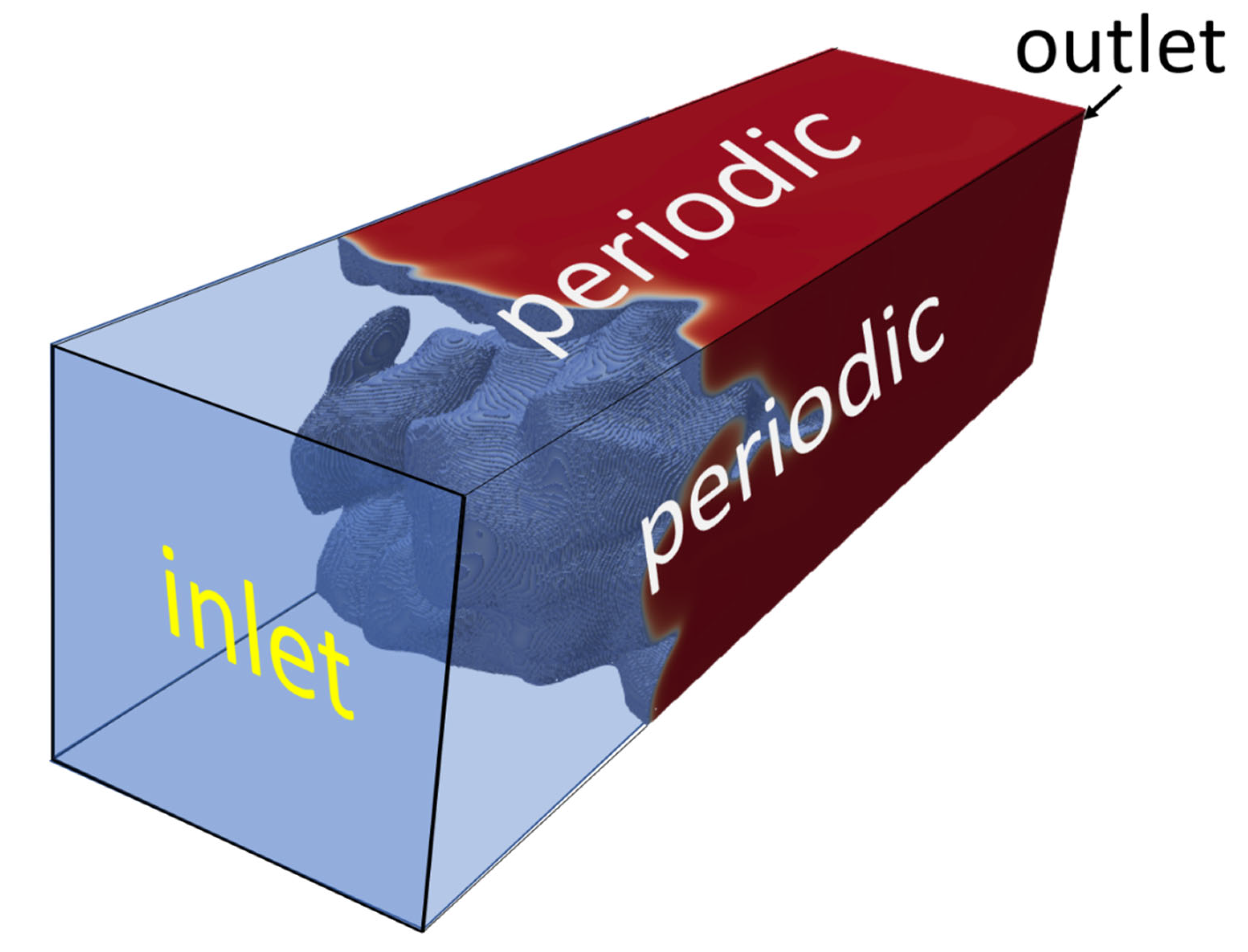
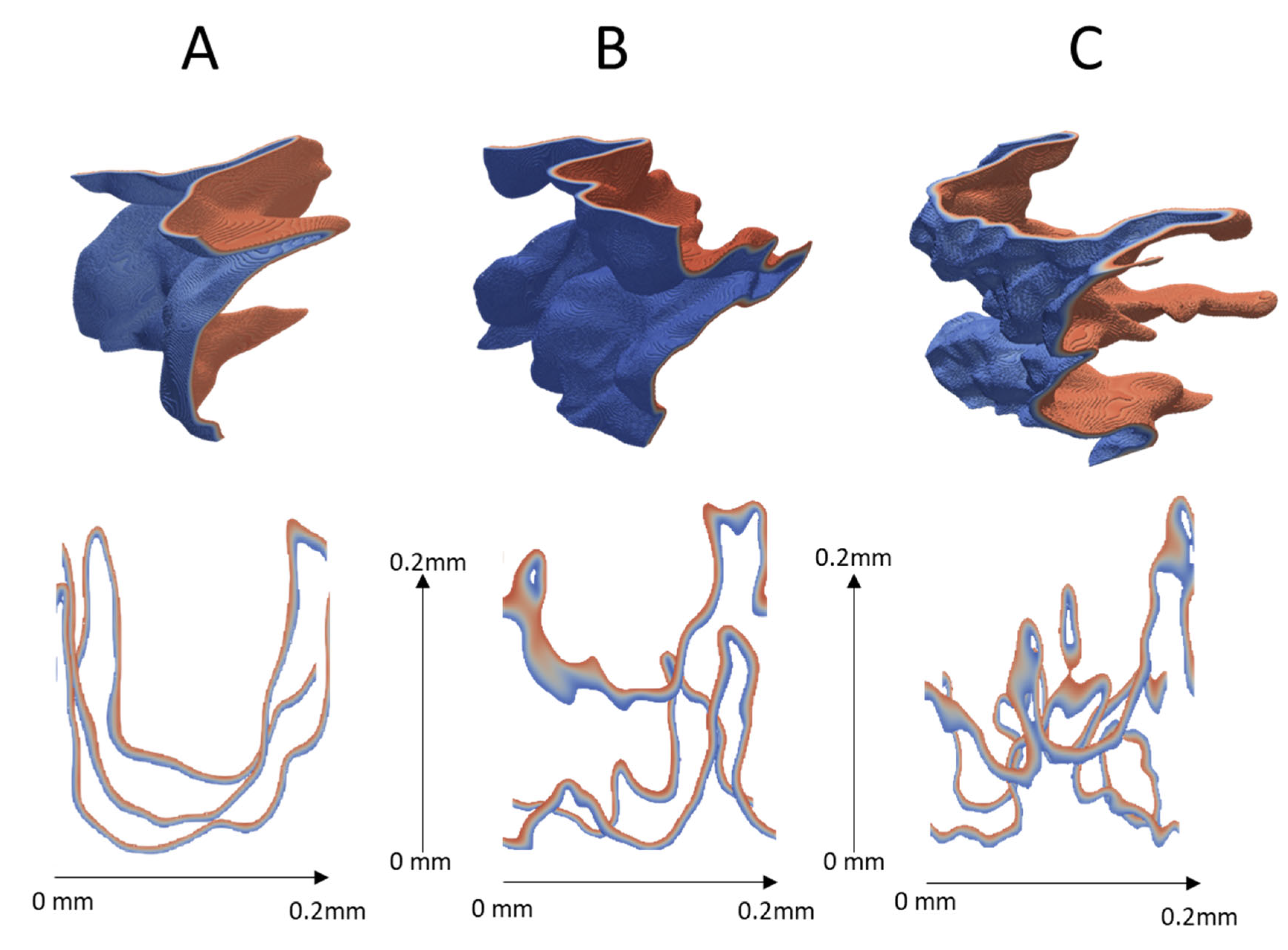

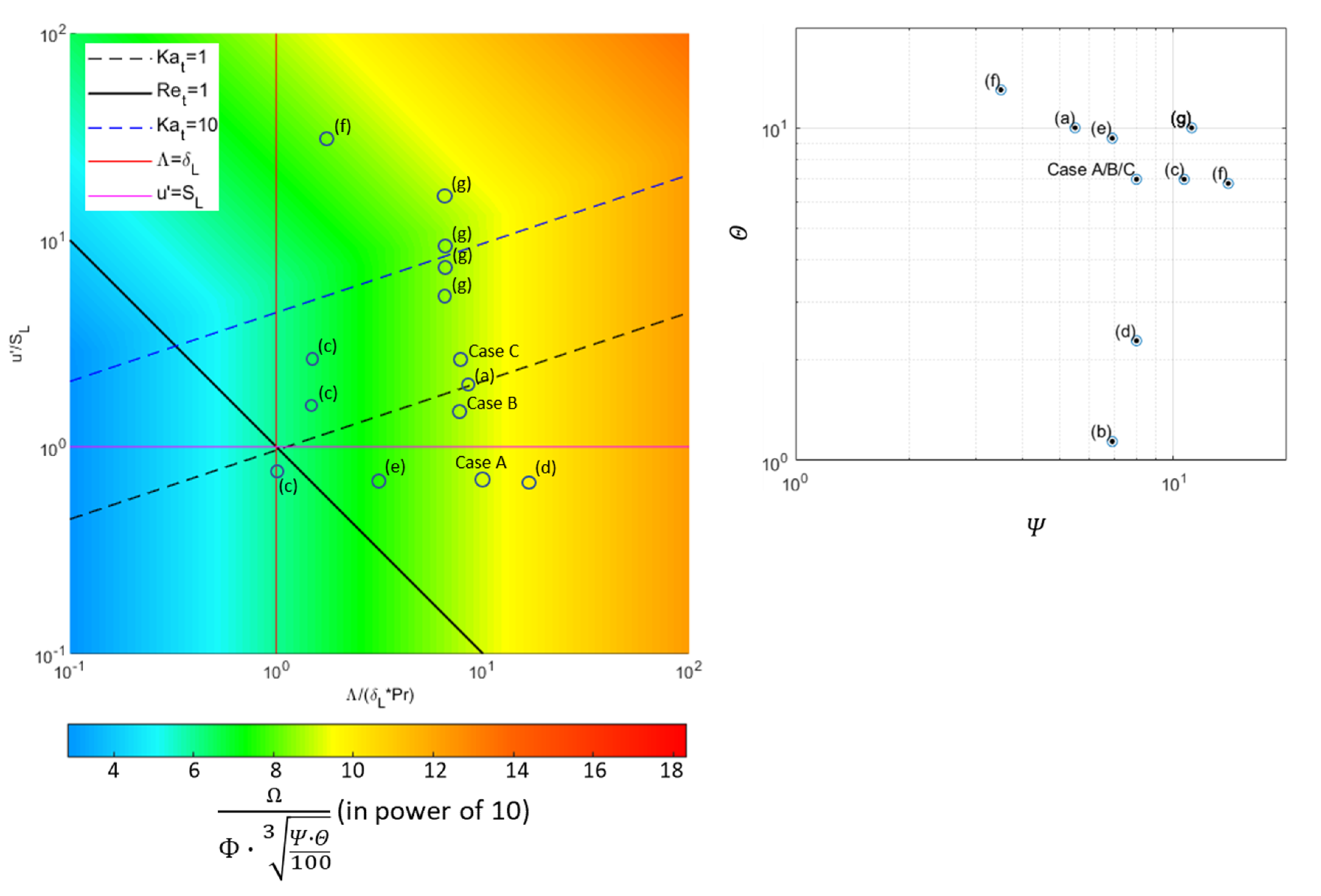
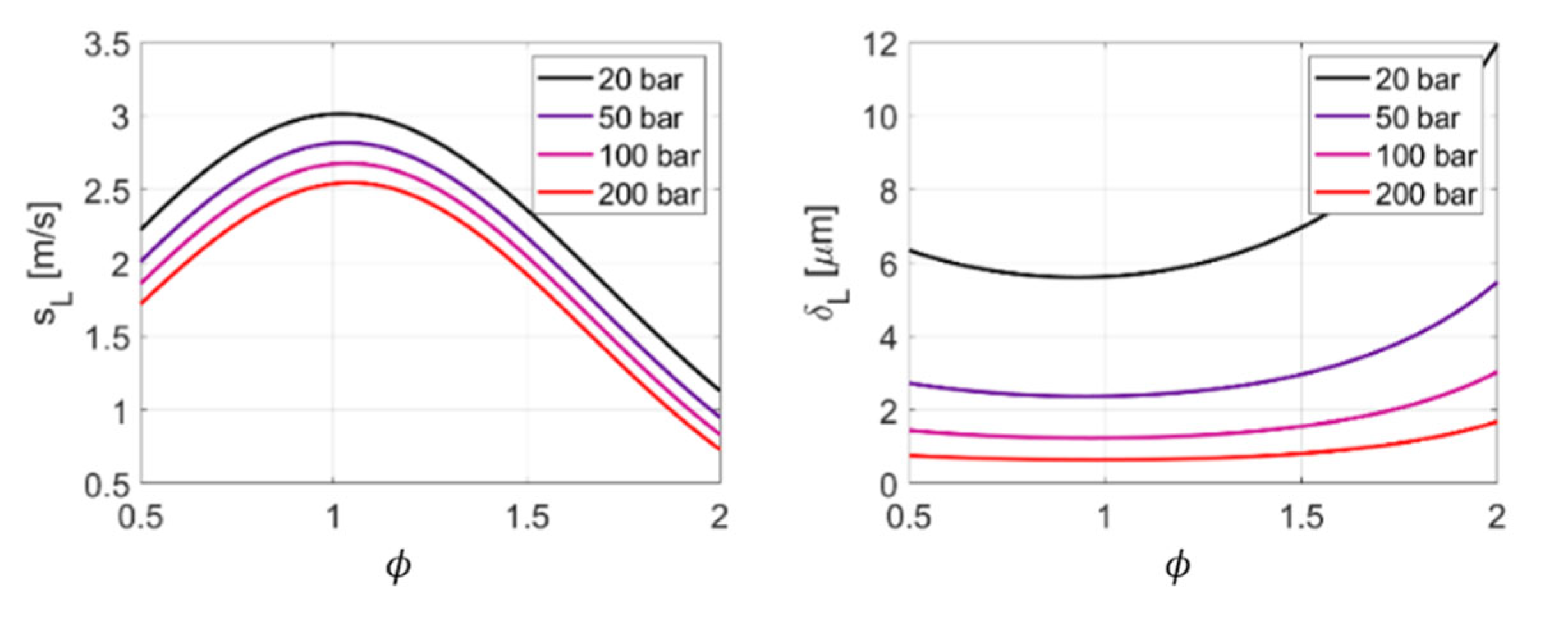

| Case | A | B | C |
|---|---|---|---|
| 2.2 | 4.59 | 7.55 | |
| 40.6 | 31 | 30.7 | |
| 1.5 | 0.81 | 0.56 | |
| 0.74 | 1.37 | 1.98 | |
| 3.072 | 3.072 | 3.072 | |
| 5.46 | 5.46 | 5.46 | |
| 1.11 | 1.11 | 1.11 | |
| 11.8 | 11.8 | 11.8 | |
| 80.5 | 128 | 209 | |
| 0.87 | 1.37 | 5.48 | |
| 10.38 | 3.8 | 2.3 | |
| 8 | 8 | 8 | |
| 7 | 7 | 7 | |
| 4 | 4 | 4 |
| Point | Definition | Determination Method | Pr | |
|---|---|---|---|---|
variable constant | from reactants | 0.066 | 1.11 | |
| Favre-averaged ν | 0.817 | 13.7 | ||
| Averaged ν | 1.564 | 26.2 | ||
| 2.014 | 33.8 | |||
Whole Pr term as a local variable | from reactants | 0.717 | 1.11 | |
| Position of autoignition temperature | 0.704 | 4.45 | ||
| Favre averaged Pr | 0.691 | 22.1 | ||
| Averaged Pr | 0.676 | 29.1 | ||
| 0.675 | 29.9 | |||
| Intersection of both definitions | 0.706 | 11.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sternin, A.; Martinez, D.; Sternin, D.; Haidn, O.; Tajmar, M. Characterisation and Design of Direct Numerical Simulations of Turbulent Statistically Planar Flames. Aerospace 2022, 9, 530. https://doi.org/10.3390/aerospace9100530
Sternin A, Martinez D, Sternin D, Haidn O, Tajmar M. Characterisation and Design of Direct Numerical Simulations of Turbulent Statistically Planar Flames. Aerospace. 2022; 9(10):530. https://doi.org/10.3390/aerospace9100530
Chicago/Turabian StyleSternin, Andrej, Daniel Martinez, Daniel Sternin, Oskar Haidn, and Martin Tajmar. 2022. "Characterisation and Design of Direct Numerical Simulations of Turbulent Statistically Planar Flames" Aerospace 9, no. 10: 530. https://doi.org/10.3390/aerospace9100530
APA StyleSternin, A., Martinez, D., Sternin, D., Haidn, O., & Tajmar, M. (2022). Characterisation and Design of Direct Numerical Simulations of Turbulent Statistically Planar Flames. Aerospace, 9(10), 530. https://doi.org/10.3390/aerospace9100530








