Application of Aeroelastic Tailoring for Load Alleviation on a Flying Demonstrator Wing †
Abstract
:1. Introduction
1.1. The FLEXOP Project
1.2. Aeroelastic Tailoring for Load Alleviation
2. Aeroelastic Tailoring Framework
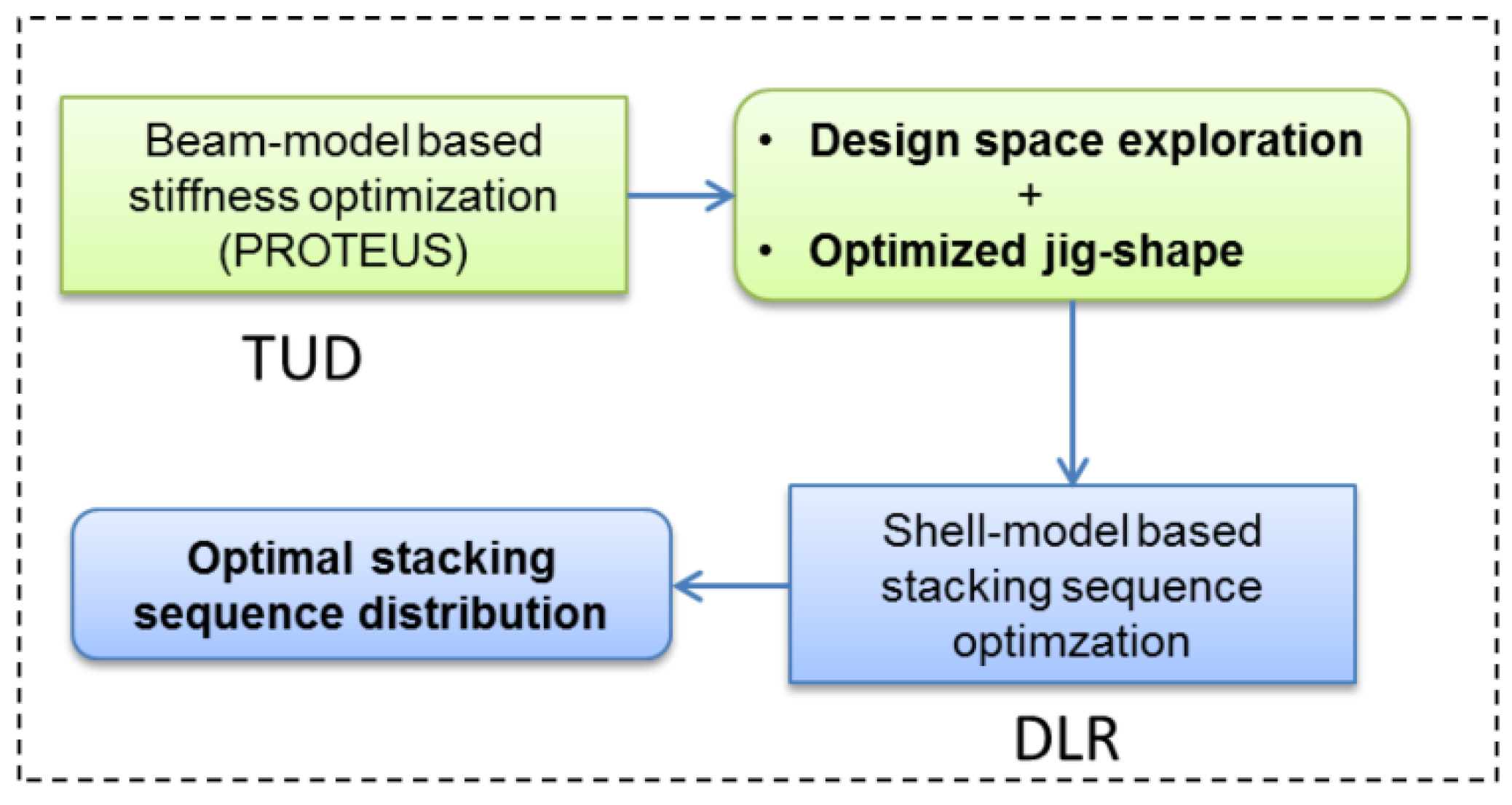
2.1. Overall Process
2.2. Beam-Model-Based Stiffness Optimization
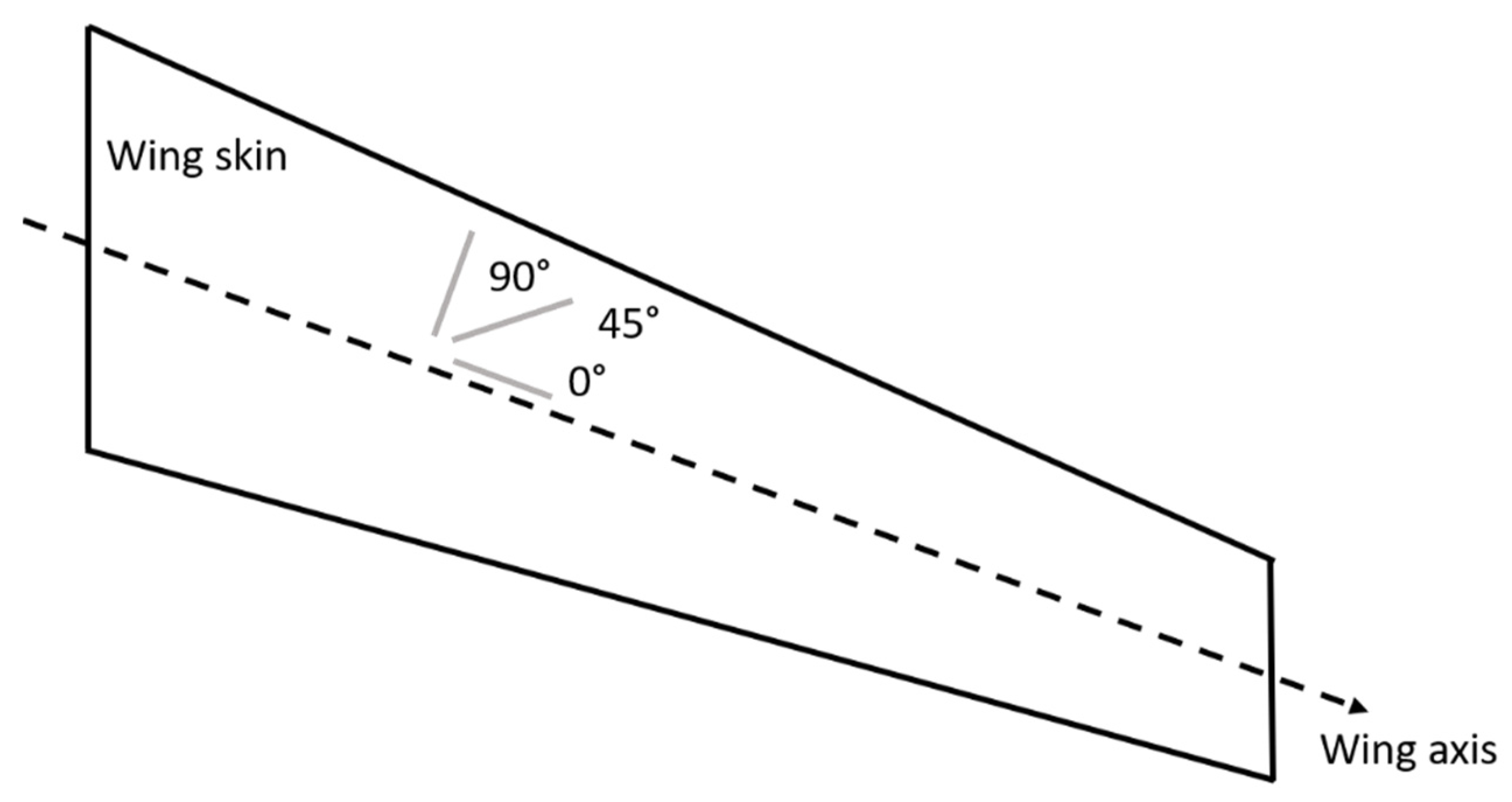
2.3. Shell-Model Based Stacking Sequence Optimization
3. Wing Design and Structural Optimization
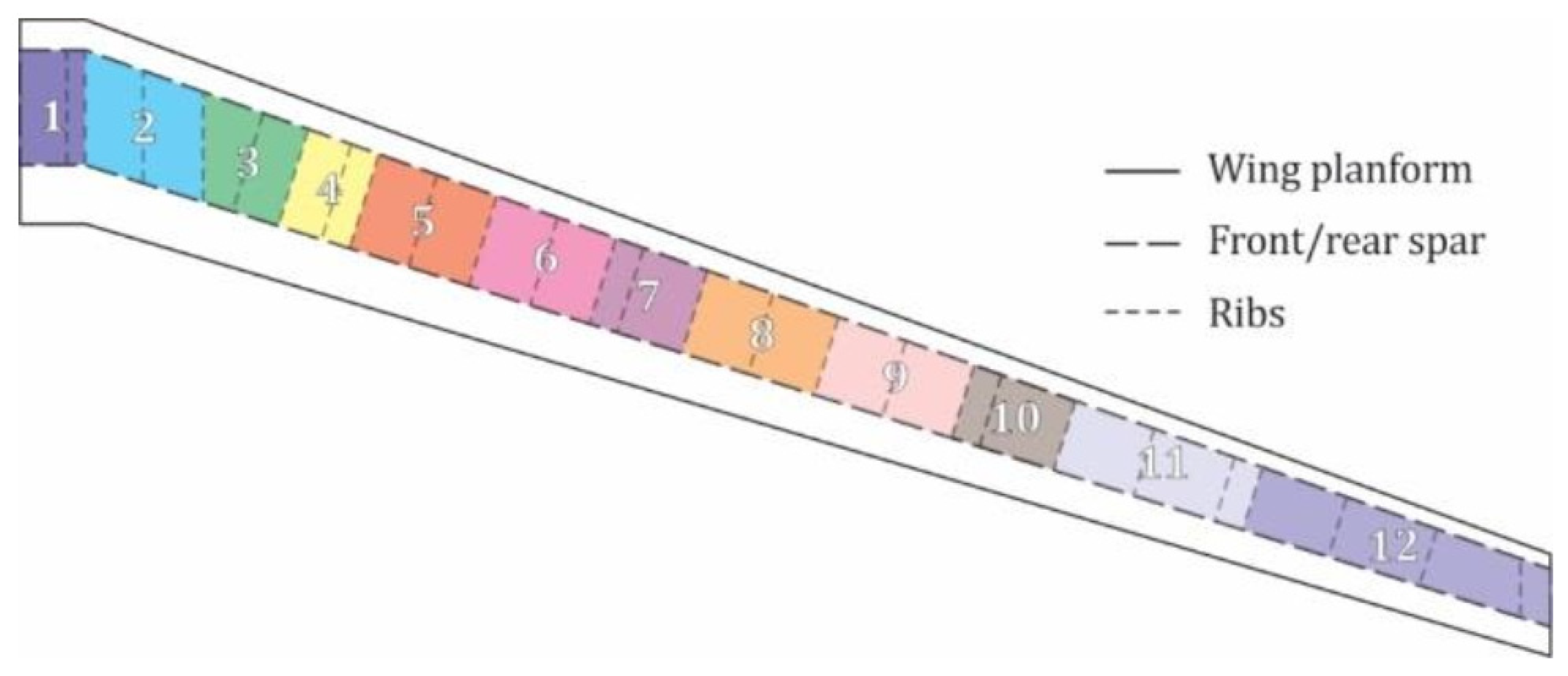
3.1. Planform and Design Specifications
3.2. Optimization Specifications
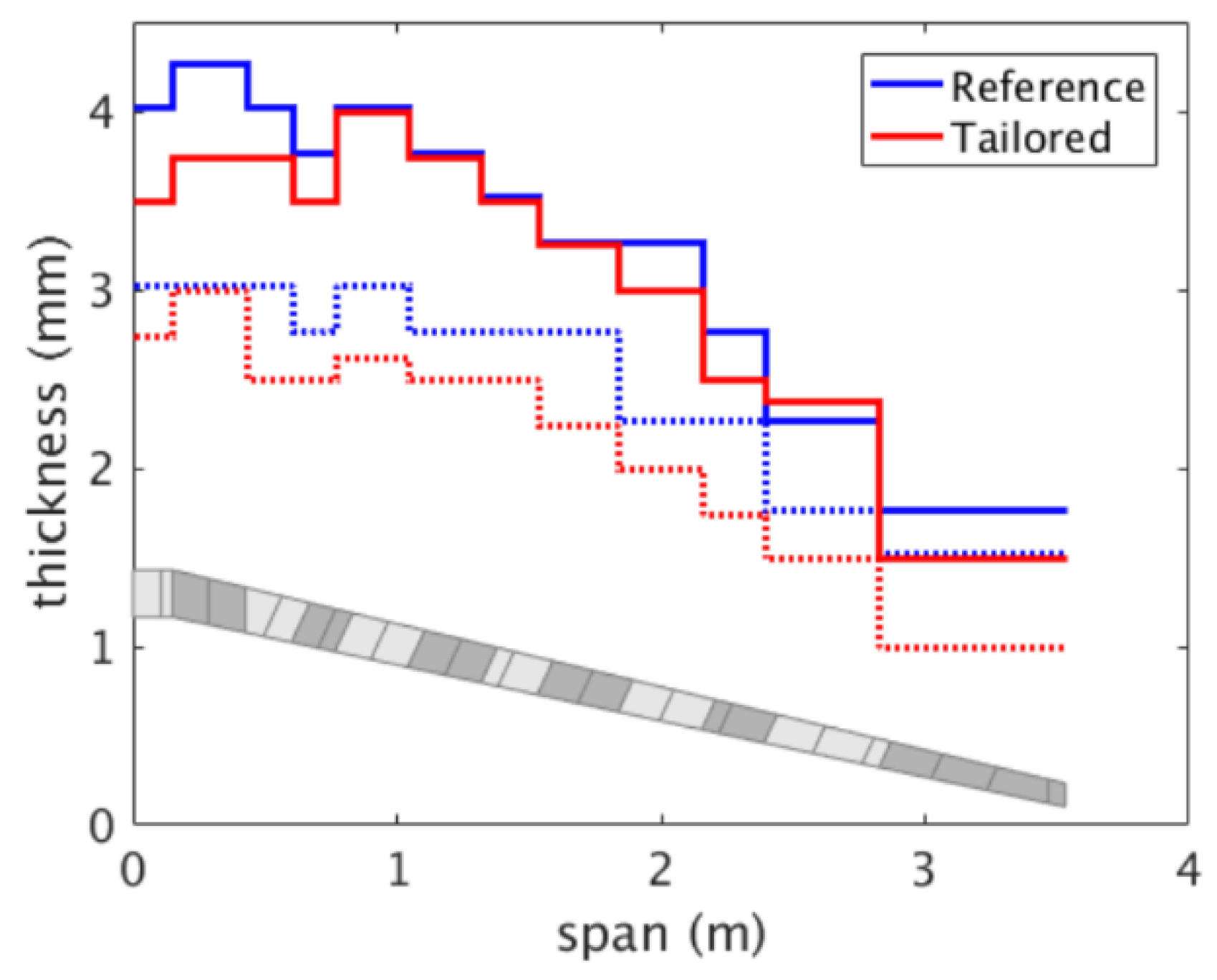
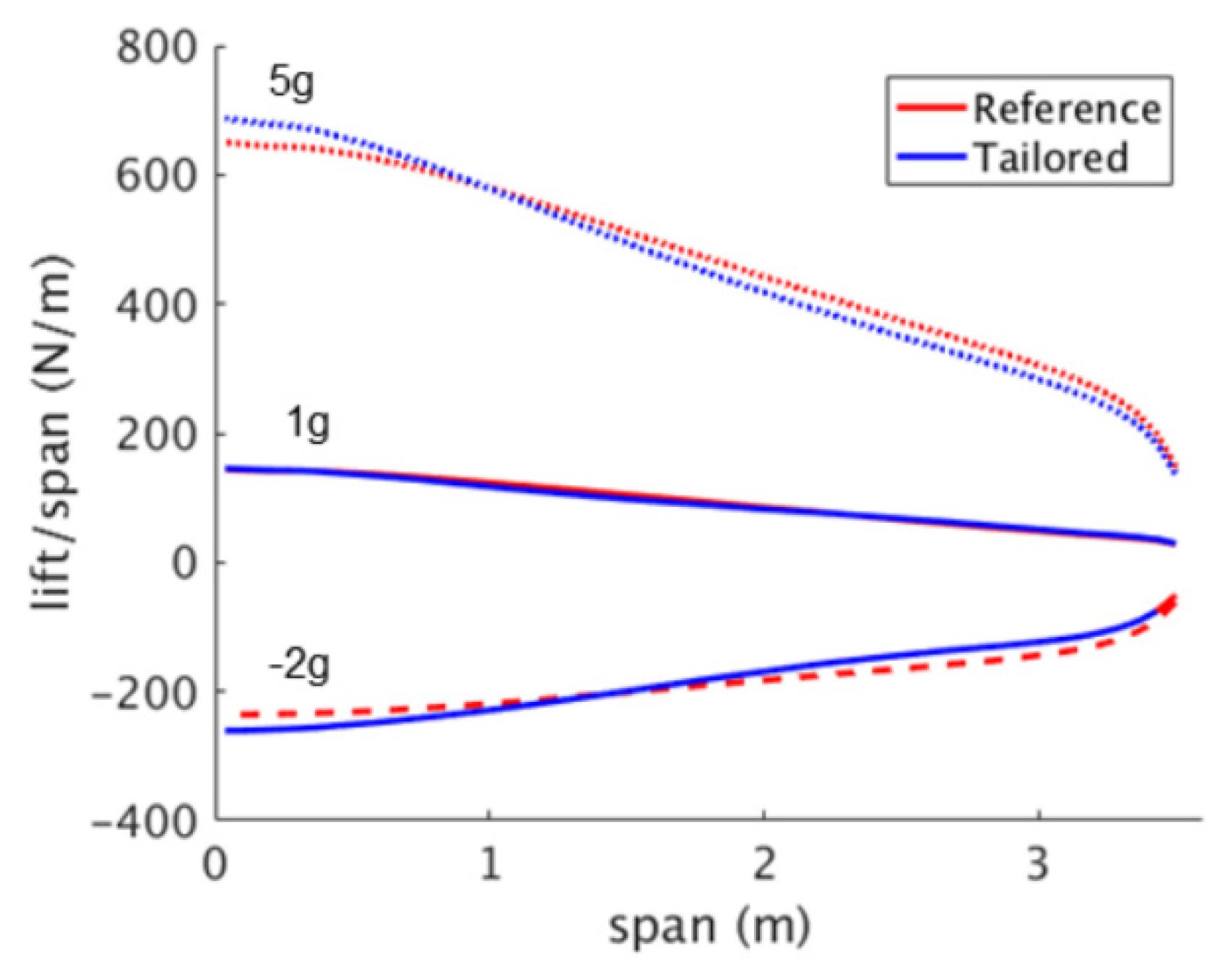
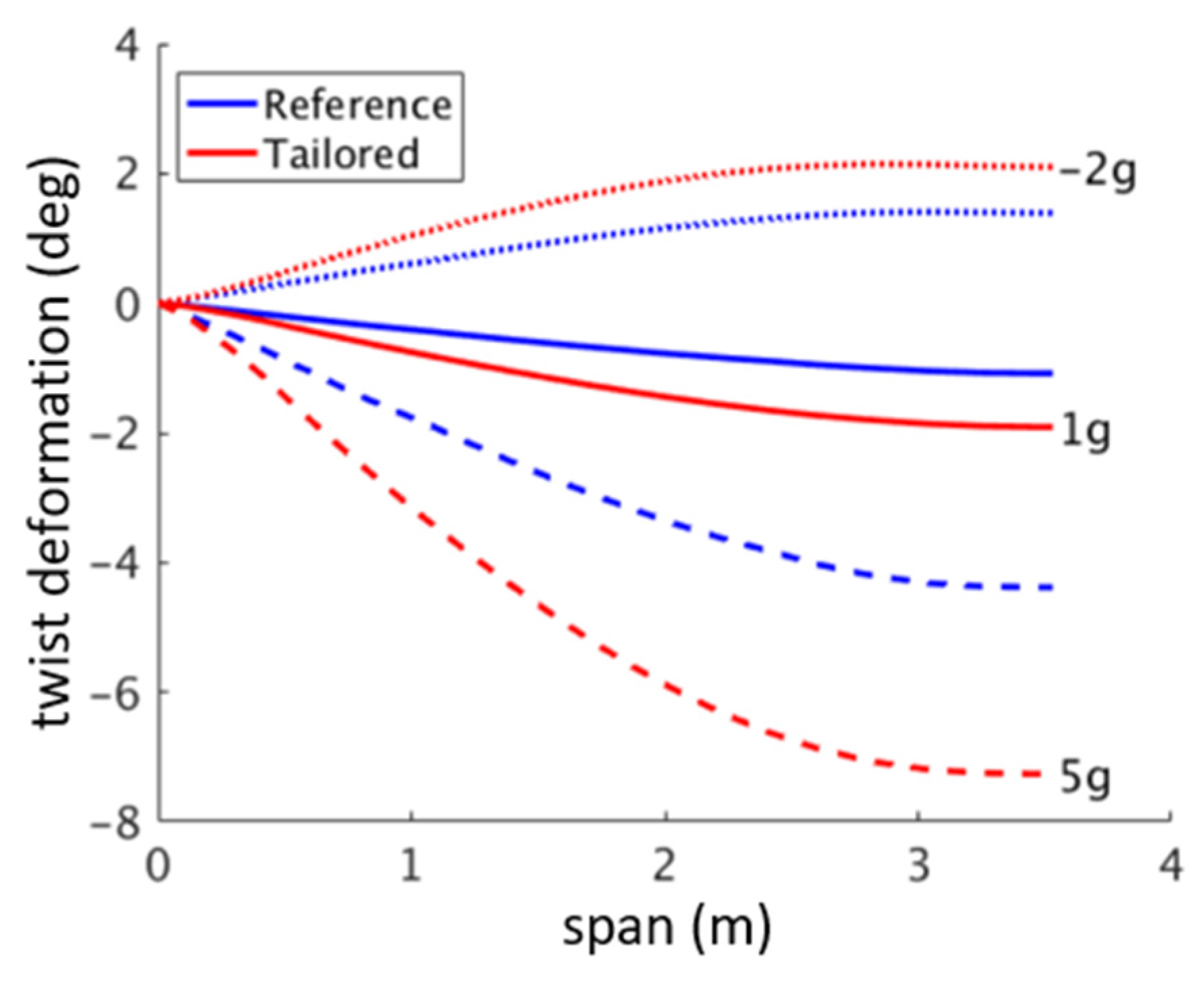
3.3. Optimization Results
3.4. Manufacturing of Wings
4. Ground Tests
4.1. Shape and Load Sensing Methodology
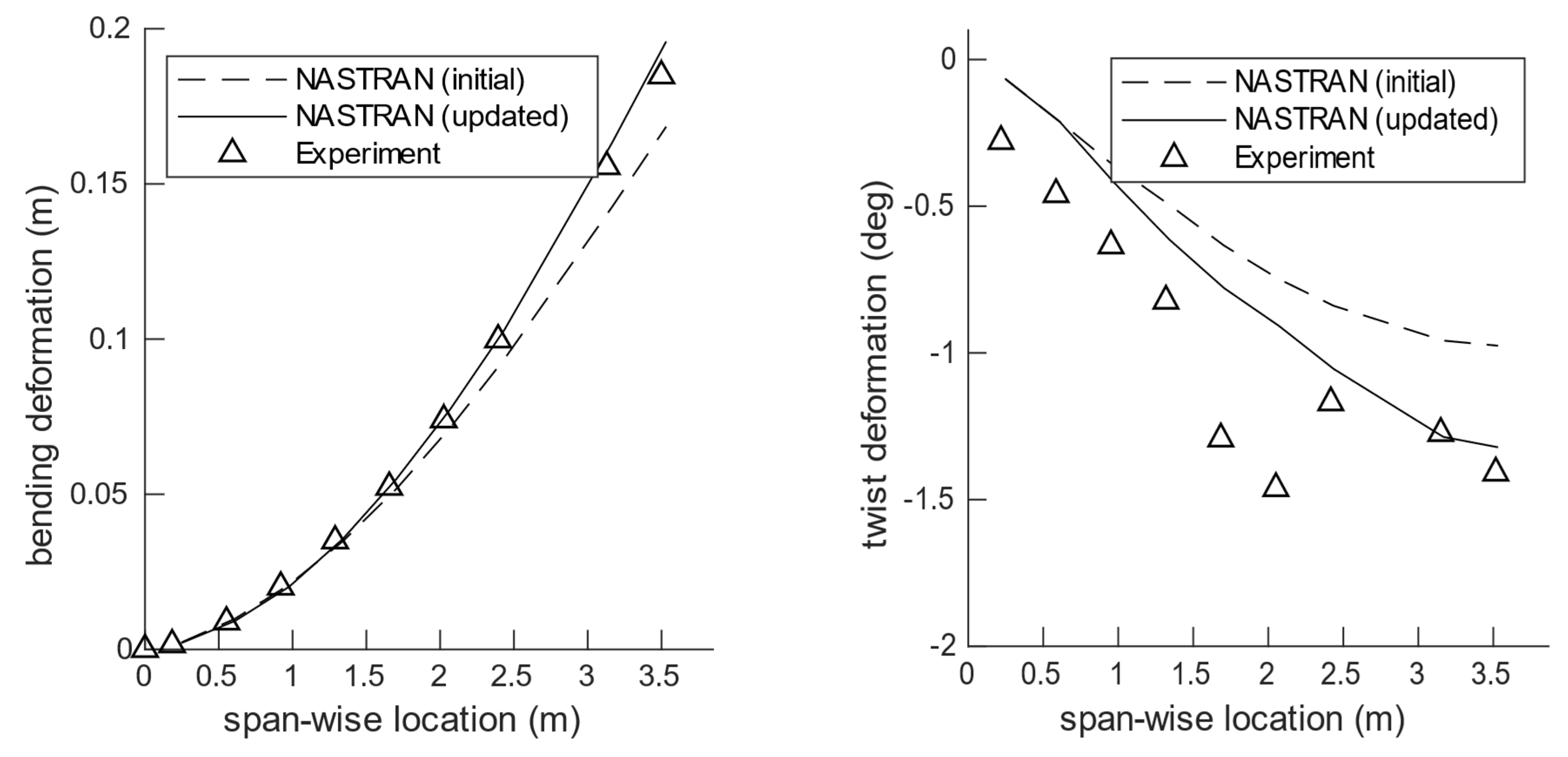
4.2. Static Test and Model Update
4.3. Airworthiness Test
4.4. Ground Vibration Tests
5. Flight Test
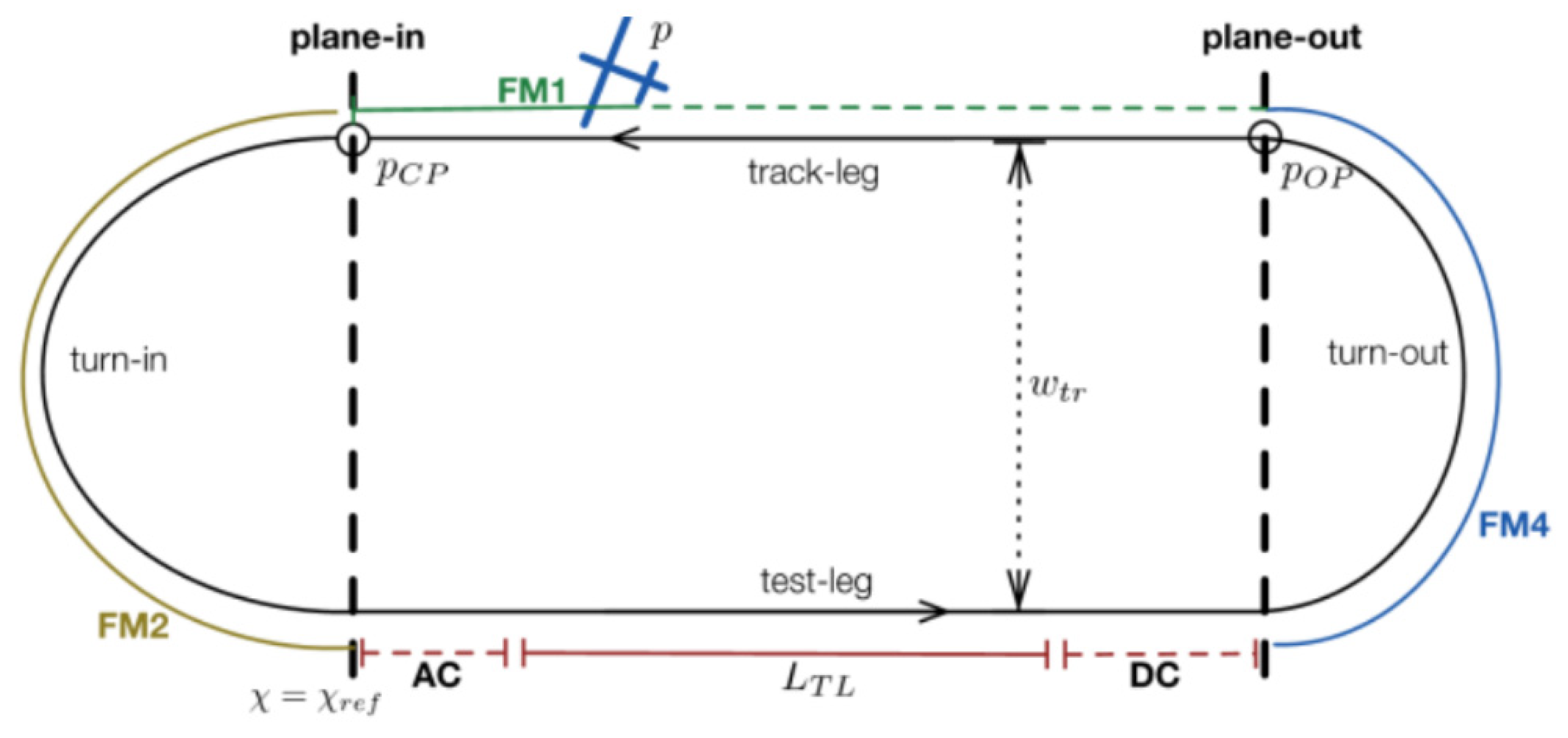
5.1. Flight Test Approach
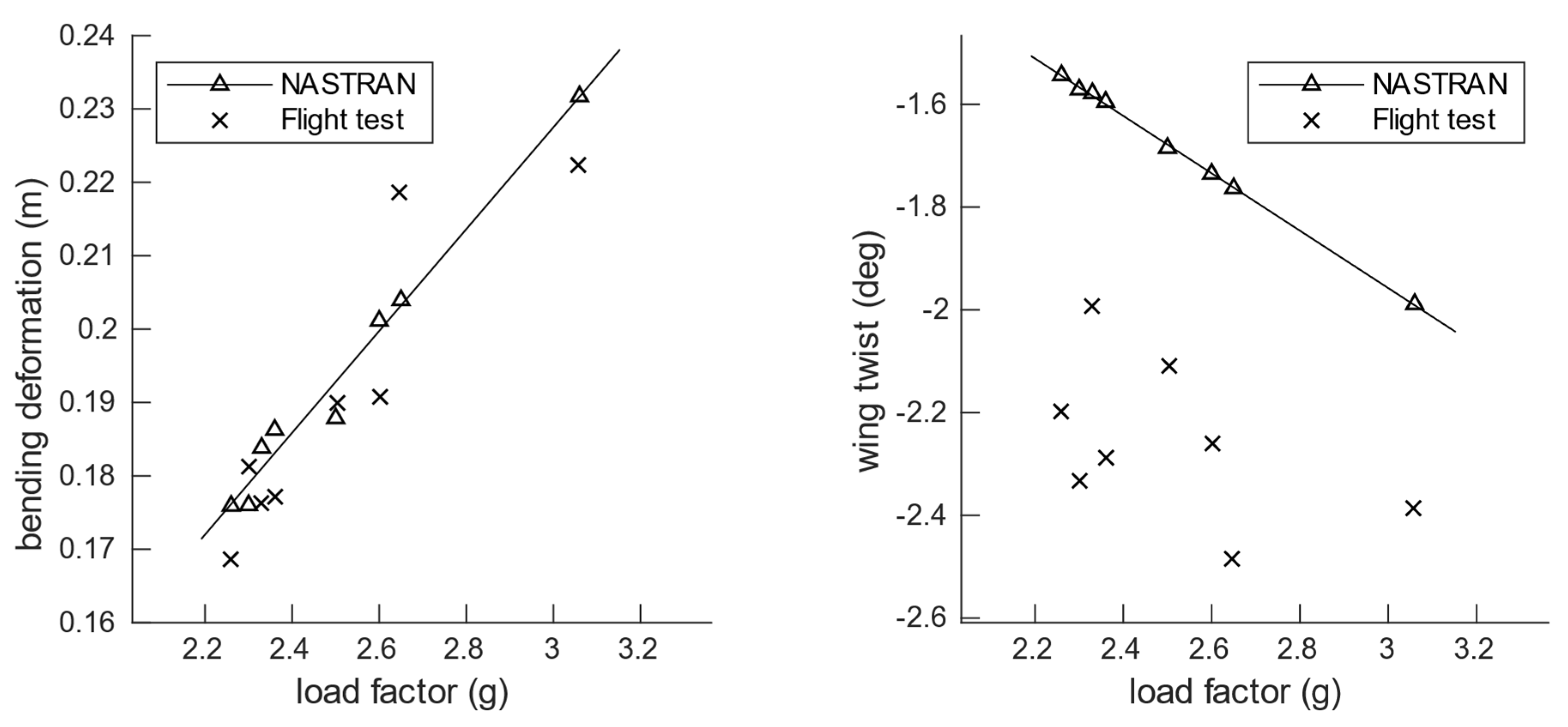
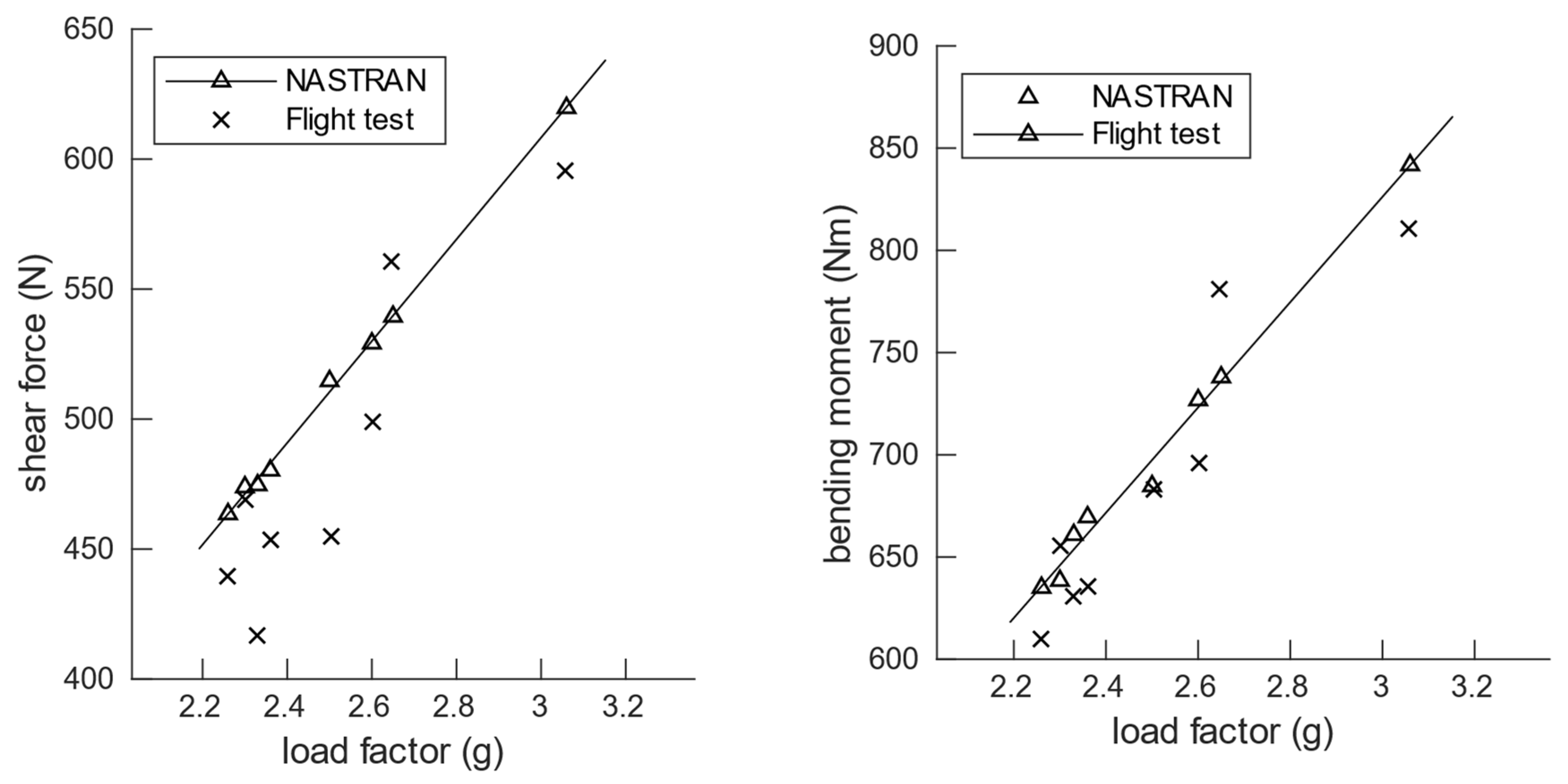
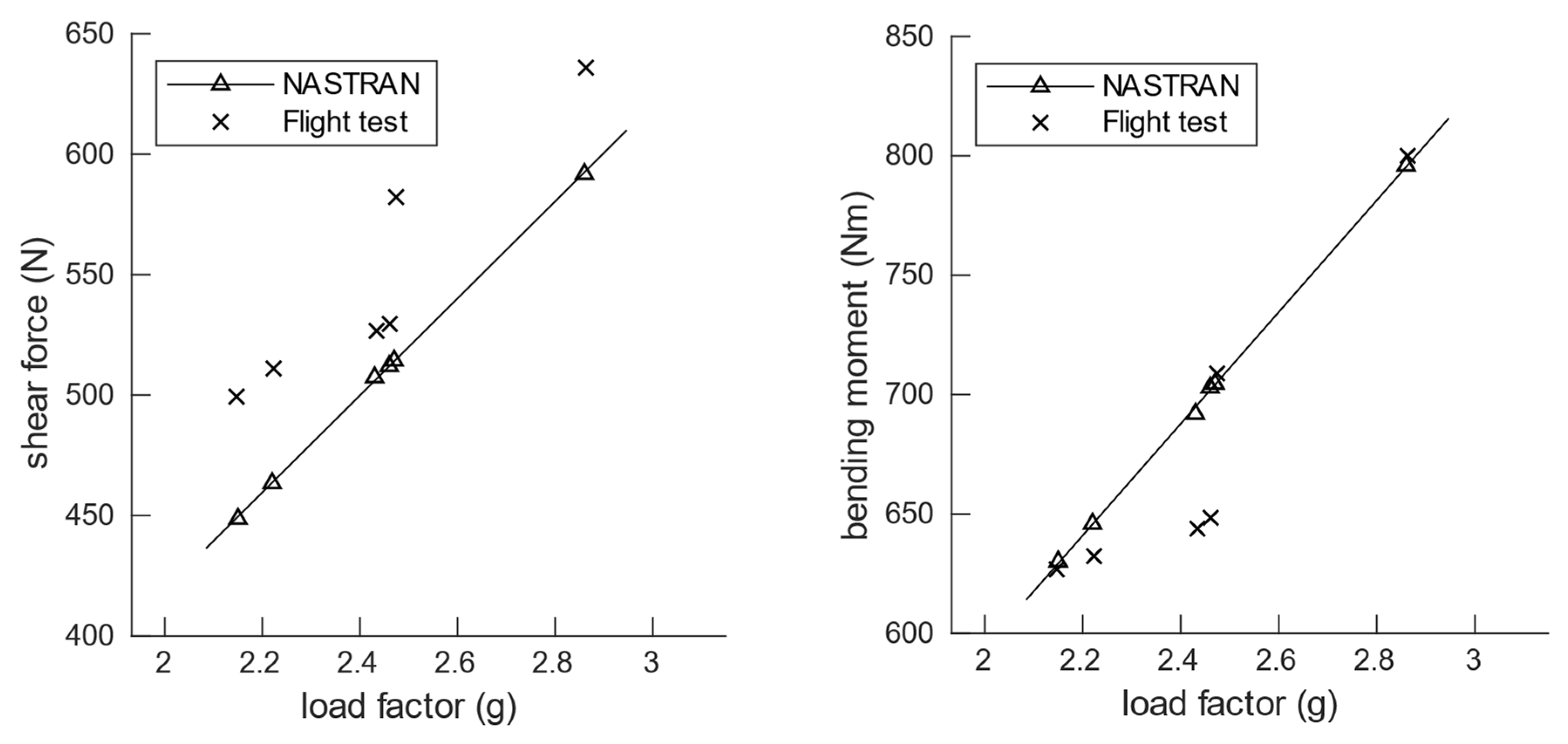
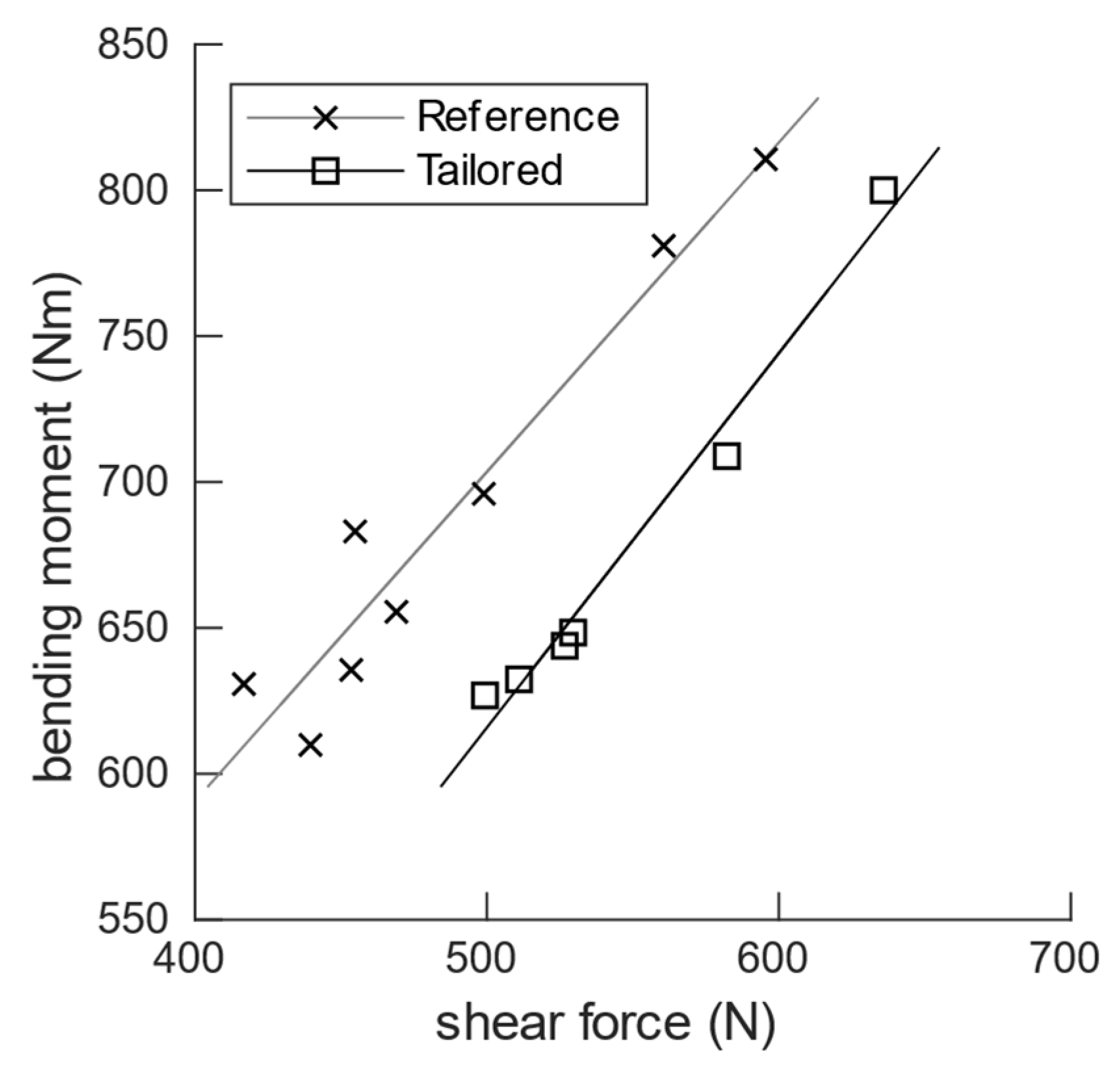
5.2. Comparison between Flight Test Results and Simulation Models
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FLEXOP Consortium. The FLEXOP Project. 2013. Available online: https://flexop.eu/ (accessed on 24 January 2022).
- Stahl, P.; Sendner, F.-M.; Hermanutz, A.; Rößler, C.; Hornung, M. Mission and Aircraft Design of FLEXOP Unmanned Flying Demonstrator to Test Flutter Suppression within Visual Line of Sight. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Meddaikar, Y.M.; Dillinger, J.; Klimmek, T.; Krueger, W.; Wuestenhagen, M.; Kier, T.M.; Hermanutz, A.; Hornung, M.; Rozov, V.; Breitsamter, C.; et al. Aircraft Aeroservoelastic Modelling of the FLEXOP Unmanned Flying Demonstrator. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Sodja, J.; Werter, N.; De Breuker, R. Design of a flying demonstrator wing for manoeuvre load alleviation with cruise shape constraint. In Proceedings of the AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Meddaikar, M.Y.; Dillinger, J.; Sodja, J.; De Breuker, R. FLEXOP—Application of Aeroelastic Tailoring to a Flying Demonstrator Wing. In Proceedings of the Deutscher Luft- und Raumfahrtkongress, Friedrichshafen, Germany, 4–6 September 2018. [Google Scholar]
- Rozov, V.; Hermanutz, A.; Breitsamter, C.; Hornung, M. Aeroelastic Analysis of a Flutter Demonstrator with a very Flexible High-Aspect-Ratio Swept Wing. In Proceedings of the IFASD 2017 (International Forum on Aeroelasticity and Structural Dynamics), Como, Italy, 25–28 June 2017; Available online: https://www.asdjournal.org/public/Proceedings/IFASD_2017/IFASD-2017-173.pdf (accessed on 24 July 2022).
- Starnes, J.H., Jr.; Haftka, R.T. Preliminary design of composite wings for buckling, strength, and displacement constraints. J. Aircr. 1979, 16, 564–570. [Google Scholar] [CrossRef]
- Hollowell, S.J.; Dungundji, J. Aeroelastic flutter and divergence of stiffness coupled, graphite epoxy cantilevered plates. J. Aircr. 1984, 21, 69–76. [Google Scholar] [CrossRef]
- Shirk, M.; Hertz, T.; Weisshaar, T. Aeroelastic tailoring—Theory, practice, and promise. J. Aircr. 1986, 23, 6–18. [Google Scholar] [CrossRef]
- Vanderplaats, G.N.; Weisshaar, T.A. Optimum design of composite structures. Int. J. Numer. Methods Eng. 1989, 27, 437–448. [Google Scholar] [CrossRef]
- Eastep, F.E.; Tischler, V.A.; Venkayya, V.B.; Khot, N.S. Aeroelastic Tailoring of Composite Structures. J. Aircr. 1999, 36, 1041–1047. [Google Scholar] [CrossRef]
- Guo, S.; Cheng, W.; Cui, D. Aeroelastic Tailoring of Composite Wing Structures by Laminate Layup Optimization. AIAA J. 2006, 44, 3146–3150. [Google Scholar] [CrossRef]
- De Leon, D.M.; de Souza, C.E.; Fonseca, J.S.; da Silva, R.G. Aeroelastic tailoring of composite plates through eigenvalues optimization. Mecánica Comput. 2010, 29, 609–623. [Google Scholar]
- Kameyama, M.; Fukunaga, H. Optimum design of composite plate wings for aeroelastic characteristics using lamination parameters. Comput. Struct. 2007, 85, 213–224. [Google Scholar] [CrossRef]
- Abdalla, M.M.; De Breuker, R.; Gurdal, Z. Aeroelastic tailoring of variable-stiffness slender wings for minimum compliance. In International Forum on Aeeroelasticity and Structural Dynamics (1–10); KTH: Stockholm, Sweden, 2007. [Google Scholar]
- Liu, D.; Toropov, V.V. A lamination parameter-based strategy for solving an integer-continuous problem arising in composite optimization. Comput. Struct. 2013, 128, 170–174. [Google Scholar] [CrossRef]
- Dillinger, J. Static Aeroelastic Optimization of Composite Wings with Variable Stiffness Laminate. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Dillinger, J.; Abdalla, M.; Klimmek, T.; Gurdal, Z. Stiffness Optimization of Composite Wings with Aeroelastic Constraints. J. Aircr. 2013, 50, 1159–1168. [Google Scholar] [CrossRef]
- Livne, E.; Weisshaar, T.A. Aeroelasticity of nonconventional airplane configurations-past and future. J. Aircr. 2003, 40, 1047–1065. [Google Scholar] [CrossRef]
- Meddaikar, Y.M.; Dillinger, J.K.; Sodja, J.; Mai, H.; De Breuker, R. Optimization, Manufacturing and Testing of a Composite Wing with Maximized Tip Deflection. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Sodja, J.; Werter, N.; Dillinger, J.K.; De Breuker, R. Dynamic Response of Aeroelastically Tailored Composite Wing: Analysis and Experiment. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Meddaikar, Y.M.; Dillinger, J.; Ritter, M.; Govers, Y. Optimization & Testing of Aeroelastically-Tailored Forward Swept Wings. In Proceedings of the IFASD 2017 (International Forum on Aeroelasticity and Structural Dynamics), Como, Italy, 25–28 June 2017; Available online: https://www.asdjournal.org/public/Proceedings/IFASD_2017/IFASD-2017-129.pdf (accessed on 24 July 2022).
- Dillinger, J.; Meddaikar, Y.M.; Lepage, A.; Fabbiane, N. Structural Optimization of an Aeroelastic Wind Tunnel Model for Unsteady Transonic Testing. In Proceedings of the Aerospace Europe Conference 2021, Warschau, Poland, 23–26 November 2021. [Google Scholar]
- DeAngelis, V.M. In-flight deflection measurement of the HiMAT aeroelastically tailored wing. J. Aircr. 1982, 19, 1088–1094. [Google Scholar] [CrossRef]
- Monaghan, R.C. Description of the HiMAT Tailored Composite Structure and Laboratory Measured Vehicle Shape under Load. NASA Technical Memorandum 81354, 1981. Available online: https://archive.org/details/NASA_NTRS_Archive_19810009523/mode/2up (accessed on 24 July 2022).
- Marano, A.D.; Belardo, M.; Beretta, J.; Starace, F.; Orlando, S.; Punzi, C.; Frajese, R.; Paletta, N.; Di Palma, L. Aeroelastic Tailoring of the Next Generation Civil Tiltrotor Technological Demonstrator Composite Wing. Aerospace 2022, 9, 335. [Google Scholar] [CrossRef]
- Krüger, W.R.; Dillinger, J.; De Breuker, R.; Haydn, K. Investigations of passive wing technologies for load reduction. CEAS Aeronaut. J. 2019, 10, 977–993. [Google Scholar] [CrossRef]
- Werter, N.; De Breuker, R. A novel dynamic aeroelastic framework for aeroelastic tailoring and structural optimisation. Compos. Struct. 2016, 158, 369–386. [Google Scholar] [CrossRef] [Green Version]
- Ferede, E.; Abdalla, M. Cross-sectional modelling of thin-walled composite beams. In Proceedings of the 55th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- De Breuker, R.; Abdalla, M.M.; Gürdal, Z. A Generic Morphing Wing Analysis and Design Framework. J. Intell. Mater. Syst. Struct. 2011, 22, 1025–1039. [Google Scholar] [CrossRef]
- Werter, N.P.M.; De Breuker, R.; Abdalla, M.M. Continuous-Time State-Space Unsteady Aerodynamic Modeling for Efficient Loads Analysis. AIAA J. 2018, 56, 905–916. [Google Scholar] [CrossRef]
- Miki, M.; Sugiyama, Y. Optimum Design of Laminated Composite Plates Using Lamination Parameters. In Proceedings of the 32nd Structures, Structural Dynamics, and Materials Conference, Baltimore, MD, USA, 8–10 April 1991. [Google Scholar]
- Fukunaga, H.; Vanderplaats, G.N. Stiffness Optimization of Orthotropic Laminated Composites Using Lamination Parameters. AIAA J. 1991, 29, 641–646. [Google Scholar] [CrossRef]
- Fukunaga, H.; Sekine, H. Stiffness design method of symmetric laminates using lamination parameters. AIAA J. 1992, 30, 2791–2793. [Google Scholar] [CrossRef]
- Sodja, J.; Georgopoulos, P.; De Breuker, R.; Meddaikar, M.Y.; Dillinger, J.K.S. Validation of an Aeroelastic Wing Design for Manoeuvre Load Alleviation Using Flight Test Data. AIAA J. 2022; submitted. [Google Scholar]
- Meddaikar, Y.M.; Irisarri, F.-X.; Abdalla, M.M. Laminate optimization of blended composite structures using a modified Shepard’s method and stacking sequence tables. Struct. Multidiscip. Optim. 2016, 55, 535–546. [Google Scholar] [CrossRef]
- Irisarri, F.-X.; Lasseigne, A.; Leroy, F.-H.; Le Riche, R. Optimal design of laminated composite structures with ply drops using stacking sequence tables. Compos. Struct. 2014, 107, 559–569. [Google Scholar] [CrossRef]
- Van Campen, J.; Seresta, O.; Abdalla, M.; Gürdal, Z. General Blending Definitions for Stacking Sequence Design of Composite Laminate Structures. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, USA, 7–10 April 2008. [Google Scholar] [CrossRef]
- Klimmek, T. Parameterization of Topology and Geometry for the Multidisciplinary Optimization of Wing Structures. In Proceedings of the CEAS 2009 European Air and Space Conference, Manchester, UK, 26–29 October 2009. [Google Scholar]
- Skopinski, T.; Aiken, W.; Huston, W.; National Advisory Committee for Aeronautics. Calibration of Strain-Gage Installations in Aircraft Structures for the Measurement of Flight Loads; NACA R-1178; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953; Available online: https://books.google.nl/books?id=xexyG1YGhp0C (accessed on 24 July 2022).
- Sodja, J.; De Breuker, R.; Meddaikar, Y.M.; Dillinger, J.K.; Soal, K.; Govers, Y.; Krueger, W.; Georgopoulos, P.; Koimtzoglou, C.; Roessler, C.; et al. Ground Testing of the FLEXOP Demonstrator Aircraft. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Roessler, C.; Bartasevicius, J.; Koeberle, S.J.; Teubl, D.; Hornung, M.; Meddaikar, Y.M.; Dillinger, J.K.; Wustenhagen, M.; Kier, T.M.; Looye, G.; et al. Results of an Aeroelastically Tailored Wing on the FLEXOP Demonstrator Aircraft. In Proceedings of the AIAA Scitech 2020 Forum, American Institute of Aeronautics and Astronautics, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]









| Planform Properties | |
| Semi-span | 3.536 m |
| Root chord | 0.4713 m |
| Tip chord | 0.2357 m |
| Leading edge sweep | 20° |
| Airfoil thickness, root | 10% chord |
| Airfoil thickness, tip | 8% chord |
| Wing Box | |
| Front spar position | 15% chord |
| Rear spar position | 71% chord |
| Operating requirements | |
| Atmosphere | ISA |
| Cruise speed | 45 m/s (TAS) |
| Cruise altitude ASL | 800 m |
| Landing speed | 20 m/s |
| Landing altitude ASL | 500 m |
| Limit load positive | 5 g at cruise speed and altitude |
| Limit load negative | −2 g at cruise speed and altitude |
| Safety requirements | |
| Safety factor (SF) | 1.5 |
| Knockdown factor (KDF) | (B-basis) 90 °C/W/BVID |
| Stiffness | Average value |
| Strength | 1/SF*KDF*material allowable |
| Buckling | SF*(B-basis KDF)*crit. load |
| One g shape requirement | |
| Twist | Linear var. root/tip: 0° to −2° |
| Twist tolerance | +/− 0.05° |
| Tip deflection | No requirement |
| Mass (kg) | Root Bending Moment (Nm) | |||
|---|---|---|---|---|
| 1 g | 5 g | −2 g | ||
| Stiffness-opt. (reference) | 5.884 | 304 | 1662 | −726 |
| Stiffness-opt. (tailored) | 5.652 (0.96) | 305 | 1555 (0.94) | −647 (0.89) |
| Stacking seq. (reference) | 6.878 | 311.0 | 1697.7 | −729.6 |
| Stacking seq. (tailored) | 6.307 (0.92) | 314.2 | 1651.9 (0.97) | −689.0 (0.94) |
| Mode | GVT (Hz) | FE (Hz) | |
|---|---|---|---|
| 2n_wing_bend-s | 3.27 | 3.28 | −0.43 |
| 3n_wing_bend-a | 8.28 | 7.07 | 14.3 |
| 1n_wing_inplane-a | 8.88 | 18.21 | - |
| 4n_wing_bend-s | 12.12 | 11.05 | 8.8 |
| tail_rock-a | 17.32 | - | - |
| 1n_wing_inplane-s | 19.26 | 18.23 | 5.4 |
| Reference Wing | Tailored Wing | |||
|---|---|---|---|---|
| Manoeuvre No. | Load Factor (g) | Airspeed (m/s) | Load Factor (g) | Airspeed (m/s) |
| 1 | 2.30 | 50.1 | 2.86 | 53.6 |
| 2 | 2.60 | 50.0 | 2.47 | 50.0 |
| 3 | 2.36 | 44.6 | 2.15 | 45.1 |
| 4 | 2.65 | 49.1 | 2.22 | 46.6 |
| 5 | 3.06 | 51.8 | 2.43 | 50.7 |
| 6 | 2.26 | 47.2 | 2.46 | 49.6 |
| 7 | 2.50 | 53.0 | ||
| 8 | 2.33 | 44.7 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krüger, W.R.; Meddaikar, Y.M.; Dillinger, J.K.S.; Sodja, J.; De Breuker, R. Application of Aeroelastic Tailoring for Load Alleviation on a Flying Demonstrator Wing. Aerospace 2022, 9, 535. https://doi.org/10.3390/aerospace9100535
Krüger WR, Meddaikar YM, Dillinger JKS, Sodja J, De Breuker R. Application of Aeroelastic Tailoring for Load Alleviation on a Flying Demonstrator Wing. Aerospace. 2022; 9(10):535. https://doi.org/10.3390/aerospace9100535
Chicago/Turabian StyleKrüger, Wolf R., Yasser M. Meddaikar, Johannes K. S. Dillinger, Jurij Sodja, and Roeland De Breuker. 2022. "Application of Aeroelastic Tailoring for Load Alleviation on a Flying Demonstrator Wing" Aerospace 9, no. 10: 535. https://doi.org/10.3390/aerospace9100535
APA StyleKrüger, W. R., Meddaikar, Y. M., Dillinger, J. K. S., Sodja, J., & De Breuker, R. (2022). Application of Aeroelastic Tailoring for Load Alleviation on a Flying Demonstrator Wing. Aerospace, 9(10), 535. https://doi.org/10.3390/aerospace9100535







