Fuzzy Logic-Based Energy Management Strategy of Hybrid Electric Propulsion System for Fixed-Wing VTOL Aircraft
Abstract
:1. Introduction
2. System Modeling
2.1. Mission Profile
2.2. Dynamic Model
2.2.1. Rotor Mode
2.2.2. Fixed-Wing Mode
2.3. Hybrid Electric Propulsion System Model
2.3.1. Hybrid Electric Propulsion System Structure
2.3.2. ICE Model
2.3.3. IOL Controller Model
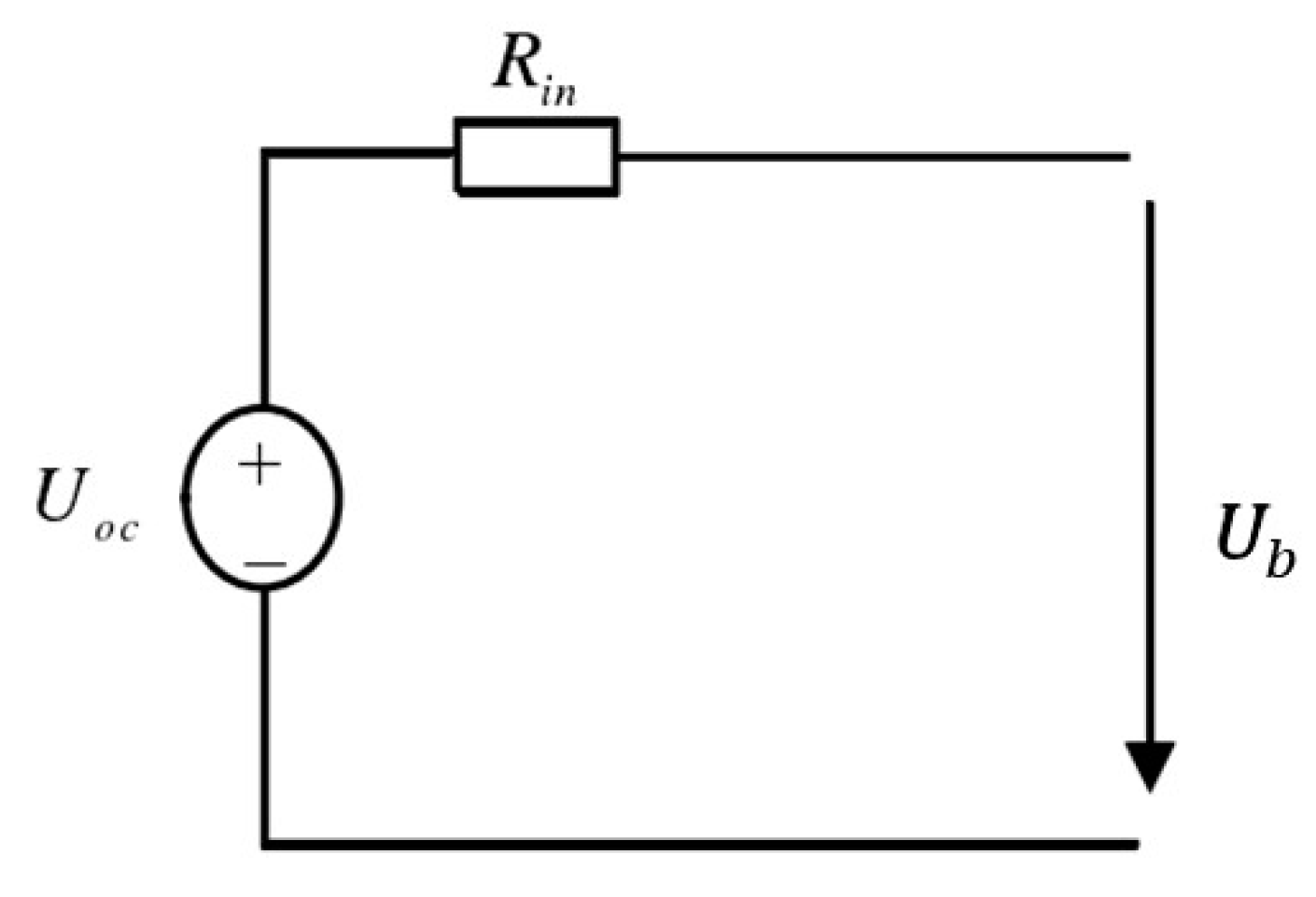
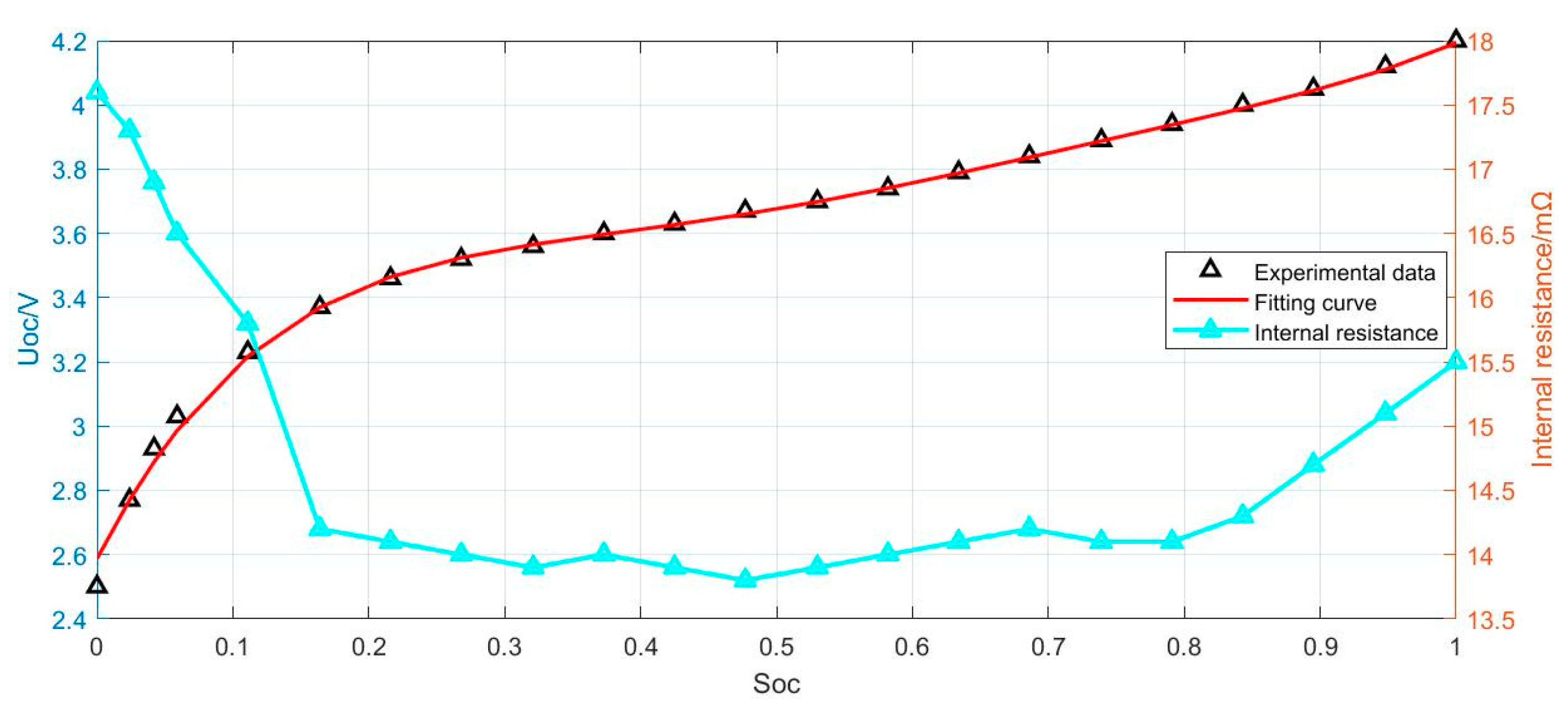
2.3.4. Battery Model
3. Energy Management Strategy
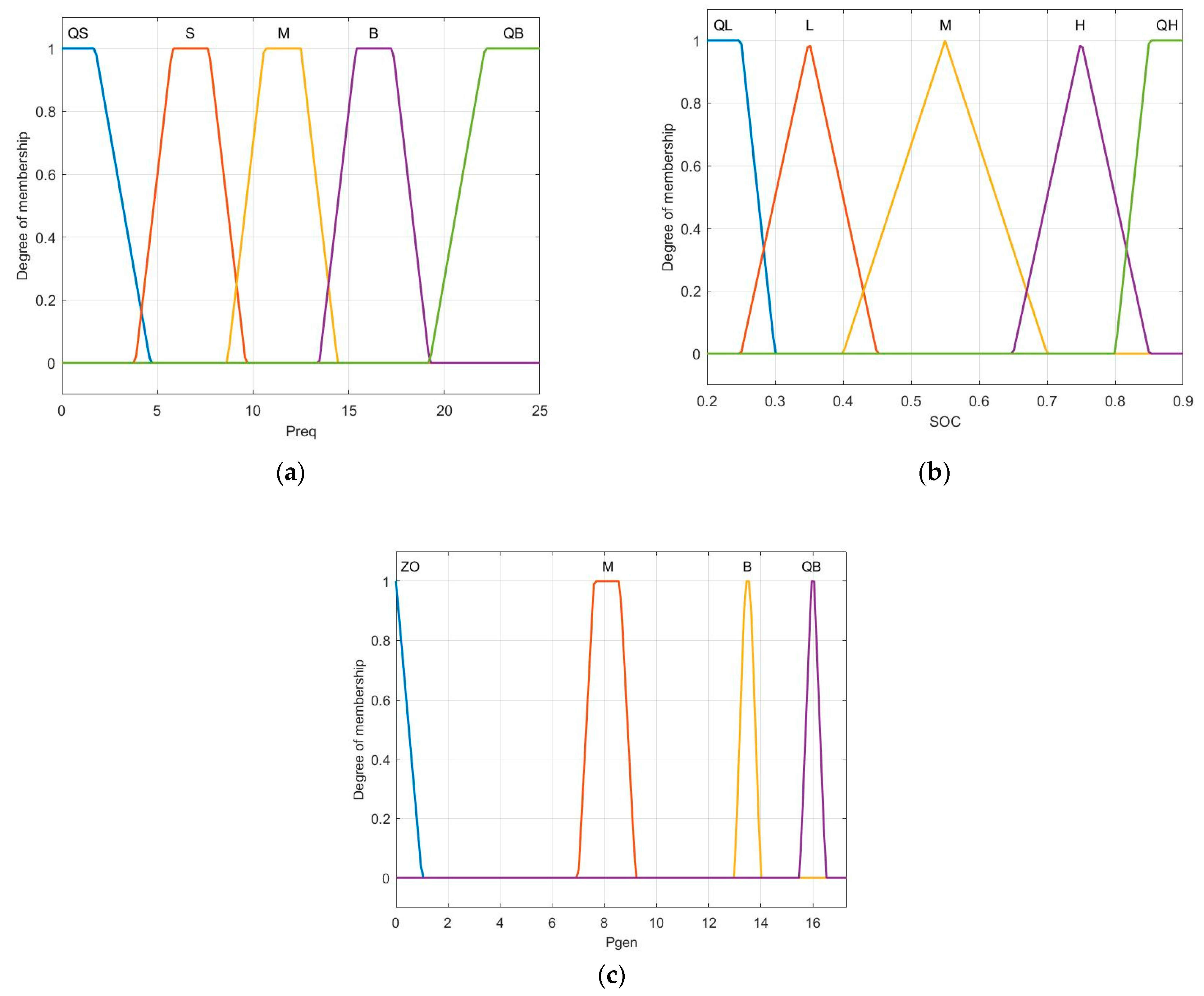
3.1. Membership Function Setting
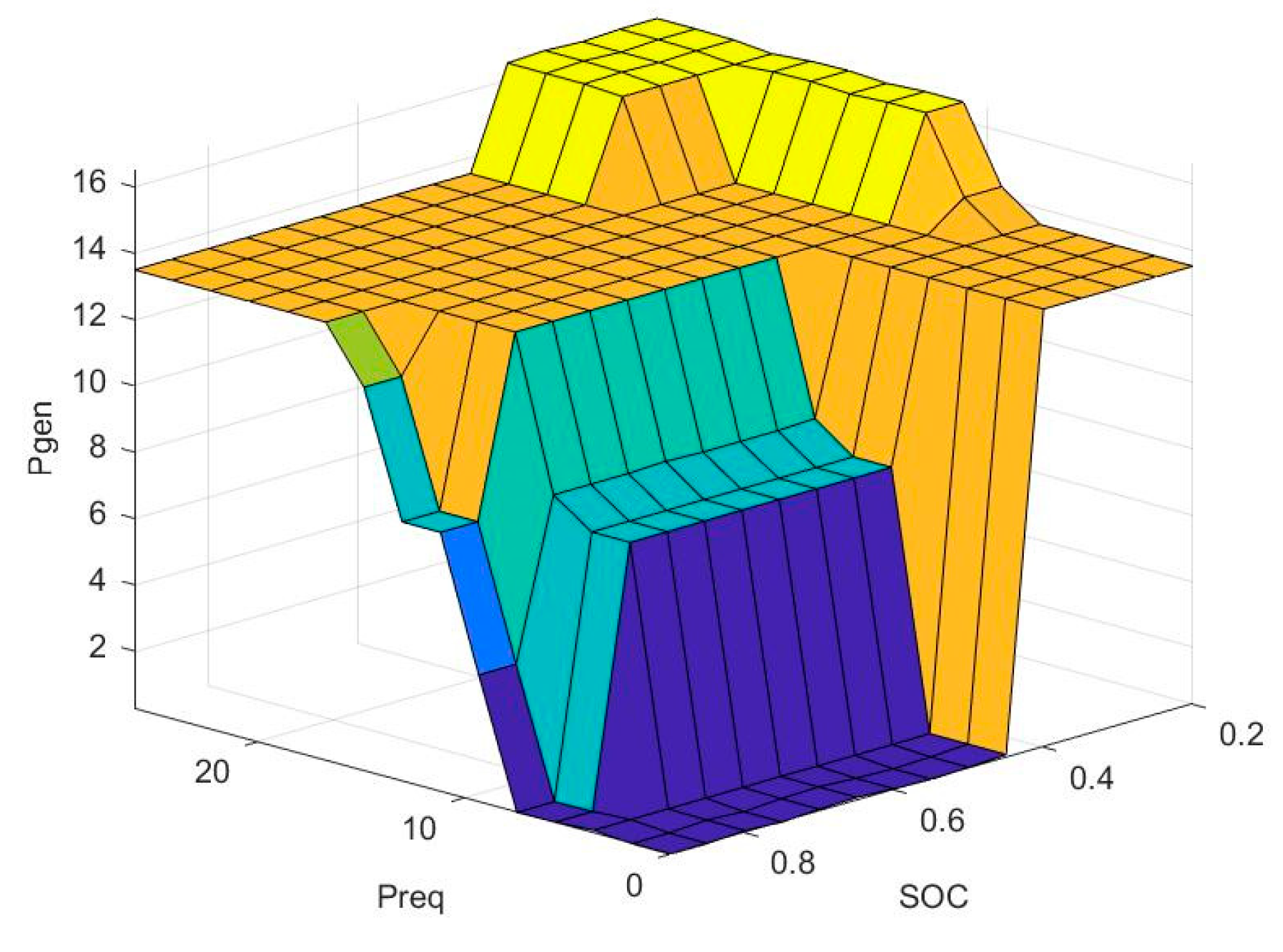
3.2. Fuzzy Logic Rule Setting
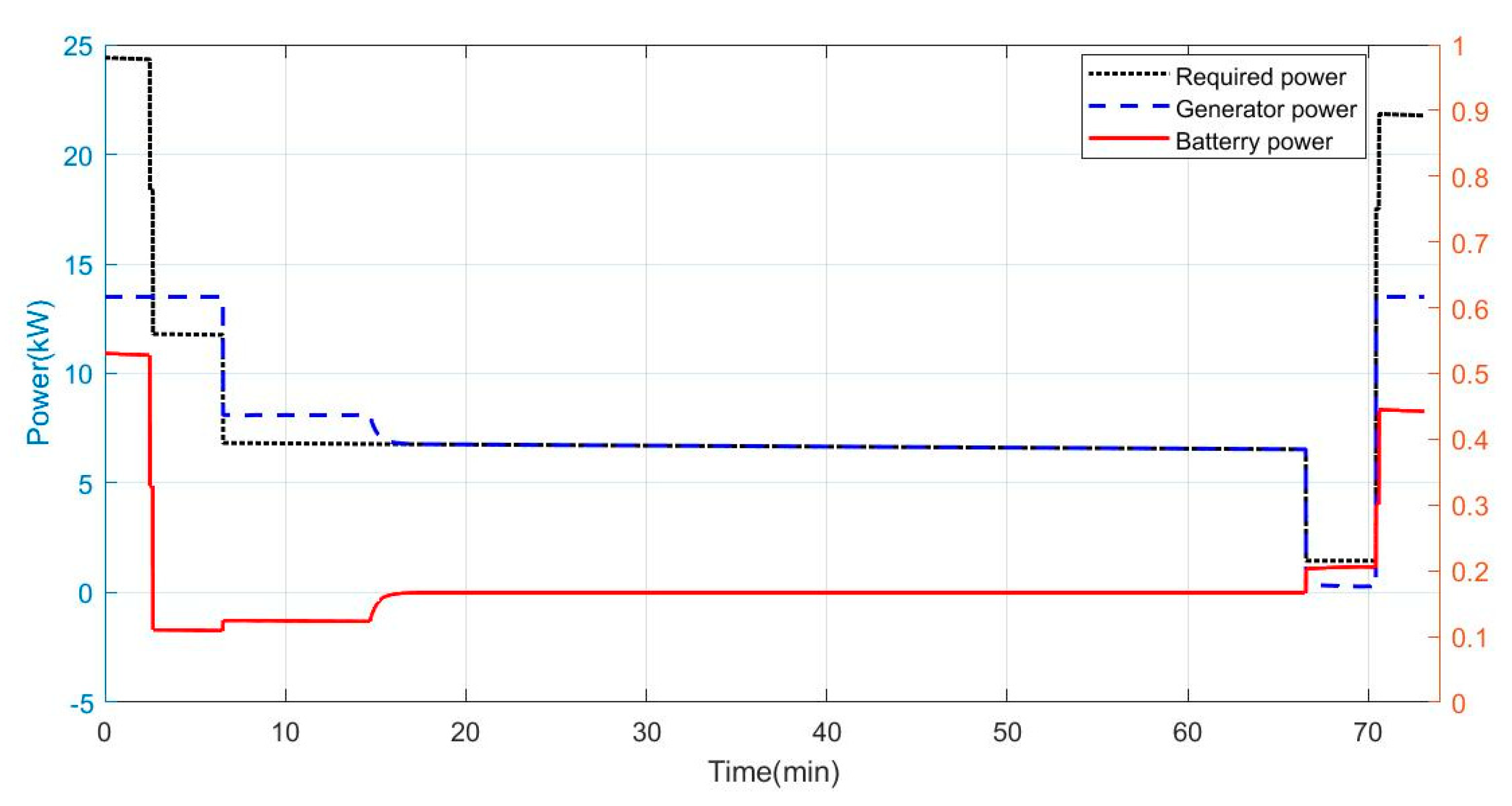
4. Simulation and Analysis
- (1)
- When the power requirement is greater than the maximum output power of the generator, the ICE outputs the maximum power, and the remaining power is supplemented by the battery pack.
- (2)
- When the power requirement is less than the maximum output power of the generator, the output power of the generator is equal to the power requirement of the aircraft.
- (3)
- After entering the cruise stage, the battery pack is charged, and the output power of the generator is equal to the sum of the power requirement of the aircraft and the charging power
5. Conclusions
- (1)
- The fixed-wing VTOL aircraft has different working modes in different flight stages, resulting in a large jump in power requirements. The power of the VTOL stage is more than three times that of the cruise stage, while the power of the descent stage is only about a quarter of that in the cruise stage. The hybrid electric propulsion system combines the high specific energy and specific power of the battery, which can not only reduce the size of the ICE, but also improve the overall efficiency of the system by rationally allocating the output power of the two energy sources.
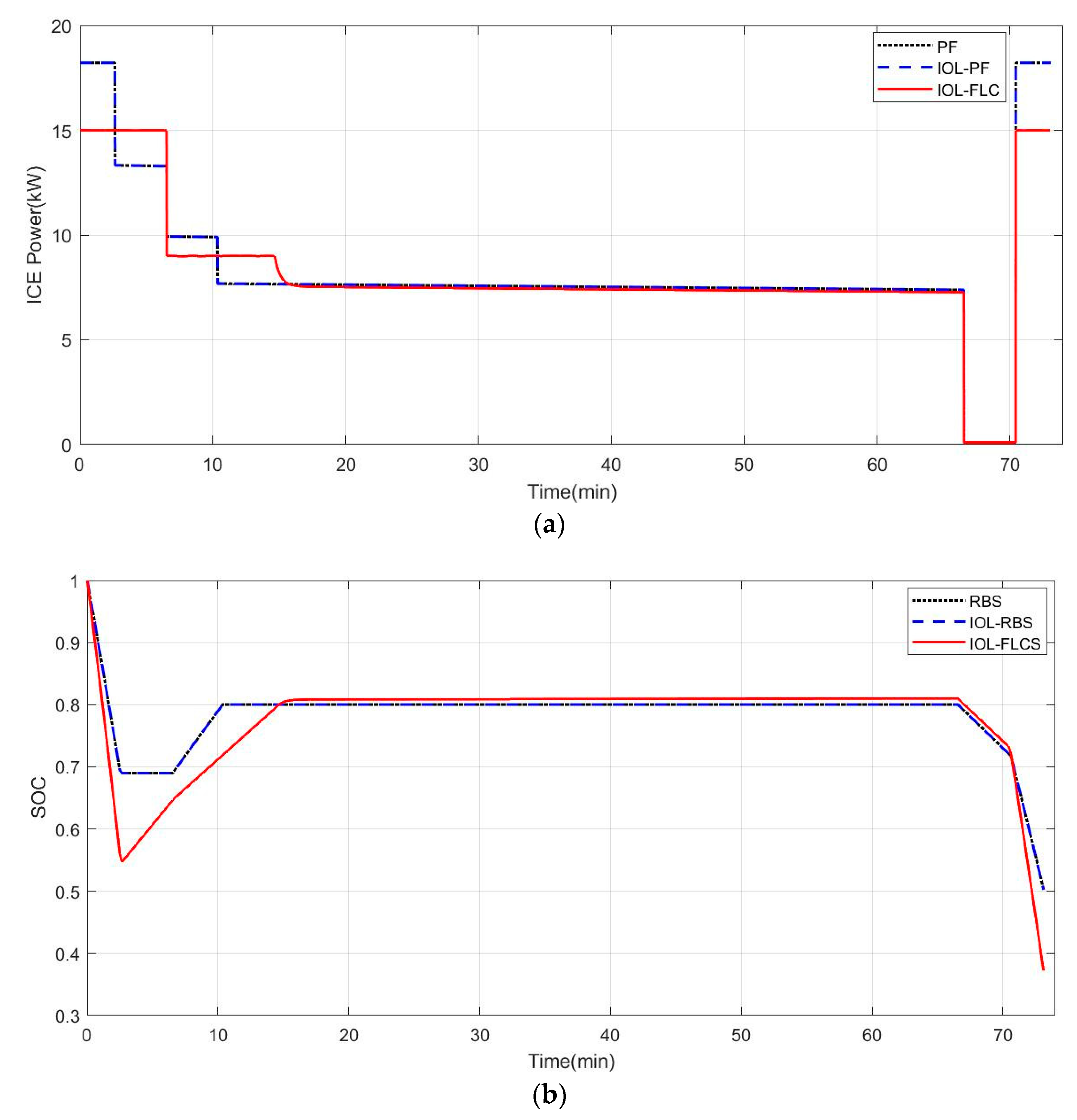
- (2)
- Combining the universal characteristic map of the ICE to find the ideal operating line, running the ICE based on the IOL can make the ICE work at the optimal operating point under the given output power, thereby improving the efficiency. Under the simulation conditions of this paper, the fuel consumption saved was 2.8%. After the introduction of the IOL, the flexible transformation between the output power and the operating point (torque, speed) of the ICE is realized, which is beneficial to the optimization of the energy management.
- (3)
- The EMS based on fuzzy logic is adopted, and the output power of the generator and the battery pack is dynamically and optimally allocated according to the power requirement of the aircraft and the SOC of the battery pack, so that the ICE works in the efficient operating area most of the time, thereby improving the fuel economy of the system and the range of the aircraft. Additionally, it is different from the dynamic programming strategy that needs to know the working conditions in advance; the EMS based on fuzzy logic can perform online optimal control under the condition of unknown working conditions.
- (1)
- The IOL-FLCS should be verified in the hardware system, combined with theoretical simulation data and experimental data to improve the practicability of the EMS.
- (2)
- An EMS can be established that comprehensively considers fuel consumption and emissions. This further study needs to be carried out based on the emission characteristic map of the ICE.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Atluri, S.N. A Four-Node Hybrid Assumed-Strain Finite Element for Laminated Composite Plates. Tech Science Press: Henderson, NV, USA, 2004. [Google Scholar]
- Lenssen, R.H. Series Hybrid Electric Aircraft. Master’s Thesis, Delft University of Technology, Delft, Holland, 2016. [Google Scholar]
- Oelberg, E. A Hybrid Optimal Control Approach to Maximum Endurance of Aircraft. Master’s Thesis, The Department of Electrical and Computer Engineering, Concordia University, Montreal, QC, Canada, 2018. [Google Scholar]
- Friedrich, C.; Robertson, P.A. Design of hybrid-electric propulsion systems for light aircraft. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Riboldi, C.E.D. An optimal approach to the preliminary design of small hybrid-electric aircraft. Aerosp. Sci. Technol. 2018, 81, 14–31. [Google Scholar] [CrossRef]
- Li, S.; Gu, C.; Zhao, P.; Cheng, S. A novel hybrid propulsion system configuration and power distribution strategy for light electric aircraft. Energy Convers. Manag. 2021, 238, 114171. [Google Scholar] [CrossRef]
- Ji, Z.; Rokni, M.M.; Qin, J.; Zhang, S.; Dong, P. Energy and configuration management strategy for battery/fuel cell/jet engine hybrid propulsion and power systems on aircraft. Energy Convers. Manag. 2020, 225, 113393. [Google Scholar] [CrossRef]
- Hung, J.Y.; Gonzalez, L.F. On parallel hybrid-electric propulsion system for unmanned aerial vehicles. Prog. Aerosp. Sci. 2012, 51, 1–17. [Google Scholar] [CrossRef]
- Xie, Y.; Savvaris, A.; Tsourdos, A. Fuzzy logic based equivalent consumption optimization of a hybrid electric propulsion system for unmanned aerial vehicles. Aerosp. Sci. Technol. 2019, 85, 13–23. [Google Scholar] [CrossRef]
- Liu, W. Hybrid Electric Vehicle System Modeling and Control; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 288–347. [Google Scholar] [CrossRef]
- Chen, G.; Ma, D.; Jia, Y.; Xia, X.; He, C. Comprehensive sizing and optimization method for series-hybrid unmanned convertiplane. Chin. J. Aeronaut. 2020, 34, 16. [Google Scholar] [CrossRef]
- Pulham, J. Designing unmanned aircraft systems: A comprehensive approach. Aeronaut. J. 2012, 116, 981–982. [Google Scholar] [CrossRef]
- Keith, J.; Hall, D. Rapid Sizing Methodologies for VTOL UAVs. In Proceedings of the AIAA Aerospace Sciences Meeting Including the New Horizons Forum & Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Tyan, M.; Van Nguyen, N.; Kim, S.; Lee, J.W. Comprehensive preliminary sizing/resizing method for a fixed wing VTOL electric UAV. Aerosp. Sci. Technol. 2012, 71, 30–41. [Google Scholar] [CrossRef]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: London, UK, 2002. [Google Scholar]
- Gao, X.Z.; Hou, Z.X.; Zheng, G.; Liu, J.X.; Chen, X.Q. Energy management strategy for solar-powered high-altitude long-endurance aircraft. Energy Convers. Manag. 2013, 70, 20–30. [Google Scholar] [CrossRef]
- Friedrich, C.; Robertson, P.A. Hybrid-Electric Propulsion for Aircraft. J. Aircr. 2015, 52, 176–189. [Google Scholar] [CrossRef]
- Available online: http://limbach.cn/ae/products/ICEs-15kw-40kw.html (accessed on 20 April 2022).
- Oudijk, M.F. Optimization of CVT Control: For Hybrid and Conventional Drive Lines. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, University of California, Davis, CA, USA, 2005. [Google Scholar]
- Kermani, S.; Delprat, S.; Guerra, T.M.; Trigui, R. Real time control of hybrid electric vehicle on a prescribed road. IFAC Proc. Vol. 2008, 41, 3356–3361. [Google Scholar] [CrossRef]
- Peukert, W. Über die Abhängigkeit der Kapazität von der Entladestromstärke bei Bleiakkumulatoren. Elektrotechnische Z. 1897, 20, 20–21. [Google Scholar]
- Su, Y.; Liahng, H.; Wu, J. Multilevel Peukert equations based residual capacity estimation method for lead-acid batteries. In Proceedings of the IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 101–105. [Google Scholar]
- Dehesa, D.A.; Menon, S.K. Modeling of Hybrid-Electric Powertrain for Unmanned Aerial Systems. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Wu, J.; Peng, J.; He, H.; Luo, J. Comparative Analysis on the Rule-based Control Strategy of Two Typical Hybrid Electric Vehicle Powertrain. Energy Procedia 2016, 104, 384–389. [Google Scholar] [CrossRef]
- Hou, C.; Ouyang, M.; Xu, L.; Wang, H. Approximate pontryagin minimum principle applied to the energy management of plug-in hybrid electric vehicles. Appl. Energy 2014, 115, 174–189. [Google Scholar] [CrossRef]
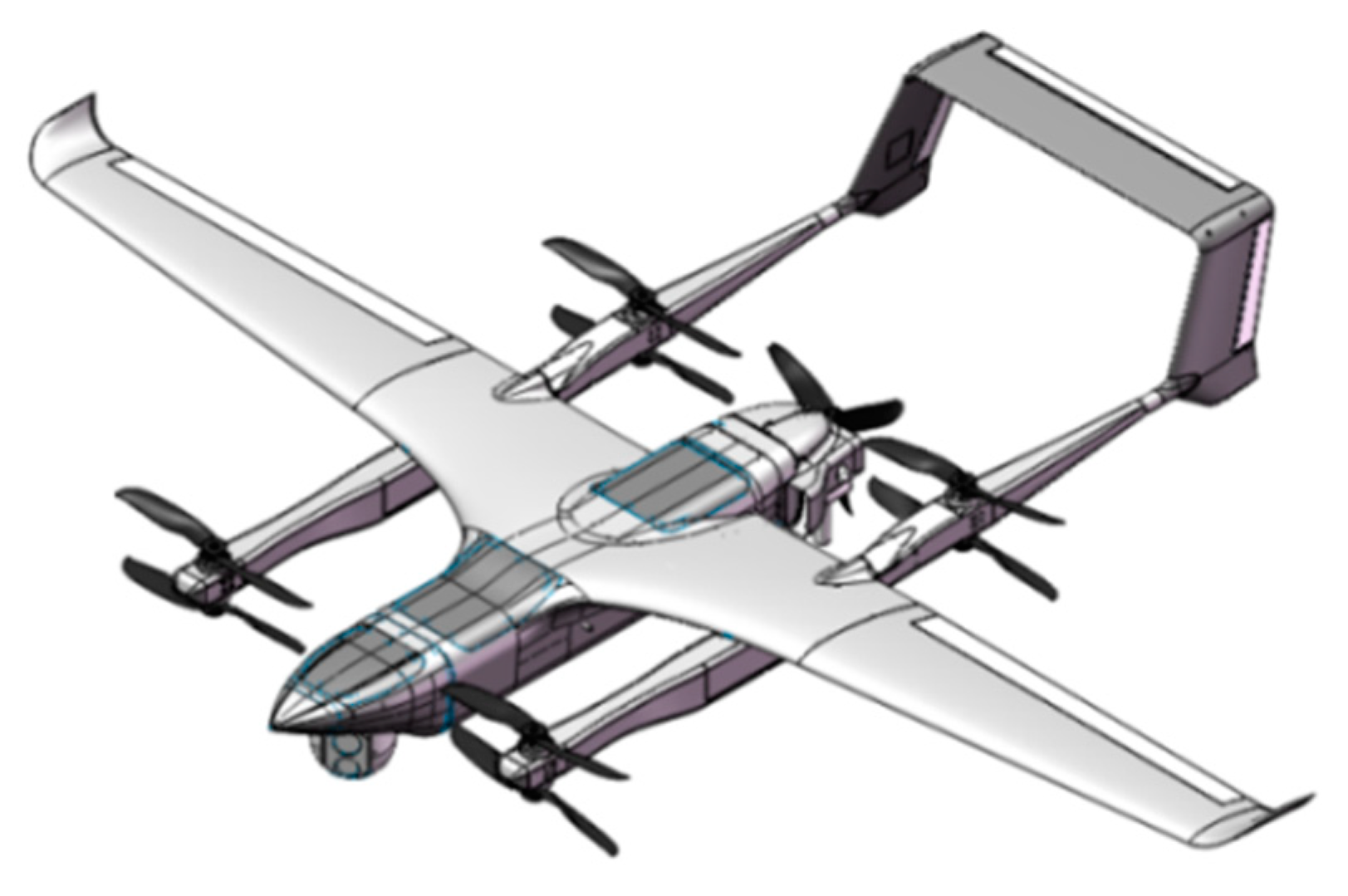

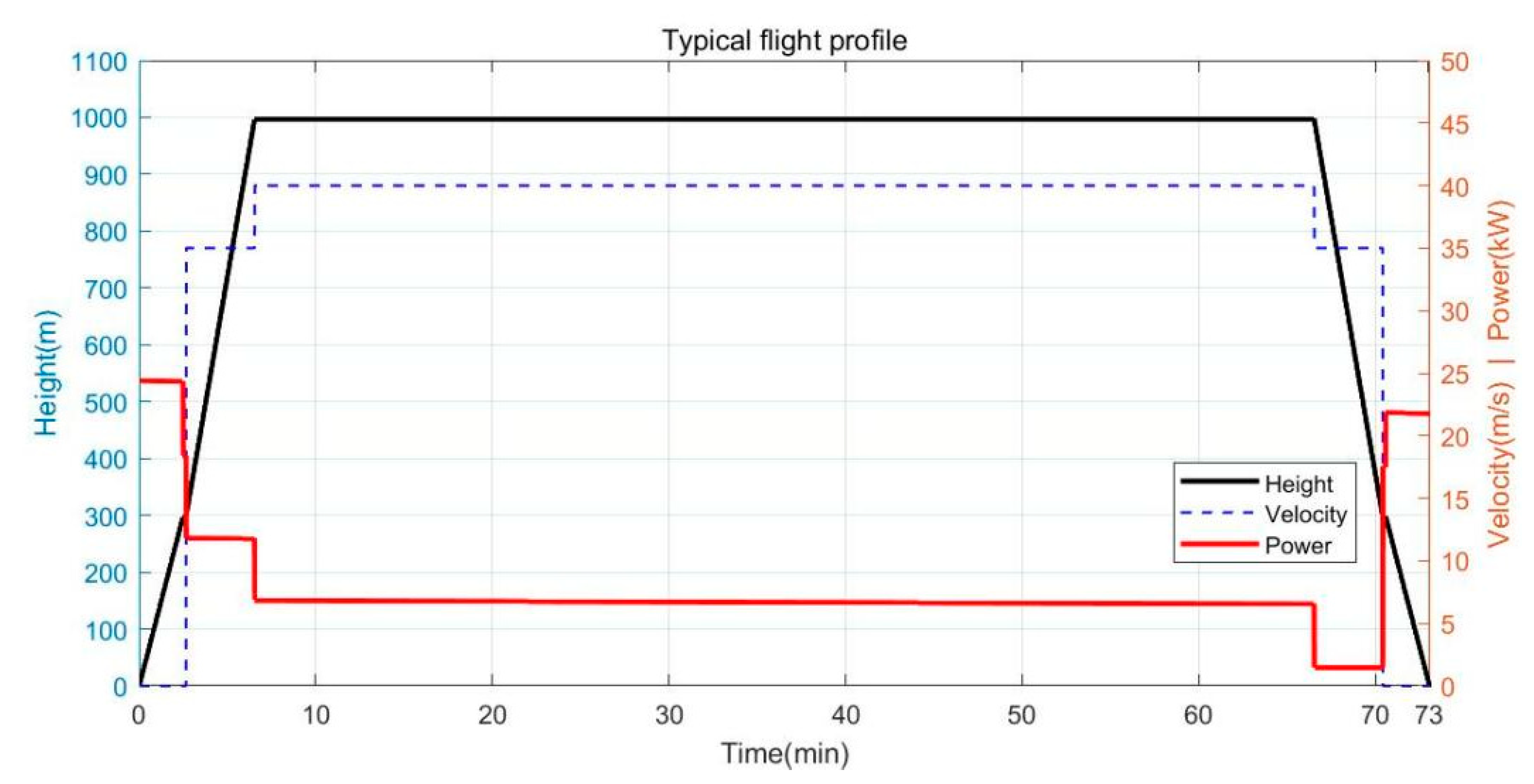


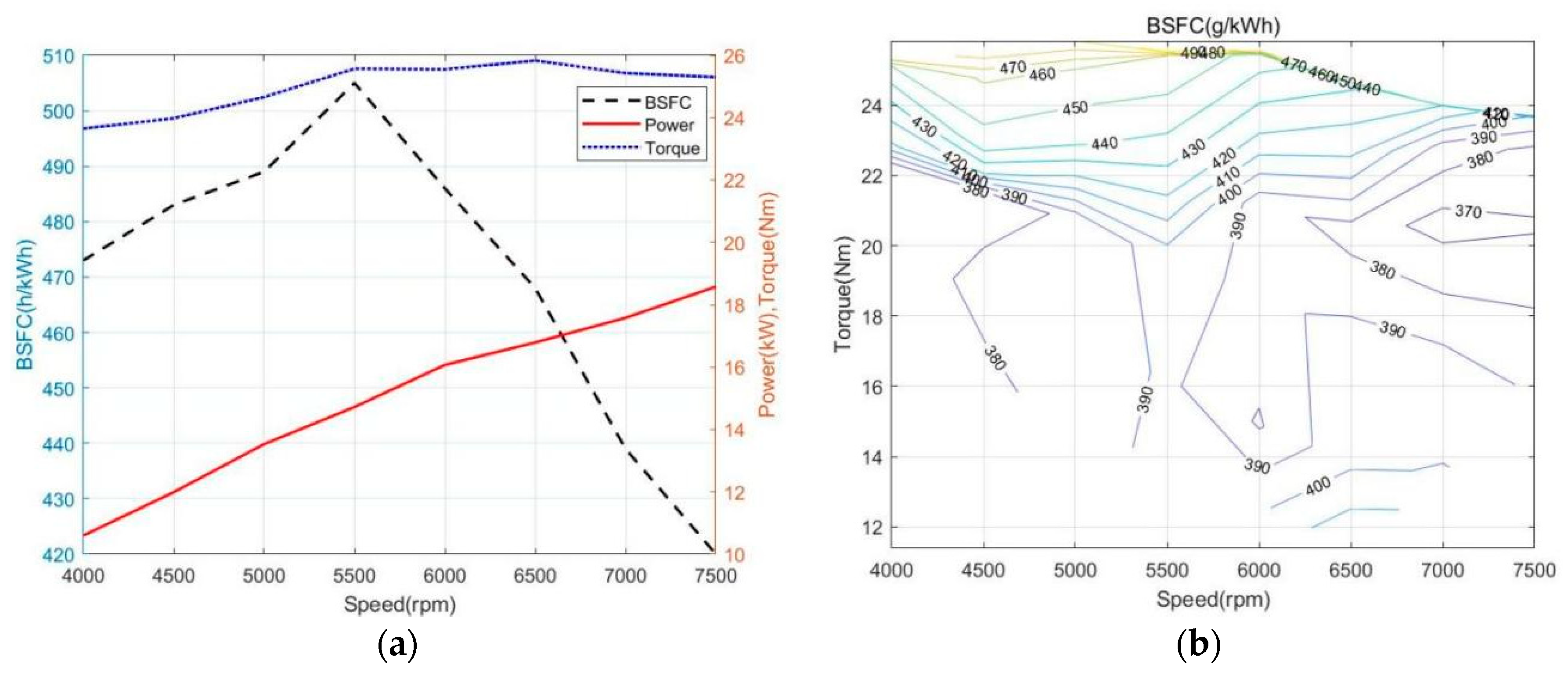
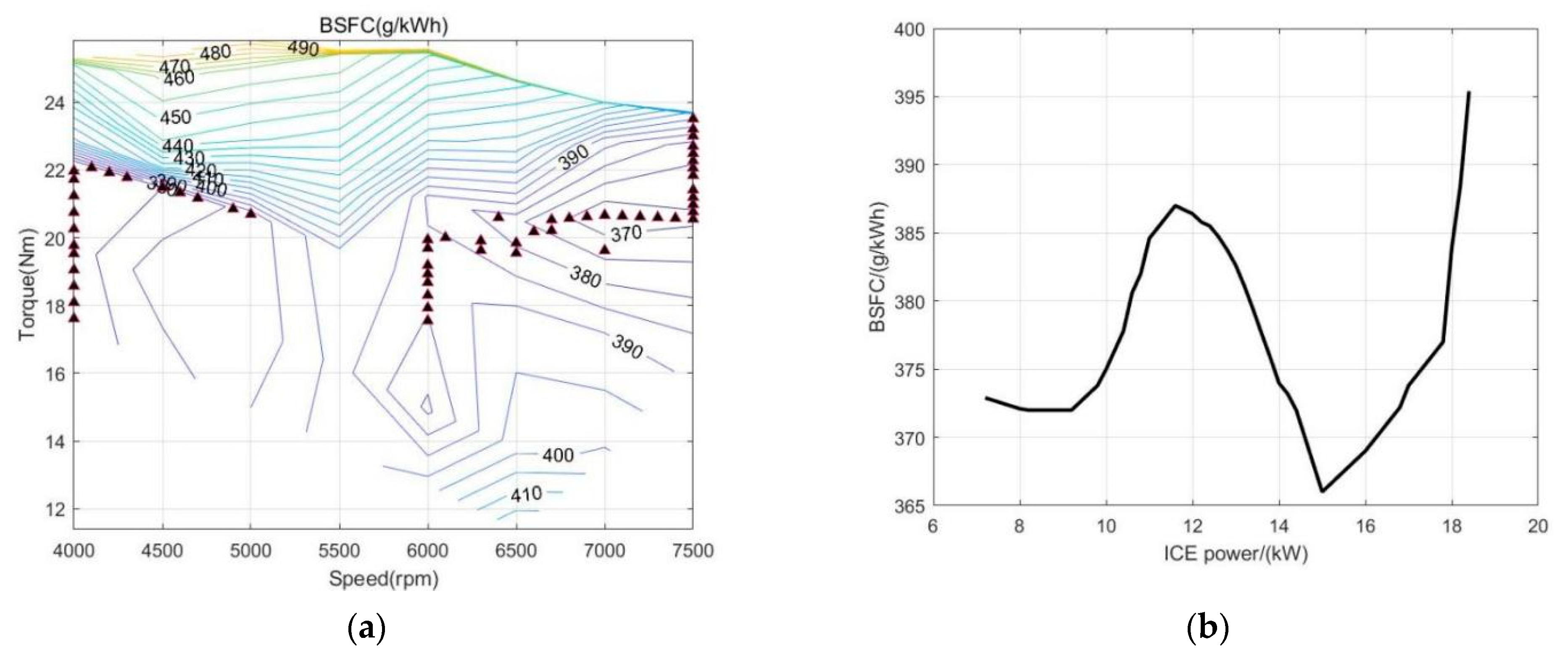



| Parameters | Value | ||
|---|---|---|---|
| Total weight | 12 | VTOL rate | 2 m/s |
| Wingspan | 4.0 m | Climbing/Descent rate | 3 m/s |
| Wing area | 2.5 m2 | VTOL altitude | 300 m |
| Cruise lift coefficient | 0.44 | Cruise altitude | 1000 m |
| Cruise drag coefficient | 0.03 | Propeller efficiency | 65% |
| Cruise lift–drag ratio | 10 | Motor efficiency | 85% |
| Parameters | Value | ||
|---|---|---|---|
| Capacity | 2800 mAh | Internal resistance | 14 mΩ |
| Maximum charge current | 6 A | Mass | 46 g |
| Maximum discharge current | 35 A | Energy density | 220 Wh/kg |
| Rated voltage | 3.6 V | Power density | 2739 W/kg |
| Cutoff voltage | 2.5 V |
| Preq | SOC | ||||
|---|---|---|---|---|---|
| QL | L | M | H | QH | |
| QS | B | B | ZO | ZO | ZO |
| S | B | B | M | M | ZO |
| M | QB | B | B | B | M |
| B | QB | QB | B | B | B |
| QB | QB | QB | B | B | B |
| Components | Parameters | Value | ||||||
|---|---|---|---|---|---|---|---|---|
| ICE | Maximum power | 18.5 kW @7500 rpm | Generator | Efficiency | 93% | Battery pack | Rated Voltage | 100 V |
| Rated power | 15 kW @7000 rpm | Rated voltage | 110 V | Capacity | 11.2 Ah | |||
| Maximum speed | 7500 rpm | Rectifier efficiency | 95% | Maximum discharge/charge current | 140 A/24 A | |||
| Mass | 7 kg | Mass | 4.2 kg | Mass (including BMS) | 5.6 kg |
| RBS | IOL | ||
|---|---|---|---|
| IOL-RBS | IOL-FLCS | ||
| Original SOC (%) | 100 | 100 | 100 |
| Final SOC (%) | 0.50 | 0.50 | 0.37 |
| Fuel consumption (kg) | 3.93 | 3.82 | 3.69 |
| Corrected SOC (%) | 50 | 50 | 50 |
| Corrected fuel consumption (kg) | 3.93 | 3.82 | 3.70 |
| Fuel saving (%) | — | 2.80 | 5.85 |
| IOL-RBS | IOL-FLCS | |
|---|---|---|
| Original SOC (%) | 100 | 100 |
| Final SOC (%) | 50 | 37 |
| Fuel consumption (kg) | 1.534 | 1.438 |
| Corrected final SOC (%) | 50 | 50 |
| Corrected fuel consumption (kg) | 1.534 | 1.453 |
| Fuel saving (%) | - | 5.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhu, B.; Yang, X.; Hou, Z.; Zong, J. Fuzzy Logic-Based Energy Management Strategy of Hybrid Electric Propulsion System for Fixed-Wing VTOL Aircraft. Aerospace 2022, 9, 547. https://doi.org/10.3390/aerospace9100547
Zhu Y, Zhu B, Yang X, Hou Z, Zong J. Fuzzy Logic-Based Energy Management Strategy of Hybrid Electric Propulsion System for Fixed-Wing VTOL Aircraft. Aerospace. 2022; 9(10):547. https://doi.org/10.3390/aerospace9100547
Chicago/Turabian StyleZhu, Yingtao, Bingjie Zhu, Xixiang Yang, Zhongxi Hou, and Jianan Zong. 2022. "Fuzzy Logic-Based Energy Management Strategy of Hybrid Electric Propulsion System for Fixed-Wing VTOL Aircraft" Aerospace 9, no. 10: 547. https://doi.org/10.3390/aerospace9100547
APA StyleZhu, Y., Zhu, B., Yang, X., Hou, Z., & Zong, J. (2022). Fuzzy Logic-Based Energy Management Strategy of Hybrid Electric Propulsion System for Fixed-Wing VTOL Aircraft. Aerospace, 9(10), 547. https://doi.org/10.3390/aerospace9100547







