Three-Dimensional Analytical Solutions for Acoustic Transverse Modes in a Cylindrical Duct with Axial Temperature Gradient and Non-Zero Mach Number
Abstract
:1. Introduction
2. Wave Equation for Three-Dimensional Acoustic Waves
3. Analytical Solutions of Three-Dimensional Acoustic Wave
3.1. Analytical Solutions of the Axial ODE Using a Modified WKB Approximation Method
3.2. Solutions of the Three-Dimensional Velocity Perturbations
4. Case of Zero Mean Flow
5. Sound Responses to Forced Inlet Pressure Perturbations
5.1. Validation Configuration
5.2. Reconstructions of Sound Responses
6. Predictions of Resonant Frequencies and Linear Instabilities for Transverse Modes
6.1. Boundary Conditions and Eigenvalue Matrix
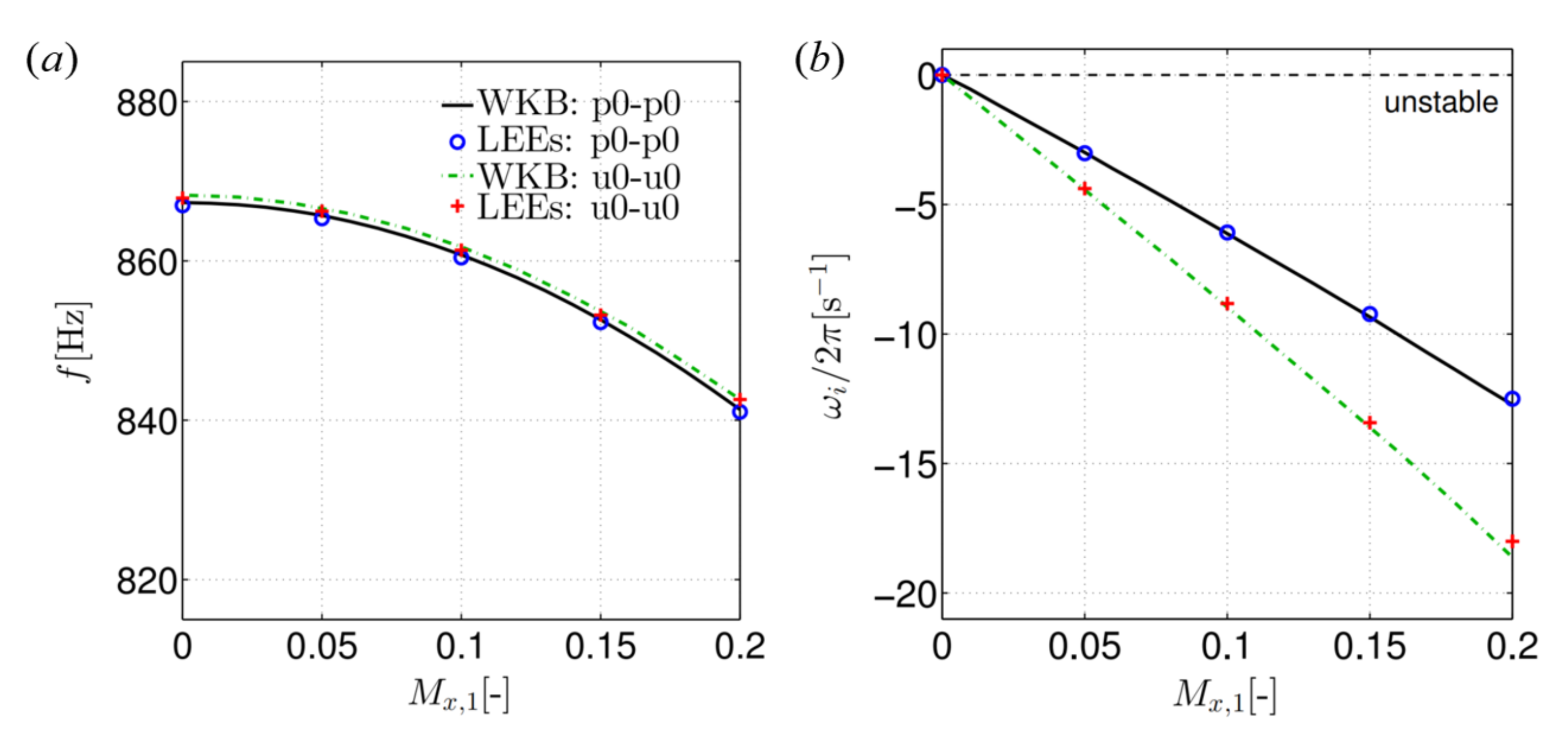
6.2. Effect of Mean Flow and Temperature Gradient on Resonant Frequencies and Instabilities
6.3. Transverse Modes with Different Boundary Conditions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c | local speed of sound |
| heat capacity at constant pressure | |
| f | frequency |
| transfer function | |
| i | imaginary unit, −i2=1 |
| local wavenumber, | |
| l | duct length |
| flow Mach number in the x direction | |
| radial wavenumber | |
| circumferential wavenumber | |
| p | pressure |
| heat flux | |
| radius of the cylindrical duct | |
| universal gas constant | |
| s | entropy |
| t | time |
| T | temperature |
| velocity vector in the cylindrical polar coordinates | |
| cylindrical polar coordinates | |
| density | |
| angular frequency | |
| specific heat ratio | |
| vorticity, | |
| dimensionless frequency, | |
| dimensionless cut-off frequency | |
| steady flow variable | |
| spatial component of unsteady flow variable | |
| flow property at the duct inlet | |
| flow property at the duct outlet |
References
- Yang, V.; Anderson, W.E. Liquid Rocket Engine Combustion Instability; AIAA, Inc.: Reston, VA, USA, 1995. [Google Scholar]
- Lieuwen, T.; Yang, V. Combustion Instabilities in Gas Turbine Engines: Operational Experience Fundamental Mechanisms and Modeling; AIAA, Inc.: Reston, VA, USA, 2005. [Google Scholar]
- Candel, S. Combustion dynamics and control: Progress and challenges. Proc. Combust. Inst. 2002, 29, 1–28. [Google Scholar] [CrossRef]
- Dowling, A.P.; Morgans, A.S. Feedback control of combustion oscillations. Annu. Rev. Fluid Mech. 2005, 37, 151–182. [Google Scholar] [CrossRef]
- Poinsot, T. Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 2017, 36, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Xia, Y.; Morgans, A.S.; Han, X. Numerical prediction of combustion instability limit cycle oscillations for a combustor with a long flame. Combust. Flame 2017, 185, 28–43. [Google Scholar] [CrossRef]
- Staffelbach, G.; Gicquel, L.; Boudier, G.; Poinsot, T. Large Eddy Simulation of self excited azimuthal modes in annular combustors. Proc. Combust. Inst. 2009, 32, 2909–2916. [Google Scholar] [CrossRef] [Green Version]
- Gicquel, L.; Staffelbach, G.; Poinsot, T. Large Eddy Simulations of gaseous flames in gas turbine combustion chambers. Prog. Energy Combust. Sci. 2012, 38, 782–817. [Google Scholar] [CrossRef] [Green Version]
- Urbano, A.; Selle, L.; Staffelbach, G.; Cuenot, B.; Schmitt, T.; Ducruix, S.; Candel, S. Exploration of combustion instability triggering using large eddy simulation of a multiple injector liquid rocket engine. Combust. Flame 2016, 169, 129–140. [Google Scholar] [CrossRef] [Green Version]
- Noiray, N.; Durox, D.; Schuller, T.; Cande, S. A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 2008, 615, 139–167. [Google Scholar] [CrossRef]
- Krediet, H.; Beck, C.; Krebs, W.; Kok, J. Saturation mechanism of the heat release response of a premixed swirl flame using LES. Proc. Combust. Inst. 2013, 34, 1223–1230. [Google Scholar] [CrossRef]
- Han, X.; Li, J.; Morgans, A.S. Prediction of combustion instability limit cycle oscillations by combining flame describing function simulations with a thermoacoustic network model. Combust. Flame 2015, 162, 3632–3647. [Google Scholar] [CrossRef]
- Schuller, T.; Poinsot, T.; Candel, S. Dynamics and control of premixed combustion systems based on flame transfer and describing functions. J. Fluid Mech. 2020, 894. [Google Scholar] [CrossRef]
- Polifke, W. Modeling and analysis of premixed flame dynamics by means of distributed time delays. Prog. Energy Combust. Sci. 2020, 79, 100845. [Google Scholar] [CrossRef]
- Polifke, W.; Poncet, A.; Paschereit, C.; Döbbeling, K. Reconstruction of acoustic transfer matrices by instationary computational fluid dynamics. J. Sound Vib. 2001, 245, 483–510. [Google Scholar] [CrossRef]
- Stow, S.R.; Dowling, A.P. A time-domain network model for nonlinear thermoacoustic oscillations. J. Eng. Gas Turbines Power 2009, 131, 031502. [Google Scholar] [CrossRef]
- Bauerheim, M.; Parmentier, J.F.; Salas, P.; Nicoud, F.; Poinsot, T. An analytical model for azimuthal thermoacoustic modes in an annular chamber fed by an annular plenum. Combust. Flame 2014, 161, 1374–1389. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Morgans, A.S. Time domain simulations of nonlinear thermoacoustic behaviour in a simple combustor using a wave-based approach. J. Sound Vib. 2015, 346, 345–360. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Morgans, A.S. Acoustic Models for Cooled Helmholtz Resonators. AIAA J. 2017, 55, 3120–3127. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Yang, D.; Li, S.; Zhu, M. An analytical study of the effect of flame response to simultaneous axial and transverse perturbations on azimuthal thermoacoustic modes in annular combustors. Proc. Combust. Inst. 2019, 37, 5279–5287. [Google Scholar] [CrossRef]
- Laurent, C.; Badhe, A.; Nicoud, F. Representing the geometrical complexity of liners and boundaries in low-order modeling for thermoacoustic instabilities. J. Comput. Phys. 2021, 428, 110077. [Google Scholar] [CrossRef]
- Li, L.; Sun, X. Effect of vorticity waves on azimuthal instabilities in annular chambers. Combust. Flame 2015, 162, 628–641. [Google Scholar] [CrossRef]
- Schulze, M.; Sattelmayer, T. Linear stability assessment of a cryogenic rocket engine. Int. J. Spray Combust. Dyn. 2017, 9, 277–298. [Google Scholar] [CrossRef] [Green Version]
- Meindl, M.; Silva, C.F.; Polifke, W. On the spurious entropy generation encountered in hybrid linear thermoacoustic models. Combust. Flame 2021, 223, 525–540. [Google Scholar] [CrossRef]
- Zhao, D. Transient growth of flow disturbances in triggering a Rijke tube combustion instability. Combust. Flame 2012, 159, 2126–2137. [Google Scholar] [CrossRef]
- Kashinath, K.; Hemchandra, S.; Juniper, M.P. Nonlinear thermoacoustics of ducted premixed flames: The influence of perturbation convection speed. Combust. Flame 2013, 160, 2856–2865. [Google Scholar] [CrossRef]
- Meindl, M.; Albayrak, A.; Polifke, W. A state-space formulation of a discontinuous galerkin method for thermoacoustic stability analysis. J. Sound Vib. 2021, 481, 115431. [Google Scholar] [CrossRef]
- Silva, C.F.; Nicoud, F.; Schuller, T.; Durox, D.; Candel, S. Combining a helmholtz solver with the flame describing function to assess combustion instability in a premixed swirled combustor. Combust. Flame 2013, 160, 1743–1754. [Google Scholar] [CrossRef] [Green Version]
- Laera, D.; Camporeale, S.M. A Weakly Nonlinear Approach Based on a Distributed Flame Describing Function to Study the Combustion Dynamics of a Full-Scale Lean-Premixed Swirled Burner. J. Eng. Gas Turbines Power 2017, 139, 091501. [Google Scholar] [CrossRef]
- Schuermans, B. Modeling and Control of Thermoacoustic Instabilities. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2003. [Google Scholar]
- Li, J.; Yang, D.; Luzzato, C.; Morgans, A.S. OSCILOS: The Open Source Combustion Instability Low Order Simulator. Technical Report. Imperial College London. 2014. Available online: http://www.oscilos.com (accessed on 26 July 2021).
- You, D.; Ku, D.D.; Yang, V. Acoustic waves in baffled combustion chamber with radial and circumferential blades. J. Propul. Power 2013, 29, 1453–1467. [Google Scholar] [CrossRef] [Green Version]
- Dowling, A.P.; Stow, S.R. Acoustic analysis of gas turbine combustors. J. Propul. Power 2003, 19, 751–764. [Google Scholar] [CrossRef]
- Schuermans, B.; Guethe, F.; Pennell, D.; Guyot, D.; Paschereit, C.O. Thermoacoustic Modeling of a Gas Turbine Using Transfer Functions Measured Under Full Engine Pressure. J. Eng. Gas Turbines Power 2010, 132, 111503. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; R.T. Edwards Inc.: Philadelphia, PA, USA, 2005. [Google Scholar]
- Palies, P.; Durox, D.; Schuller, T.; Candel, S. Nonlinear combustion instability analysis based on the flame describing function applied to turbulent premixed swirling flames. Combust. Flame 2011, 158, 1980–1991. [Google Scholar] [CrossRef]
- Orchini, A.; Juniper, M.P. Flame double input describing function analysis. Combust. Flame 2016, 171, 87–102. [Google Scholar] [CrossRef] [Green Version]
- Morgans, A.; Stow, S. Model-based control of combustion instabilities in annular combustors. Combust. Flame 2007, 150, 380–399. [Google Scholar] [CrossRef]
- Schmitt, P.; Poinsot, T.; Schuermans, B.; Geigle, K.P. Large-eddy simulation and experimental study of heat transfer, nitric oxide emissions and combustion instability in a swirled turbulent high-pressure burner. J. Fluid Mech. 2007, 570, 17–46. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Lee, J.; Quay, B.; Santavicca, D. Spatially distributed flame transfer functions for predicting combustion dynamics in lean premixed gas turbine combustors. Combust. Flame 2010, 157, 1718–1730. [Google Scholar] [CrossRef]
- Heinig, K. Sounding propagation in multistage axial flow turbomachines. AIAA J. 1983, 21, 98–105. [Google Scholar] [CrossRef]
- Nicoud, F.; Wieczorek, K. About the zero Mach number assumption in the calculation of thermoacoustic instability. Int. J. Spray Combust. Dyn. 2009, 101, 67–111. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Morgans, A.S. The one-dimensional acoustic field in a duct with arbitrary mean axial temperature gradient and mean flow. J. Sound Vib. 2017, 400, 248–269. [Google Scholar] [CrossRef]
- Marble, F.E.; Candel, S.M. Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 1977, 55, 225–243. [Google Scholar] [CrossRef]
- Rienstra, S.; Hirschberg, A. An Introduction to Acoustics; Eindhoven University of Technology: Eindhoven, The Netherlands, 2016. [Google Scholar]
- Lieuwen, T. Unsteady Combustor Physics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Sujith, R.; Waldherr, G.; Zinn, B. An exact solution for one-dimensional acoustic fields in ducts with an axial temperature gradient. J. Sound Vib. 1995, 184, 389–402. [Google Scholar] [CrossRef]
- Duran, I.; Moreau, S. Solution of the quasi-one-dimensional linearized Euler equations using flow invariants and the Magnus expansion. J. Fluid Mech. 2013, 723, 190–231. [Google Scholar] [CrossRef]
- Duran, I.; Morgans, A. On the reflection and transmission of circumferential waves through nozzles. J. Fluid Mech. 2015, 773, 137–153. [Google Scholar] [CrossRef] [Green Version]
- Peat, K. The transfer matrix of a uniform duct with a linear temperature gradient. J. Sound Vib. 1988, 123, 43–53. [Google Scholar] [CrossRef]
- Cummings, A. Ducts with axial temperature gradients: An approximate solution for sound transmission and generation. J. Sound Vib. 1977, 51, 55–67. [Google Scholar] [CrossRef]
- Sirignano, W.A.; Popov, P.P. Two-dimensional model for liquid-rocket transverse combustion instability. AIAA J. 2013, 51, 2919–2934. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Nan, J.; Yang, L. Analytical solutions for the acoustic field in a thin annular duct with temperature gradient and mean flow. J. Sound Vib. 2020, 467, 115043. [Google Scholar] [CrossRef]
- Li, J.; Morgans, A.S.; Yang, L. The three-dimensional acoustic field in cylindrical and annular ducts with an axially varying mean temperature. Aerosp. Sci. Technol. 2020, 99, 105712. [Google Scholar] [CrossRef]
- Karimi, N.; Brear, M.J.; Moase, W.H. Acoustic and disturbance energy analysis of a flow with heat communication. J. Fluid Mech. 2008, 597, 67–89. [Google Scholar] [CrossRef]
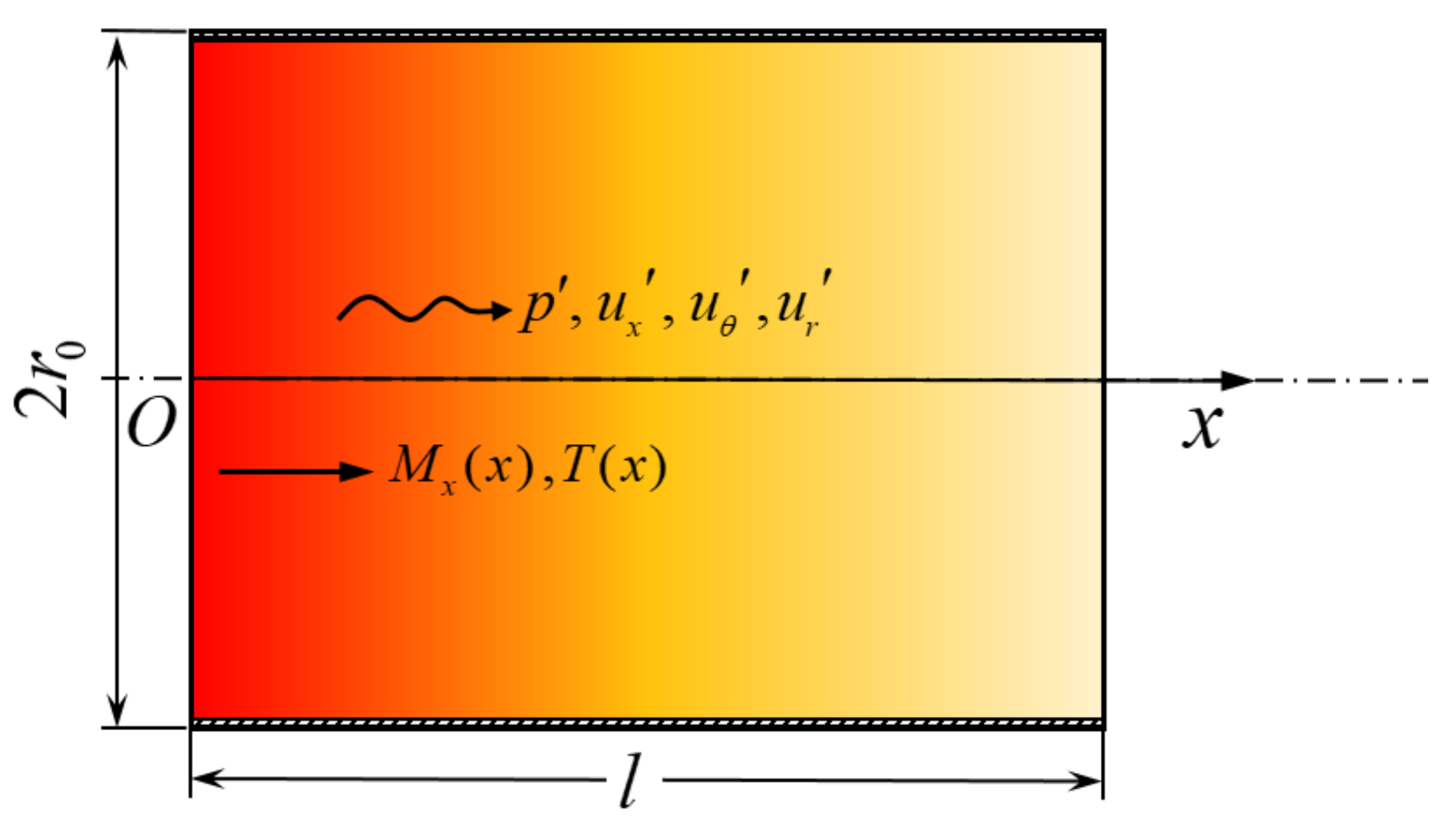
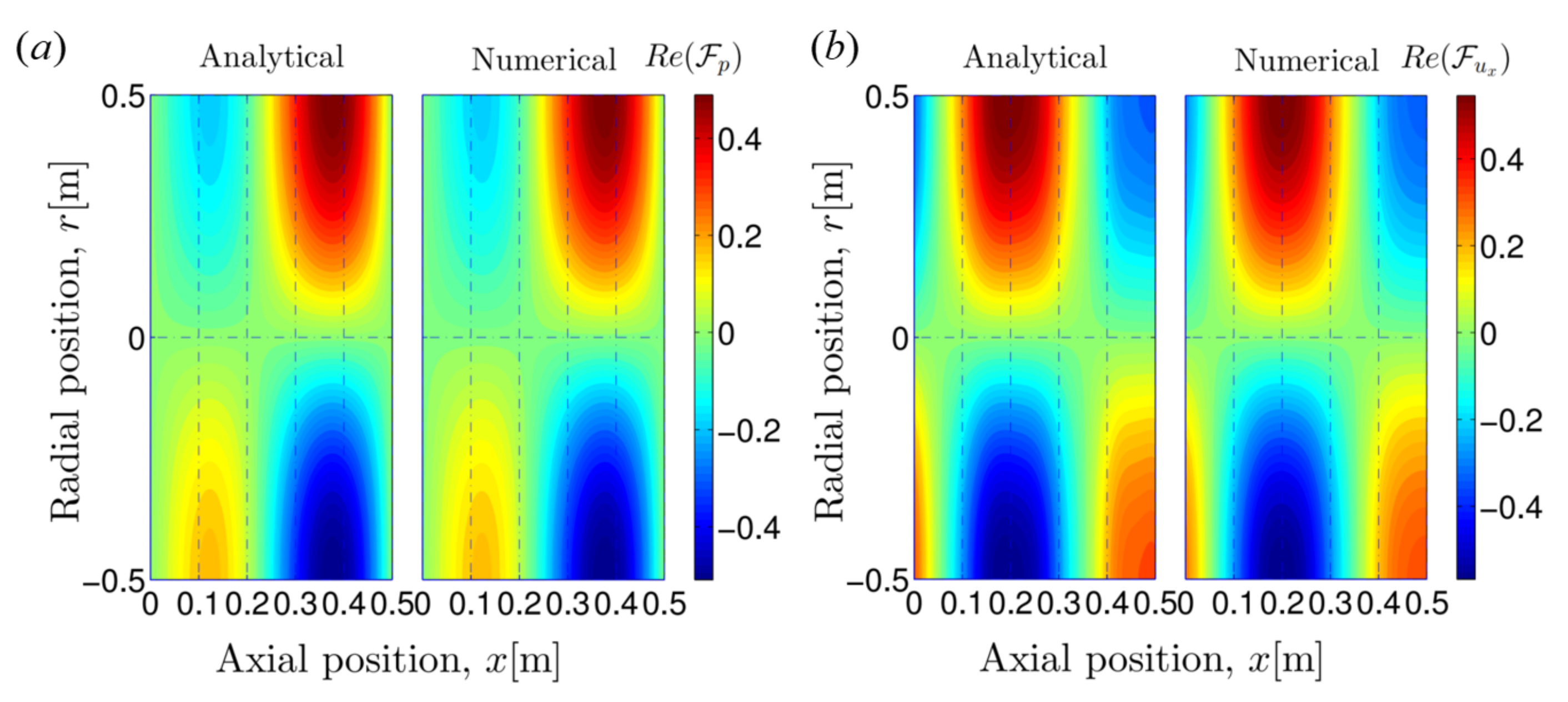
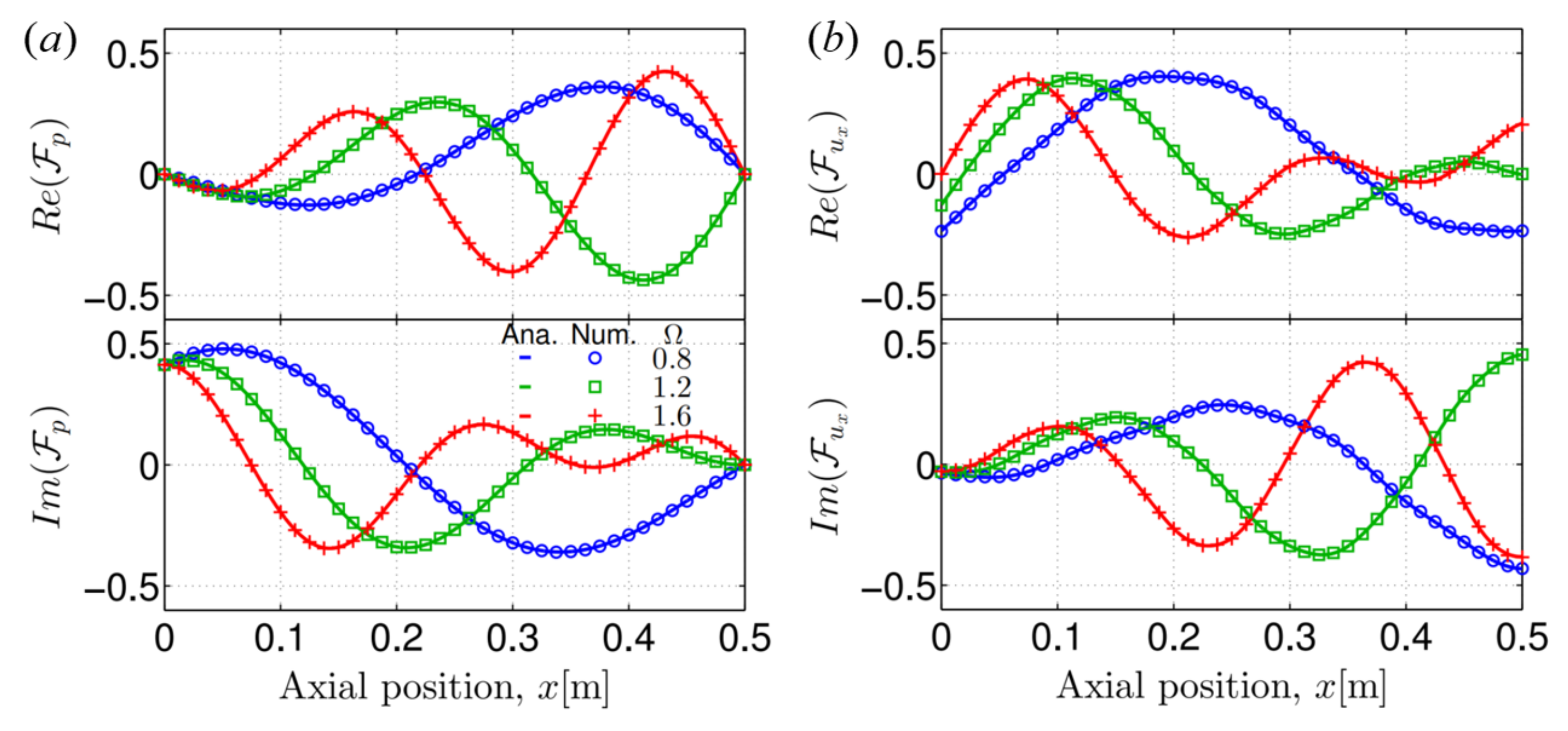
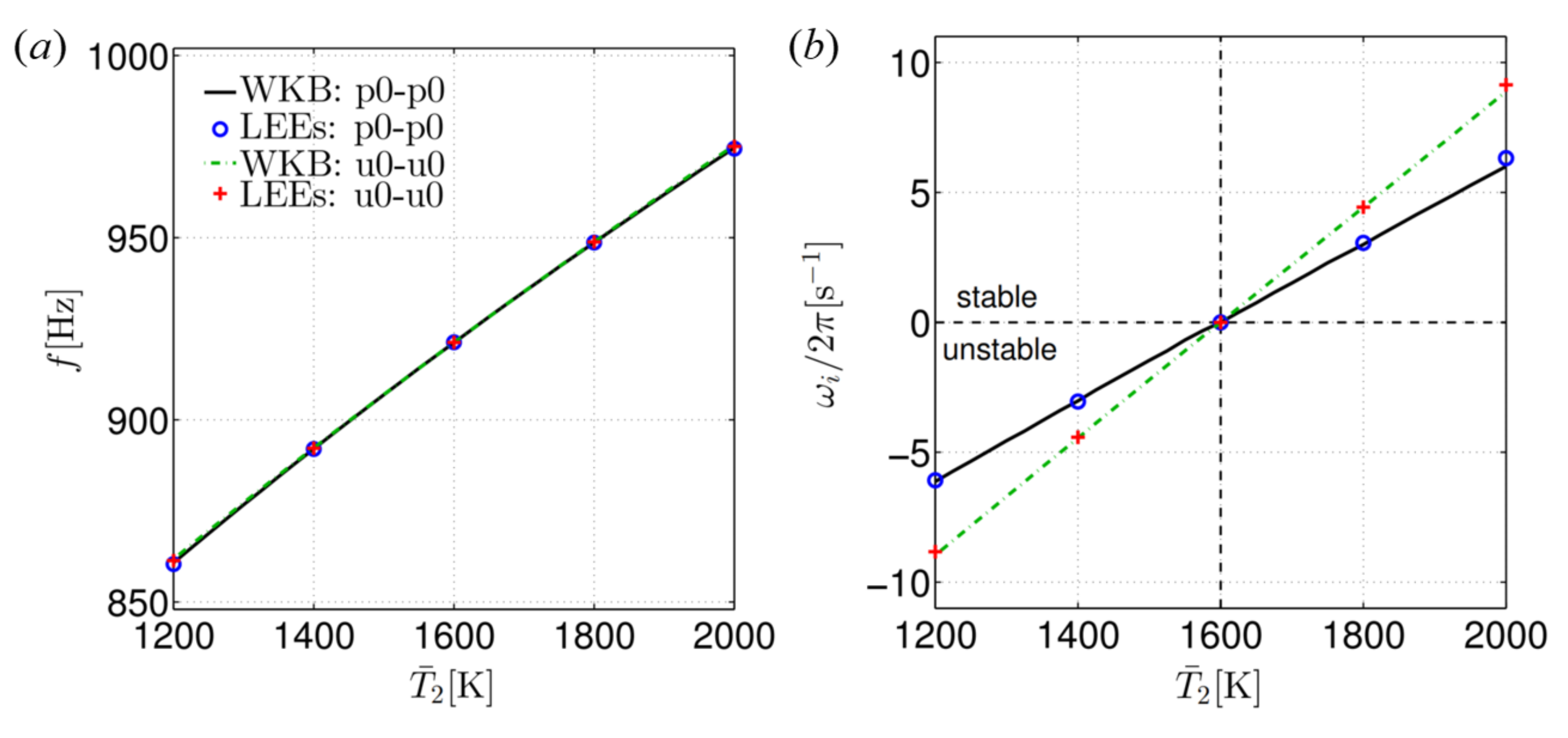
| l [m] | [m] | [m] | [Pa] | [K] | [K] | [-] | [J K kg−1] |
|---|---|---|---|---|---|---|---|
| 0.5 | 0.5 | 0 | 1× 10 | 1600 | 1200 | 1.4 | 287 |
| Open-Open Ends | Closed-Closed Ends | |||||
|---|---|---|---|---|---|---|
| [Hz] | WKB | LEEs | WKB | LEEs | ||
| 1T1L | 860.77 | 860.42 | 0.041% | 861.65 | 861.35 | 0.035% |
| 1R1L | 1174.18 | 1172.60 | 0.135% | 1178.64 | 1176.50 | 0.182% |
| 2T1L | 1037.32 | 1036.30 | 0.098% | 1039.66 | 1038.40 | 0.121% |
| [] | WKB | LEEs | WKB | LEEs | ||
| 1T1L | −6.1275 | −6.0813 | 0.760% | −8.9604 | −8.8245 | 1.540% |
| 1R1L | −3.9789 | −3.8839 | 2.446% | −12.653 | −12.392 | 2.106% |
| 2T1L | −4.6951 | −4.6000 | 2.067% | −10.918 | −10.739 | 1.667% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, J.; Li, J.; Yang, L. Three-Dimensional Analytical Solutions for Acoustic Transverse Modes in a Cylindrical Duct with Axial Temperature Gradient and Non-Zero Mach Number. Aerospace 2022, 9, 588. https://doi.org/10.3390/aerospace9100588
Nan J, Li J, Yang L. Three-Dimensional Analytical Solutions for Acoustic Transverse Modes in a Cylindrical Duct with Axial Temperature Gradient and Non-Zero Mach Number. Aerospace. 2022; 9(10):588. https://doi.org/10.3390/aerospace9100588
Chicago/Turabian StyleNan, Jiaqi, Jingxuan Li, and Lijun Yang. 2022. "Three-Dimensional Analytical Solutions for Acoustic Transverse Modes in a Cylindrical Duct with Axial Temperature Gradient and Non-Zero Mach Number" Aerospace 9, no. 10: 588. https://doi.org/10.3390/aerospace9100588
APA StyleNan, J., Li, J., & Yang, L. (2022). Three-Dimensional Analytical Solutions for Acoustic Transverse Modes in a Cylindrical Duct with Axial Temperature Gradient and Non-Zero Mach Number. Aerospace, 9(10), 588. https://doi.org/10.3390/aerospace9100588







