Multi-Scenario Trajectory Optimization for Vertical Takeoff and Vertical Landing Vehicles Using the Gauss Pseudospectral Method
Abstract
:1. Introduction
2. Multi-Scenario Overview
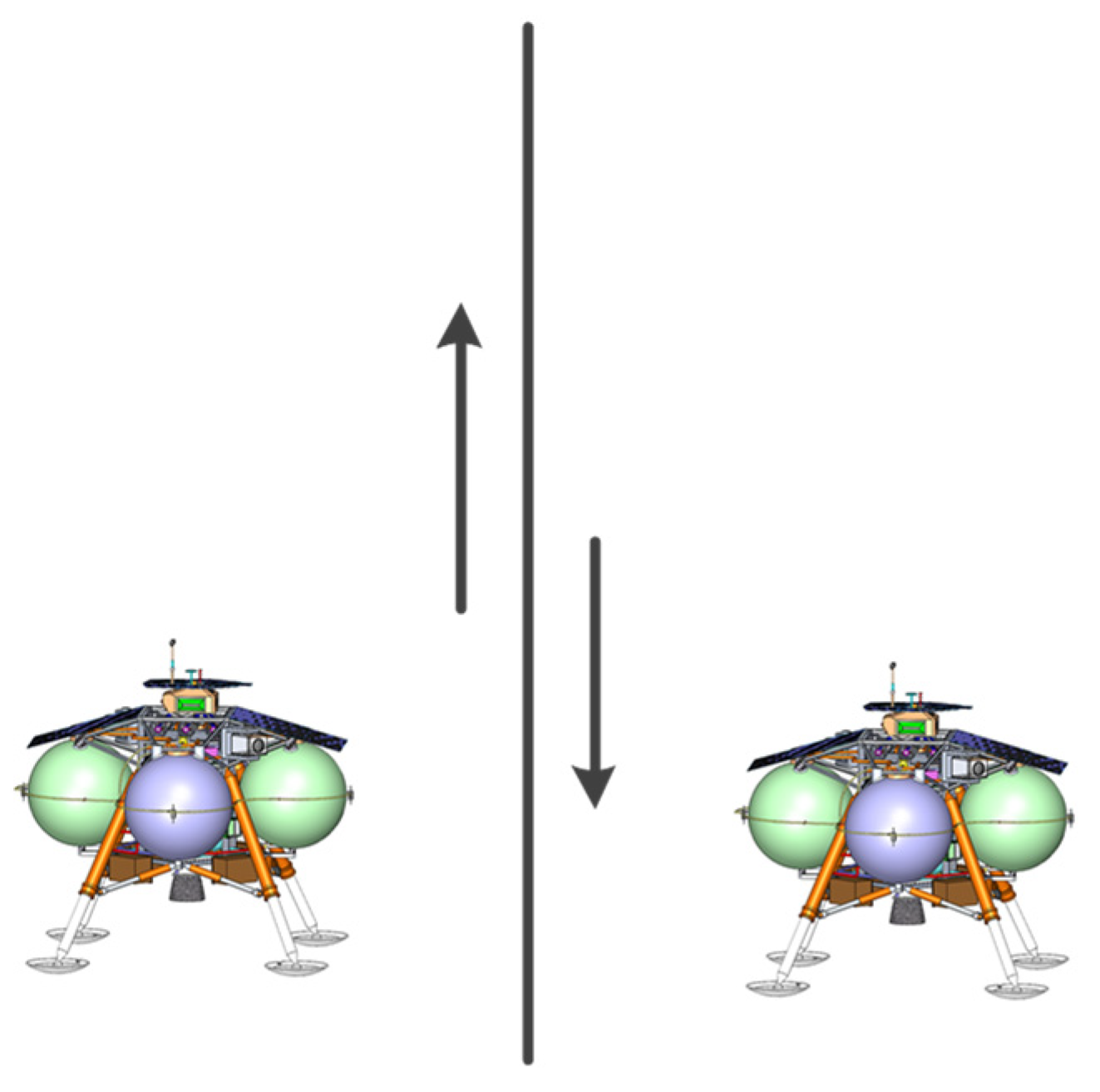
2.1. VTVL Vehicles without Horizontal Movement: First Flight Scenario
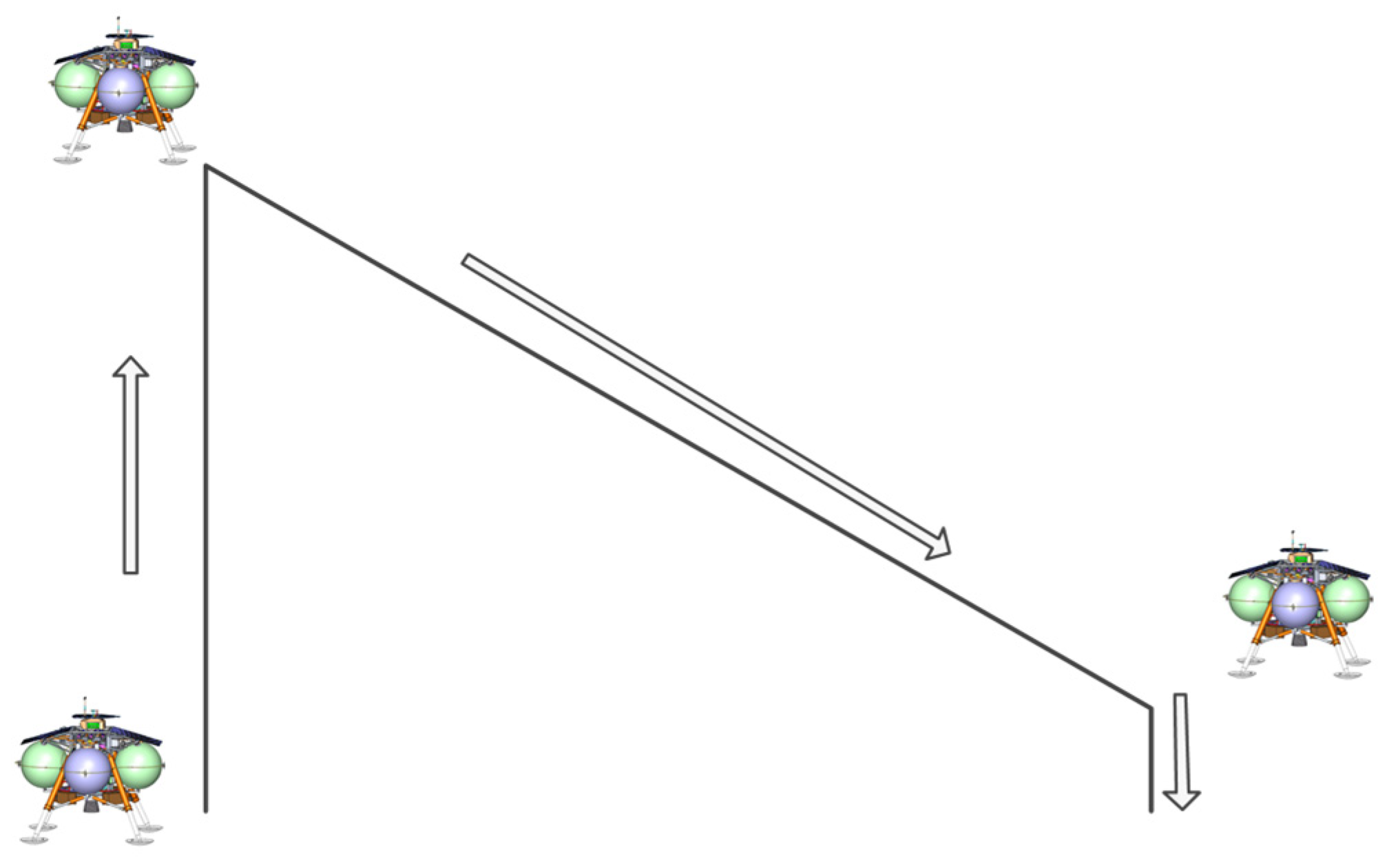
2.2. VTVL Vehicles with Horizontal Movement: Second Flight Scenario
2.3. Vertical Takeoff and Autonomous Landing with Horizontal Movement: Third Flight Scenario
3. Dynamic Model
4. Trajectory Optimization Method Based on the Gauss Pseudospectral Method
4.1. Problem Formulation
4.2. Gauss Pseudospectral Method
4.3. Multi-Objective Processing
5. Numerical Simulation Results and Discussions
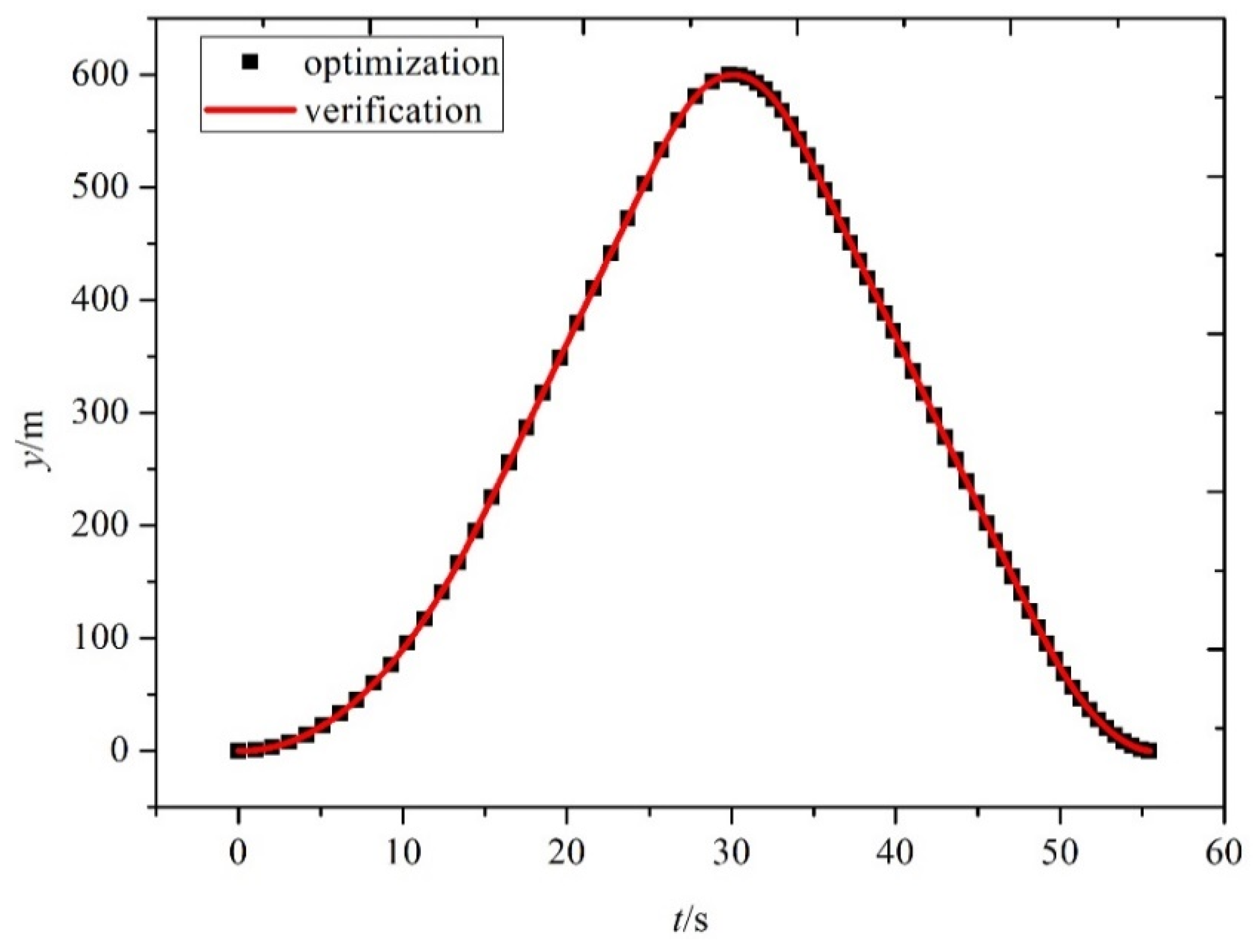
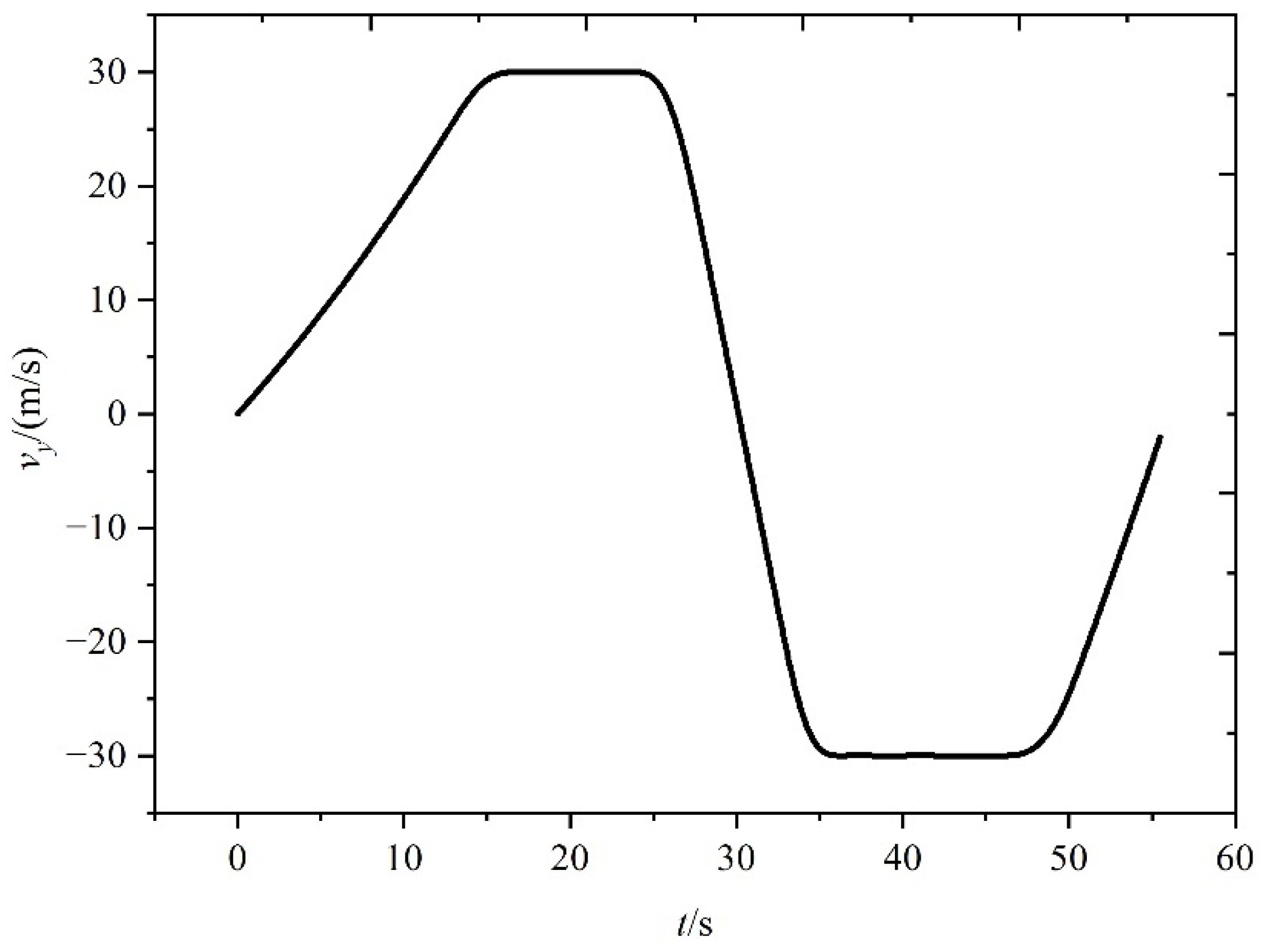
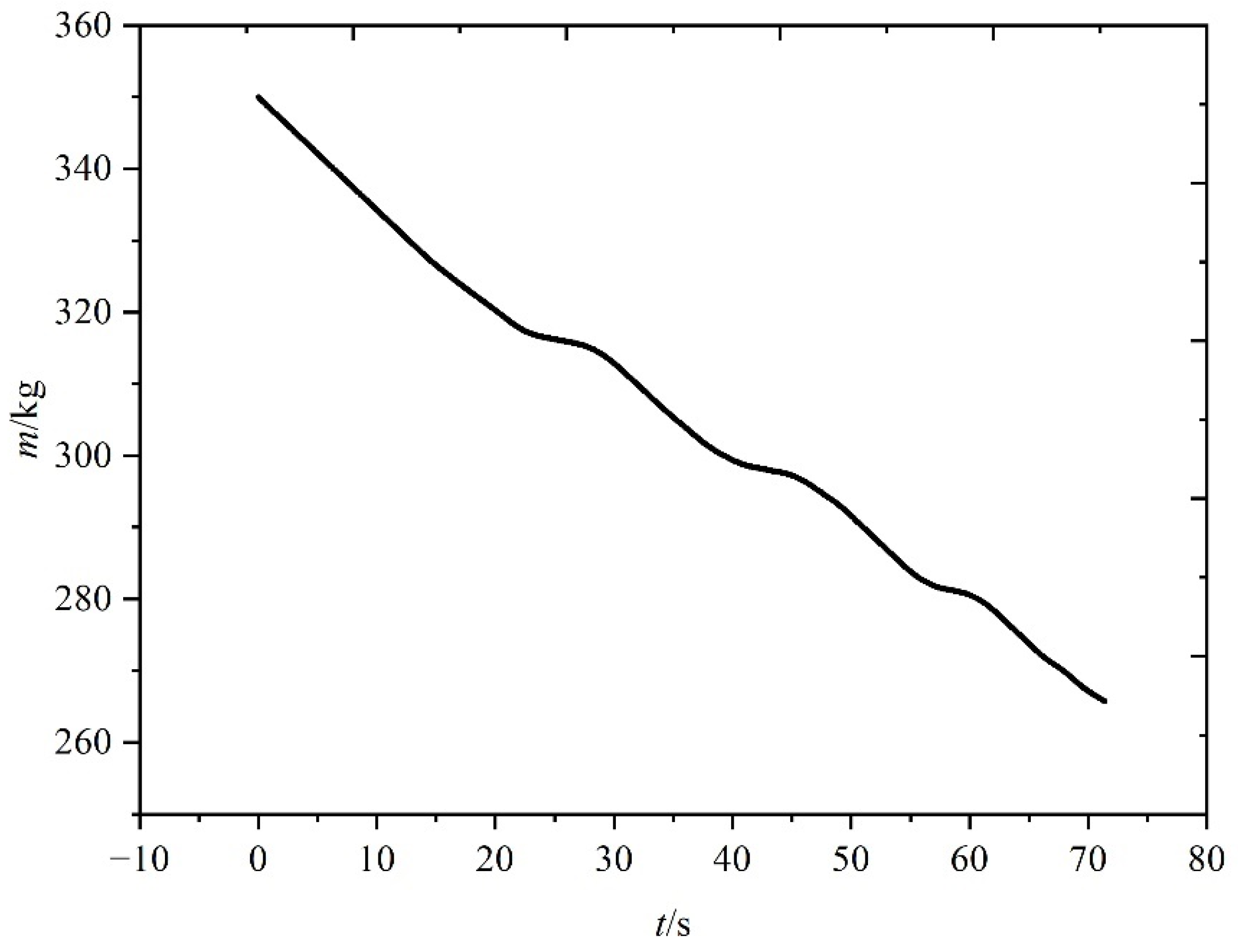
5.1. Simulation Results for the First Scenario
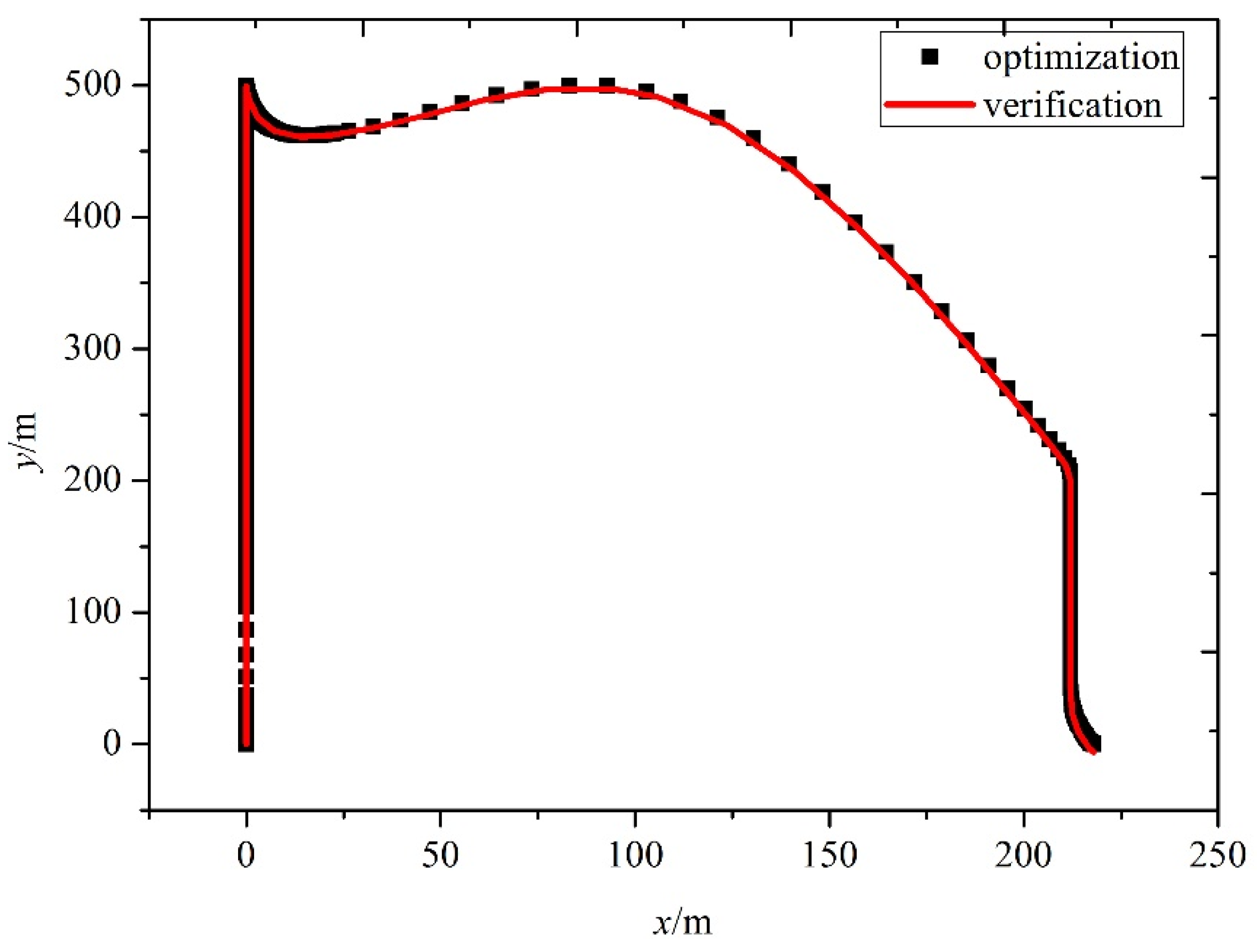
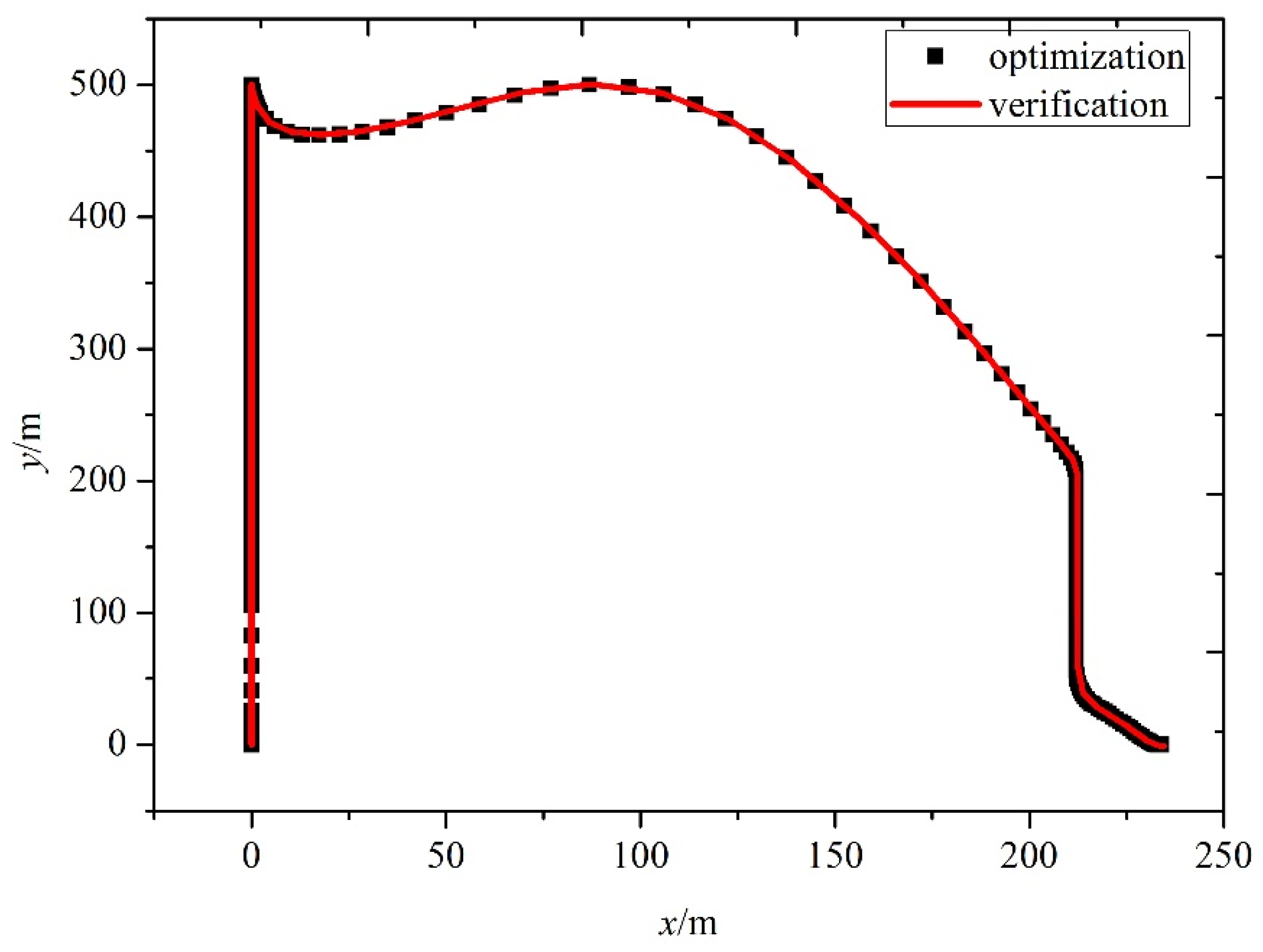
5.2. Simulation Results for the Second Scenario
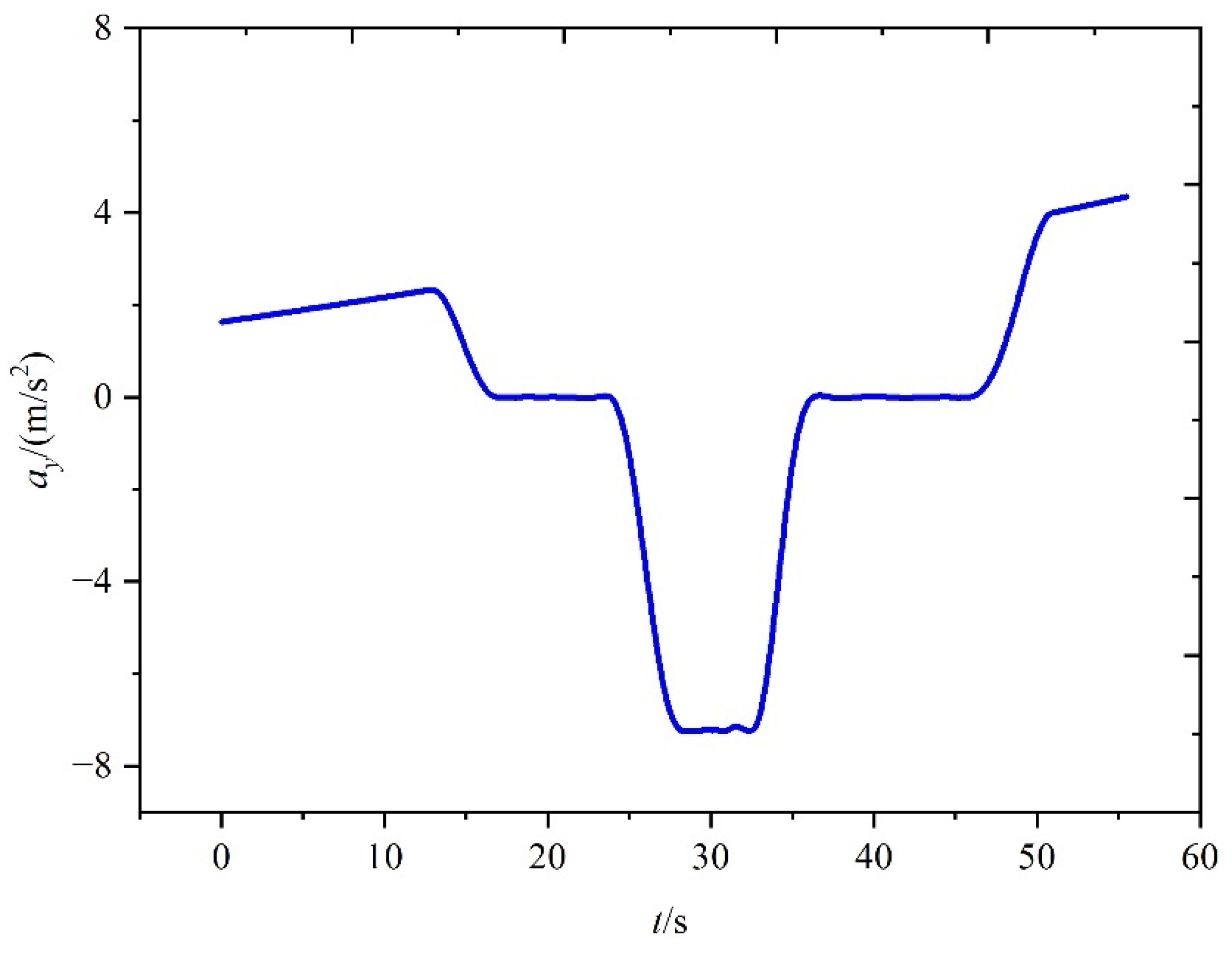
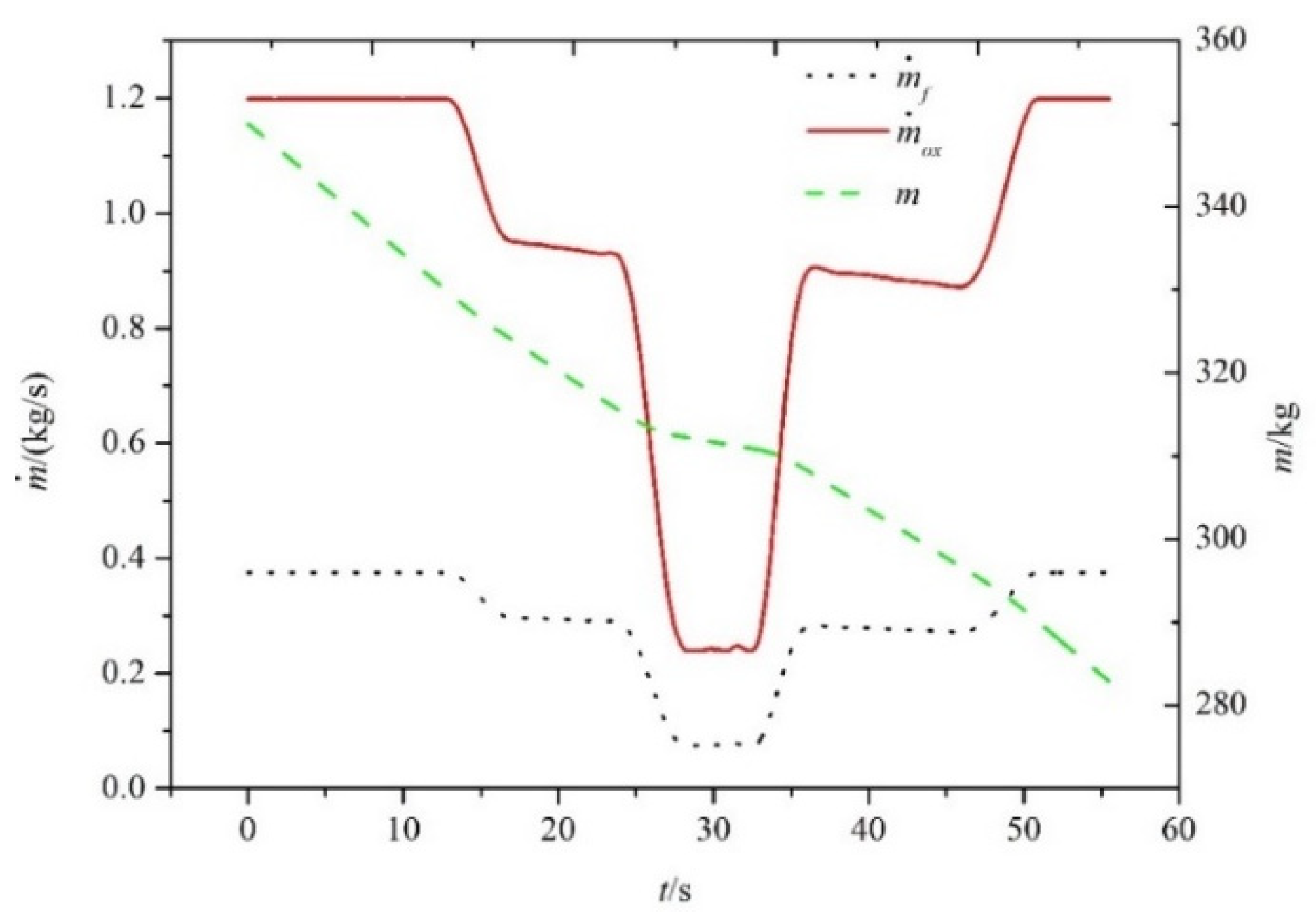
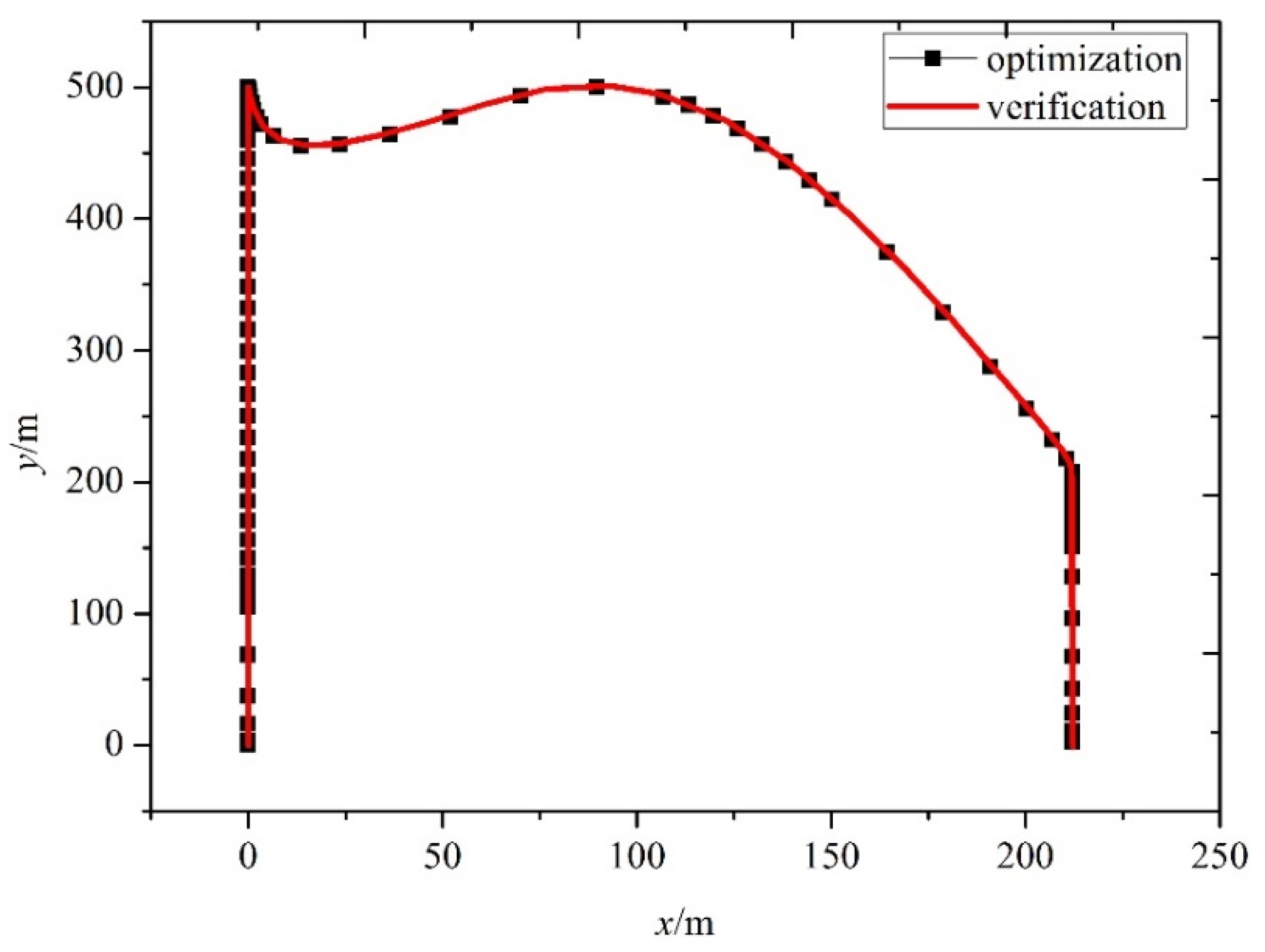
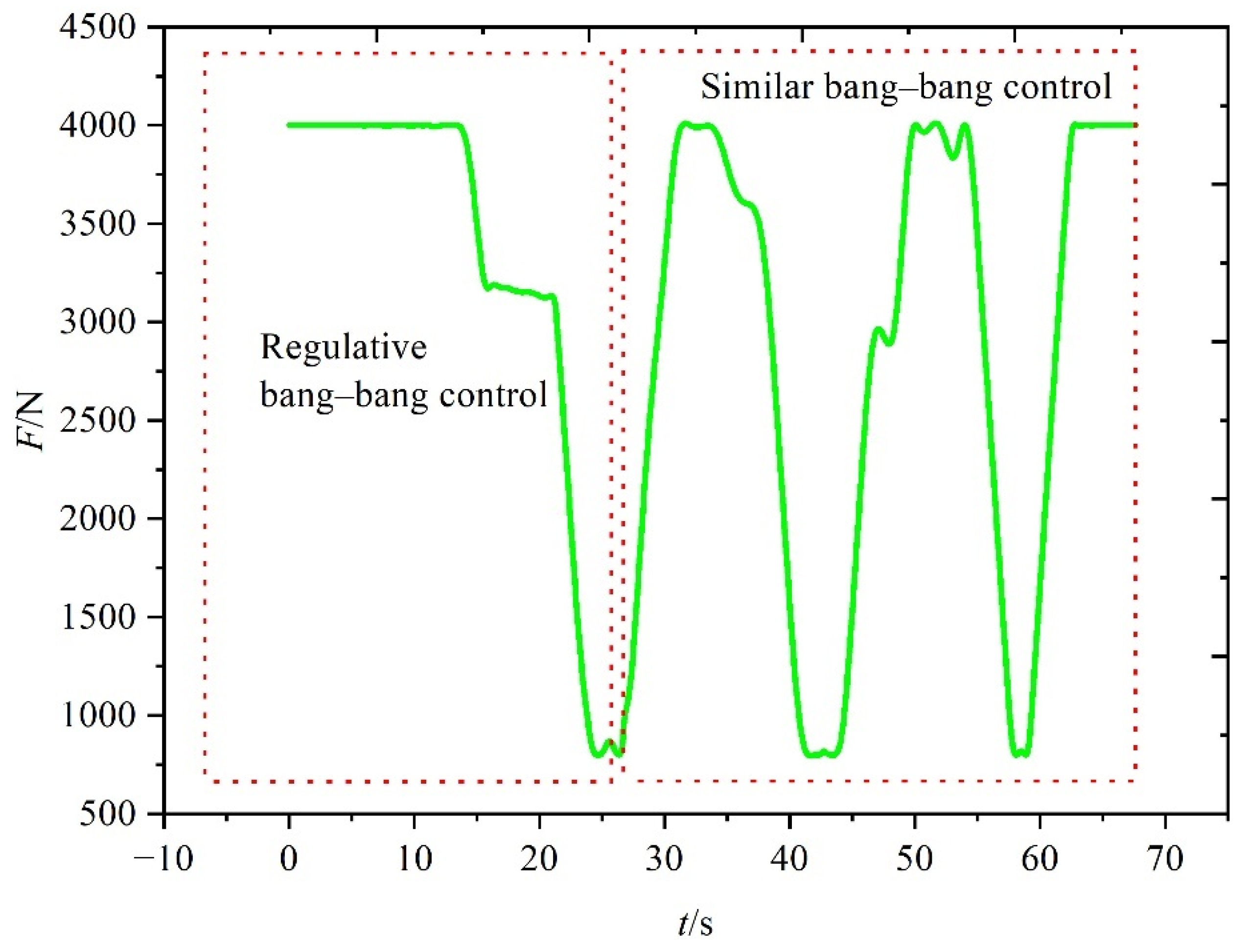
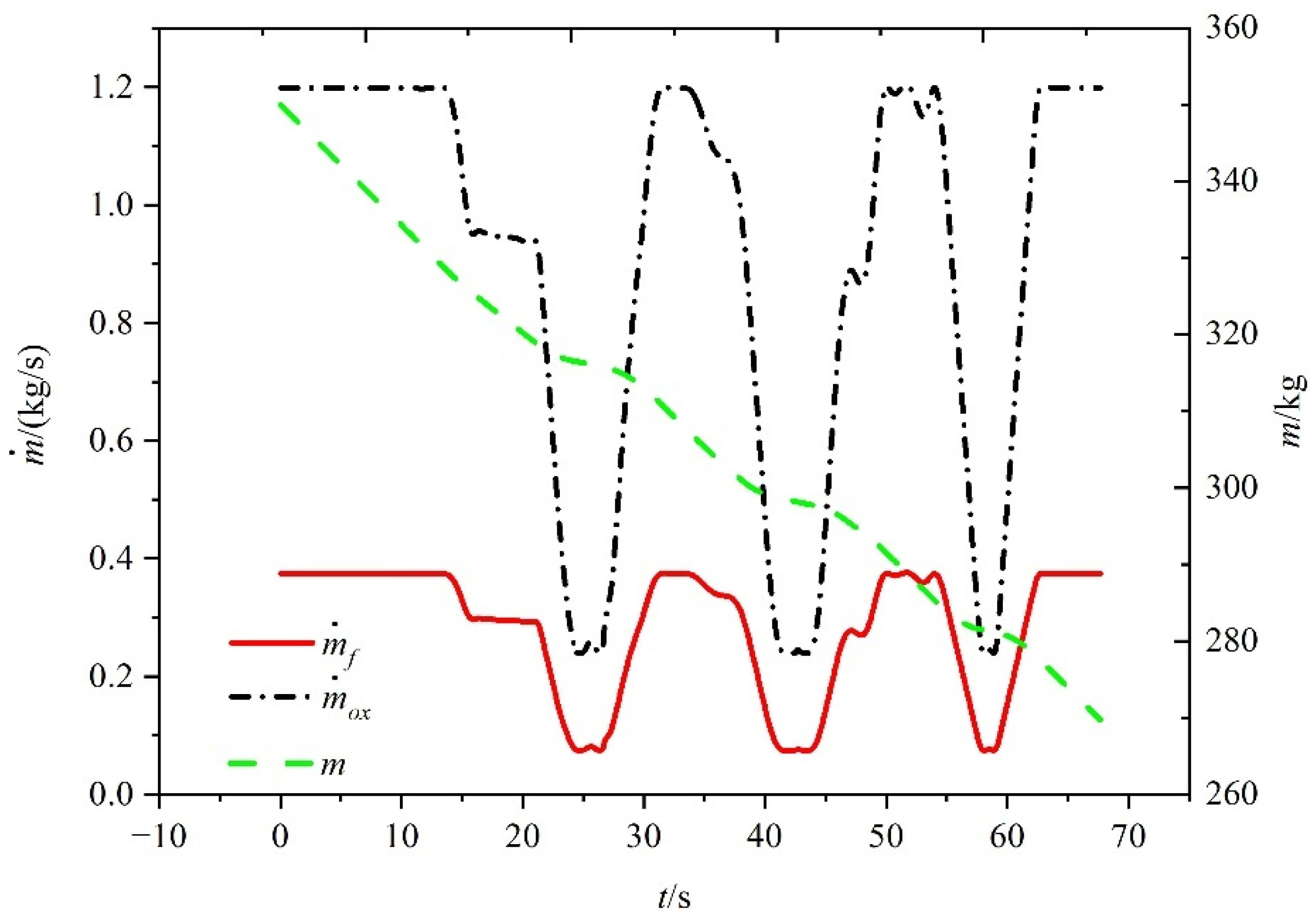
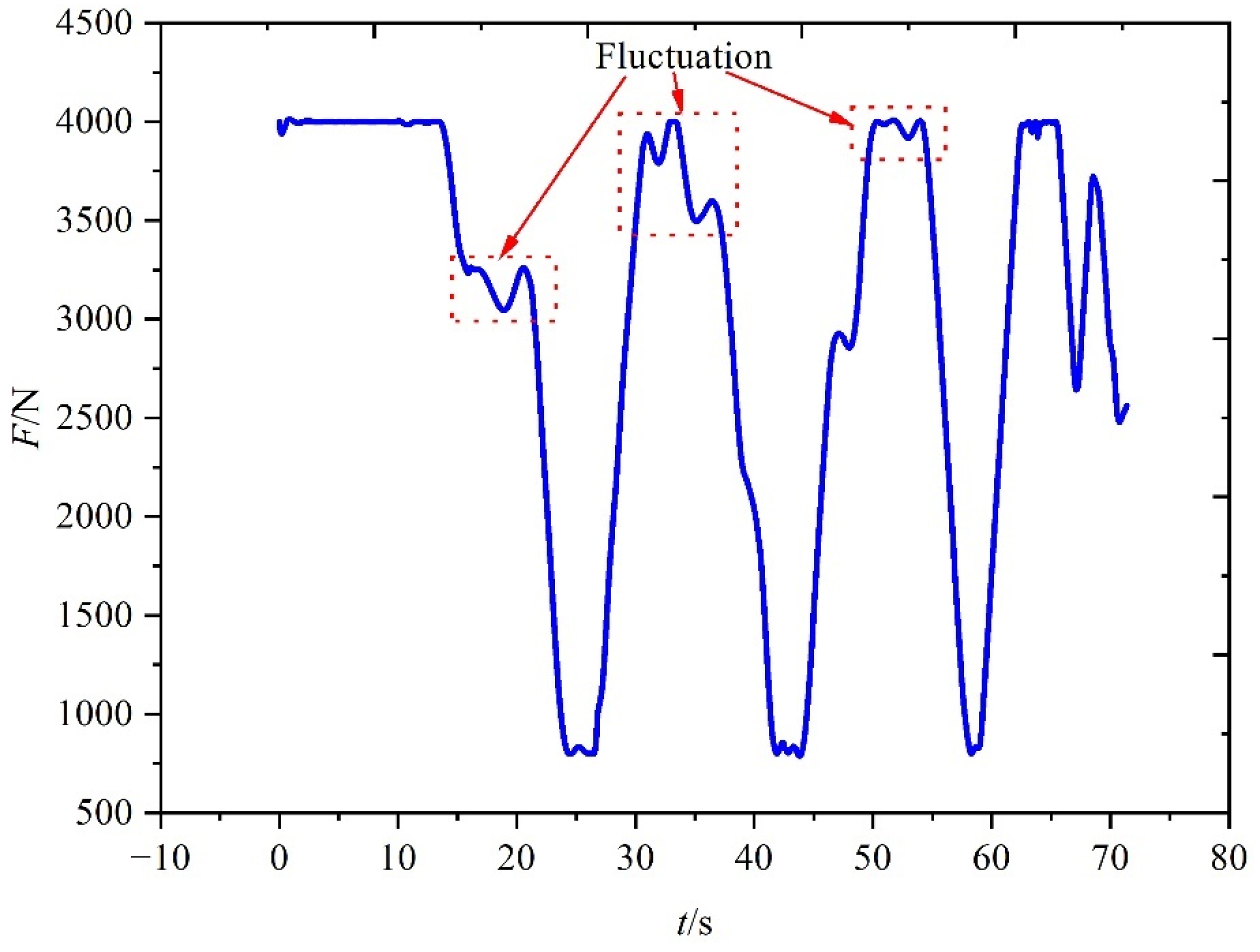
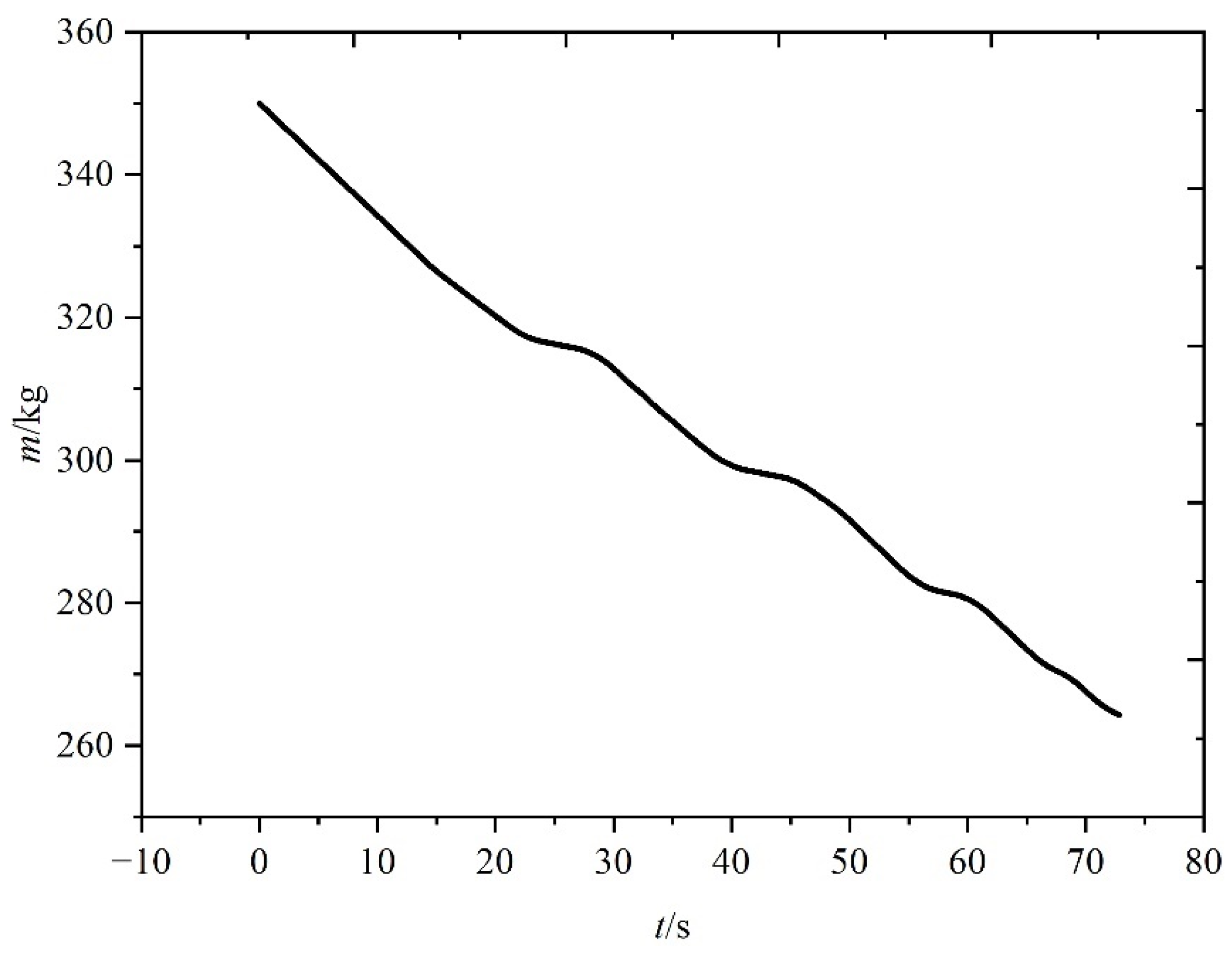
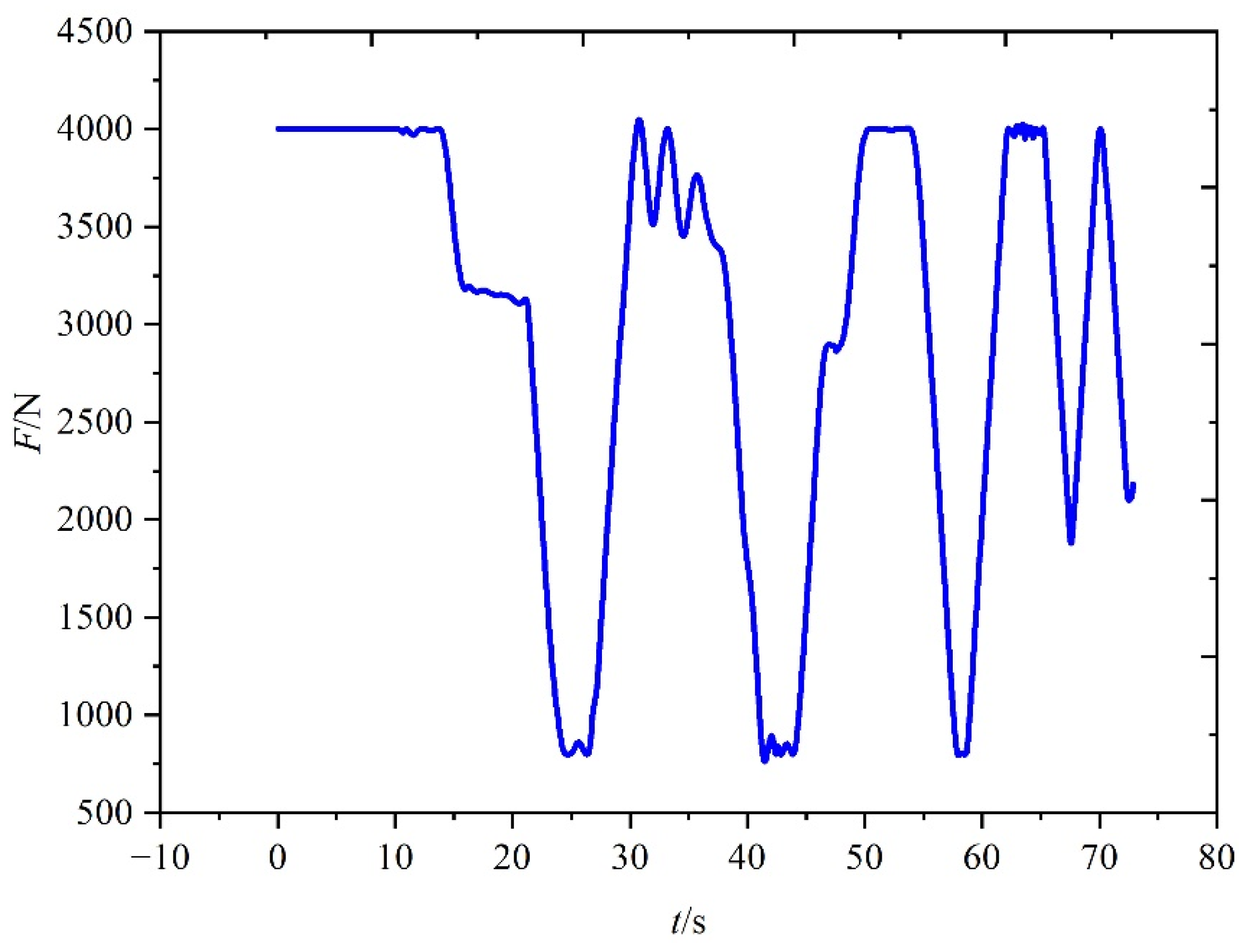
5.3. Simulation Results for the Third Scenario
5.3.1. Results under Case 1 in the Third Scenario
5.3.2. Results under Case 2 in the Third Scenario
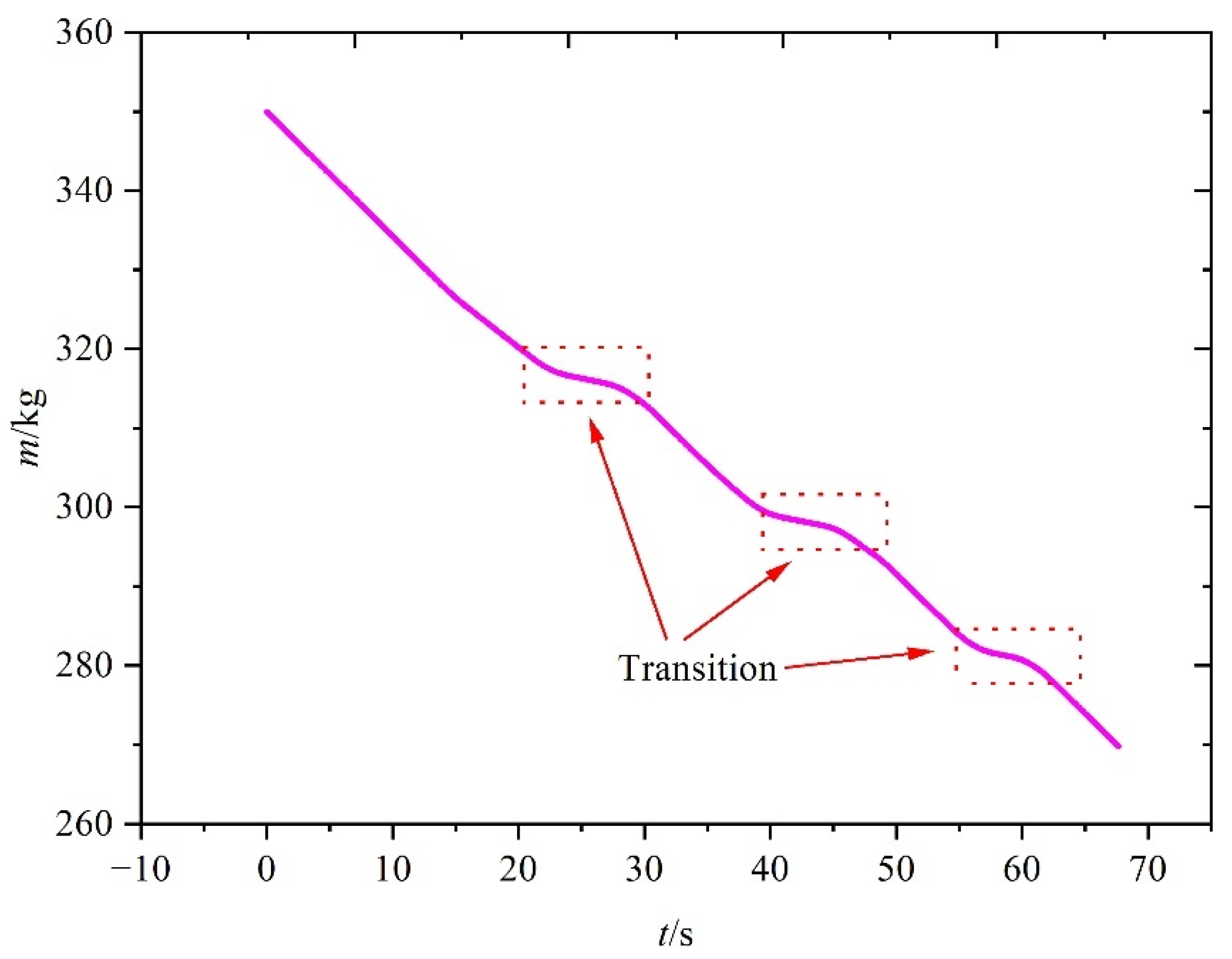
5.4. Comparison among Three Scenarios
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, T.D.; Klem, M.D.; Fisher, K.L. Propulsion Risk Reduction Activities for Nontoxic Cryogenic Propulsion. In Proceedings of the Space 2010 Conference and Exposition, Anaheim, CA, USA, 30 August–2 September 2010. [Google Scholar]
- Zhang, L.; Wei, C.; Wu, R.; Cui, N. Adaptive Fault-Tolerant Control for a Vtvl Reusable Launch Vehicle. Acta Astronaut. 2019, 159, 362–370. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Xu, Z.; Shao, Z.; Song, Z.; Biegler, L.T. Trajectory Optimization for Lunar Rover Performing Vertical Takeoff Vertical Landing Maneuvers in the Presence of Terrain. Acta Astronaut. 2018, 146, 289–299. [Google Scholar] [CrossRef]
- Casiano, M.J.; Hulka, J.R.; Yang, V. Liquid-Propellant Rocket Engine Throttling: A Comprehensive Review. J. Propuls. Power 2010, 26, 897–923. [Google Scholar] [CrossRef] [Green Version]
- Yue, C.; Li, J.; Hou, X.; Feng, X.; Yang, S. Summarization on Variable Liquid Thrust Rocket Engines. Sci. China Ser. E Technol. Sci. 2009, 52, 2918–2923. [Google Scholar] [CrossRef]
- Hurlbert, E.; McManamen, J.; Studak, J. Advanced Development of a Compact 5-15 Lbf Lox/Methane Thruster for an Integrated Reaction Control and Main Engine Propulsion System. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2011. [Google Scholar]
- Melcher, J.C.; Morehead, R.L. Combustion Stability Characteristics of the Project Morpheus Liquid Oxygen/Liquid Methane Main Engine. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2014. [Google Scholar]
- Crain, T.; Bishop, R.H.; Carson, J.M.; Trawny, N.; Sullivan, J.; Christian, J.A.; Kyle, J.D.; Joel, G.; Chad, H. Approach-Phase Precision Landing with Hazard Relative Navigation: Terrestrial Test Campaign Results of the Morpheus/Alhat Project. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2016. [Google Scholar]
- Carson, J.M.; Robertson, E.; Trawny, N.; Amzajerdian, F. Flight Testing Alhat Precision Landing Technologies Integrated Onboard the Morpheus Rocket Vehicle. In Proceedings of the AIAA SPACE 2015 Conference and Exposition, Pasadena, CA, USA, 31 August–2 September 2015; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 2015. [Google Scholar]
- Marc, W. Rl10a-5—An Assessment of Reusability Demonstrated During the Ssrt Program. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Buena Vista, FL, USA, 1–3 July 1996; American Institute of Aeronautics and Astronautics: Reston, VI, USA, 1996. [Google Scholar]
- Pavlov Rachov, P.A.; Tacca, H.; Lentini, D. Electric Feed Systems for Liquid Propellant Rockets. J. Propuls. Power 2013, 29, 1171–1180. [Google Scholar] [CrossRef] [Green Version]
- Soldà, N.; Lentini, D. Opportunities for a Liquid Rocket Feed System Based on Electric Pumps. J. Propuls. Power 2008, 24, 1340–1346. [Google Scholar] [CrossRef]
- Song, Y.; Gong, S. Solar Sail Trajectory Optimization of Multi-Asteroid Rendezvous Mission. Acta Astronaut. 2019, 157, 111–122. [Google Scholar] [CrossRef]
- Betts, J.T. Survey Numerical Methods for Trajectory Optimization. J. Guid. Control. Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef] [Green Version]
- Peng, Q.; Shen, H.; Li, H. Free Return Orbit Design and Characteristics Analysis for Manned Lunar Mission. Sci. China Technol. Sci. 2011, 54, 3243–3250. [Google Scholar]
- Cao, X. Optimal Control for a Chaotic System by Means of Gauss Pseudospectral Method. Acta Phys. Sin. 2013, 62, 71–78. (In Chinese) [Google Scholar]
- Zhu, Y.W.; Cai, W.W.; Yang, L.P.; Huang, H. Flatness-Based Trajectory Planning for Electromagnetic Spacecraft Proximity Operations in Elliptical Orbits. Acta Astronaut. 2018, 152, 342–351. [Google Scholar] [CrossRef]
- Benson, D.A.; Huntington, G.T.; Thorvaldsen, T.P.; Rao, A.V. Direct Trajectory Optimization and Costate Estimation via an Orthogonal Collocation Method. J. Guid. Control. Dyn. 2006, 29, 1435–1439. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S.; Furfaro, R. Integrated Guidance for Mars Entry and Powered Descent Using Reinforcement Learning and Pseudospectral Method. Acta Astronaut. 2018, 163, 114–129. [Google Scholar] [CrossRef]
- Ross, I.M.; Sekhavat, P.; Fleming, A.; Qi, G. Optimal Feedback Control: Foundations, Examples, and Experimental Results for a New Approach. J. Guid. Control. Dyn. 2008, 31, 307–321. [Google Scholar] [CrossRef]
- Fahroo, F.; Ross, I.M. Advances in Pseudospectral Methods for Optimal Control. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Zhang, J.; Chu, X.; Zhang, Y.; Hu, Q.; Zhai, G.; Li, Y. Safe-Trajectory Optimization and Tracking Control in Ultra-Close Proximity to a Failed Satellite. Acta Astronaut. 2018, 144, 339–352. [Google Scholar] [CrossRef]
- Meng, S.; Xiang, J.; Luo, Z.; Ren, Y. Optimal Trajectory Planning for Small-Scale Unmanned Helicopter Obstacle Avoidance. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 246–251. (In Chinese) [Google Scholar]
- Zhong, W.; Qu, Q.; Yuan, J.; Wu, W. Research on Reentry Integrated Guidance Law of Hypersonic Velocity Aircraft Based on the Gauss Pseudo-Spectral Method. Comput. Meas. Control. 2017, 25, 106–109+113. (In Chinese) [Google Scholar]
- Yang, X.; Zhang, W. Rapid Optimization of Ascent Trajectory for Solid Launch Vehicles Based on Gauss Pseudospectral Method. J. Astronaut. 2011, 32, 15–21. (In Chinese) [Google Scholar]
- Gao, X.Z.; Hou, Z.X.; Guo, Z.; Wang, P.; Zhang, J.T. Research on Characteristics of Gravitational Gliding for High-Altitude Solar-Powered Unmanned Aerial Vehicles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 1911–1923. [Google Scholar] [CrossRef]
- Chu, Z.; Wei, T.; Shen, T.; Di, J.; Cui, J.; Sun, J. Optimal Commands Based Multi-Stage Drag De-Orbit Design for a Tethered System During Large Space Debris Removal. Acta Astronaut. 2019, 163, 238–249. [Google Scholar] [CrossRef]
- Chu, Z.; Di, J.; Cui, J. Hybrid Tension Control Method for Tethered Satellite Systems During Large Tumbling Space Debris Removal. Acta Astronaut. 2018, 152, 611–623. [Google Scholar]
- Luo, J.; Wang, M.; Yuan, J. Rapid Lunar Soft-Landing Trajectory Optimization by a Legendre Pseudospectral Method. In Proceedings of the 57th International Astronautical Congress, Valenica, Spain, 2–6 October 2006. [Google Scholar]
- Sostaric, R.; Rea, J. Powered Descent Guidance Methods for the Moon and Mars. In Proceedings of the AIAA Guidance Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar]
- Tang, X. Numerical Solution of Optimal Control Problems Using Multiple-Interval Integral Gegenbauer Pseudospectral Methods. Acta Astronaut. 2016, 121, 63–75. [Google Scholar]
- Zhao, W.; Wang, L.; Yin, Y.; Wang, B.; Tang, Y. Sequential Quadratic Programming Enhanced Backtracking Search Algorithm. Front. Comput. Sci. 2018, 12, 316–330. [Google Scholar] [CrossRef]
- Curtis, F.E.; Han, Z.; Robinson, D.P. A Globally Convergent Primal-Dual Active-Set Framework for Large-Scale Convex Quadratic Optimization. Comput. Optim. Appl. 2015, 60, 311–341. [Google Scholar] [CrossRef]
- Gould, N.I.M.; Robinson, D.P. A Second Derivative Sqp Method: Global Convergence. SIAM J. Optim. 2010, 20, 2023–2048. [Google Scholar] [CrossRef] [Green Version]
- Gill, P.E.; Murray, W.; Saunders, M.A. Snopt: An Sqp Algorithm for Large-Scale Constrained Optimization. Siam Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Zhong, Y. Optimal Control; Tsinghua University Press: Beijing, China, 2015. (In Chinese) [Google Scholar]




| No. | Parameters | Values |
|---|---|---|
| 1 | Altitude, m | 600 |
| 2 | Takeoff mass, kg | ≤350 |
| 3 | g, m/s2 | 9.8 |
| 4 | Specific impulse, m/s | 2537 |
| NO. | Parameters | Values |
|---|---|---|
| 1 | Maximum altitude, m | 500 |
| 2 | Translation distance, m | 212 |
| 3 | Landing-point altitude, m | 200 |
| 4 | Takeoff mass, kg | ≤350 |
| 5 | g, m/s2 | 9.8 |
| 6 | Specific impulse, m/s | 2537 |
| No. | Parameters | Case 1 | Case 2 |
|---|---|---|---|
| 1 | Maximum altitude, m | 500 | 500 |
| 2 | Translation distance, m | 212 | 212 |
| 3 | Landing-point altitude, m | 200 | 200 |
| 4 | Autonomous landing-point altitude, m | 50 | 60 |
| 5 | Obstacle size, m | 4 | 18 |
| 6 | Takeoff mass, kg | ≤350 | ≤350 |
| 7 | g, m/s2 | 9.8 | 9.8 |
| 8 | Specific impulse, m/s | 2537 | 2537 |
| Scenario 1 | Values | Scenario 2 | Values | Scenario 3 | Values |
|---|---|---|---|---|---|
| Rise | 0.04 | Rise | 0.04 | Rise | 0.04 |
| Accelerated translation | 0.04 | ||||
| Accelerated translation | 0.035 | ||||
| Decelerated translation | 0.04 | ||||
| Descent | 0.06 | Decelerated translation | 0.037 | Descent | 0.04 |
| Accelerated autonomous landing | 0.04/0.042 | ||||
| Descent | 0.06 | ||||
| Decelerated Autonomous landing | 0.06 |
| No. | Parameters | First Scenario | Second Scenario | Third Scenario | |
|---|---|---|---|---|---|
| Case 1 | Case 2 | ||||
| 1 | Maximum altitude/m | 600 | 500 | 500 | |
| 2 | Maximum distance/m | 212 | 212 | 218 | 233.9 |
| 3 | Time/s | 55.5 | 67.7 | 71.4 | 72.9 |
| 4 | Consumed propellant/kg | 67.2 | 80.2 | 84.3 | 85.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, C.; Zhu, X.; Han, Q.; Cui, P.; Zhang, D. Multi-Scenario Trajectory Optimization for Vertical Takeoff and Vertical Landing Vehicles Using the Gauss Pseudospectral Method. Aerospace 2022, 9, 638. https://doi.org/10.3390/aerospace9110638
Liu Y, Li C, Zhu X, Han Q, Cui P, Zhang D. Multi-Scenario Trajectory Optimization for Vertical Takeoff and Vertical Landing Vehicles Using the Gauss Pseudospectral Method. Aerospace. 2022; 9(11):638. https://doi.org/10.3390/aerospace9110638
Chicago/Turabian StyleLiu, Yang, Chenyang Li, Xiongfeng Zhu, Qiulong Han, Peng Cui, and Dongdong Zhang. 2022. "Multi-Scenario Trajectory Optimization for Vertical Takeoff and Vertical Landing Vehicles Using the Gauss Pseudospectral Method" Aerospace 9, no. 11: 638. https://doi.org/10.3390/aerospace9110638




