Limits of Fluid Modeling for High Pressure Flow Simulations
Abstract
1. Introduction
2. Materials and Methods
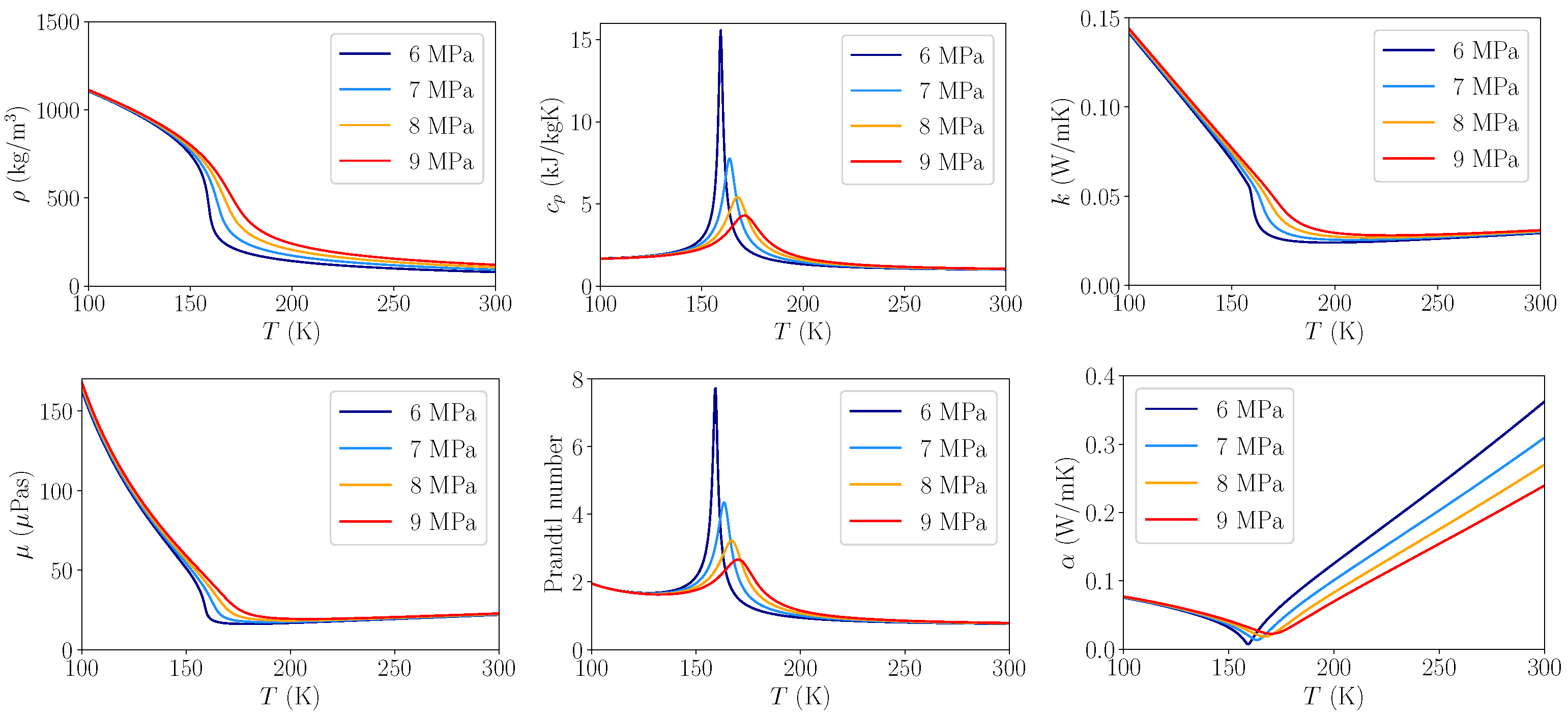
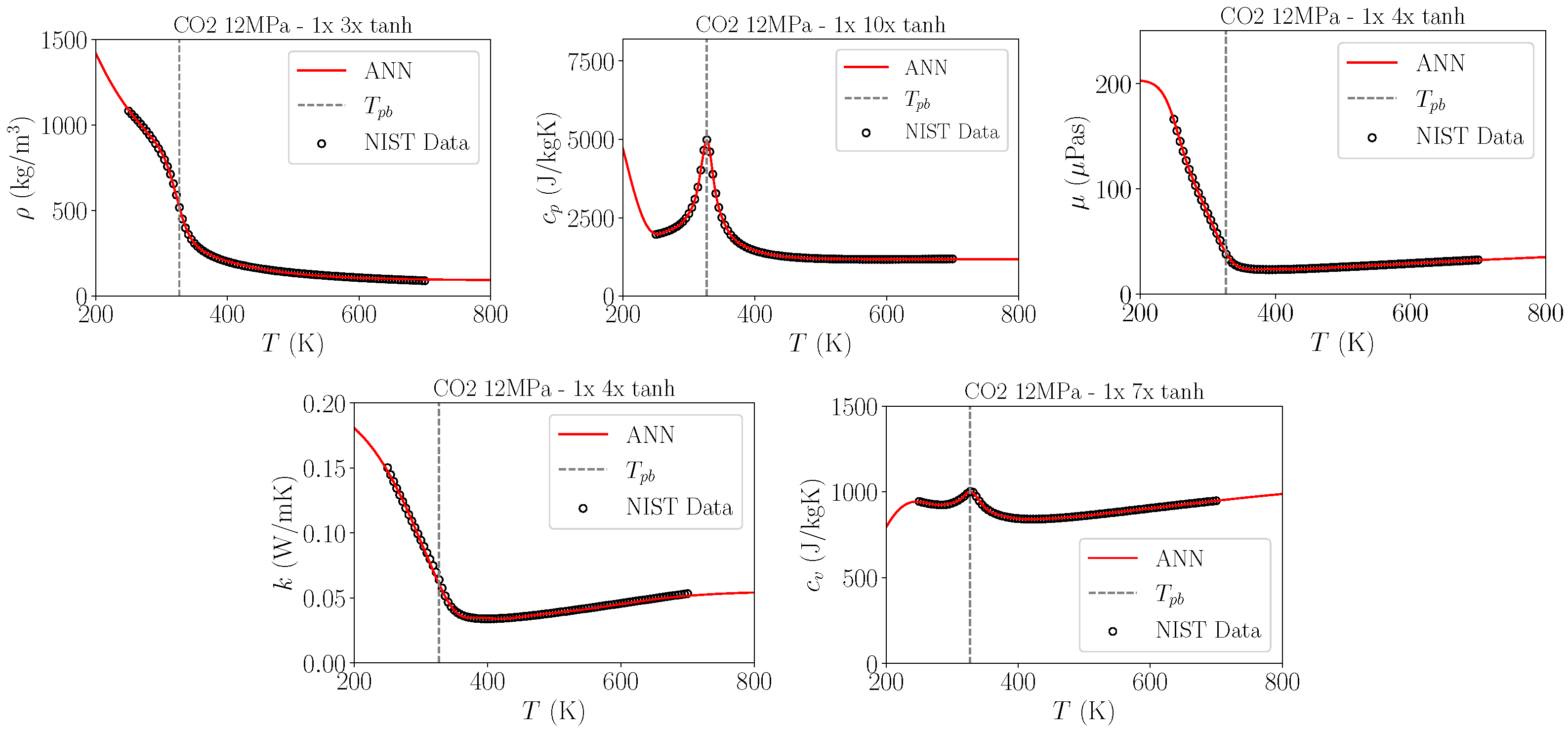
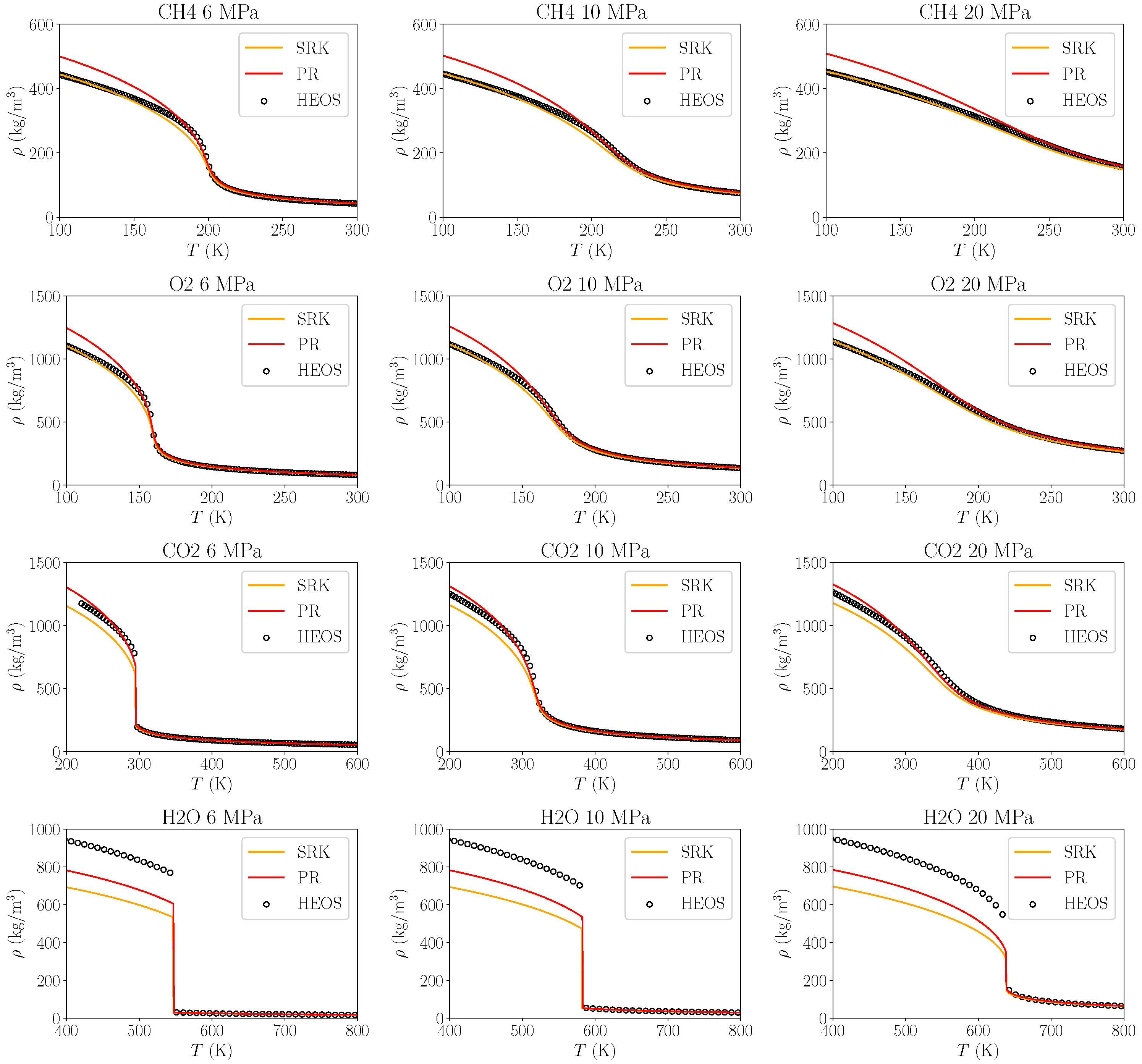
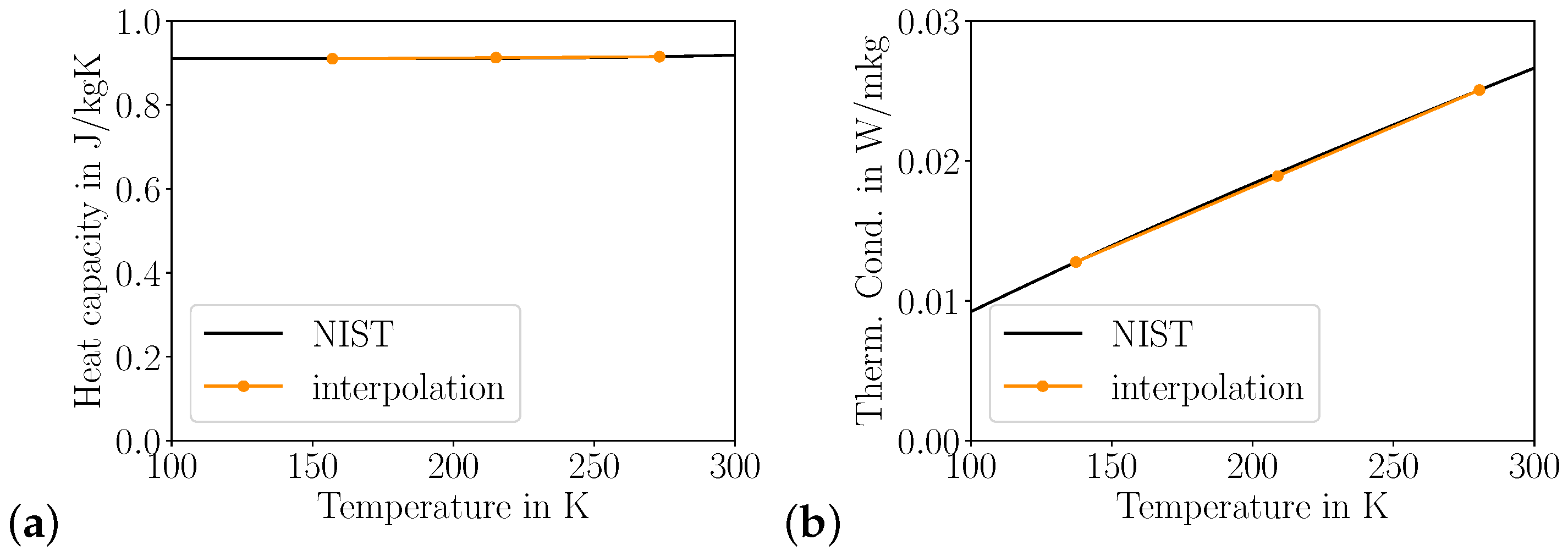
2.1. Fluid Properties
2.2. Computational Fluid Dynamics
3. Results
3.1. Property Representation Error
3.1.1. Density Errors
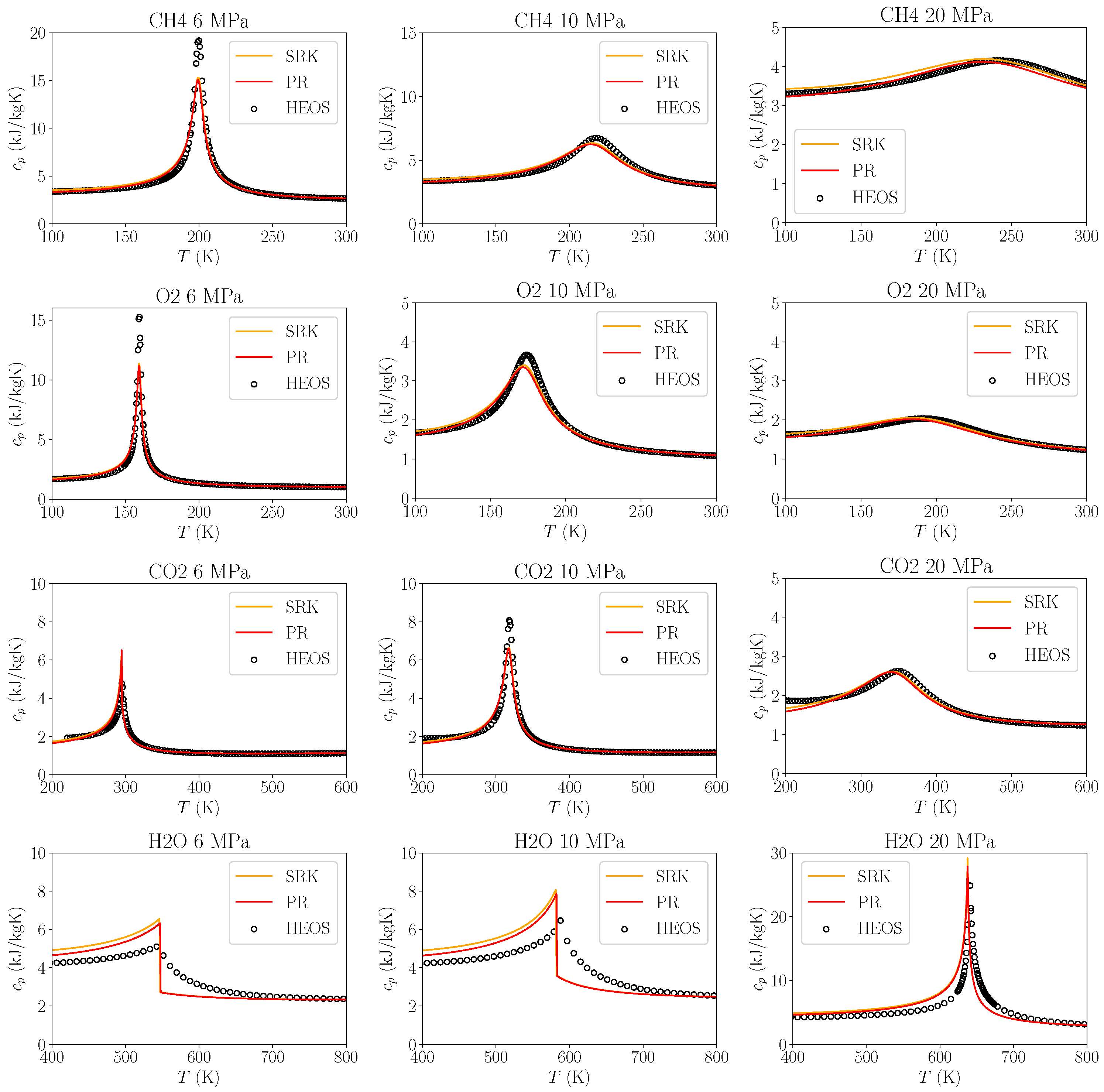
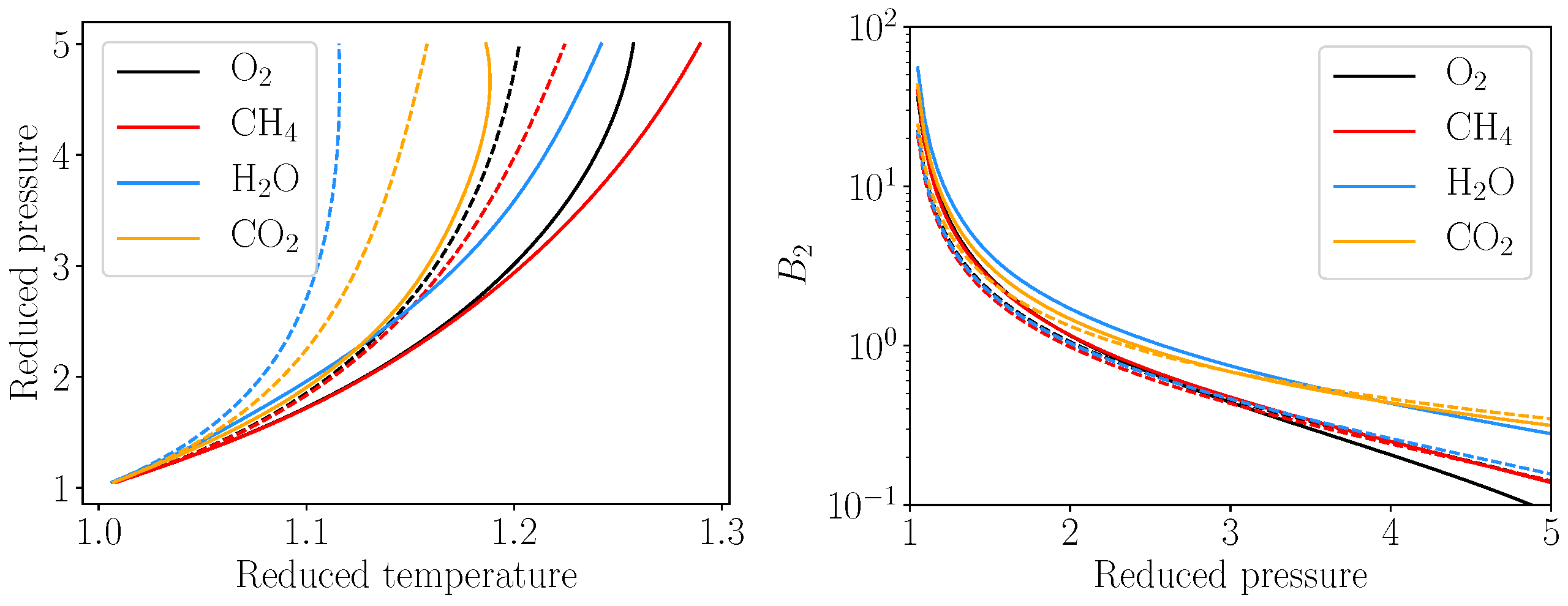
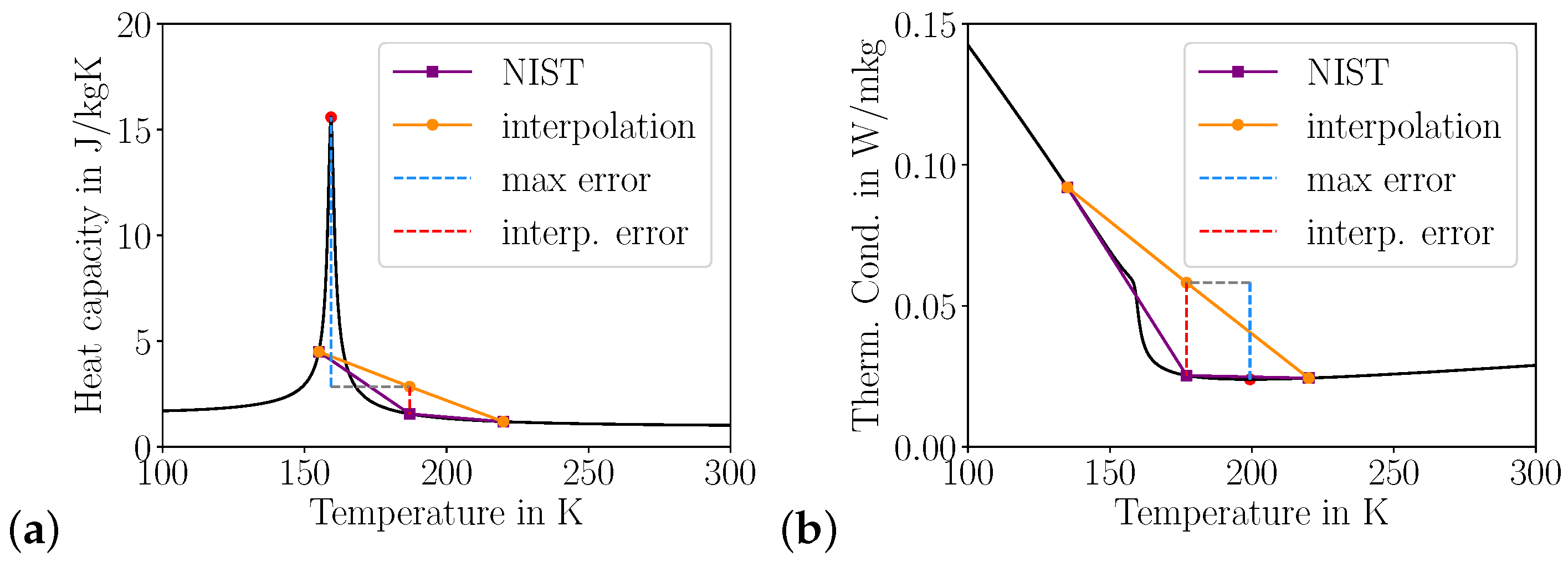
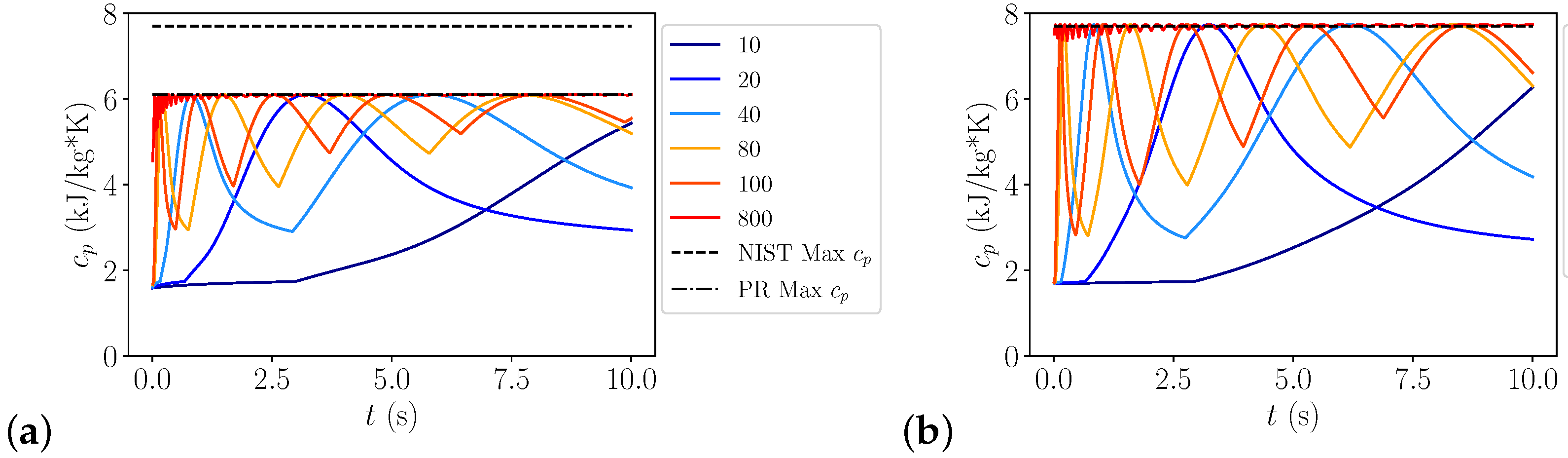
3.1.2. Heat Capacity Errors
Heat Transfer
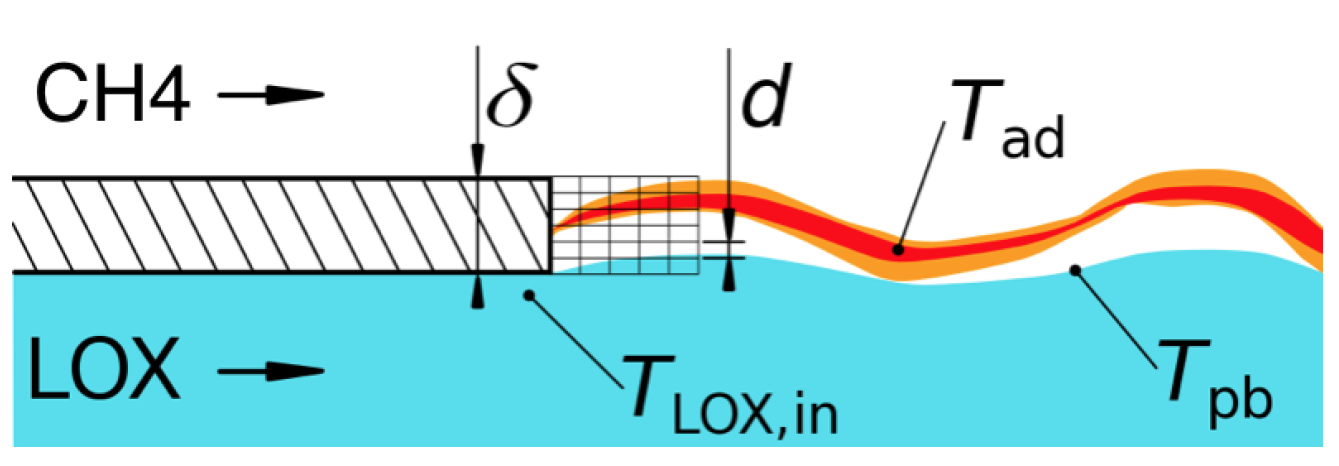
Pseudo Boiling
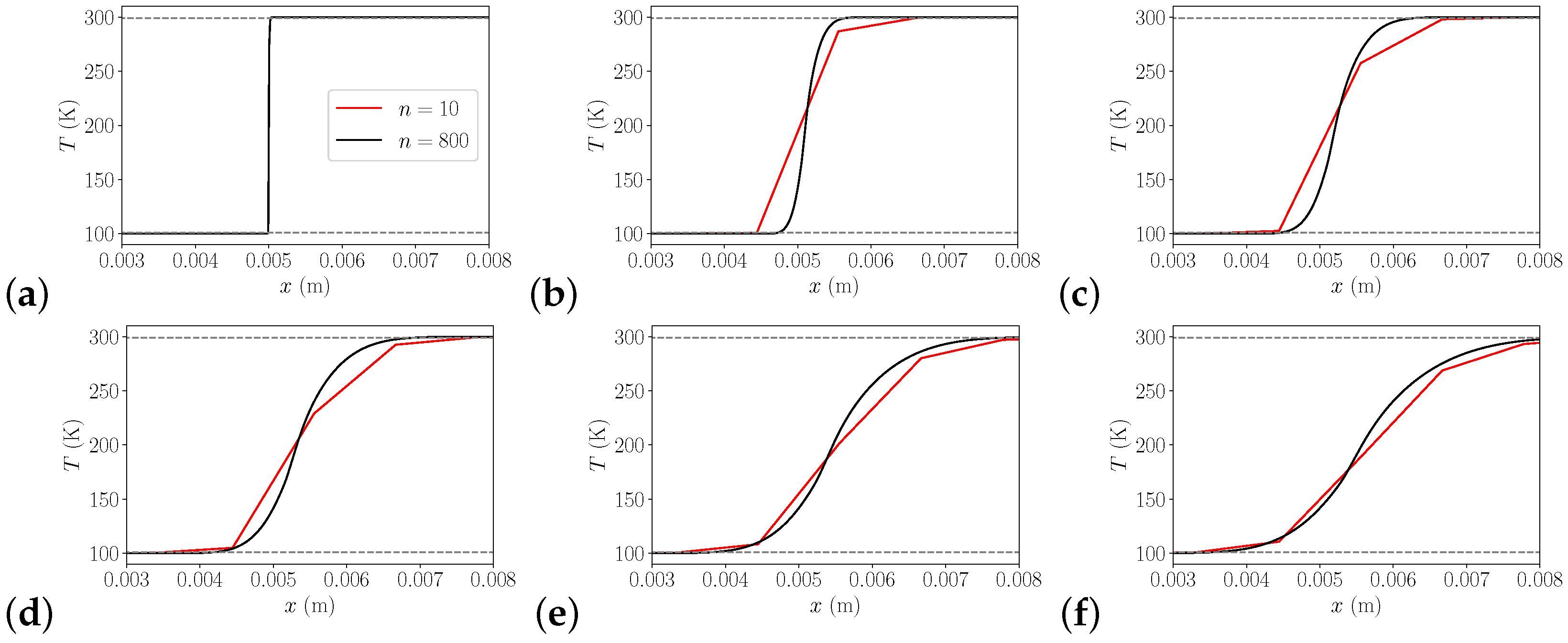
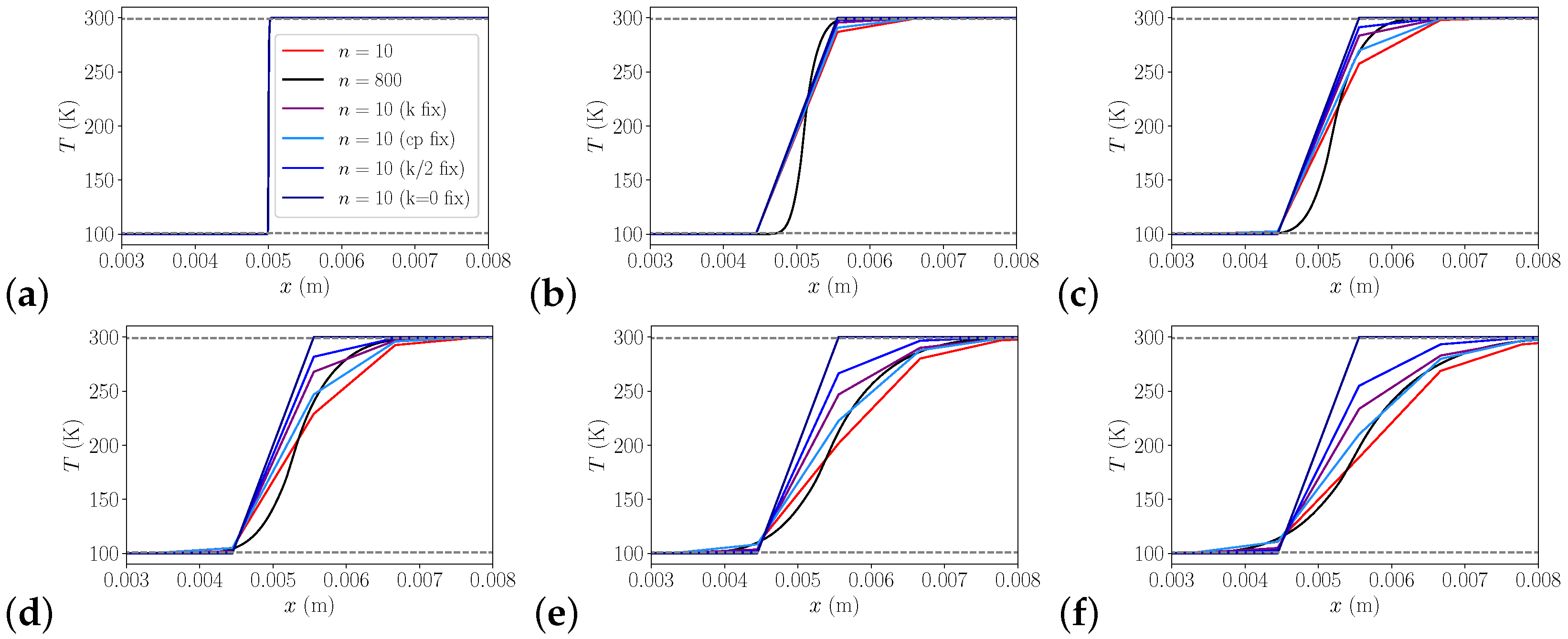
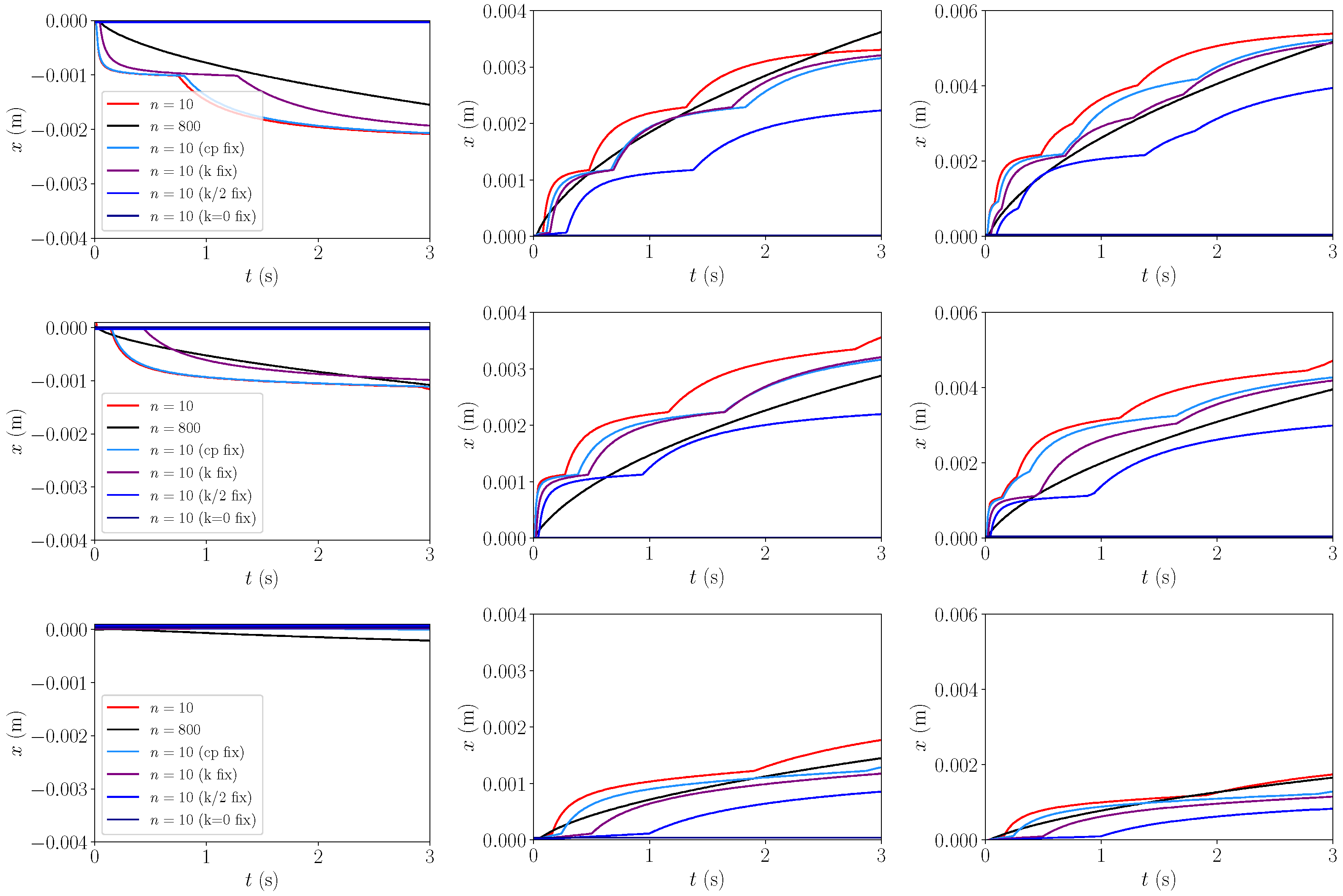
3.1.3. 2D Heat Transfer
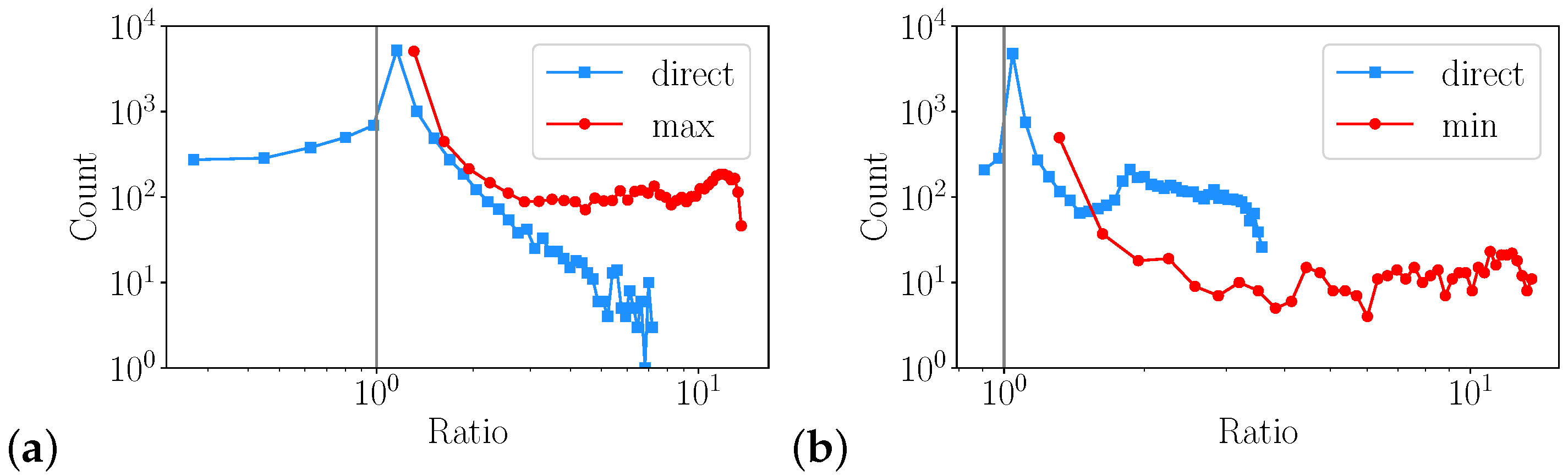
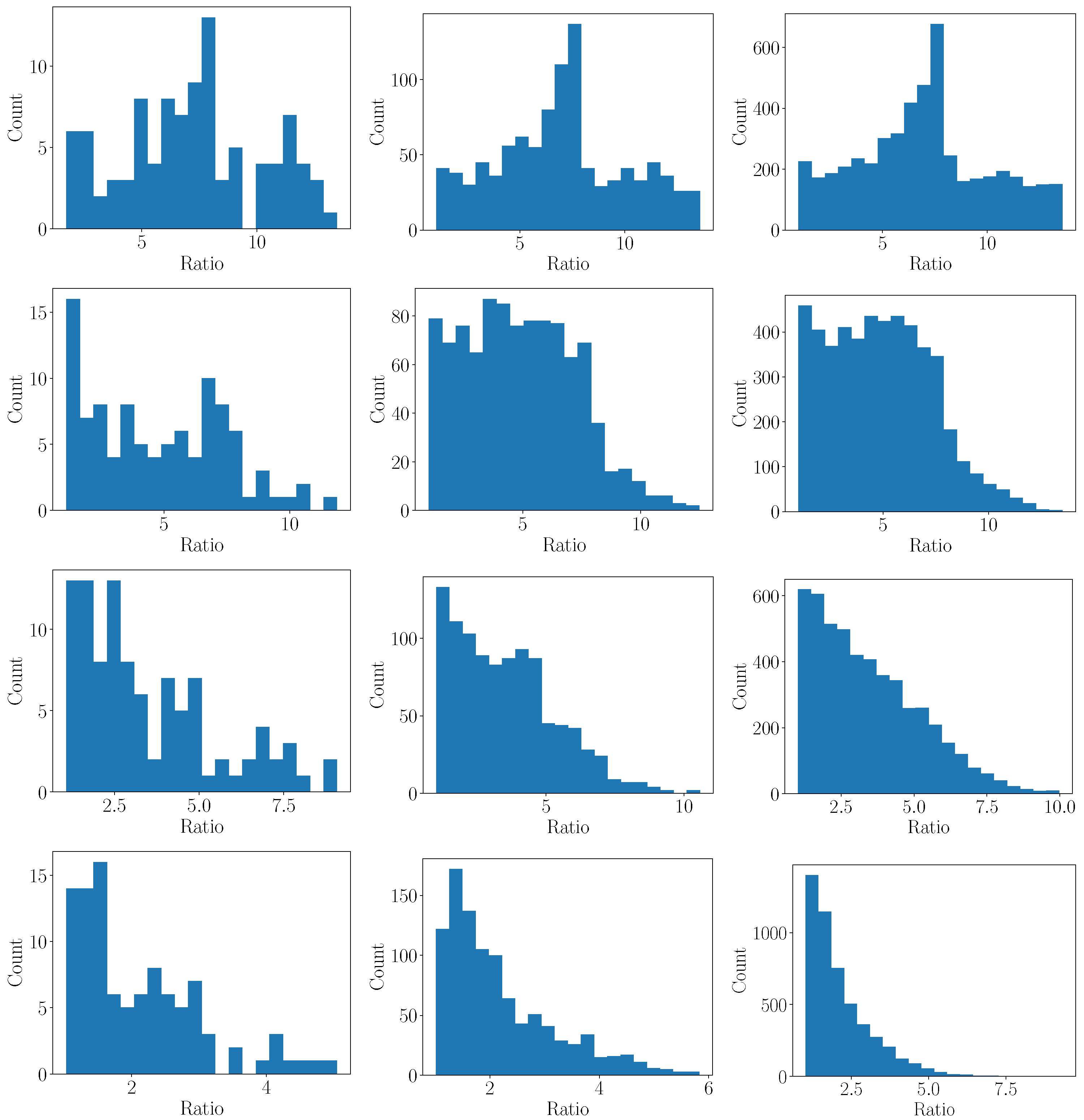
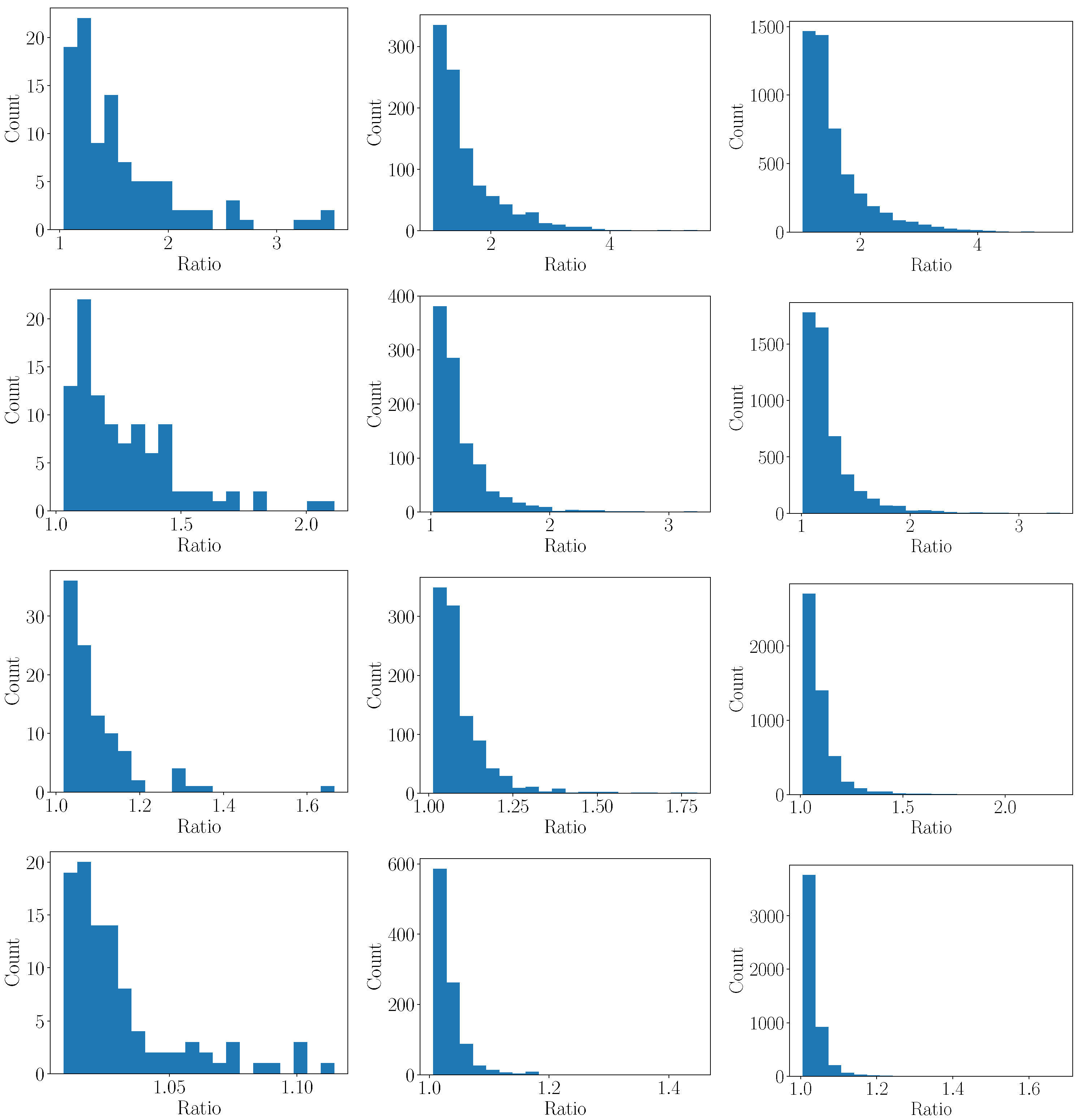
3.2. Sampling Error
3.2.1. Monte Carlo
- 1
- Within bounds defined by the boundary conditions, states can be randomly sampled from the physical fluid properties to obtain information about how numerical properties are reconstructed on a discrete representation.
- 2
- Extremal values of fluid properties that minimize transport need to be taken into account as they act as bottle necks.
- 1
- Prescribe a mesh resolution n and the boundary conditions and .
- 2
- Determine random temperatures (uniform distribution) in the interval . Together with the boundary conditions and , n temperature intervals are thus identified.
- 3
- For each interval, perform the analysis illustrated in Figure 11.
- 4
- Save the maximum error obtained across all intervals .
- 5
- Repeat the above steps N times to analyze a distribution of the error for a given resolution n.
- 6
- Repeat the above steps for different n to study the impact of the resolution.
3.2.2. 1D Heat Transfer
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| EOS | Equation Of State |
| HEOS | Helmholtz EOS |
| SRK | Soave Redlich Kwong EOS |
| PR | Peng Robinson EOS |
References
- Villermaux, E. Mixing and spray formation in coaxial jets. J. Propuls. Power 1998, 14, 807–817. [Google Scholar] [CrossRef]
- Yang, V.; Anderson, W. (Eds.) Liquid Rocket Engine Combustion Instability; AIAA: Washington, DC, USA, 1995. [Google Scholar]
- Candel, S.; Herding, G.; Synder, R.; Scouflaire, P.; Rolon, C.; Vingert, L.; Habiballah, M.; Grisch, F.; Péalat, M.; Bouchardy, P.; et al. Experimental Investigation of Shear Coaxial Cryogenic Jet Flames. J. Propuls. Power 1998, 14, 826–834. [Google Scholar] [CrossRef]
- Delplanque, J.P.; Sirignano, W. Numerical study of the transient vaporization of an oxygen droplet at sub- and super-critical conditions. Int. J. Heat Mass Transf. 1993, 36, 303–314. [Google Scholar] [CrossRef]
- Yang, V.; Lin, N.; Shuen, J. Vaporization of Liquid Oxygen (LOX) Droplets in Supercritical Hydrogen Environments. Combust. Sci. Technol. 1994, 97, 247–270. [Google Scholar] [CrossRef]
- Sirignano, W.; Delplanque, J.P. Transcritical vaporization of liquid fuels and propellants. J. Propuls. Power 1999, 15, 896–902. [Google Scholar] [CrossRef]
- Mayer, W.; Tamura, H. Propellant Injection in a Liquid Oxygen/Gaseous Hydrogen Rocket Engine. J. Propul. Power 1996, 12, 1137–1147. [Google Scholar] [CrossRef]
- Mayer, W.; Ivancic, B.; Schik, A.; Hornung, U. Propellant Atomization and Ignition Phenomena in Liquid Oxygen/Gaseous Hydrogen Rocket Combustors. J. Propuls. Power 2001, 17, 794–799. [Google Scholar] [CrossRef]
- Oschwald, M.; Schik, A. Supercritical nitrogen free jet investigated by spontaneous Raman scattering. Exp. Fluids 1999, 27, 497–506. [Google Scholar] [CrossRef]
- Oschwald, M.; Smith, J.J.; Branam, R.; Hussong, J.; Schik, A.; Chehroudi, B.; Talley, D. Injection of Fluids into Supercritical Environments. Combust. Sci. Technol. 2006, 178, 49–100. [Google Scholar] [CrossRef]
- Habiballah, M.; Orain, M.; Grisch, F.; Vingert, L.; Gicquel, P. Experimental studies of high-pressure cryogenic flames on the mascotte facility. Combust. Sci. Technol. 2006, 178, 101–128. [Google Scholar] [CrossRef]
- Candel, S.; Juniper, M.; Singla, G.; Scouflaire, P.; Rolon, C. Structures and dynamics of cryogenic flames at supercritical pressure. Combust. Sci. Technol. 2006, 178, 161–192. [Google Scholar] [CrossRef]
- Chehroudi, B.; Talley, D.; Coy, E. Initial growth rate and visual characteristics of a round jet into sub- and supercritical environment of relevance to rocket, gas turbine, and Diesel engines. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11 January–14 January 1999. [Google Scholar]
- Chehroudi, B.; Talley, D.; Coy, E. Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures. Phys. Fluids 2002, 14, 850–861. [Google Scholar] [CrossRef]
- Davis, D.; Chehroudi, B. The effects of pressure and acoustic field on a cryogenic coaxial jet. In Proceedings of the 42nd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5 January–8 January 2004. [Google Scholar]
- Davis, D.; Chehroudi, B. Measurements in an acoustically driven coaxial jet under sub-, near-, and supercritical conditions. J. Propuls. Power 2007, 23, 364–374. [Google Scholar] [CrossRef]
- Banuti, D.T. Thermodynamic Analysis and Numerical Modeling of Supercritical Injection. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2015. [Google Scholar]
- Habiballah, M.; Zurbach, S. Test case RCM-3—Mascotte single injector 60 bar. In Proceedings of the 2nd International Workshop Rocket Combustion Modeling—Atomization, Combustion and Heat Transfer, DLR, Lampoldshausen, Germany, 25–27 March 2001. [Google Scholar]
- Vingert, L.; Nicole, A.; Habiballah, M. Test Case RCM-2, Mascotte single injector. In Proceedings of the 3rd International Workshop on Rocket Combustion Modeling, Vernon, France, 13–15 March 2006. [Google Scholar]
- Oefelein, J.C.; Dahms, R.N.; Lacaze, G.; Manin, J.L.; Pickett, L.M. Effects of pressure on fundamental physics of fuel injection in Diesel engines. In Proceedings of the ICLASS, Heidelberg, Germany, 2–6 September 2012. [Google Scholar]
- Banuti, D.T. A thermodynamic look at injection in aerospace propulsion systems. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Banuti, D.T.; Hannemann, V.; Hannemann, K.; Weigand, B. An efficient multi-fluid-mixing model for real gas reacting flows in liquid propellant rocket engines. Combust. Flame 2016, 168, 98–112. [Google Scholar] [CrossRef]
- Oefelein, J.C.; Yang, V. Modeling High-Pressure Mixing and Combustion Processes in Liquid Rocket Engines. J. Propul. Power 1998, 14, 843–857. [Google Scholar] [CrossRef]
- Ely, J.F.; Hanley, H. Prediction of transport properties. 1. Viscosity of fluids and mixtures. Ind. Eng. Chem. Res. 1981, 20, 323–332. [Google Scholar] [CrossRef]
- Ely, J.F.; Hanley, H. Prediction of transport properties. 2. Thermal conductivity of pure fluids and mixtures. Ind. Eng. Chem. Res. 1983, 22, 90–97. [Google Scholar] [CrossRef]
- Benedict, M.; Webb, G.; Rubin, L. An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures: I. Methane, Ethane, Propane, and n-Butane. J. Chem. Phys. 1940, 8, 334–345. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Res. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium Constants from a Modified Redlich-Kwong Equation of State. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Banuti, D.T. Crossing the Widom-line—Supercritical pseudo-boiling. J. Supercrit. Fluids 2015, 98, 12–16. [Google Scholar] [CrossRef]
- Banuti, D.T. The latent heat of supercritical fluids. Period. Polytech. Chem. Eng. 2019, 63, 270–275. [Google Scholar] [CrossRef]
- Banuti, D.; Raju, M.; Ihme, M. Between supercritical liquids and gases–reconciling dynamic and thermodynamic state transitions. J. Supercrit. Fluids 2020, 165, 104895. [Google Scholar] [CrossRef]
- Banuti, D.T.; Hannemann, K. The absence of a dense potential core in supercritical injection: A thermal break-up mechanism. Phys. Fluids. 2016, 28, 035103. [Google Scholar] [CrossRef]
- Longmire, N.; Banuti, D. Onset of heat transfer deterioration caused by pseudo-boiling in CO2 laminar boundary layers. Int. J. Heat Mass Transf. 2022, 193, 122957. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef]
- Ghosal, S. Analysis of Discretization Errors in LES; Center for Turbulence Research Annual Research Briefs: Moffett Field, CA, USA, 1995. [Google Scholar]
- Chow, F.K.; Moin, P. A further study of numerical errors in large-eddy simulations. J. Comput. Phys. 2003, 184, 366–380. [Google Scholar] [CrossRef]
- Lacaze, G.; Oefelein, J.C. A non-premixed combustion model based on flame structure analysis at supercritical pressures. Combust. Flame 2012, 159, 2087–2103. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. NIST Chemistry Webbook, NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. Available online: http://webbook.nist.gov/chemistry (accessed on 1 March 2021).
- Prausnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 1985. [Google Scholar]
- van der Waals, J. Over de Continuiteit van den Gas- en Vloeistoftoestand. Ph.D. Thesis, University of Leiden, Leiden, The Netherlands, 1873. [Google Scholar]
- Banuti, D.T. A critical assessment of adaptive tabulation for fluid properties using neural networks. In Proceedings of the AIAA Aerospace Sciences Meeting, Virtual Event, 11–15, 19–21 January 2021. [Google Scholar]
- Harstad, K.G.; Miller, R.S.; Bellan, J. Efficient high-pressure state equations. AIChE J. 1997, 43, 1605–1610. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids, 4th ed.; McGraw Hill: New York, NY, USA, 1987. [Google Scholar]
- Pini, M.; Vitale, S.; Colonna, P.; Gori, G.; Guardone, A.; Economon, T.; Alonso, J.; Palacios, F. SU2: The Open-Source Software for Non-ideal Compressible Flows. J. Phys. Conf. Ser. 2017, 821, 012013. [Google Scholar] [CrossRef]
- Economon, T.D. Simulation and Adjoint-Based Design for Variable Density Incompressible Flows with Heat Transfer. AIAA J. 2020, 58, 757–769. [Google Scholar] [CrossRef]
- Longmire, N.P.; Banuti, D. Extension of SU2 using neural networks for thermo-fluids modeling. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. [Google Scholar] [CrossRef]
- Longmire, N.; Banuti, D.T. Modeling of the supercritical boiling curve by forced convection for supercritical fluids in relation to regenerative cooling. In Proceedings of the AIAA Aerospace Sciences Meeting, Virtual Event, 11–15, 19–21 January 2021. [Google Scholar]
- Schmidt, E.; Eckert, E.; Grigull, E. Jahrbuch der Deutschen Luftfahrtforschung Bd. II, AAF Translation Nr. 527, Air Material Command; Wright Field: Dayton, OH, USA, 1939; p. 53158. [Google Scholar]
- Schmidt, E. Wärmetransport durch natürliche Konvektion in Stoffen bei kritischem Zustand. Int. J. Heat Mass Transf. 1960, 1, 92–101. [Google Scholar] [CrossRef]
- Banuti, D.T.; Ma, P.C.; Hickey, J.P.; Ihme, M. Thermodynamic structure of supercritical LOX–GH2 diffusion flames. Combust. Flame 2018, 196, 364–376. [Google Scholar] [CrossRef]
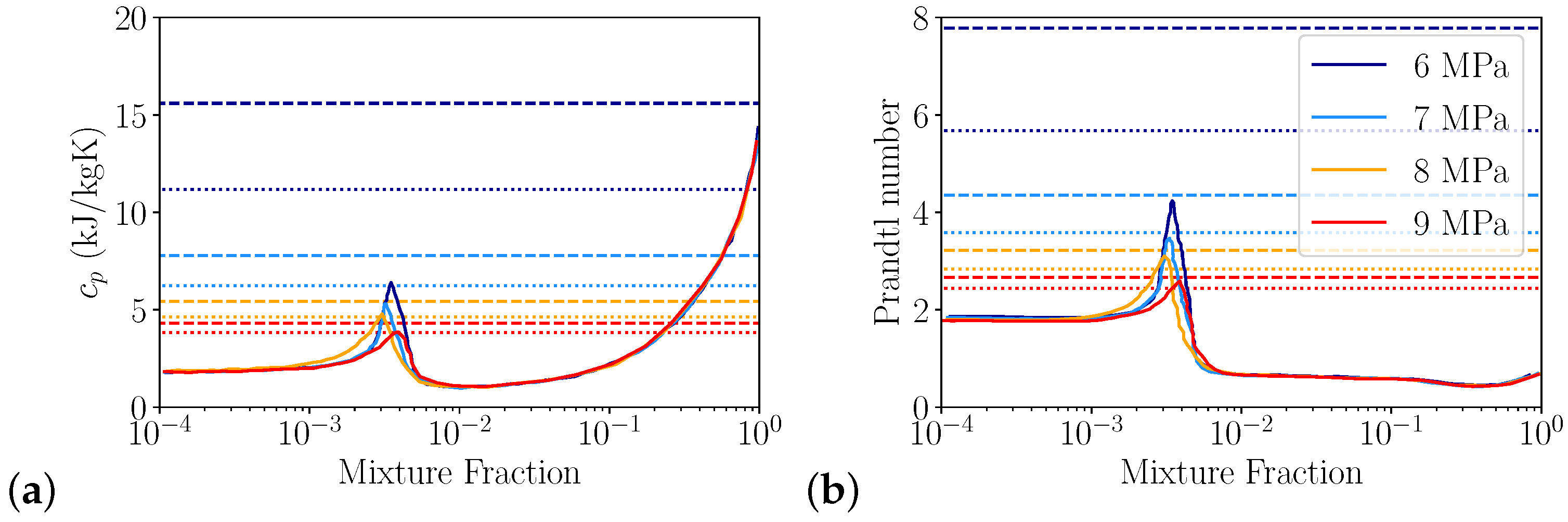




| Pressure in MPa | J/kg/K | J/kg/K | Ratio | Rel. Error | Pr | Pr | Ratio | Rel. Error |
|---|---|---|---|---|---|---|---|---|
| 60 | 15.6 | 6.46 | 2.41 | 58.59% | 9.38 | 4.24 | 2.21 | 54.83% |
| 70 | 7.78 | 5.40 | 1.44 | 30.59% | 5.13 | 3.47 | 1.48 | 32.29% |
| 80 | 5.42 | 4.84 | 1.12 | 10.73% | 3.76 | 3.14 | 1.20 | 16.52% |
| 90 | 4.31 | 4.00 | 1.08 | 7.19 % | 3.10 | 2.58 | 1.20 | 16.69% |
| # Elements | Spacing d in mm |
|---|---|
| 10 | 1.0 |
| 20 | 0.5 |
| 40 | 0.25 |
| 80 | 0.125 |
| 100 | 0.1 |
| 800 | 0.0125 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Longmire, N.P.; Banuti, D.T. Limits of Fluid Modeling for High Pressure Flow Simulations. Aerospace 2022, 9, 643. https://doi.org/10.3390/aerospace9110643
Longmire NP, Banuti DT. Limits of Fluid Modeling for High Pressure Flow Simulations. Aerospace. 2022; 9(11):643. https://doi.org/10.3390/aerospace9110643
Chicago/Turabian StyleLongmire, Nelson P., and Daniel T. Banuti. 2022. "Limits of Fluid Modeling for High Pressure Flow Simulations" Aerospace 9, no. 11: 643. https://doi.org/10.3390/aerospace9110643
APA StyleLongmire, N. P., & Banuti, D. T. (2022). Limits of Fluid Modeling for High Pressure Flow Simulations. Aerospace, 9(11), 643. https://doi.org/10.3390/aerospace9110643





