Optimal Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints
Abstract
:1. Introduction
2. Model Description
2.1. Nonlinear Engagement Kinematics
2.2. Linear Engagement Kinematics
2.3. Timeline
2.4. Missile Guidance Law
3. Two-Way Cooperation Guidance Strategies with Impact Angle Constraints
3.1. Two-Way Cooperation Dynamics with Impact Angle Constraints
3.2. Problem Statement with Impact Angle Constraints for Two-Way Cooperation
3.3. Order Reduction
3.4. Optimal Solution
3.5. Solution of the Terminal Miss Distance and Terminal Impact Angle
3.6. Special Cases
4. One-Way Cooperation Guidance Strategy with Impact Angle Constraints for Independent Defender
4.1. One-Way Cooperation Dynamics with Impact Angle Constraints for Independent Defender
4.2. One-Way Problem Statement with Impact Angle Constraints for Independent Defender
4.3. Order Reduction
4.4. Optimal Solution
4.5. Solution of the Terminal Miss Distance and Terminal Impact Angle
5. One-Way Cooperation Guidance Strategy with Impact Angle Constraints for Independent Target
5.1. One-Way Cooperation Dynamics with Independent Target
5.2. One-Way Problem Statement with Independent Target
5.3. Order Reduction
5.4. Optimal Solution
5.5. Solution of the Terminal Miss Distance and Terminal Impact Angle
6. Simulation Analysis
6.1. Two-Way Cooperation
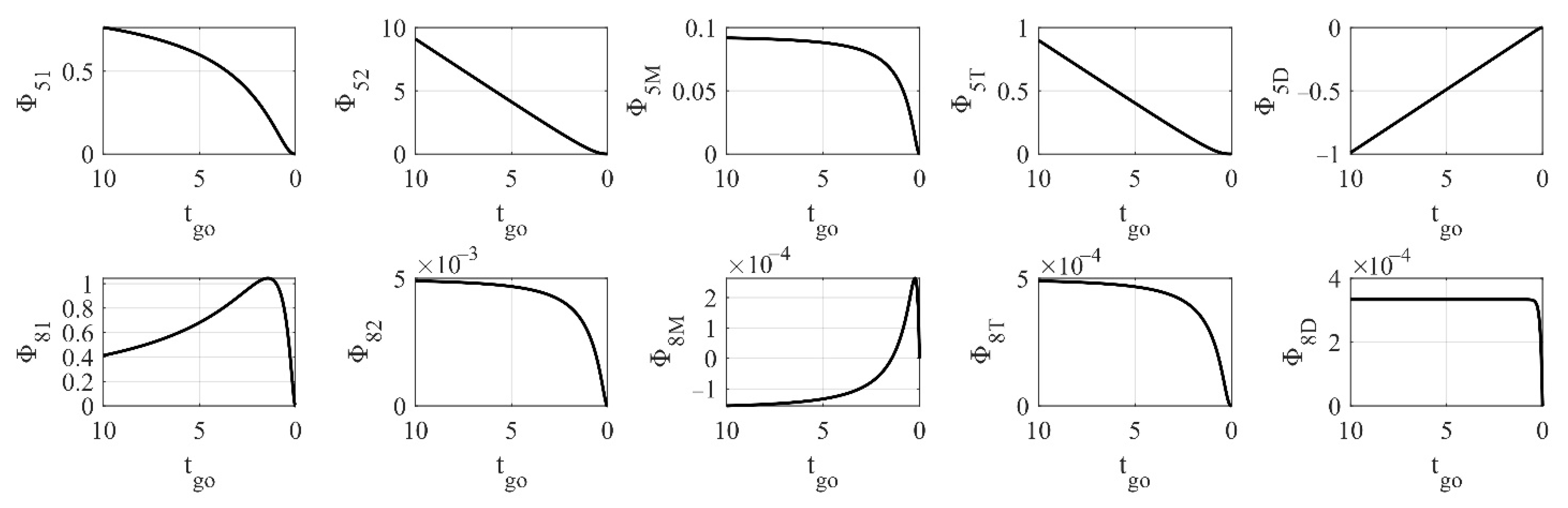
6.1.1. Transfer Matrix
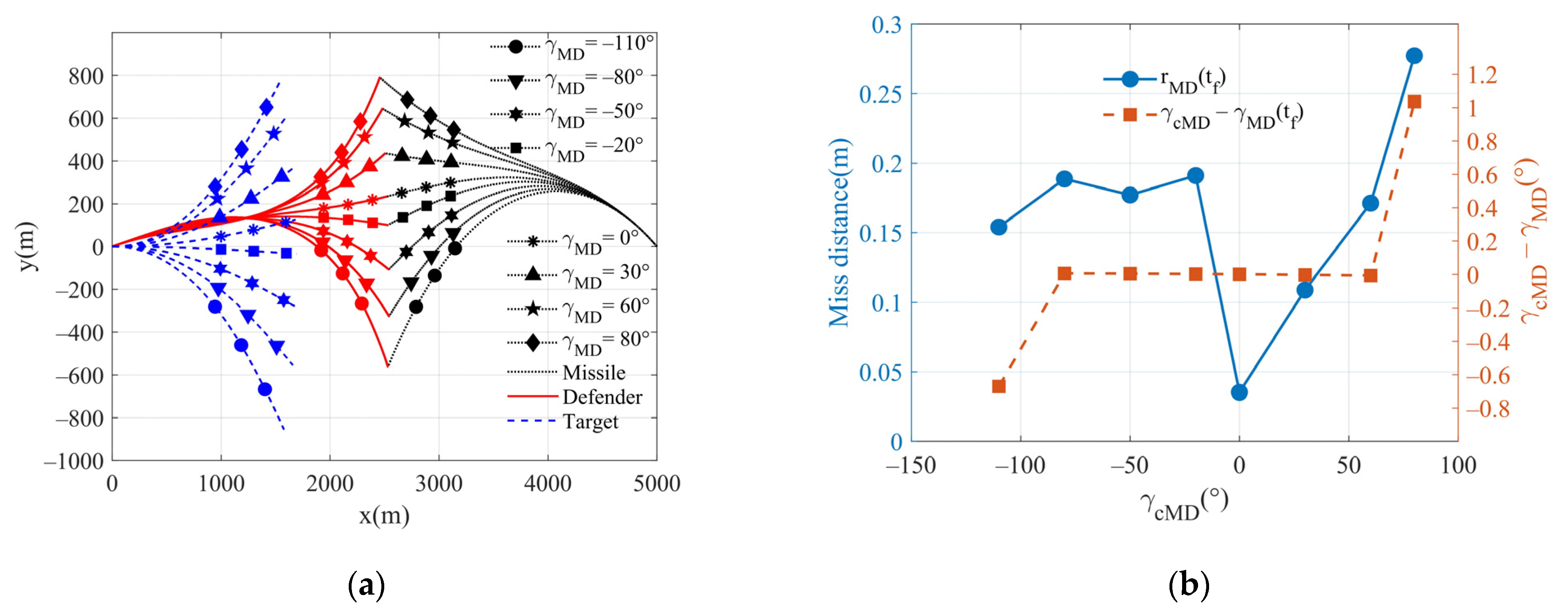
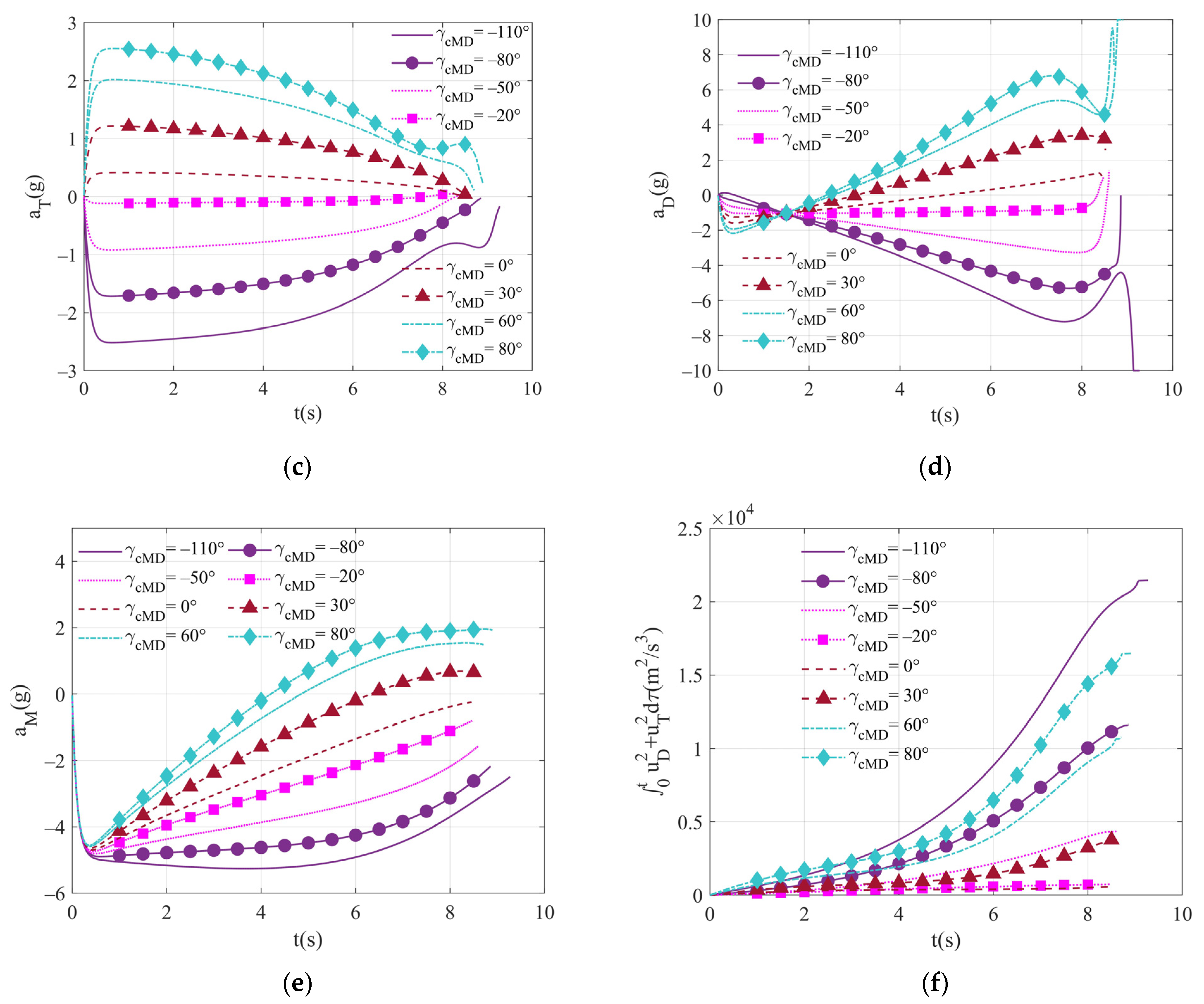
6.1.2. Simulation of Different Terminal Impact Angle Commands
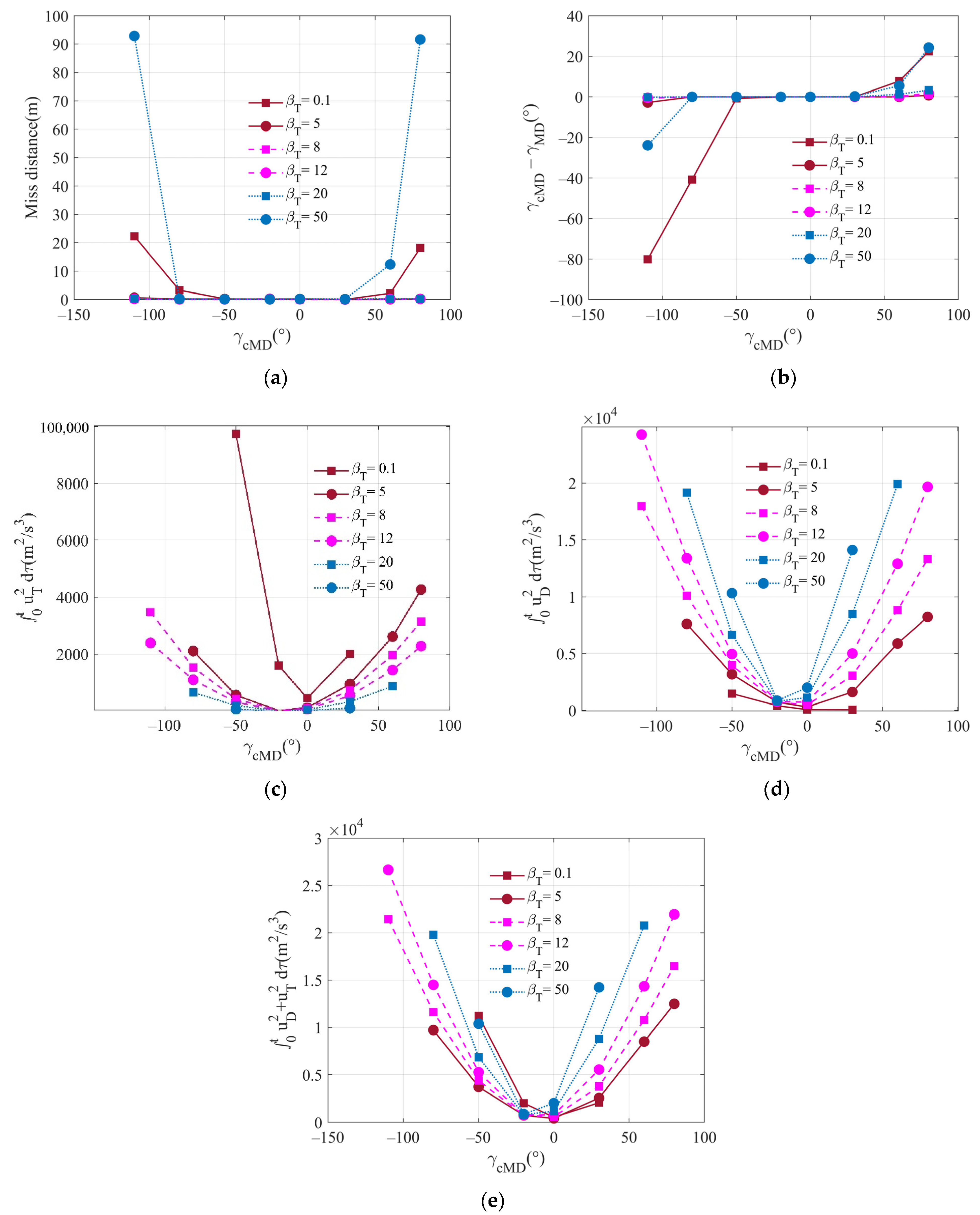
6.1.3. Variation Curves for Different Weight Coefficients
6.2. One-Way Cooperation with Independent Defender
6.2.1. Transfer Matrix
6.2.2. Simulation of Different Terminal Impact Angle Commands
6.3. One-Way Cooperation with Independent Target
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Computation of ZIA for Two-Way Cooperation
References
- Yamasaki, T.; Takano, H. Modified command to line-of-sight intercept guidance for aircraft defense. J. Guid. Control. Dyn. 2013, 36, 898–902. [Google Scholar] [CrossRef]
- Ratnoo, A.; Shima, T. Guidance Strategies Against Defended Aerial Targets. J. Guid. Control. Dyn. 2012, 35, 1059–1068. [Google Scholar] [CrossRef]
- Ratnoo, A.; Shima, T. Line-of-Sight Interceptor Guidance for Defending an Aircraft. J. Guid. Control. Dyn. 2011, 34, 522–532. [Google Scholar] [CrossRef]
- Kumar, R.S.; Mukherjee, D. Cooperative active aircraft protection guidance using line-of-sight approach. IEEE Trans. Aerosp. Electron. Syst. 2020, 27, 957–967. [Google Scholar] [CrossRef]
- Luo, H.; Ji, H.; Wang, X.; Qu, X. Cooperative robust line-of-sight guidance law for aerial target defense. In Proceedings of the International Conference on Unmanned Aircraft Systems, IEEE, Athens, Greece, 1–4 September 2020; pp. 1501–1507. [Google Scholar]
- Kumar, R.S.; Mukherjee, D. Mukherjee Cooperative guidance strategies for active aircraft protection. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 10–12 July 2019; pp. 4641–4646. [Google Scholar]
- Shaferman, V.; Shima, T. Cooperative Multiple-Model Adaptive Guidance for an Aircraft Defending Missile. J. Guid. Control. Dyn. 2010, 33, 1801–1813. [Google Scholar] [CrossRef]
- Fang, F.; Cai, Y.; Yu, Z. Adaptive estimation and cooperative guidance for active aircraft defense in stochastic scenario. Sensors 2019, 19, 979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prokopov, O.; Shima, T. Linear Quadratic Optimal Cooperative Strategies for Active Aircraft Protection. J. Guid. Control. Dyn. 2013, 36, 753–764. [Google Scholar] [CrossRef]
- Weiss, M.; Shima, T. Minimum Effort Pursuit/Evasion Guidance with Specified Miss Distance. J. Guid. Control. Dyn. 2016, 39, 1069–1079. [Google Scholar] [CrossRef]
- Weiss, M.; Shima, T.; Castaneda, D.; Rusnak, I. Combined and Cooperative Minimum-Effort Guidance Algorithms in an Active Aircraft Defense Scenario. J. Guid. Control. Dyn. 2017, 40, 1241–1254. [Google Scholar] [CrossRef]
- Fang, F.; Cai, Y.-L. Optimal cooperative guidance with guaranteed miss distance in three-body engagement. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 232, 492–504. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Cooperative Strategies for Optimal Aircraft Defense from an Attacking Missile. J. Guid. Control. Dyn. 2015, 38, 1510–1520. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Active target defense using first order missile models. Automatica 2017, 78, 139–143. [Google Scholar] [CrossRef]
- Weintraub, E.I.; Garcia, E.; Casbeer, D.; Pachter, M. Optimal evasion in an active target defense scenario. In AIAA Scitech 2021 Forum; AIAA: Reston, VA, USA, 2021; p. 1881. [Google Scholar]
- Perelman, A.; Shima, T.; Rusnak, I. Cooperative Differential Games Strategies for Active Aircraft Protection from a Homing Missile. J. Guid. Control. Dyn. 2011, 34, 761–773. [Google Scholar] [CrossRef]
- Saurav, A.; Kumar, S.R.; Maity, A. Cooperative guidance strategies for aircraft defense with impact angle constraints. In SciTech Forum; AIAA: San Diego, CA, USA, 2019; p. 0356. [Google Scholar]
- Rubinsky, S.; Gutman, S. Three-Player Pursuit and Evasion Conflict. J. Guid. Control. Dyn. 2014, 37, 98–110. [Google Scholar] [CrossRef]
- Sun, Q.; Shen, M.; Gu, X.; Hou, K.; Qi, N. Evasion-Pursuit Strategy against Defended Aircraft Based on Differential Game Theory. Int. J. Aerosp. Eng. 2019, 2019, 7980379. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, W.D.; Fuchs, E.Z.; Pachter, M. Cooperative missile guidance for active defense of air vehicles. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 706–721. [Google Scholar] [CrossRef]
- Liu, S.; Yan, B.; Zhang, X.; Liu, W.; Yan, J. Fractional-order sliding mode guidance law for intercepting hypersonic vehicles. Aerospace 2022, 9, 53. [Google Scholar] [CrossRef]
- Kumar, S.R.; Shima, T. Cooperative Nonlinear Guidance Strategies for Aircraft Defense. J. Guid. Control. Dyn. 2017, 40, 124–138. [Google Scholar] [CrossRef]
- Li, Q.; Fan, Y.; Yan, T.; Liang, X.; Yan, J. Cooperative smooth nonsingular terminal sliding mode guidance with tracking differentiator for active aircraft defense. Aerospace 2022, 9, 221. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghose, D.; Raha, S. Composite Guidance for Impact Angle Control Against Higher Speed Targets. J. Guid. Control. Dyn. 2016, 39, 98–117. [Google Scholar] [CrossRef]
- Kumar, S.R.; Rao, S.; Ghose, D. Sliding-Mode Guidance and Control for All-Aspect Interceptors with Terminal Angle Constraints. J. Guid. Control. Dyn. 2012, 35, 1230–1246. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Zhang, P. Optimal guidance law for intercepting the active defense aircraft with terminal angle constraint. J. Phys. Conf. Ser. Beijing Chin. 2021, 1828, 012160. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Optimal Guidance Laws for Imposing a Relative Intercept Angle. J. Guid. Control. Dyn. 2015, 38, 1395–1408. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative Differential Games Guidance Laws for Imposing a Relative Intercept Angle. J. Guid. Control. Dyn. 2017, 40, 2465–2480. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Linear Quadratic Guidance Laws for Imposing a Terminal Intercept Angle. J. Guid. Control. Dyn. 2008, 31, 1400–1412. [Google Scholar] [CrossRef]
- Taub, I.; Shima, T. Intercept Angle Missile Guidance Under Time Varying Acceleration Bounds. J. Guid. Control. Dyn. 2013, 36, 686–699. [Google Scholar] [CrossRef]
- Fonod, R.; Shima, T. Estimation Enhancement by Cooperatively Imposing Relative Intercept Angles. J. Guid. Control. Dyn. 2017, 40, 1711–1725. [Google Scholar] [CrossRef]
- Fonod, R.; Shima, T. Estimation enhancement by imposing a relative intercept angle for defending missiles. In SciTech Forum; AIAA: Grapevine, TX, USA, 2017; p. 1018. [Google Scholar]
- Zarchan, P. Tactical and Strategic Missile Guidance, 7th ed.; AIAA: Reston, VA, USA, 2019; Chapter 8. [Google Scholar]
- Shima, T. Optimal Cooperative Pursuit and Evasion Strategies Against a Homing Missile. J. Guid. Control. Dyn. 2011, 34, 414–425. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, J. Smooth Sliding Mode Control for Missile Interception with Finite-Time Convergence. J. Guid. Control. Dyn. 2015, 38, 1311–1318. [Google Scholar] [CrossRef]


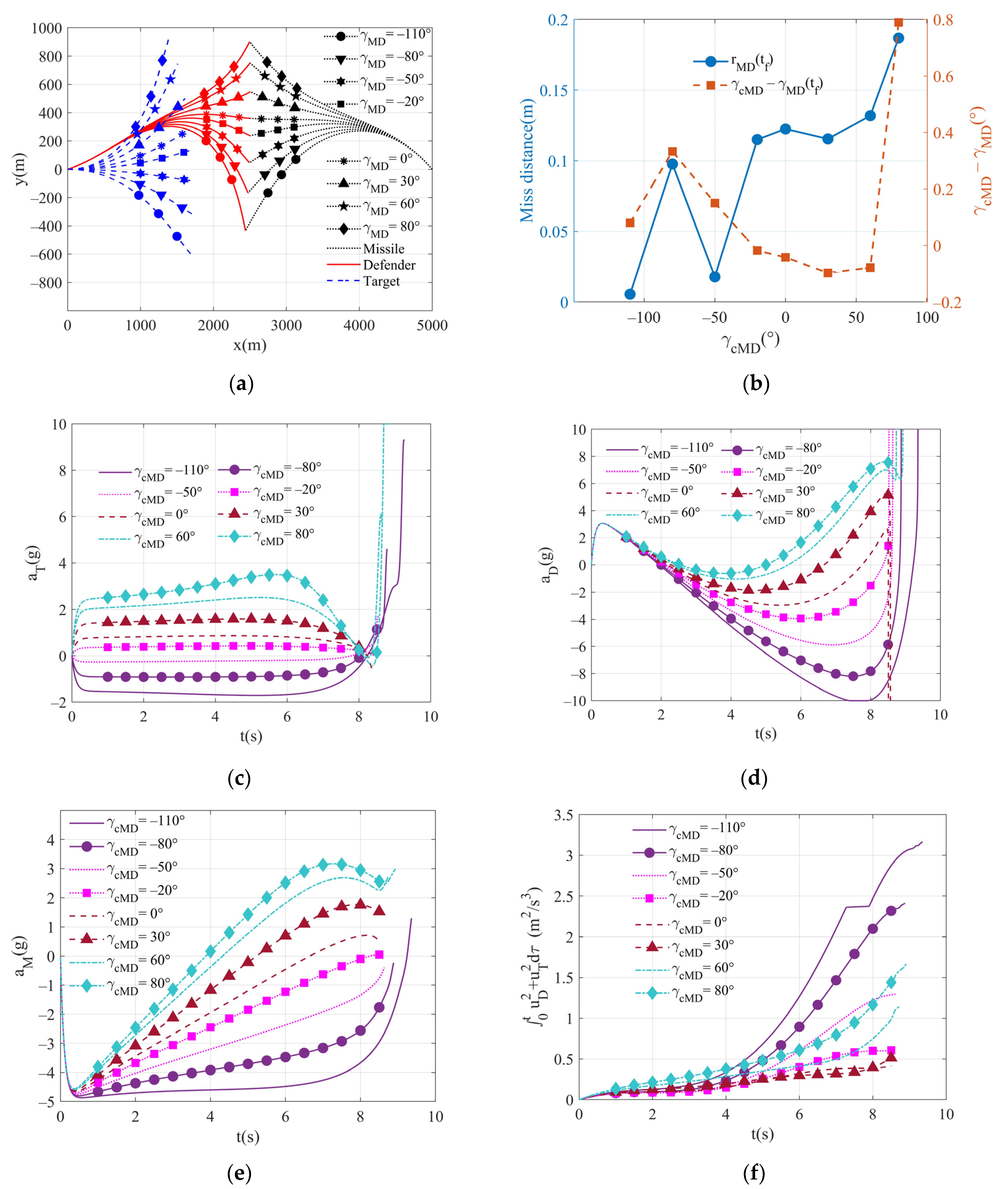
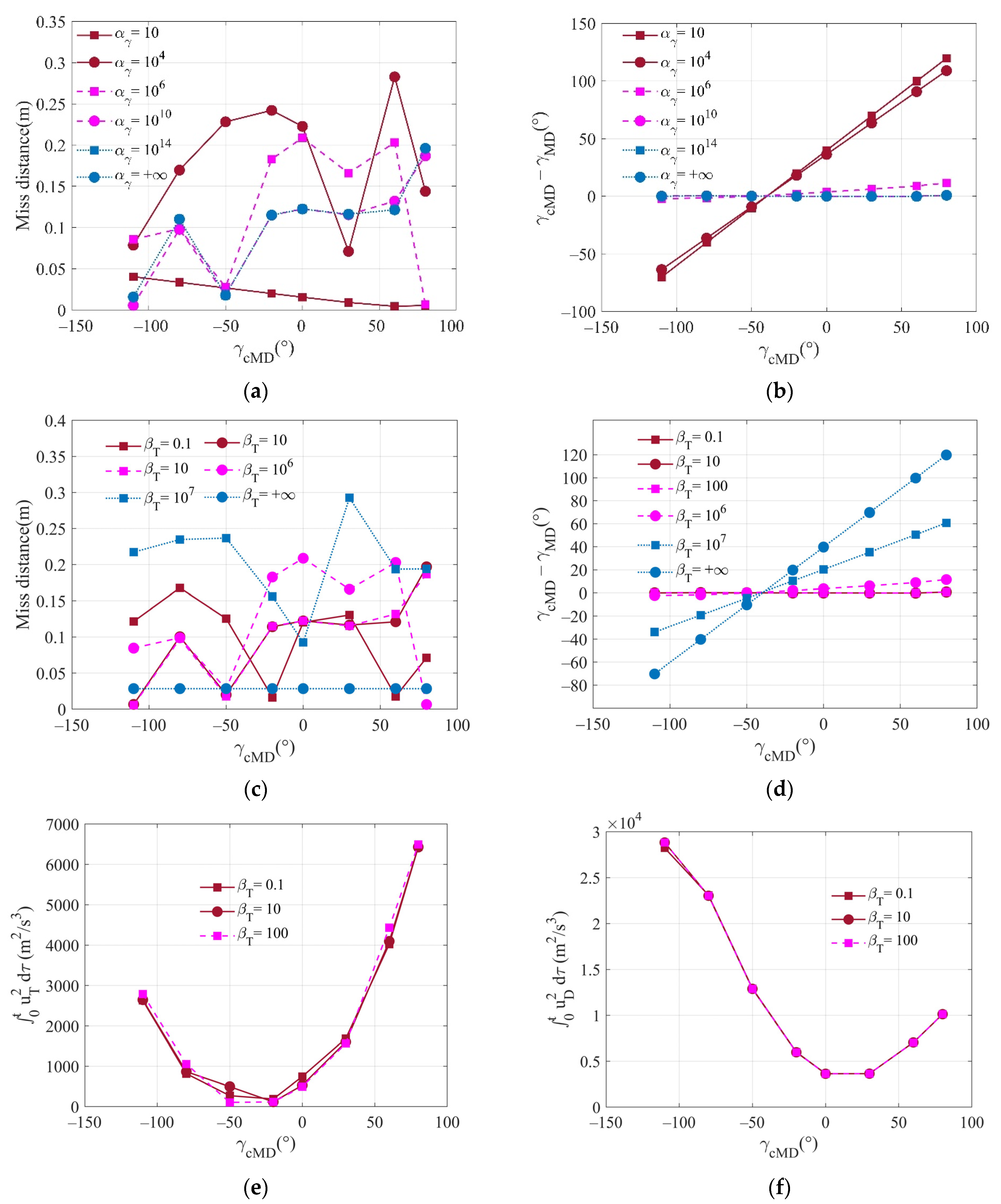

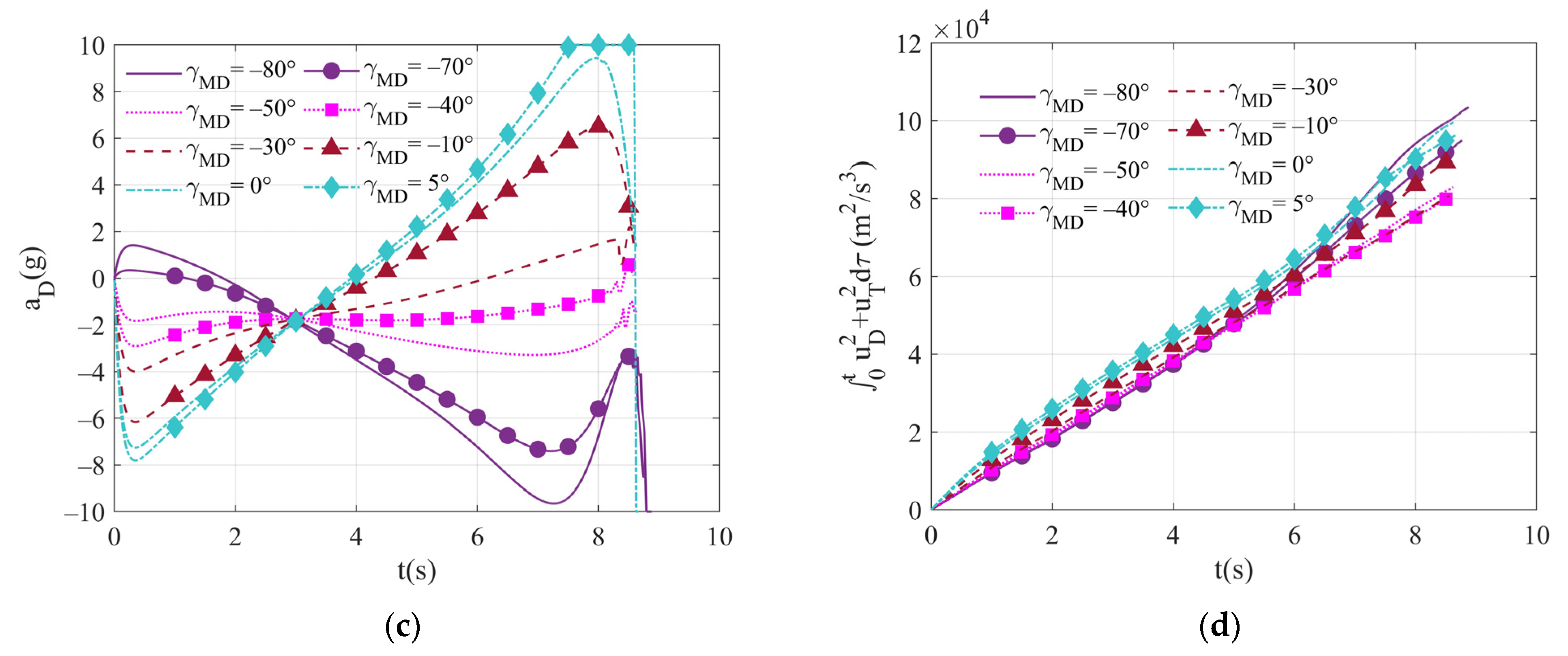
| Special Cases | ||||
|---|---|---|---|---|
| Parameters | Values | Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|---|---|
| 200 m/s | 30 g | 0.1 s | |||||
| 300 m/s | 10 g |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Yan, T.; Gao, M.; Fan, Y.; Yan, J. Optimal Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints. Aerospace 2022, 9, 710. https://doi.org/10.3390/aerospace9110710
Li Q, Yan T, Gao M, Fan Y, Yan J. Optimal Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints. Aerospace. 2022; 9(11):710. https://doi.org/10.3390/aerospace9110710
Chicago/Turabian StyleLi, Quancheng, Tian Yan, Mengjing Gao, Yonghua Fan, and Jie Yan. 2022. "Optimal Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints" Aerospace 9, no. 11: 710. https://doi.org/10.3390/aerospace9110710






