Effects of Aeroelastic Walls on the Aeroacoustics in Transonic Cavity Flow †
Abstract
:1. Introduction
2. Numerical Methods
2.1. Method for Flow Simulation
| Mach Number | Speed, | Static Pressure | Static Temperature |
|---|---|---|---|
| 0.85 | 278.16 m·s | 62,100.00 Pa | 266.53 K |
2.2. Method for Structural Simulation
3. Simulations with Rigid Cavity Models
3.1. Wind Tunnel Model
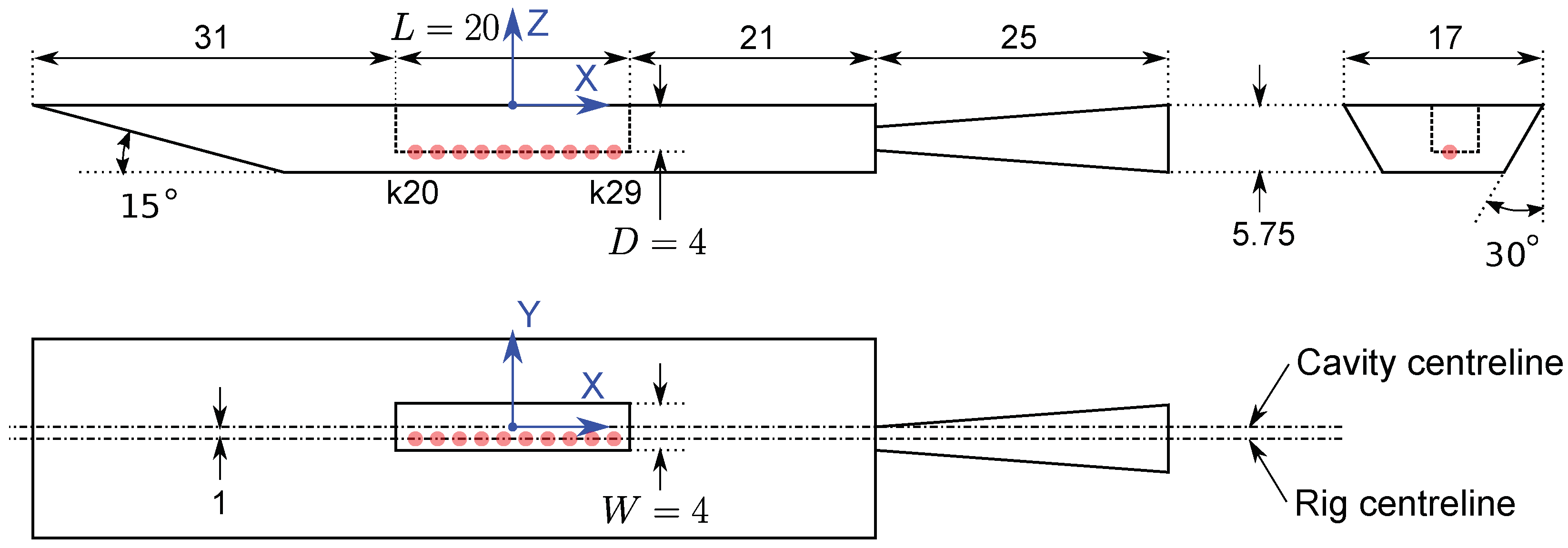

| Probe | x (inch) | y (inch) | z (inch) |
|---|---|---|---|
| K20 | −9.0 | −1.0 | −4.0 |
| K21 | −7.0 | −1.0 | −4.0 |
| K22 | −5.0 | −1.0 | −4.0 |
| K23 | −3.0 | −1.0 | −4.0 |
| K24 | −1.0 | −1.0 | −4.0 |
| K25 | 1.0 | −1.0 | −4.0 |
| K26 | 3.0 | −1.0 | −4.0 |
| K27 | 5.0 | −1.0 | −4.0 |
| K28 | 7.0 | −1.0 | −4.0 |
| K29 | 9.0 | −1.0 | −4.0 |


3.2. Simplified Geometry

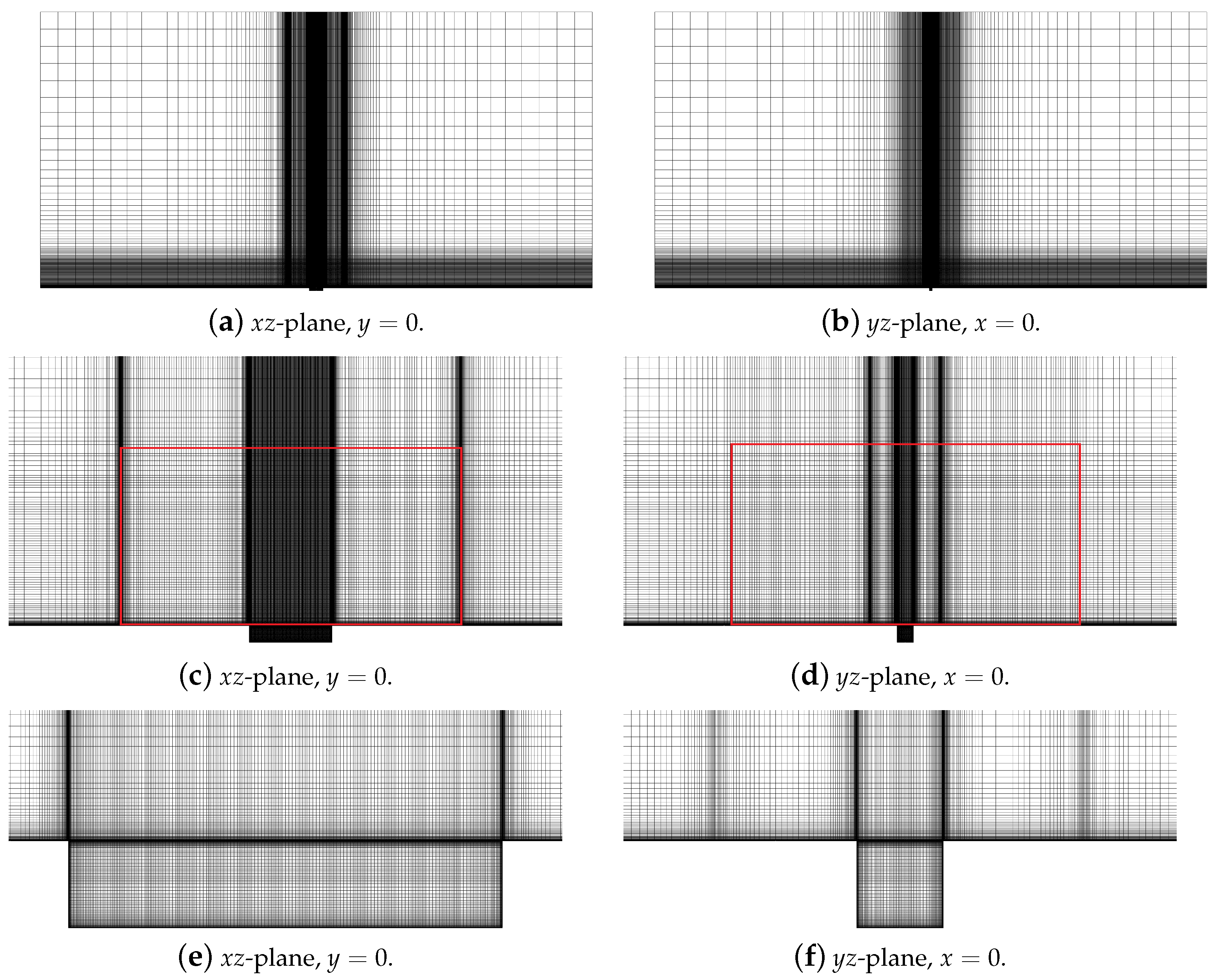
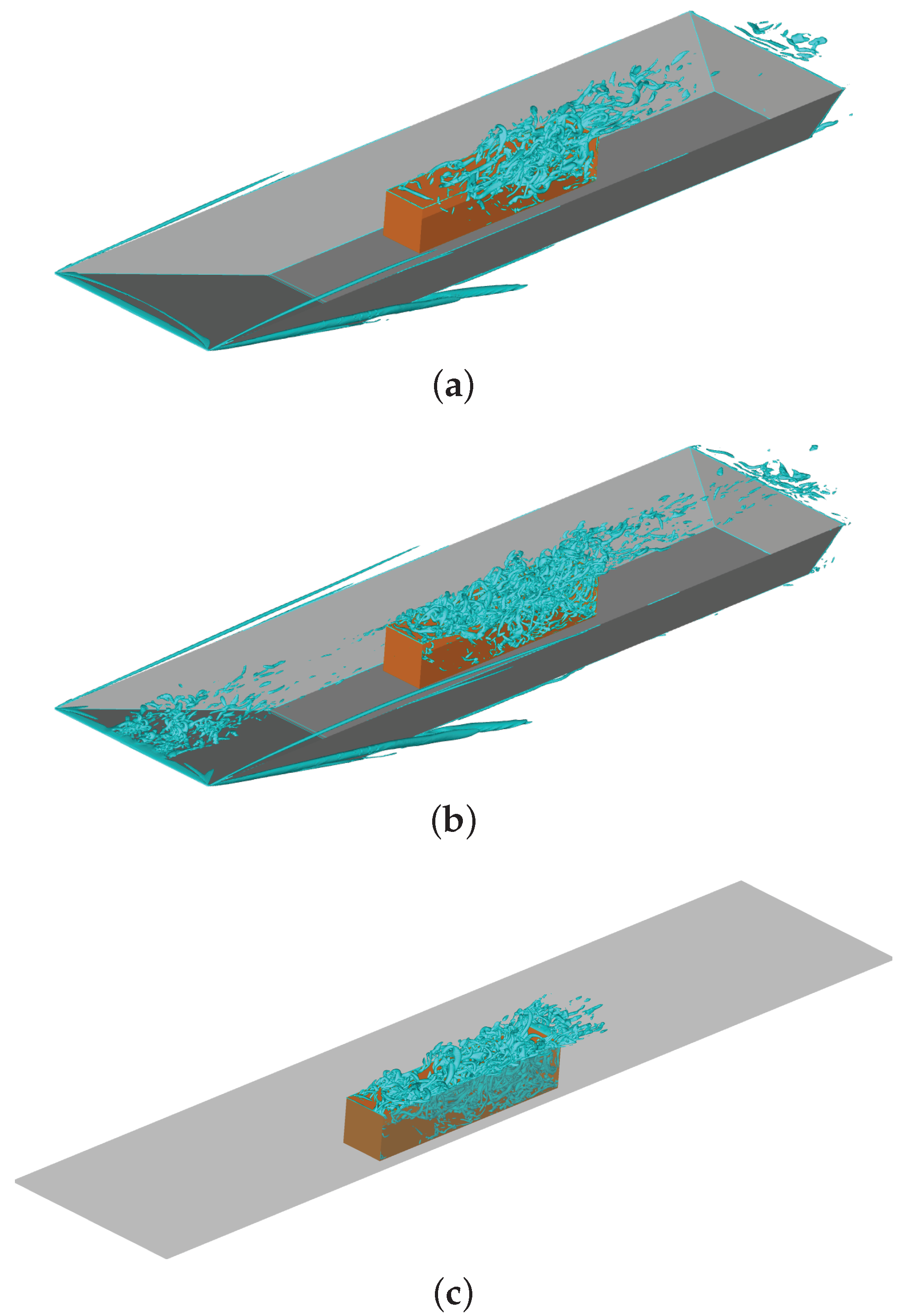
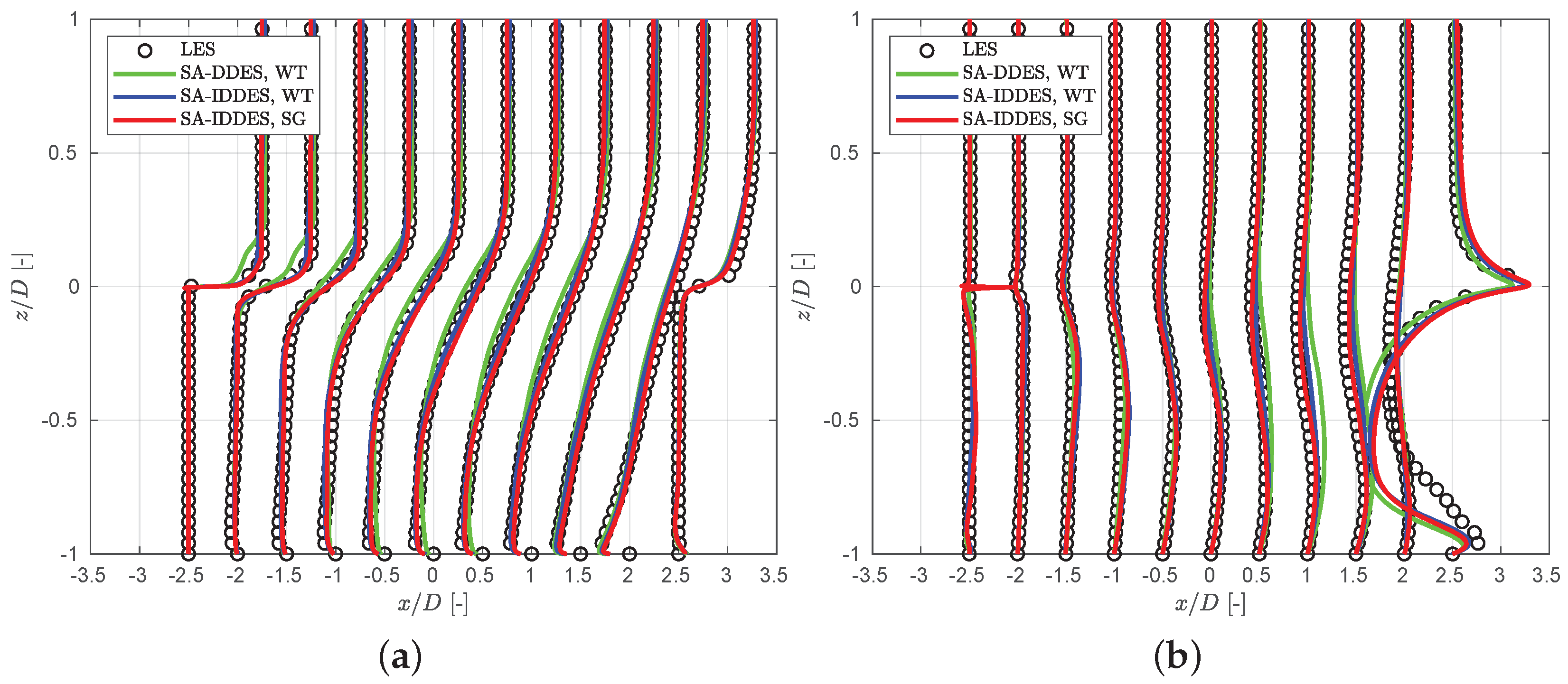
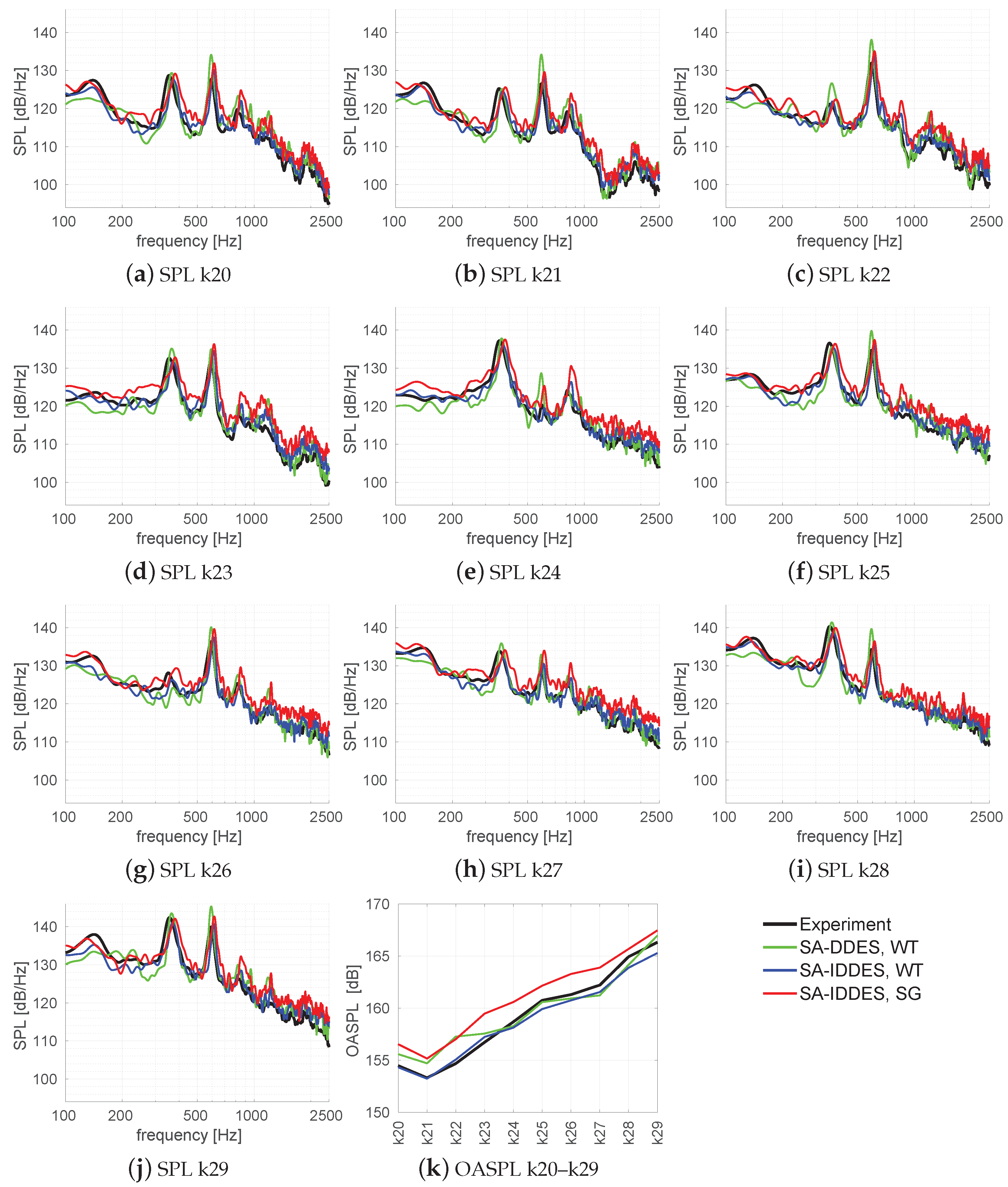
3.3. Results with Rigid Cavities

| Mode | Experimental (Hz) | SA-DDES, WT (Hz) | SA-IDDES, WT (Hz) | SA-IDDES, SG (Hz) |
|---|---|---|---|---|
| 1 | 140 | - | 138 | 130 |
| 2 | 352 | 365 | 370 | 381 |
| 3 | 592 | 592 | 611 | 614 |
| 4 | 812 | 822 | 854 | 852 |
4. Finite Element Model and the Modal Representation
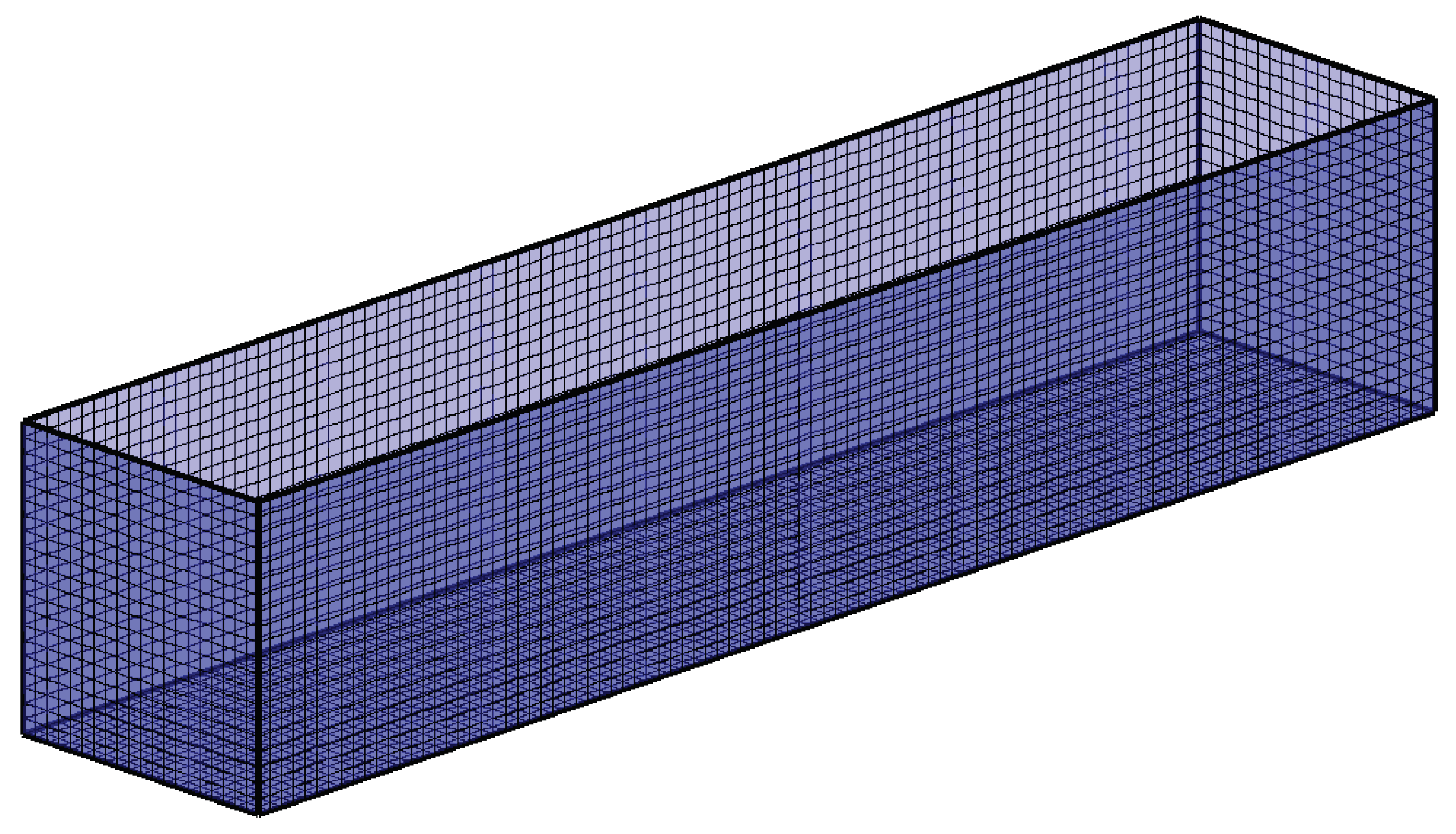
4.1. Finite Element Model
4.2. Modal Representation of the Structural Model
| Mode | f (Hz) | Mode | f (Hz) | Mode | f (Hz) | Mode | f (Hz) |
|---|---|---|---|---|---|---|---|
| 1 | 468 | 14 | 949 | 27 | 1546 | 40 | 2026 |
| 2 | 509 | 15 | 956 | 28 | 1587 | 41 | 2082 |
| 3 | 577 | 16 | 992 | 29 | 1642 | 42 | 2087 |
| 4 | 646 | 17 | 1042 | 30 | 1664 | 43 | 2087 |
| 5 | 675 | 18 | 1087 | 31 | 1665 | 44 | 2120 |
| 6 | 702 | 19 | 1107 | 32 | 1732 | 45 | 2163 |
| 7 | 759 | 20 | 1139 | 33 | 1762 | 46 | 2177 |
| 8 | 801 | 21 | 1214 | 34 | 1823 | 47 | 2214 |
| 9 | 812 | 22 | 1242 | 35 | 1849 | 48 | 2255 |
| 10 | 836 | 23 | 1278 | 36 | 1893 | 49 | 2265 |
| 11 | 841 | 24 | 1350 | 37 | 1942 | 50 | 2280 |
| 12 | 877 | 25 | 1363 | 38 | 1992 | ||
| 13 | 933 | 26 | 1446 | 39 | 2005 |
5. Results with the Elastic Cavity
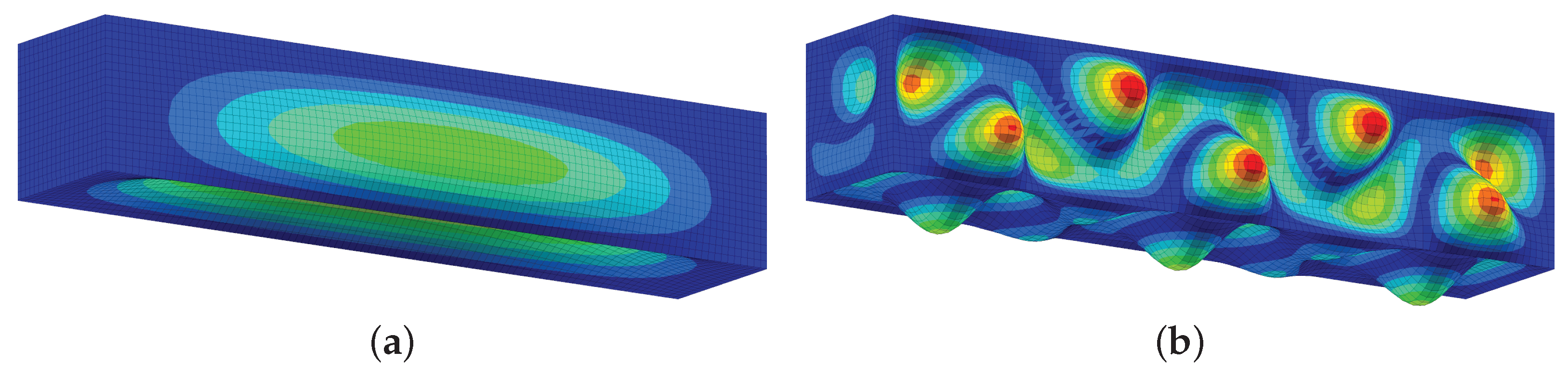
5.1. Analysis of Noise in the Free-Stream Flow
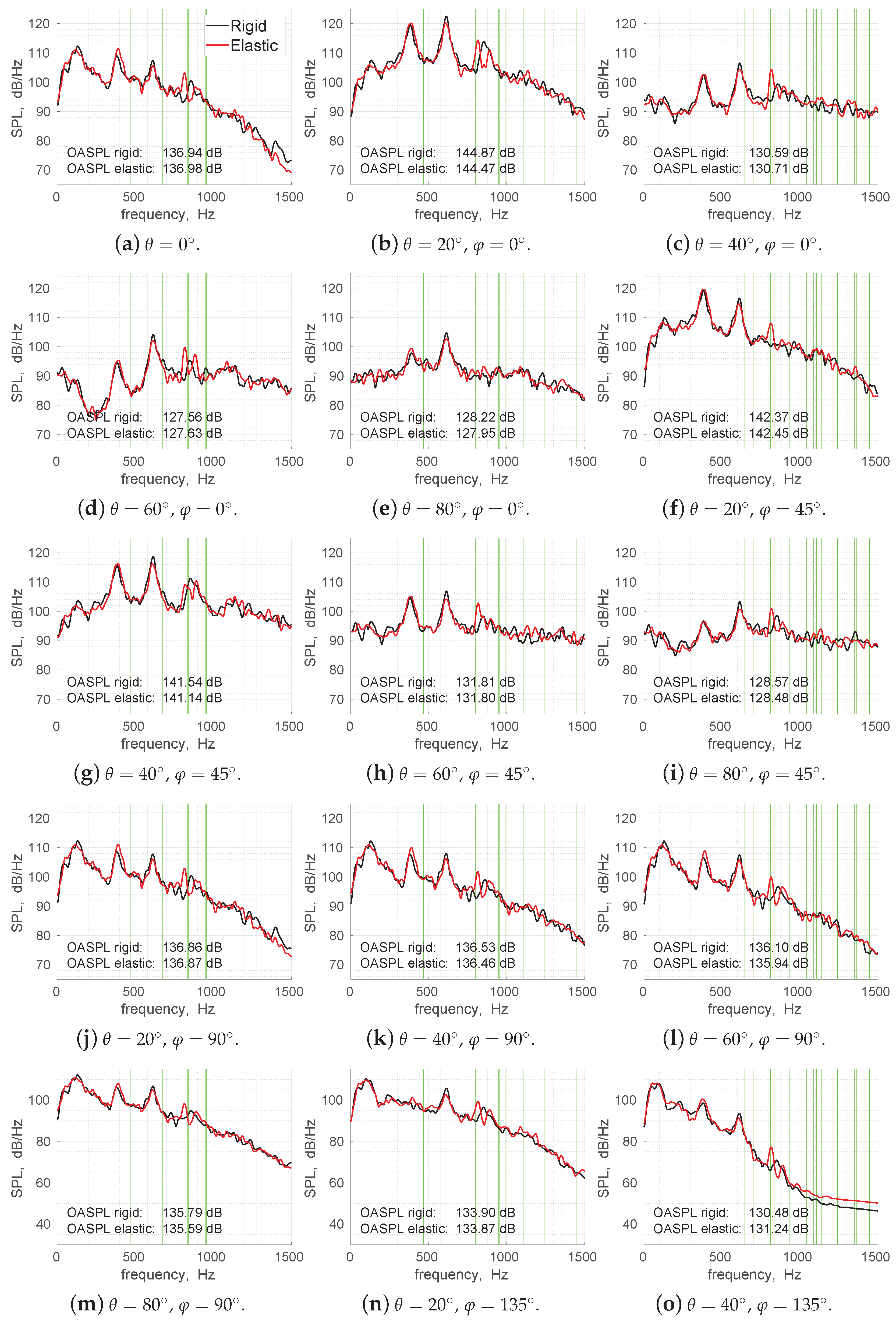
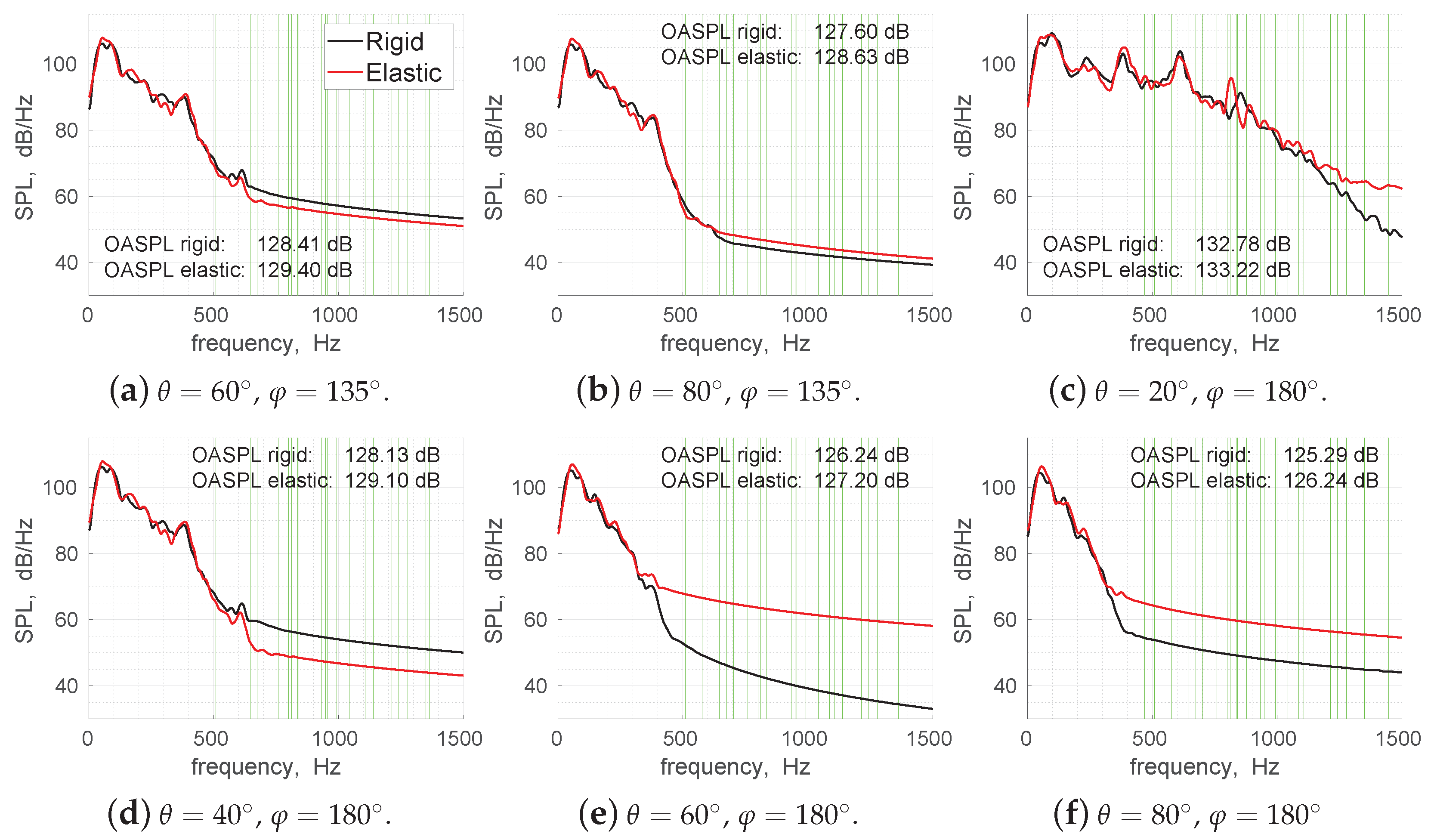
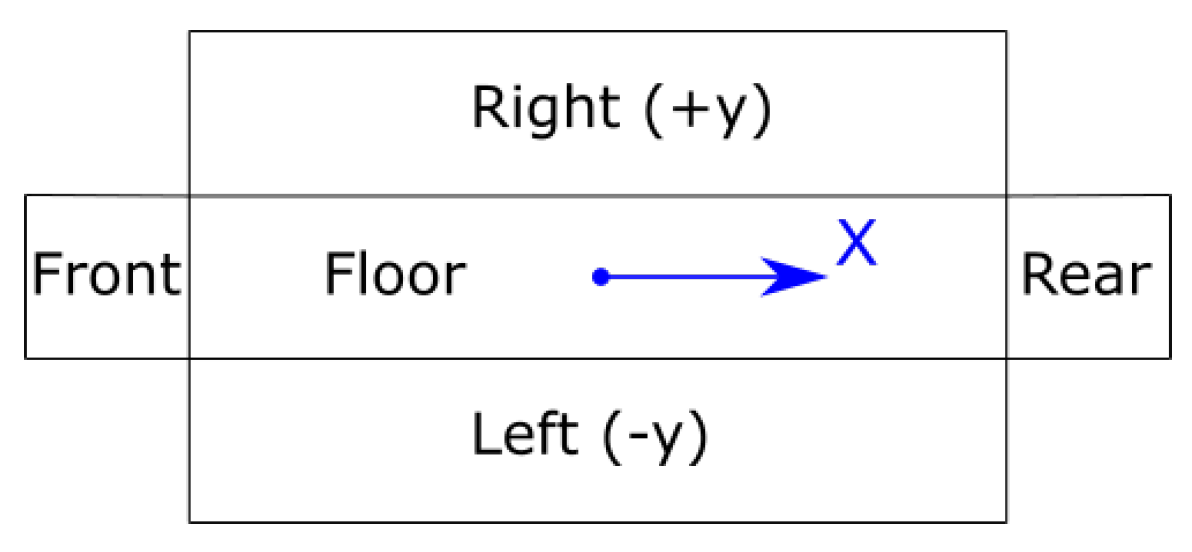
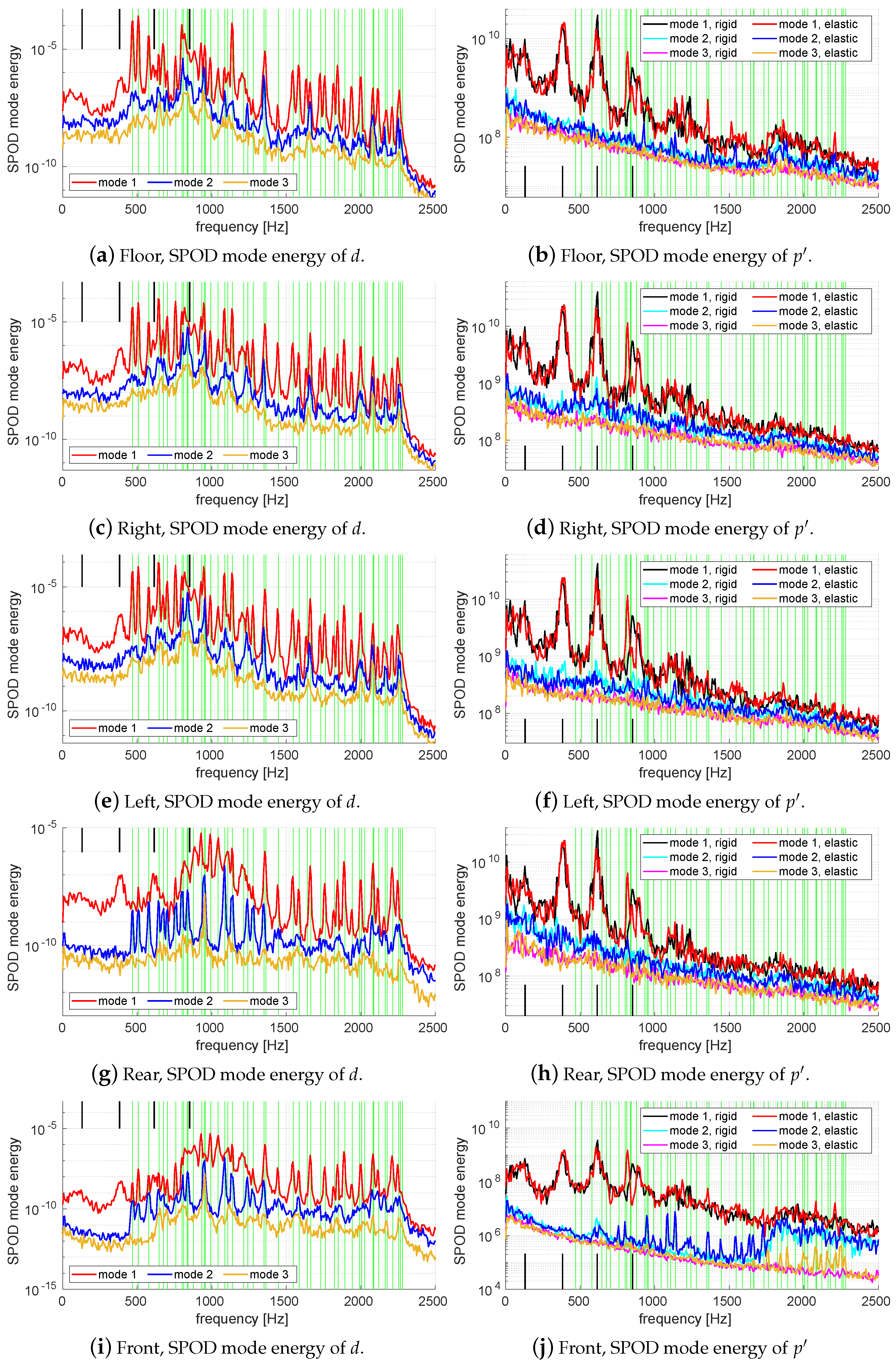
5.2. Spectral Proper Orthogonal Decomposition of Wall Pressures and Displacements
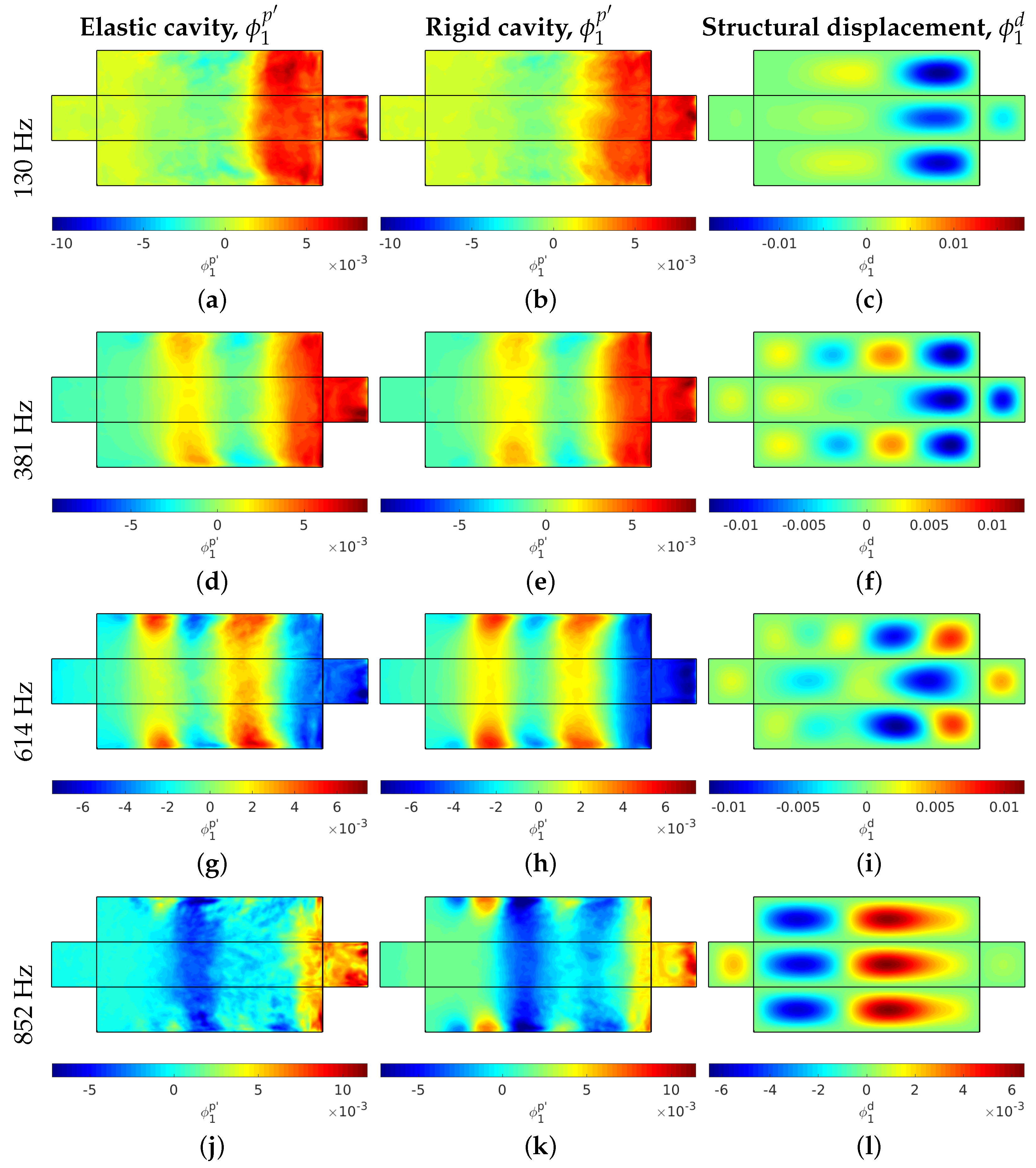

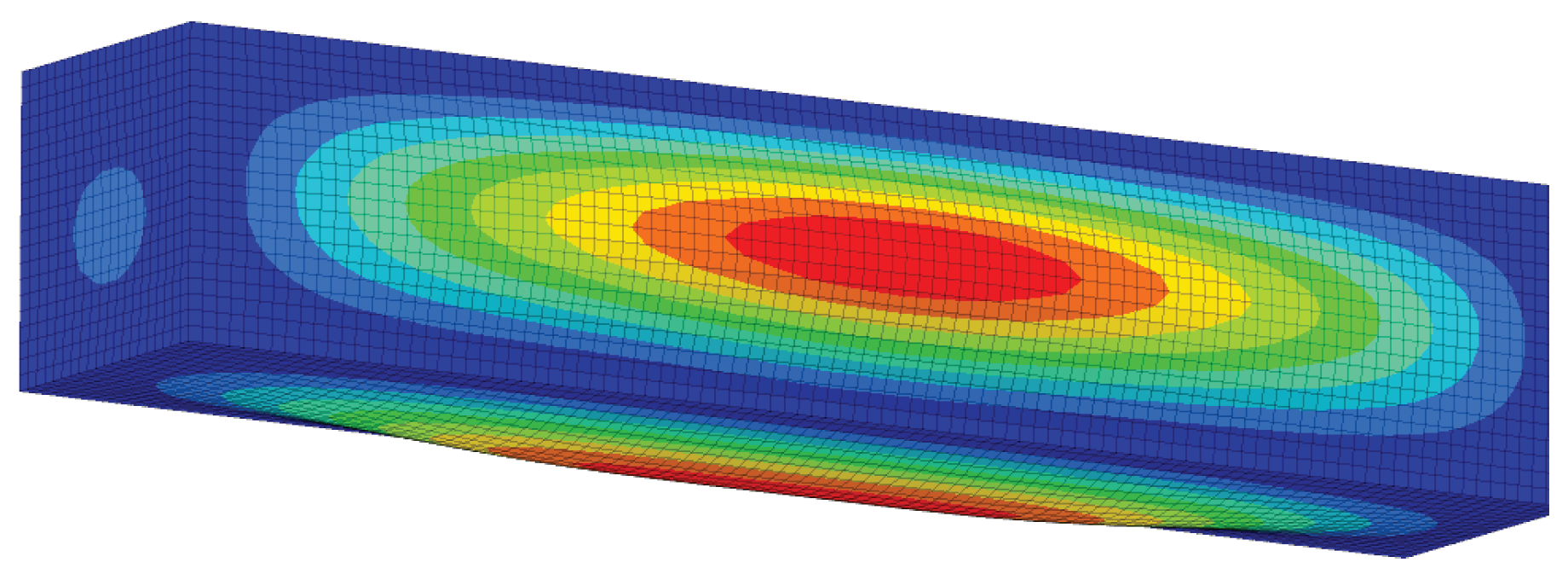
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| DDES | delayed detached-eddy simulation |
| FE | finite element |
| FSI | fluid–structure interaction |
| IDDES | improved delayed detached-eddy simulation |
| LES | large-eddy simulation |
| OASPL | overall sound pressure level |
| RANS | Reynolds-averaged Navier–Stokes |
| SA | Spalart–Allmaras |
| SPL | sound pressure level |
| SPOD | spectral proper orthogonal decomposition |
| PSD | power spectral density |
References
- Rossiter, J.E. Wind-Tunnel Experiments on the Flow over Rectangular Cavities at Subsonic and Transonic Speeds; Reports and Memoranda No. 3438, Ministry of Aviation; Her Majesty’s Stationery Office: London, UK, 1966.
- Peng, S.H. Simulation of Turbulent Flow Past a Rectangular Open Cavity Using DES and Unsteady RANS. In Proceedings of the 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Lawson, S.J.; Barakos, G.N. Review of numerical simulations for high-speed, turbulent cavity flows. Prog. Aerosp. Sci. 2011, 47, 186–216. [Google Scholar] [CrossRef]
- Larchevêque, L.; Sagaut, P.; Lê, T.H.; Comte, P. Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number. J. Fluid Mech. 2004, 516, 265–301. [Google Scholar] [CrossRef]
- Luo, K.; Xiao, Z. Improved Delayed Detached-Eddy Simulation of Transonic and Supersonic Cavity Flows. In Progress in Hybrid RANS-LES Modelling; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Cham, Switzerland, 2015; Volume 130, pp. 163–174. [Google Scholar]
- Peng, S.H.; Leicher, S. DES and Hybrid RANS-LES Modelling of Unsteady Pressure Oscillations and Flow Features in a Rectangular Cavity. In Advances in Hybrid RANS-LES Modelling; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Cham, Switzerland, 2008; Volume 97, pp. 132–141. [Google Scholar]
- Allen, R.; Mendonça, F. RANS and DES turbulence model predictions of noise on the M219 cavity at M = 0.85. Int. J. Aeroacoust. 2005, 4, 135–151. [Google Scholar] [CrossRef]
- Łojec, P.; Czajka, I.; Gołaś, A.; Suder-Dębska, K. Influence of the Elastic Cavity Walls on Cavity Flow Noise. Vib. Phys. Syst. 2021, 32, 2021109. [Google Scholar]
- Henshaw, M.J.d.C. Verification and Validation Data for Computational Unsteady Aerodynamics; M219 Cavity Case Technical Report; British Aerospace (Operations) Ltd., Military Aircraft and Aerostructures: Brough, UK, 1991. [Google Scholar]
- Gritskevich, M.S.; Garbaruk, A.V.; Menter, F.R. A Comprehensive Study of Improved Delayed Detached Eddy Simulation with Wall Functions. Flow Turbul. Combust 2017, 98, 461–479. [Google Scholar] [CrossRef]
- Mockett, C.; Fuchs, M.; Thiele, F. Progress in DES for wall-modelled LES of complex internal flows. Comput. Fluids 2012, 65, 44–55. [Google Scholar] [CrossRef]
- Eliasson, P. Edge: A Navier-Stokes Solver for Unstructured Grids. In Finite Volumes for Complex Applications III; CP849; Kogan Page: London, UK, 2002; pp. 527–534. [Google Scholar]
- Eliasson, P.; Weinerfelt, P. Recent applications of the flow solver Edge. In Proceedings of the 7th Asian CFD Conference, Bangalore, India, 26–30 November 2007. [Google Scholar]
- Spalart, P.; Deck, S.; Shur, M.; Squires, K.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theory Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. La Rech. AéRospatiale 1994, 1, 5–21. [Google Scholar]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Kegerise, M.A.; Spina, E.F.; Garg, S.; Cattafesta, L. Mode-Switching and Nonlinear Effects In Compressible Flow Over a Cavity. Phys. Fluids 2004, 16, 678–687. [Google Scholar] [CrossRef]
- Loupy, G.J.M.; Barakos, G.N. Understanding Transonic Weapon Bay Flows. In Proceedings of the 6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7), Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Smith, J. Aeroelastic Functionality in Edge Initial Implementation and Validation; Scientific Report FOI-R–1485–SE; FOI, Swedish Defence Research Agency: Stockholm, Sweden, 2005.
- Pahlavanloo, P. Dynamic Aeroelastic Simulation of the AGARD 445.6 Wing Using Edge; Technical Report FOI-R–2259–SE; FOI, Swedish Defence Research Agency: Stockholm, Sweden, 2007.
- Palombo, C.L. Development and Validation of an Improved Wall-Function Boundary Condition for Computational Aerodynamics. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2021. [Google Scholar]
- Mockett, C.; Haase, W.; Schwamborn, D. (Eds.) Go4Hybrid: Grey Area Mitigation for Hybrid RANS-LES Methods—Results of the 7th Framework Research Project Go4Hybrid, Funded by the European Union, 2013–2015, 1st ed.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Arvidson, S. Methodologies for RANS-LES Interfaces in Turbulence-Resolving Simulations. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2017. [Google Scholar]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Pwelch, Welch’s Power Spectral Density Estimate. Available online: https://se.mathworks.com/help/signal/ref/pwelch.html (accessed on 20 October 2022).
- MSC Software Corporation, Nastran. MSC Nastran 2012.2 Quick Reference Guide; 2 MacArthur Place: Santa Ana, CA, USA, 2012. [Google Scholar]
- Scope. Available online: www.larosterna.com (accessed on 20 October 2022).
- Nekkanti, A.; Schmidt, O.T. Frequency-time analysis, low-rank reconstruction and denoising of turbulent flows using SPOD. J. Fluid Mech. 2021, 926, A26. [Google Scholar] [CrossRef]
- Towne, A.; Schmidt, O.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nilsson, S.; Yao, H.-D.; Karlsson, A.; Arvidson, S. Effects of Aeroelastic Walls on the Aeroacoustics in Transonic Cavity Flow. Aerospace 2022, 9, 716. https://doi.org/10.3390/aerospace9110716
Nilsson S, Yao H-D, Karlsson A, Arvidson S. Effects of Aeroelastic Walls on the Aeroacoustics in Transonic Cavity Flow. Aerospace. 2022; 9(11):716. https://doi.org/10.3390/aerospace9110716
Chicago/Turabian StyleNilsson, Stefan, Hua-Dong Yao, Anders Karlsson, and Sebastian Arvidson. 2022. "Effects of Aeroelastic Walls on the Aeroacoustics in Transonic Cavity Flow" Aerospace 9, no. 11: 716. https://doi.org/10.3390/aerospace9110716
APA StyleNilsson, S., Yao, H.-D., Karlsson, A., & Arvidson, S. (2022). Effects of Aeroelastic Walls on the Aeroacoustics in Transonic Cavity Flow. Aerospace, 9(11), 716. https://doi.org/10.3390/aerospace9110716







