Influence of Aerodynamic Interaction on Performance of Contrarotating Propeller/Wing System
Abstract
:1. Introduction
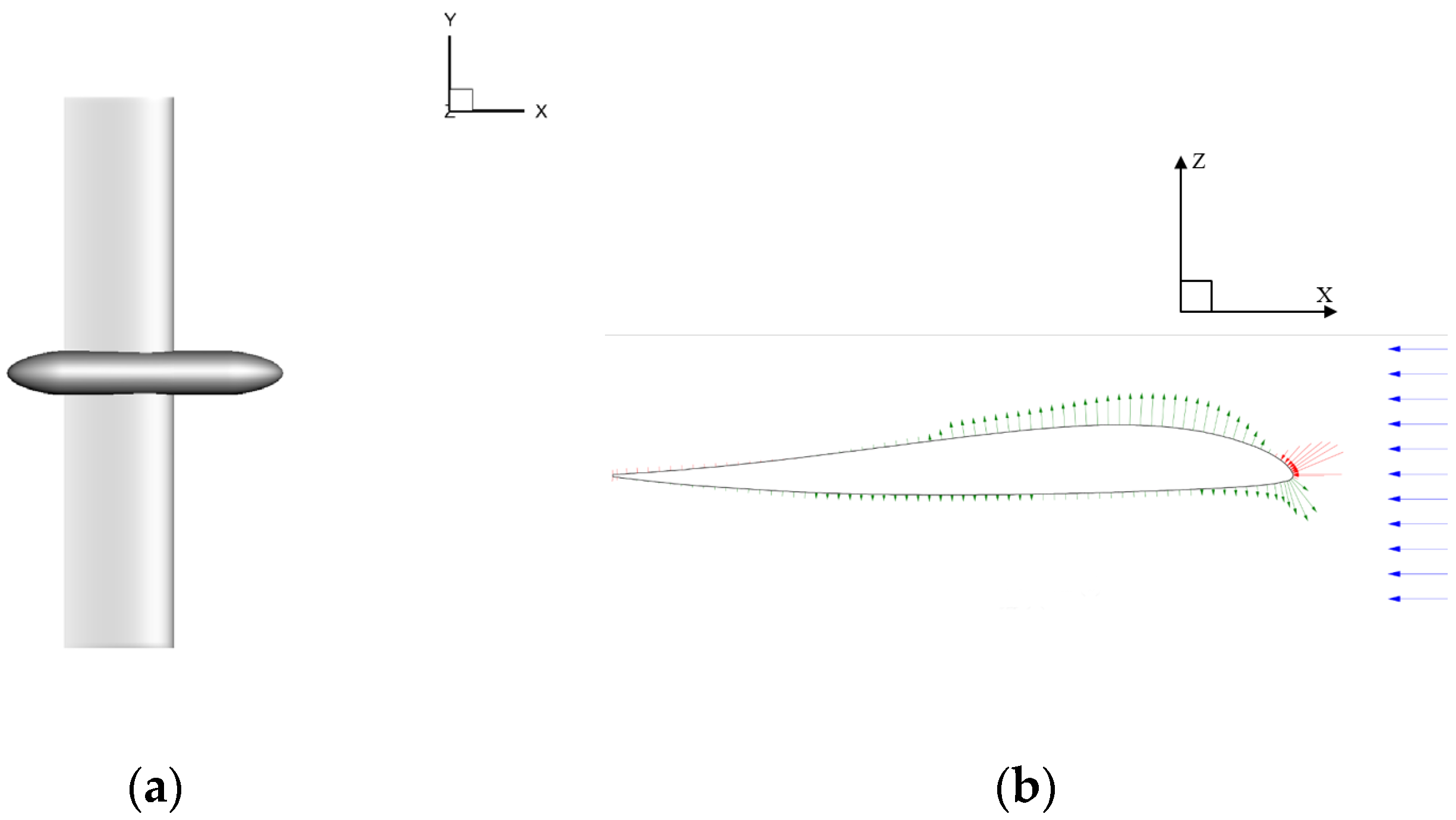
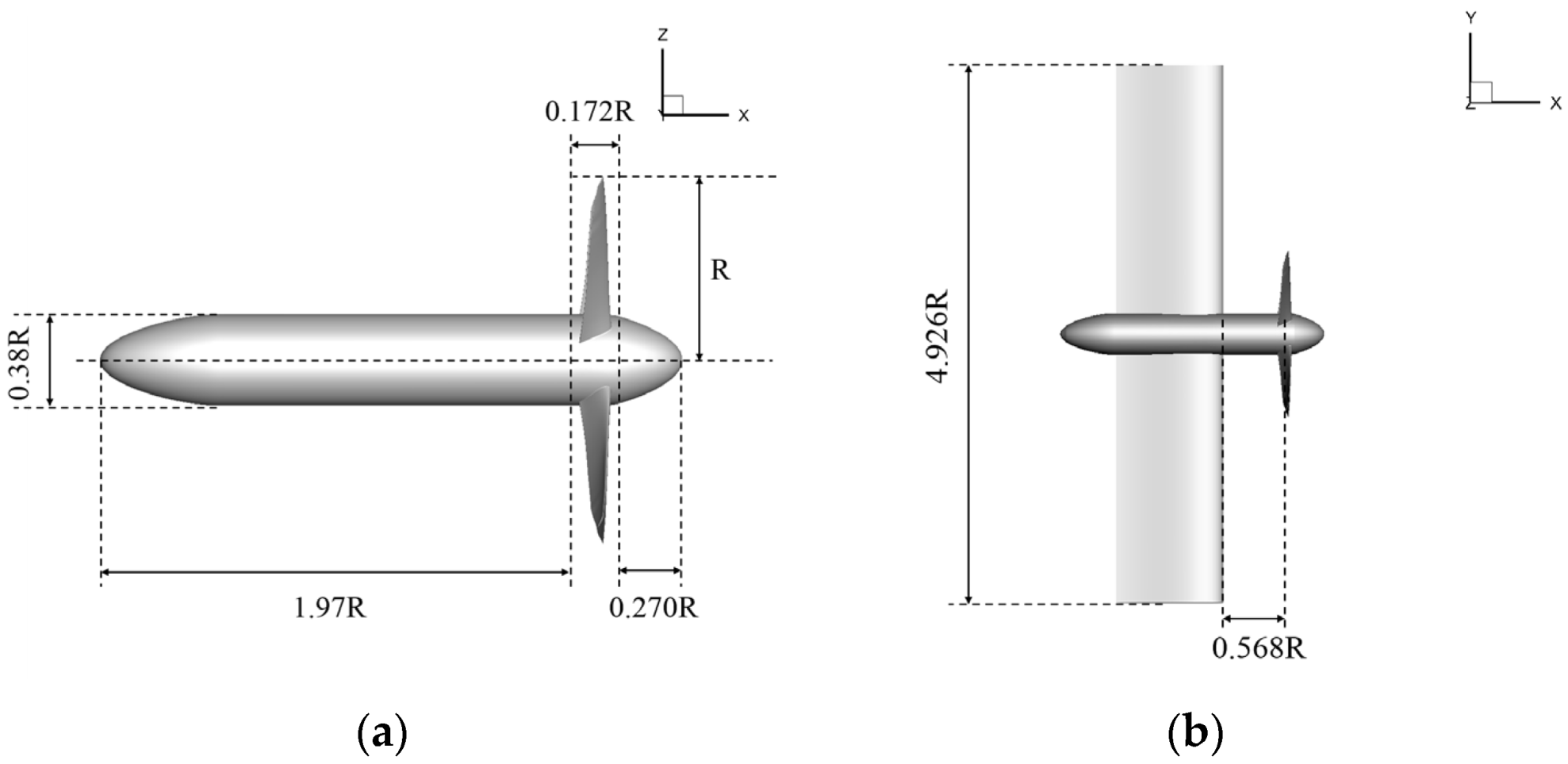
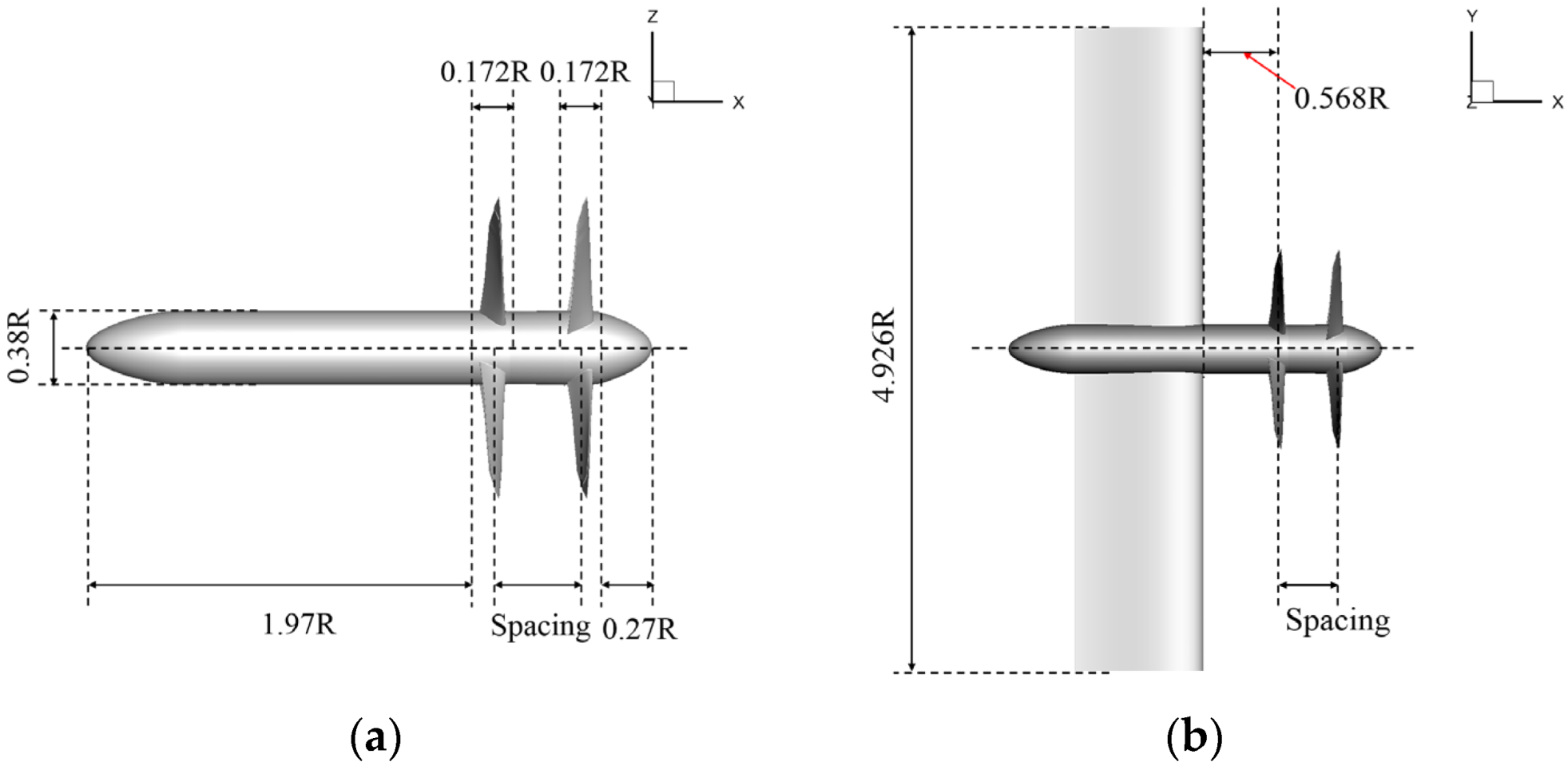
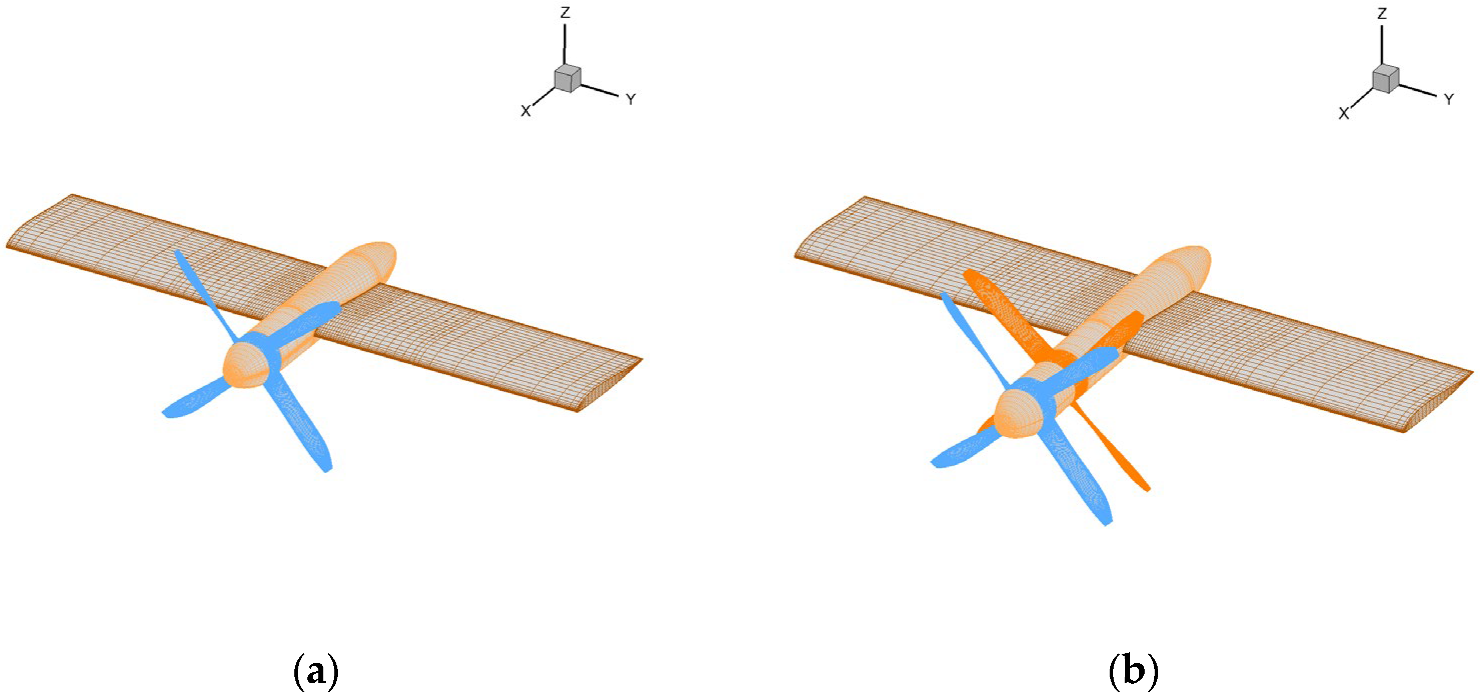
2. Model Description
3. Computational Strategy
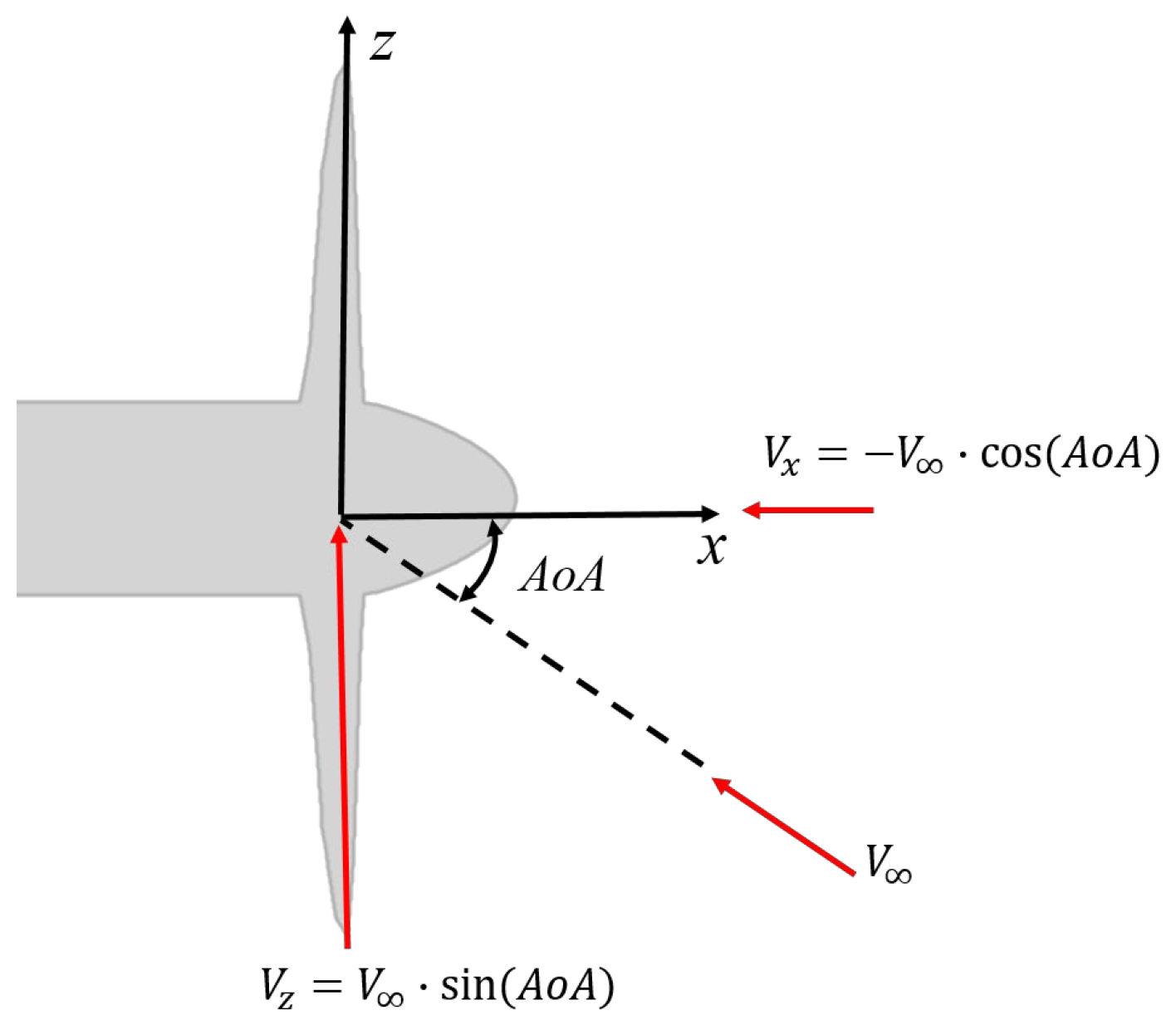
3.1. CFD Settings
- The velocity inlet for the far field and inlet domain was established via the freestream AoA and freestream velocity of V∞ = 30 m/s. The corresponding Reynolds number based on the freestream velocity and a section of the blade of the propeller at r/R = 70% was 64,000.
- The condition of the pressure outlet was set at the domain of the outlet, where the magnitude of gauge pressure and pressure profile multiplier were set to default.
- Solid surfaces of the simulated geometry, including the propellers, nacelle, and wing, were modeled as a stationary wall with the no-slip shear boundary condition.
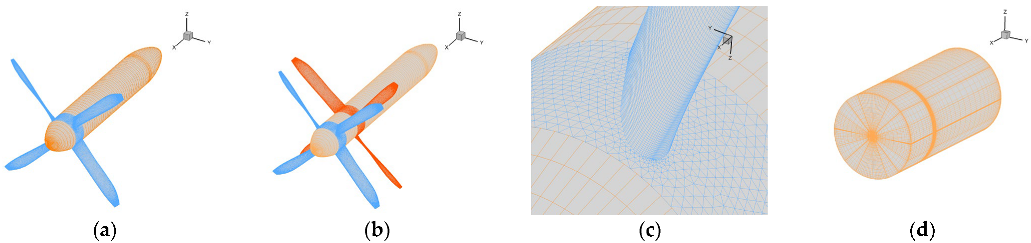
3.2. Grid Generation
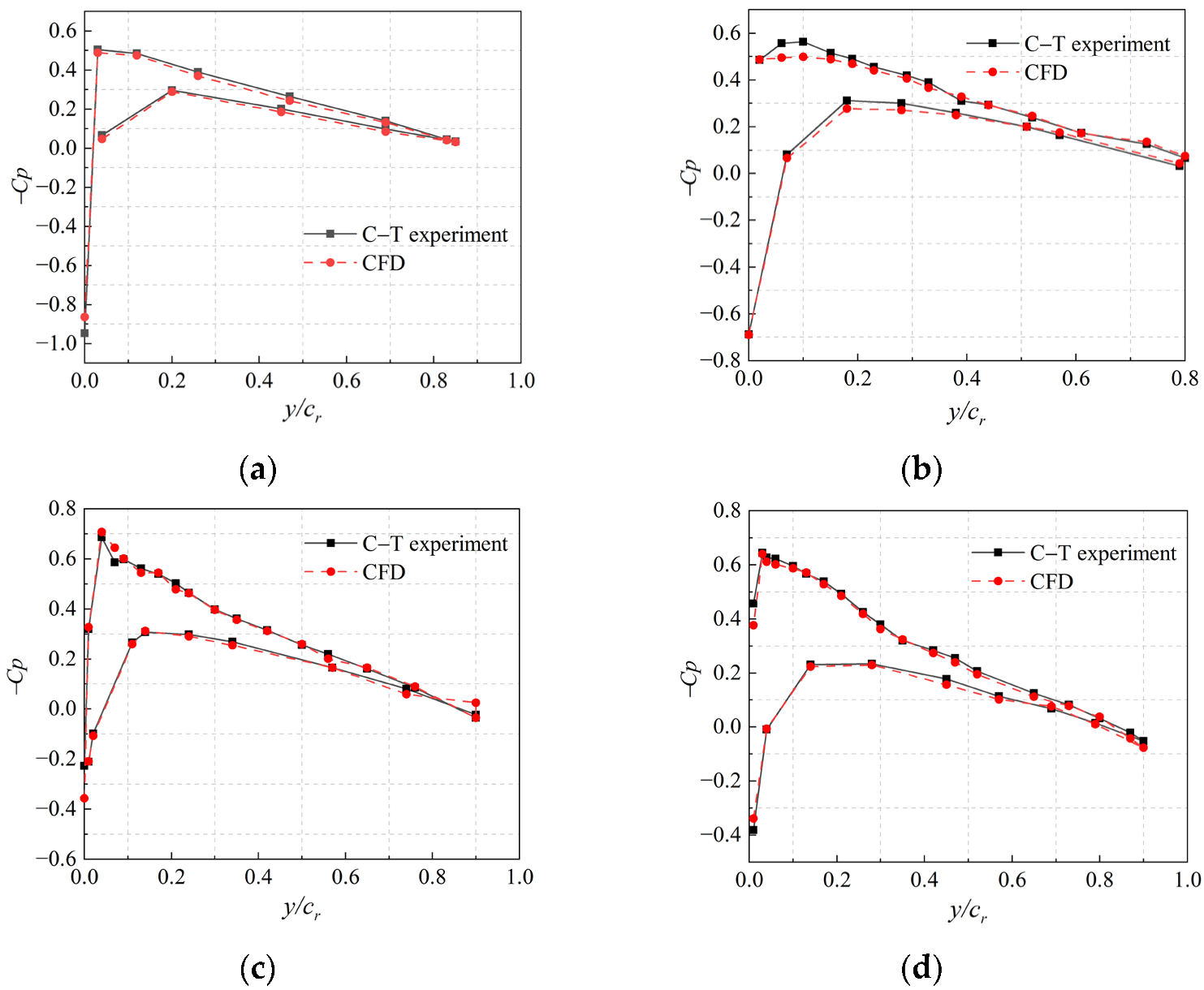
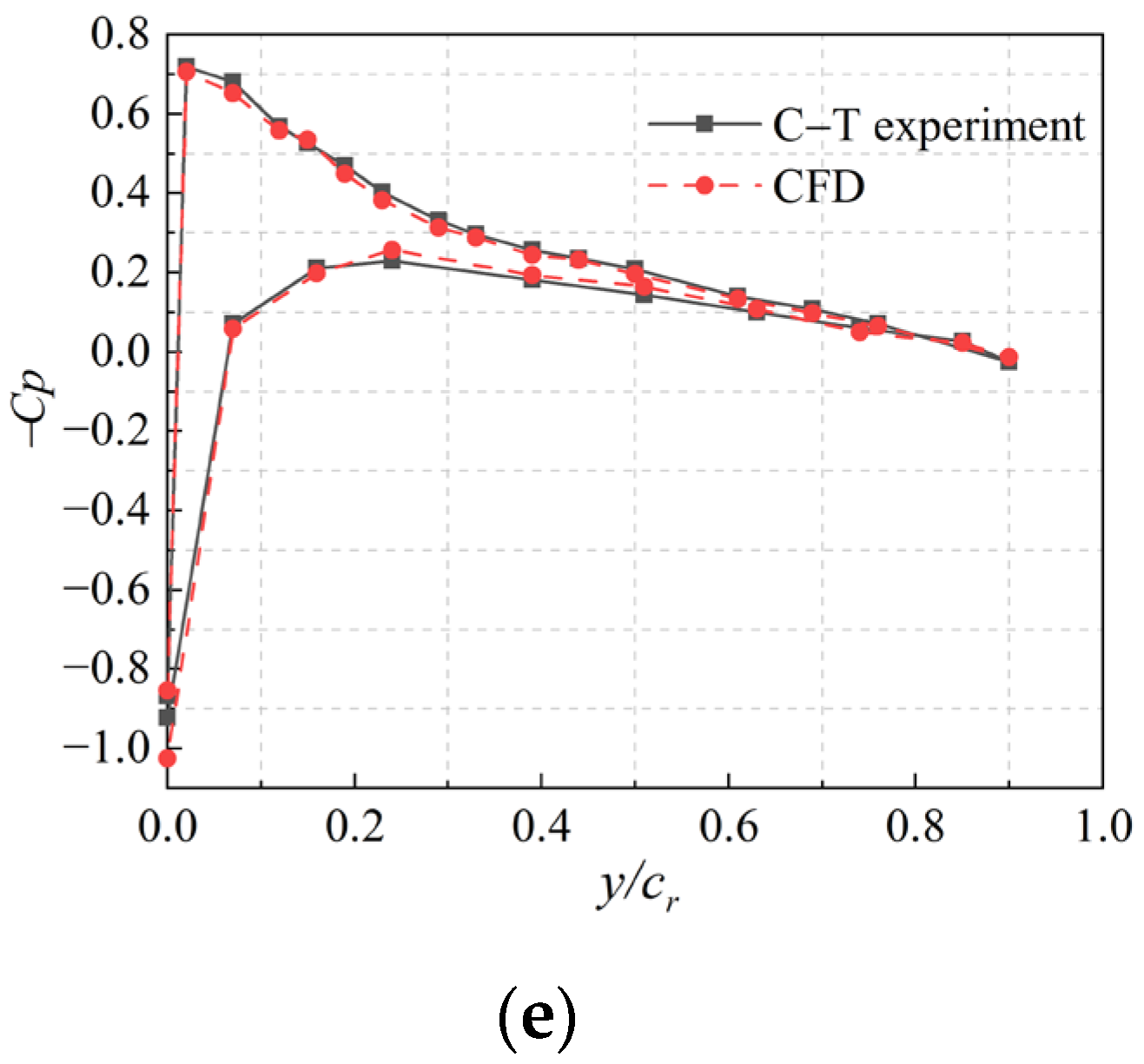
3.3. Test Validation
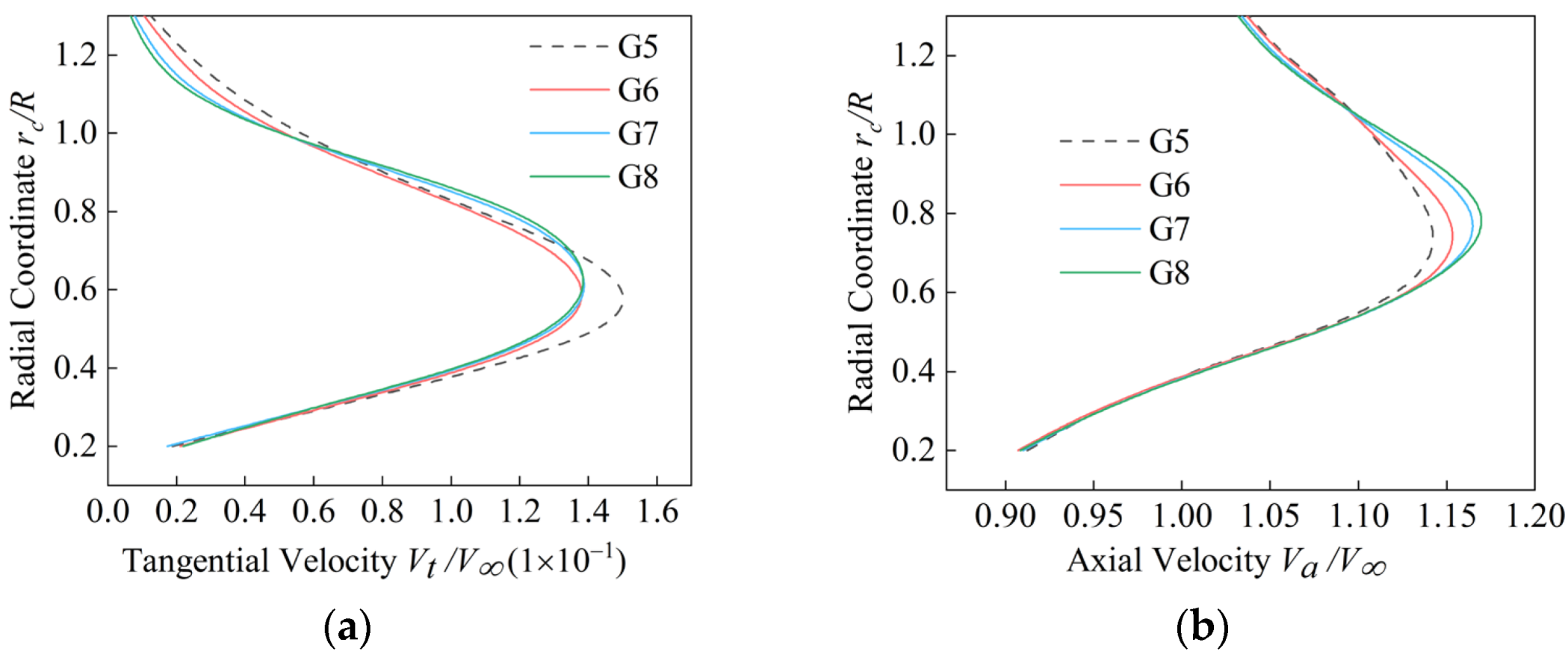
3.4. Grid Convergence Study
4. Results and Discussion
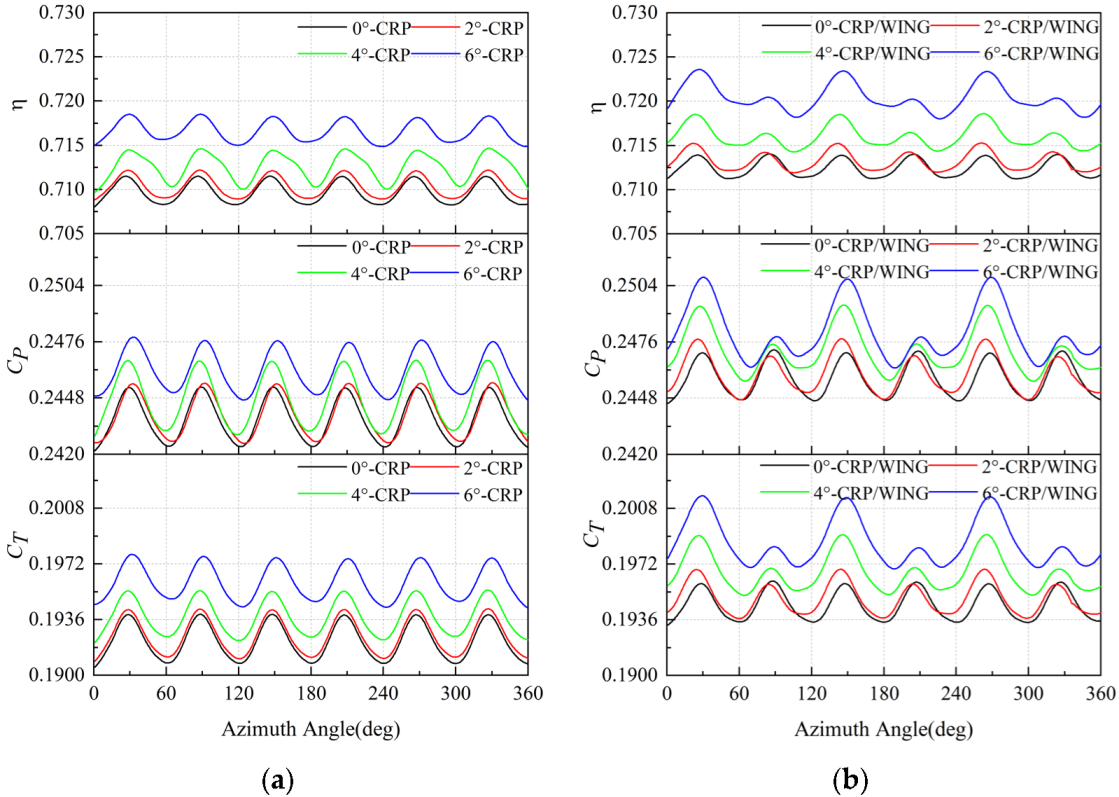
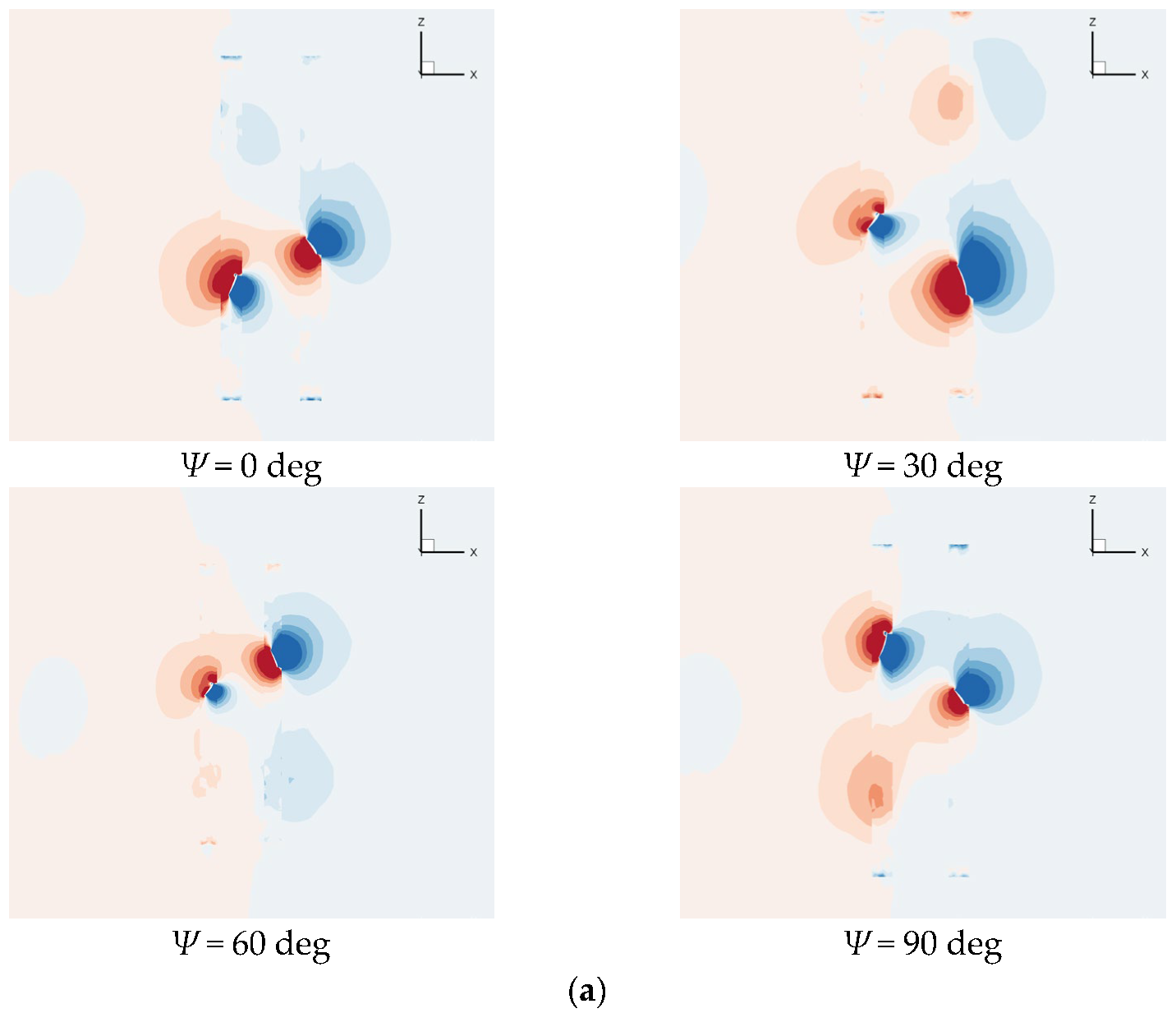
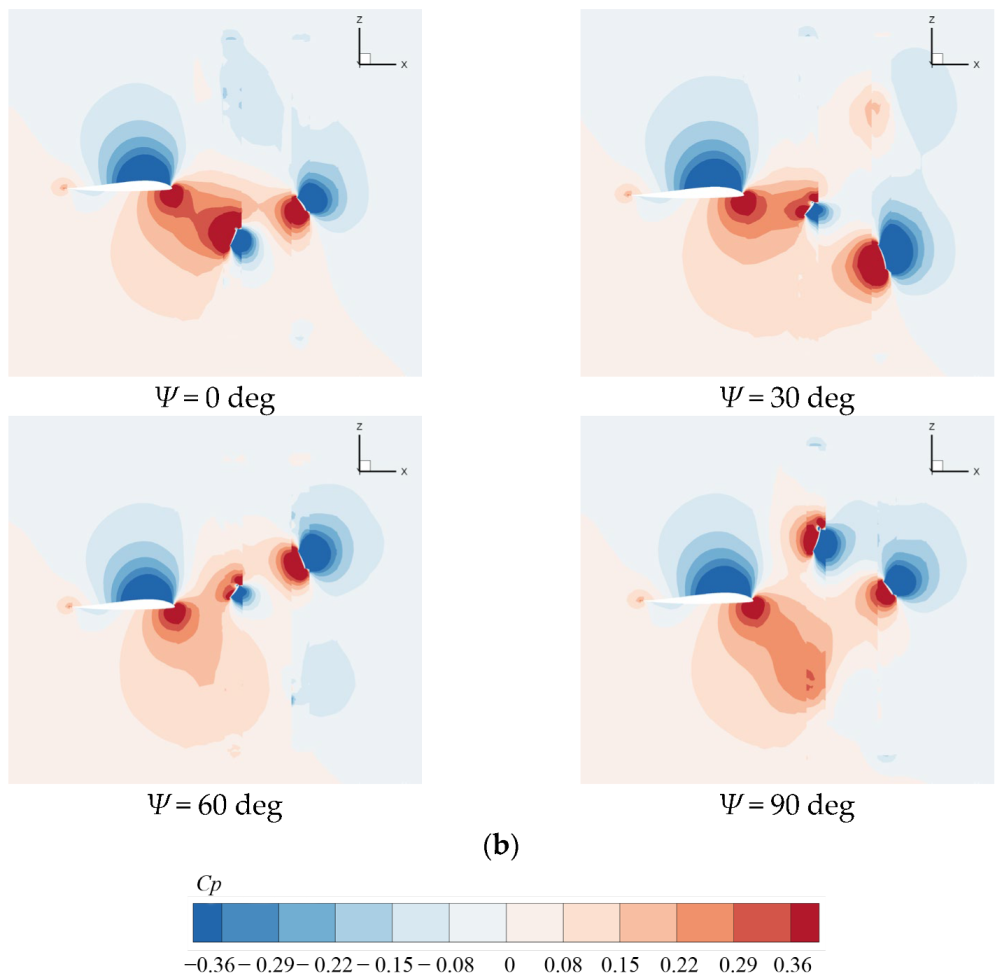
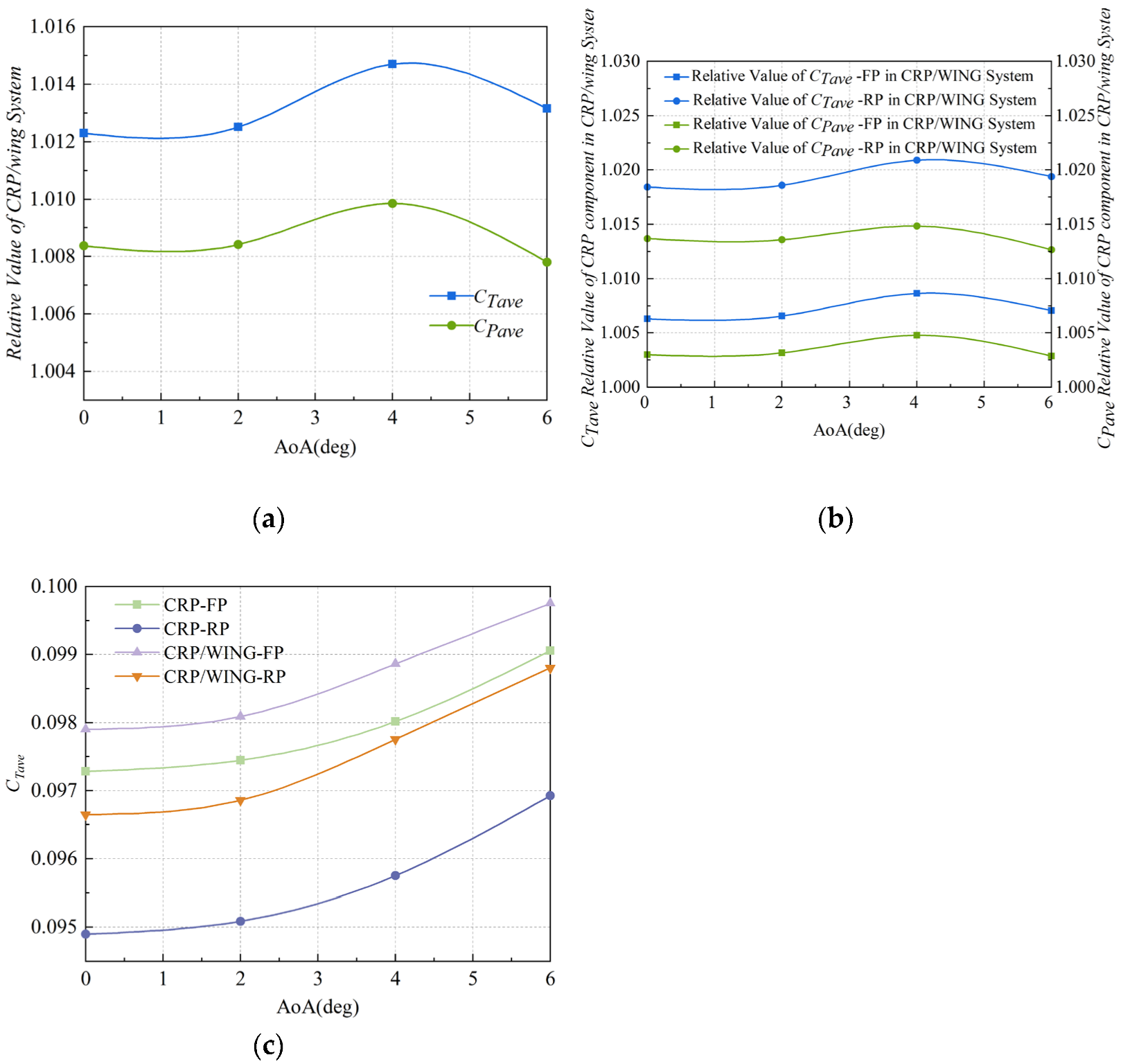
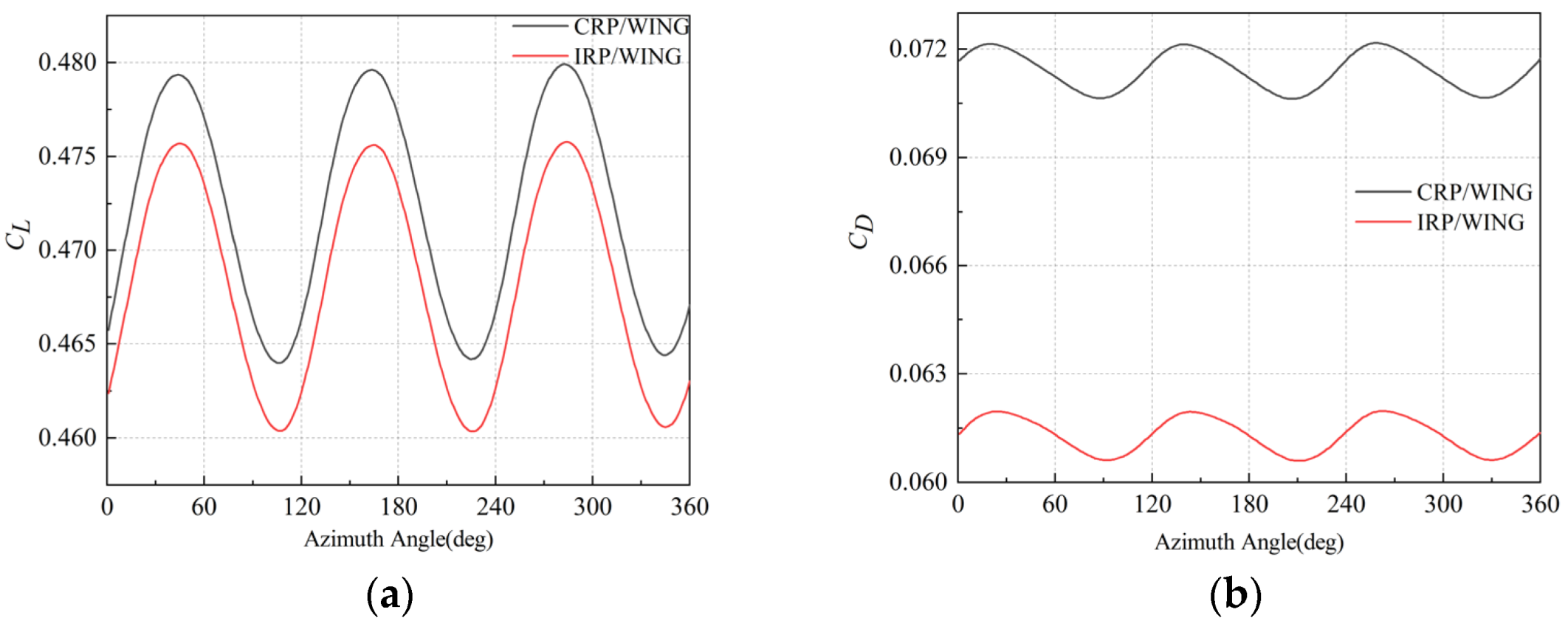
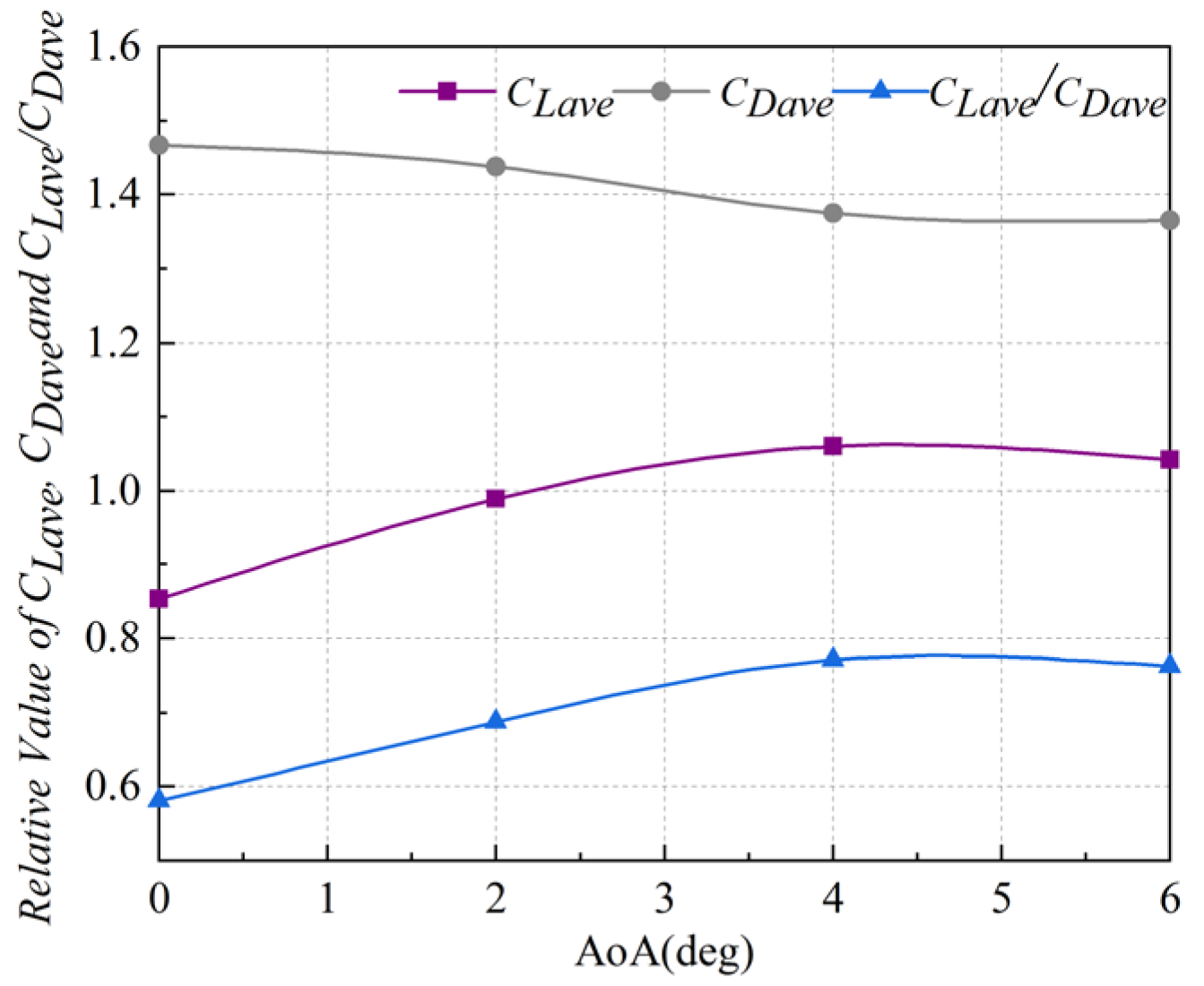
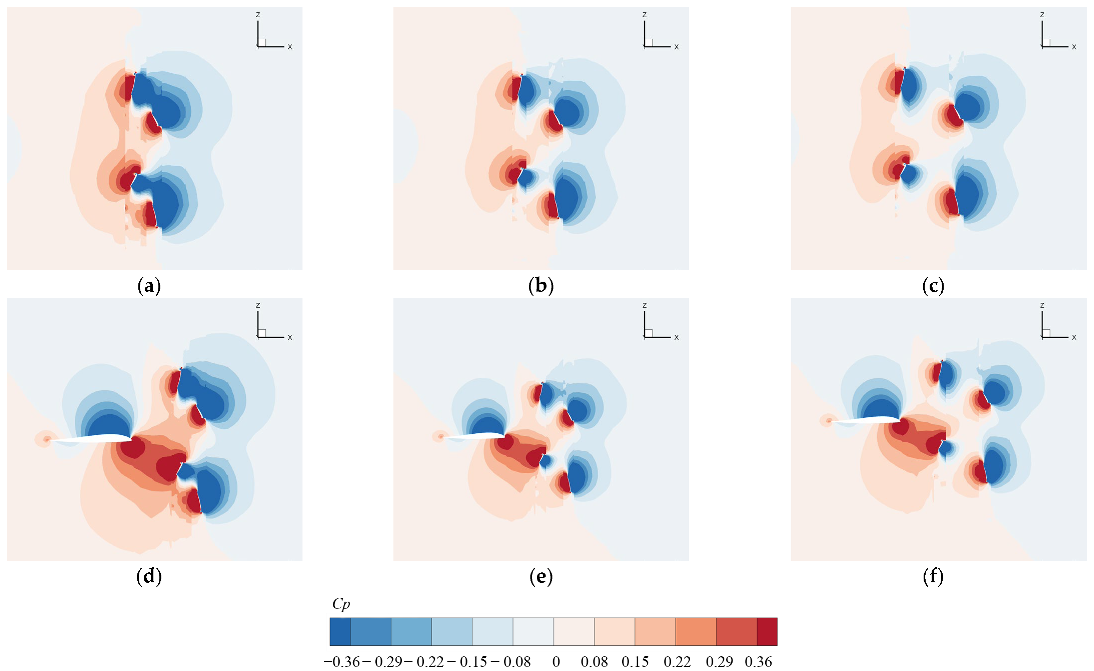
4.1. Effect of AoA
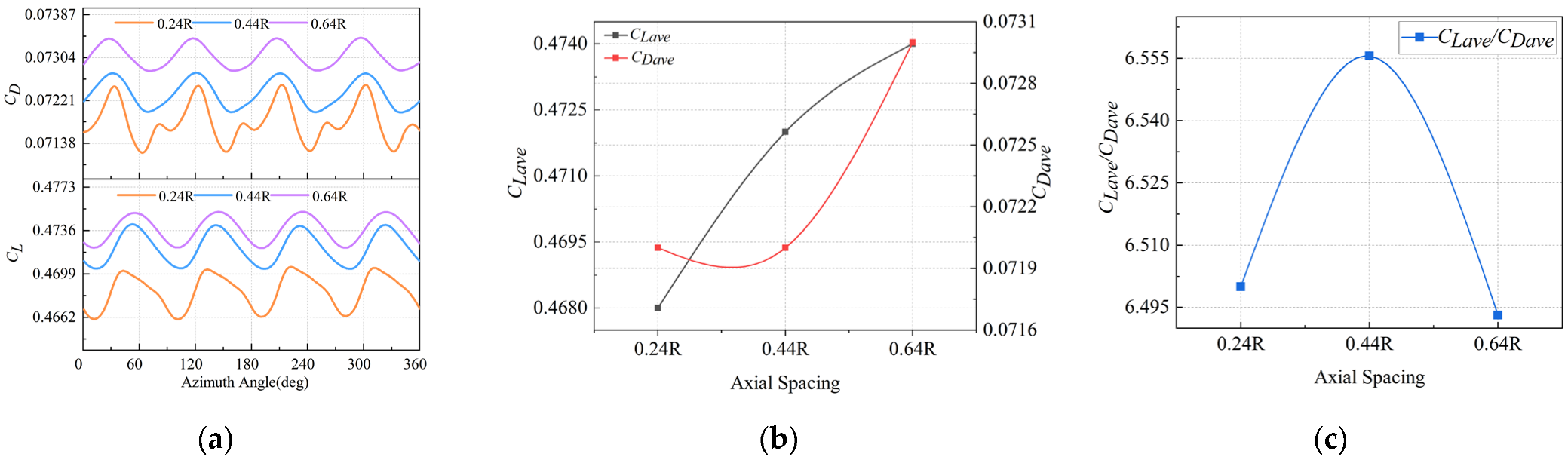
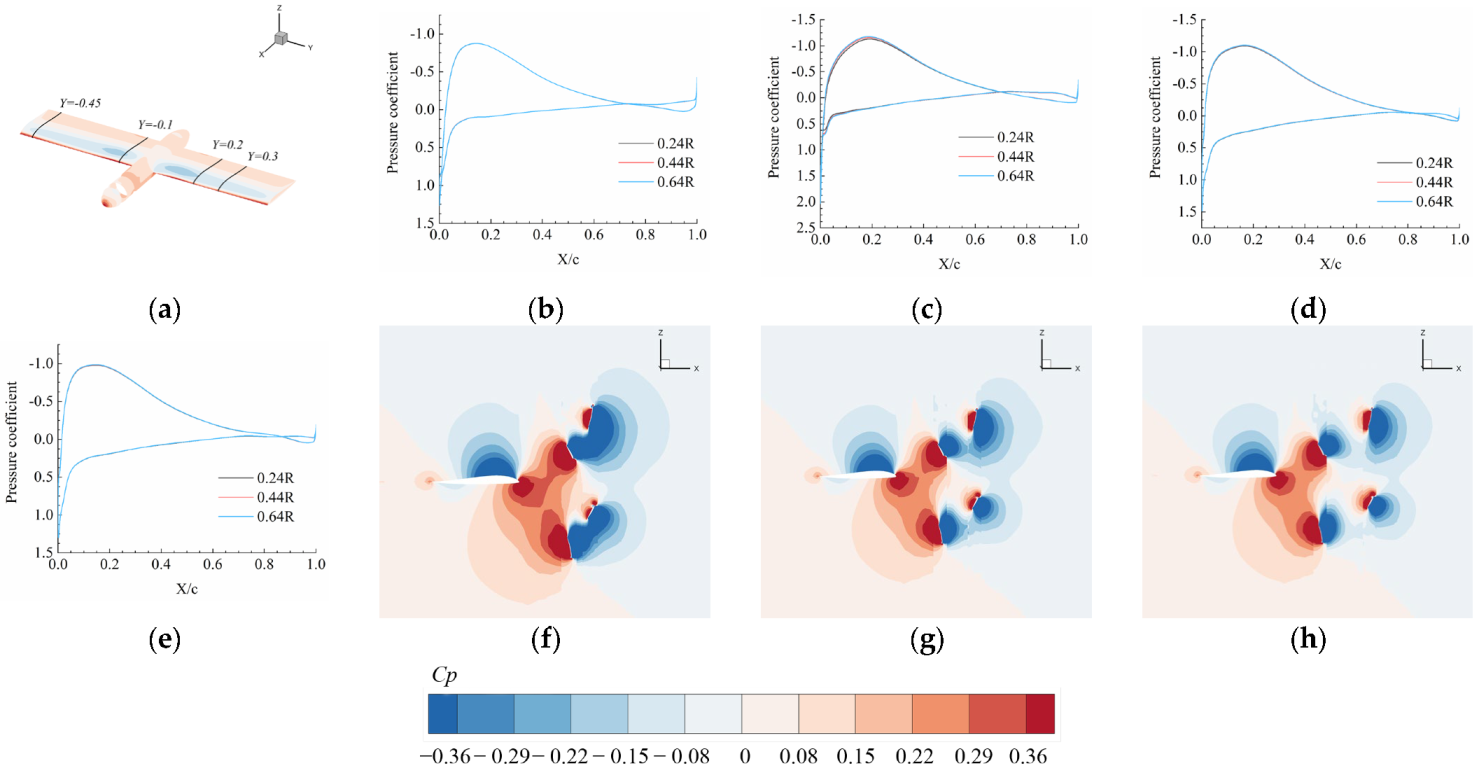
4.2. Effect of Axial Spacing between FP and RP
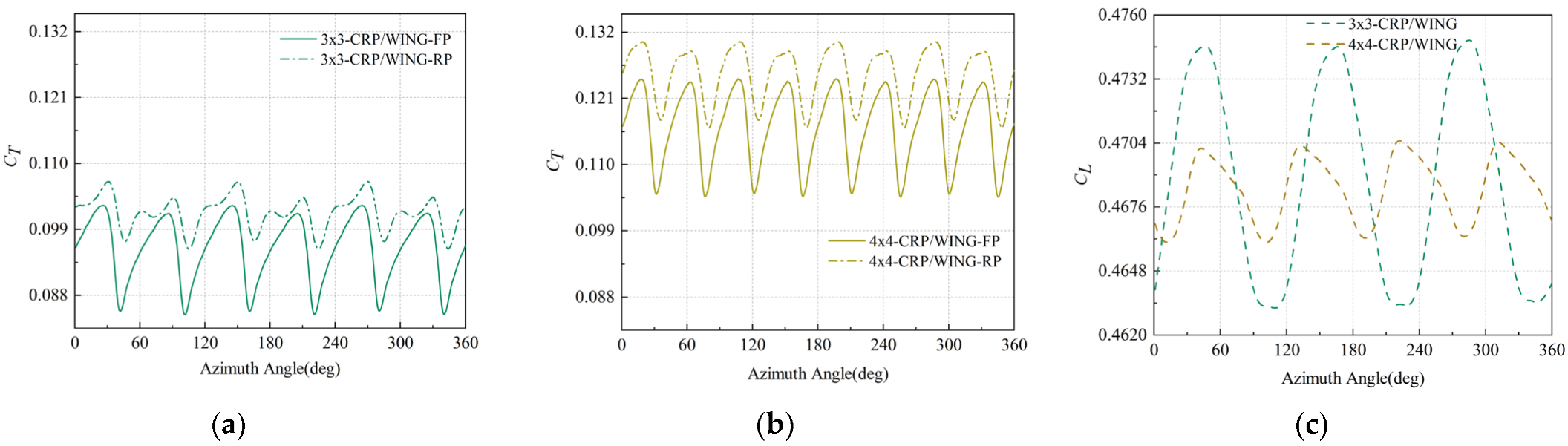
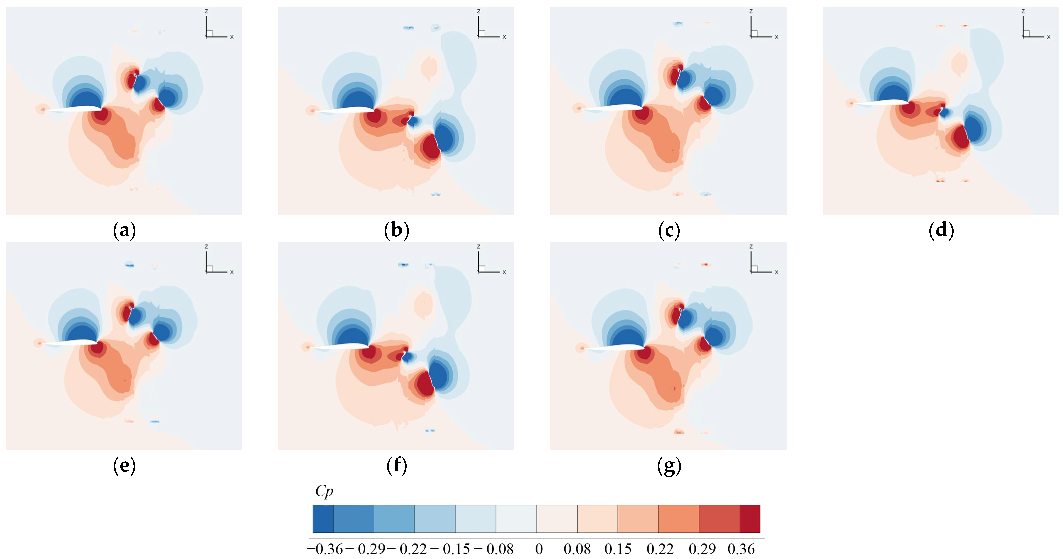
4.3. Effect of NoB
4.4. Effect of Rotational Speed
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Definition |
| CRP | Contrarotating propeller |
| IRP | Isolated rotating propeller |
| FP | Front propeller |
| RP | Rear propeller |
| CFD | Computational fluid dynamics |
| uRANS | Unsteady Reynolds-averaged Navier–Stokes |
| MRFs | Multiple reference frames |
| SMM | Sliding mesh method |
| OMM | Overset mesh method |
| AoA | Freestream angle of attack, deg |
| NoB | Number of blades |
| RPM | Revolutions per minute |
| n | Rotational speed of propeller, rev/s |
| T | Propeller thrust, N |
| P | Propeller power, W |
| Q | Propeller torque, N · m |
| L | Wing lift, N |
| D | Wing drag, N |
| M | Pitching moment |
| CT | Thrust coefficient |
| CTave | Time-averaged thrust coefficient |
| CP | Power coefficient |
| CPave | Time-averaged power coefficient |
| CQ | Torque coefficient |
| CL | Lift coefficient |
| CLave | Time-averaged lift coefficient |
| CD | Drag coefficient |
| CDave | Time-averaged drag coefficient |
| CM | Pitching moment coefficient |
| CMave | Time-averaged pitching moment coefficient |
| CL/CD | Wing lift-to-drag ratio |
| Vt | Tangential velocity, m/s |
| Va | Axial velocity, m/s |
| J | Propeller advance ratio |
| V∞ | Freestream velocity, 30 m/s |
| R | Propeller radius, m |
| rc | Radial coordinate, m |
| r | C–T rotor radius, m |
| Cp | Pressure coefficient |
| c | Chord length, m |
| l | Span length, m |
| deg | Degree |
| Greek symbols | |
| η | Propulsion efficiency |
| ρ | Freestream air density, 1.225 kg/m3 |
| Subscripts | |
| ave | Time-averaged value |
| ∞ | Freestream value |
| a | Axial |
| t | Tangential |
References
- Benzakein, M.J. What does the future bring? A look at technologies for commercial aircraft in the years 2035–2050. Propuls. Power Res. 2014, 3, 165–174. [Google Scholar] [CrossRef] [Green Version]
- Strack, W.C.; Knip, G.; Weisbrih, A.L.; Godston, J.; Bradley, E. Technology and Benefits of Aircraft Counter Rotation Propellers; Techniacl Report, NASA Technical Memornadum 81232; NASA: Washington, DC, USA, 1981. [Google Scholar]
- Ferraro, G.; Kipouros, T.; Savill, A.M.; Rampurawala, A.; Agostinelli, C. Propeller-wing interaction prediction for early design. In Proceedings of the 52nd Aerospace Science Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA Paper 2014-0564. [Google Scholar]
- Aref, P.; Ghoreyshi, M.; Jirasek, A.; Satchell, M.J.; Bergeron, K. Computational study of propeller-wing aerodynamic interaction. Aerospace 2018, 5, 79. [Google Scholar] [CrossRef] [Green Version]
- Alba, C.; Elham, A.; German, B.J.; Veldhuis, L.L.M. A surrogate-based multi-disciplinary design optimization framework modeling wing–propeller interaction. Aerosp. Sci. Technol. 2018, 78, 721–733. [Google Scholar] [CrossRef]
- Bohari, B.; Borlon, Q.; Santos, P.B.M.; Sgueglia, A.; Benard, E.; Bronz, M.; Defoort, S. Conceptual design of distributed propellers aircraft: Non-linear aerodynamic model verification of propeller-wing interaction in high-lift configuration. In Proceedings of the 2018 AIAA Aerospace Science Meeting, Kissimmee, FL, USA, 8–12 January 2018. AIAA Paper 2018-1742. [Google Scholar]
- Veldhuis, L.L.M. Review of propeller-wing aerodynamic interference. In Proceedings of the 24th International Congress of the Aeronautical Science, Yokohama, Japan, 29 August–3 September 2014. [Google Scholar]
- Bouquet, T. Modelling the Propeller Slipstream Effect on the Longitudinal Stability and Control; Delft University Technology: Delft, The Netherlands, 2016. [Google Scholar]
- Marretta, R.M.A. Different wings flowfields interaction on the wing-propeller coupling. J. Aircr. 1997, 34, 740–747. [Google Scholar] [CrossRef]
- Cole, J.A.; Krebs, T.; Barcelos, D.; Bramesfeld, G. Influence of propeller location, diameter, and rotation direction on aerodynamic efficiency. J. Aircr. 2021, 58, 63–71. [Google Scholar] [CrossRef]
- Catalano, F.M. On the effects of an installed propeller slipstream on wing aerodynamic characteristics. Acta Polytech. 2004, 44. [Google Scholar] [CrossRef]
- Müller, L.; Friedrichs, J.; Kozulovic, D. Unsteady flow simulations of an over-the-wing propeller configuration. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. AIAA Paper 2014-3886. [Google Scholar]
- Kroo, I. Propeller-wing integration for minimum induced loss. J. Aircr. 2008, 23, 561–565. [Google Scholar] [CrossRef]
- Agostinelli, C.; Liu, C.; Allen, C.B.; Rampurawala, A.; Ferraro, G. Propeller-flexible wing interaction using rapid computational methods. In Proceedings of the 31st AIAA Applied Aerodynamic Conference, San Diego, CA, USA, 24–27 June 2013. AIAA Paper 2013-2418. [Google Scholar]
- Teixeira, P.C.; Cesnik, C.E.S. Propeller effects on the response of high-altitude long-endurance aircraft. AIAA J. 2019, 57, 4328–4342. [Google Scholar] [CrossRef]
- Hoover, C.B.; Shen, J.; Kreshock, A.R. Propeller whirl flutter stability and its influence on X-57 aircraft design. J. Aircr. 2018, 55, 2168–2174. [Google Scholar] [CrossRef]
- Playle, S.C.; Korkan, K.D.; Von lavante, E. A numerical method for the design and analysis of counter-rotating propellers. J. Propuls. Power. 1986, 2, 57–63. [Google Scholar] [CrossRef]
- Korkan, K.D.; Gazzaniga, J.A. Off-design analysis of counter-rotating propeller configurations. J. Propuls. Power. 1987, 3, 91–93. [Google Scholar] [CrossRef]
- Stürmer, A.; Marquez Gutierrez, C.O.; Roosenboom, E.W.M.; Schröder, A.; Geisler, R.; Pallek, D.; Agocs, J.; Neitzke, K.P. Experimental and numerical investigation of a contra rotating open-rotor flowfield. J. Aircr. 2012, 49, 1868–1877. [Google Scholar] [CrossRef]
- Stuermer, A. Unsteady CFD simulations of contra-rotating propeller propulsion systems. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008. AIAA Paper 2008-5218. [Google Scholar]
- Akkermans, R.A.D.; Stuermer, A.; Delfs, J.W. Active flow control for interaction noise reduction of contra-rotating open rotors. AIAA J. 2016, 54, 1413–1423. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, P.; Chen, Y.; Guo, H. Experimental study of counter-rotating propellers for high-altitude airships. J. Guid. Control. Dyn. 2015, 38, 1491–1496. [Google Scholar] [CrossRef]
- Fiore, M.; Daroukh, M.; Montagnac, M. Loss assessment of a counter rotating open rotor using URANS/LES with phase-lagged assumption. Comput. Fluids 2021, 228, 105025. [Google Scholar] [CrossRef]
- Sinnige, T.; Stokkermans, T.C.A.; Ragni, D.; Eitelberg, G.; Veldhuis, L.L.M. Aerodynamic and aeroacoustic performance of a propeller propulsion system with swirl-recovery vanes. J. Propuls. Power. 2018, 34, 1376–1390. [Google Scholar] [CrossRef]
- Li, Q.; Öztürk, K.; Sinnige, T.; Ragni, D.; Eitelberg, G.; Veldhuis, L.; Wang, Y. Design and experimental validation of swirl-recovery vanes for propeller propulsion systems. AIAA J. 2018, 56, 4719–4729. [Google Scholar] [CrossRef] [Green Version]
- Kingan, M.J.; Parry, A.B. Acoustic theory of the many-bladed contra-rotating propeller: The effect of sweep on noise enhancement and reduction. J. Sound Vib. 2020, 468, 115089. [Google Scholar] [CrossRef]
- Meng, Y.; An, C.; Xie, C.; Yang, C. Conceptual design and flight test of two wingtip-docked multi-body aircraft. Chin. J. 2022, 35, 144–155. [Google Scholar] [CrossRef]
- Ruiz-Calavera, L.P.; Perdones-Diaz, D. CFD computation of in-plane propeller shaft loads. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013. AIAA Paper 2013-3798. [Google Scholar]
- Roosenboom, E.W.M.; Stürmer, A.; Schröder, A. Advanced experimental and numerical validation and analysis of propeller slipstream flows. J. Aircr. 2010, 47, 284–291. [Google Scholar] [CrossRef]
- De Rosa, D.; Morales Tirado, E.; Mingione, G. Paremetric invesgation of a distributed propulsion system on a regional aircraft. Aerospace 2022, 9, 176. [Google Scholar] [CrossRef]
- Ciliberti, D.; Nicolosi, F. Design, analysis, and testing of a scaled propeller for an innovative regional turboprop aircraft. Aerospace 2022, 9, 264. [Google Scholar] [CrossRef]
- Wang, H.; Gan, W.; Li, D. An investigation of the aerodynamic performance for a propeller-aided lift-enhancing double wing configuration. Aerosp. Sci. Technol. 2020, 105, 105991. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Zhang, Y. Wing optimization of propeller aircraft based on actuator disc method. Chin. J. Aeronaut. 2021, 34, 65–78. [Google Scholar] [CrossRef]
- Stajuda, M.; Obidowski, D.; Karczewski, M.; Józwik, K. Modified virtual blade method for propeller modelling. Mech. Mech. Eng. 2018, 22, 603–617. [Google Scholar] [CrossRef]
- Huang, Z.; Yao, H.; Sjögren, O.; Lundbladh, A.; Davidson, L. Aeroacoustic analysis of aerodynamically optimized joined-blade propeller for future electric aircraft at cruise and take-off. Aerosp. Sci. Technol. 2020, 107, 106336. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Martins, J.R.R.A. RANS-based aerodynamic shape optimization of a wing considering propeller–wing interaction. J. Aircr. 2021, 58, 497–513. [Google Scholar] [CrossRef]
- Caradonna, F.X.; Tung, C. Experimental and analytical studies of a model helicopter rotor in hover. Vertica 1980, 5, 149–161. [Google Scholar]




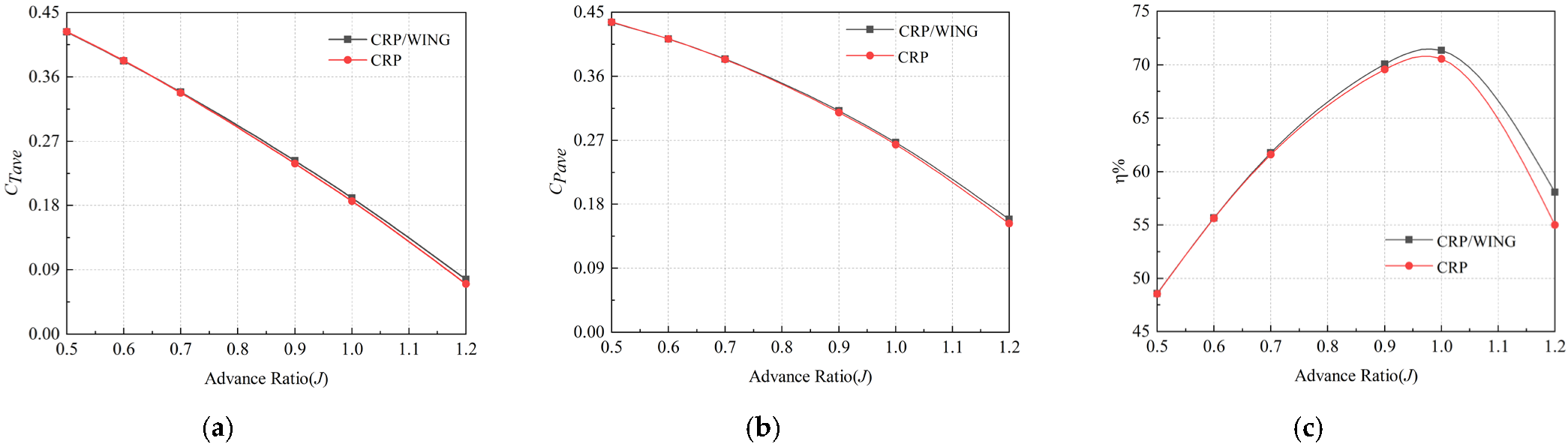
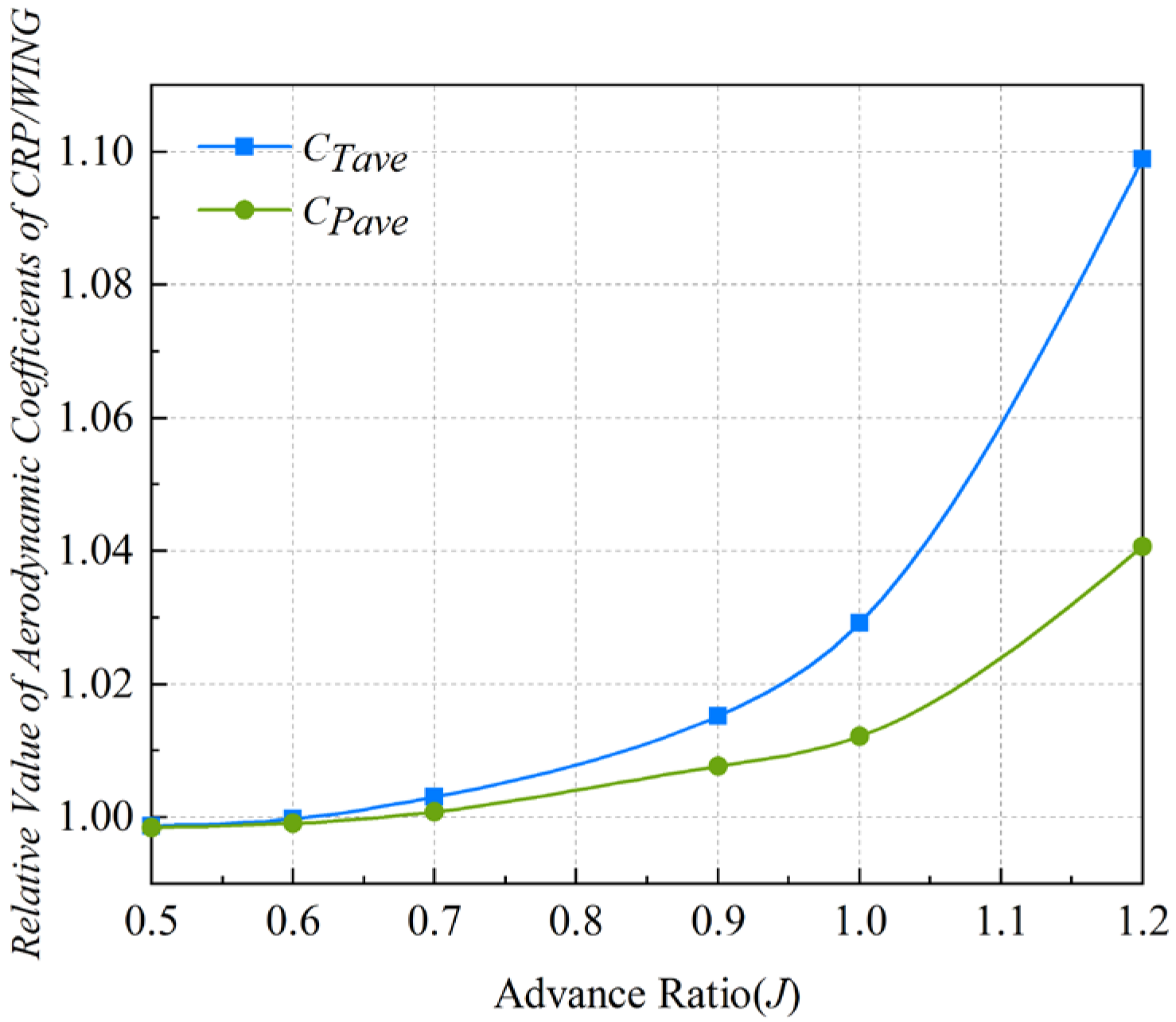
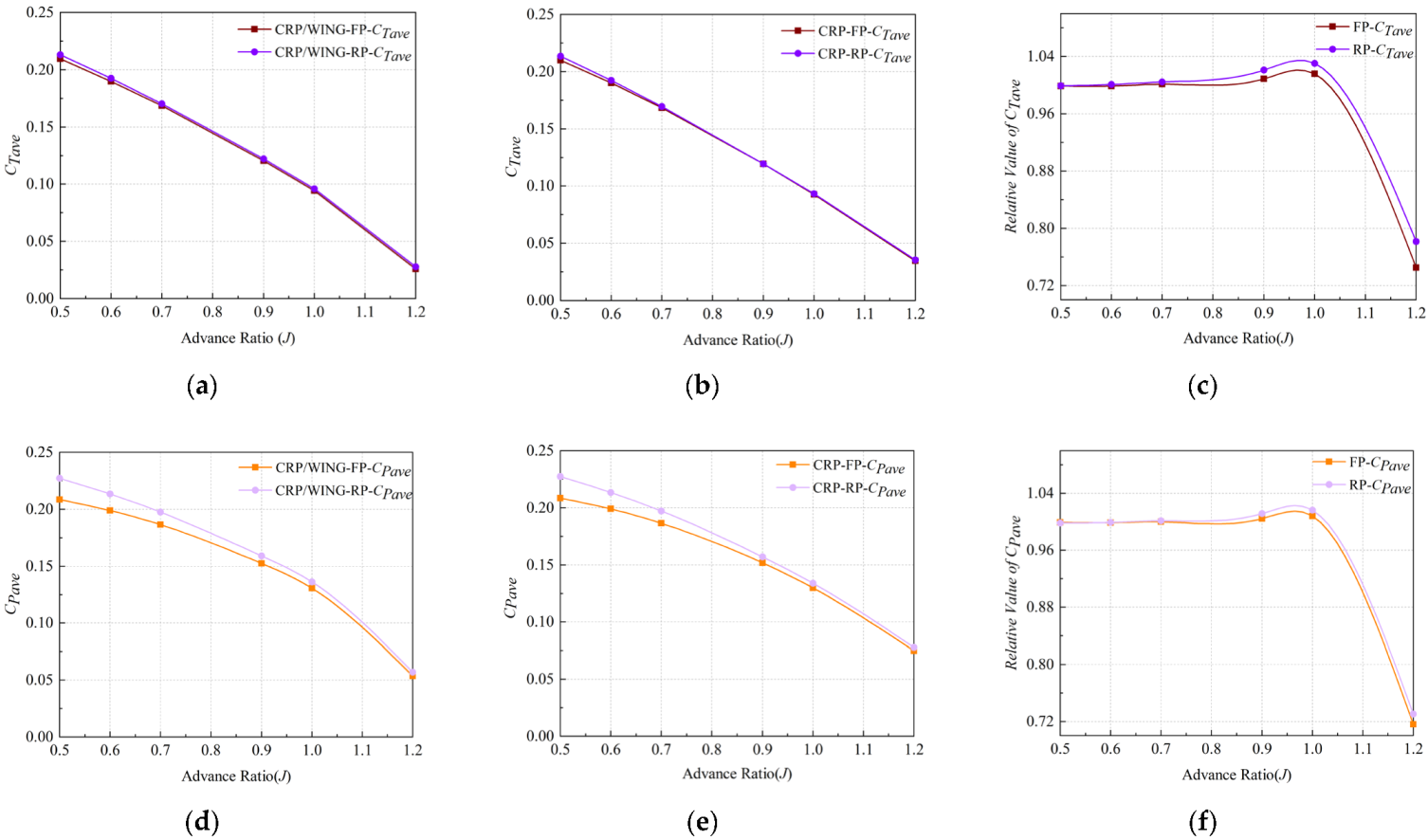

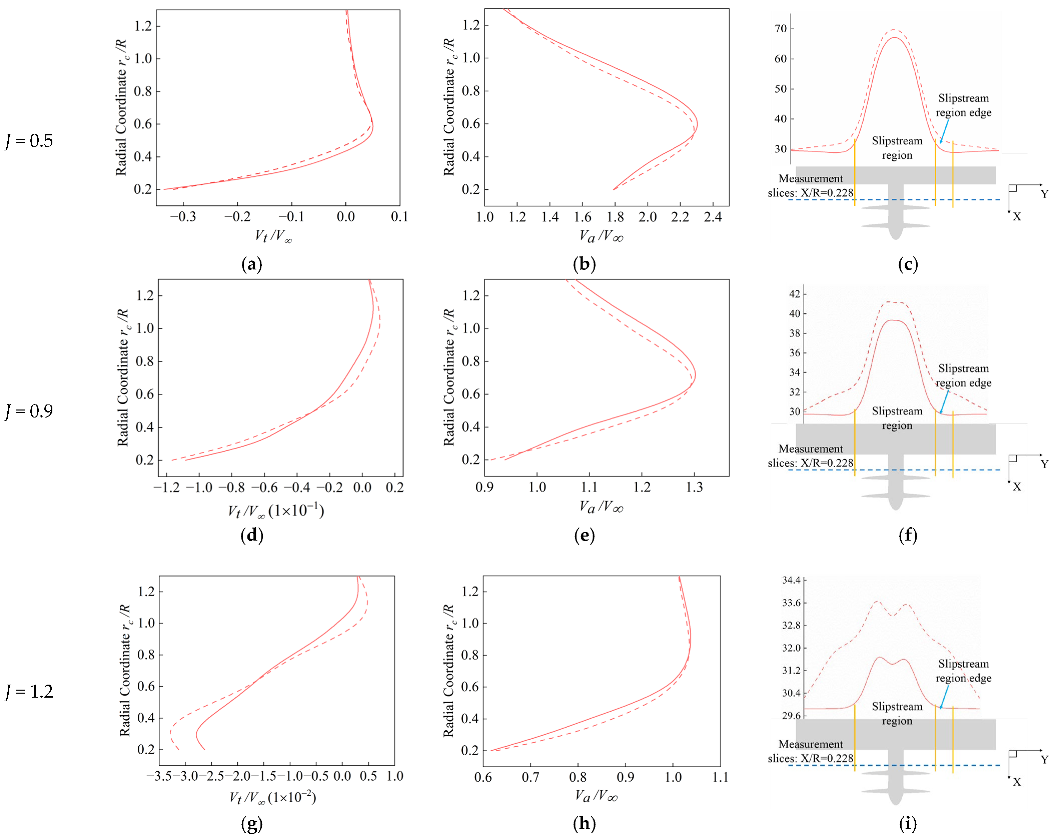
| Configuration | Axial Spacing | Number of Nodes /Million | Number of Elements /Million |
|---|---|---|---|
| 3 × 3-CRP | 0.24R | 2.50 | 4.77 |
| 0.44R | 2.52 | 4.79 | |
| 0.64R | 2.55 | 4.82 | |
| 3-IRP | 1.85 | 2.97 | |
| Configuration | Axial Spacing | Number of Nodes /Million | Number of Elements /Million |
| 4 × 4-CRP | 0.24R | 2.93 | 5.92 |
| 0.44R | 2.95 | 5.96 | |
| 0.64R | 2.97 | 5.98 | |
| 4-IRP | 2.06 | 3.55 |
| Configuration | Axial Spacing | Number of Nodes /Million | Number of Elements /Million |
|---|---|---|---|
| 3 × 3-CRP/wing | 0.24R | 3.07 | 5.34 |
| 0.44R | 3.09 | 5.36 | |
| 0.64R | 3.13 | 5.40 | |
| 3-IRP/wing | 2.23 | 3.34 | |
| Configuration | Axial Spacing | Number of Nodes /Million | Number of Elements /Million |
| 4 × 4-CRP/wing | 0.24R | 3.49 | 6.48 |
| 0.44R | 3.51 | 6.50 | |
| 0.64R | 3.55 | 6.55 | |
| 4-IRP/wing | 2.44 | 3.92 |
| Grid | IRP | Grid | IRP/Wing System | ||
|---|---|---|---|---|---|
| Number of Cells (Million) | Number of Nodes (Million) | Number of Cells (Million) | Number of Nodes (Million) | ||
| G1 | 1.68 | 1.16 | G5 | 1.92 | 1.40 |
| G2 | 3.55 | 2.06 | G6 | 3.92 | 2.44 |
| G3 | 4.90 | 2.73 | G7 | 5.62 | 3.45 |
| G4 | 6.61 | 3.61 | G8 | 7.70 | 4.72 |
| Grid | High Loading Condition | Medium Loading Condition | ||||||
|---|---|---|---|---|---|---|---|---|
| CTave | △% | CQave | △% | CTave | △% | CQave | △% | |
| G1 | 0.1945 | 3.951 | 0.0343 | 4.893 | 0.1228 | 4.510 | 0.0267 | 5.534 |
| G2 | 0.2025 | 0 | 0.0327 | 0 | 0.1286 | 0 | 0.0253 | 0 |
| G3 | 0.2030 | 0.247 | 0.0326 | 0.306 | 0.1286 | 0 | 0.0252 | 0.395 |
| G4 | 0.2032 | 0.346 | 0.0325 | 0.612 | 0.1287 | 0.078 | 0.0251 | 0.791 |
| Grid | Medium Loading Condition | |||||||
| CTave | △% | CQave | △% | CLave | △% | CDave | △% | |
| G5 | 0.1263 | 3.661 | 0.0271 | 5.447 | 0.4755 | 0.870 | 0.0678 | 9.709 |
| G6 | 0.1311 | 0 | 0.0257 | 0 | 0.4714 | 0 | 0.0618 | 0 |
| G7 | 0.1311 | 0 | 0.0255 | 0.778 | 0.4710 | 0.085 | 0.0588 | 4.854 |
| G8 | 0.13109 | 0.007 | 0.0255 | 0.778 | 0.4709 | 0.106 | 0.0580 | 6.149 |
| Model Configuration | Axial Spacing | AoA (deg) |
|---|---|---|
| 3 × 3-CRP | 0.64R | 0 |
| 2 | ||
| 4 | ||
| 6 | ||
| 3 × 3-CRP/wing system | 0.64R | 0 |
| 2 | ||
| 4 | ||
| 6 | ||
| Clean wing | 0 | |
| 2 | ||
| 4 | ||
| 6 | ||
| IRP/wing system | 6 |
| Configuration | △CTave/% | △CPave/% | △η/% |
|---|---|---|---|
| FP | 0.863 | 0.477 | 0.384 |
| RP | 2.092 | 1.484 | 0.597 |
| CRP | 1.47 | 0.985 | 0.480 |
| Configuration | Axial Spacing | AoA(deg) | Rotation Speed/RPM |
|---|---|---|---|
| 4 × 4-CRP | 0.24R | 6 | 4926 |
| 0.44R | |||
| 0.64R | |||
| 4 × 4-CRP/wing | 0.24R | 6 | 4926 |
| 0.44R | |||
| 0.64R |
| Axial Spacing | CRP/Wing System | ||
|---|---|---|---|
| CLave | CDave | CMave | |
| 0.24R | 0.468 | 0.072 | 0.0314 |
| 0.44R | 0.472 | 0.072 | 0.0339 |
| 0.64R | 0.474 | 0.073 | 0.0368 |
| Configuration | Axial Spacing | AoA/deg | Rotational Speed/RPM |
|---|---|---|---|
| 3 × 3-CRP | 0.24R | 6 | 4926 |
| 4 × 4-CRP | |||
| 3 × 3-CRP/wing | |||
| 4 × 4-CRP/wing | |||
| 3 × 3-CRP | 0.64R | 6 | 4926 |
| 4 × 4-CRP | |||
| 3 × 3-CRP/wing | |||
| 4 × 4-CRP/wing |
| Configuration | CTave | △% | CPave | △% | η% | △% |
|---|---|---|---|---|---|---|
| 3 × 3-CRP | 0.1954 | 0 | 0.2457 | 0 | 71.59 | 0 |
| 4 × 4-CRP | 0.2374 | 21.49 | 0.3074 | 25.11 | 69.48 | −2.95 |
| Configuration | CTave | △% | CPave | △% | η% | △% |
|---|---|---|---|---|---|---|
| 3 × 3-CRP/wing | 0.1975 | 0 | 0.2467 | 0 | 72.06 | 0 |
| 4 × 4-CRP/wing | 0.2412 | 22.13 | 0.3100 | 25.66 | 70.03 | −2.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xie, C.; Huang, K.; Yang, C. Influence of Aerodynamic Interaction on Performance of Contrarotating Propeller/Wing System. Aerospace 2022, 9, 813. https://doi.org/10.3390/aerospace9120813
Zhang Z, Xie C, Huang K, Yang C. Influence of Aerodynamic Interaction on Performance of Contrarotating Propeller/Wing System. Aerospace. 2022; 9(12):813. https://doi.org/10.3390/aerospace9120813
Chicago/Turabian StyleZhang, Zhitao, Changchuan Xie, Kunhui Huang, and Chao Yang. 2022. "Influence of Aerodynamic Interaction on Performance of Contrarotating Propeller/Wing System" Aerospace 9, no. 12: 813. https://doi.org/10.3390/aerospace9120813
APA StyleZhang, Z., Xie, C., Huang, K., & Yang, C. (2022). Influence of Aerodynamic Interaction on Performance of Contrarotating Propeller/Wing System. Aerospace, 9(12), 813. https://doi.org/10.3390/aerospace9120813





