Numerical and Experimental Analysis of Drag and Lift Forces on a Bullet Head
Abstract
:1. Introduction
2. Experimental
2.1. Sample Bullet Head and Its Conditions
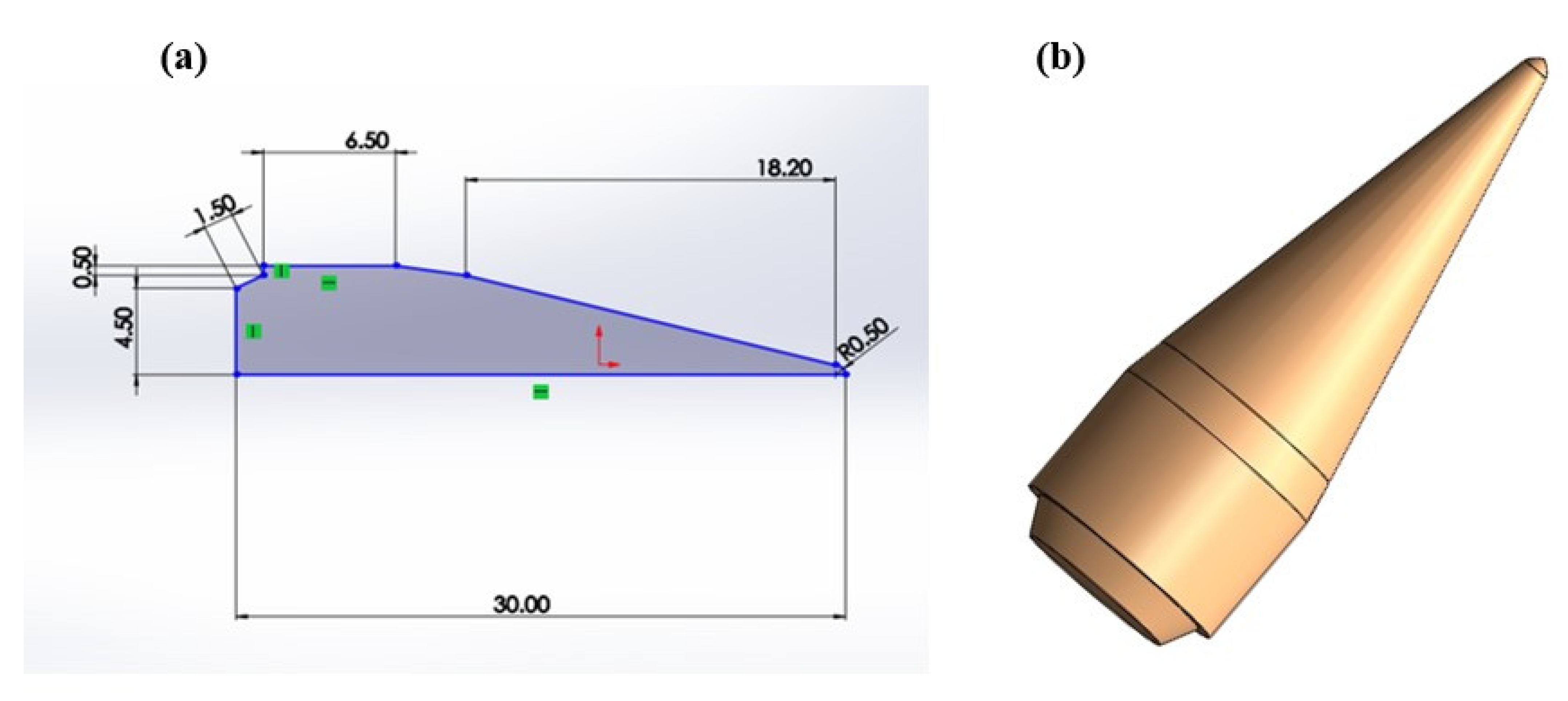
2.2. Bullet Head (Design I)
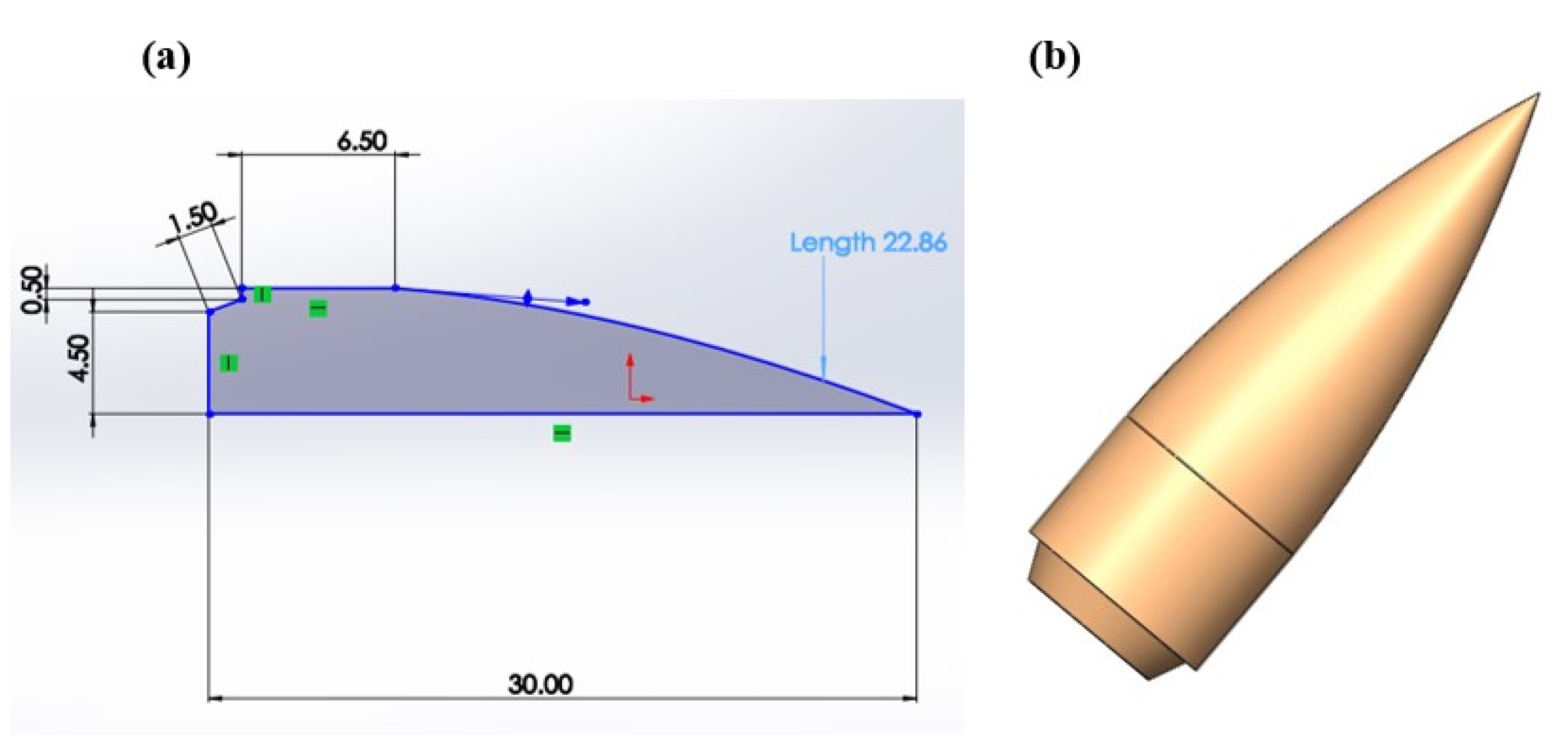
2.3. Bullet Head (Design II)
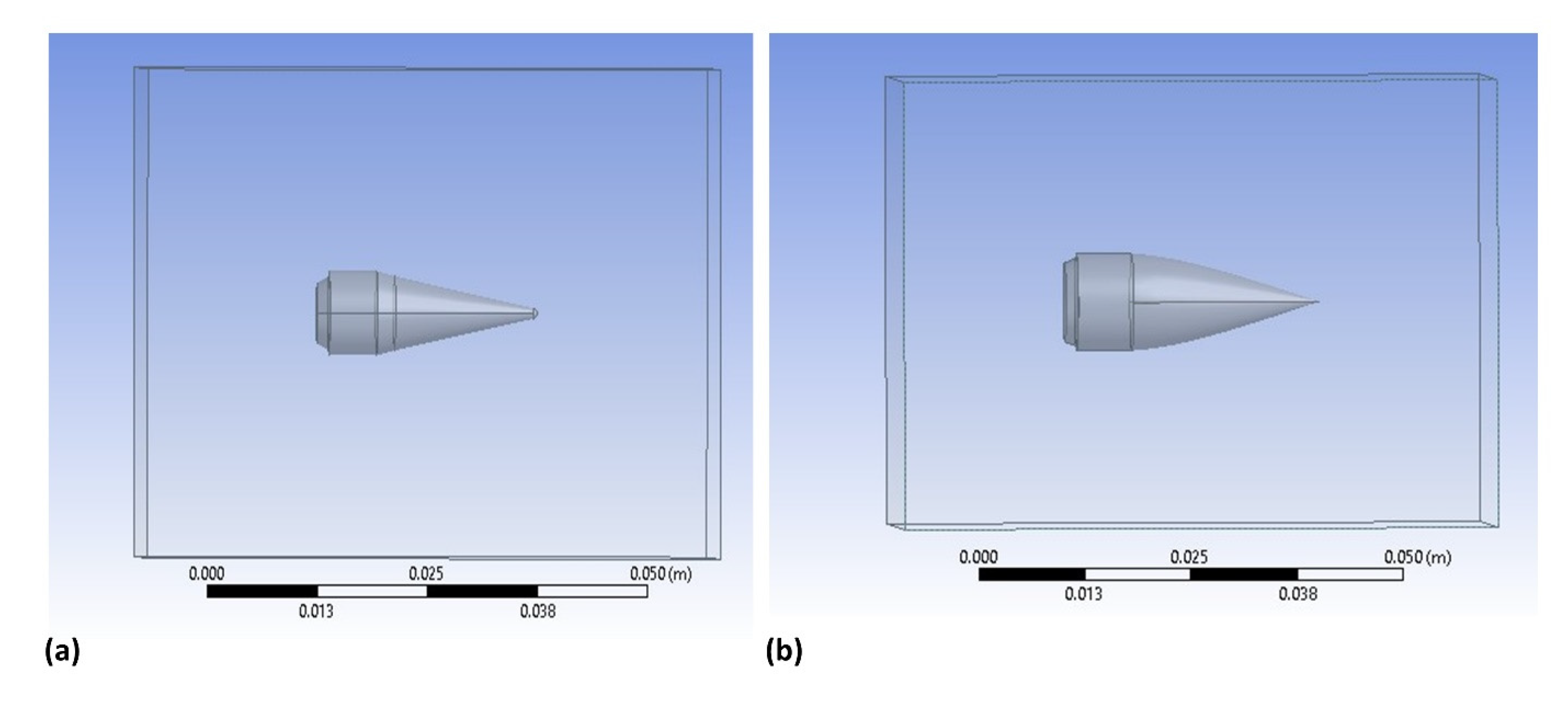
2.4. Experimental Model
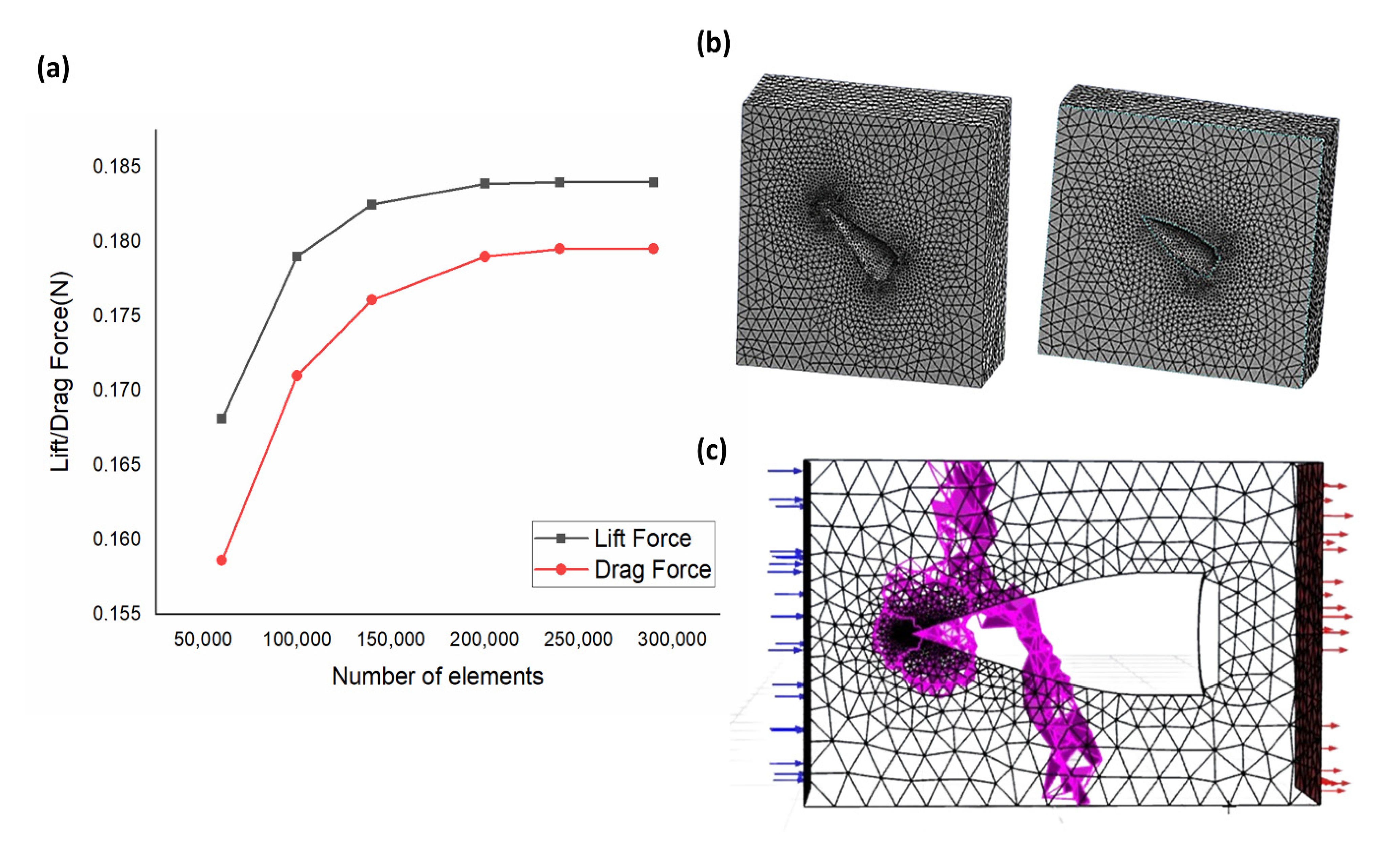
2.5. Mathematical Model and Simulations
3. Results and Discussion
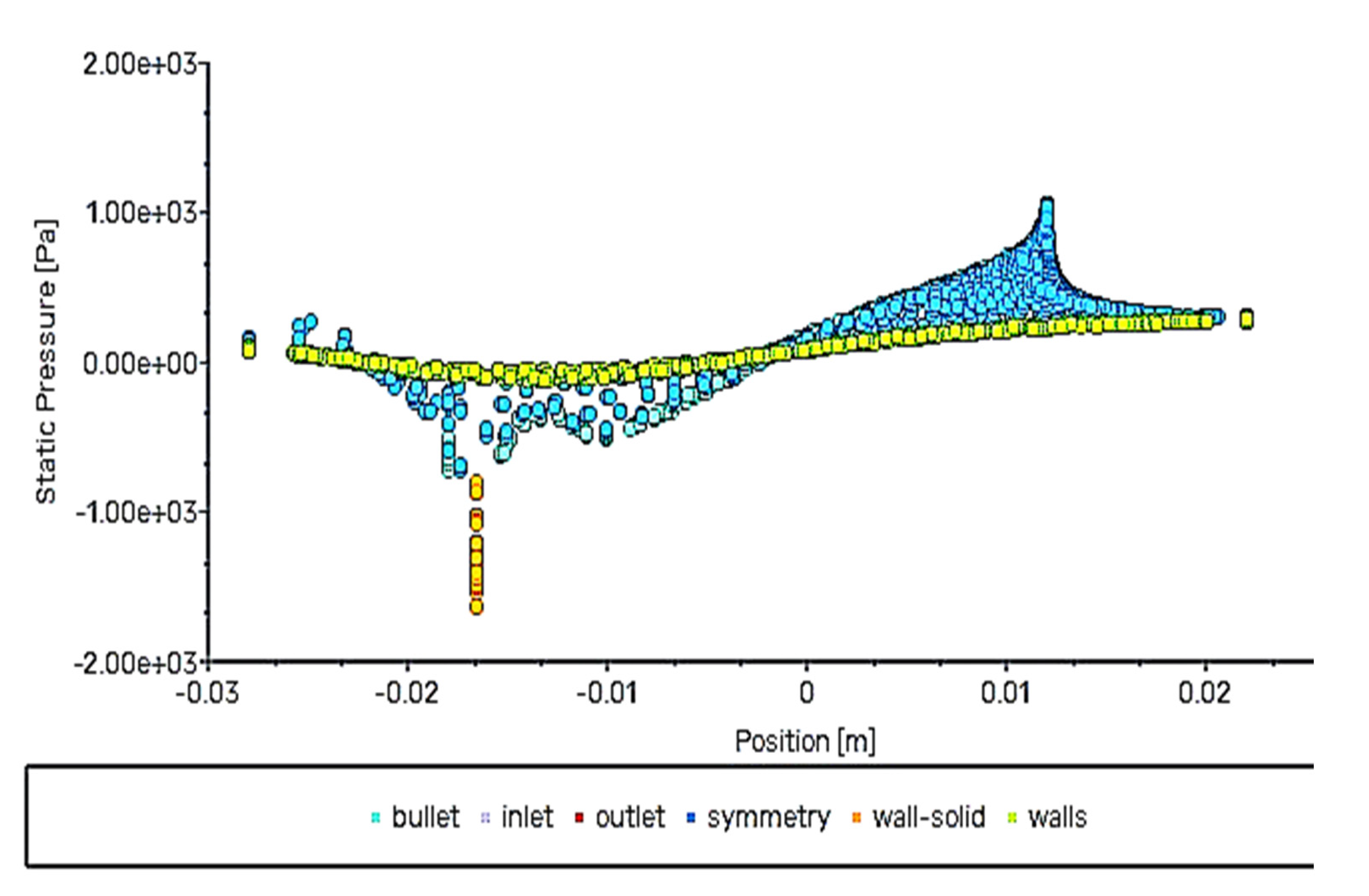
- The wind tunnel may have some adjustment errors that cause a difference between the CL (EXP) and CL (CFD).
- The wind tunnel may have blockage effects that cause a difference between the experimental and CFD coefficients.
4. Conclusions
- The above research work focuses on the drag and lifts coefficients of a bullet head because these are the parameters on which the hitting precision and range of a bullet head are dependent.
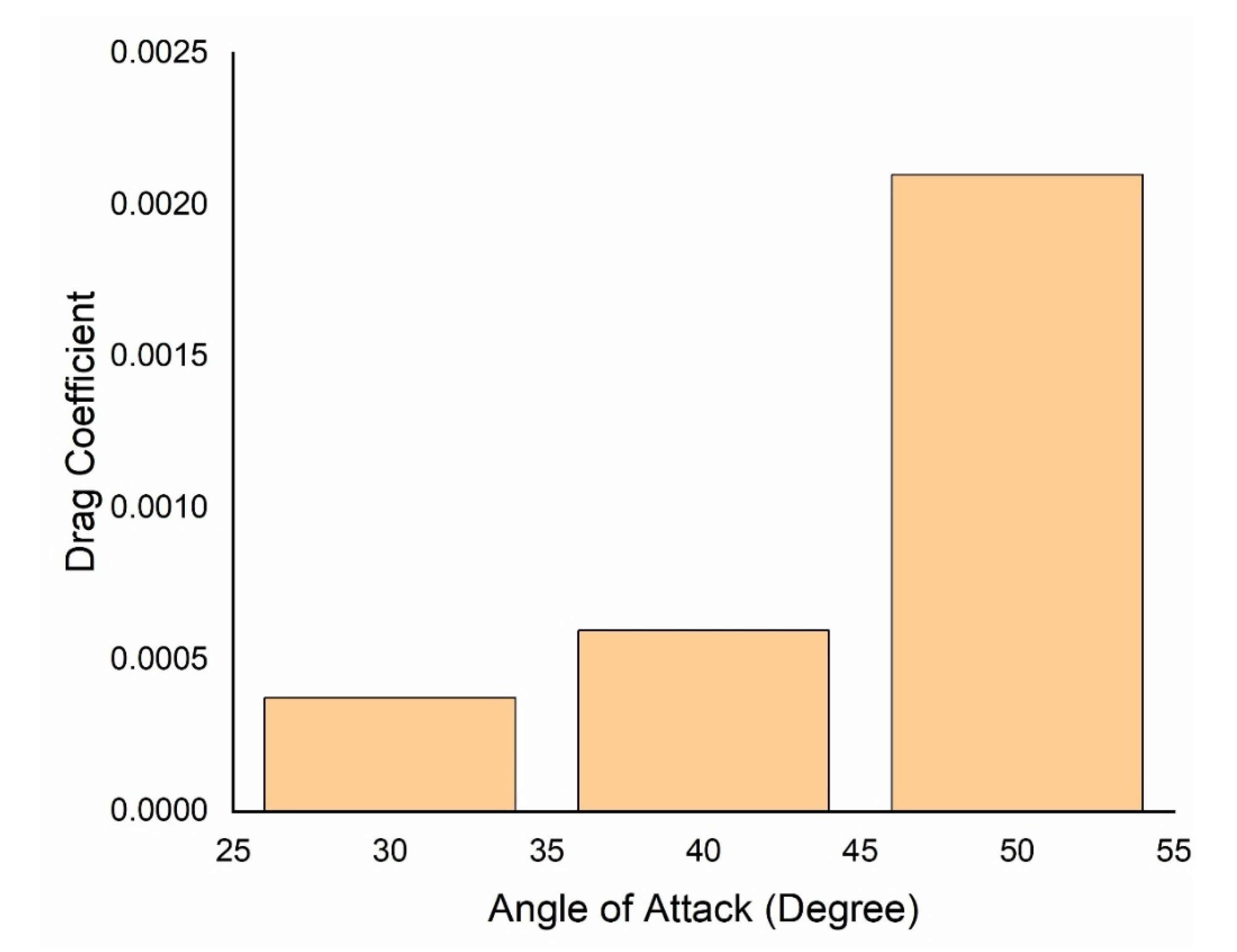
- The above numerical and simulation results show that the lift and drag coefficients of a bullet head are directly proportional to the angle of attack and length of a bullet; when increasing these parameters, the lift and drag coefficients also increase.
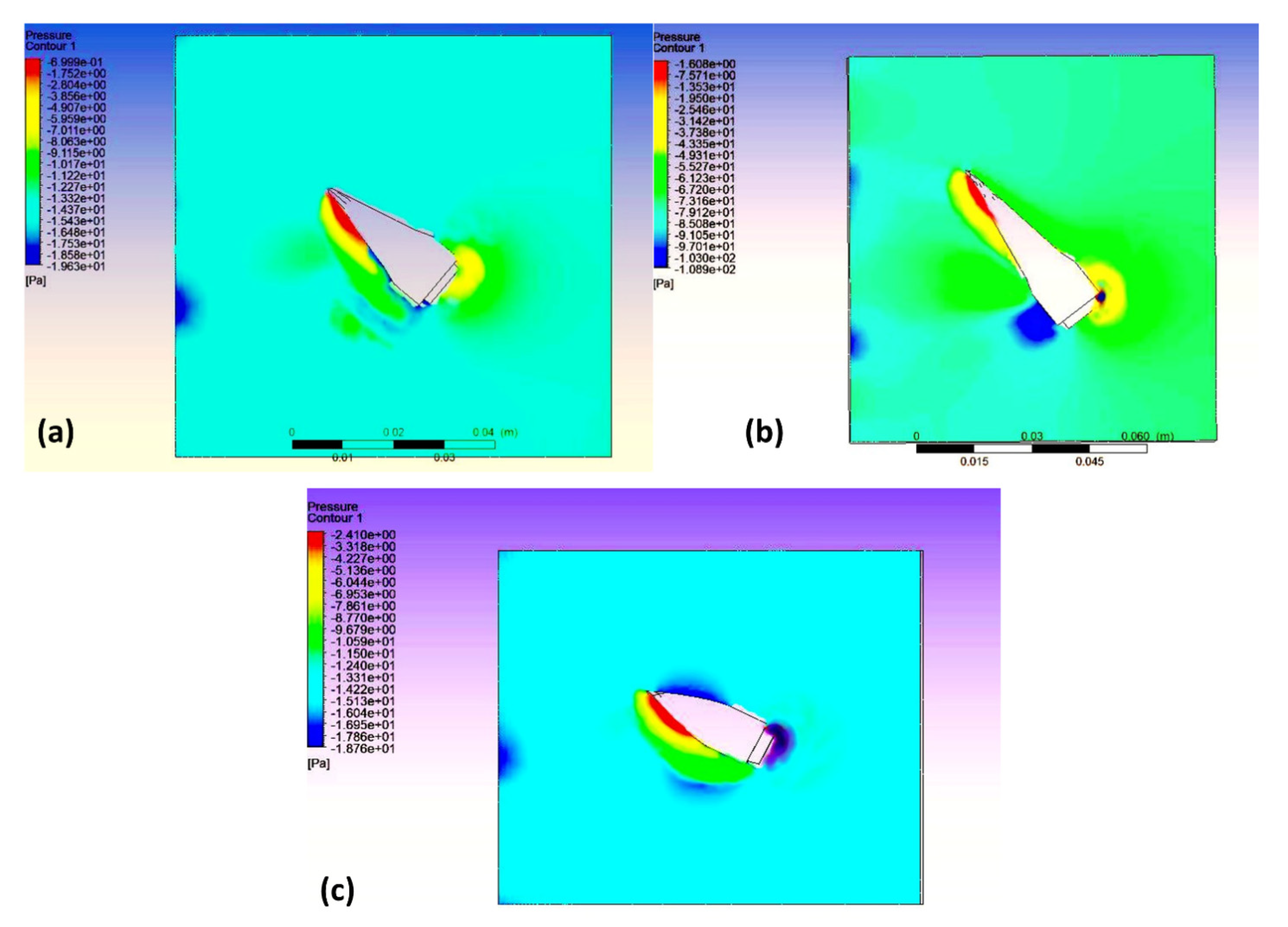
- Velocity streamlines are inversely proportional to the drag coefficient because there are no streamlines at a 50 mm bullet head, due to which a large drag force act on it.
- When increasing the angle of attack, the increase in the drag coefficient is greater than the increase in the lift coefficient. Hence, we can state that these two parameters are due to the combined effect of the size, shape, and angle of attack.
- In the real-time framework, the flight of a bullet is in the supersonic region, whereas this research work focused on the simulation of the subsonic region because it presents the initial flight scenario; however, when numerical simulations were performed in the supersonic region, we observed the same trend.
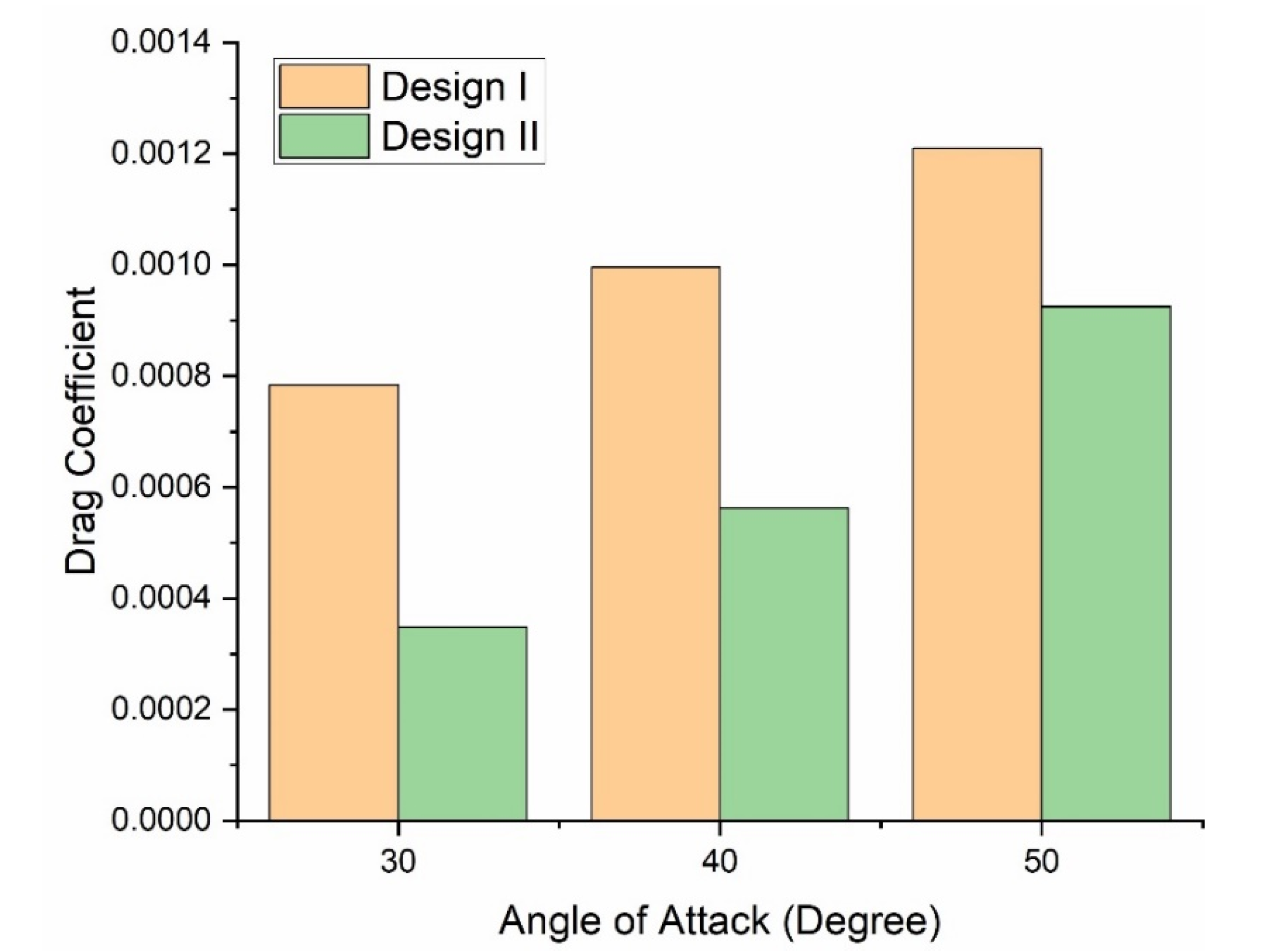
- The drag coefficient of the modified design of the bullet head is smaller than the drag coefficient of the original design of the bullet head under the same conditions, because the modified design of the bullet head has a smaller projected area, so, according to the results, the drag coefficient is inversely proportional to the projected area.
- Numerical and experimental investigation of a bullet head will be performed in the future, in which the behavior of a bullet head will be analyzed and interpreted at multiple points in its trajectory.
- Experimental and numerical investigation of a bullet head will be performed with the optimization of its shape so that it has less drag and a greater lift coefficient.
- In the actual framework, both the wind and bullet heads are moving; to evaluate this, numerical and experimental testing can be performed in the future at different speeds.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Rhee, P.M.; Moore, E.E.; Joseph, B.; Tang, A.; Pandit, V.; Vercruysse, G. Gunshot wounds: A review of ballistics, bullets, weapons, and myths. J. Trauma Acute Care Surg. 2016, 80, 853–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bateman, M.J.K.; Force, U.A. Maximizing Engagement Area Lethality. Mil. Rev. 2022. [Google Scholar]
- Ahmad, G.; Alanazi, S.; Alruwaili, M.; Ahmad, F.; Khan, M.A.; Abbas, S.; Tabassum, N. Intelligent Ammunition Detection and Classification System Using Convolutional Neural Network; Tech Science Press: Henderson, NV, USA, 2021; Volume 2, p. 340. [Google Scholar]
- Carlucci, D.E. Ballistics: Theory and Design of Guns and Ammunition; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Zamanian, S.; Terranova, B.; Shafieezadeh, A. Significant variables affecting the performance of concrete panels impacted by wind-borne projectiles: A global sensitivity analysis. Int. J. Impact Eng. 2020, 144, 103650. [Google Scholar] [CrossRef]
- Pai, A.; Kini, C.R.; Shenoy, S. Development of materials and structures for shielding applications against Blast and Ballistic impact: A Detailed Review. Thin-Walled Struct. 2022, 179, 109664. [Google Scholar] [CrossRef]
- Rahman, M.R. Computational Analysis of Aerodynamic Parameters for Supersonic Artillery Projectiles International journal of mechanical engineering. J. Mech. Civ. Eng. 2020, 6, 1–18. [Google Scholar]
- Lin, L.; Ju, R. Analysis and Research on the Impact of Bullet Head Eccentricity on Air Resistance. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; p. 012064. [Google Scholar]
- Yang, Y.-L.; Guo, R.; Liu, R.-Z.; Chen, L.; Xing, B.Y.; Zhao, B.B. Quasi-steady aerodynamic characteristics of terminal sensitive bullets with short cylindrical portion. Def. Technol. 2021, 17, 633–649. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, R.; Liu, R.; Guo, Z.; Qu, Y.; Chen, L. Numerical analysis on aerodynamic characteristics of short cylindrical terminal-sensitive bullet. Vibroengineering Procedia 2018, 18, 150–156. [Google Scholar] [CrossRef] [Green Version]
- Bolonkin, A. Long distance bullets and shells. Int. J. Aerosp. Sci. 2013, 2, 29–36. [Google Scholar]
- Novak, L.; Bajcar, T.; Širok, B.; Orbanić, A.; Bizjan, B. Investigation of vortex shedding from an airfoil by computational fluid dynamics simulation and computer-aided flow visualization. Therm. Sci. 2018, 22, 3023–3033. [Google Scholar] [CrossRef]
- Jang, Y.; Huh, J.; Lee, N.; Lee, S.; Park, Y. Comparative study on the prediction of aerodynamic characteristics of aircraft with turbulence models. Int. J. Aeronaut. Space Sci. 2018, 19, 13–23. [Google Scholar] [CrossRef]
- Dali, M.A.; Jaramaz, S. Optimization of artillery projectiles base drag reduction using hot base flow. Therm. Sci. 2019, 23, 353–364. [Google Scholar] [CrossRef]
- Wessam, M.; Chen, Z. Flow field investigations and aerodynamic characteristics of artillery projectile. In Proceedings of the International Conference of Electrical, Automation and Mechanical Engineering (EAME 2015), Phuket, Thailand, 26–27 July 2015. [Google Scholar]
- Burris, J.L.; Hester, B.C.; Mamola, K.C. The two-bullet problem with constant magnitude drag force. Phys. Teach. 2018, 56, 340–343. [Google Scholar] [CrossRef]
- Munir, A.; Aved, A.; Blasch, E. Situational Awareness: Techniques, Challenges, and Prospects. AI 2022, 3, 55–77. [Google Scholar] [CrossRef]
- Sahoo, S.; Laha, M. Coefficient of drag and trajectory simulation of 130 mm supersonic artillery shell with recovery plug or fuze. Def. Sci. J. 2014, 64, 502. [Google Scholar] [CrossRef]
- Bhuiyan, N.; Baghel, A.; Wilson, J. A sustainable continuous improvement methodology at an aerospace company. Int. J. Product. Perform. Manag. 2006, 4, 498. [Google Scholar] [CrossRef]
- Suliman, M.; Mahmoud, O.; Al-Sanabawy, M.; Abdel-Hamid, O.E. Computational investigation of base drag reduction for a projectile at different flight regimes. In International Conference on Aerospace Sciences and Aviation Technology; The Military Technical College: Cairo, Eqypt, 2009; pp. 1–13. [Google Scholar]
- Uddin, M.N.; Mostofa, G.; Rana, M.S. Numerical Analysis of Drag and Lift Forces Acting on Long Range Projectiles. Int. J. Acad. Res. Reflect. 2021, 9, 15–27. [Google Scholar]
- Ahmed, M.; Qin, N. Recent advances in the aerothermodynamics of spiked hypersonic vehicles. Prog. Aerosp. Sci. 2011, 47, 425–449. [Google Scholar] [CrossRef]
- Xiao, S.; Hu, K.; Huang, B.; Deng, H.; Ding, X. A review of research on the mechanical design of hoverable flapping wing micro-air vehicles. J. Bionic Eng. 2021, 18, 1–20. [Google Scholar] [CrossRef]
- Truscott, T.; Techet, A.; Beal, D. Shallow angle water entry of ballistic projectiles. In Proceedings of the 7th International Symposium on Cavitation, Ann Arbor, MI, USA, 16–20 August 2009. [Google Scholar]
- Susu, L.; Cheng, X.; Yaoke, W.; Xiaoyun, Z. A new motion model of rifle bullet penetration into ballistic gelatin. Int. J. Impact Eng. 2016, 93, 1–10. [Google Scholar] [CrossRef]
- Götten, F.; Havermann, M.; Braun, C.; Gómez, F.; Bil, C. On the applicability of empirical drag estimation methods for unmanned air vehicle design. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3192. [Google Scholar]
- Sethuraman, V.; Rajendran, P.; Khan, S.A. Base and wall pressure control using cavities and ribs in suddenly expanded flows-an overview. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 66, 120–134. [Google Scholar]
- Khan, A.; Rajendran, P.; Sidhu, J.S.S. Passive Control of Base Pressure: A Review. Appl. Sci. 2021, 11, 1334. [Google Scholar] [CrossRef]
- Patel, K.S.; Patel, S.B.; Patel, U.B.; Ahuja, A.P. CFD Analysis of an Aerofoil. Int. J. Eng. Res. 2014, 3, 154–158. [Google Scholar] [CrossRef]
- Seifert, J. A review of the Magnus effect in aeronautics. Prog. Aerosp. Sci. 2012, 55, 17–45. [Google Scholar] [CrossRef]


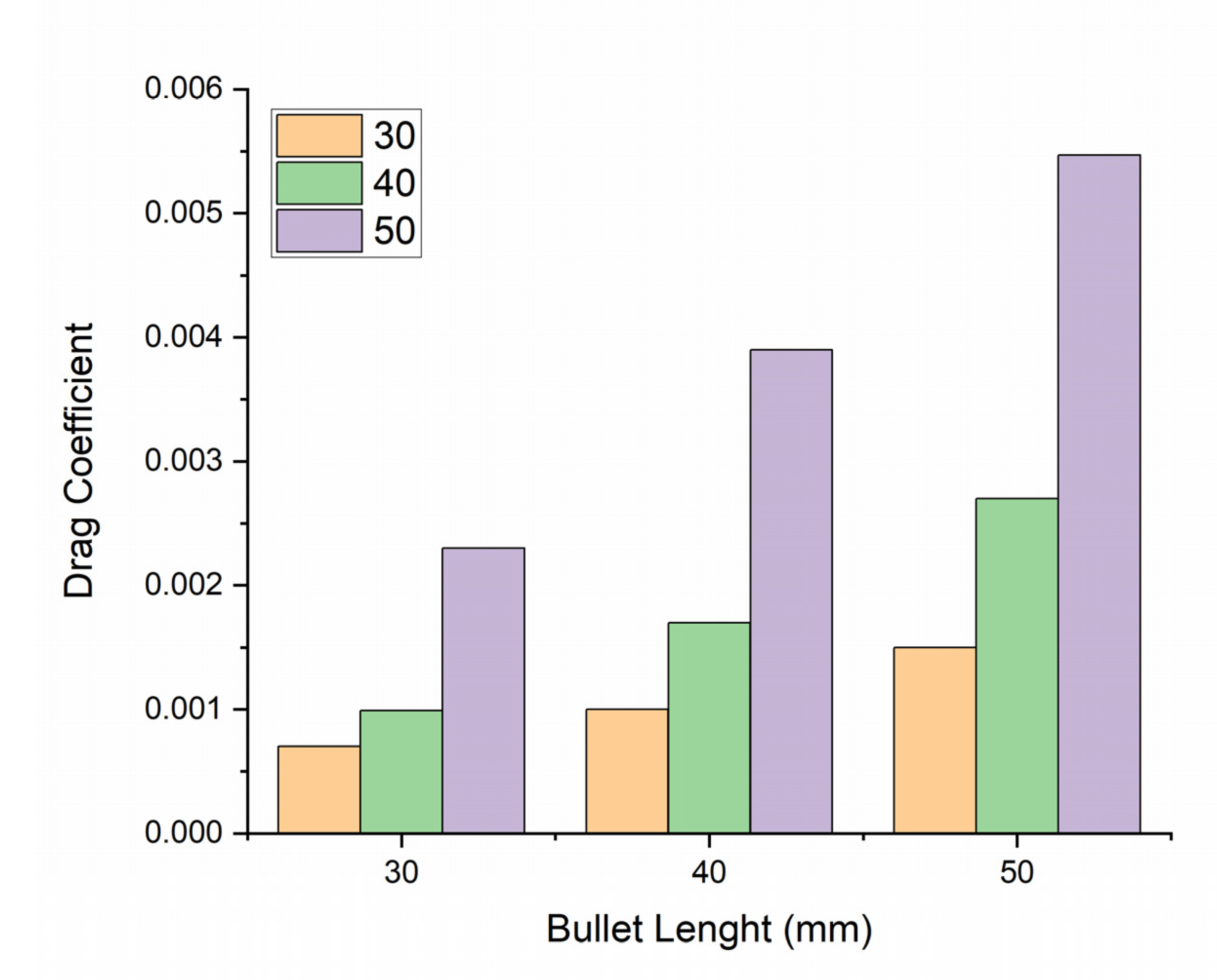
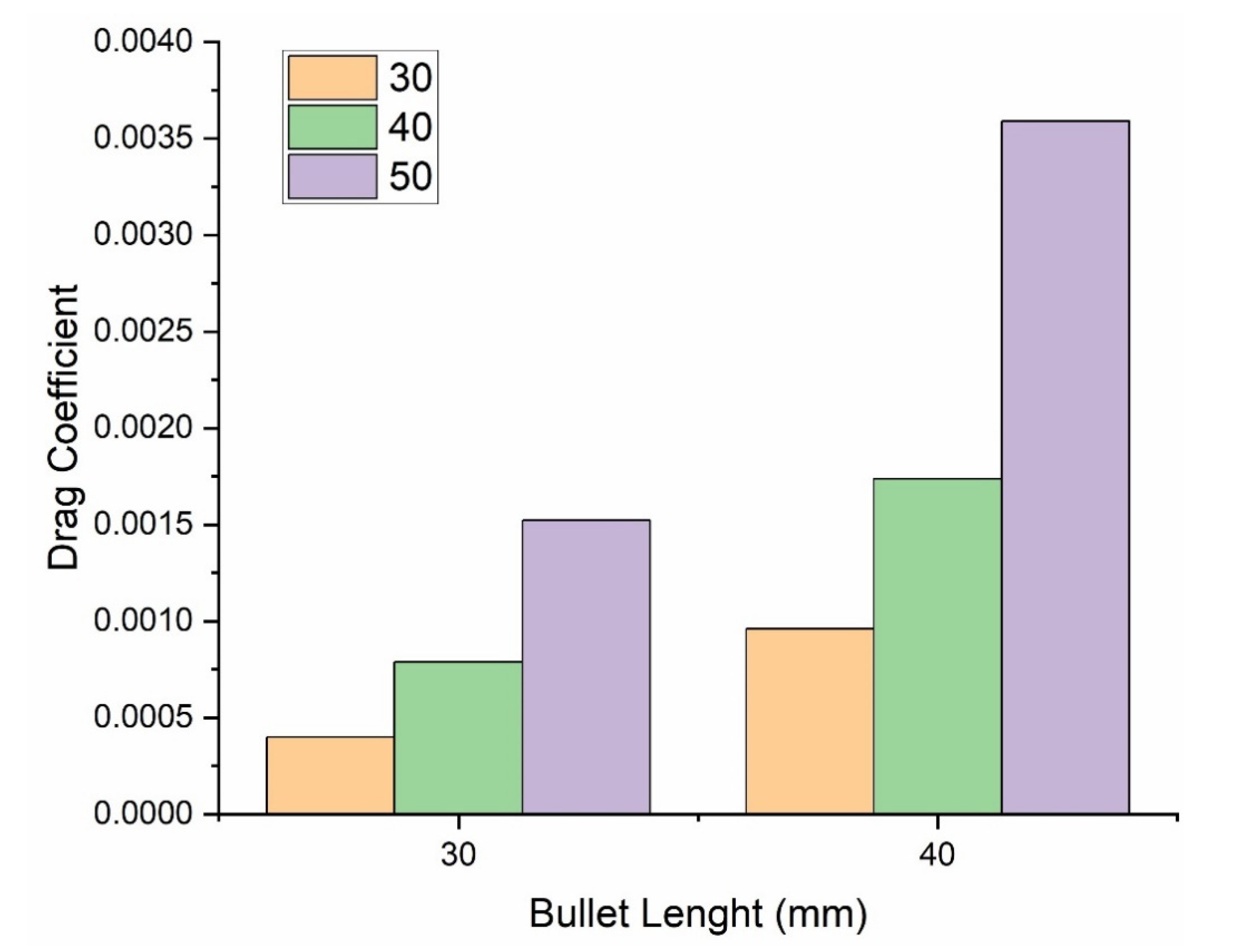
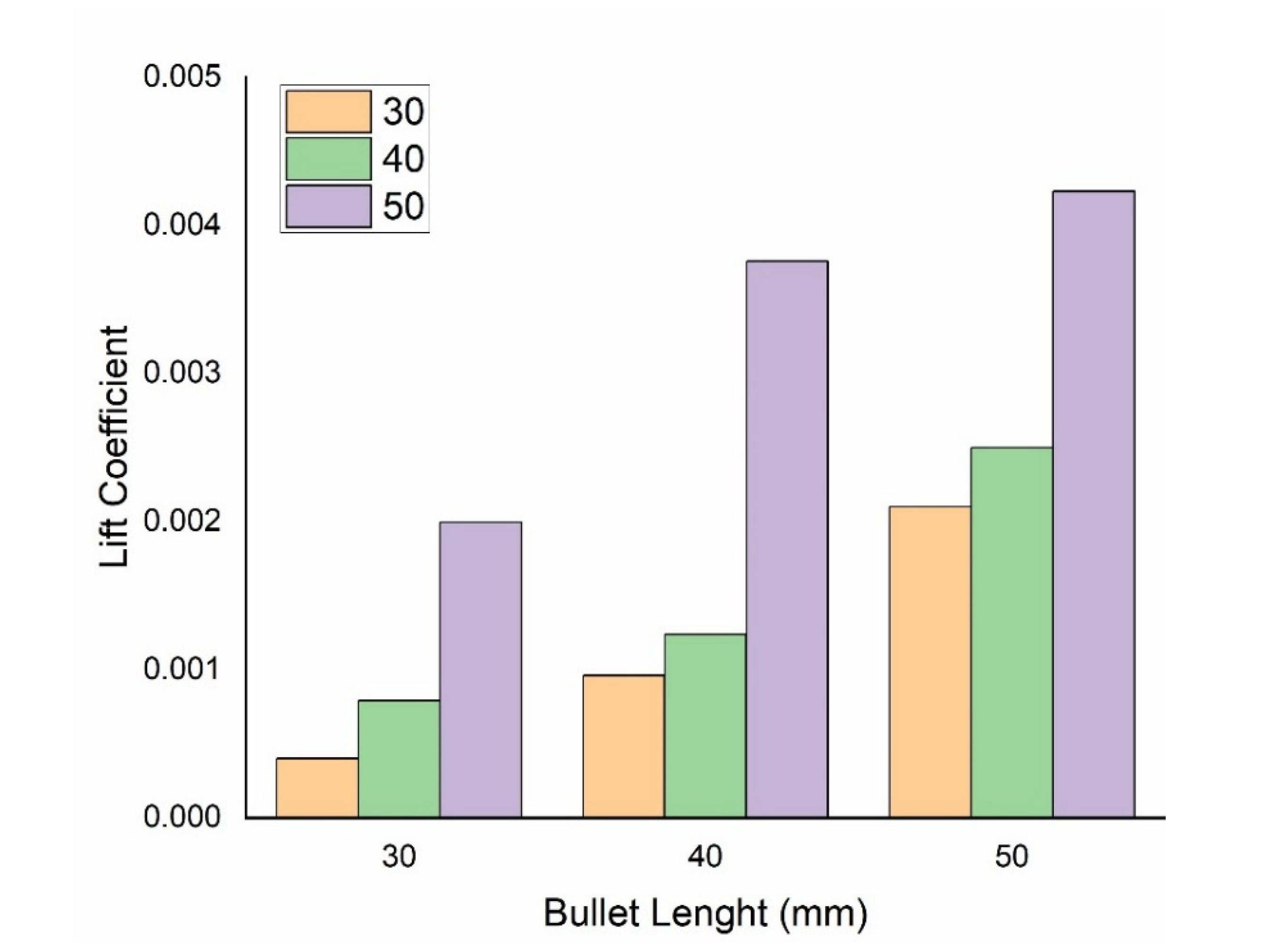
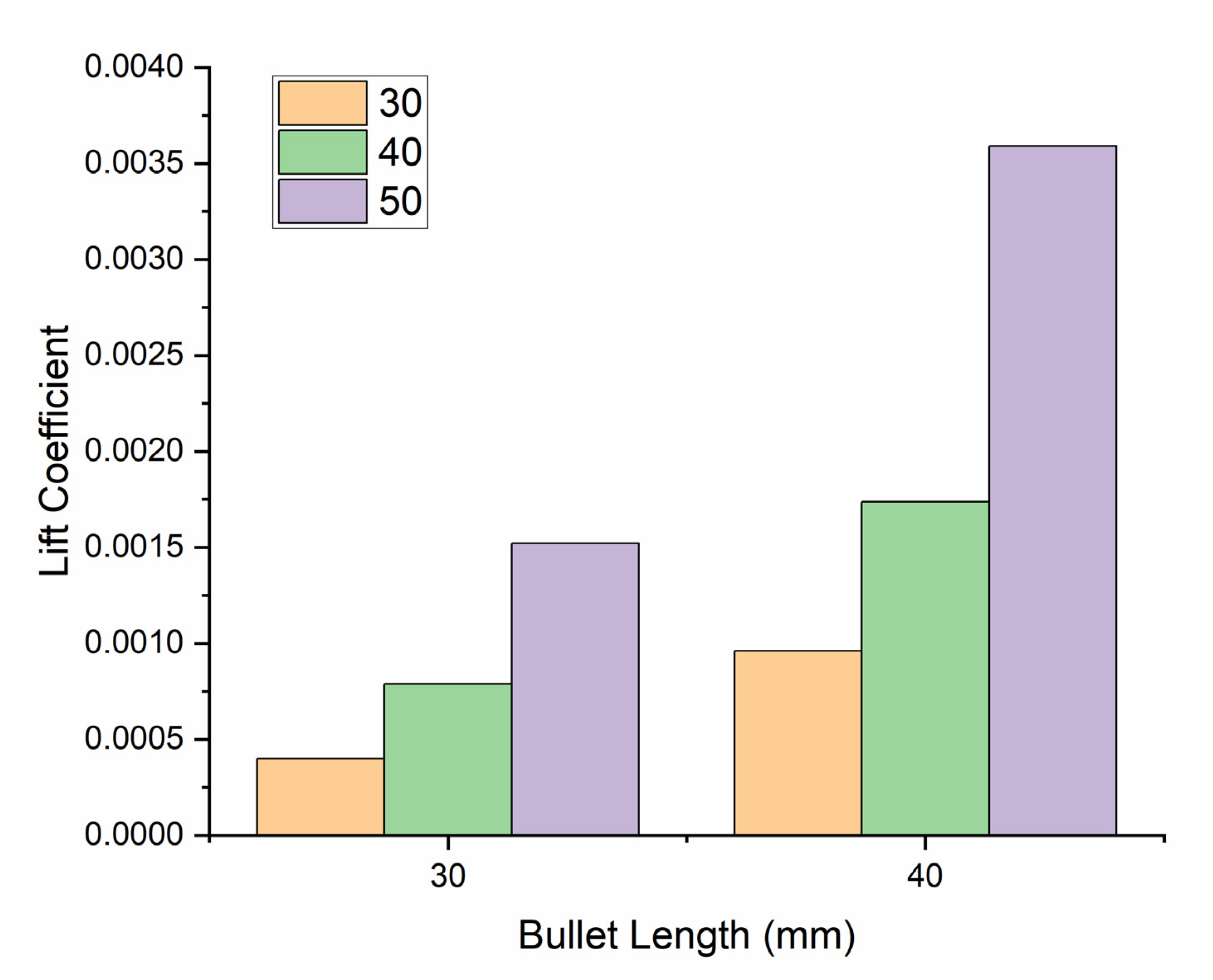
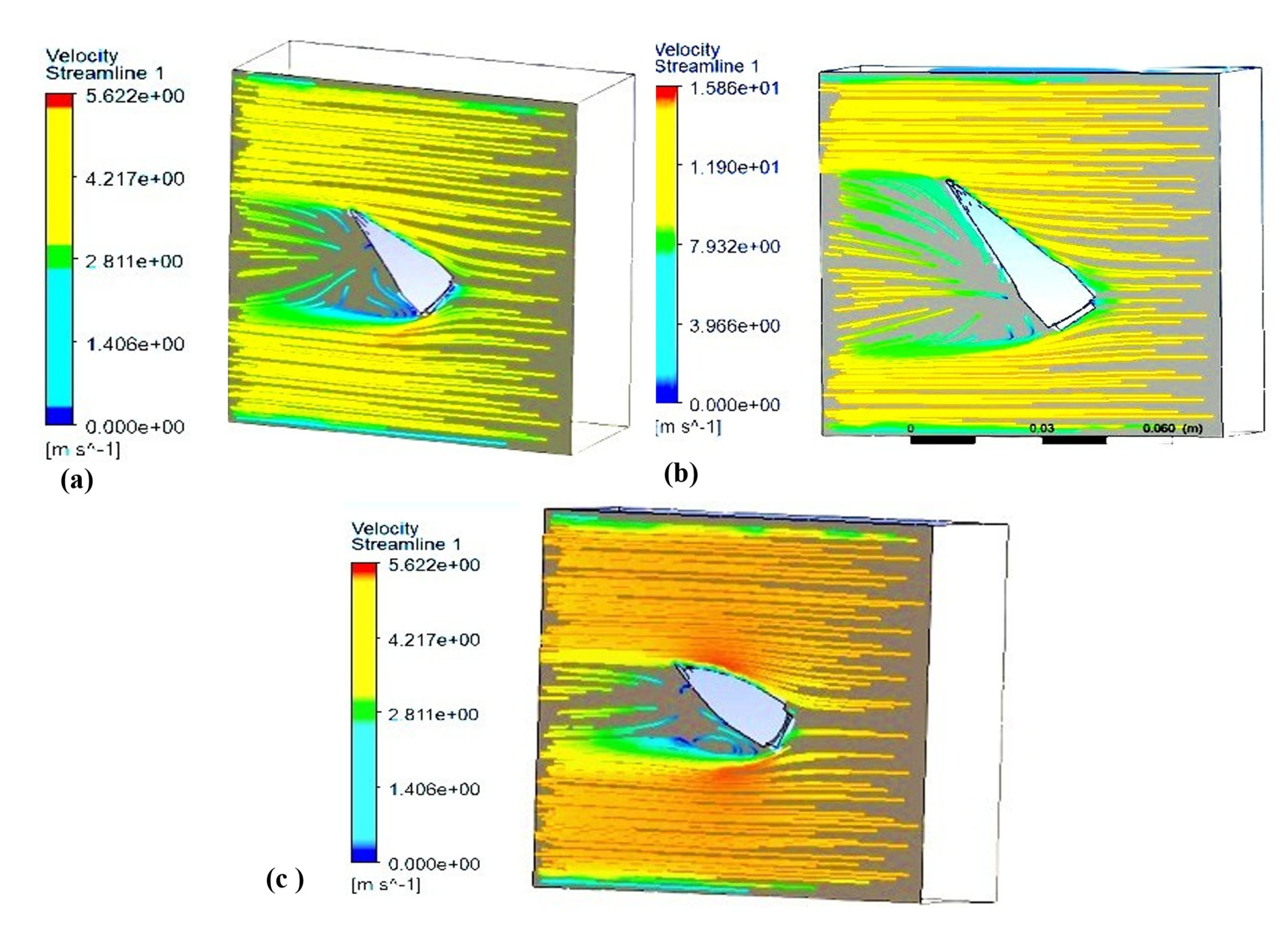
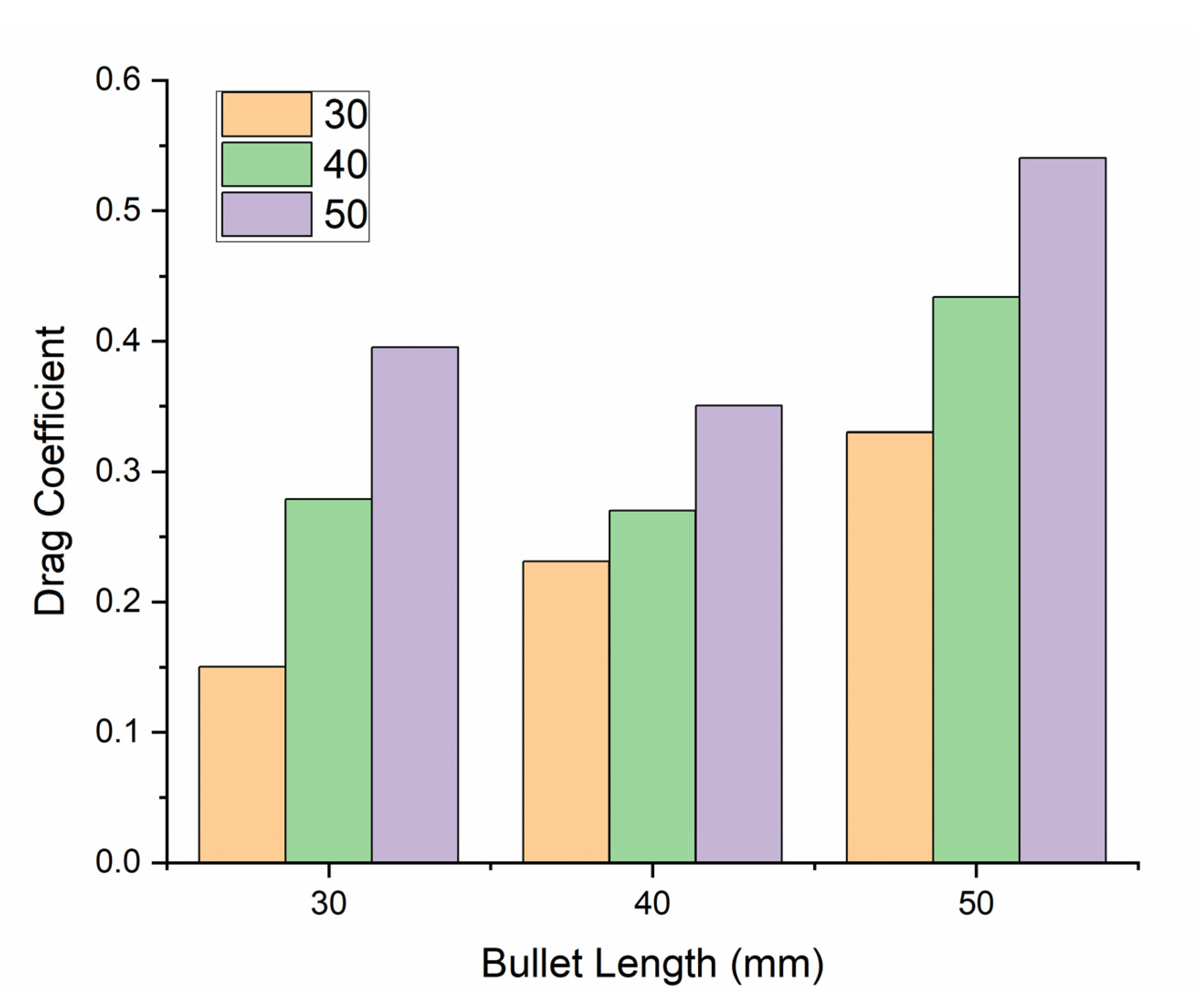
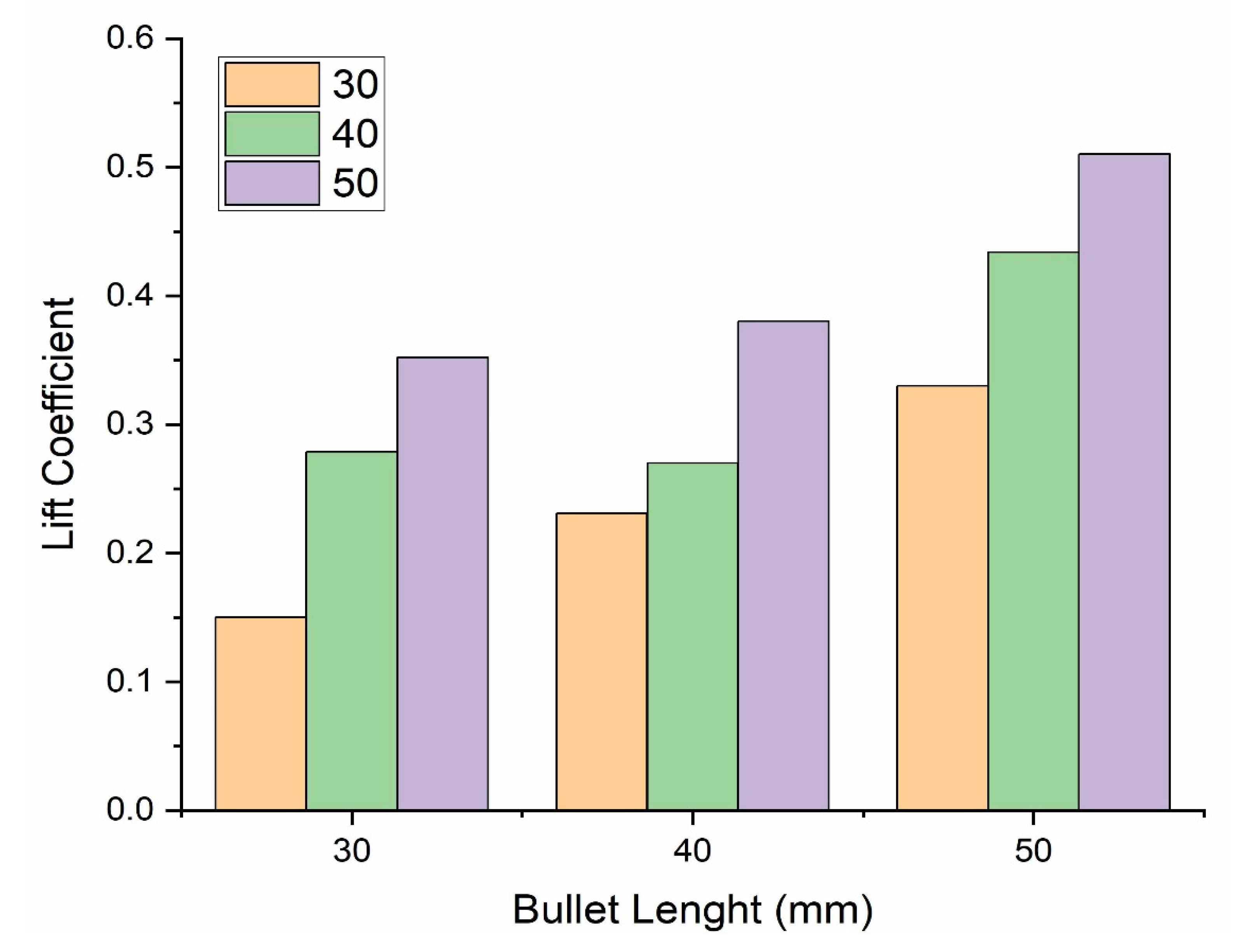
| Bullet Head Size (mm) | AOA (Degree) | Air Velocity (m/s) | Tapping Points (mm) | Area of the Bullet Head (mm2) |
|---|---|---|---|---|
| 30 | 30, 40, 50 | 5.2 | 30 | 902.4 |
| 40 | 30, 40, 50 | 5.2 | 30 | 1108 |
| 50 | 30, 40, 50 | 5.2 | 30 | 1148.5 |
| Bullet Size (mm) | AOA (Degree) | Air Velocity (m/s) | Tapping Points (mm) | Area of the Bullet Head (mm2) |
|---|---|---|---|---|
| 30 mm | 30, 40, 50 | 5.2 | 30 | 629.5 |
| Angle of Attack (Degrees) | 30 mm (Simulation) | 40 mm (Simulation) | 50 mm (Simulation) | 30 mm (Experimental) | 40 mm (Experimental) |
|---|---|---|---|---|---|
| 30 | 0.000720 | 0.000820 | 0.003987 | 0.000732 | 0.000897 |
| 40 | 0.000825 | 0.002045 | 0.004091 | 0.000900 | 0.002990 |
| 50 | 0.001145 | 0.003235 | 0.008957 | 0.001681 | 0.003871 |
| Angle of Attack (Degrees) | 30 mm (Simulation) | 40 mm (Simulation) | 50 mm (Simulation) | 30 mm (Experimental) | 40 mm (Experimental) |
|---|---|---|---|---|---|
| 30 | 0.000170 | 0.000370 | 0.002287 | 0.000260 | 0.000463 |
| 40 | 0.000221 | 0.000444 | 0.005591 | 0.000349 | 0.000598 |
| 50 | 0.001545 | 0.002835 | 0.003051 | 0.002168 | 0.003309 |
| Angle of Attack (Degrees) | 30 mm (Simulation) | 30 mm (Experimental) |
|---|---|---|
| 30 | 0.000416 | 0.000598 |
| 40 | 0.000489 | 0.000672 |
| 50 | 0.000522 | 0.000921 |
| Normal Section | Dimpled Section |
|---|---|
| CFD | CFD |
| CL = 0.0002207 | CL = 0.000354 |
| CD = 0.00031 | CD = 0.000265 |
| Experimental | Experimental |
| CL = 0.000278 | CL = 0.000391 |
| CD = 0.00037 | CD = 0.000256 |
| Uncertainty | Uncertainty |
|
|
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.; Shah, I.; Aziz, S.; Waqas, M.; Zaman, U.K.u.; Jung, D.-W. Numerical and Experimental Analysis of Drag and Lift Forces on a Bullet Head. Aerospace 2022, 9, 816. https://doi.org/10.3390/aerospace9120816
Khan A, Shah I, Aziz S, Waqas M, Zaman UKu, Jung D-W. Numerical and Experimental Analysis of Drag and Lift Forces on a Bullet Head. Aerospace. 2022; 9(12):816. https://doi.org/10.3390/aerospace9120816
Chicago/Turabian StyleKhan, Abdullah, Imran Shah, Shahid Aziz, Muhammad Waqas, Uzair Khaleeq uz Zaman, and Dong-Won Jung. 2022. "Numerical and Experimental Analysis of Drag and Lift Forces on a Bullet Head" Aerospace 9, no. 12: 816. https://doi.org/10.3390/aerospace9120816
APA StyleKhan, A., Shah, I., Aziz, S., Waqas, M., Zaman, U. K. u., & Jung, D.-W. (2022). Numerical and Experimental Analysis of Drag and Lift Forces on a Bullet Head. Aerospace, 9(12), 816. https://doi.org/10.3390/aerospace9120816









