Numerical Simulations of Spray Combustion in Jet Engines
Abstract
:1. Introduction and Background
2. Computational Methodology
2.1. The Gas-Phase Large Eddy Simulation (LES) Methodology
2.2. LES Subgrid Flow Modeling
2.3. LES Combustion Modeling
2.4. Spray Combustion Models
2.5. Numerical Methods
3. Kerosene-Grade Fossil and Non-Fossil Jet Fuels
4. Combustion Chemistry
5. Results from LES
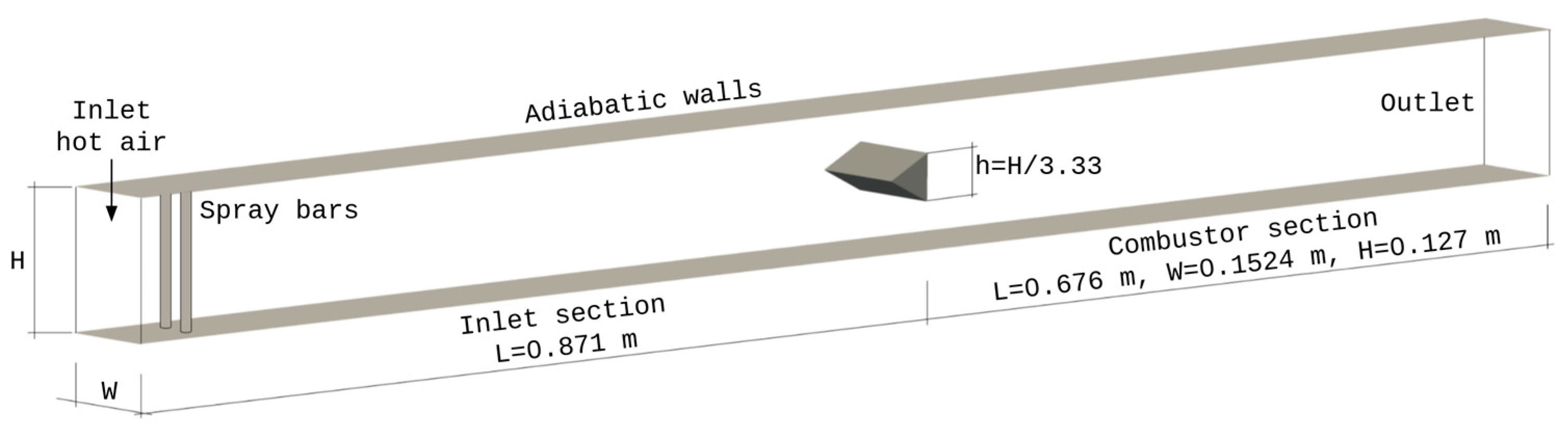
5.1. Air Force Research Laboratory (AFRL) Combustor
5.2. DLR Single-Cup Swirl Combustor
5.3. Helicopter Combustor
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrison, R.M.; Maisol, M.; Vardoulakis, S. Civil Aviation, Air Pollution and Human Health. Environ. Res. Lett. 2015, 10, 41001. [Google Scholar] [CrossRef] [Green Version]
- Kärcher, B. Aviation Produced Aerosols and Contrails. Surv. Geophys. 1999, 20, 113. [Google Scholar] [CrossRef]
- Lee, D.S.; Fahey, D.W.; Skowron, A.; Allen, M.R.; Burkhardt, U.; Chen, Q.; Doherty, S.J.; Freeman, S.; Forster, P.M.; Fuglestvedt, J.; et al. The Contribution of Global Aviation to Anthropogenic Climate Forcing for 2000 to 2018, 2021. Atm. Environ. 2021, 244, 117834. [Google Scholar] [CrossRef] [PubMed]
- Standard D1655; Standard Specification for Aviation Turbine Fuels. ASTM: West Conshohocken, PA, USA, 2022.
- Kumar, K.; Sung, C.-J. An Experimental Study of the Autoignition Characteristics of Conventional Jet Fuel/Oxidizer Mixtures: Jet-A and JP-8. Comb. Flame 2010, 157, 676. [Google Scholar] [CrossRef]
- Blakely, S.; Rye, L.; Wilson, C.W. Aviation Gas Turbine Alternative Fuels: A. Review. Proc. Comb. Inst. 2011, 33, 2863. [Google Scholar] [CrossRef]
- Braun-Unkhoff, M.; Riedel, U. Alternative Fuels in Aviation. CEAS Aeronaut. J. 2015, 6, 83. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Xin, Z.; Quan, H.; Corscadden, K.; Niu, H. An Overview on Performance Characteristics of Bio-Jet Fuels. Fuel 2019, 237, 916. [Google Scholar] [CrossRef]
- Kick, T.; Herbst, J.; Kathrodia, T.; Marquetand, J.; Braun-Unkhoff, M.; Riedel, U. An Experimental and Modeling Study of Burning Velocities of Possible Future Synthetic Jet Fuels. Energy 2012, 43, 111. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Hui, X.; Lin, Y.; Sung, C.-J. Recent Development in Studies of Alternative Jet Fuel Combustion: Progress, Challenges, and Opportunities. Ren. Sust. Energy Rev. 2016, 54, 120. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://www.icao.int/environmental-protetion/GFAAF/Pages/Conversion-processes.aspx (accessed on 13 October 2022).
- Available online: https://web.stanford.edu/group/haiwanglab/HyChem/fuels/C1_spec.html (accessed on 13 October 2022).
- Echekki, T.; Mastorakos, E. Turbulent Combustion Modeling, Fluid Mechanics and its Applications; Springer Science + Business Media: Berlin, Germany, 2011; Volume 95. [Google Scholar]
- Menon, S.; Fureby, C. Computational Combustion. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Faeth, G.M. Mixing, Transport and Combustion in Sprays. Prog. Energy Comb. Sci. 1987, 13, 293. [Google Scholar] [CrossRef]
- Giacomazzi, E.; Picchia, F.R.; Arcidiacono, N. On the Distribution of Lewis and Schmidt Numbers in Turbulent Flames. In Proceedings of the 30th Event of the Italian Section of the Combustion Institute, Ischia, Italy, 20–23 June 2007. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows; Springer Verlag: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather. Rev. 1963, 91, 99. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W. A Dynamic Subgrid-Scale Eddy Viscosity Model. Phys. Fluids A 1991, 3, 1760. [Google Scholar] [CrossRef] [Green Version]
- Yoshizawa, A. A Statistically-derived Subgrid-scale Kinetic Energy Model for the Large Eddy Simulation of Turbulent Flows. J. Phys. Soc. Jpn. 1985, 54, 2834. [Google Scholar] [CrossRef]
- Kim, W.-W.; Menon, S. A New Dynamic One Equation Subgrid-scale Model for Large Eddy Simulations. In Proceedings of the 19th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1995. AIAA 95-0356. [Google Scholar]
- Wang, Z.J.; Li, Y. A Mathematical Analysis of Scale Similarity. Com. Comp. Phys. 2017, 21, 149. [Google Scholar] [CrossRef]
- Cook, A.W.; Riley, J.J. A Subgrid Model for Equilibrium Chemistry in Turbulent Flows. Phys. Fluids 1994, 6, 2868. [Google Scholar] [CrossRef]
- Branley, N.; Jones, W.P. Large Eddy Simulation of a Turbulent Non-Premixed Flame. Comb. Flame 2001, 127, 1914. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Fureby, C. Large Eddy Simulation of Combustion Instabilities in a Jet-Engine Afterburner Model. Comb. Sci. Technol. 2000, 161, 213. [Google Scholar] [CrossRef]
- Hawkes, E.R.; Cant, R.S. Implications of a Flame Surface Density Approach to Large Eddy Simulation of Premixed Turbulent Combustion. Comb. Flame 2001, 126, 1617. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Gosman, A.D.; Fureby, C. Application of a Flame-Wrinkling LES Combustion Model to a Turbulent Shear Layer Formed at a Rearward Facing Step. Proc. Comb. Inst. 1998, 27, 899. [Google Scholar] [CrossRef]
- Veynante, D. Investigation of Flame Surface Density Modeling for Large Eddy Simulation of Turbulent Premixed Flames by Comparison with a Prescribed Reference Solution. Comb. Flame 2022, 239, 111663. [Google Scholar] [CrossRef]
- Bai, X.-S.; Fureby, C. Non-Premixed and Partially Premixed Combustion. In Turbulent Combustion; Swaminathan, N., Bai, X.-S., Brethouwer, G., Haugen, N.E.L., Fureby, C., Eds.; Cambridge University Press: Cambridge, UK, 2019; p. 162. [Google Scholar]
- Ma, T.; Stein, O.T.; Chakraborty, N.; Kempf, A. A Posteriori Testing of Algebraic Flame Surface Density Models for LES. Comb. Theory Model. 2013, 17, 431. [Google Scholar] [CrossRef]
- Colin, O.; Ducros, F.; Veynante, D.; Poinsot, T. A Thickened Flame Model for Large Eddy Simulation of Turbulent Premixed Combustion. Phys. Fluids. 2000, 12, 1843. [Google Scholar] [CrossRef]
- Fureby, C. LES Modeling of Combustion for Propulsion Applications. Phil. Trans. R. Soc. A 2009, 367, 2957. [Google Scholar] [CrossRef] [PubMed]
- Giacomazzi, E.; Bruno, C.; Favini, B. Fractal Modeling of Turbulent Combustion. Comb. Theory Model. 2000, 4, 391. [Google Scholar] [CrossRef]
- Sabelnikov, V.; Fureby, C. LES Combustion Modeling for High Re Flames using a Multi-phase Analogy. Comb. Flame 2013, 160, 83. [Google Scholar] [CrossRef]
- Jones, W.P.; Marquis, A.-J.; Wang, F. Large Eddy Simulation of a Premixed Propane Turbulent Bluff Body Flame using the Eulerian Stochastic Field Method. Fuel 2015, 140, 514. [Google Scholar] [CrossRef]
- Menon, S. Subgrid Combustion Modeling for Large Eddy Simulations. Int. J. Engine Res. 2000, 1, 209. [Google Scholar] [CrossRef]
- Bulat, G.; Fedina, E.; Fureby, C.; Meier, W.; Stopper, U. Reacting Flow in an Industrial Gas Turbine Combustor: LES and Experimental Analysis. Proc. Comb. Inst. 2014, 35, 3175. [Google Scholar] [CrossRef]
- Nilsson, T.; Zhong, S.; Fureby, C. LES of H2-air Jet Combustion in High Enthalpy Supersonic Crossflow. Phys. Fluids 2021, 33, 35133. [Google Scholar] [CrossRef]
- Magnussen, B.F. On the Structure of Turbulence and Generalized Eddy Dissipation Concept for Chemical Reactions in Turbulent Flow. In Proceedings of the 19th Aerospace Sciences Meeting, St. Louis, MO, USA, 12–15 January 1981. AIAA 1981-0042. [Google Scholar]
- Chomiak, J. A Possible Propagation Mechanism of Turbulent Flames at High Reynolds Numbers. Comb. Flame 1970, 15, 319. [Google Scholar] [CrossRef]
- Batchelor, G.K.; Townsend, A.A. The Nature of Turbulent Motion at Large Wave-numbers. Proc. Roy. Soc. London A 1949, 199, 238. [Google Scholar]
- Dukowicz, J.K. A Particle-Fluid Numerical Model for Liquid Sprays. J. Comp. Phys. 1980, 35, 229. [Google Scholar] [CrossRef]
- Apte, S.V.; Goroskhovski, M.; Moin, P. LES of Atomizing Spray with Stochastic Modeling of Secondary Breakup. Int. J. Multiph. Flow 2003, 29, 1503. [Google Scholar] [CrossRef]
- Faeth, G.M. Evaporation and Combustion of Sprays. Prog. Energy Comb. Sci. 1983, 9, 1. [Google Scholar] [CrossRef]
- Faeth, G.M. Spray Combustion Phenomena. Proc. Comb. Inst. 1996, 26, 1593. [Google Scholar] [CrossRef]
- Reitz, R.D. Mechanisms of Atomization Processes in High-Pressure Vaporizing Sprays. At. Spray Technol. 1987, 3, 309. [Google Scholar]
- Reitz, R.D.; Diwakar, R. Effect of Drop Breakup on Fuel Sprays. SAE Technol. Pap. 1986, 95, 860469. [Google Scholar]
- Crowe, C.T.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press LLC: Boca Raton, FL, USA, 1998. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from Drops. Chem. Eng. Prog. 1952, 48, 141. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to CFD using Object Oriented Techniques. Comp. Phys. 1997, 12, 620. [Google Scholar] [CrossRef]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1973. [Google Scholar]
- Issa, R.I. Solution of the Implicitly Discretized Fluid Flow Equations by Operator Splitting. J. Comp. Phys. 1986, 62, 40. [Google Scholar] [CrossRef]
- Strang, G. On the Construction and Comparison of Difference Schemes. SIAM J. Numer. Anal. 1968, 506. [Google Scholar] [CrossRef] [Green Version]
- Rosenbrock, H.H. Some General Implicit Processes for the Numerical Solution of Differential Equations. Comput. J. 1963, 5, 329. [Google Scholar] [CrossRef] [Green Version]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Handbook of Aviation Fuels, Society of Automotive Engineers; Report No. 635; Coordinating Research Council, SAE: Alpharetta, GA, USA, 2004.
- Maurice, L.Q.; Lander, H.; Edwards, T.; Harrison, W.E. Advanced Aviation Fuels: A Look Ahead via a Historical Perspective. Fuel 2001, 80, 747. [Google Scholar] [CrossRef]
- Bowden, J.N.; Westbrook, S.R.; LePera, M.E. Jet Kerosene Fuels for Military Diesel Application, SAE Transactions. J. Fuels Lubr. 1989, 98, 810. [Google Scholar]
- Aicholtz, J.; Holland, T.; Andac, G.; Boehm, R.; Seto, S.; Lewis, R.; Williams, R.; Ludwig, D.; James, S.; Mosbacher, M.; et al. Development of Combustion Rules and Tools for the Characterization of Alternative Fuels. AFRL-RZ-WP-TR-2010-2134 MACCCR 3rd Annual Fuels Summit Princeton, NJ, 20 September 2010. Available online: https://kinetics.nist.gov/RealFuels/macccr/macccr2010/MACCCR_2010_Colket.pdf (accessed on 13 October 2022).
- Colket, M.; Heyne, J.; Rumizen, M.; Gupta, M.; Edwards, T.; Roquemore, W.M.; Andac, R.; Boehm, R.; Lovett, J.; Williams, R.; et al. Overview of the National Jet Fuels Combustion Program. AIAA J. 2017, 55, 1087. [Google Scholar] [CrossRef]
- Edwards, T. Reference Jet Fuels for Combustion Testing. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TA, USA, 9–13 January 2017. AIAA 2017-0146. [Google Scholar]
- Yao, T.; Pei, Y.; Zhong, B.-J.; Som, S.; Lu, T.; Luo, K.H. A Compact Skeletal Mechanism for n-dodecane with Optimized Semi-Global Low-Temperature Chemistry for Diesel Engine Simulations. Fuel 2017, 191, 339. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xu, R.; Wang, K.; Bowman, C.T.; Davidson, D.F.; Hanson, R.K.; Brezinsky, K.; Egolfopoulos, F.N. A Physics-Based Approach to Modeling Real-Fuel Combustion Chemistry—I. Evidence from Experiments, and Thermodynamic, Chemical Kinetic and Statistical Considerations. Comb. Flame 2018, 193, 502. [Google Scholar] [CrossRef]
- Kumar, K.; Sung, C.-J. Laminar Flame Speeds and Extinction Limits of Preheated n-decane/O2/N2 and n-dodecane/O2/N2 Mixtures. Comb. Flame 2007, 151, 209. [Google Scholar] [CrossRef]
- Xu, R.; Wang, K.; Banerjee, S.; Shao, J.; Parise, T.; Zhu, Y.; Wang, S.; Movaghar, A.; Lee, D.J.; Zhao, R.; et al. A Physics-Based Approach to Modeling Real-Fuel Combustion Chemistry—II. Reaction Kinetic Models of Jet and Rocket Fuels. Comb. Flame 2018, 193, 520. [Google Scholar] [CrossRef]
- Dooley, S.; Hee Won, S.; Heyne, J.; Farouk, T.; Ju, Y.; Dryer, F.; Kumar, K.; Hui, X.; Sung, C.-J.; Wang, H.; et al. The Experimental Evaluation of a Methodology for Surrogate Fuel Formulation to Emulate Gas Phase Combustion Kinetic Phenomena. Comb. Flame 2012, 159, 1444. [Google Scholar] [CrossRef]
- Hui, X.; Sung, C.-J. Laminar Flame Speeds of Transportation-relevant Hydrocarbons and Jet Fuels at Elevated Temperatures and Pressures. Fuel 2013, 109, 191. [Google Scholar] [CrossRef]
- Kumar, K.; Sung, C.-J.; Hui, X. Laminar Flame Speeds and Extinction Limits of Conventional and Alternative Jet Fuels. Fuel 2011, 90, 1004. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, R.; Xu, R.; Egolfopoulos, F.N.; Wang, H. Binary Diffusion Coefficients and Non-premixed Flames Extinction of Long-chain Alkanes. Proc. Comb. Inst. 2017, 36, 1523. [Google Scholar] [CrossRef]
- Mao, Y.; Raza, M.; Wu, Z.; Zhu, J.; Yu, L.; Wang, S.; Zhu, L.; Lu, X. An Experimental Study of n-dodecane and the Development of an Improved Kinetic Model. Comb. Flame 2020, 212, 388. [Google Scholar] [CrossRef]
- Ansys Chemkin-Pro; Ansys Inc.: Canonsburg, PA, USA, 2016.
- Paxton, B.T.; Fugger, C.A.; Tomlin, A.S.; Caswell, A.W. Experimental Investigation of Fuel Type on Combustion Instabilities in a Premixed Bluff- Body Combusto. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. AIAA 2020-0174. [Google Scholar]
- Fugger, C.A.; Yi, T.; Sykes, J.P.; Rankin, B.; Miller, J.D.; Gord, J.R. The Structure and Dynamics of a Bluff-Body Stabilized Premixed Reacting Flow. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. AIAA 2018-1190. [Google Scholar]
- Fugger, C.A.; Roy, S.; Caswell, A.W.; Rankin, B.; Gord, J.R. Structure and Dynamics of CH2O, OH, and the Velocity Field of a Confined Bluff-body Premixed Flame, using Simultaneous PLIF and PIV at 10 kHz. Proc. Comb. Inst. 2019, 37, 1461. [Google Scholar] [CrossRef]
- Sjunesson, A.; Nelson, C.; Max, E. LDA Measurements of Velocities and Turbulence in a Bluff Body Stabilized Flame; Aero Technical Report S-461 81; Volvo: Gothenburg, Sweden, 1991. [Google Scholar]
- Sjunesson, A.; Henriksson, R.; Löfström, C. CARS Measurements and Visualization of Reacting Flows in Bluff Body Stabilized Flame. In Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. AIAA 1992–3650. [Google Scholar]
- Fureby, C. The Volvo Validation Rig—A Comparative Study of Large Eddy Simulation Combustion Models at Different Operating Conditions. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January. AIAA 2018–0149. [Google Scholar]
- Fureby, C. A Large Eddy Simulation (LES) Study of the VOLVO and AFRL Bluff Body Combustors at Different Operating Conditions. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. AIAA 2019-0453. [Google Scholar]
- Erickson, R.R.; Soteriou, M.C.; Mehta, P.G. The Influence of Temperature Ratio on the Dynamics of the Bluff Body Stabilized Flames. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. AIAA 2006-0753. [Google Scholar]
- Ehn, A. Towards Quantitative Diagnostics using Short-Pulse Laser Techniques. Ph.D. Thesis, Division of Combustion Physics, Faculty of Engineering, Lund University, Lund, Sweden, 2012. [Google Scholar]
- Behrendt, T.; Frodermann, M.; Hassa, C.; Heinze, J.; Lehmann, B.; Stursberg, K. Optical Measurements of Spray Combustion in a Single Sector Combustor from a Practical Fuel Injector at Higher Pressures. In Proceedings of the Symposium on Gas Turbine Engine Combustion, Emissions and Alternative Fuels, Lisboa, Portugal, 12–16 October 1999. [Google Scholar]
- Meier, U.; Heinze, J.; Freitag, S.; Hassa, C. Spray and Flame Structure of a Generic Injector at Aero-engine Conditions. J. Eng. Gas Turbines Power 2012, 134, 31503. [Google Scholar] [CrossRef]
- Jones, W.P.; Marquis, A.J.; Vogiatzaki, K. Large-Eddy Simulation of Spray Combustion in a Gas Turbine Combustor. Comb. Flame 2014, 161, 222. [Google Scholar] [CrossRef]
- Andreini, A.; Bertini, D.; Mazzei, L.; Puggelli, S. Assessment of a Numerical Procedure for Scale Resolved Simulations of Turbulent Spray Flames. In Proceedings of the XXXIX Meeting of the Italian Section of the Combustion Institute, Naples, Italy, 4–6 July 2016. [Google Scholar]
- Puggelli, S.; Paccati, S.; Bertini, D.; Mazzei, L.; Giusti, A.; Andreini, A. Multi-coupled Numerical Simulations of the DLR Generic Single Sector Combustor. Comb. Sci. Technol. 2018, 190, 1409. [Google Scholar] [CrossRef]
- Åkerblom, A. The Impact of Reaction Mechanism Complexity in LES of Liquid Kerosene Spray Combustion. In Proceedings of the 33rd Congress of the International Council of the Aeronautical Sciences, Stockholm, Sweden, 4–9 September 2022. [Google Scholar]
- Von Kármán, T. Mechanische Ähnlichkeit und Turbulenz, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Fachgruppe 1. Mathematik 1930, 5, 58. [Google Scholar]
- Yamashita, H.; Shimada, M.; Takeno, T. A Numerical Study on Flame Stability at the Transition Point of Jet Diffusion Flames. Proc. Comb. Inst. 1996, 26, 27. [Google Scholar] [CrossRef]
- PT6—Descriptive Course and Guide to Troubleshooting; United Turbine Corp.: MIAMI, FL, USA, 2022.
- Boudier, G.; Gicquel, L.Y.M.; Poinsot, T.J. Effects of Mesh Resolution on Large Eddy Simulation of Reacting Flows in Complex Geometry Combustors. Comb. Flame 2008, 155, 196. [Google Scholar] [CrossRef]
- Poinsot, T.J.; Lele, S.K. Boundary Conditions for Direct Simulations of Compressible Viscous Flows. J. Comp. Phys. 1992, 101, 104. [Google Scholar] [CrossRef]
- Taylor, J.W.R. Jane’s All the World’s Aircraft 1962–63; McGraw-Hill Book Company: New York, NY, USA, 1962. [Google Scholar]
- Available online: https://www.aviationpros.com/home/article/10381485/pt6-fuel-nozzles (accessed on 13 October 2022).
- Sivathanu, Y.; Lim, J.; Muliadi, A.; Nitulescu, O.; Shieh, T. Estimating Velocity in Gasoline Direct Injection Sprays using Statistical Pattern Imaging Velocimetry. Int. J. Spray and Comb. Dyn. 2019, 11, 1. [Google Scholar] [CrossRef]
- Ballal, D.R.; Lefebvre, A.H. Gas Turbine Combustion: Alternative Fuels and Emissions, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Boudier, G.; Gicquel, L.Y.M.; Poinsot, T.J.; Bissières, D.; Bérat, C. Comparison of LES, RANS and Experiments in an Aeronautical Gas Turbine Combustion Chamber. Proc. Comb. Inst. 2007, 31, 3075. [Google Scholar] [CrossRef]

 ), Jet A (
), Jet A ( ), and C1 (
), and C1 ( ). Lines denote the numerical predictions, while symbols the experimental data from Kumar et al., [65] (▲), Xu et al. [66] (■, ■), Dooley et al. [67] (▼), Hui et al. [68] (
). Lines denote the numerical predictions, while symbols the experimental data from Kumar et al., [65] (▲), Xu et al. [66] (■, ■), Dooley et al. [67] (▼), Hui et al. [68] ( ), Kumar et al. [69] (●), Liu et al. [70] (►), and Mao et al. [71] (◄).
), Kumar et al. [69] (●), Liu et al. [70] (►), and Mao et al. [71] (◄).
 ), Jet A (
), Jet A ( ), and C1 (
), and C1 ( ). Lines denote the numerical predictions, while symbols the experimental data from Kumar et al., [65] (▲), Xu et al. [66] (■, ■), Dooley et al. [67] (▼), Hui et al. [68] (
). Lines denote the numerical predictions, while symbols the experimental data from Kumar et al., [65] (▲), Xu et al. [66] (■, ■), Dooley et al. [67] (▼), Hui et al. [68] ( ), Kumar et al. [69] (●), Liu et al. [70] (►), and Mao et al. [71] (◄).
), Kumar et al. [69] (●), Liu et al. [70] (►), and Mao et al. [71] (◄).




 ), Jet A (
), Jet A ( ), C1 (
), C1 ( ).
).
 ), Jet A (
), Jet A ( ), C1 (
), C1 ( ).
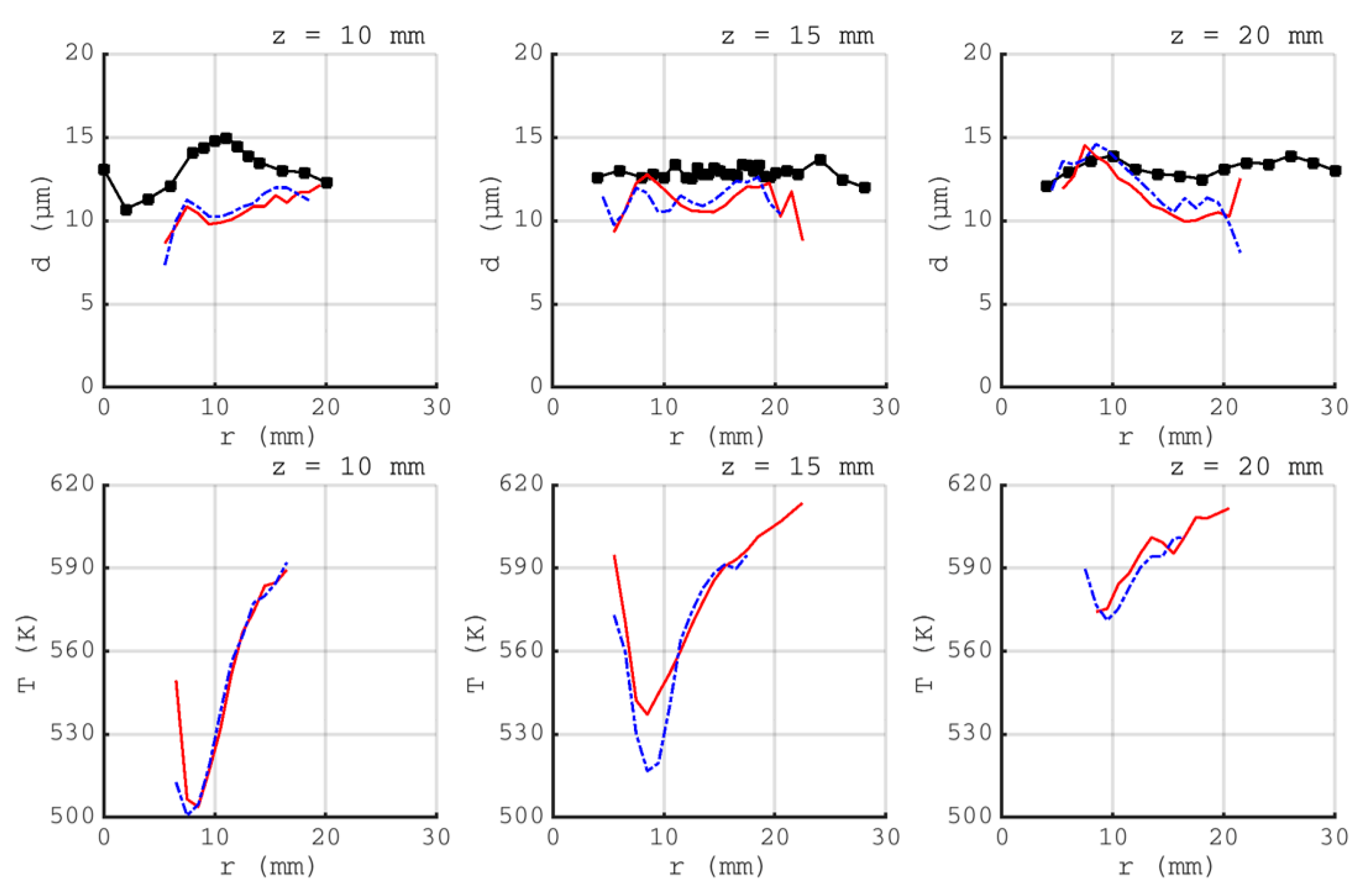
).
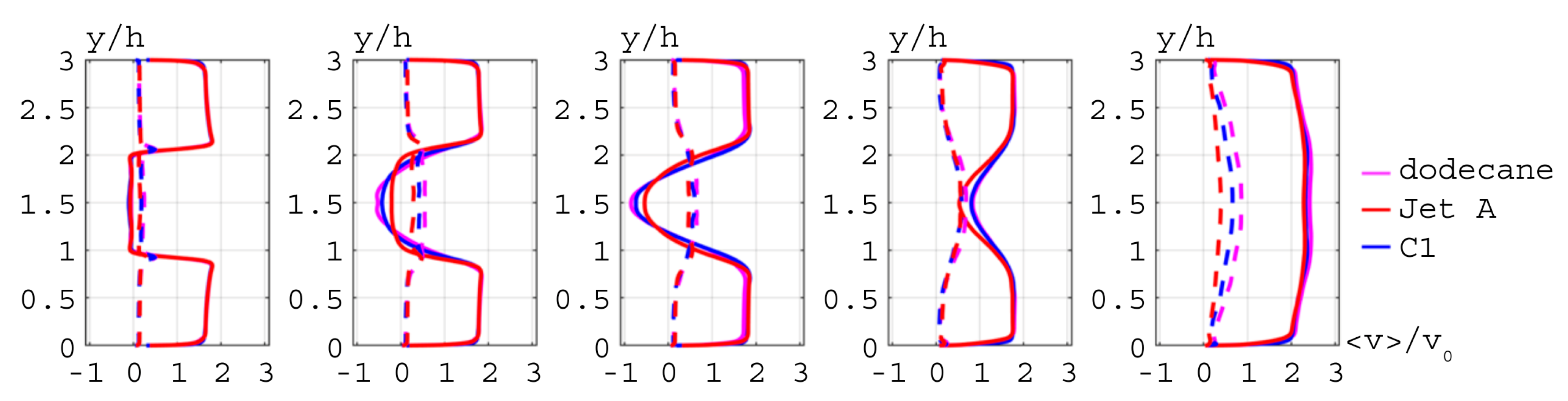
 ), Jet A (
), Jet A ( ), and C1 (
), and C1 ( ).
).
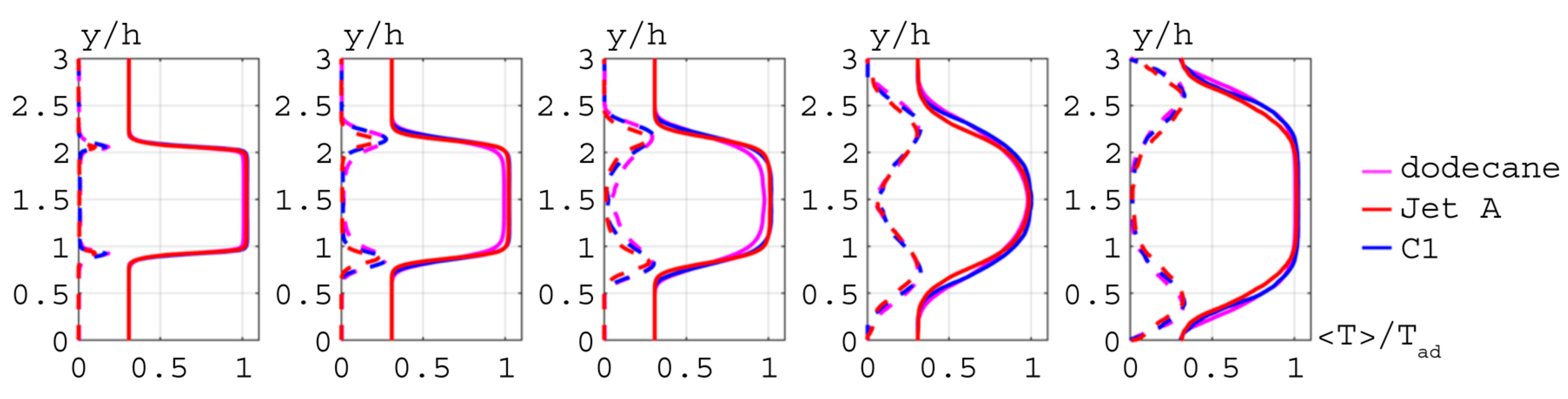
 ), Jet A (
), Jet A ( ), and C1 (
), and C1 ( ).
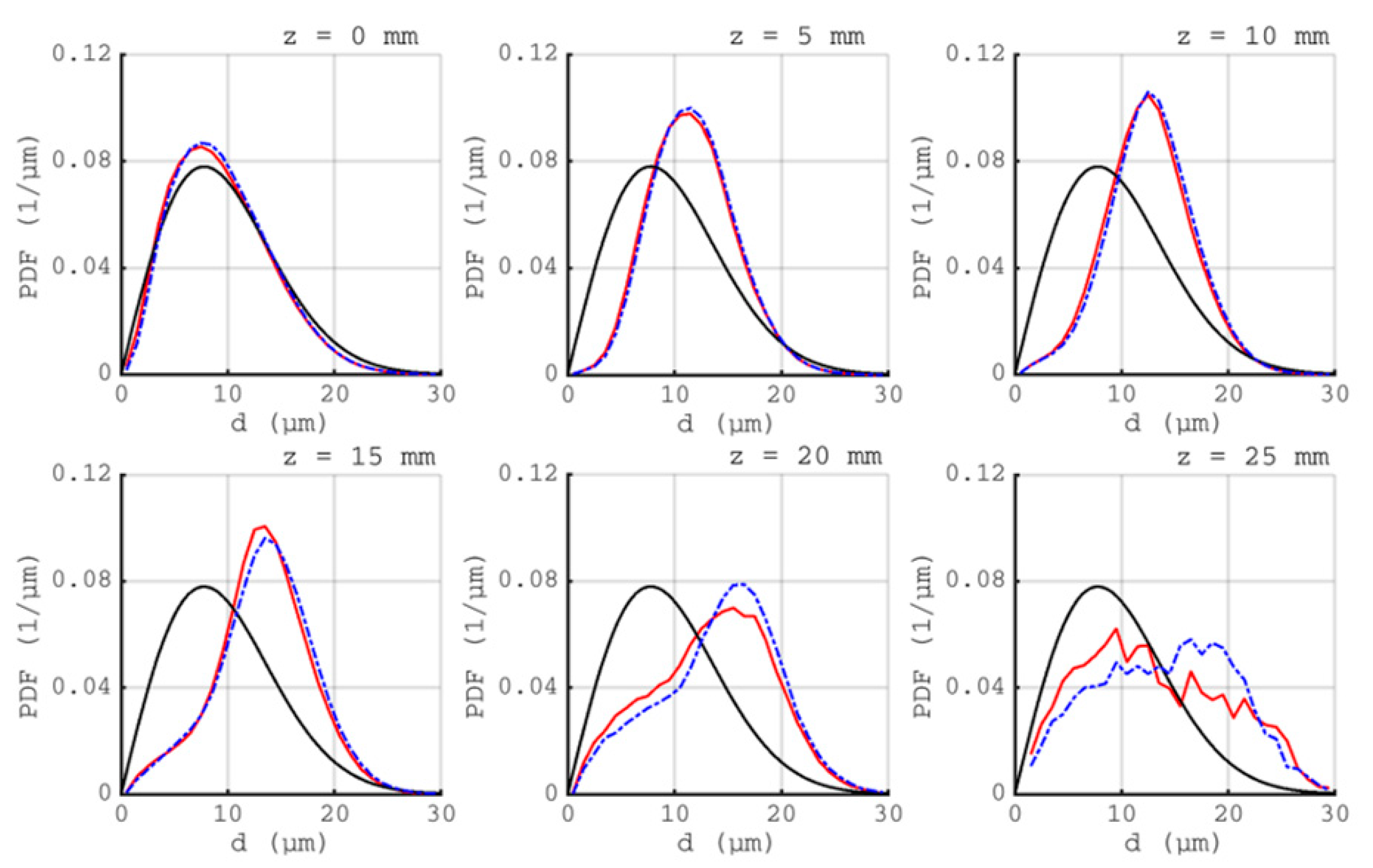
).
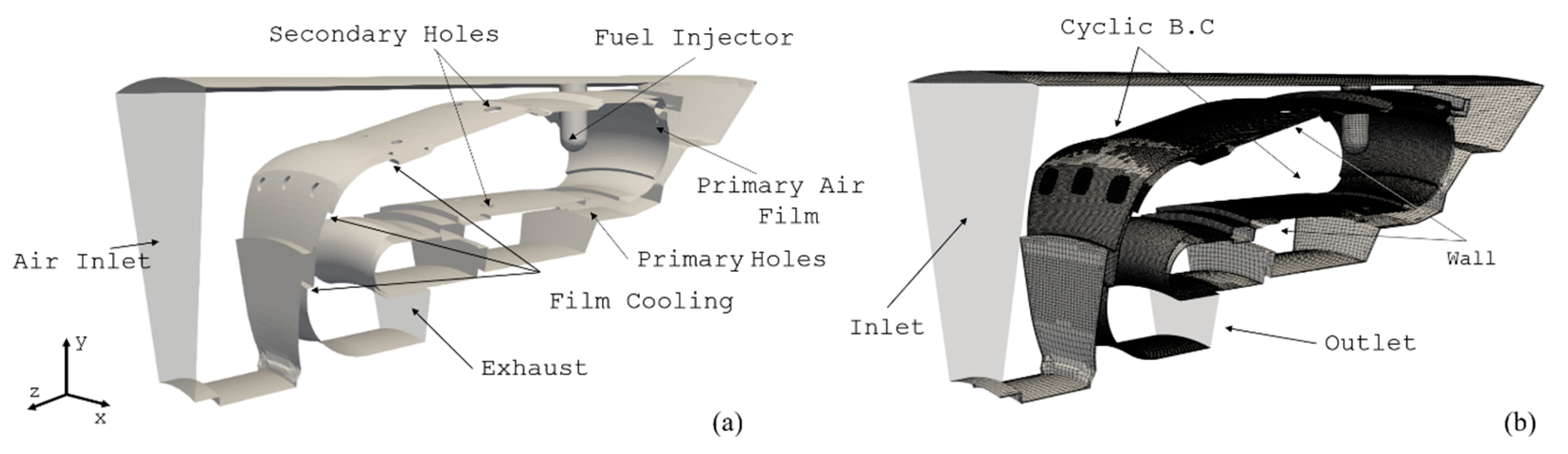
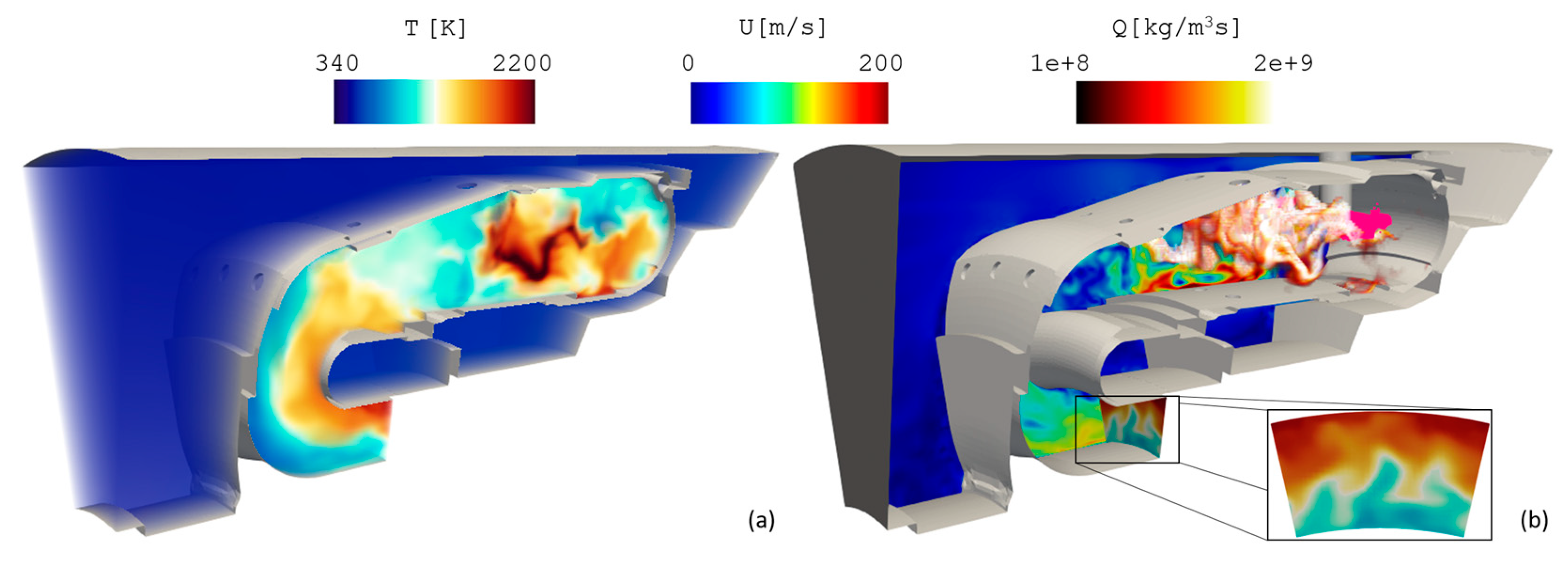

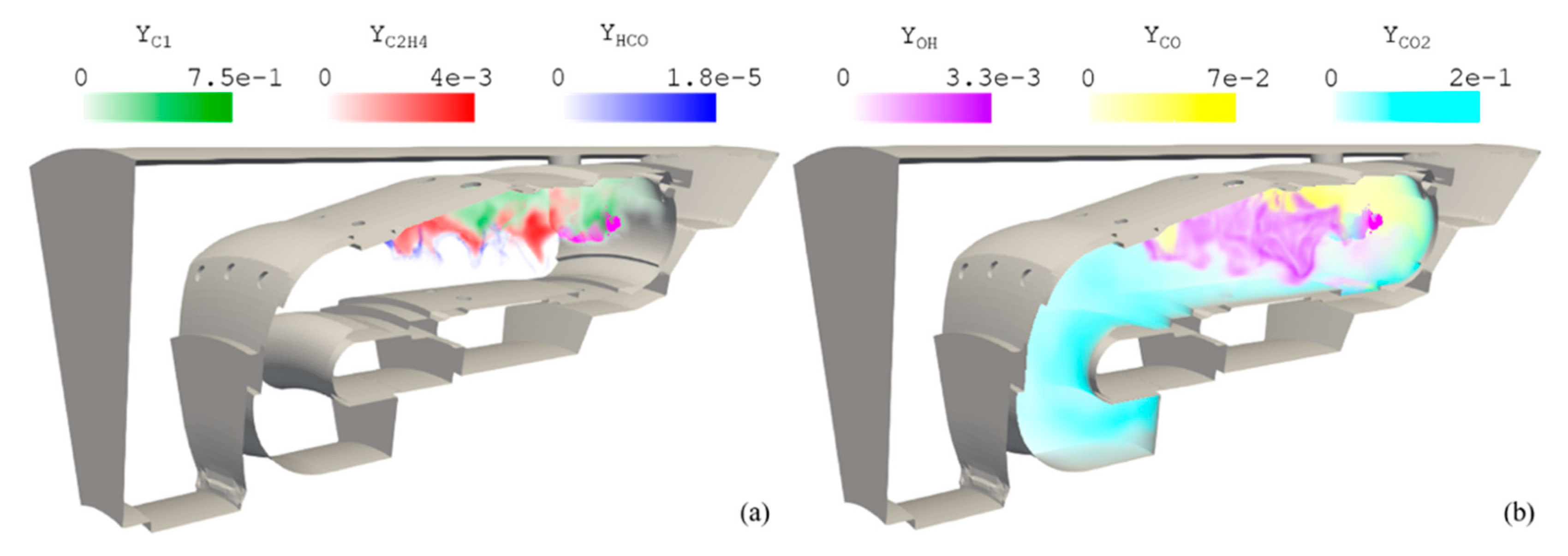
 ) and C1 (
) and C1 ( ).
).
 ) and C1 (
) and C1 ( ).
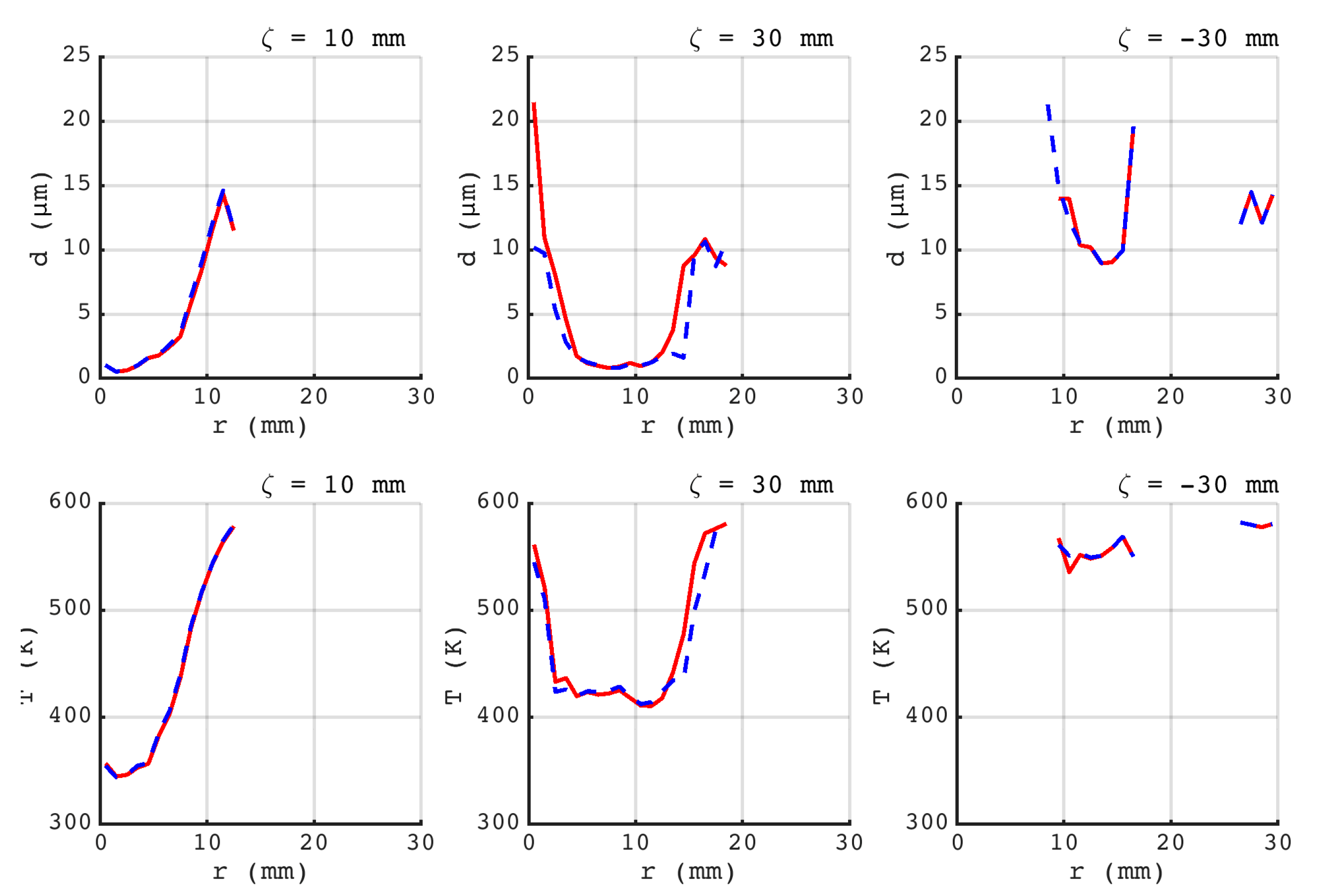
).
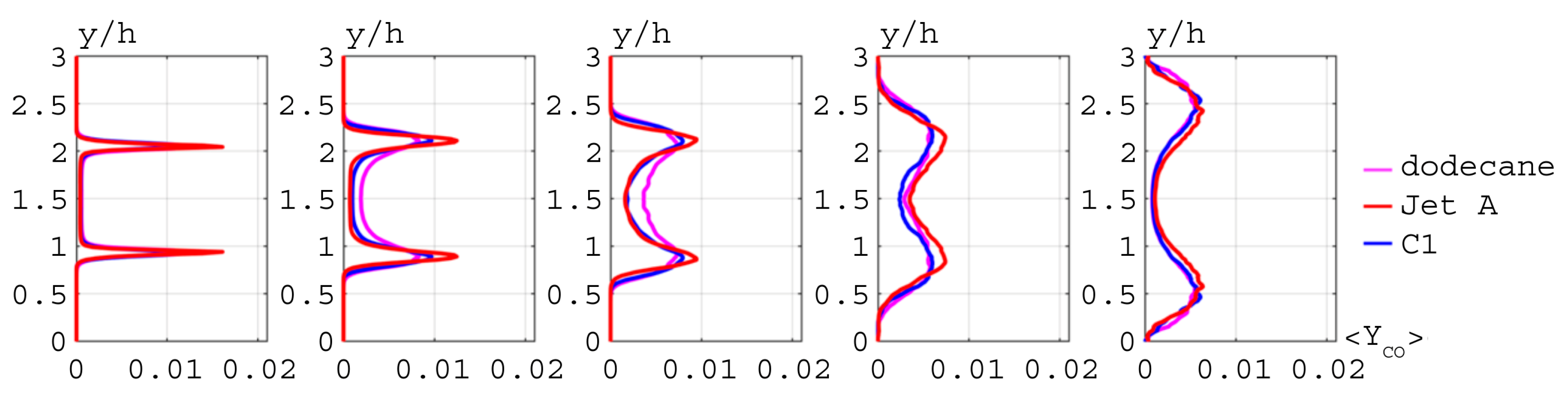
 ), Jet A (
), Jet A ( ), C1 (
), C1 ( ).
).
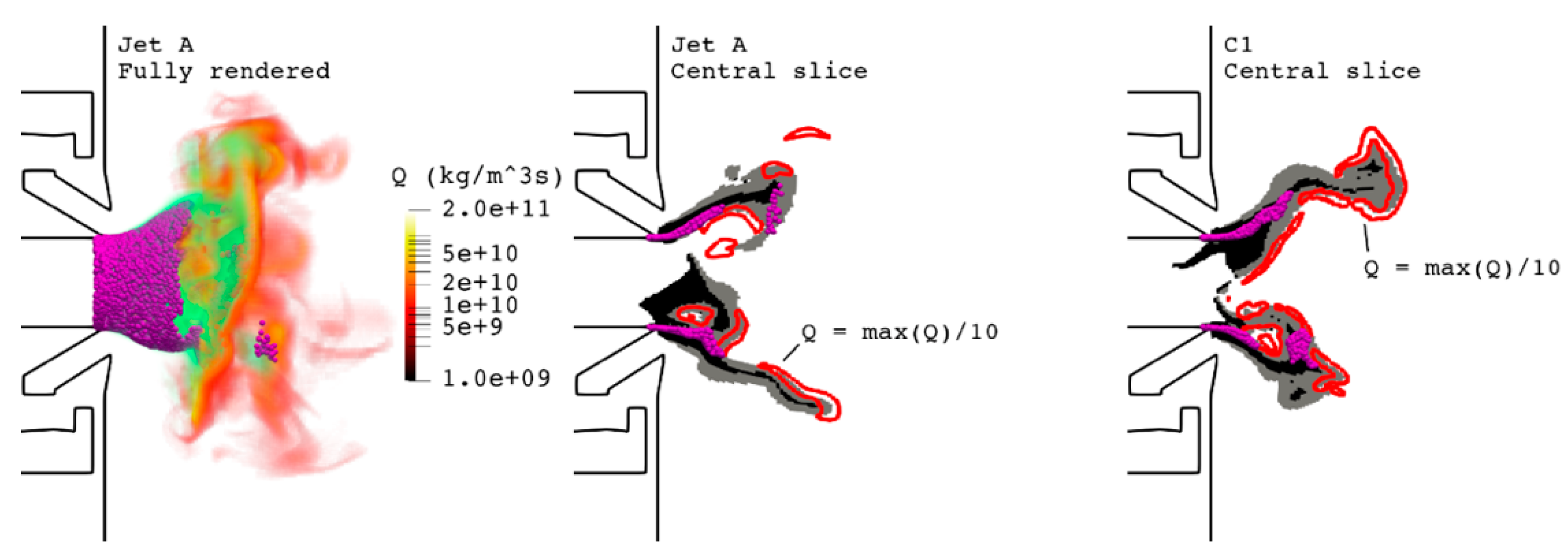
 ), Jet A (
), Jet A ( ), C1 (
), C1 ( ).
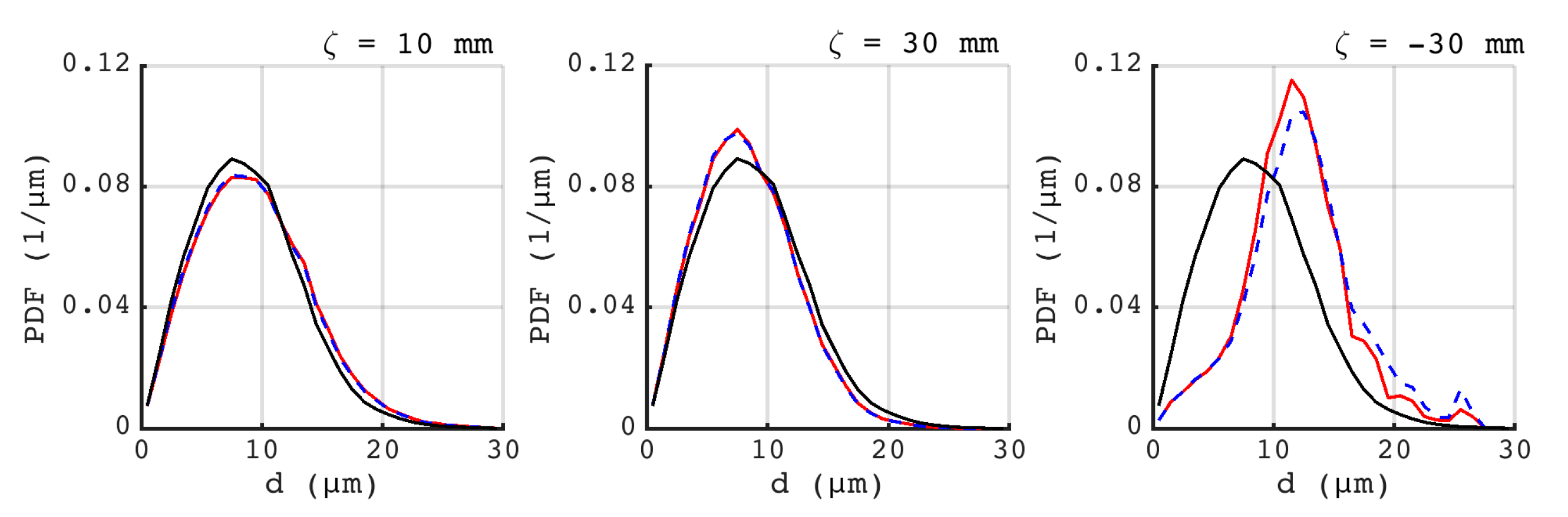
).
| Property | n-Dodecane | Jet A, A2 (POSF 10325) | JP5, A3 (POSF 10289) | C1 (POSF 11498) | C4 (POSF 12344) |
|---|---|---|---|---|---|
| Density (kg/m3) | 749 | 803 | 827 | 760 | 760 |
| Viscosity @ 20 °C (cSt) | 1.34 | 4.5 | 6.5 | 4.9 | 3.9 |
| Surface tension (mN/m) | 22.1 | 25.8 | 26.1 | 22.4 | — |
| Aromatics (vol. %) | 0 | 17.0 | 18.0 | 1.0 | 2.3 |
| Heat of combustion (MJ/kg) | 46.5 | 43.3 | 43.1 | 44.2 | 43.8 |
| H content (wt. %) | 15.2 | 14.0 | 13.7 | 15.3 | 15.5 |
| Cetane number | 74.7 | 48.3 | 39.2 | 17.1 | 28 |
| Inlet Air Velocity (m/s) | 10.2 |
| Inlet Air Temperature (K) | 490 |
| Fuel Mass Rate (kg/s) | 0.04885 |
| Injection Speed (m/s) | 50.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Åkerblom, A.; Pignatelli, F.; Fureby, C. Numerical Simulations of Spray Combustion in Jet Engines. Aerospace 2022, 9, 838. https://doi.org/10.3390/aerospace9120838
Åkerblom A, Pignatelli F, Fureby C. Numerical Simulations of Spray Combustion in Jet Engines. Aerospace. 2022; 9(12):838. https://doi.org/10.3390/aerospace9120838
Chicago/Turabian StyleÅkerblom, Arvid, Francesco Pignatelli, and Christer Fureby. 2022. "Numerical Simulations of Spray Combustion in Jet Engines" Aerospace 9, no. 12: 838. https://doi.org/10.3390/aerospace9120838
APA StyleÅkerblom, A., Pignatelli, F., & Fureby, C. (2022). Numerical Simulations of Spray Combustion in Jet Engines. Aerospace, 9(12), 838. https://doi.org/10.3390/aerospace9120838







