Atmospheric Disturbance Modelling for a Piloted Flight Simulation Study of Airplane Safety Envelope over Complex Terrain
Abstract
:1. Introduction
2. Stochastic Method of Atmospheric Turbulence Modelling
- low-altitude , wherewith the typical values of the wind speed being 15 knots for light turbulence, 30 knots for moderate turbulence, 45 knots for severe turbulence [47];
- between low and medium/high altitudes 1000 2000 , where turbulence quantities are determined by linearly interpolating between the values from the low altitude model at 1000 and the values from the high altitude model at 2000 [47].
3. Numerical Procedure
3.1. Governing Equations
3.2. Turbulence Closure
3.2.1. Deardorff Subgrid-Scale Model
3.2.2. Dynamic Subgrid-Scale Model
3.3. Discretization and Numerics
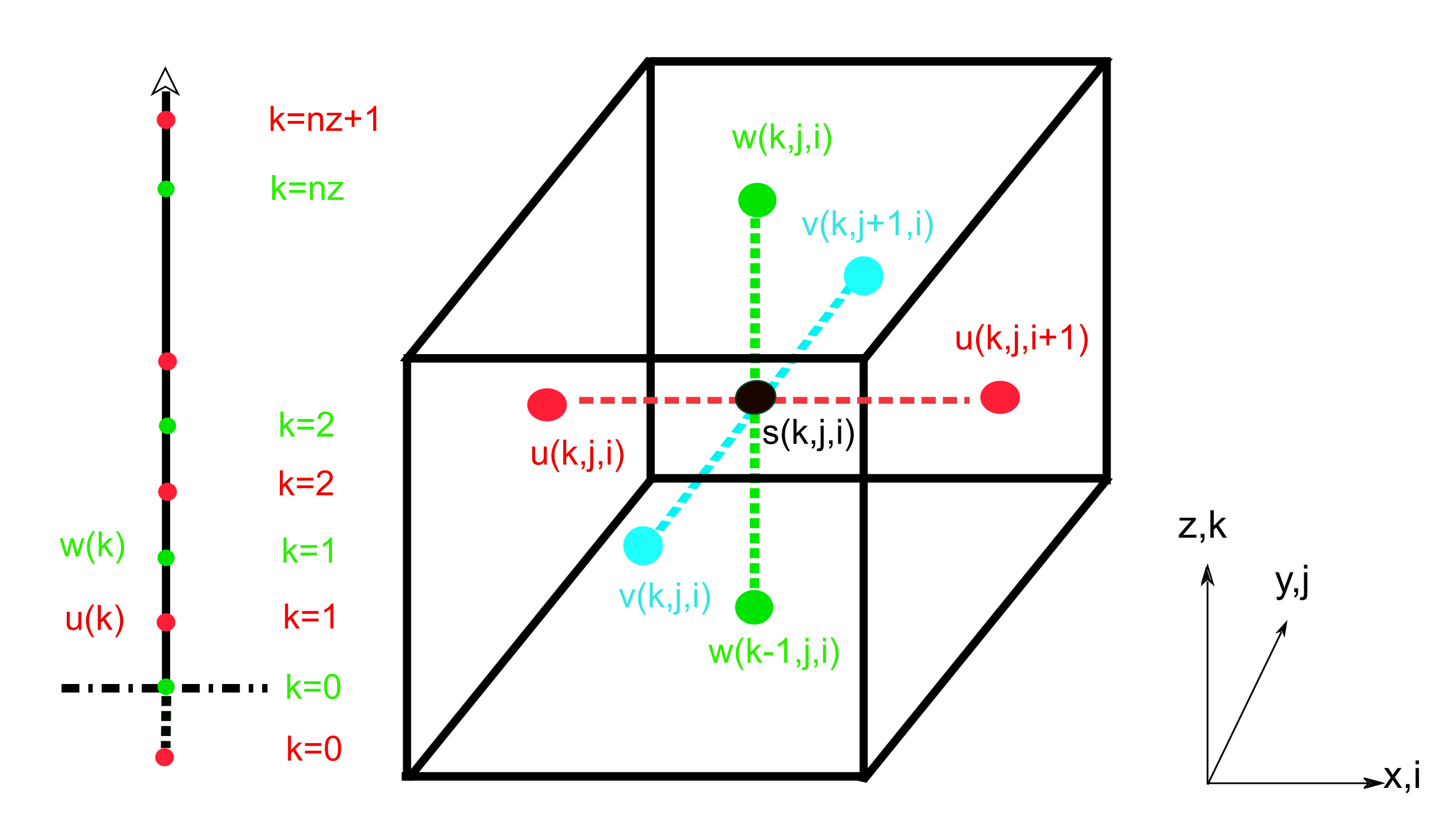
3.3.1. Numerical Grid
3.3.2. Numerical Scheme
3.3.3. Pressure Solver
3.4. Boundary Conditions
3.4.1. Topography and Surface Boundary Condition
- (i)
- grid cells in free atmosphere without adjacent solid surfaces,
- (ii)
- grid cells within orography,
- (iii)
- grid cells adjacent to solid surfaces, where a local surface layer is assumed.
3.4.2. Mesoscale Nesting and Synthetic Turbulence Generation
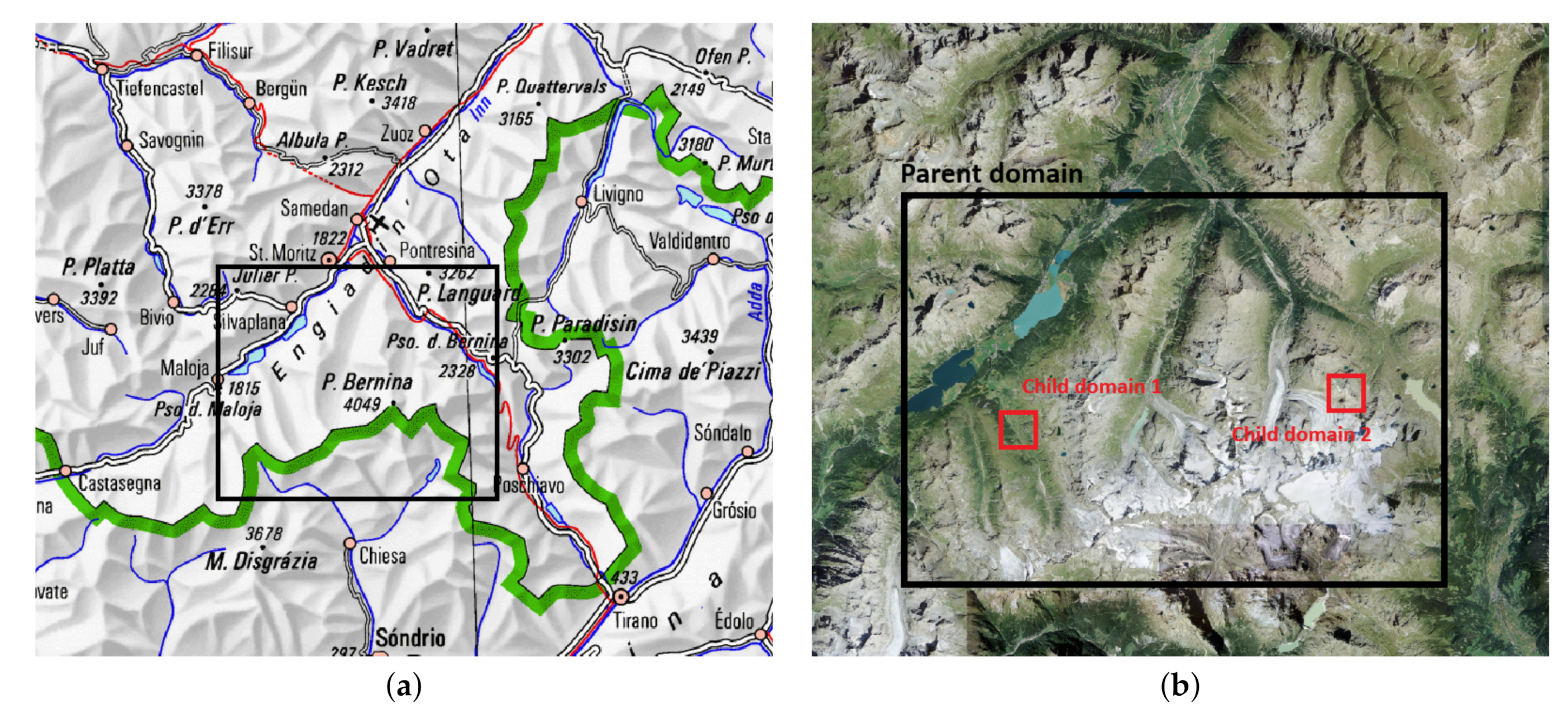
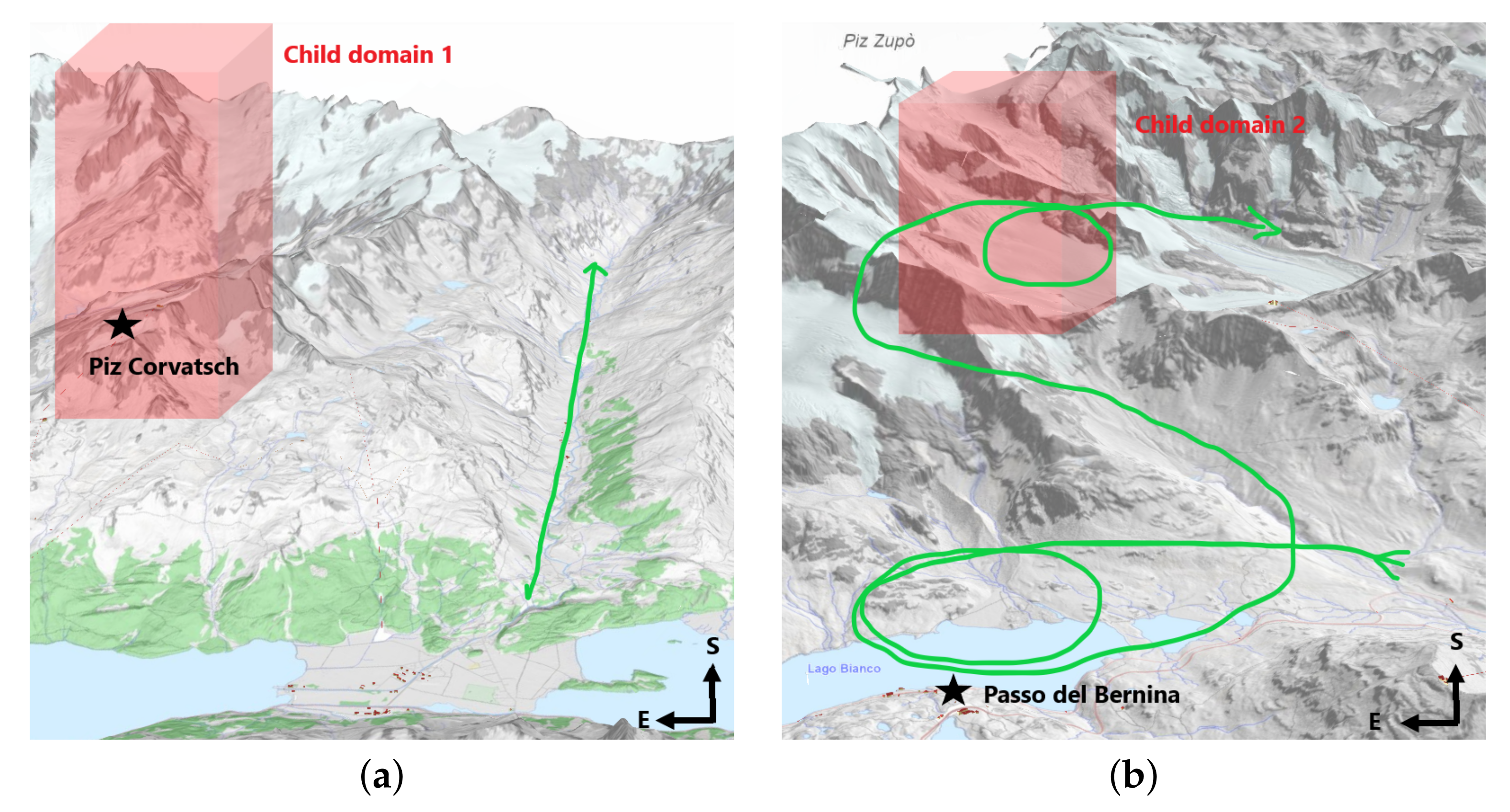
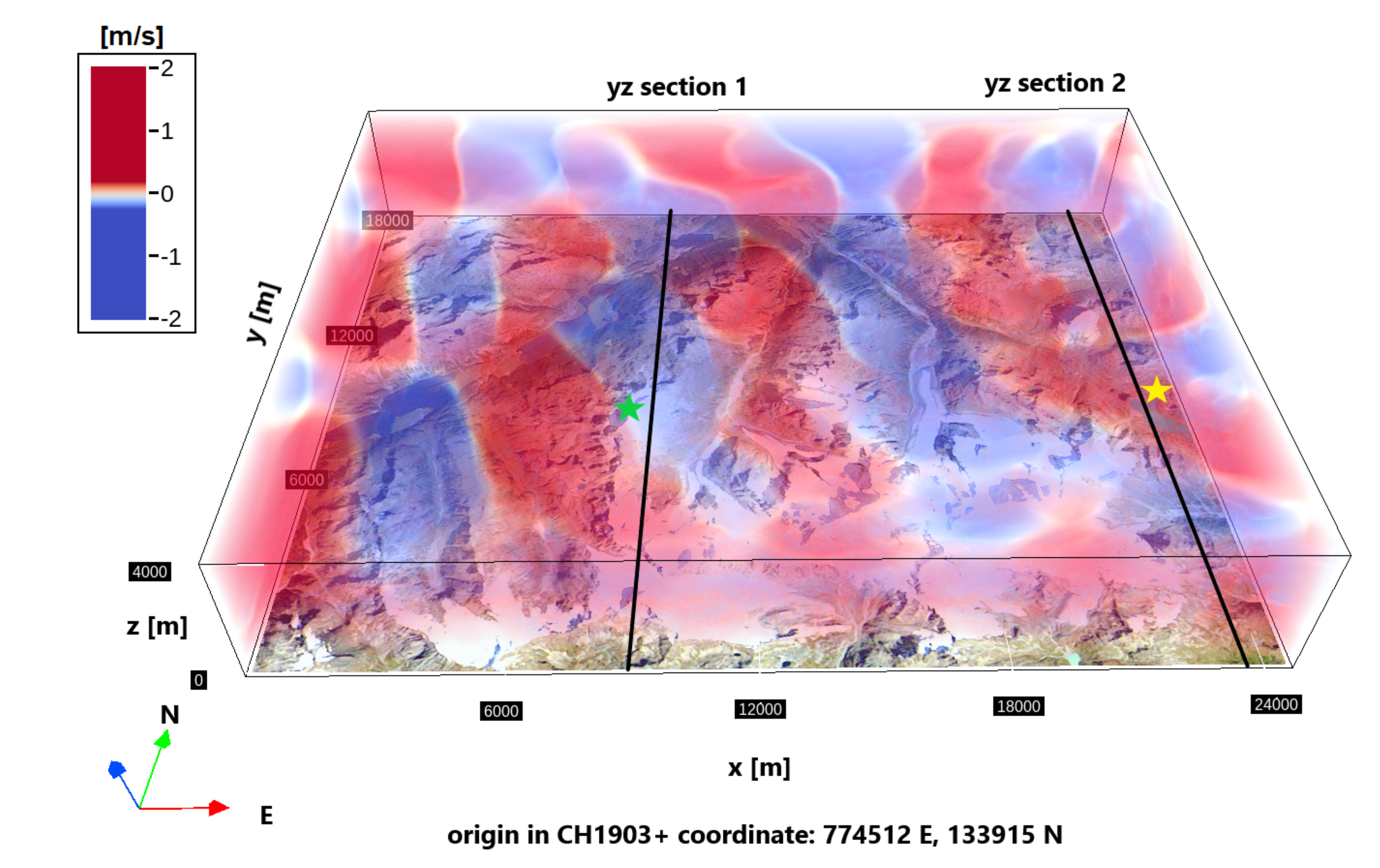
3.5. Grid Nesting and Computational Domain
4. Flight Simulation Test Campaign
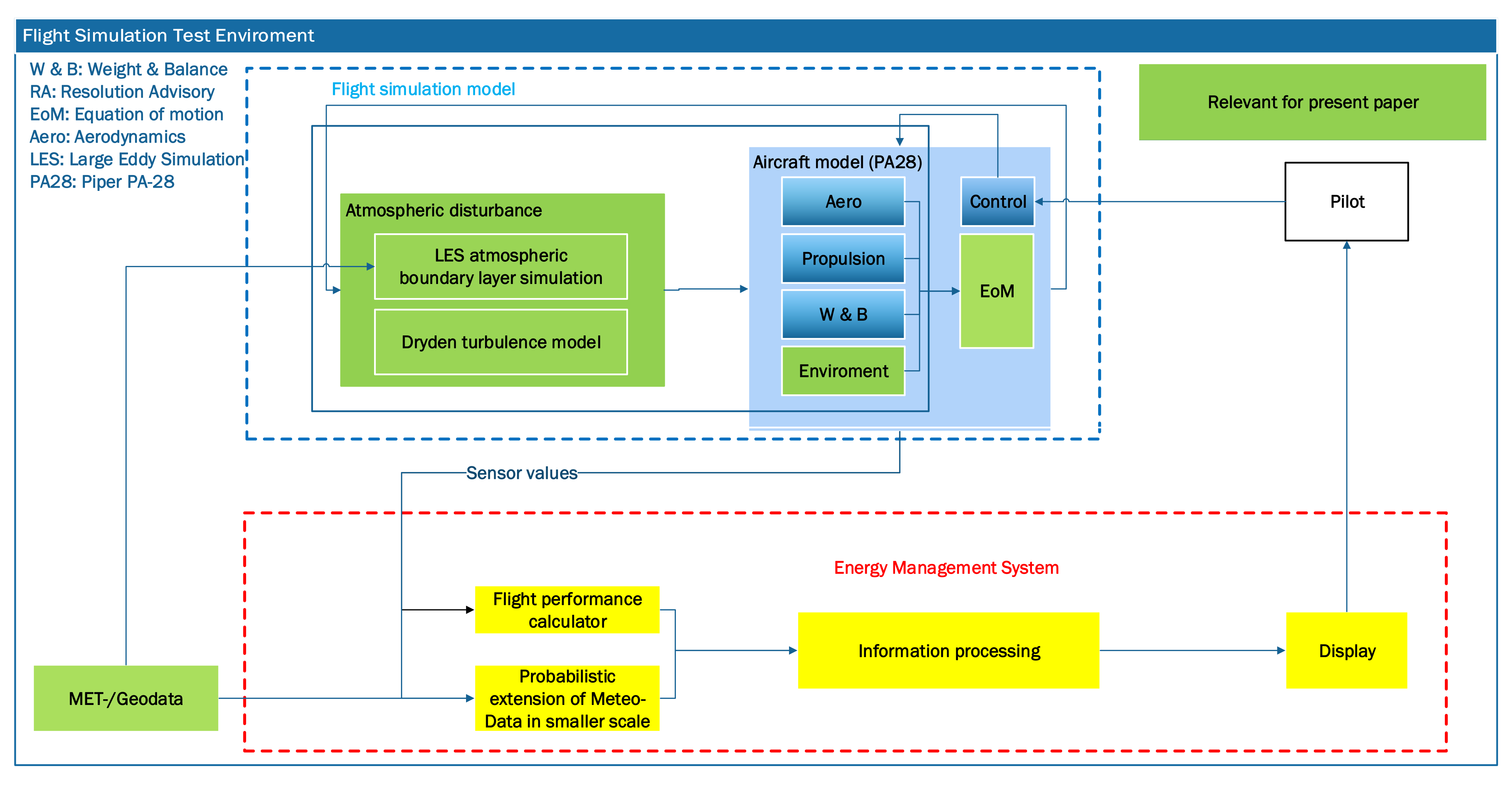
4.1. Concept of Flight Simulation Test Environment
- (i)
- by importing PALM instantaneous data with high temporal resolution with local mesh refinements (hereafter called turbulence case PALM),
- (ii)
- by activating Dryden turbulence model plus temporally mean data from PALM simulations without local mesh refinements (hereafter called turbulence case Dryden).
4.2. Summary of Test Procedure
5. Results and Discussion
5.1. PALM Simulation Evaluation
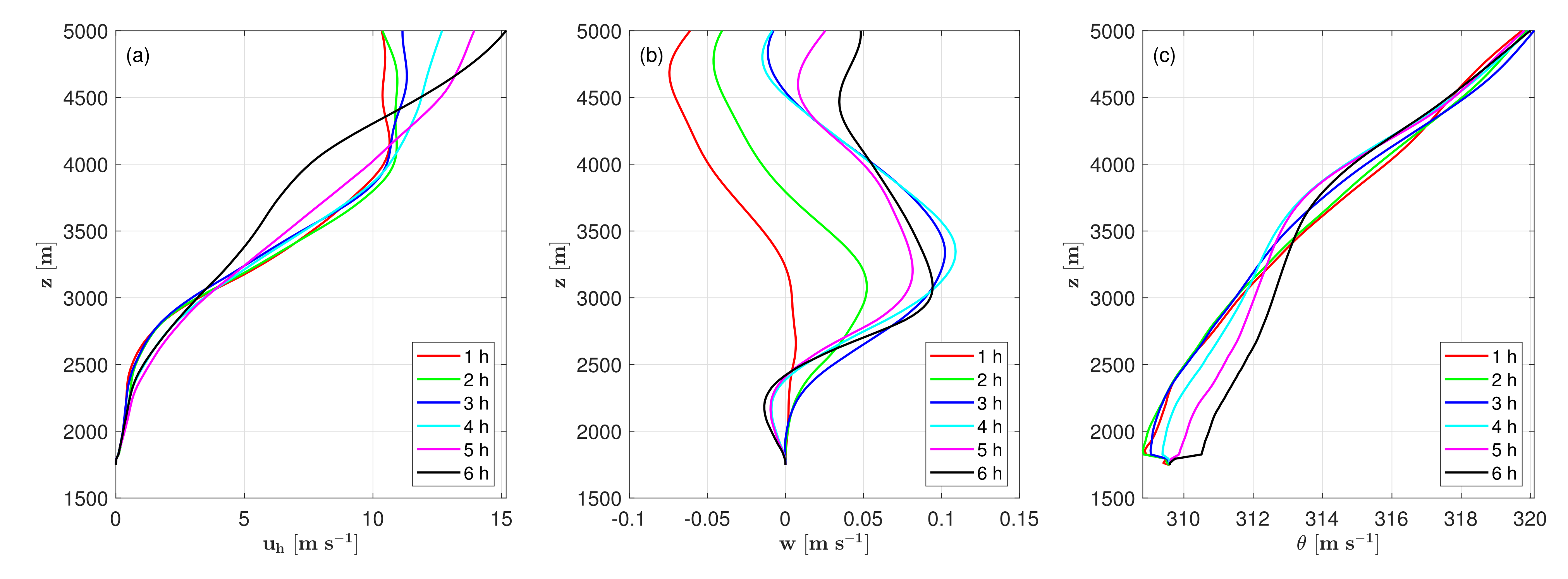
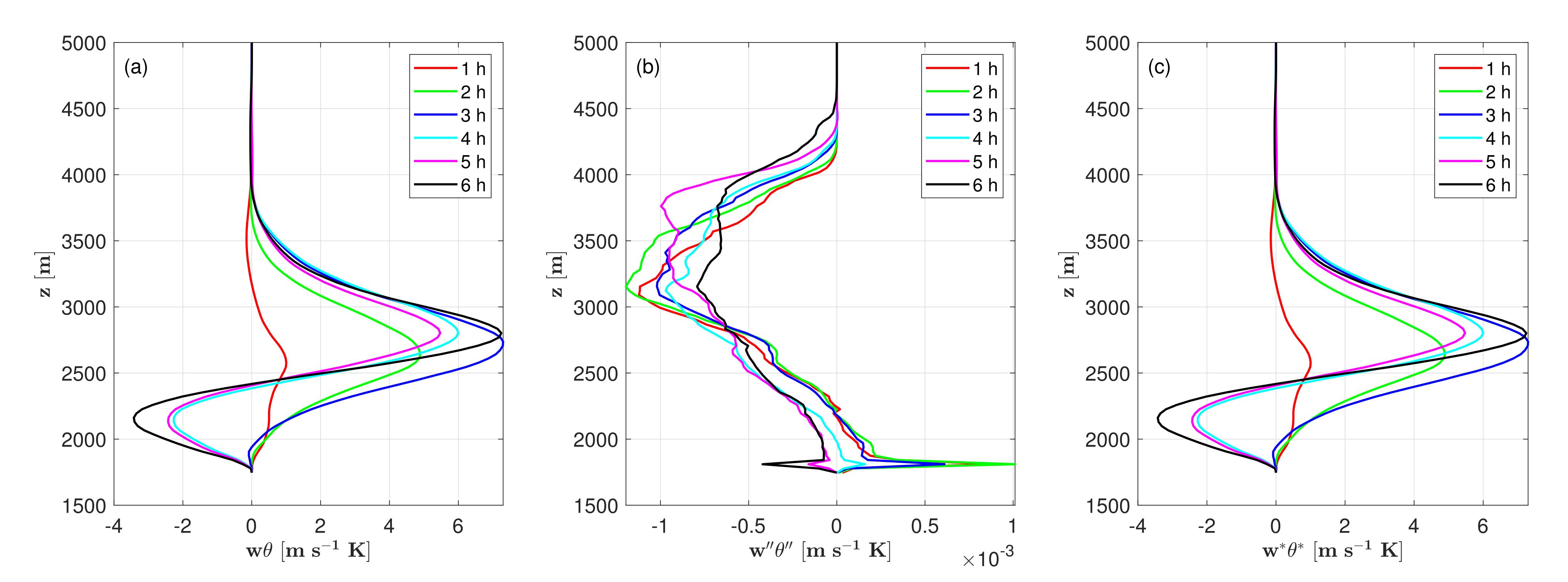
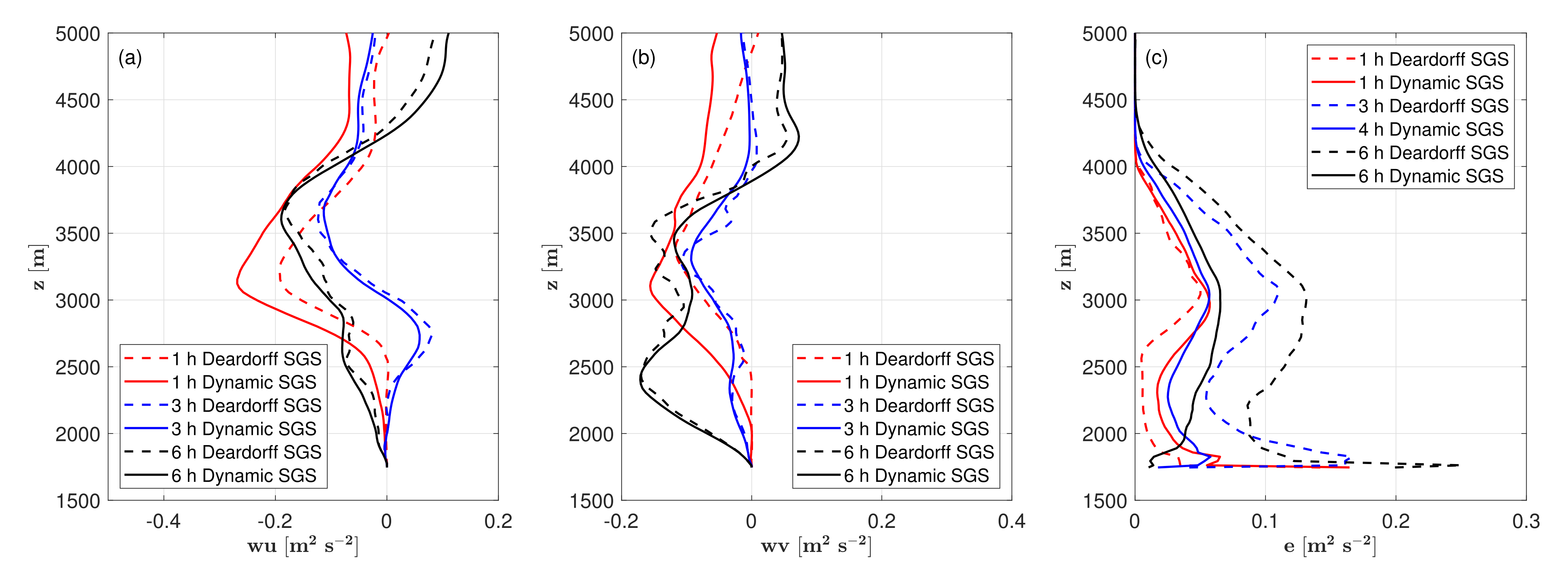
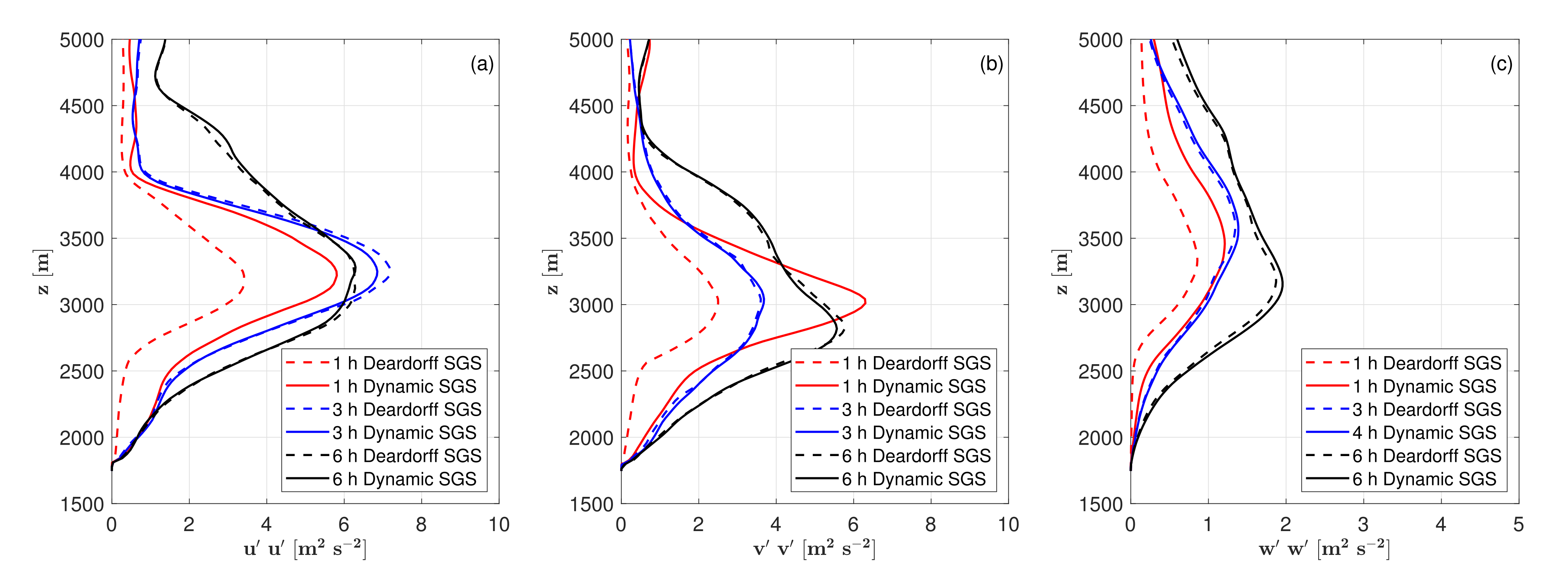
5.1.1. Vertical Profiles
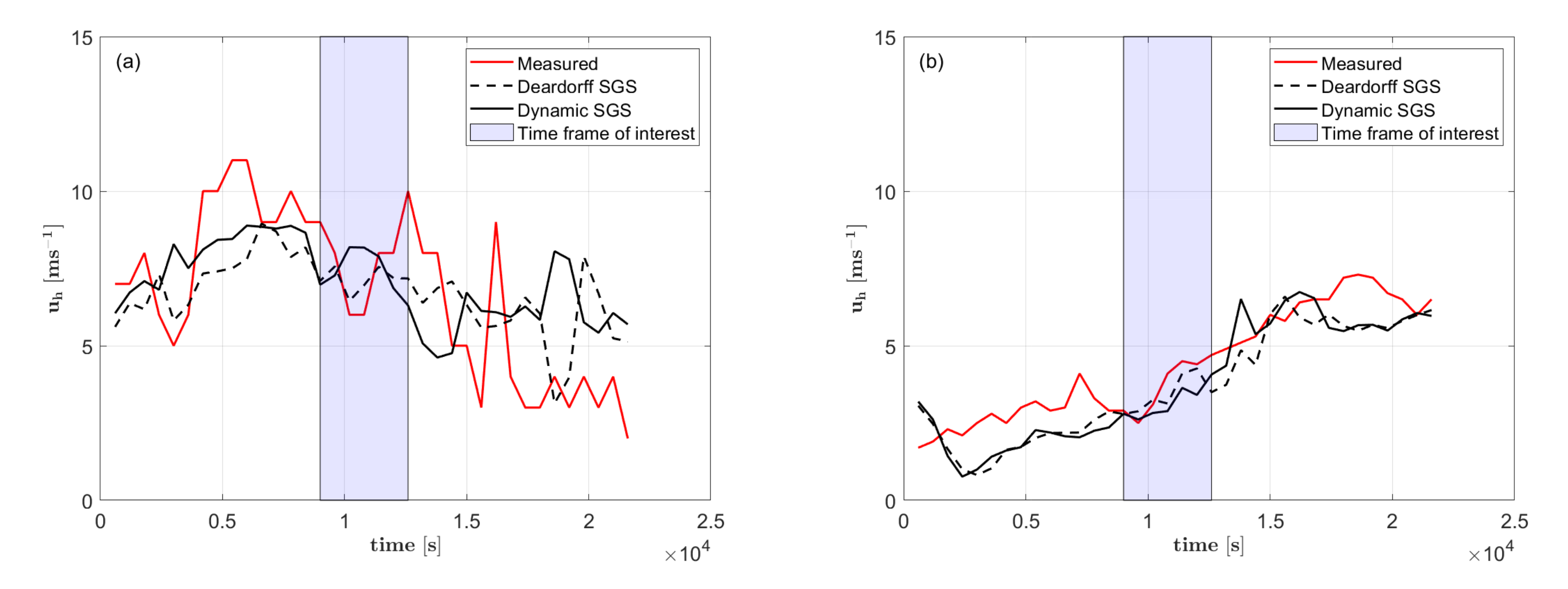
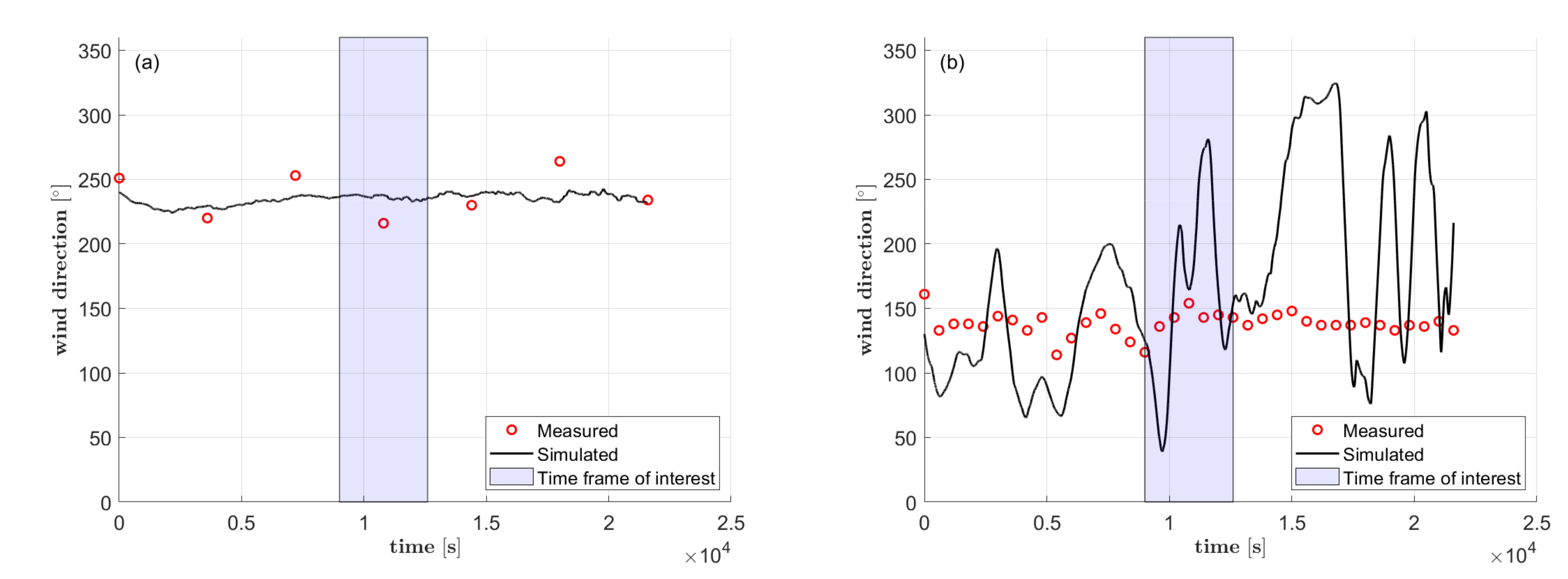
5.1.2. Temporal Evolution
5.2. Results of Flight Simulation Test
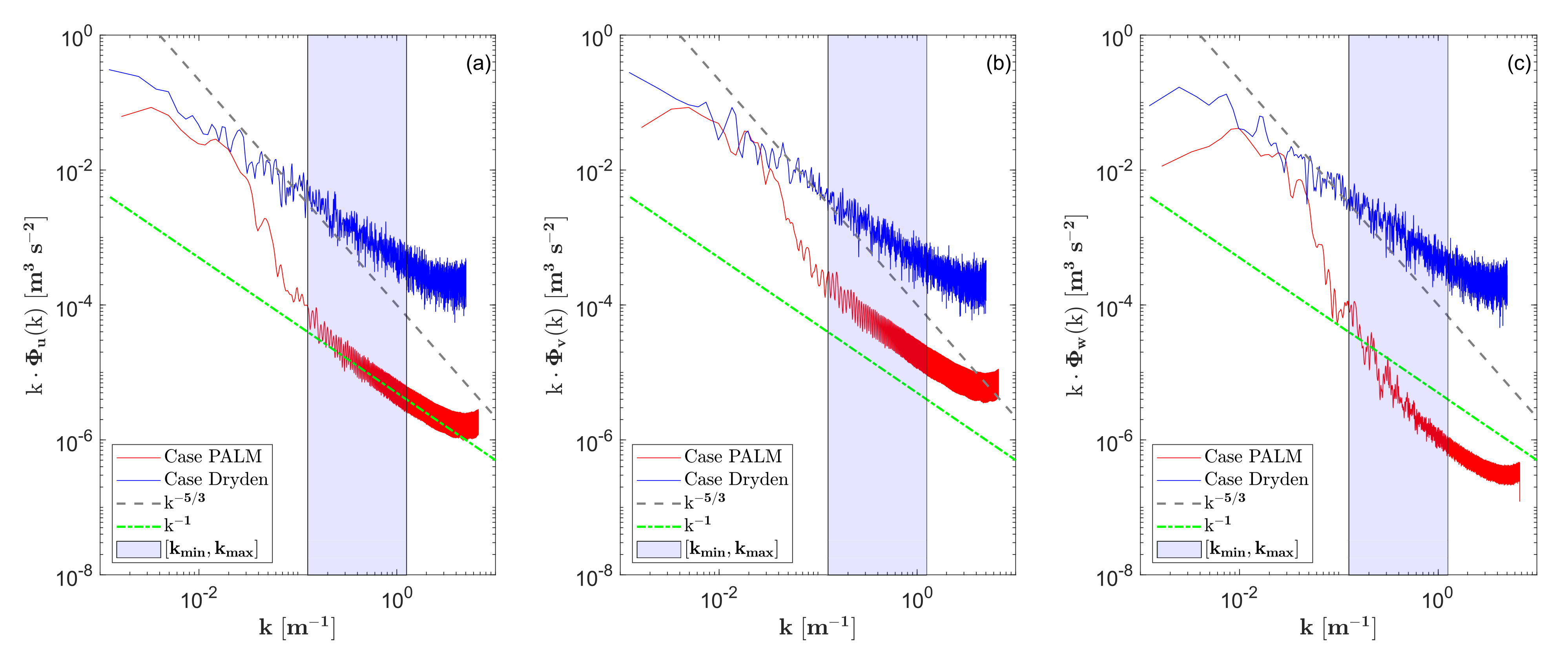
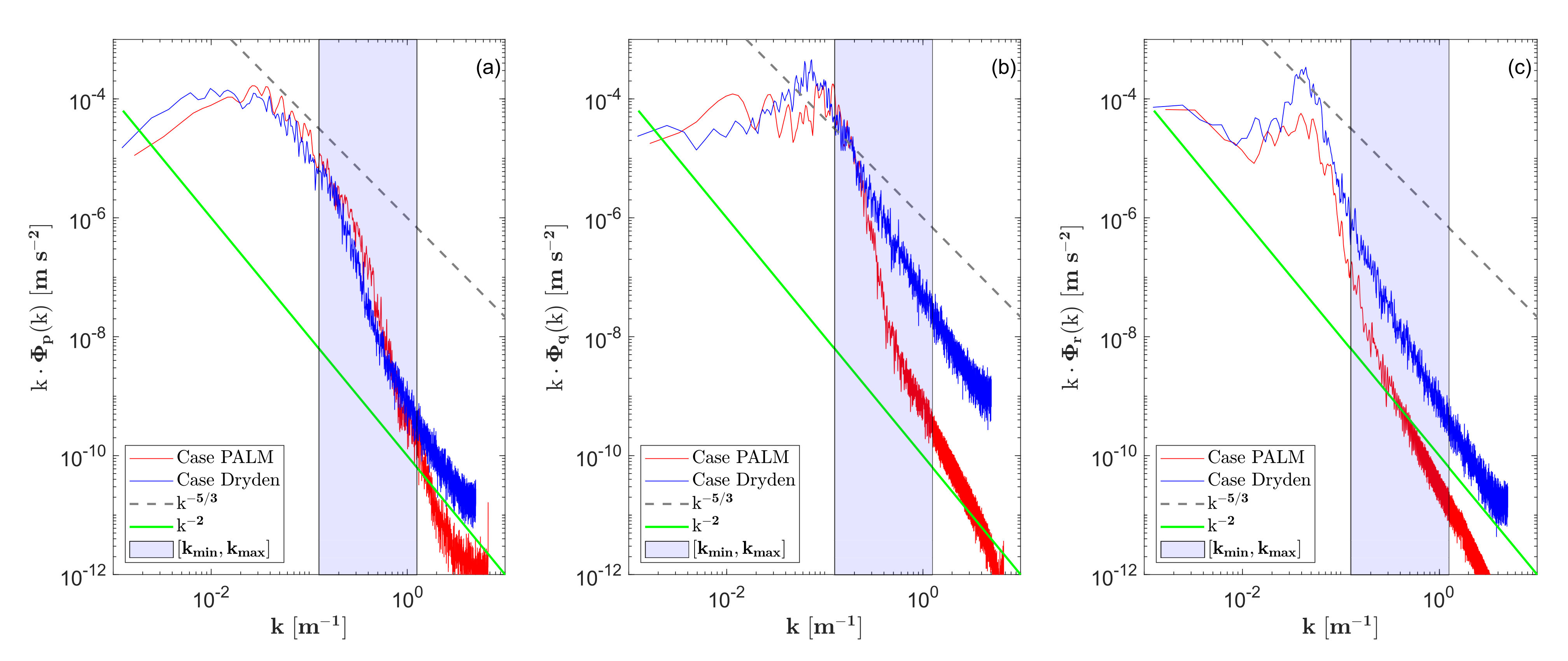
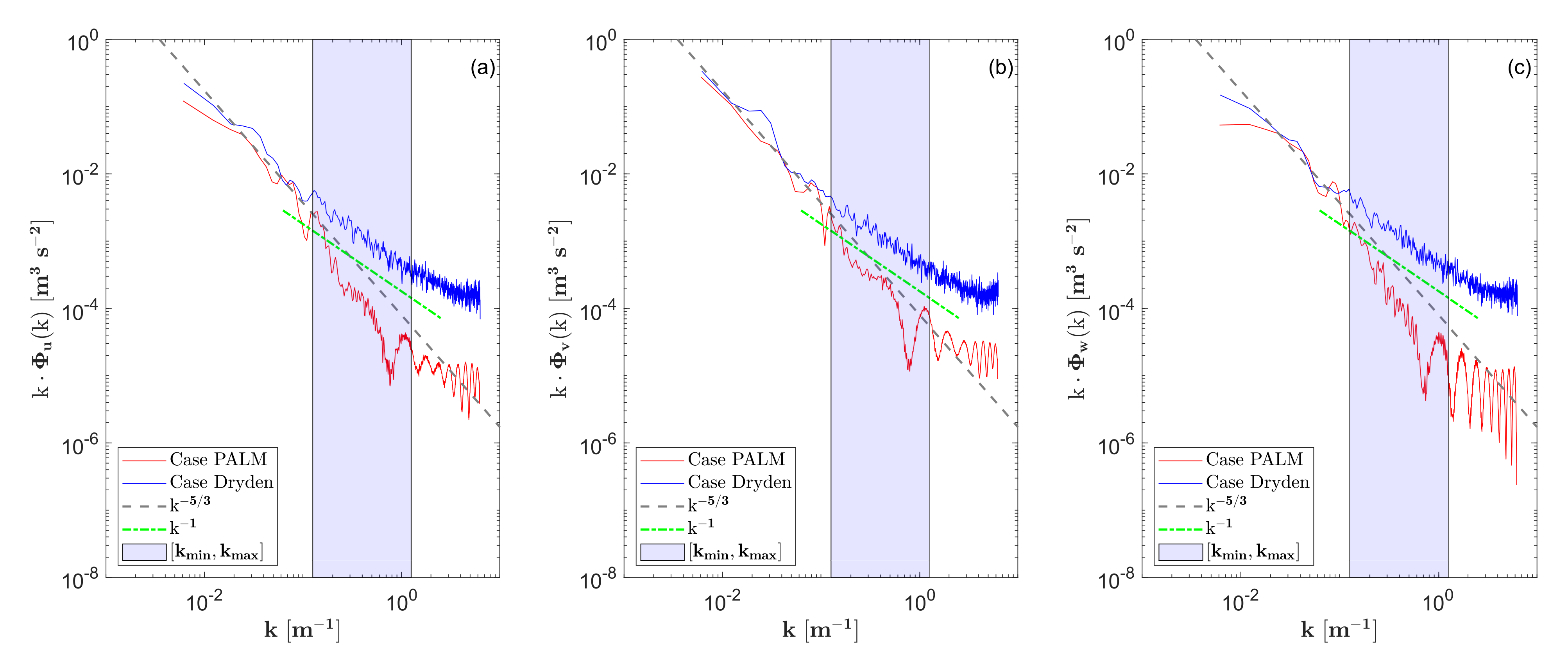
5.2.1. Spectral Analysis
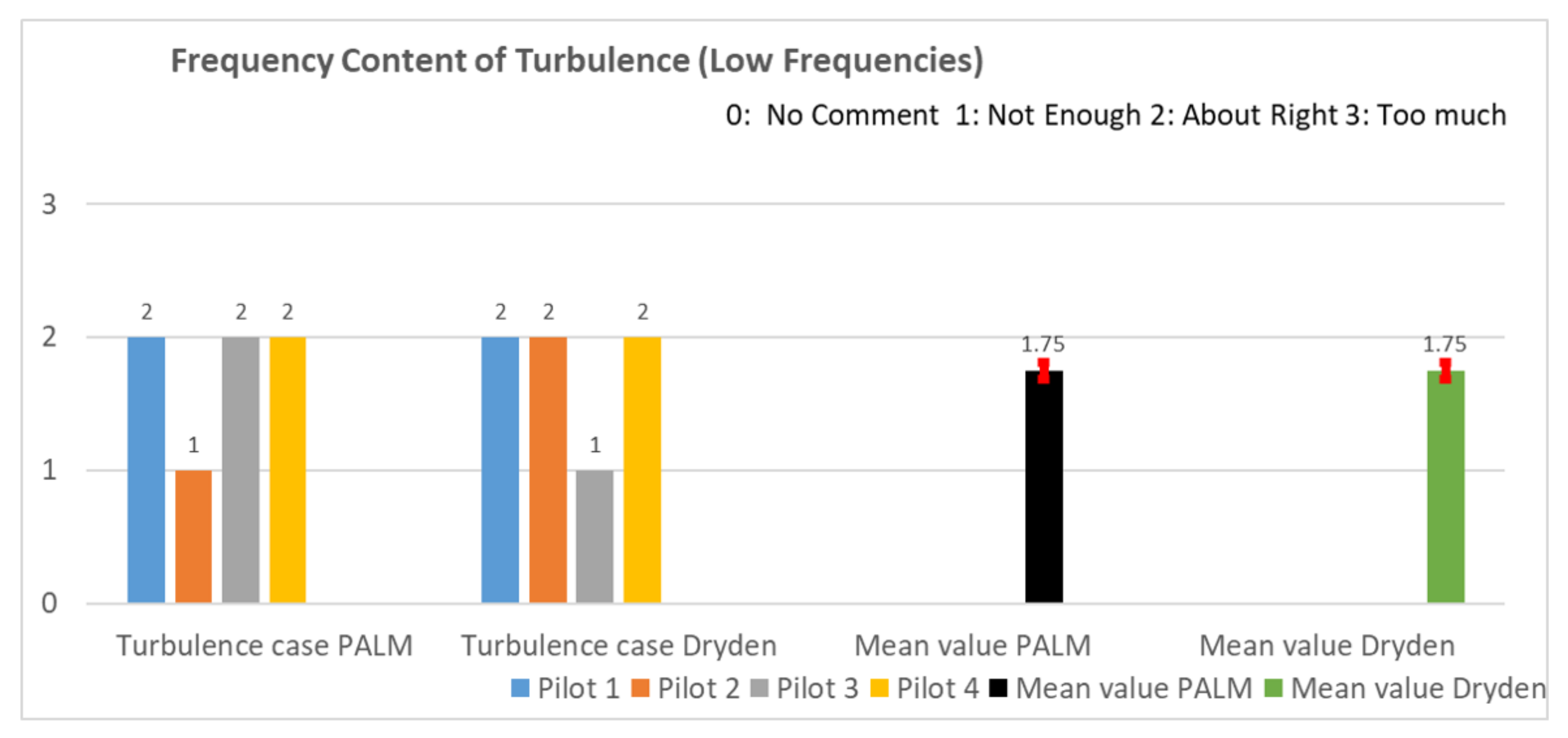
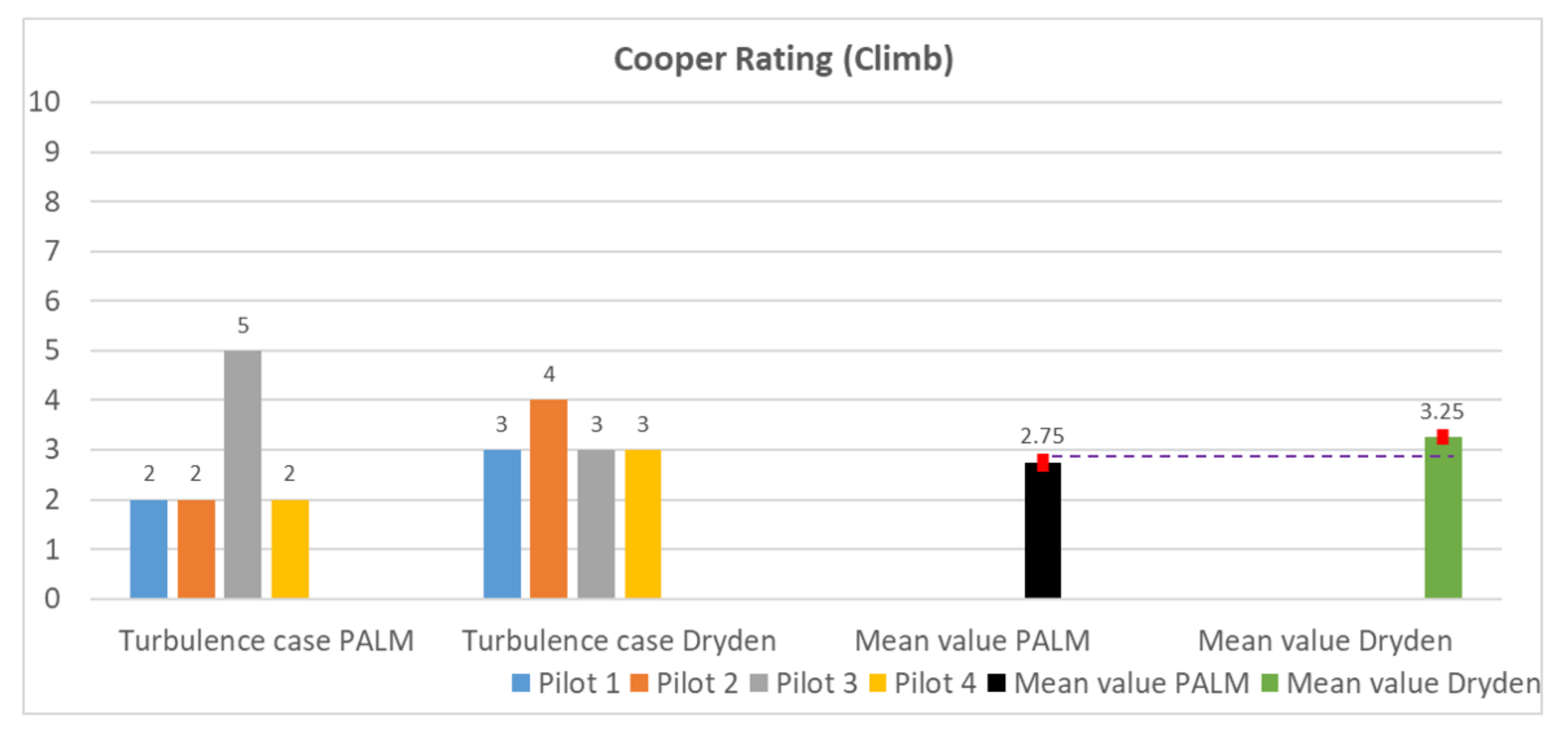
5.2.2. Results of Pilot Questionnaire
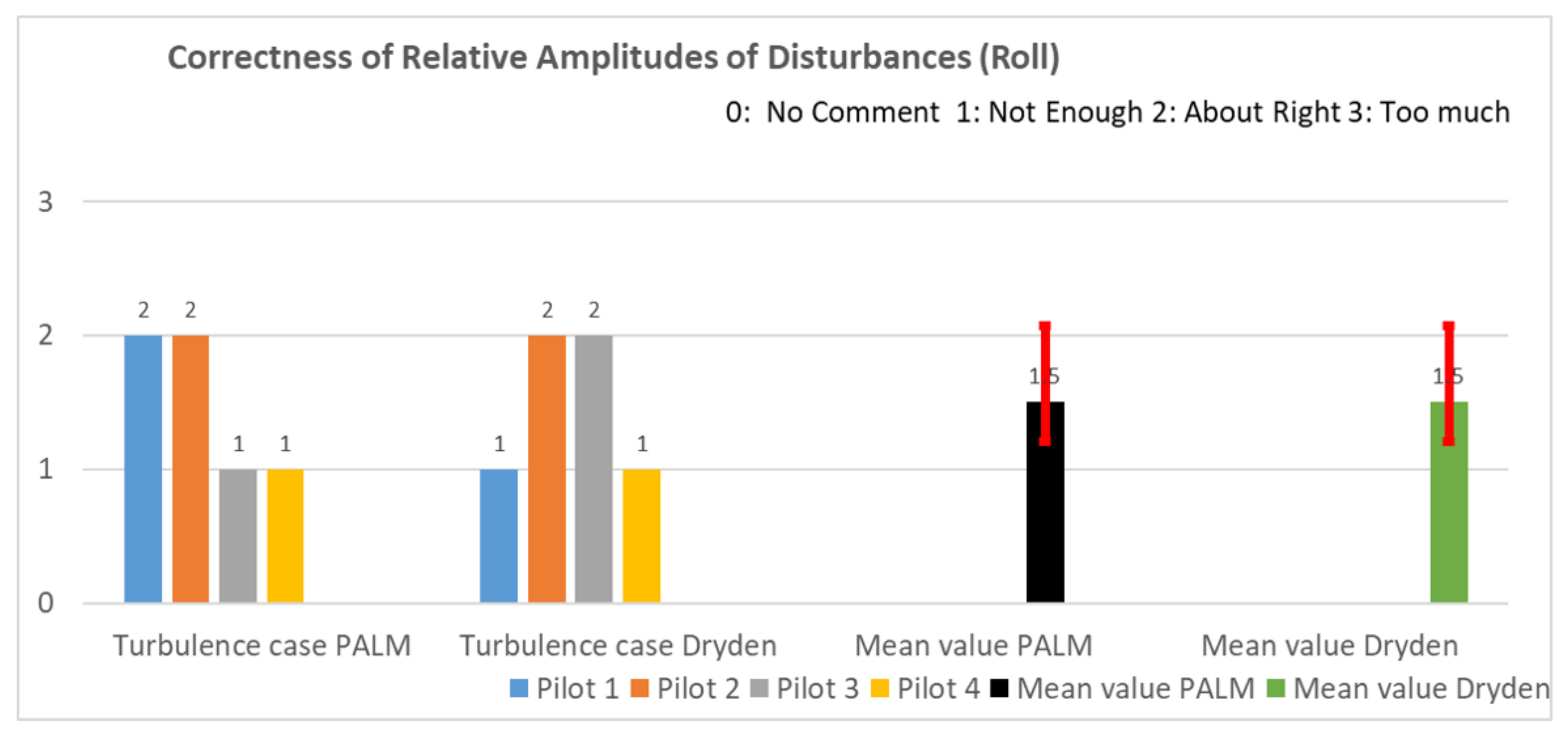
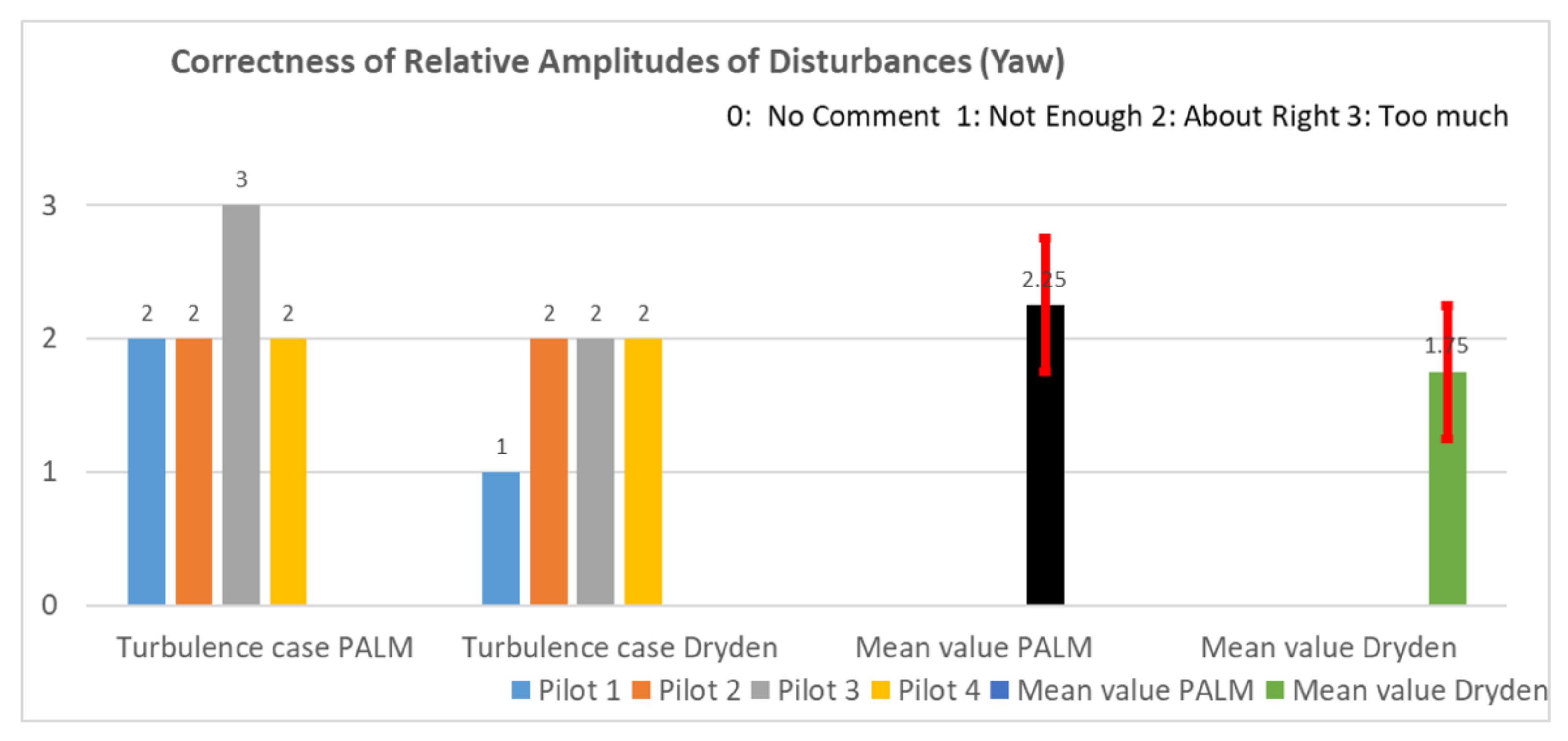
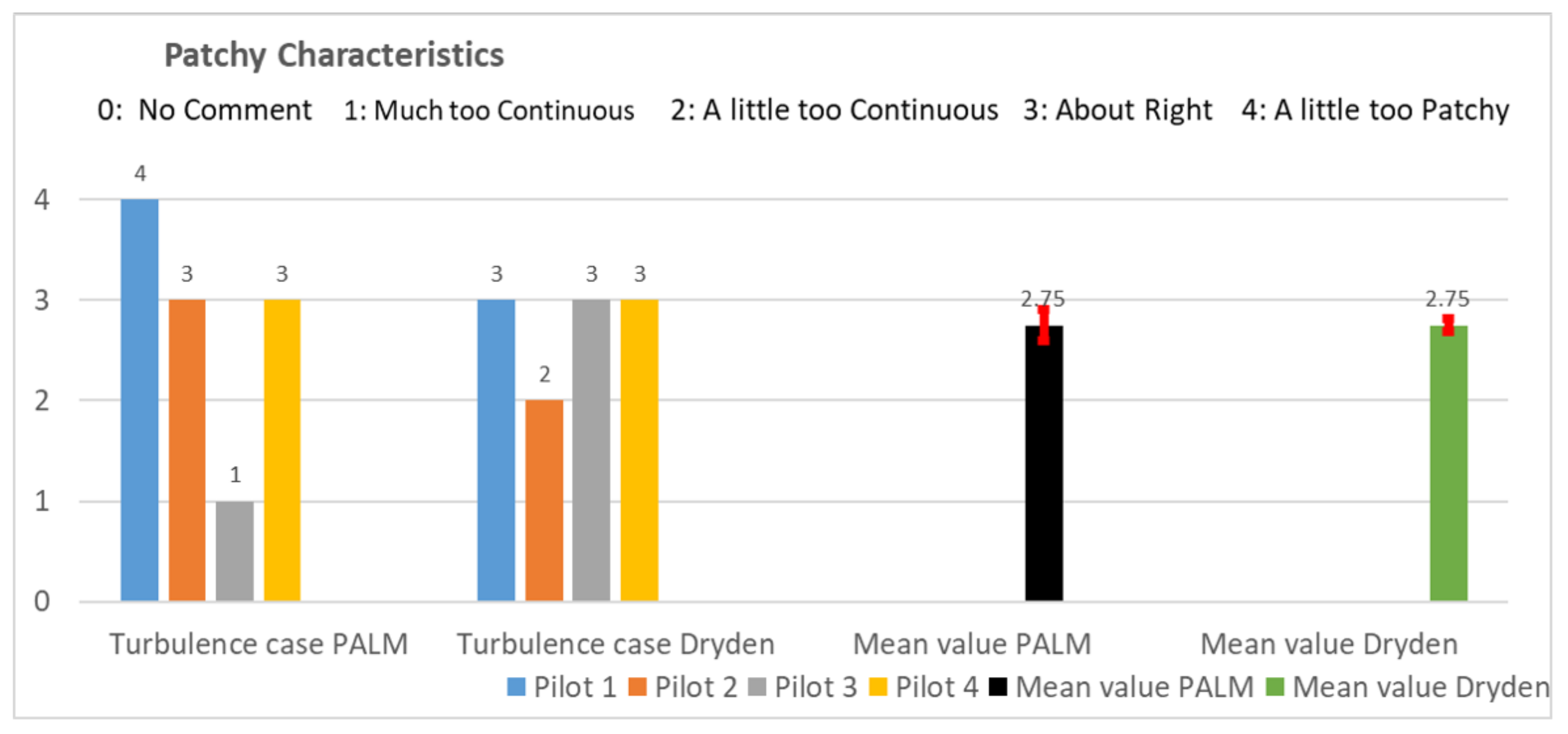
- (i)
- the mean value of case PALM must lie outside the confidence interval of case Dryden;
- (ii)
- the mean value of case Dryden must lie outside the confidence of case PALM.
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric Boundary Layer |
| AMSL | Above Mean Sea Level |
| BEH | Passo del Bernina |
| COV | Piz Corvatsch |
| COSMO | Consortium for Small-scale Modeling |
| CFD | Computational Fluid Dynamics |
| CLS | Control Loading System |
| COV | Piz Corvatsch |
| DNS | Direct Numerical Simulation |
| FEAST | Finite Element Aircraft Simulation of Turbulence |
| FFT | Fast Fourier Transform |
| GUI | Graphic User Interface |
| IMIS | Intercantonal Measurement and Information System |
| INIFOR | Initialization and Forcing |
| LES | Large Eddy Simulations |
| LiDAR | Light Detection And Ranging |
| NetCDF | Network Common Data |
| PALM | Parallelized Large-Eddy Simulation |
| PPL | Private Pilot License |
| QGIS | Quantum Geographic Information System |
| RANS | Reynolds-averaged Navier–Stokes |
| SOBERT | Rotor Blade Element Turbulence |
| SLEVE | Smooth LEvel VErtical |
| SMN | SwissMetNet |
| SRTM | Shuttle Radar Topography Mission |
| STSB | Swiss Transportation Safety Investigation Board |
| SGS | Sub-grid scale |
| TKE | Turbulence Kinetic Energy |
| UTC | Coordinated Universal Time |
| WSL | Swiss Federal Institute for Forest, Snow and Landscape Research |
| ZAV | Centre for Aviation |
| ZHAW | Zurich University of Applied Sciences |
Appendix A. Flight Simulation Test Campaign
Appendix A.1. Weight and Balance
| MASS | ARM | ||||
|---|---|---|---|---|---|
| in | |||||
| Empty Mass | 1500 | ||||
| Position 1 | 80 | ||||
| Position 2 | 50 | ||||
| Position 3 | 50 | ||||
| Position 4 | 50 | ||||
| Fuel | 80 | ||||
| Overall | M.A.C. | ||||
Appendix A.2. Flight Test Card
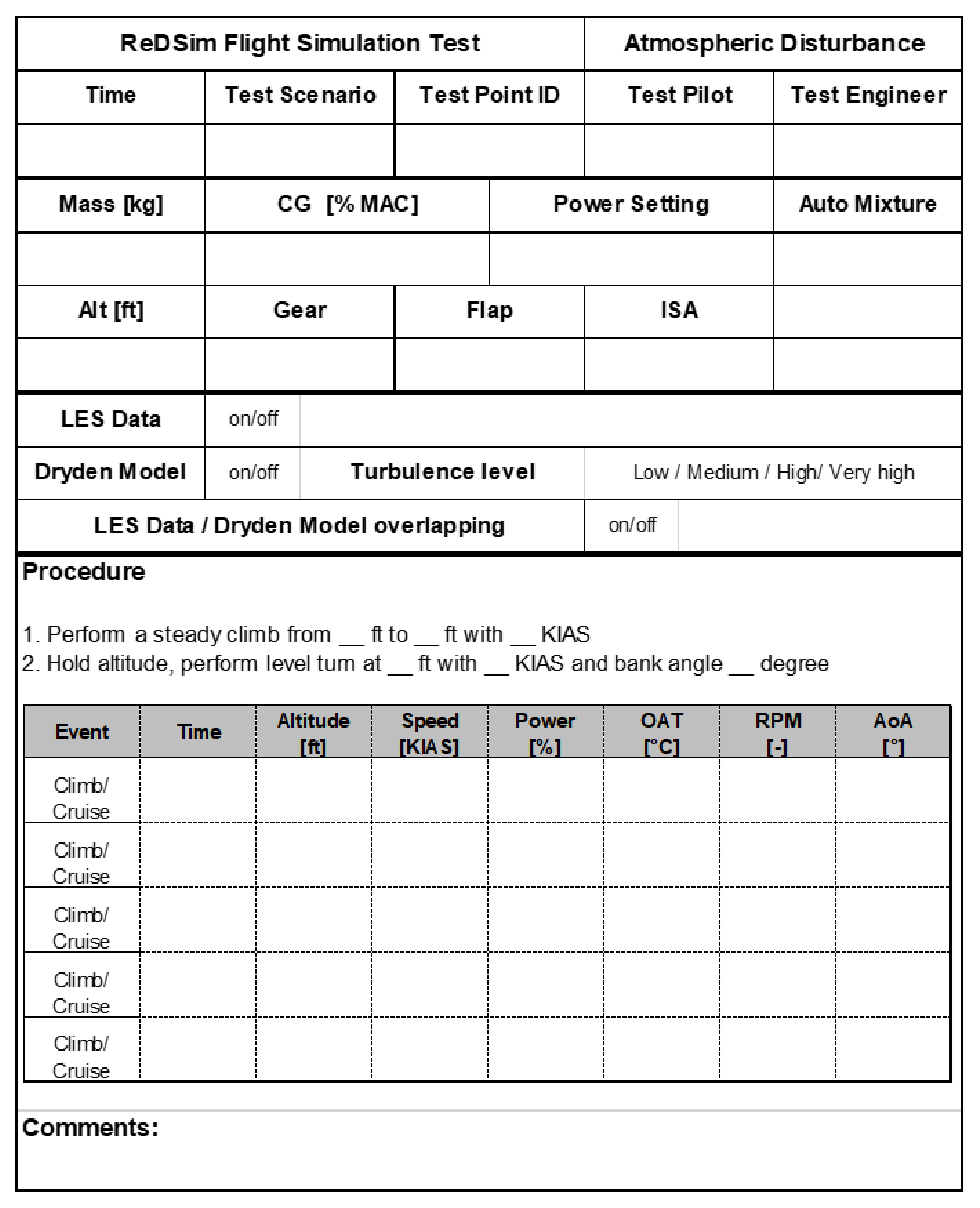
Appendix A.3. Question Sheet


Appendix A.4. Pilot’s Experience
| Pilot | Total No. of Hours | Hours under Similar Conditions | Technical Background |
|---|---|---|---|
| Pilot A | 95 | 10 | Aeronautical engineer |
| Pilot B | 175 | 25 | Aeronautical engineer |
| Pilot C | 55 | 5 | Aeronautical engineer |
| Pilot D | 155 | 20 | Meteorologist |
Appendix A.5. Questionnaire Results





References
- Liu, X.; Manfriani, L.; Fu, Y. Concept of a new system synthesizing meteorological and orographic influences on the airplane safe energy envelope. In Proceedings of the 32rd Congress of the International Council of the Aeronautical Sciences, Shanghai, China, 6–10 September 2021. [Google Scholar]
- Von Kármán, T. Progress in the Statistical Theory of Turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dryden, H.L. A review of statistical theory of turbulence. Q. Appl. Math. 1943, 1, 7–42. [Google Scholar] [CrossRef] [Green Version]
- Gault, J.D.; Gunter, D.E. Atmospheric turbulence considerations for future aircraft operated at low altitudes. In Proceedings of the Aircraft Design for 1980’s Operations Meeting, Washington, DC, USA, 12–14 February 1968. [Google Scholar]
- Taylor, G.I. The spectrum of turbulence. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef] [Green Version]
- Reeves, P.M. A Non-Gaussian Turbulence Simulation; US Air Force Flight Dynamics Laboratory Technical Report AFFDL-TR-69-97; Wright-Patterson Air Force Base: Dayton, OH, USA, 1969.
- Reeves, P.M.; Campbell, G.S.; Ganzer, V.M.; Victor, M.; Joppa, R.G. Development and Application of a Non-Gaussian Atmospheric Turbulence Continuous Atmospheric Turbulence Model for Use Turbulence for Use in Aircraft Design; NASA Contractor Report 2451; National Aeronautics and Space Administration: Washington, DC, USA, 1974.
- Reeves, P.M.; Ganzer, V.M.; Victor, M.; Joppa, R.G. A Non-Gaussian Model of Continuous Atmospheric Turbulence for Use in Aircraft Design; NASA Contractor Report 2639; National Aeronautics and Space Administration: Washington, DC, USA, 1976.
- Jones, J.G. Statistical Discrete Gust Theory for Aircraft Loads; Royal Aircraft Establishment Progress Report 73167; Royal Aircraft Establishment: Farnborough, UK, 1973.
- Van de Moesdijk, G.A.J.G. The Description of Patch Atmospheric Turbulence, Based On a Non-Gaussian Simulation Technique; Report VTH-192; Delft University of Technology, Department of Aeronautical Engineering: Delft, The Netherlands, 1975. [Google Scholar]
- Van de Moesdijk, G.A.J.G. Non-Gaussian Structure of the Simulated Turbulence Environment in Piloted Flight Simulation, Memorandum M-304; Delft University of Technology, Department of Aeronautical Engineering: Delft, The Netherlands, 1978. [Google Scholar]
- Fichtl, G.H.; Perlmutter, M. Nonstationary Atmospheric Boundary-Layer Turbulence Simulation. J. Aircr. 1975, 12, 639–647. [Google Scholar] [CrossRef]
- Fichtl, G.H. A Technique for Simulating Turbulence for Aerospace Vehicle Flight Simulation Studies; NASA Technical Memorandum 78141; National Aeronautics and Space Administration: Washington, DC, USA, 1977.
- Jones, J.G. Modelling of gusts and wind shear for aircraft assessment and certification. Proc. Indian Acad. Sci. Sect. C Eng. Sci. 1980, 3, 1–30. [Google Scholar]
- MIL-F-8785C. United States Military Specification: Flying Qualities of Piloted Airplanes; US Department of Defense: Washington, DC, USA, 1980.
- MIL-STD-1787A. United States Department of Defense Handbook: Flying Qualities of Piloted Airplanes; US Department of Defense: Washington, DC, USA, 1997.
- Fujita, T.T. Manual of Downburst Identification for Project NLMROD; The University of Chicago, Department of the Geophysical Sciences, Satellite and Mesometeorology Research Project 156; University of Chicago, Department of the Geophysical Sciences: Chicago, IL, USA, 1978. [Google Scholar]
- Wilson, J.W.; Roberts, R.D.; Kessinger, C.; McCarthy, J. Microburst Wind Structure and Evaluation of Doppler Radar for Airport Wind Shear Detection. J. Appl. Clim. Meteorol. 1984, 23, 898–915. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, J.; Wilson, J.W.; Fujita, T.T. The Joint Airport Weather Studies Project. Bull. Am. Meteorol. Soc. 1948, 63, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Campbell, C. A Spatial Model of Wind Shear and Turbulence for Flight Simulation. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1984. [Google Scholar]
- Bowles, R.; Laituri, T.; Trevino, G. A Monte Carlo Simulation Technique for Low Altitude, Wind-Shear Turbulence. In Proceedings of the 28th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 1990. [Google Scholar]
- Trevino, G.; Laituri, T.R. Power Spectral Density Analysis of Wind-Shear Turbulence for Related Flight Simulations; NASA Contractor Report 182721; Michigan Technological University: Houghton, MI, USA, 1988. [Google Scholar]
- Trevino, G.; Laituri, T.R. Structure of Wind-Shear Turbulence; NASA Contractor Report 4213; National Aeronautics and Space Administration, Scientific and Technical Information Division: Hampton, VA, USA, 1989.
- McFarland, R.E.; Duisenberg, K. Simulation of Rotor Blade Element Turbulence; NASA Technical Memorandum 108862; National Aeronautics and Space Administration, Ames Research Center: Moffett Field, CA, USA, 1995.
- McFarland, R.E. Finite Element Aircraft Simulation of Turbulence; NASA Technical Memorandum 110437; National Aeronautics and Space Administration, Ames Research Center: Moffett Field, CA, USA, 1997.
- Ji, H.; Chen, R.; Li, P. Distributed atmospheric turbulence model for helicopter flight simulation and handling-quality analysis. J. Aircr. 2017, 54, 190–198. [Google Scholar] [CrossRef]
- Labows, S.J. UH-60 Black Hawk Disturbance Rejection Study for Hover/Low Speed Handling Qualities Criteria and Turbulence Modeling. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, March 2000. [Google Scholar]
- Lusardi, J.A.; Tischler, M.B.; Blanken, C.L. Piloted evaluation of a UH-60 mixer equivalent turbulence simulation model. In Proceedings of the American Helicopter 59th Annual Forum, Phoenix, AZ, USA, 6–8 January 2003. [Google Scholar]
- Lusardi, J.A.; Tischler, M.B.; Blanken, C.L.; Labows, S.J. Empirically Derived Helicopter Response Model and Control System Requirements for Flight in Turbulence. J. Am. Helicopter Soc. 2004, 49, 340–349. [Google Scholar] [CrossRef]
- Seher-Weiss, S.; Von Grünhagen, W.; Tischler, M.B. Development of EC 135 Turbulence Models via System Identification. In Proceedings of the 35th European Rotorcraft Forum, Hamburg, Germany, 22–25 September 2009. [Google Scholar]
- Courtney, M.; Wagner, R.; Lindelöw, P. Testing and comparison of lidars for profile and turbulence measurements in wind energy. IOP Conf. Ser. Earth Environ. Sci. 2008, 19, 1–14. [Google Scholar]
- Mikkelsen, T.; Hansen, K.H.; Angelou, N.; Sjöholm, M.; Harris, M.; Hadley, P.; Scullion, R.; Ellis, G.; Vives, G. Lidar Wind Speed Measurements from a Rotating Spinner. In Proceedings of the European Wind Energy Conference and Exhibition, Warsaw, Poland, 22–25 April 2010. [Google Scholar]
- Towers, P.; Jones, B.L. Real-time wind field reconstruction from LiDAR measurements using a dynamic wind model and state estimation. Wind Energy 2014, 19, 133–150. [Google Scholar] [CrossRef] [Green Version]
- Keating, A.; Piomelli, U.; Balaras, E. A priori and a posteriori tests of inflow conditions for large-eddy simulation. Phys. Fluids 2004, 16, 4696–4712. [Google Scholar] [CrossRef]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef] [Green Version]
- Lund, T.S.; Wu, X.; Kyle, D.S. Generation of Turbulent Inflow Data for Spatially-Developing Boundary Layer Simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef] [Green Version]
- Jarrin, N.; Prosser, R.; Uribe, J.C.; Benhamadouche, S.; Laurence, D. Reconstruction of turbulent fluctuations for hybrid RANS/LES simulations using a Synthetic-Eddy Method. Int. J. Heat Fluid Flow 2009, 30, 435–442. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.W.; Haeri, S. An advanced synthetic eddy method for the computation of aerofoil-turbulence interaction noise. J. Comput. Phys. 2015, 287, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Huecas, S.H.; White, M.; Barakos, G.A. Turbulence Model for Flight Simulation and Handling Qualities Analysis based on a Synthetic Eddy Method. In Proceedings of the Vertical Flight Society’s 76th Annual Forum and Technology Display, Montreal, QC, Canada, 19–21 May 2020. [Google Scholar]
- Xie, Z.-T.; Castro, L.P. Efficient generation of inflow conditions for large-eddy simulation of street-scale flows. Flow Turbul. Combust. 2008, 81, 449–470. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Castro, L.P.; Xie, Z.-T. Divergence-free turbulence inflow conditions for large-eddy simulations with incompressible flow solvers. Comput. Fluids 2013, 84, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Raasch, S.; Schröter, M. PALM—A large-eddy simulation model performing on massively parallel computers. Meteorol. Z. 2001, 84, 363–372. [Google Scholar] [CrossRef]
- Maronga, B.; Gryschka, M.; Heinze, R.; Hoffmann, F.; Kanani-Sühring, F.; Keck, M.; Ketelsen, K.; Letzel, M.O.; Sühring, M.; Raasch, S. The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: Model formulation, recent developments, and future perspectives. Geosci. Model Dev. 2015, 8, 2515–2551. [Google Scholar] [CrossRef] [Green Version]
- Giersch, S. Flugsimulationen in Mit LES Generierten Bodennahen Turbulenten Windfeldern. Master’s Thesis, Leibniz Universität Hannover, Hannover, Germany, 11 May 2017. [Google Scholar]
- Maronga, B.; Banzhaf, S.; Burmeister, C.; Esch, T.; Forkel, R.; Fröhlich, D.; Fuka, V.; Gehrke, K.F.; Geletič, J.; Giersch, S.; et al. Overview of the PALM model system 6.0. Geosci. Model Dev. 2020, 13, 1335–1372. [Google Scholar] [CrossRef]
- Kadasch, E.; Sühring, M.; Gronemaier, T.; Raasch, S. Mesoscale nesting interface of the PALM model system 6.0. Geosci. Model Dev. 2021, 14, 5435–5465. [Google Scholar] [CrossRef]
- Dryden Wind Turbulence Model (Discrete). Available online: https://www.mathworks.com/help/aeroblks/drydenwindturbulece-modeldiscrete.html (accessed on 20 October 2021).
- Van der Vaart, J.C. The Cross-Covariance of Gust Velocities and Their Time-Derivatives; Report VTH-207; Delft University of Technology, Department of Aeronautical Engineering: Delft, The Netherlands, 1975. [Google Scholar]
- Van der Vaart, J.C. The Calculation of the R.M.S. value of an Aircraft’s Normal Acceleration due to Gaussian Random Atmospheric Turbulence; Report VTH-213; Delft University of Technology, Department of Aeronautical Engineering: Delft, The Netherlands, 1976. [Google Scholar]
- Jessi, C.Y. Implementation and Testing of Turbulence Models for the F18-HARV Simulation; NASA Contractor Report 206937; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 1998.
- PALM Website. Available online: https://palm.muk.uni-hannover.de/ (accessed on 20 October 2021).
- Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef] [Green Version]
- Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Moeng, C.-H.; Wyngaard, J.C. Spectral Analysis of Large-Eddy Simulations of the Convective Boundary Layer. Bound.-Layer Meteorol. 1988, 18, 495–527. [Google Scholar] [CrossRef] [Green Version]
- Saiki, E.M.; Moeng, C.-H.; Sullivan, P.P. Large-Eddy Simulation of the stably-stratified atmospheric boundary layer. Bound.-Layer Meteorol. 2000, 95, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2008; p. 666. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef] [Green Version]
- Heinz, S. Realizability of dynamic subgrid-scale stress models via stochastic analysis. Monte Carlo Methods Appl. 2008, 14, 311–329. [Google Scholar] [CrossRef]
- Mokharpoor, R.; Piomelli, U.; Moin, P. Dynamic large eddy simulation: Stability via realizability. Phys. Fluids 2017, 29, 105104. [Google Scholar]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. Methods Comput. Phys. Adv. Res. Appl. 1977, 17, 173–265. [Google Scholar]
- Wicker, L.J.; Skamarock, W.C. Time-Splitting Methods for Elastic Models Using Forward Time Schemes. Mon. Weather Rev. 2002, 130, 2088–2097. [Google Scholar] [CrossRef]
- Williamson, J.H.; Skamarock, W.C. Low-storage Runge-Kutta schemes. J. Comput. Phys. 1980, 35, 48–56. [Google Scholar] [CrossRef]
- Hackbusch, W. Multi-Grid Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1985; p. 378. [Google Scholar]
- Briscolini, M.; Santangelo, P. Development of the mask method for incompressible unsteady flows. J. Comput. Phys. 1980, 35, 48–56. [Google Scholar] [CrossRef]
- Fluck, S. Bodenturbulenzen um Flugplätze, Durchführung und Benchmarking von Turbulenzsimulationen Sowie Entwicklung eines Frameworks für zukünftige Problemstellungen. Master’s Thesis, Zurich University of Applied Sciences, Winterthur, Switzerland, 12 June 2020. [Google Scholar]
- Koller, M.; Fuhrer, P.; Schär, C. Notes and Correspondence. A Generalization of the SLEVE Vertical Coordinate. Am. Meteorol. Soc. 2010, 138, 3683–3689. [Google Scholar]
- Hellsten, A.; Ketelsen, E.; Sühring, M.; Auvinen, M.; Maronga, B.; Knigge, C.; Barmpas, F.; Tsegas, G.; Moussiopoulos, N.; Raasch, S. A nested multi-scale system implemented in the large-eddy simulation model PALM model system 6.0. Geosci. Model Dev. 2021, 14, 3185–3214. [Google Scholar] [CrossRef]
- Cooper, G.E.; Harper, R.P. The Use of Pilot Rating in the Evaluation Aircraft Handling Qualities. NASA Report TN-D-5133; National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- Heimo, A.; Begert, M.; Mühlhäuser, C.; Konzelmann, T.; Suter, S. SwissMetNet: The New Automatic Meteorological Network of Switzerland. In Proceedings of the 6th European Conference on Applied Climatology, Ljubljana, Slovenia, 4–8 September 2006. [Google Scholar]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Lindborg, C. The energy cascade in a strongly stratified fluid. J. Fluid Mech. 2006, 550, 207–242. [Google Scholar] [CrossRef]
- Dougherty, J. The anisotropy of turbulence at the meteor level. J. Atmos. Terr. Phys. 1961, 30, 210–213. [Google Scholar] [CrossRef]
- Ozmidov, R.V. On the Turbulent Exchange in a Stably Stratified Ocean. Zzv. Atm. Ocean Phys. 1965, 1, 853–860. [Google Scholar]
- Cheng, Y.; Li, Q.; Argentini, S.; Sayde, C.; Gentine, P. A Model for Turbulence Spectra in the Equilibrium Range of the Stable Atmospheric Boundary Layer. J. Geophys. Res. Atmos. 2020, 125, e2019JD032191. [Google Scholar] [CrossRef]
- Knigge, C.; Raasch, S. Improvement and development of one- and two-dimensional discrete gust models using a large-eddy simulation model. J. Wind Eng. Ind. Aerodyn. 2016, 153, 46–59. [Google Scholar] [CrossRef] [Green Version]




| Symbol | Value | Description |
|---|---|---|
| SGS model constant | ||
| Heat capacity of dry air at constant pressure | ||
| g | Gravitational acceleration | |
| Reference pressure | ||
| Specific gas constant for dry air | ||
| Specific gas constant for water vapor | ||
| Von Kármán constant | ||
| Angular velocity of the Earth |
| Spatial Domain | Number of Grid | Grid Resolution | Domain Origin in Coordinates System | Time Domain | |
|---|---|---|---|---|---|
| Parent domain | (774,572 E, 133,915 N) | E, N) | |||
| Child domain 1 | (778,864 E, 140,087 N) | E, N) | UTC 06:00–UTC 12:00 | ||
| Child domain 2 | (793,612 E, 141,947 N) | E, N) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Abà, A.; Capone, P.; Manfriani, L.; Fu, Y. Atmospheric Disturbance Modelling for a Piloted Flight Simulation Study of Airplane Safety Envelope over Complex Terrain. Aerospace 2022, 9, 103. https://doi.org/10.3390/aerospace9020103
Liu X, Abà A, Capone P, Manfriani L, Fu Y. Atmospheric Disturbance Modelling for a Piloted Flight Simulation Study of Airplane Safety Envelope over Complex Terrain. Aerospace. 2022; 9(2):103. https://doi.org/10.3390/aerospace9020103
Chicago/Turabian StyleLiu, Xinying, Anna Abà, Pierluigi Capone, Leonardo Manfriani, and Yongling Fu. 2022. "Atmospheric Disturbance Modelling for a Piloted Flight Simulation Study of Airplane Safety Envelope over Complex Terrain" Aerospace 9, no. 2: 103. https://doi.org/10.3390/aerospace9020103
APA StyleLiu, X., Abà, A., Capone, P., Manfriani, L., & Fu, Y. (2022). Atmospheric Disturbance Modelling for a Piloted Flight Simulation Study of Airplane Safety Envelope over Complex Terrain. Aerospace, 9(2), 103. https://doi.org/10.3390/aerospace9020103






