Characterization of Residual Stresses and Grain Structure in Hot Forging of GH4169
Abstract
:1. Introduction
2. Materials and Methods
2.1. Details of Forging Process
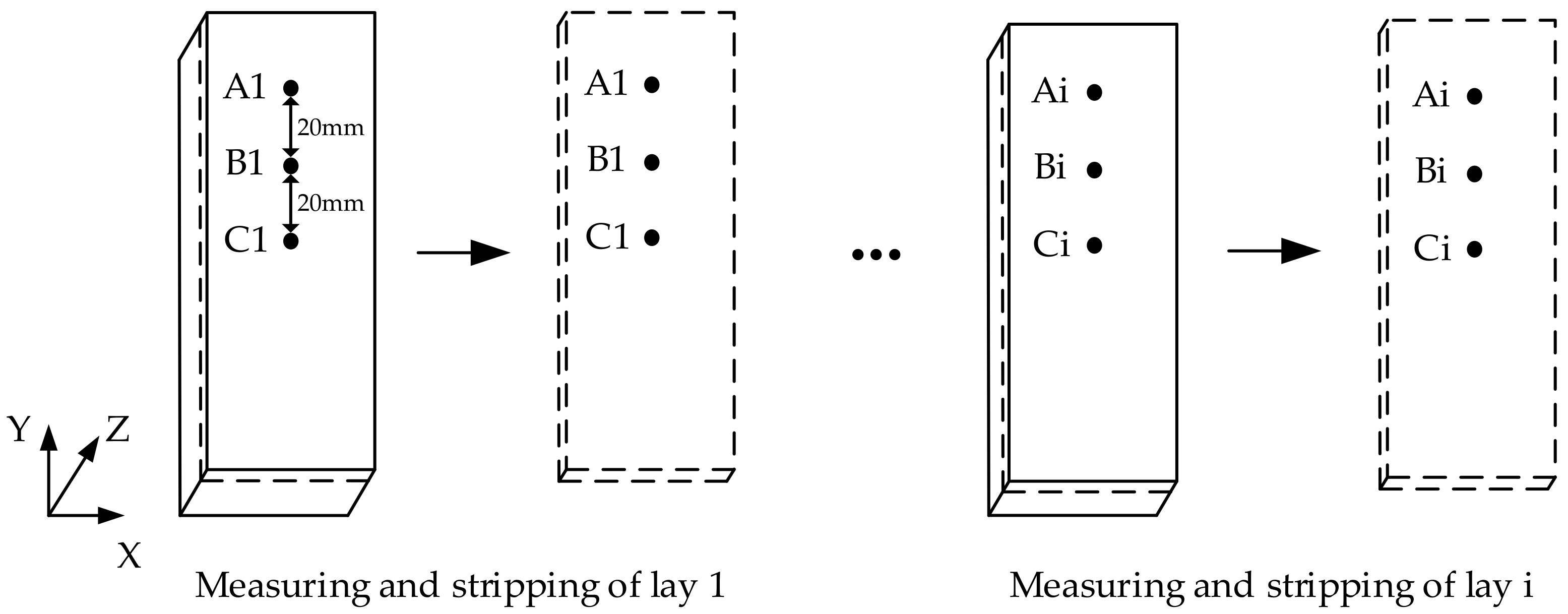
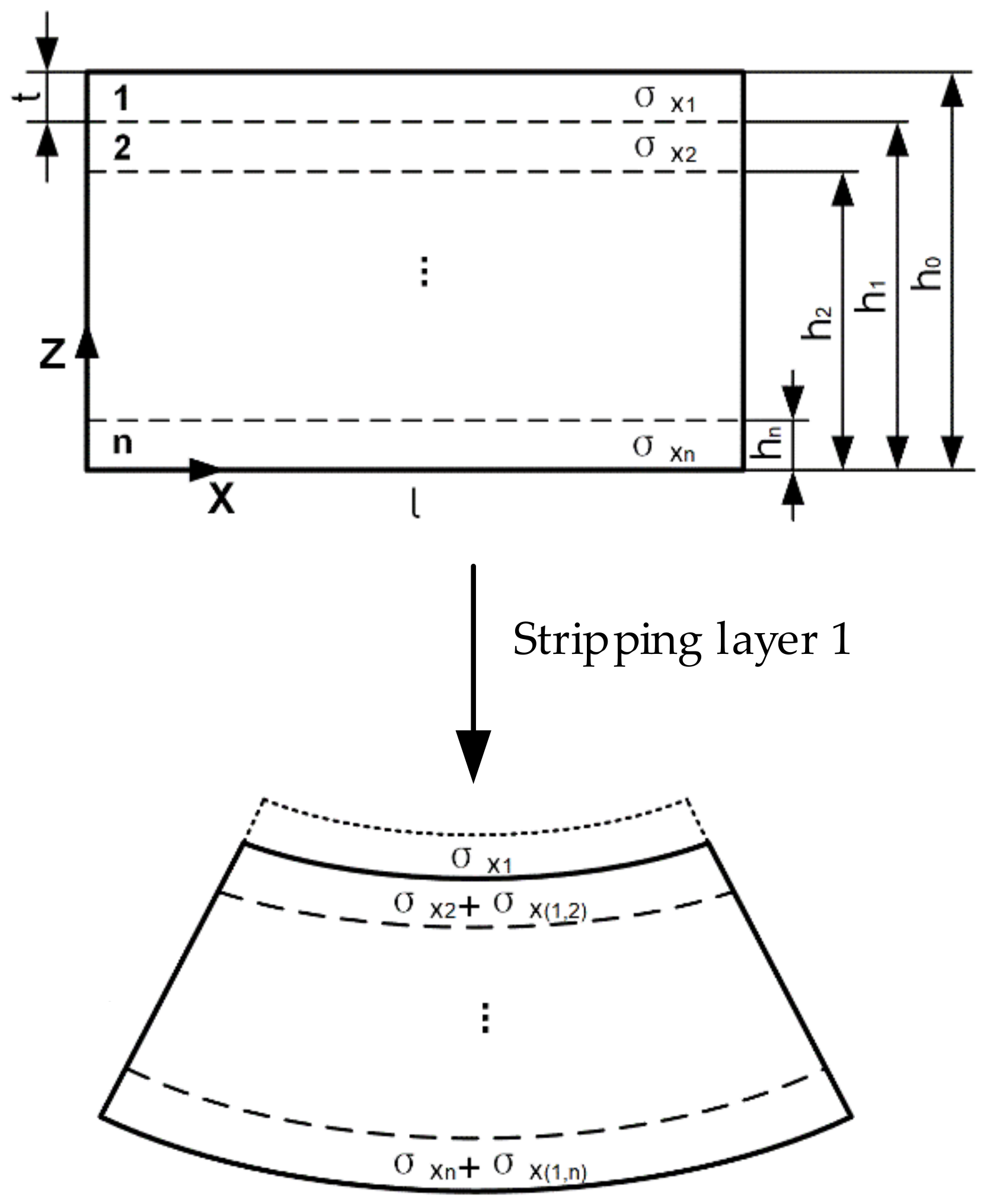
2.2. Measurement Method of Residual Stresses
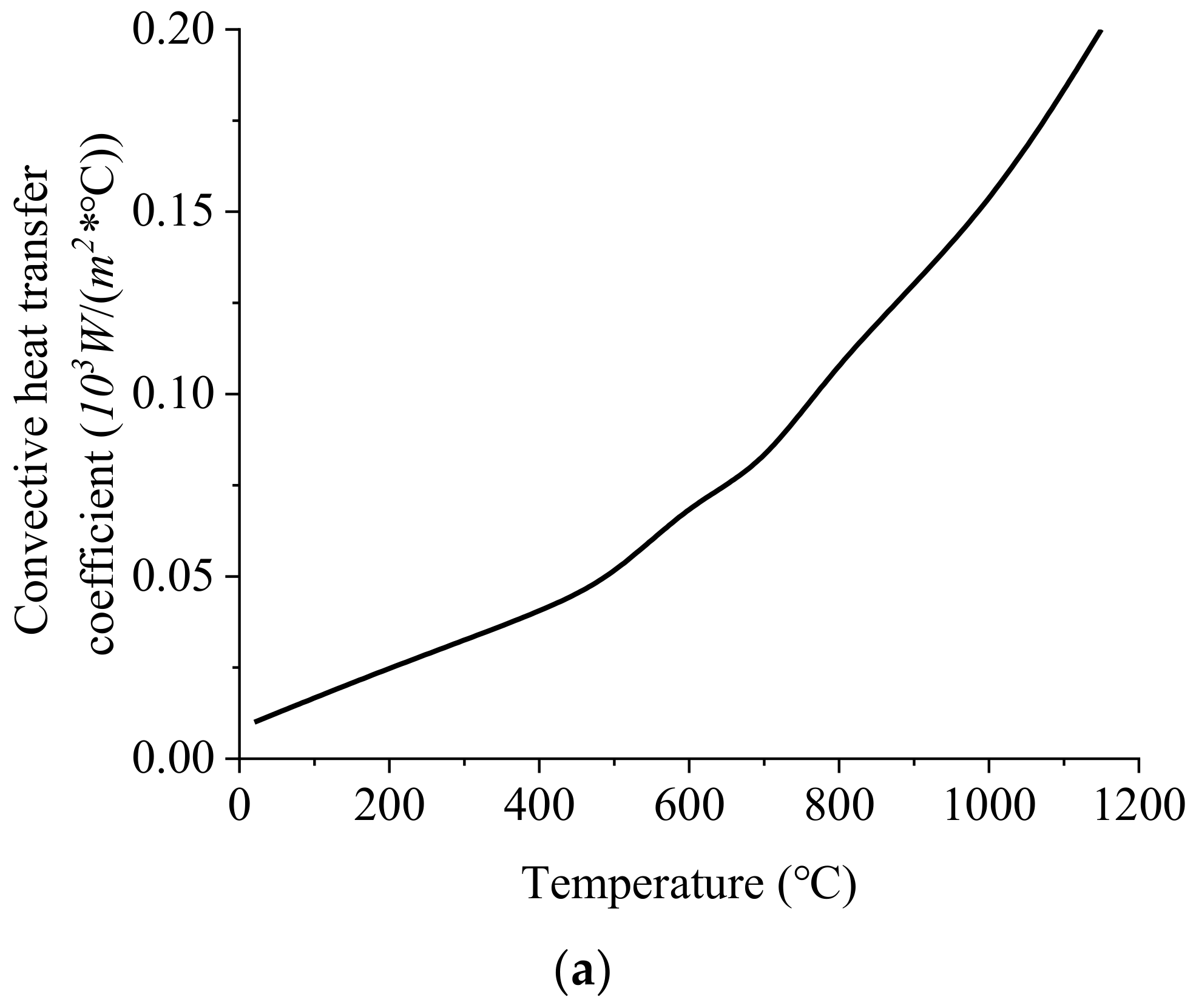
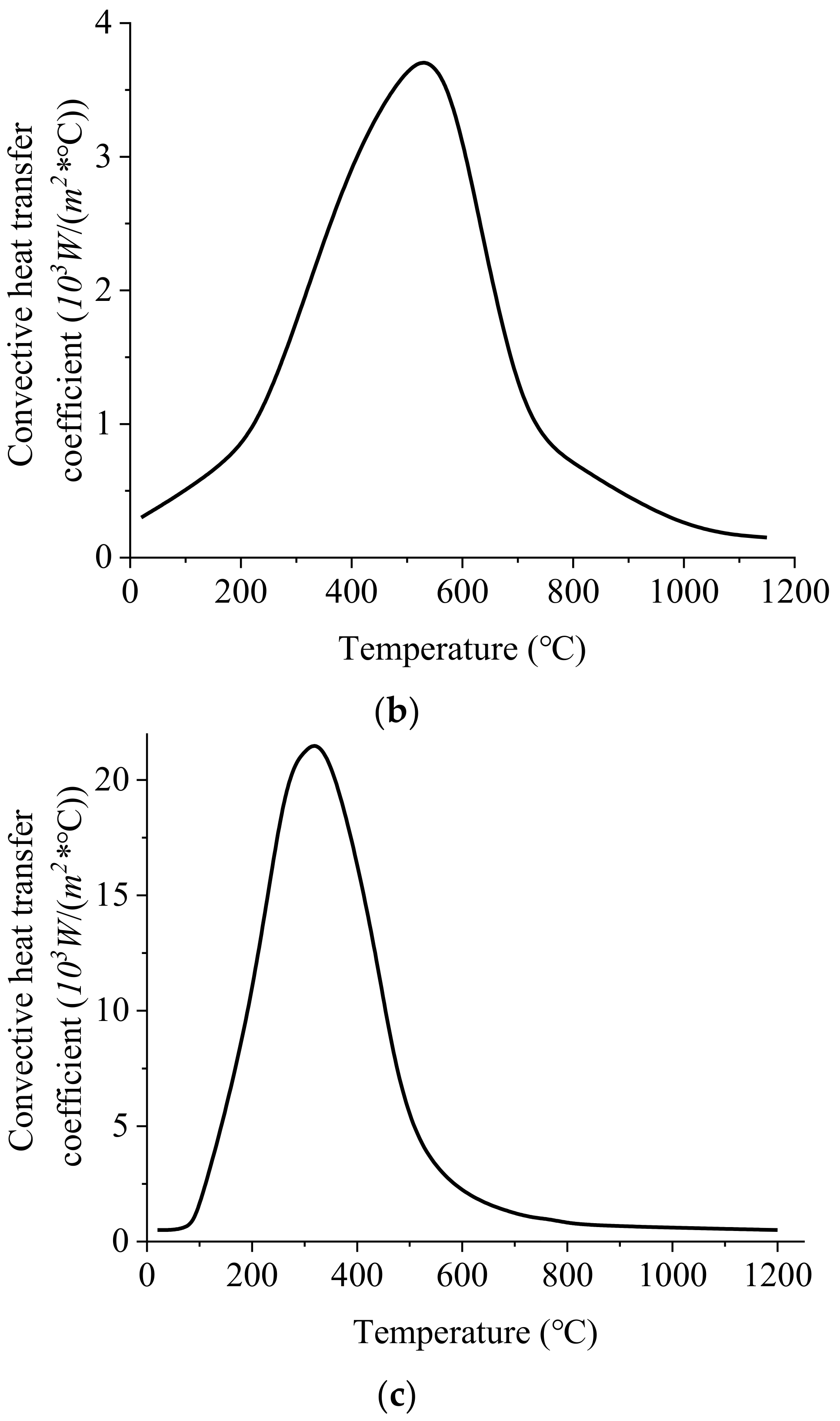
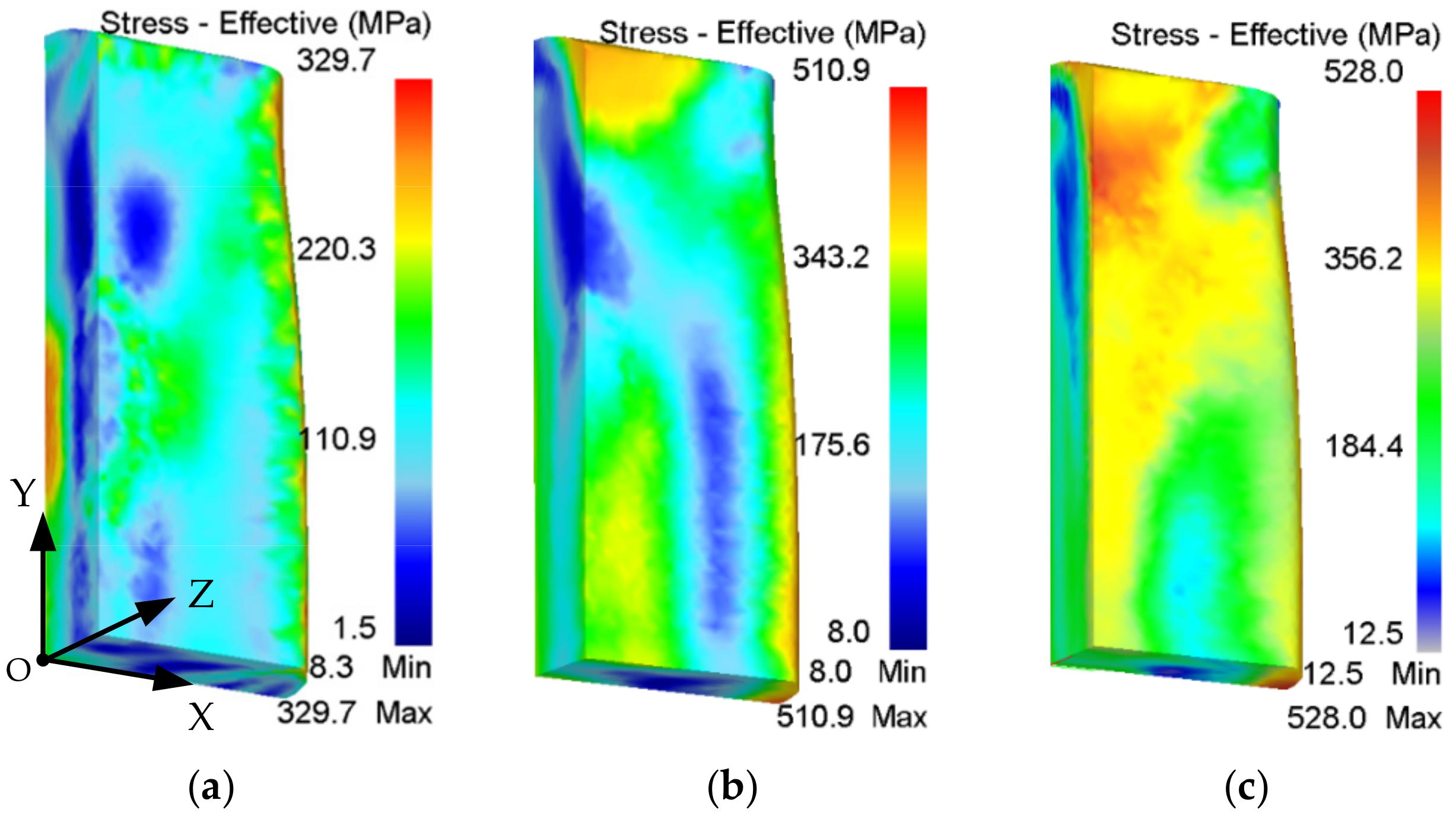
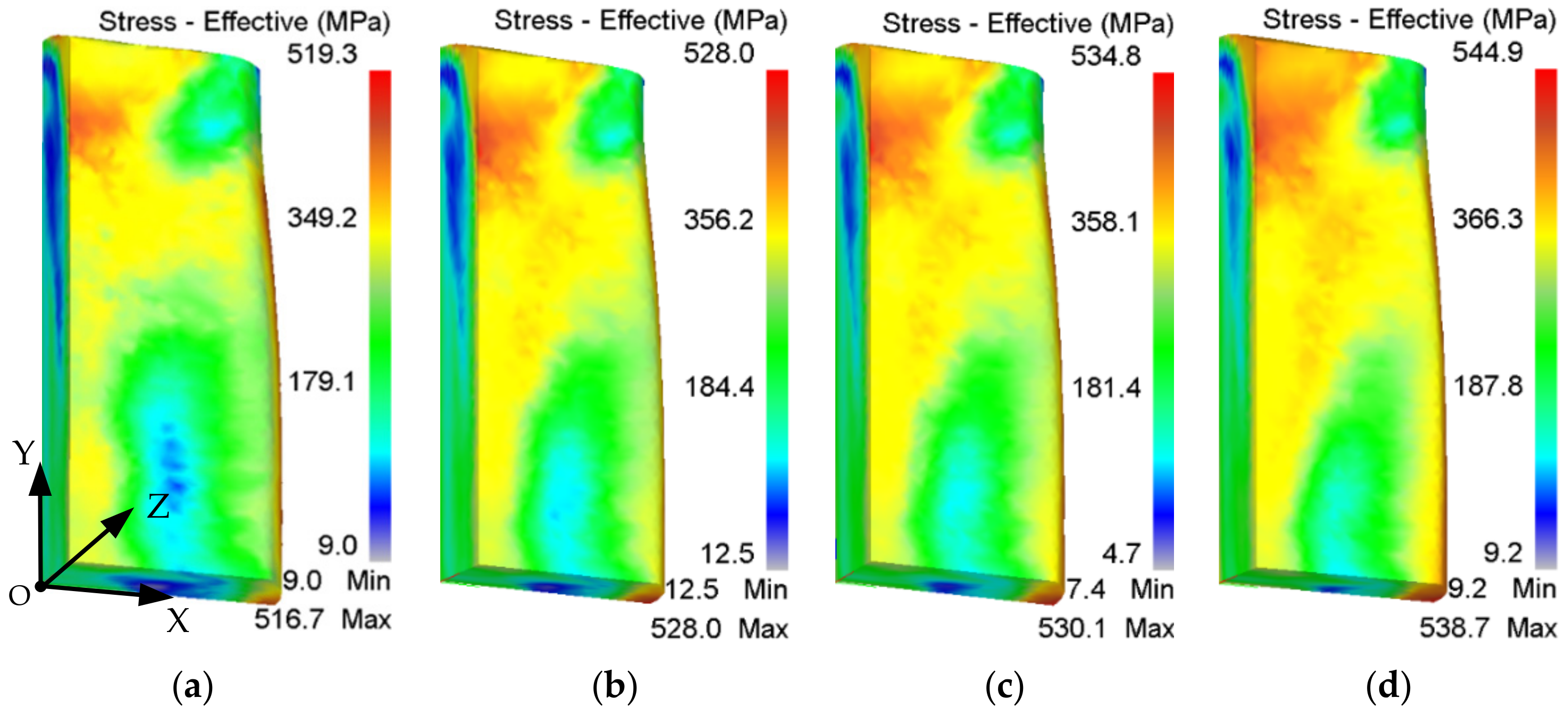
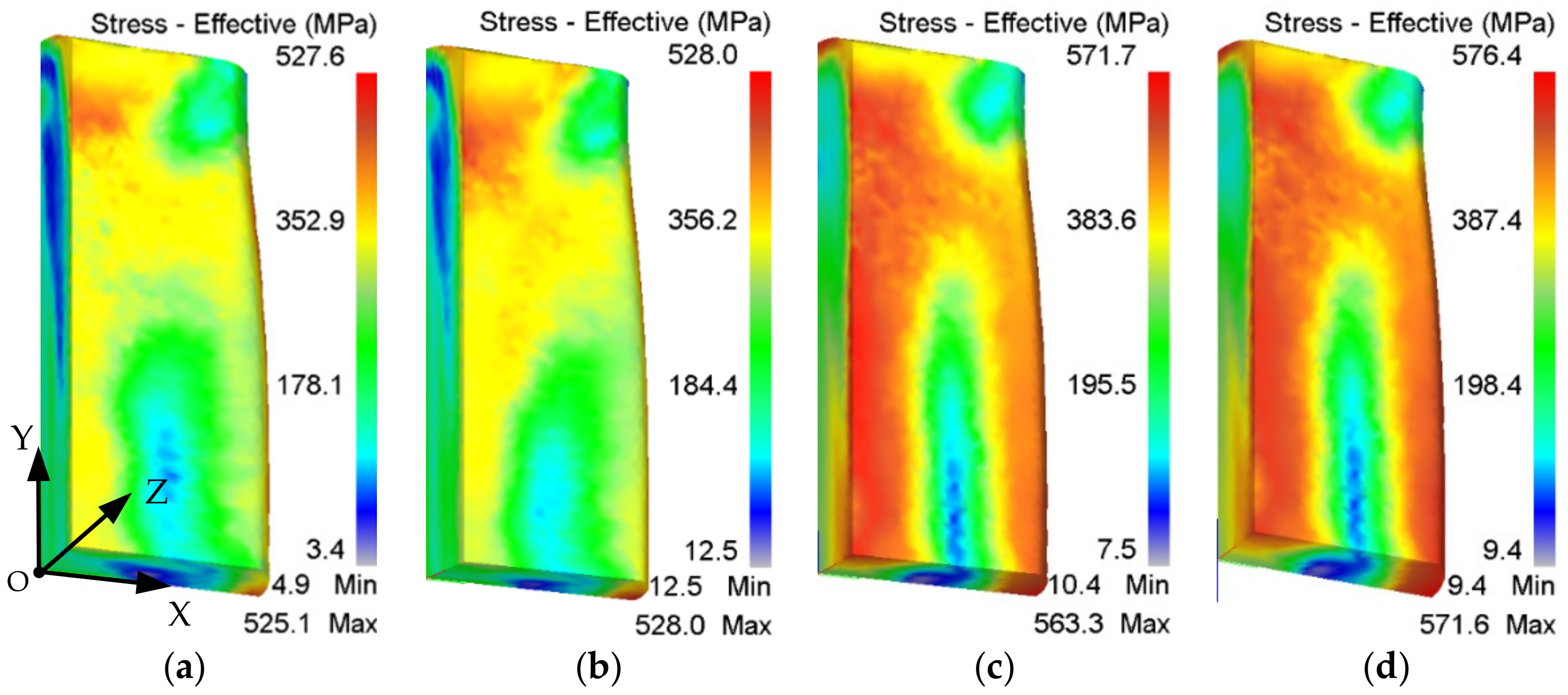
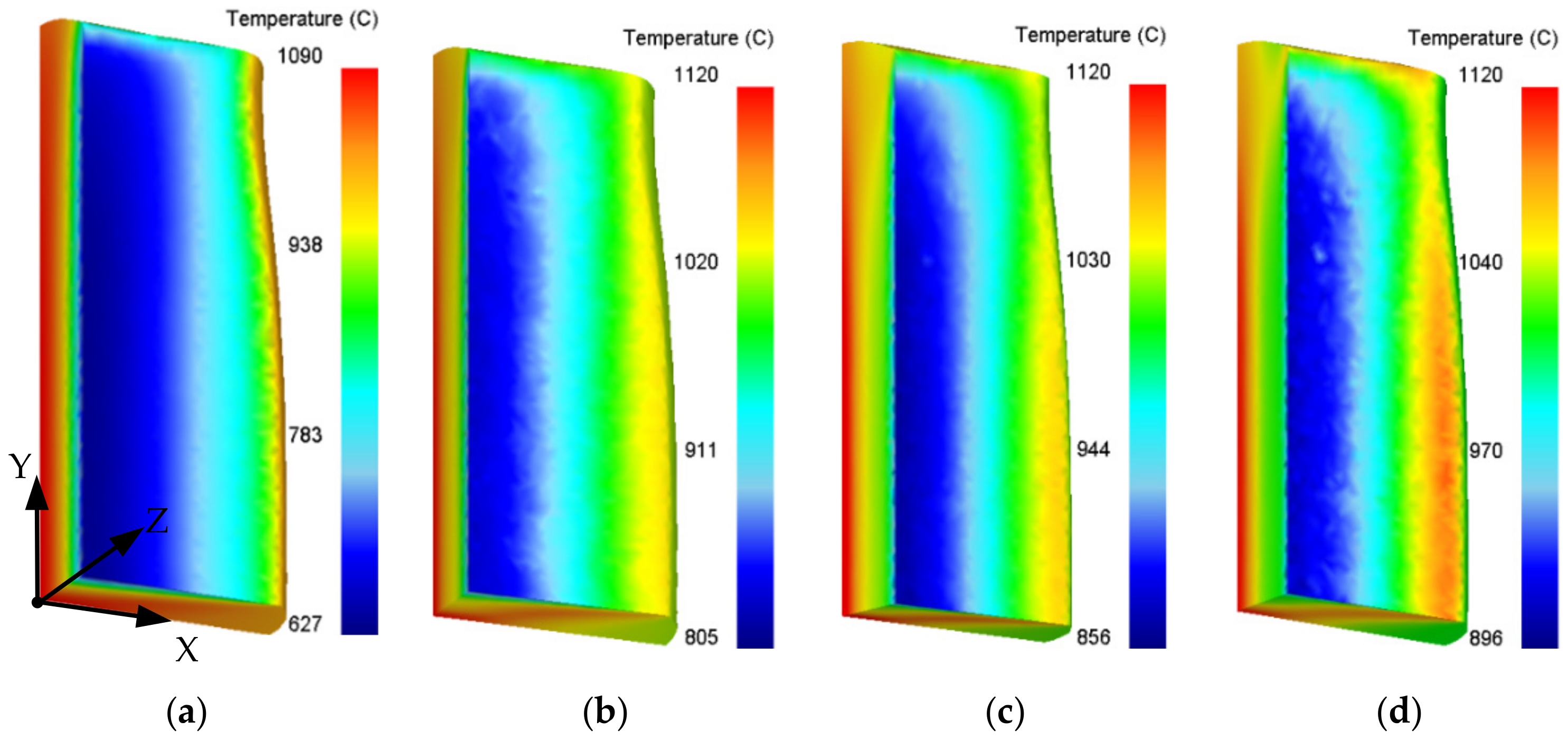
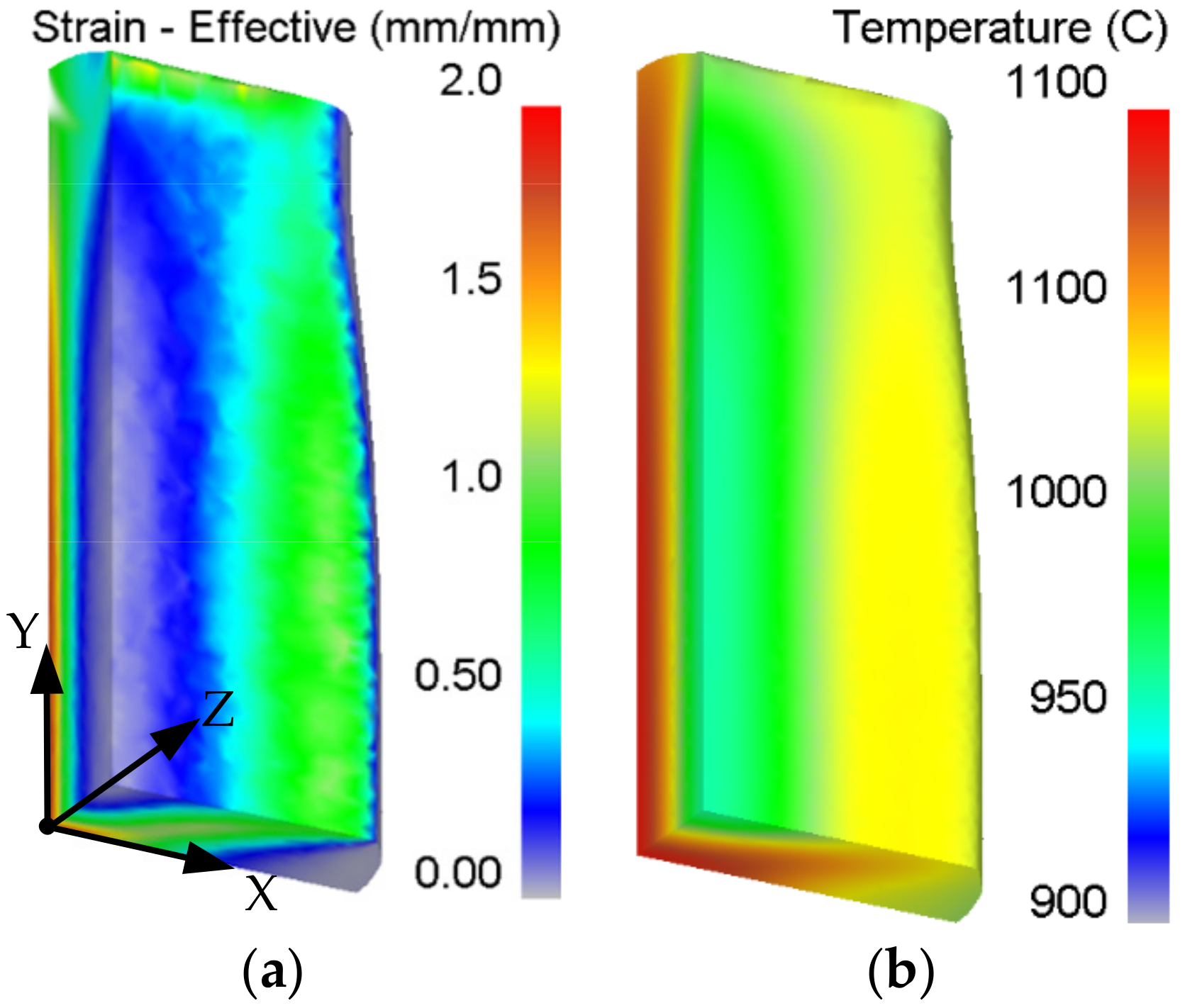
3. Simulations of Residual Stresses with Different Parameters
4. Experimental Results and Discussion
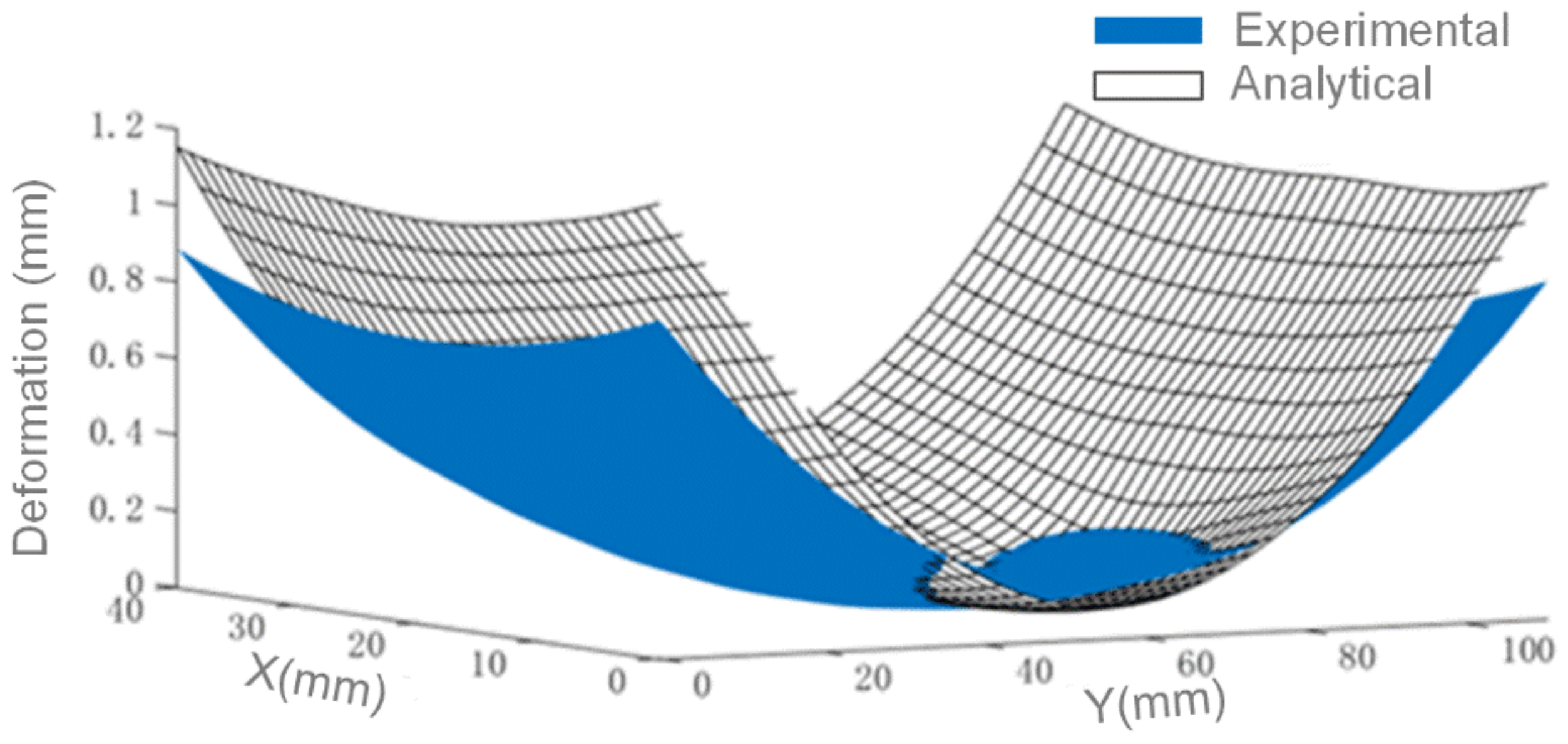
4.1. Experimental Results of Residual Stresses
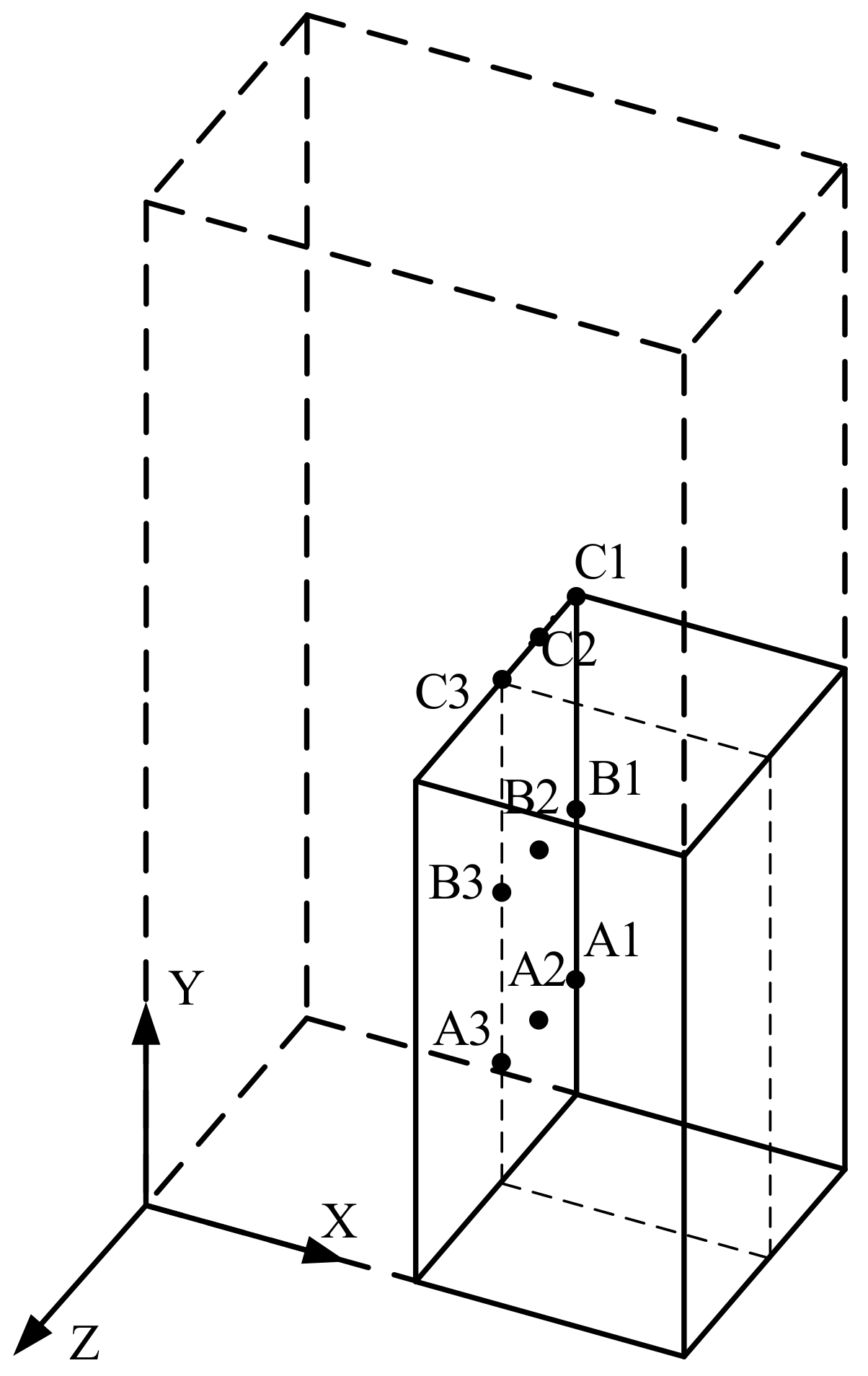
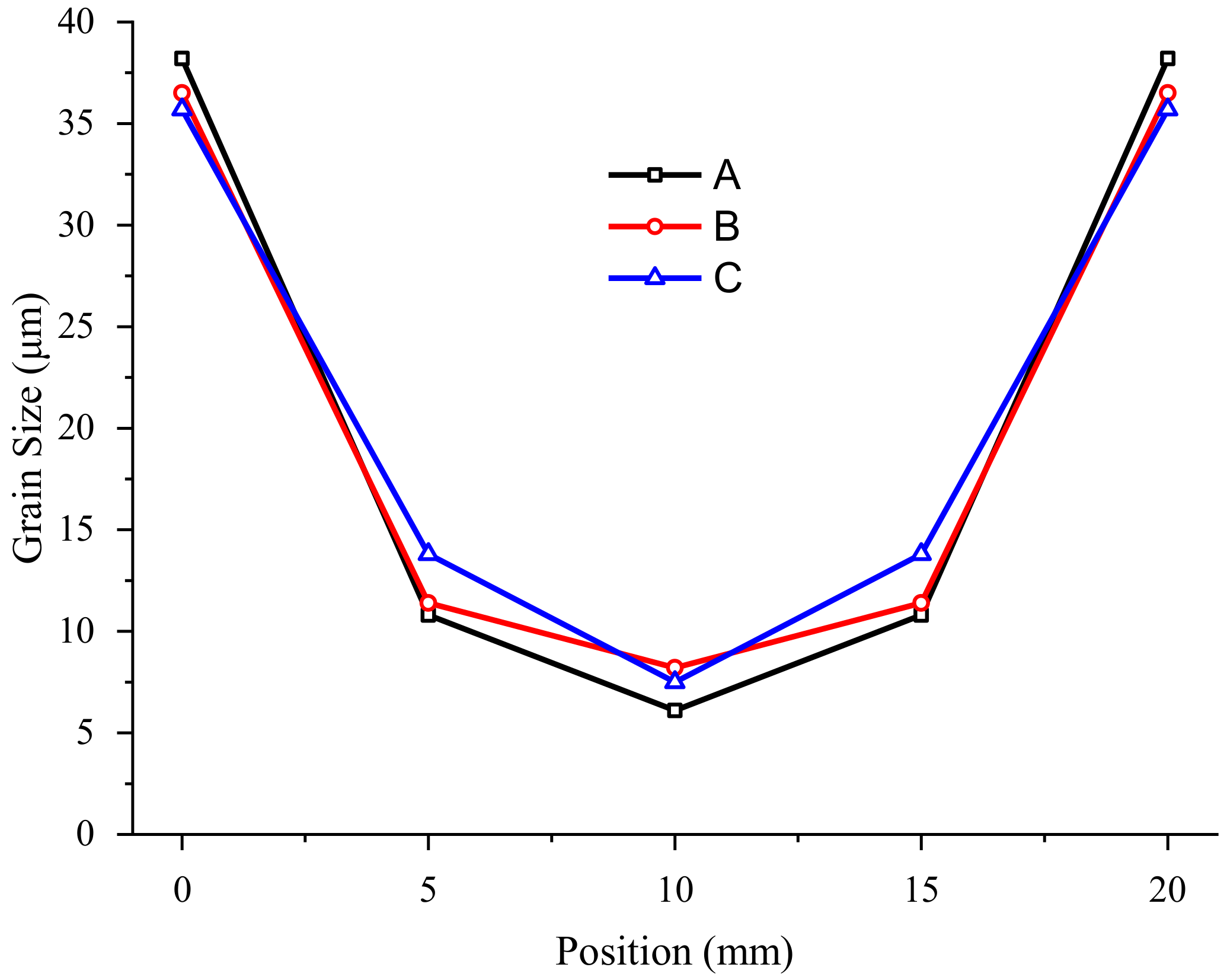
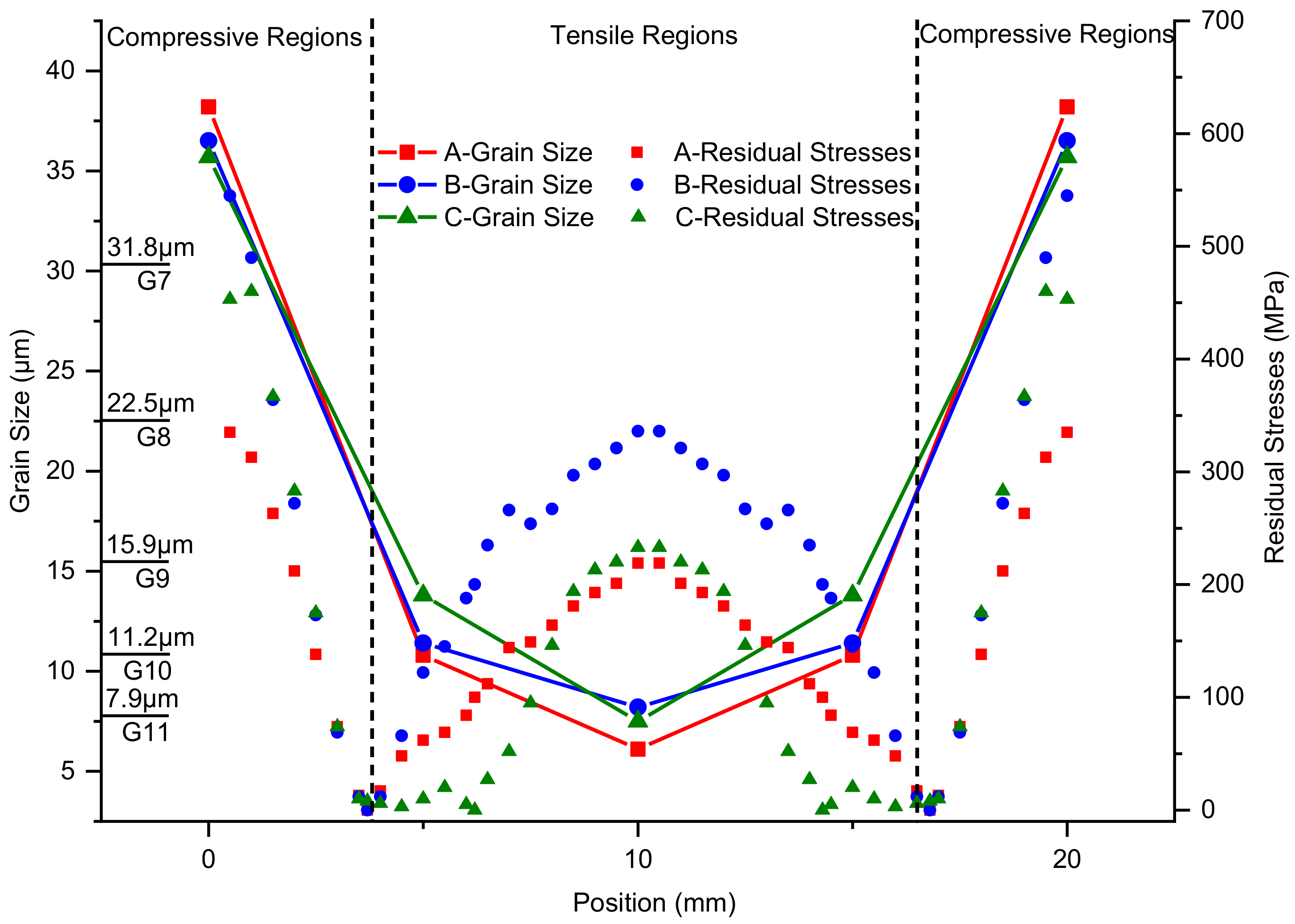
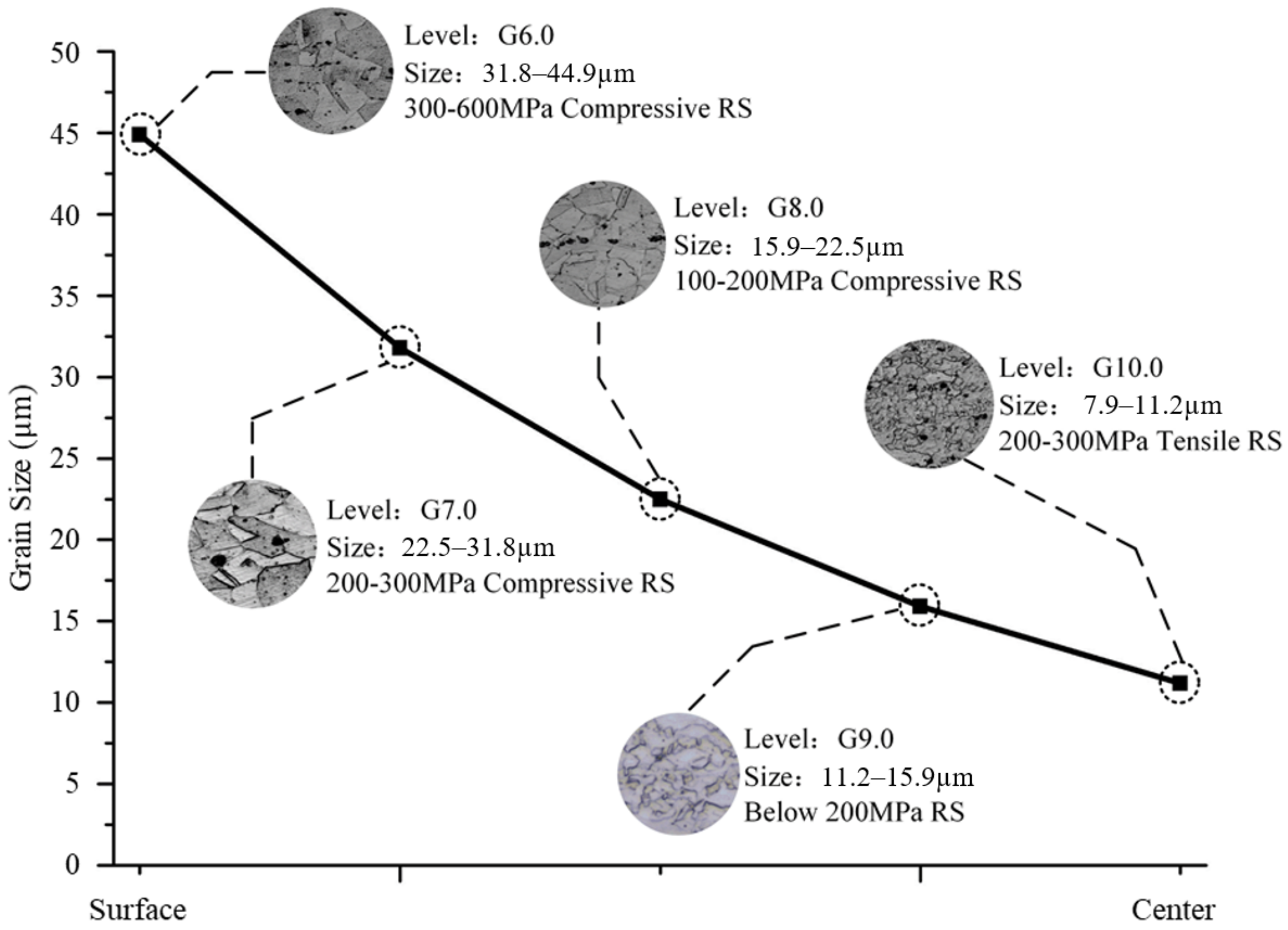
4.2. Experimental Results of Grain Structures
5. Conclusions
- (1)
- The level of RS rises with the increase in forging temperature, loading speed, and cooling speed. Among them, loading speed mainly influences the stress value, and the cooling method has remarkable effects on both the value and distribution of RS. A small convective heat transfer coefficient and loading speed are recommended to obtain stable parts with uniform and low-level RS.
- (2)
- A new layer-stripping method is put forward for interior RS measurement. The method is able to realize stress measurement in deep positions with high resolution. Measurement results are more accurate as they compensate for the stress redistribution caused by material removal. Compared with the traditional strain gauge layer-stripping method, the measurement efficiency of the new layer-stripping method is increased by 10 times.
- (3)
- RS curves are nearly parabolic in depth, as the compressive RS change to tensile from the surfaces to the center. The transition layer with low-level RS should be retained in the subsequent machining. The peak values of compressive and tensile stresses appear on the surfaces and center, respectively. Three-fifths in the center are tensile layers, while the remainder shows compressive stresses. Nonuniform plastic deformation and temperature gradient are the two main factors that induce the RS during forging.
- (4)
- Differences in grain size during single-pass compression are principally caused by the DRX. Grain size decreases from the surfaces to the center. Incomplete DRX results in the coexistence of stretched grains and refined grains. In the compressive regions, stress values share the same rules as grain size, while, in the tensile regions, they are contrary. In the average grain size range of G7.0~G9.0, the variety of RS is around 100 MPa for every 1.0 change in grain size. According to the residual stress and grain distribution law of the blank, the optimal positions of the part in the blank ought to be arranged close to a quarter of the forging blank to guarantee low residual stresses and a homogeneous and refined grain. Compared with the center position of the part in the blank, the residual stress of the part is reduced by 70%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.S.; Niu, S.; Zhang, Q.L.; Fu, S.X.; Qu, N.S. Investigation of material removal in inner-jet electrochemical grinding of GH4169 alloy. Sci. Rep. 2017, 7, 3482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brand, A.J.; Karhausen, K.; Kopp, R. Microstructure simulation of nickel base alloy Inconel 718 in production of turbine disks. Mater. Sci. Technol. 1996, 12, 963–969. [Google Scholar] [CrossRef]
- Zouari, M.; Bozzolo, N.; Loge, R.E. Mean field modelling of dynamic and post-dynamic recrystallization during hot deformation of Inconel 718 in the absence of deta phase particles. Mater. Sci. Eng. A 2016, 655, 408–424. [Google Scholar] [CrossRef]
- Geng, L.; Na, Y.S.; Park, N.K. Continuous cooling transformation behavior of Alloy 718. Mater. Lett. 1997, 30, 401. [Google Scholar] [CrossRef]
- Tang, X.F.; Wang, B.Y.; Ji, H.C.; Fu, X.B.; Xiao, W.C. Behavior and modeling of microstructure evolution during metadynamic recrystallization of a Ni-based superalloy. Mater. Sci. Eng. A 2016, 675, 192–203. [Google Scholar] [CrossRef]
- Rist, M.A.; James, J.A.; Tin, S.; Roder, B.A.; Daymond, M.R. Residual stress in a quenched superalloy turbine disk: Measurement and modeling. Metall. Mater. Trans. A 2006, 37, 459–467. [Google Scholar] [CrossRef]
- Aba-Perea, P.E.; Pirling, T.; Preuss, M. In-situ residual stress analysis during annealing treatment using neutron diffraction in combination with a novel furnace design. Mater. Des. 2016, 110, 925–931. [Google Scholar] [CrossRef]
- Wallis, R.A.; Bhowal, P.R.; Bhathena, N.M.; Raymand, E.L. Modeling the heat treatment of superalloy forgings. JOM 1989, 41, 35–37. [Google Scholar] [CrossRef]
- Cihak, U.; Staron, P.; Marketz, W.; Leitner, H.; Tockner, J.; Clemens, H. Residual stress in forged IN718 turbine disks. Int. J. Mater. Res. 2004, 95, 663–667. [Google Scholar] [CrossRef]
- Marcelin, J.L. Optimization of the cooling regime of hot-rolled complex beams. Int. J. Adv. Manuf. Technol. 2006, 32, 711–718. [Google Scholar] [CrossRef]
- Ameli, A.; Movahhedy, M.R. A parametric study on residual stresses and forging load in cold radial forging process. Int. J. Adv. Manuf. Technol. 2007, 33, 7–17. [Google Scholar] [CrossRef]
- Chen, X.M.; Lin, Y.C.; Chen, M.S.; Li, H.B.; Wen, D.X.; Zhang, J.L.; He, M. Microstructural evolution of a nickel based superalloy during hot deformation. Mater. Des. 2015, 77, 41–49. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M.; Cabrera, J.M.; Calvo, J. Microstructural evolution and constitutive equations of Inconel 718 alloy under quasi-static and quasi-dynamic conditions. Mater. Des. 2015, 94, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Loyda, A.; Gernandez-Munoz, G.M.; Reyes, L.A.; Zambrano-Robledo, P. Microstructure Modeling of a Ni-Fe-Based Superalloy During the Rotary Forging Process. J. Mater. Eng. Perform. 2016, 25, 2128–2137. [Google Scholar] [CrossRef]
- Li, J.B.; Wang, X.Y.; Jin, J.S. Research on residual stresses during hot stamping with flat and local-thickened plates. Int. J. Adv. Manuf. Technol. 2017, 92, 2987–2999. [Google Scholar] [CrossRef]
- Xu, X.Y.; Ma, X.D.; Wang, H.; Ye, Z.; Chang, J.W.; Xu, Y.; Sun, G.A.; Lv, W.J.; Gao, Y.K. Characterization of residual stresses and microstructural features in an Inconel 718 forged compressor disk. Trans. Nonferr. Met. Soc. China 2019, 29, 569–578. [Google Scholar] [CrossRef]
- Loyda, A.; Reyes, L.A.; Hernandez-Munoz, G.M.; Garcia-Castillo, F.A.; Zambrano-Robledo, P. Influence of the incremental deformation during rotary forging on the microstructure behavior of a nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2018, 97, 2383–2396. [Google Scholar] [CrossRef]
- Ma, Q.; Lin, Z.Q.; Yu, Z.Q. Prediction of deformation behavior and microstructure evolution in heavy forging by FEM. Int. J. Adv. Manuf. Technol. 2009, 40, 253–260. [Google Scholar] [CrossRef]
- Toro, L.; Cavazos, A.; Colas, R. Grain Size Estimation of Superalloy Inconel 718 After Upset Forging by a Fuzzy Inference System. J. Mater. Eng. Perform. 2009, 18, 1183–1192. [Google Scholar] [CrossRef]
- Berti, G.A.; Quagliato, L.; Monti, M. Set-up of radial-axial ring rolling precess: Process worksheet and ring geometry expansion prediction. Int. J. Mech. Sci. 2015, 99, 58–71. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, D.; Hu, Y.; Yang, Y.H.; Zhu, X.L. Effect of Grain Size Distribution on Processing Maps for Isothermal Compression of Inconel 718 Superalloy. J. Mater. Eng. Perform. 2016, 25, 677–686. [Google Scholar] [CrossRef]
- Zhu, X.L.; Liu, D.; Xing, L.J.; Hu, Y.; Yang, Y.H. Microstructure evolution of Inconel 718 alloy during ring rolling process. Int. J. Precis. Eng. Manuf. 2016, 17, 775–783. [Google Scholar] [CrossRef]
- Tang, X.F.; Wang, B.Y.; Zhang, H.; Fu, X.B.; Ji, H.C. Study on the microstructure evolution during radial axial ring rolling of IN718 using a unified internal state variable material model. Int. J. Mech. Sci. 2017, 128–129, 235–252. [Google Scholar] [CrossRef]
- Tang, X.F.; Wang, B.Y.; Huo, Y.M.; Ma, W.Y.; Zhou, J.; Ji, H.C.; Fu, X.B. Unified modeling of flow behavior and microstructure evolution in hot forming of a Ni-based superalloy. Mater. Sci. Eng. A 2016, 662, 54–62. [Google Scholar] [CrossRef]
- Zhbankov, I.G.; Pering, A.V.; Aliieva, L.I. New schemes of forging plates, shafts, and disks. Int. J. Adv. Manuf. Technol. 2016, 82, 287–301. [Google Scholar] [CrossRef]
- Dohepty, R.D.; Hughes, D.A.; Humphreys, F.J.; Jones, J.J.; Jensen, D.J.; Kassner, M.E.; King, W.E.; Mcnelley, T.R.; Mcqueen, H.I.; Rollett, A.D. Current issues in recrystallization: A review. Mater. Sci. Eng. A 1997, 238, 219–274. [Google Scholar]
- Zheng, P.; Zheng, Y.; Wei, H.; Qian, Y. Characteristics and effects of residual stress distributed along the thickness in 2324 aluminum alloy plate. J. Acta Aeronaut. Astronaut. Sin. 1996, 17, 330–336. [Google Scholar]
- Liu, L.; Sun, J.; Chen, W.; Sun, P. Modified Layer-Removal Method for Measurement of Residual Stress in Pre-stretched Aluminium Alloy Plate. J. Harbin Inst. Technol. 2015, 22, 34–40. [Google Scholar]
- Steinzig, M.; Ponslet, E. Residual stress measurement using the hole drilling method and laser speckle interferometry part I. J. Exp. Tech. 2003, 27, 43–46. [Google Scholar] [CrossRef]
- Ponslet, E.; Steinzig, M. Residual stress measurement using the hole drilling method and laser speckle interferometry part II: Analysis technique. J. Exp. Tech. 2003, 27, 17–21. [Google Scholar] [CrossRef]
- Ponslet, E.; Steinzig, M. Residual stress measurement using the hole drilling method and laser speckle interferometry part III: Analysis technique. J. Exp. Tech. 2003, 27, 45–48. [Google Scholar] [CrossRef]
- Steinzig, M.; Takahashi, T. Residual stress measurement using the hole drilling method and laser speckle interferometry part IV: Measurement Accuracy. J. Exp. Tech. 2003, 27, 59–63. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, J.; Li, T.; Zhang, L.; Zhang, S. Slope Measurement Method for Three-dimensional Residual Stress in 7075-T651 Aluminum Alloy Plate. J. Acta Armamentarii 2021, 42, 2004–2012. [Google Scholar]
- Wang, Z.B.; Sun, J.F.; Liu, L.B.; Wang, R.Q.; Chen, W.Y. An analytical model to predict the machining deformation of frame parts caused by residual stress. J. Mater. Process. Technol. 2019, 274, 116282. [Google Scholar] [CrossRef]
- Davey, K.; Ward, M.J. A practical method for finite element ring rolling simulation using the ALE flow formulation. Int. J. Mech. Sci. 2002, 44, 165–190. [Google Scholar] [CrossRef]
- Reti, T.; Fried, Z.; Felde, I. Computer simulation of steel quenching process using a multi-phase transformation model. Comput. Mater. Sci. 2001, 22, 261–278. [Google Scholar] [CrossRef]
- Song, R.H.; Qin, H.L.; Li, D.; Bi, Z.N.; Zhang, J. An experimental and numerical study of quenching-induced residual stresses under the effect of dsa in an in718 superalloy disc. J. Eng. Mater. Technol. 2021, 144, 011002. [Google Scholar]
- Deng, H.Z.; Wang, L.; Liu, Y.; Song, X.; Meng, F.Q.; Huang, S. The evolution law of δ phase of in 718 superalloy in temperature/stress coupled field. Mater. Charact. 2021, 184, 111684. [Google Scholar] [CrossRef]






| Elements | C | Cr | Co | Al | Ti | Nb | Ni |
|---|---|---|---|---|---|---|---|
| wt% | 17.0~21.0 | 0.30~0.70 | 0.75~1.15 | 4.75~5.50 | Bal. | ||
| Mechanical properties | Temperature (20 ) | ||||||
| Tensile strength (MPa) | 1372 | ||||||
| Elongation (%) | 14.6 | ||||||
| Coefficient of thermal expansion () | 13.2 | ||||||
| Thermal conductivity (W/(m °C)) | 13.4 | ||||||
| Material | Q (J/mol) | A | n | ||
|---|---|---|---|---|---|
| GH4169 | 413,118 | 8.314 | 5.05 | 0.0024 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Hou, G.; Zhao, Y.; Sun, J.; Guo, J.; Chen, W. Characterization of Residual Stresses and Grain Structure in Hot Forging of GH4169. Aerospace 2022, 9, 92. https://doi.org/10.3390/aerospace9020092
Wang Z, Hou G, Zhao Y, Sun J, Guo J, Chen W. Characterization of Residual Stresses and Grain Structure in Hot Forging of GH4169. Aerospace. 2022; 9(2):92. https://doi.org/10.3390/aerospace9020092
Chicago/Turabian StyleWang, Zibiao, Guangsha Hou, Yang Zhao, Jianfei Sun, Jiangzhen Guo, and Wuyi Chen. 2022. "Characterization of Residual Stresses and Grain Structure in Hot Forging of GH4169" Aerospace 9, no. 2: 92. https://doi.org/10.3390/aerospace9020092
APA StyleWang, Z., Hou, G., Zhao, Y., Sun, J., Guo, J., & Chen, W. (2022). Characterization of Residual Stresses and Grain Structure in Hot Forging of GH4169. Aerospace, 9(2), 92. https://doi.org/10.3390/aerospace9020092






