Improvement of Airport Surface Operation at Tokyo International Airport Using Optimization Approach
Abstract
:1. Introduction
2. Current Surface Operation
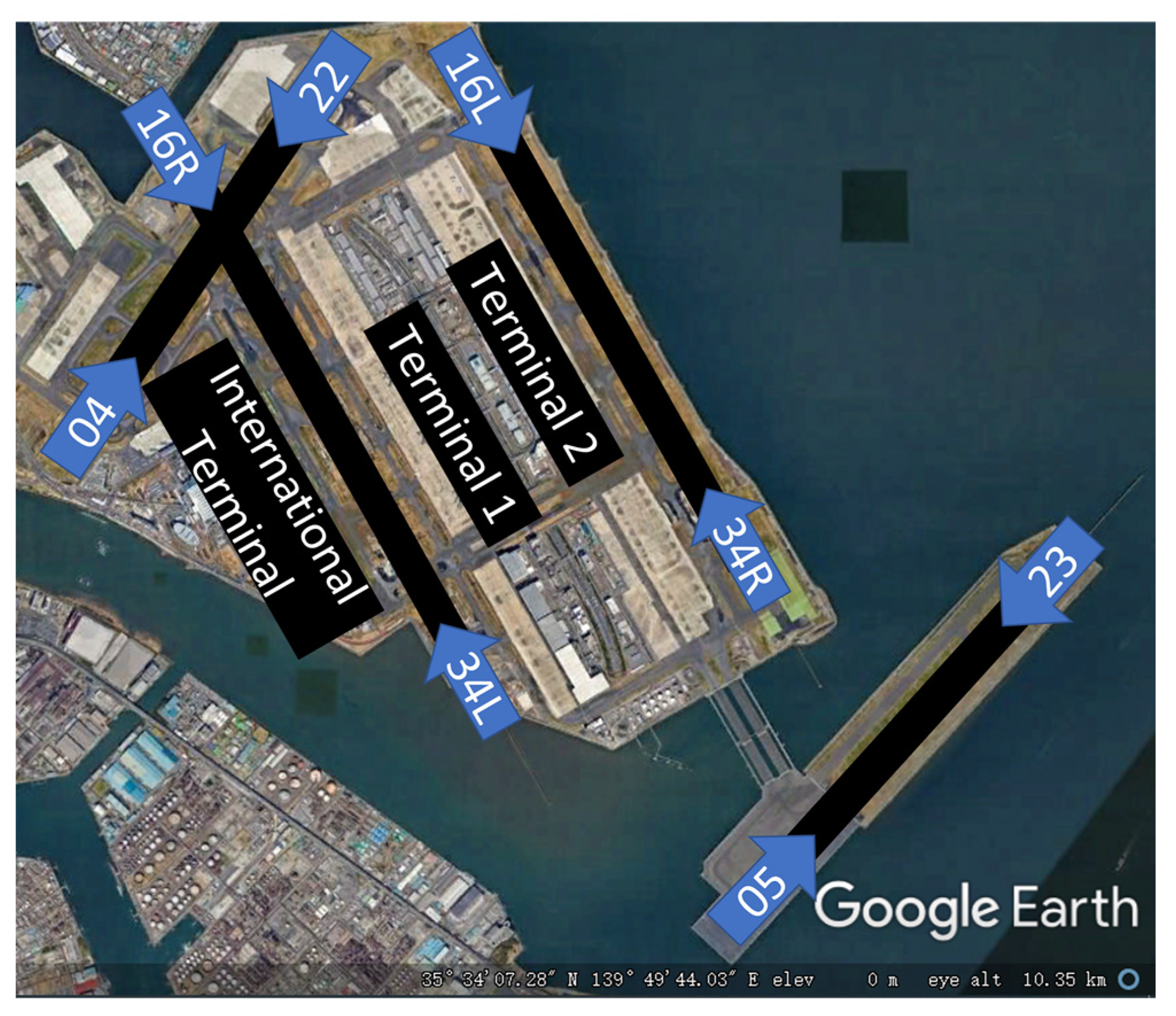
2.1. Overview of the Tokyo International Airport
2.2. CARATS Open Data
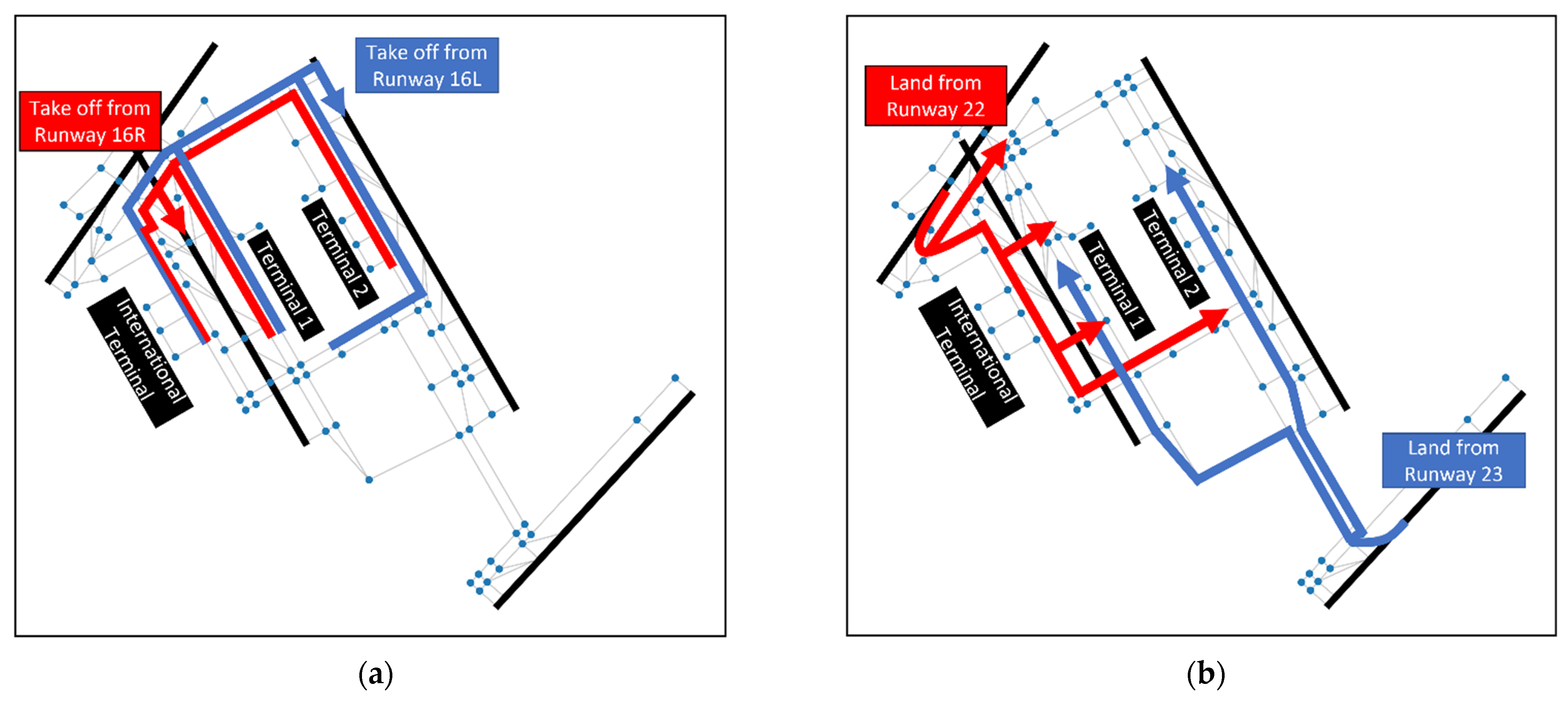
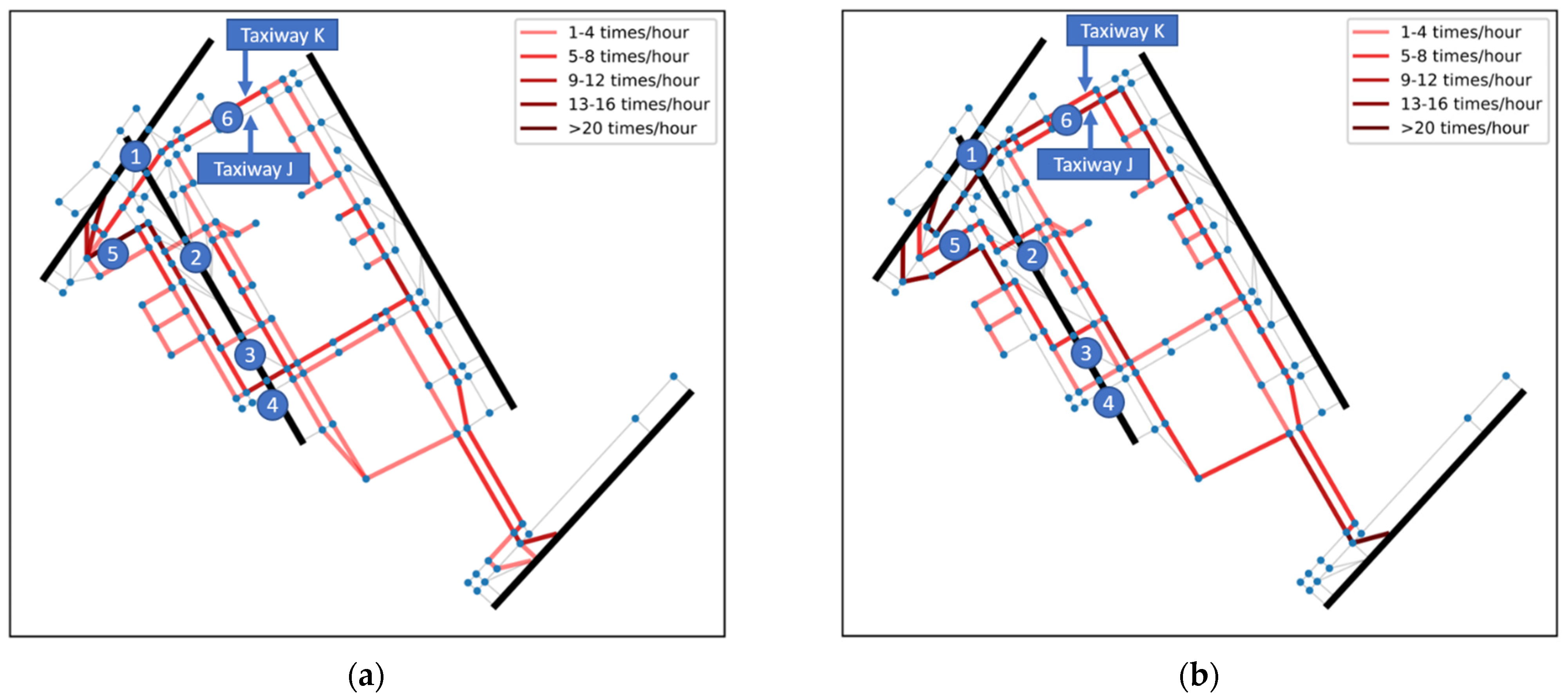
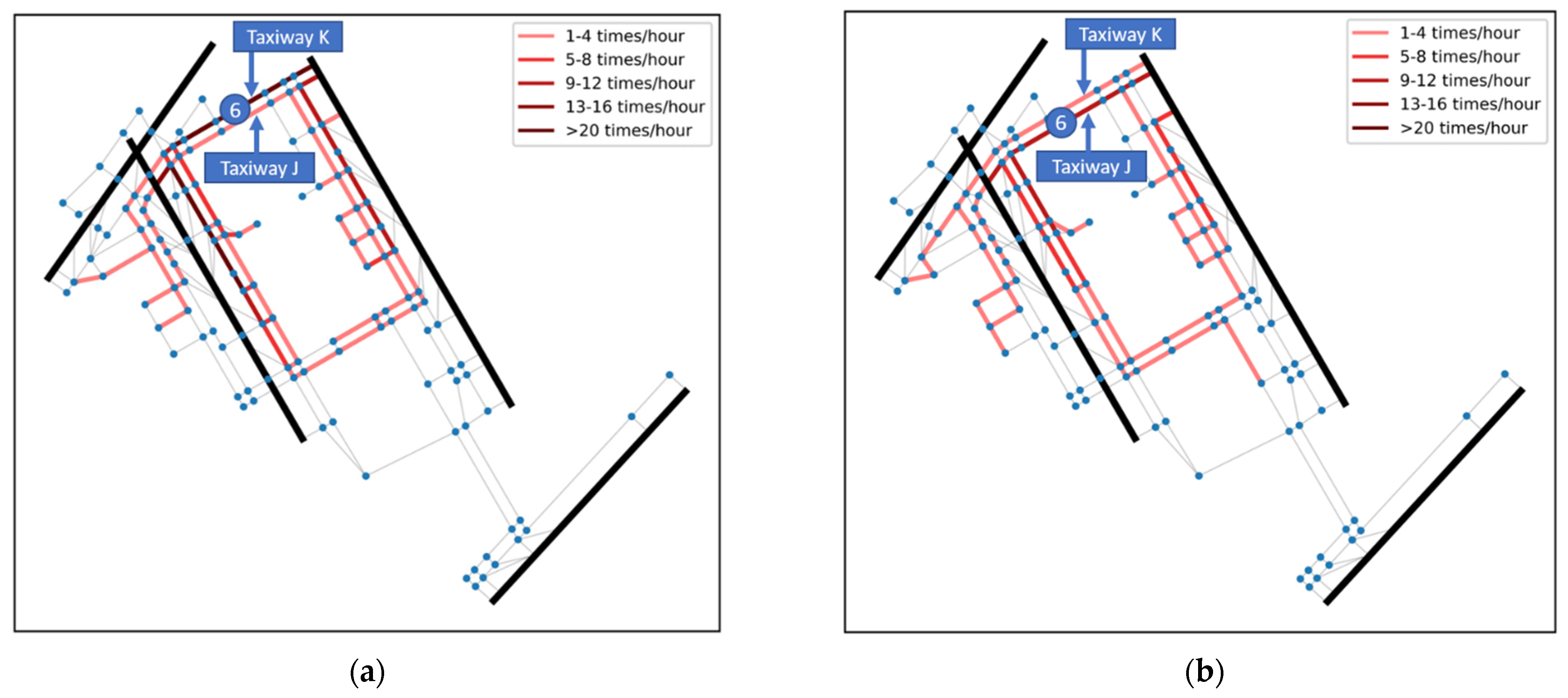
2.3. Taxiway Selection Patterns
3. Model Development
3.1. Mixed-Integer Linear Programming and Receding Horizon
3.2. Model Parameters
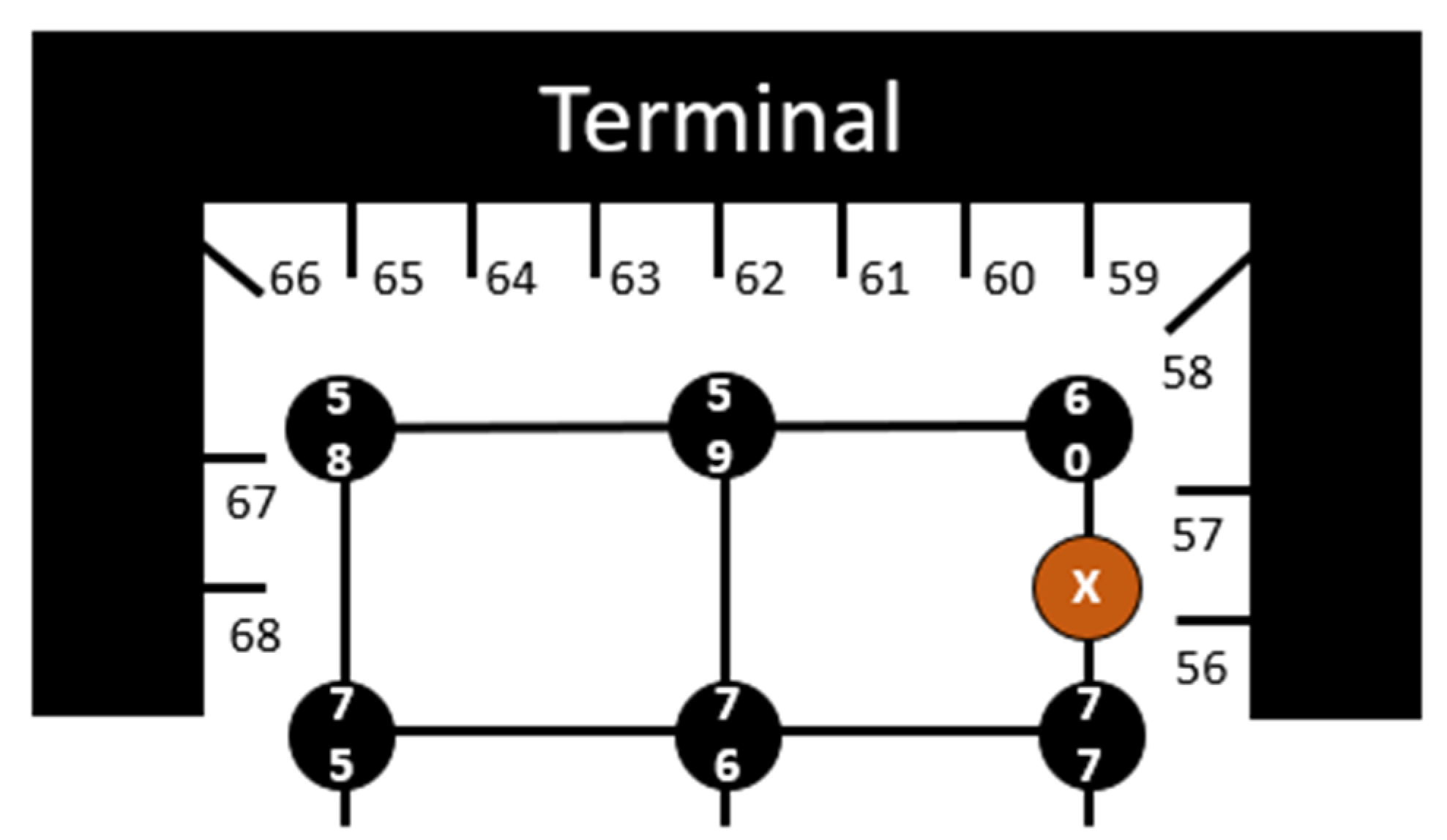
3.2.1. Airport Graph Model
| Algorithm1 Floyd (G(N,E)). |
| let s be a |N| × |N| array initialized to ∞ (infinity) |
| foreach edge(u,v) in E do |
| s[u][v] ← l(u,v) //l(u,v) is the length of the edge (u,v) |
| foreach v in N do |
| s[u][v] ← 0 |
| for k from 1 for k from 1 to |N| |
| for i from 1 to |N| |
| for j from 1 to |N| |
| if s[i][j] > s[i][k] + s[k][j] |
| s[i][j] ← s[i][k] + s[k][j] |
| end if |
| return s |
3.2.2. Virtual Pushback Node
3.2.3. Runway Virtual Node and Cross Node
3.2.4. Aircraft Data
3.3. Decision Variables
3.4. Objective Function
3.5. Constraints
3.5.1. Constraints for Taxi Rules on the Graph Model
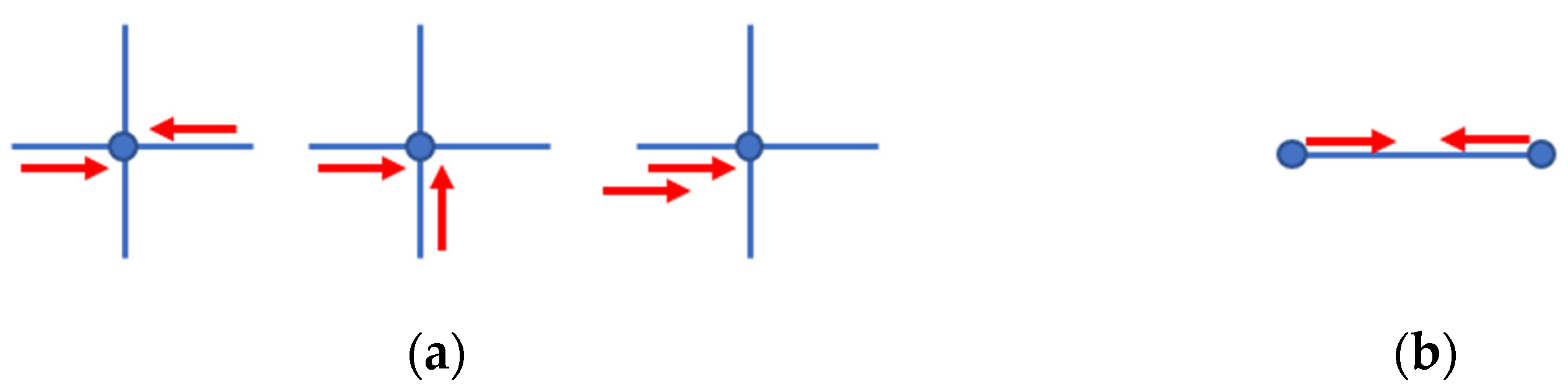
3.5.2. Constraints to Avoid Conflict on Taxiways
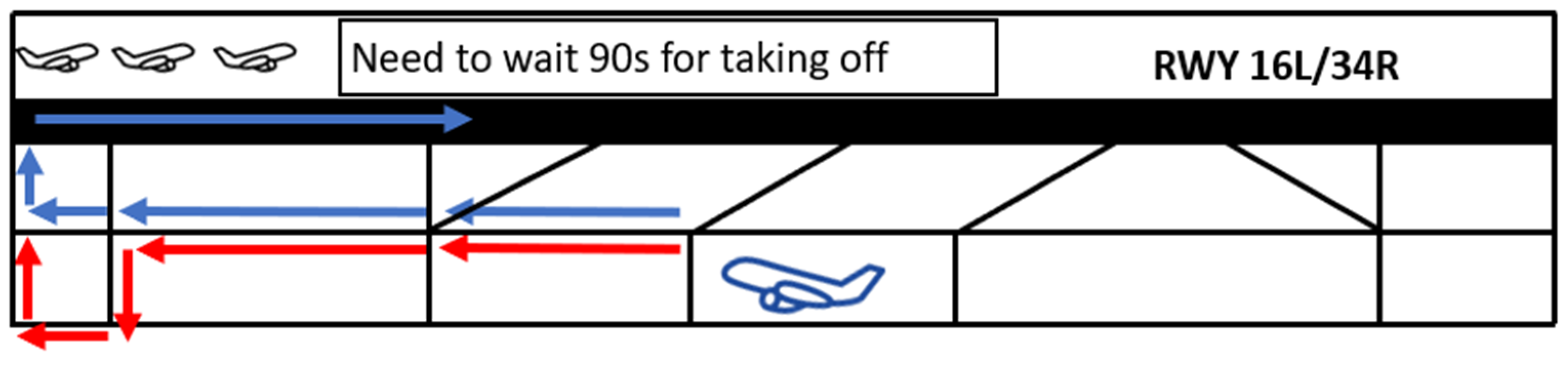
3.5.3. Constraints to Avoid Conflict in the Runway
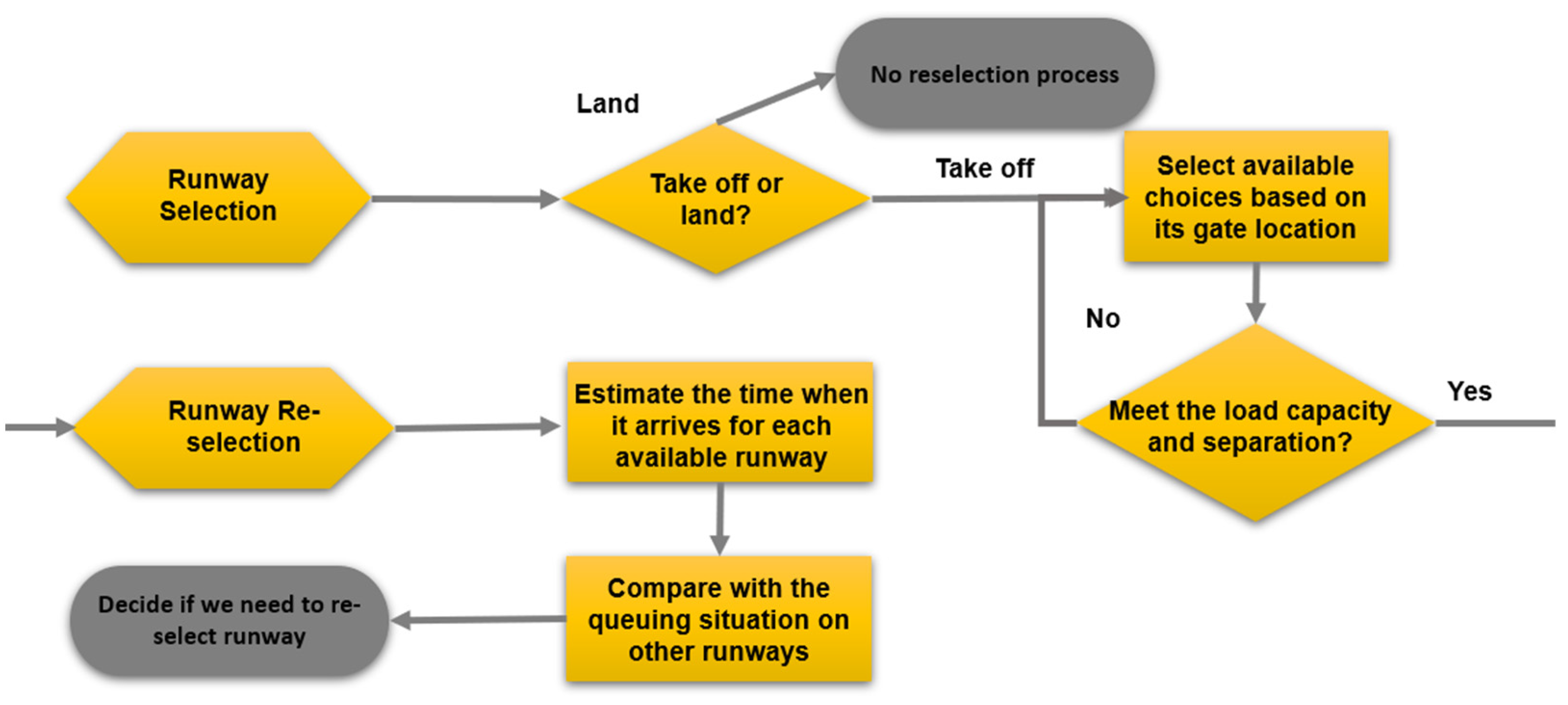
3.6. Runway Decider
4. Results and Discussion
4.1. Implementation
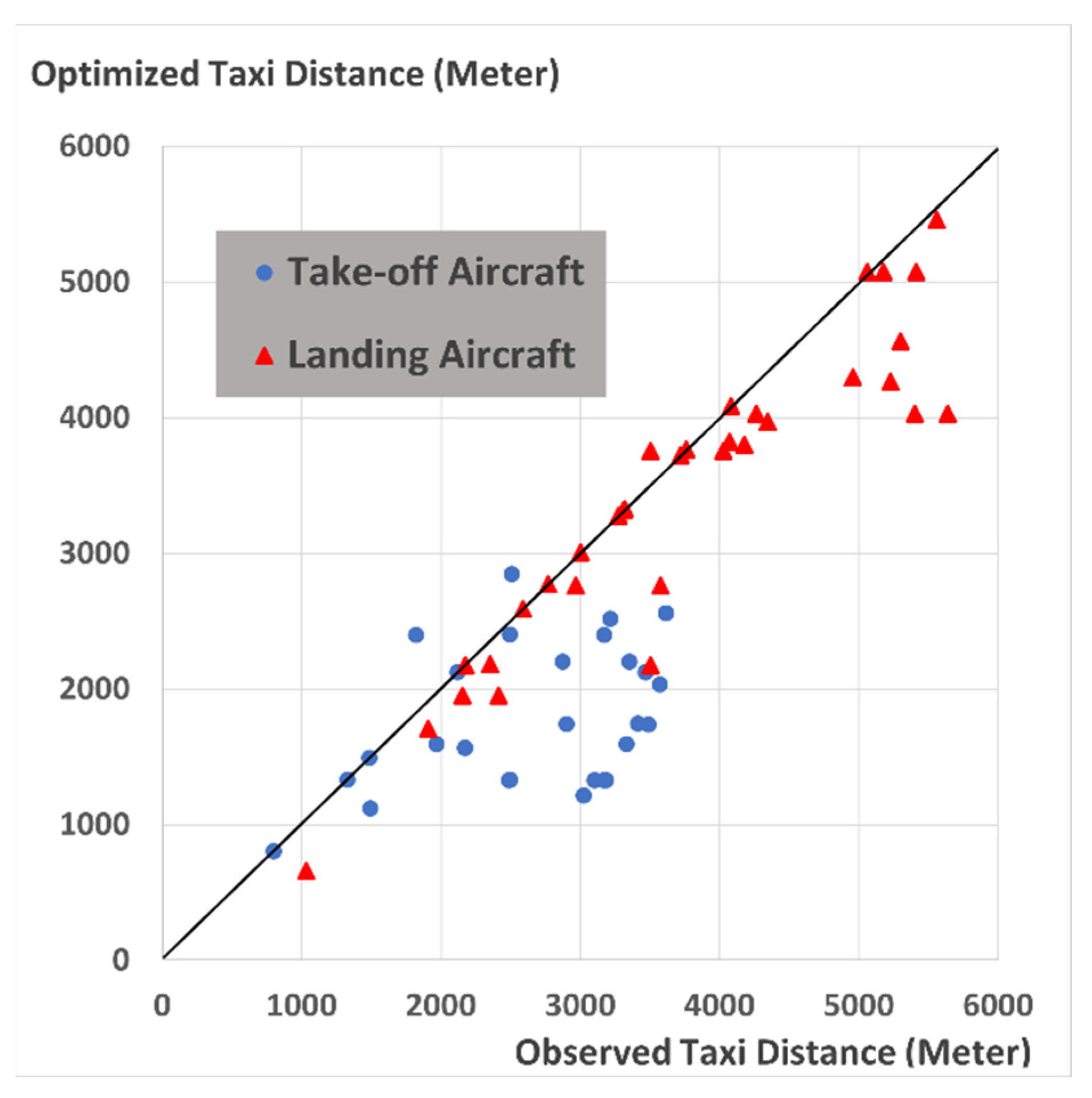
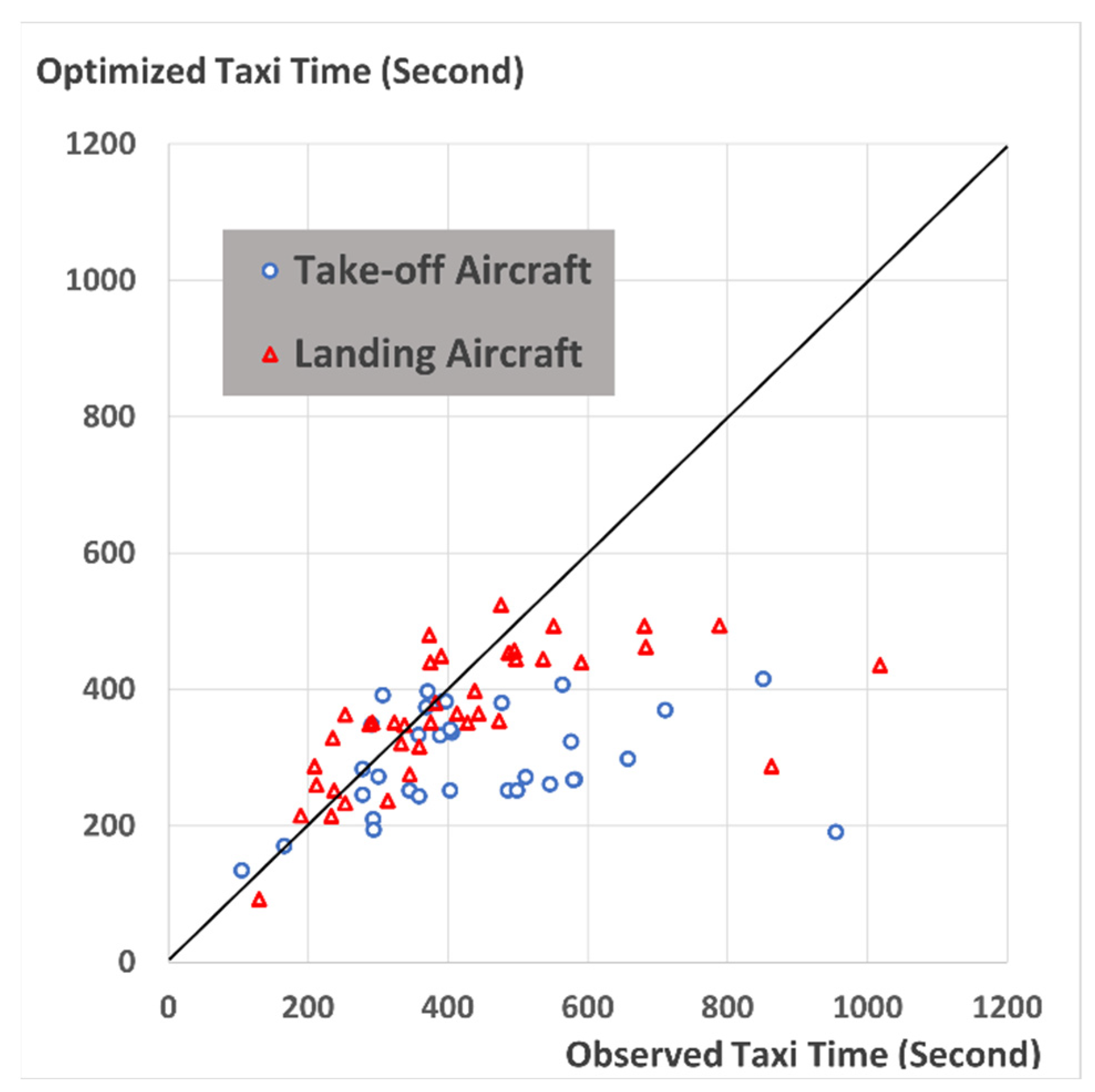
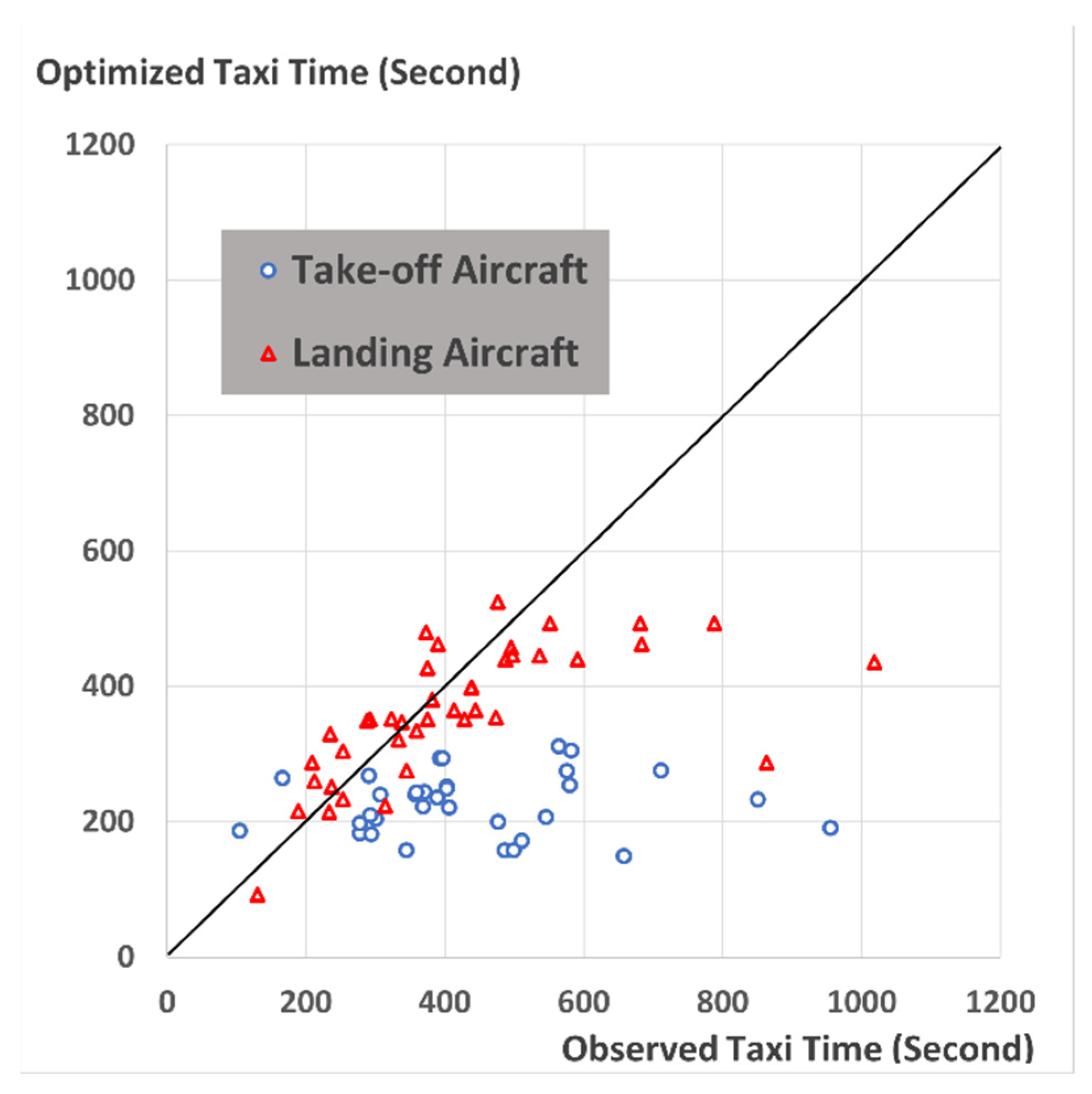
4.2. Result Comparison
4.3. Identification of Operation Differences
4.4. MILP Weight Parameter Analysis
4.5. Phenomenon due to Receding Horizon
4.6. Gate Re-Assignment and Analysis of Airline–Terminal Relationships
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simaiakis, I.; Khadilkar, H.; Balakrishnan, H.; Reynolds, T.G.; Hansman, R.J. Demonstration of reduced airport congestion through pushback rate control. Transp. Res. Part A Policy Pract. 2014, 66, 251–267. [Google Scholar] [CrossRef]
- Gudmundsson, S.V.; Cattaneo, M.; Redondi, R. Forecasting temporal world recovery in air transport markets in the presence of large economic shocks: The case of COVID-19. J. Air Transp. Manag. 2021, 91, 102007. [Google Scholar] [CrossRef]
- Airports Council International. Annual World Airport Traffic Report 2020; Airports Council International: Montreal, QC, Canada, 2020. [Google Scholar]
- Watabe, Y.; Noguchi, T. Site-investigation and geotechnical design of D-runway construction in Tokyo Haneda airport. Soils Found. 2011, 51, 1003–1018. [Google Scholar] [CrossRef] [Green Version]
- Gotteland, J.B.; Durand, N. Genetic algorithms applied to airport ground traffic optimization. In Proceedings of the 2003 Congress on Evolutionary Computation, CEC ’03, Canberra, Australia, 8–12 December 2003; Volume 1, pp. 544–551. [Google Scholar] [CrossRef] [Green Version]
- Atkin, J.A.D.; Burke, E.K.; Ravizza, S. The airport ground movement problem: Past and current research and future directions. In Proceedings of the 4th International Conference on Research in Air Transportation (ICRAT), Budapest, Hungary, 1–4 June 2010; pp. 131–138. [Google Scholar]
- Daş, G.S.; Gzara, F.; Stützle, T. A review on airport gate assignment problems: Single versus multi objective approaches. Omega 2020, 92, 102146. [Google Scholar] [CrossRef]
- Smeltink, J.W.; Soomer, M.J.; de Waal, P.R.; van der Mei, R.D. An Optimisation Model for Airport Taxi Scheduling. In Proceedings of the INFORMS Annual Meeting, Denver, CO, USA, 24–27 October 2004. [Google Scholar]
- Pesic, B.; Durand, N.; Alliot, J.-M. Aircraft Ground Traffic Optimisation Using a Genetic Algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference, San Francisco, CA, USA, 7–11 July 2001. [Google Scholar]
- Ravizza, S.; Atkin, J.A.D.; Burke, E.K. A more realistic approach for airport ground movement optimisation with stand holding. J. Sched. 2014, 17, 507–520. [Google Scholar] [CrossRef] [Green Version]
- Brownlee, A.E.I.; Weiszer, M.; Chen, J.; Ravizza, S.; Woodward, J.R.; Burke, E.K. A fuzzy approach to addressing uncertainty in Airport Ground Movement optimisation. Transp. Res. Part C Emerg. Technol. 2018, 92, 150–175. [Google Scholar] [CrossRef]
- Chen, J.; Weiszer, M.; Locatelli, G.; Ravizza, S.; Atkin, J.A.; Stewart, P.; Burke, E.K. Toward a More Realistic, Cost-Effective, and Greener Ground Movement Through Active Routing: A Multiobjective Shortest Path Approach. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3524–3540. [Google Scholar] [CrossRef] [Green Version]
- Clare, G.; Richards, A.G. Optimization of taxiway routing and runway scheduling. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1000–1013. [Google Scholar] [CrossRef]
- Behrends, J.A.; Usher, J.M. Aircraft gate assignment: Using a deterministic approach for integrating freight movement and aircraft taxiing. Comput. Ind. Eng. 2016, 102, 44–57. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, D.; Henry Lau, H.Y.K. A heuristic approach for solving an integrated gate reassignment and taxi scheduling problem. J. Air Transp. Manag. 2017, 62, 189–196. [Google Scholar] [CrossRef]
- MLIT Collaborative Actions for Renovation of Air Traffic Systems (CARATS). Available online: http://www.mlit.go.jp/common/001046514.pdf (accessed on 1 June 2020).
- Google earth V 7.3.3.7786 Tokyo International Airport, Tokyo, Japan. 35° 33′24.11″ N, 139° 45′48.42″ E, Eye alt 10.35 km. Available online: http://earth.google.com (accessed on 30 June 2020).
- Bellingham, J.; Kuwata, Y.; How, J. Stable receding horizon trajectory control for complex environments. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar]
- Schouwenaars, T.; De Moor, B.; Feron, E.; How, J. Mixed integer programming for multi-vehicle path planning. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 2603–2608. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Clare, G.; Richards, A.; Sharma, S. Receding Horizon, iterative optimization of taxiway routing and runway scheduling. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Chicago, IL, USA, 10–13 August 2009. [Google Scholar] [CrossRef]
- Bellingham, J.; Richards, A.; How, J.P. Receding horizon control of autonomous aerial vehicles. In Proceedings of the 2002 American Control Conference (IEEE Cat. No. CH37301), Anchorage, AK, USA, 8–10 May 2002; pp. 3741–3746. [Google Scholar] [CrossRef]





| Symbol | Description |
|---|---|
| N | Set of nodes in graph model. |
| Set of taxiway intersection nodes in graph model. | |
| Set of runway entrance nodes in graph model. | |
| Set of runway exit nodes in graph model. | |
| Set of gate nodes in graph model. | |
| Set of virtual push-back nodes in graph model. | |
| Set of runway cross nodes in graph model. | |
| Set of directed edges in graph model. | |
| Graph model of Tokyo International Airport. | |
| Identified nodes in graph model. | |
| Length of shortest path between and . | |
| Graph matrix of graph model. | |
| Maximum taxi speed of taxiway between and . | |
| Time separation requirement at node . | |
| Time separation requirement of runway cross node. | |
| Time separation requirement for aircraft type when taking off on same runway after aircraft type . | |
| Set of all aircraft. | |
| Set of all active aircraft in current planning horizon. | |
| Identity of aircraft. | |
| Gate node of aircraft . | |
| Push-back ready time for a take-off aircraft; runway arrival time for a landing aircraft. | |
| Runway node of aircraft . | |
| Aircraft type of aircraft . | |
| Destination node of aircraft . | |
| Start time of aircraft in current planning horizon. | |
| Last node passed by aircraft before current planning horizon. | |
| Node ahead of aircraft in current planning horizon. | |
| Rest distance of aircraft to in current planning horizon. | |
| Number of steps that can be planned in one horizon. | |
| Duration of the planning horizon. | |
| Step number. | |
| Decision Variable. = 1 means aircraft taxis from to at step. | |
| Decision Variable. The time when aircraft a passing step’s node . | |
| The estimated taxi time from to . | |
| Time when aircraft last passed node in the previous planning horizon. | |
| Time gap between aircraft at step and at step . | |
| Equals 1 when step of aircraft and step of aircraft use the same node, . | |
| Equals 1 when the step of aircraft is performed earlier than the step of aircraft . | |
| Equals 1 if aircraft crosses the runway cross point at step when aircraft takes off or lands on the same runway at step . | |
| Equals 1 when takes off before . |
| Items | Values without Runway Reselection | Values with Runway Reselection |
|---|---|---|
| Observed total taxi distance | 237.55 km | 237.55 km |
| Optimized total taxi distance | 214.21 km | 193.51 km |
| Decreasing rate | 9.82% | 18.54% |
| Items | Values without Runway Reselection | Values with Runway Reselection |
|---|---|---|
| Observed total taxi time | 31,240 s | 31,240 s |
| Optimized total taxi time | 24,367 s | 21,941 s |
| Decreasing rate | 22.00% | 29.77% |
| Terminal | T1 | T2 | T3 | |||
|---|---|---|---|---|---|---|
| Airlines | JAL, Skymark | ANA | JAL, Skymark | ANA | All | |
| Observed data | Take-off | 17 | 0 | 0 | 11 | 3 |
| Landing | 13 | 0 | 0 | 20 | 5 | |
| After re-assignment | Take-off | 4 | 4 | 13 | 7 | 3 |
| Landing | 8 | 13 | 5 | 7 | 5 | |
| Taxi Distance | Taxi Time | |||||
|---|---|---|---|---|---|---|
| Take-Off | Landing | Total | Take-Off | Landing | Total | |
| Optimized result | 11.15% | 9.03% | 9.82% | 32.29% | 13.08% | 22.00% |
| Optimized result with runway reselection | 34.12% | 9.16% | 18.54% | 48.56% | 13.49% | 29.77% |
| Optimized result with gate re-assignment | 35.7 6% | 26.07% | 29.71% | 47.22% | 28.78% | 37.34% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Hanaoka, S. Improvement of Airport Surface Operation at Tokyo International Airport Using Optimization Approach. Aerospace 2022, 9, 145. https://doi.org/10.3390/aerospace9030145
Chen T, Hanaoka S. Improvement of Airport Surface Operation at Tokyo International Airport Using Optimization Approach. Aerospace. 2022; 9(3):145. https://doi.org/10.3390/aerospace9030145
Chicago/Turabian StyleChen, Tong, and Shinya Hanaoka. 2022. "Improvement of Airport Surface Operation at Tokyo International Airport Using Optimization Approach" Aerospace 9, no. 3: 145. https://doi.org/10.3390/aerospace9030145
APA StyleChen, T., & Hanaoka, S. (2022). Improvement of Airport Surface Operation at Tokyo International Airport Using Optimization Approach. Aerospace, 9(3), 145. https://doi.org/10.3390/aerospace9030145







