Correction-Efficiency-Coefficient-Based Trajectory Optimization for Two-Dimensional Trajectory Correction Projectile
Abstract
:1. Introduction
2. Correction Efficiency Coefficient
2.1. Equation of Motion
- (1)
- The principal axes of inertia of the forward and aft bodies are parallel to that of the combination.
- (2)
- The force and moment are uniformly applied to the whole projectile;
- (3)
- The aerodynamic coupling of forces and moments acted on the projectile is neglected.
- (4)
- Magnus force and Coriolis inertial force are ignored;
- (5)
- The influence of wind is not considered
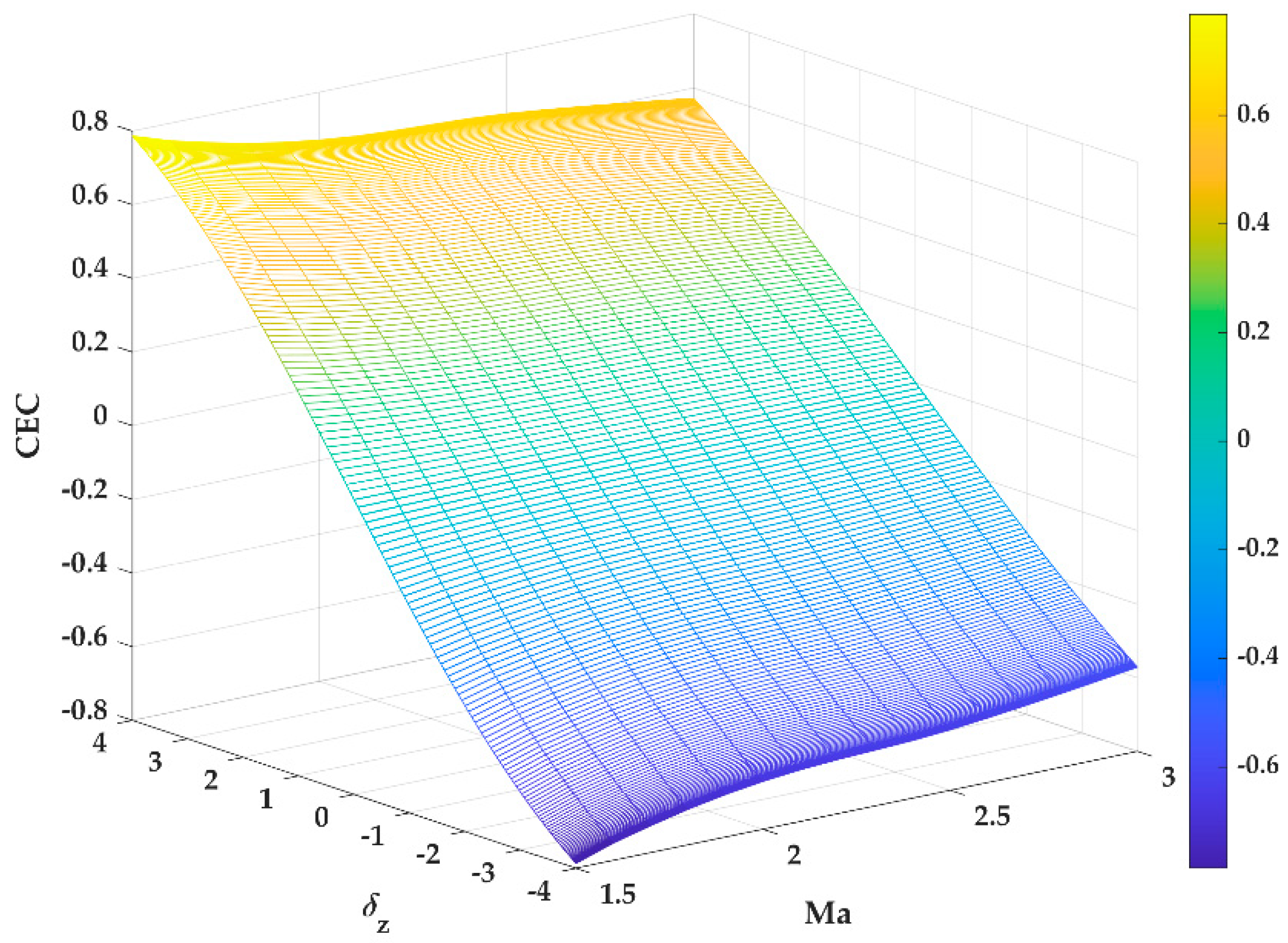
2.2. Correction Efficiency Coefficient
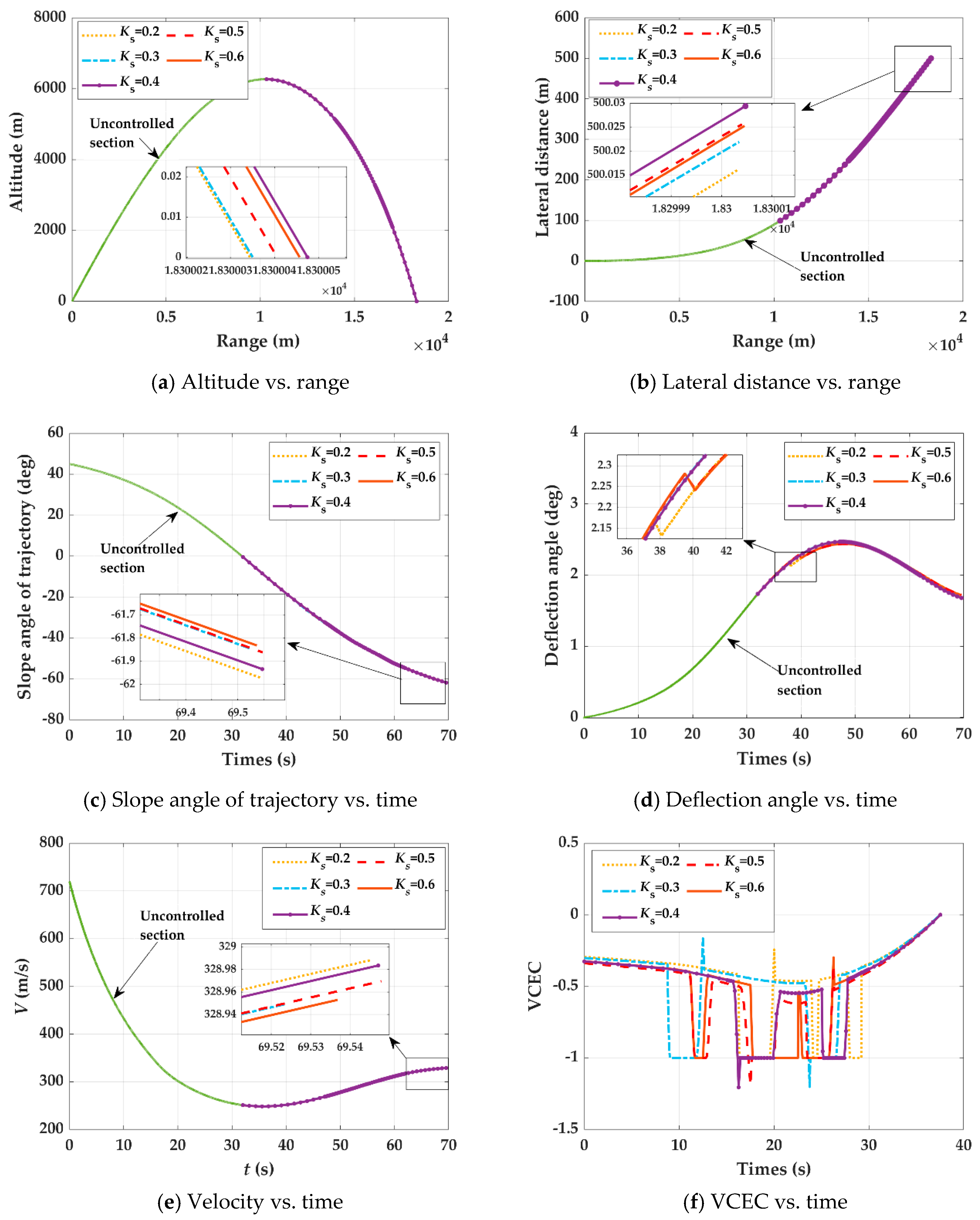
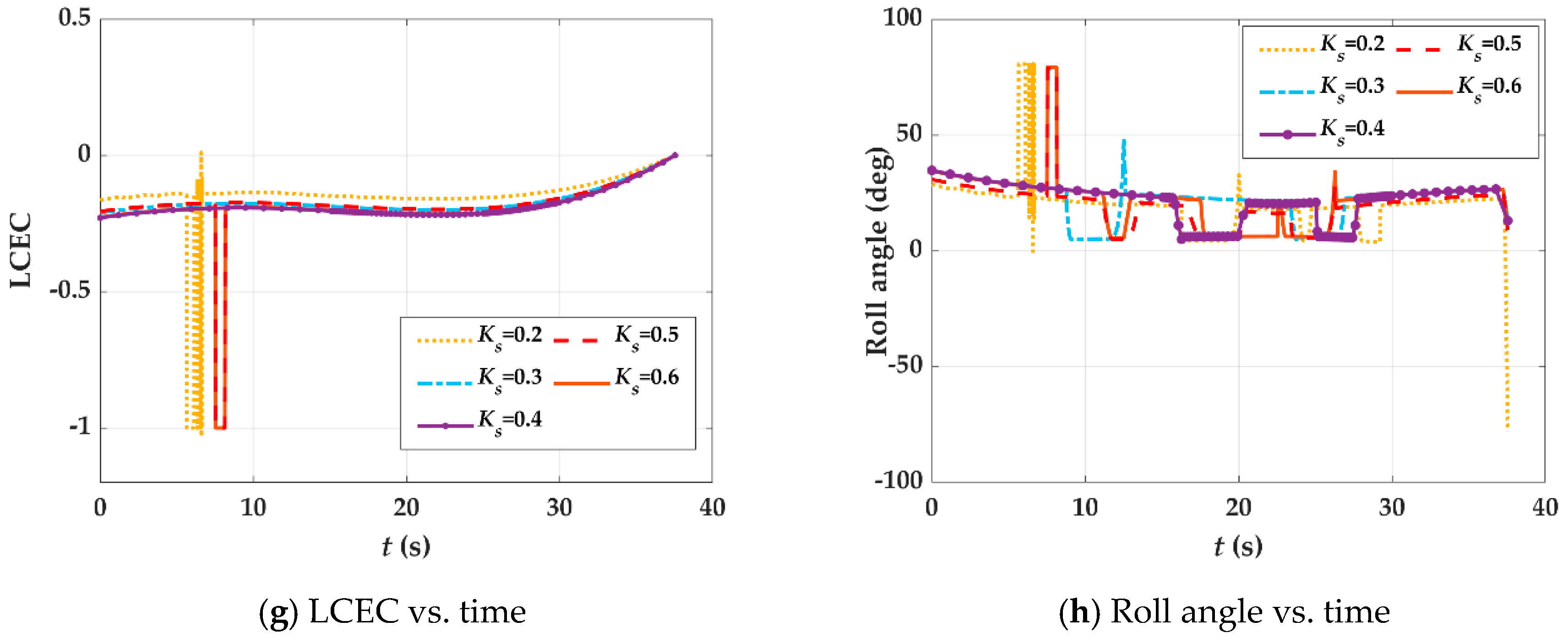
3. Trajectory Characteristics Based on CEC
- (1)
- VCEC and LCEC can reflect the changing law of the roll angle, as shown in Equation (28).
- (2)
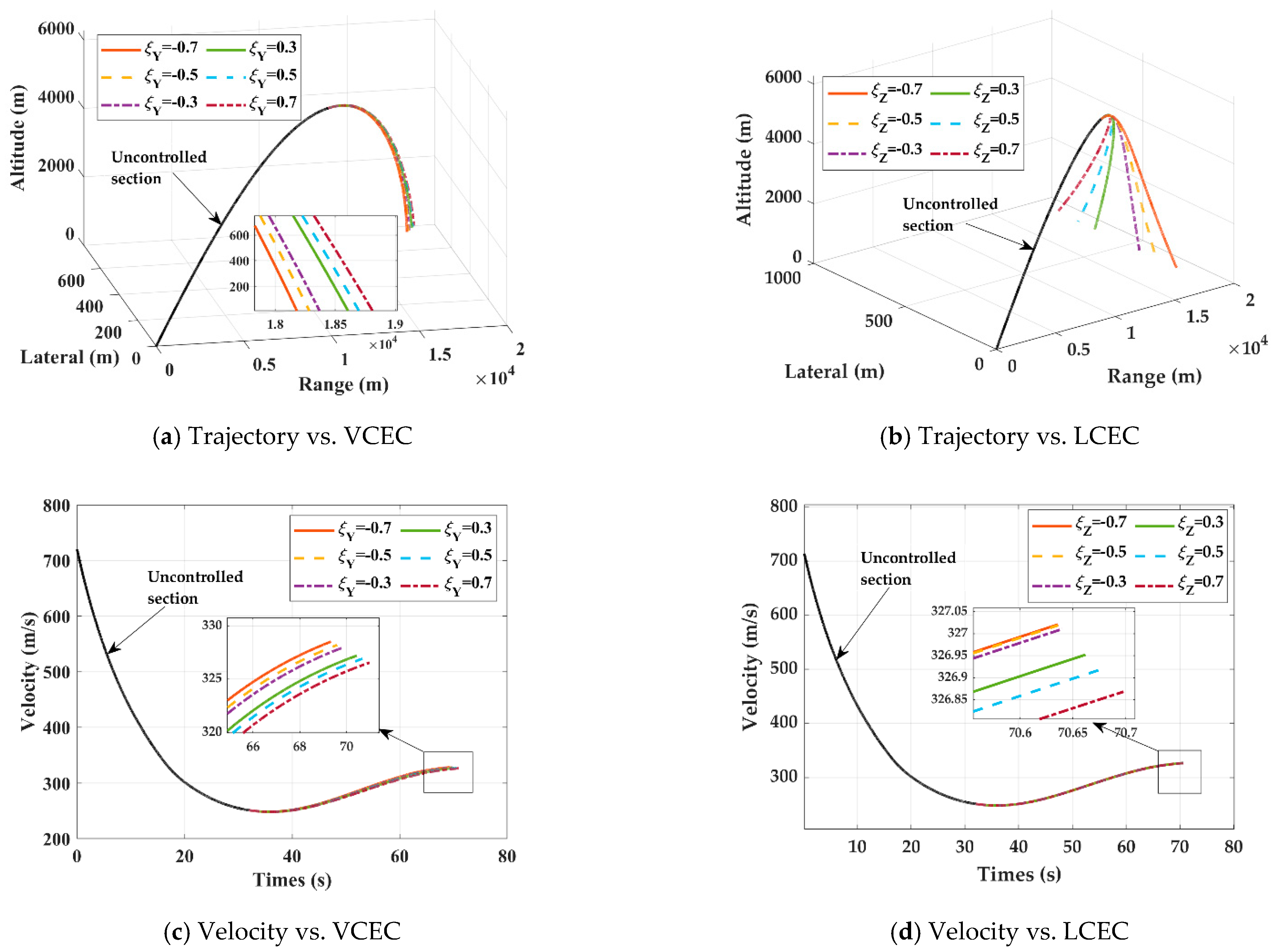
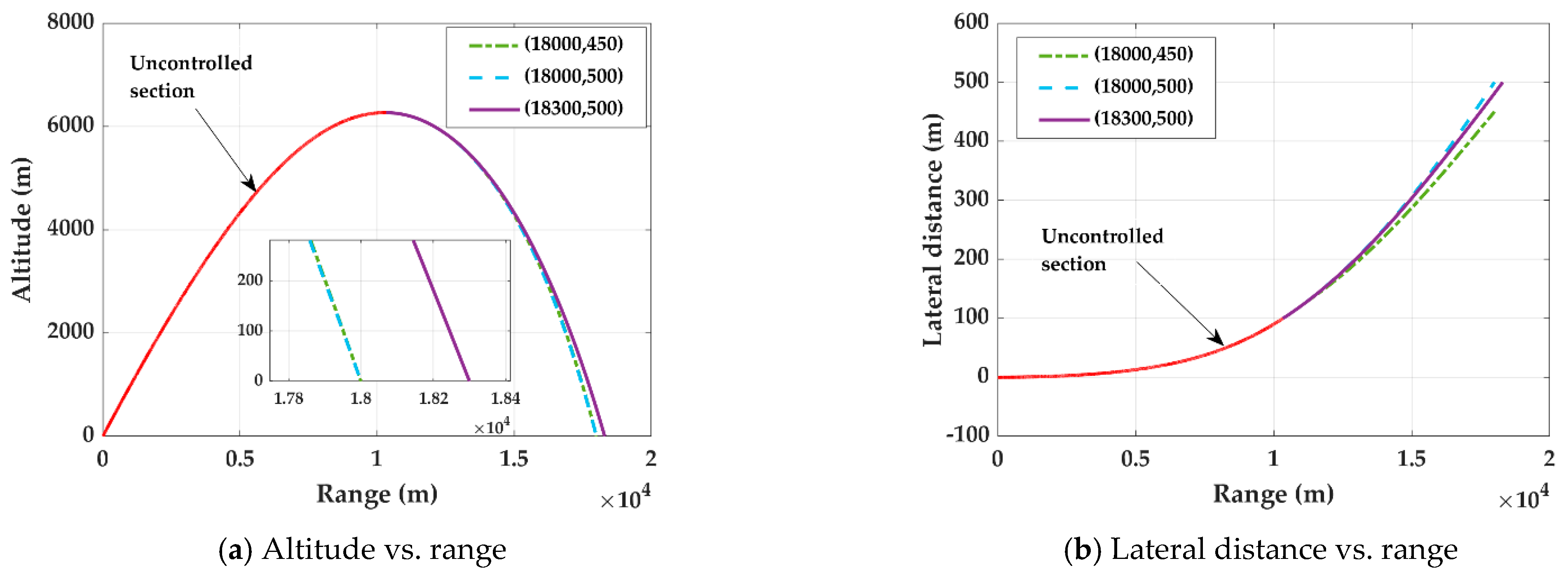
- The effect of CEC on impact point
- (3)
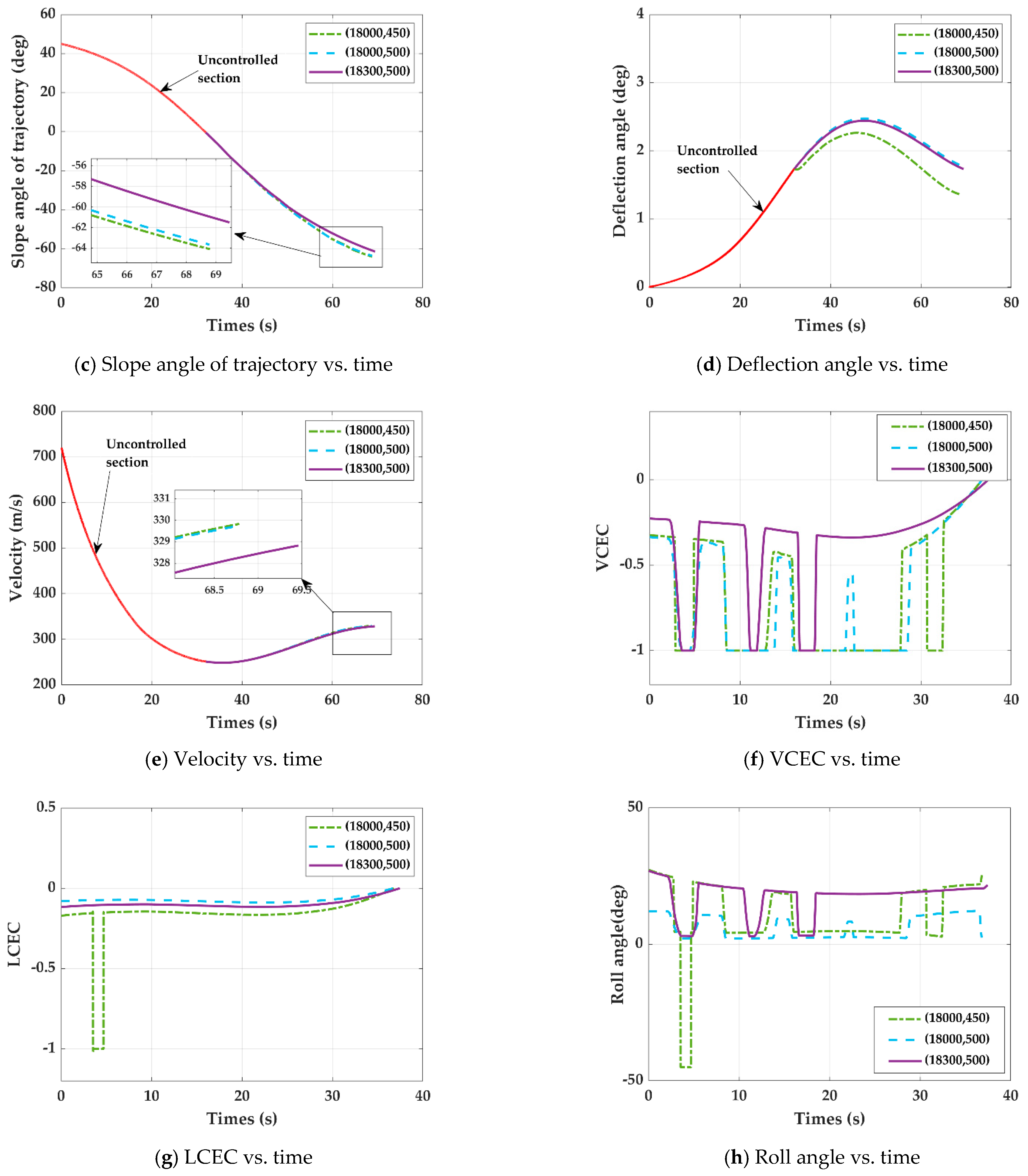
- The effect of CEC on velocity
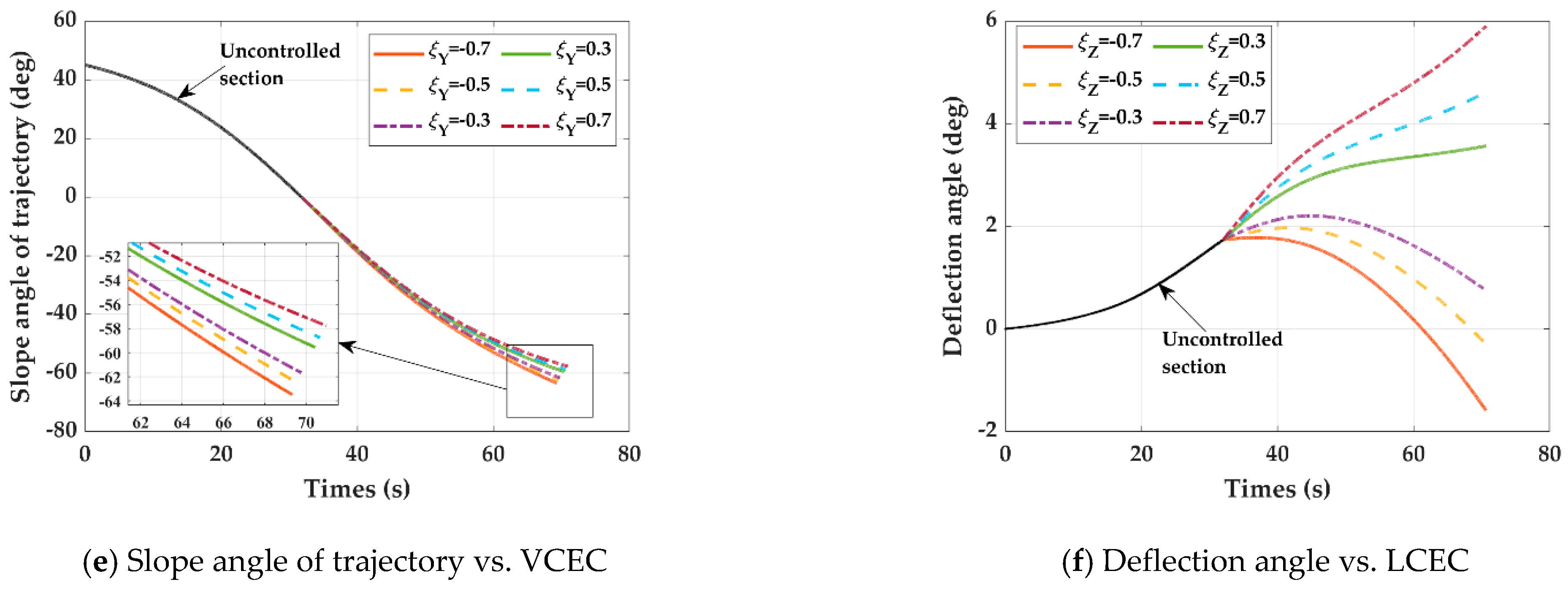
- (4)
- The effect of CEC on slope angle of trajectory
- (5)
- The effect of CEC on deflection angle
4. CEC-Based Trajectory Optimization
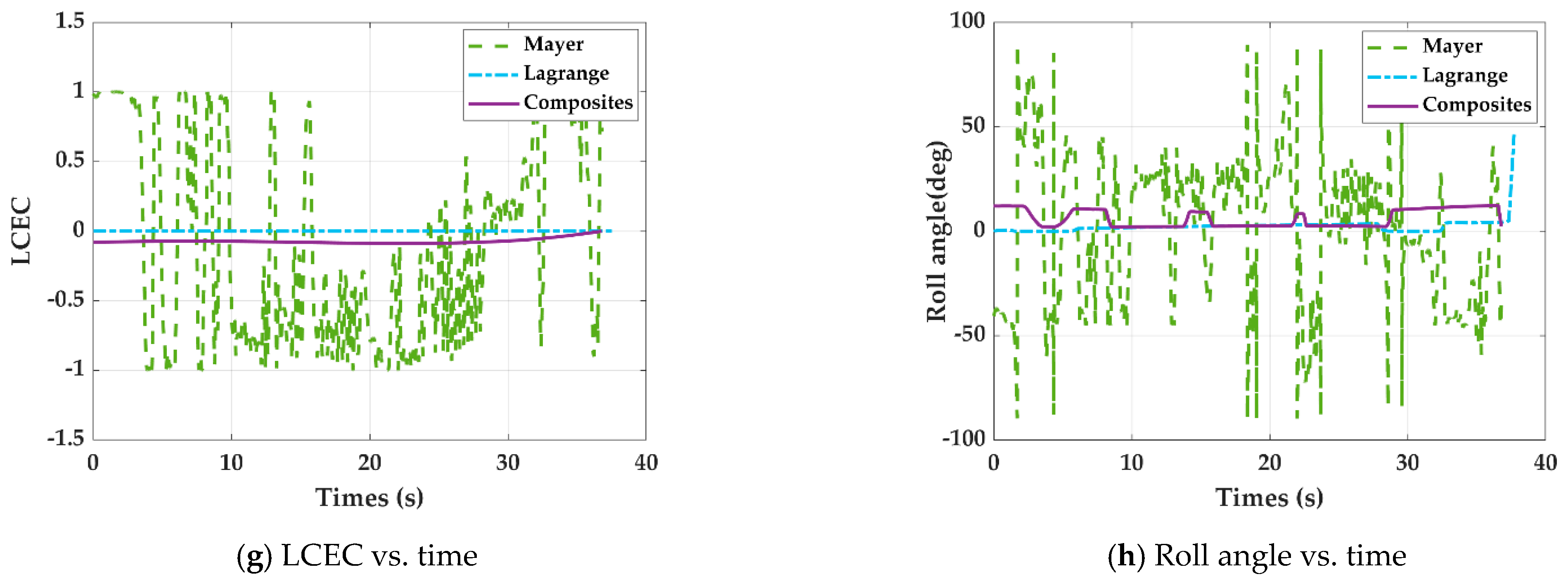
- (1)
- Mayer functions
- (2)
- Lagrange functions
- (3)
- Composite function
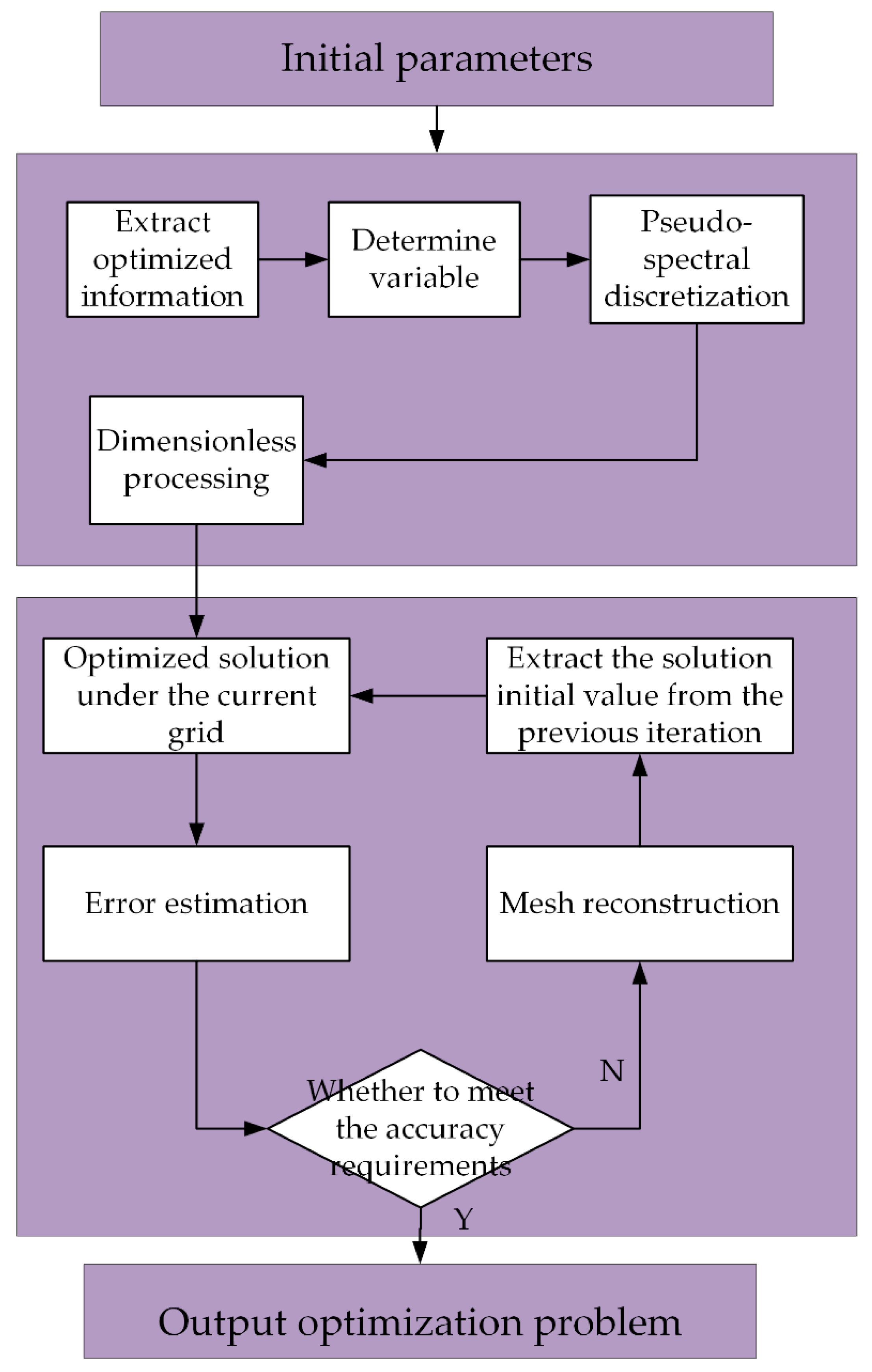
4.1. Gauss Pseudo-Spectral Method
4.2. Trajectory Optimization for Different Targets
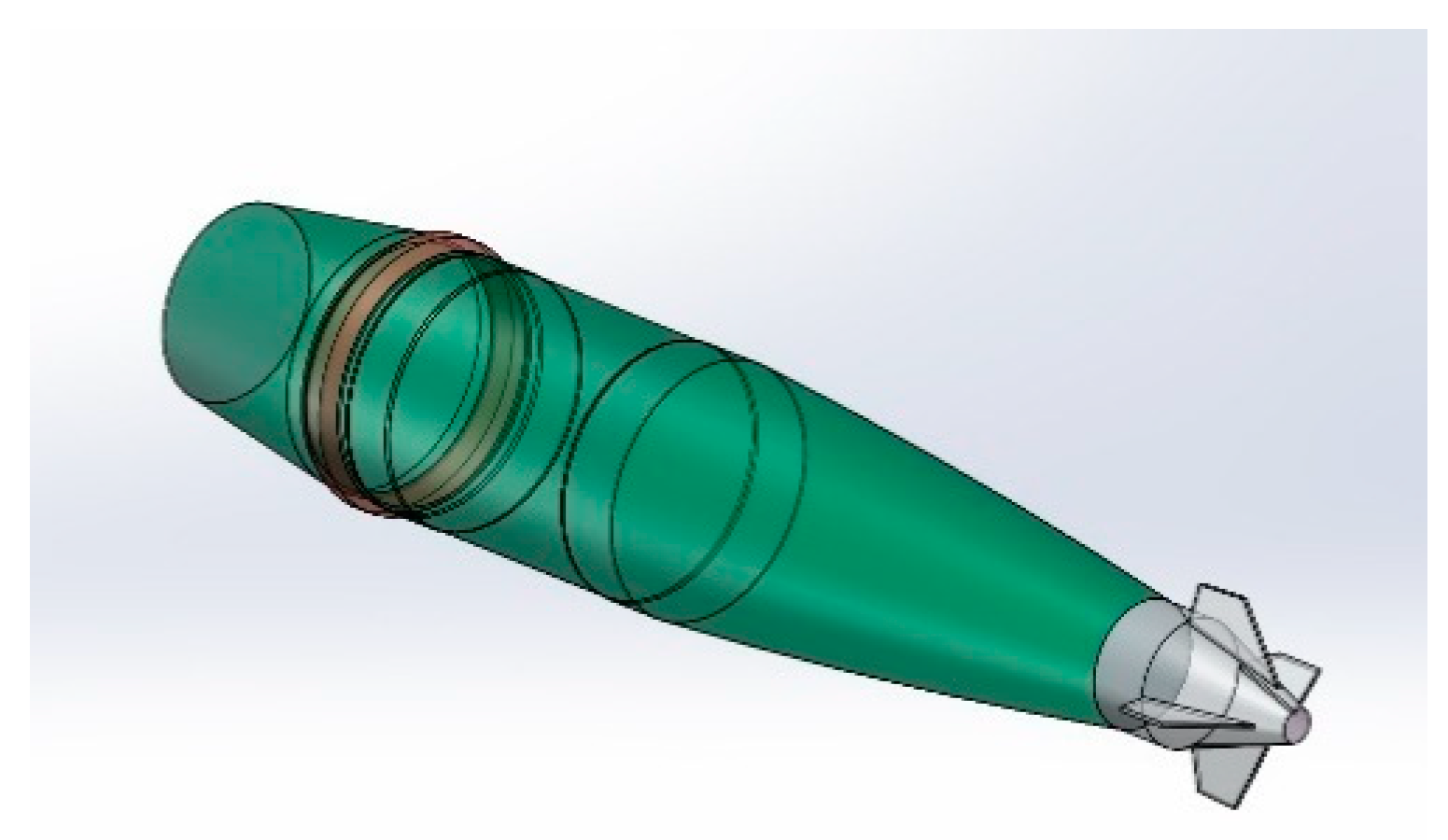
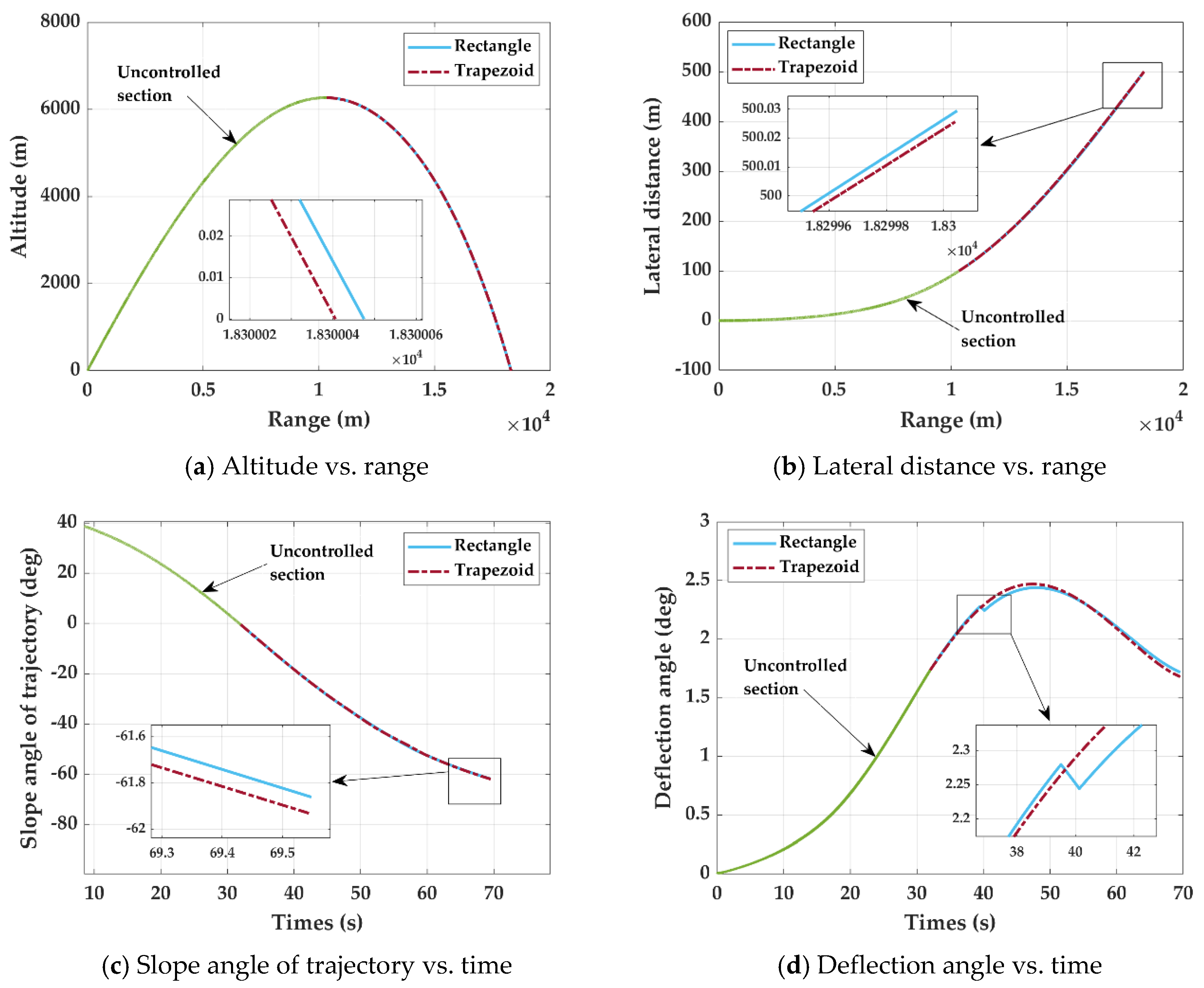
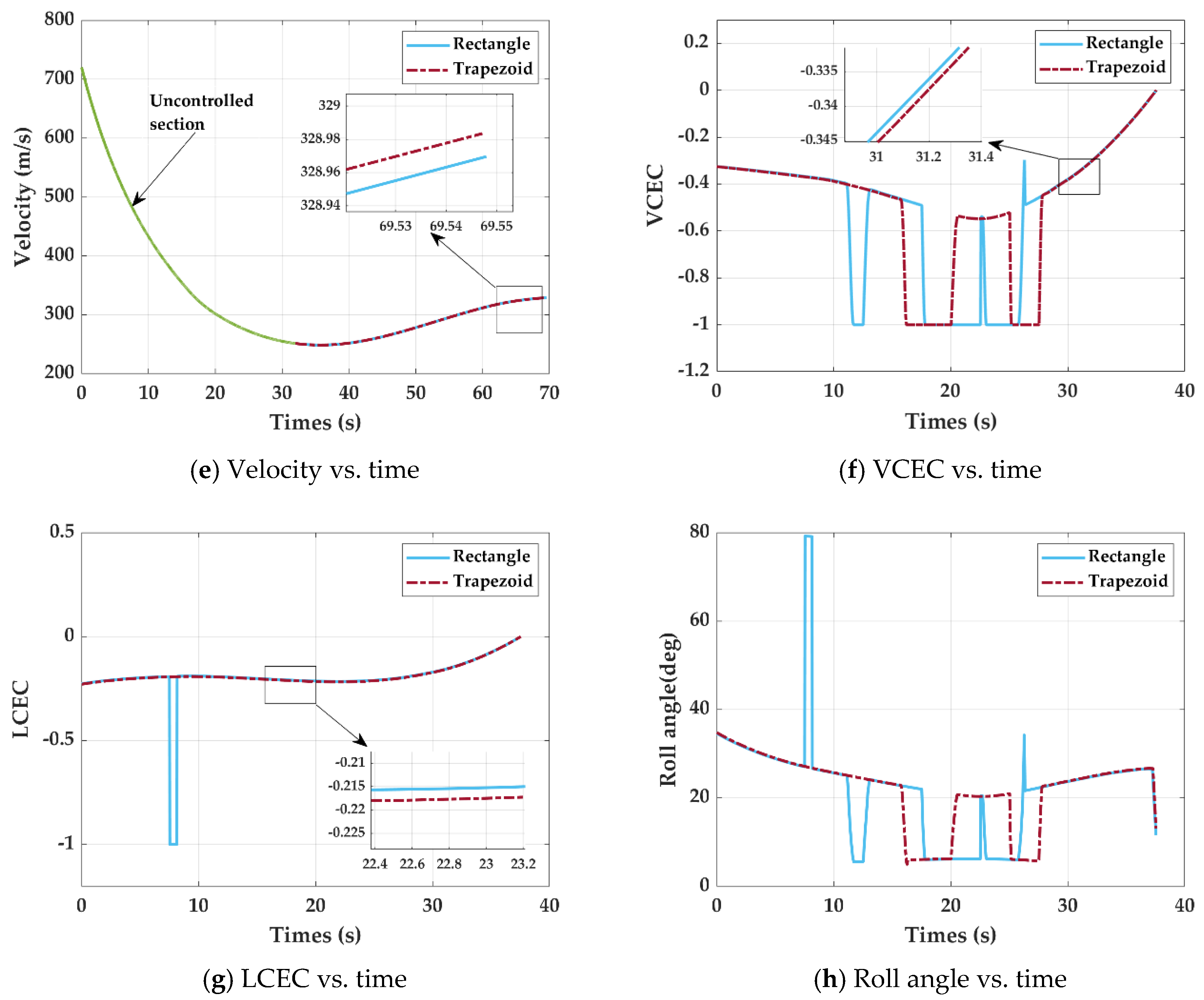
5. Design of Canard Geometry Based on CEC
5.1. Canard Wingspan Design
5.2. Canard Shape Design
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, Q.; Li, D.; Ji, X. Technology of Trajectory Correction Fuze; National Defense Industry Press: Beijing, China, 2016; pp. 1–10. [Google Scholar]
- Norris, J.; Hameed, A.; Economou, J.; Parker, S. A Review of Dual-spin Projectile Stability. Def. Technol. 2020, 16, 1–9. [Google Scholar] [CrossRef]
- Costello, M.F. Modeling and Simulation of a Differential Roll Projectile. In Proceedings of the 1998 AIAA Modeling and Simulation Technologies Conference, Boston, MA, USA, 10–12 August 1998; AIAA: Reston, VA, USA, 1998; pp. 490–499. [Google Scholar]
- Wernert, P.; Theodoulis, S. Modelling and Stability Analysis for a Class of 155 mm Spin-stabilized Projectiles with Course Correction Fuse (CCF). In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, OR, USA, 8–11 August 2011; pp. 1–14. [Google Scholar]
- Chang, S. Dynamic Response to Canard Control and Gravity for a Dual-Spin Projectile. J. Spacecr. Rocket. 2016, 53, 558–566. [Google Scholar] [CrossRef]
- Brauer, G.L.; Cornick, D.E.; Stevenson, R. Capabilities and Applications of the Program to Optimize and Simulate Trajectories; NASA-CR-2770; NASA: Springfield, VA, USA, 1977. [Google Scholar]
- Darby, C.L.; Hager, W.W.; Rao, A.V. Direct trajectory optimization using a variable low-order adaptive pseudo-spectral method. J. Spacecr. Rocket. 2011, 48, 433–445. [Google Scholar] [CrossRef]
- Huo, P.; Shi, K.; Yuan, W. Research on Trajectory Controlled Optimization for Trajectory Correction Fuze Using Maximum Principle. Acta Armamentarii 2007, 28, 301–304. [Google Scholar]
- Vormer, F.J.; Mulder, M.; van Paassen, M.M.; Mulder, J.A. Optimization of Flexible Approach Trajectories Using a Genetic Algorithm. J. Aircr. 2006, 43, 941–952. [Google Scholar] [CrossRef]
- Kitayama, S.; Yamazaki, K.; Arakawa, M. Adaptive Range Particle Swarm Optimization. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; pp. 1–10. [Google Scholar]
- Berguin, S.H.; Dunn, A.K.; Sonnenburg, C.; Allison, D.L. Surrogate-Based Trajectory Optimization Using Gradient-Enhanced Neural Networks. In Proceedings of the AIAA Aviation 2021 Forum, Virtual, 2–6 August 2021. [Google Scholar]
- Costello, M. Range Optimization of a Fin Stabilized Projectile. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–19 August 1997; pp. 695–699. [Google Scholar]
- Liu, C.; Zhang, C. Multi-stage Trajectory Optimization of Tactical Two-stage Booster Rocket Based on Gauss Pseudo-spectral Method. Acta Armamentarii 2019, 40, 292–302. [Google Scholar]
- Chen, Q.; Wang, Z.; Chang, S.; Fu, J. Multiphase Trajectory Optimization for Gun-Launched Glide Guided Projectiles. J. Aerosp. Eng. 2015, 6, 995–1010. [Google Scholar] [CrossRef]
- Xu, Q.; Chang, S.; Wang, Z. Composite-Efficiency-Factor-Based Trajectory Optimization for Gliding Guided Projectiles. J. Spacecr. Rocket. 2018, 55, 66–76. [Google Scholar] [CrossRef]
- Burchett, B.T. A Gauss Pseudo-spectral Collocation for Rapid Trajectory Prediction and Guidance. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Grapevine, TX, USA, 9–13 January 2017; pp. 1–20. [Google Scholar]
- Yao, J.; Wang, X.; Wang, X.B. Solution for Trajectory Correction Optimization Based on Generalized Work Principle. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; pp. 232–236. [Google Scholar]
- Wu, Y.; Deng, J.; Li, L.; Su, X.; Lin, L. A hybrid particle swarm optimization-gauss pseudo method for reentry trajectory optimization of hypersonic vehicle with navigation information model. Aerosp. Sci. Technol. 2021, 118, 107046. [Google Scholar] [CrossRef]
- Arnoult, G.; Zeidler, M.; Garnier, E. Control Surface Geometry Surrogate-Based Optimization for Spin-Stabilized Projectile Course Correction. AIAA J. 2020, 58, 550–560. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, J.; Ni, Q.; Hao, Y.; Liang, Y. Research on Parametric Modeling Optimization of Trajectory Correction Projectile Based on FVM. Teh. Vjesn. Tech. Gaz. 2021, 28, 907–913. [Google Scholar]
- Wang, Z. Optimal trajectories and normal load analysis of hypersonic glide vehicles via convex optimization. Aerosp. Sci. Technol. 2019, 87, 357–368. [Google Scholar] [CrossRef]
- Kwon, H.-H.; Hong, S.-M.; Kim, G.-H.; Kim, Y.-H. Mid-course Trajectory Optimization for Boost-Glide Missiles Based on Convex Programming. J. Korean Soc. Aeronaut. Space Sci. 2021, 49, 21–30. [Google Scholar]
- Laad, D.; Elango, P.; Mohan, R. Fourier Pseudo-spectral Method for Trajectory Optimization with Stability Requirements. J. Guid. Control. Dyn. 2020, 43, 2073–2090. [Google Scholar] [CrossRef]
- Elsisi, M. Optimal design of nonlinear model predictive controller based on new modified multitracker optimization algorithm. Int. J. Intell. Syst. 2020, 35, 1857–1878. [Google Scholar] [CrossRef]
- Elsisi, M.; Ebrahim, M.A. Optimal design of low computational burden model predictive control based on SSDA towards autonomous vehicle under vision dynamics. Int. J. Intell. Syst. 2021, 36, 6968–6987. [Google Scholar] [CrossRef]
- Elsisi, M. Improved grey wolf optimizer based on opposition and quasi learning approaches for optimization: Case study autonomous vehicle including vision system. Artif. Intell. Rev. 2022. [Google Scholar] [CrossRef]
- Han, Z.P. Exterior Ballistics of Shells and Rockets, 2nd ed.; Beijing University of Technology Press: Beijing, China, 2008; pp. 179–180. [Google Scholar]
- Benson, D.A. A Gauss Pseudo-Spectral Transcription for Optimal Control; Massachusetts Institute of Technology: Cambridge, MA, USA, 2005. [Google Scholar]
- Rao, A.V.; Benson, D.; Darby, C.L.; Mahon, B.; Francolin, C.; Patterson, M.; Sanders, I.; Huntington, G.T. User’s Manual for GPOPS Version 5.0: A MATLAB Software for Solving Multiple-Phase Optimal Control Problems Using hp-Adaptive Pseudo-spectral Methods; University of Florida: Gainesville, FL, USA, 2011. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. SIAM J. Optim. 2002, 12, 979–1006. [Google Scholar] [CrossRef] [Green Version]

| Aerodynamic Force | Expressions |
|---|---|
| Drag | |
| Lift | |
| Control force for canards | |
| Static moment | |
| Pitch damping moment | |
| Control moment for canards |
| Parameters of Projectile | Values |
|---|---|
| Mass , kg | 22 |
| Reference area , m2 | 1.17 × 10−2 |
| Reference length , m | 0.75 |
| 4.5 × 10−2 | |
| 2.25 × 10−3 | |
| , m/s | 720 |
| , deg | 45 |
| Start control time , s | 32 |
| Parameters | Values |
|---|---|
| free | |
| free | |
| free | |
| free | |
| (18,000, 500) |
| Description | Definition in GPOPS | Values |
|---|---|---|
| Mesh refinement tolerance | Setup.mesh.tolerance | 10−4 |
| Number of mesh refinement iterations | Setup.mesh.iteration | 25 |
| Minimum number of allowed collocation points in a mesh interval | Setup.nodesPerInterval.min | 4 |
| Maximum number of allowed collocation points in a mesh interval | Setup.nodesPerInterval.max | 12 |
| Automatic scaling | Setup.autoscale | on |
| Derivative computation | Setup.derivatives | finite-difference |
| Cost Function | Velocity, m/s | Impact Angle, deg | Deflection Angle, deg | Impact Point |
|---|---|---|---|---|
| Mayer | 329.9 | 65.87 | 2.77 | (17,999, 500) |
| Lagrange | 328.65 | 61.35 | 2.1 | (18,397, 542) |
| Composite | 329.78 | 63.98 | 1.8 | (18,000, 500) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhang, J.; Jiao, Z.; Ni, Q.; Guo, Q. Correction-Efficiency-Coefficient-Based Trajectory Optimization for Two-Dimensional Trajectory Correction Projectile. Aerospace 2022, 9, 149. https://doi.org/10.3390/aerospace9030149
Zhang D, Zhang J, Jiao Z, Ni Q, Guo Q. Correction-Efficiency-Coefficient-Based Trajectory Optimization for Two-Dimensional Trajectory Correction Projectile. Aerospace. 2022; 9(3):149. https://doi.org/10.3390/aerospace9030149
Chicago/Turabian StyleZhang, Dejian, Jian Zhang, Zhigang Jiao, Qingjie Ni, and Qiuping Guo. 2022. "Correction-Efficiency-Coefficient-Based Trajectory Optimization for Two-Dimensional Trajectory Correction Projectile" Aerospace 9, no. 3: 149. https://doi.org/10.3390/aerospace9030149
APA StyleZhang, D., Zhang, J., Jiao, Z., Ni, Q., & Guo, Q. (2022). Correction-Efficiency-Coefficient-Based Trajectory Optimization for Two-Dimensional Trajectory Correction Projectile. Aerospace, 9(3), 149. https://doi.org/10.3390/aerospace9030149





