A Multidisciplinary Possibilistic Approach to Size the Empennage of Multi-Engine Propeller-Driven Light Aircraft
Abstract
:1. Introduction
2. Methodology
2.1. Aircraft TSC Requirements
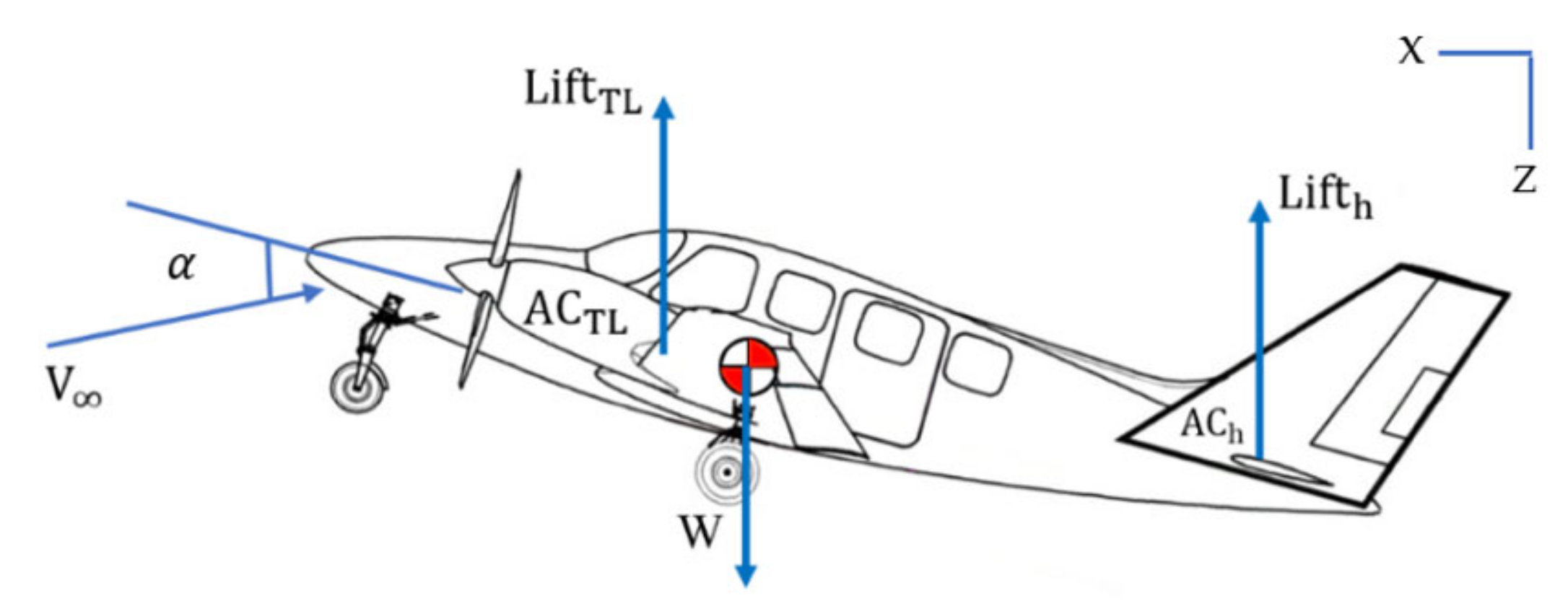
2.1.1. Longitudinal TSC
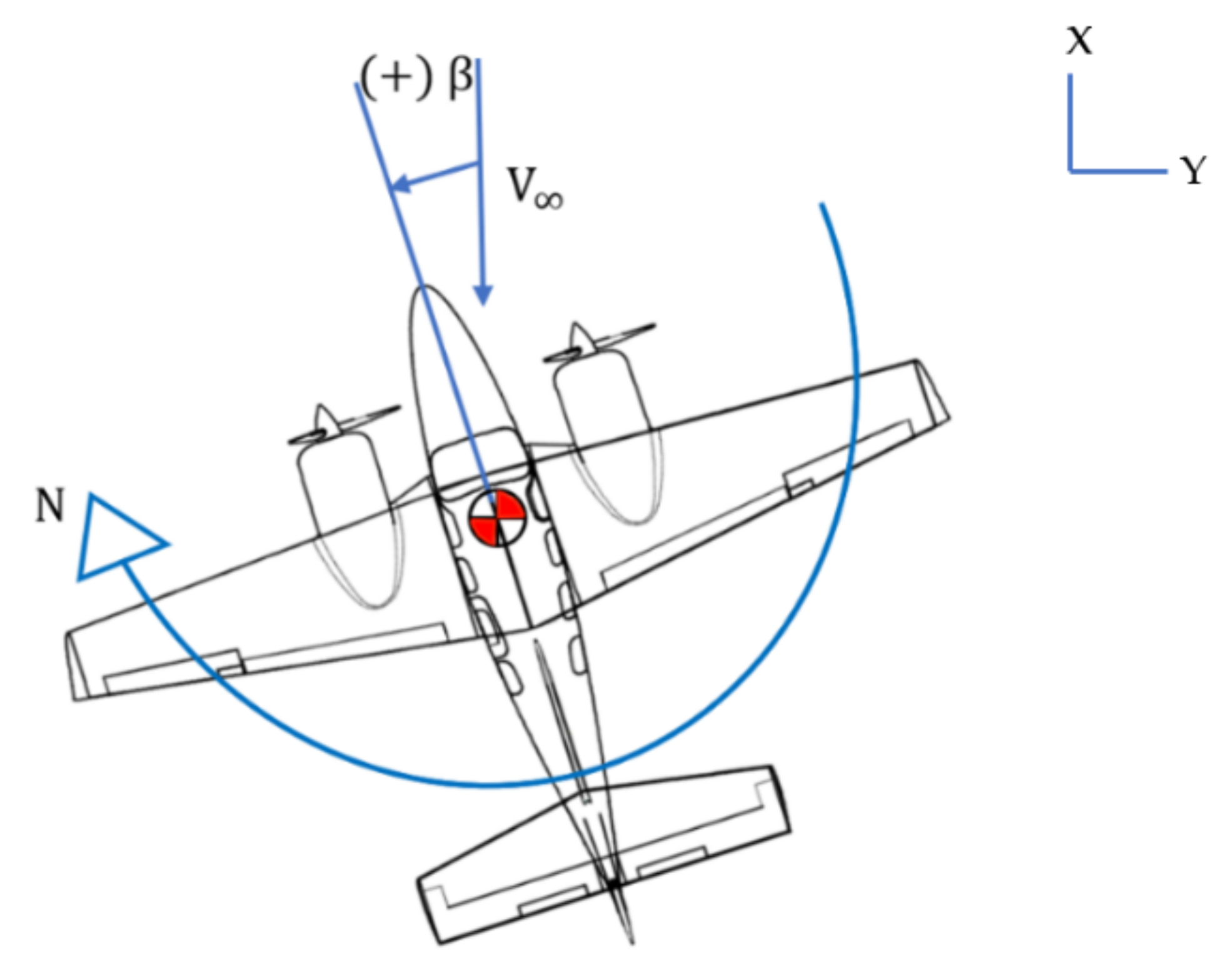
2.1.2. Directional TSC
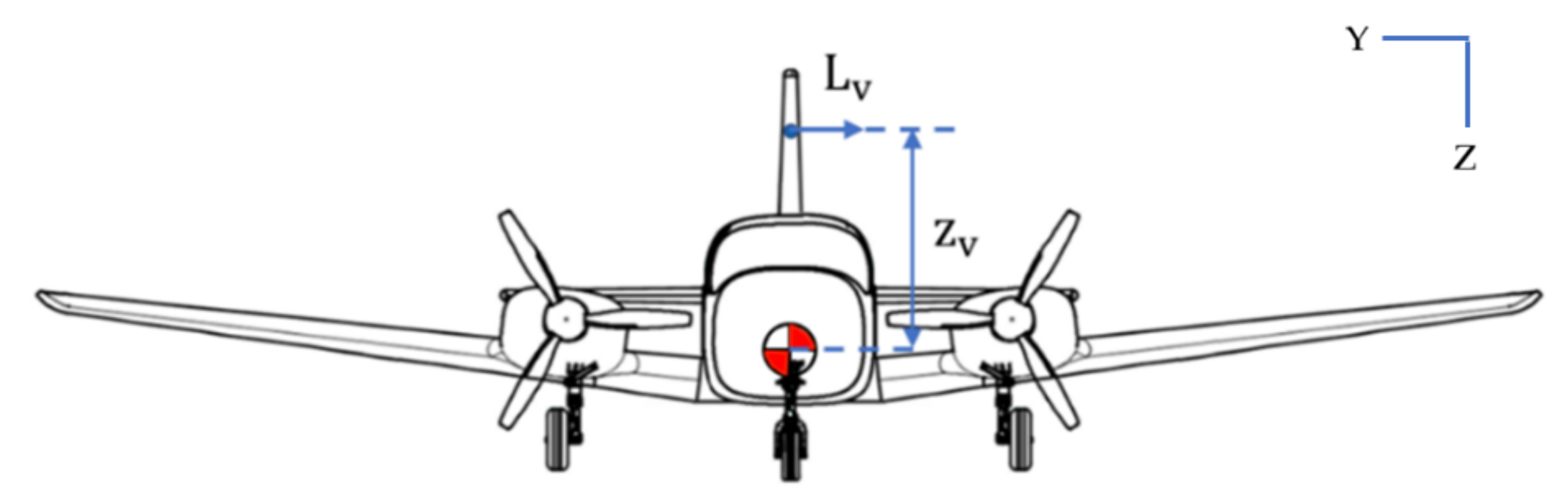
2.1.3. Lateral TSC
2.2. MAPLA
2.3. PBDO Method Outline
3. MDO Framework
3.1. Methods
- 1.
- Find the analysis error distributions
- (I)
- Model each entry based on the aircraft empennage model
- (II)
- Determine the entire aircraft aerodynamic characteristics
- (III)
- Implement the uncertainty analysis
- (IV)
- Implement a best fit PDF curve for each individual source of uncertainty
- 2.
- Choose the starting vector and a list of reliability indices
- 3.
- Run the IDF-based deterministic optimization
- 4.
- Run the MDF-based PMA reliability evaluation at the current reliability index, and alter variables according to the sequential procedure
- 5.
- Check for convergence with current reliability goal
- (I)
- if yes, update starting vector with the current optimum point, select next reliability goal, return to 3
- (II)
- if no, return to 3
- 6.
- Advance to next target reliability level
- (I)
- retain solution as new starting vector
- (II)
- return to 3
3.2. Disciplines
3.3. Design Variables
3.4. Objective Functions
3.5. Constraints
3.6. Sources of Uncertainty
4. Results
4.1. Resulting Geometry
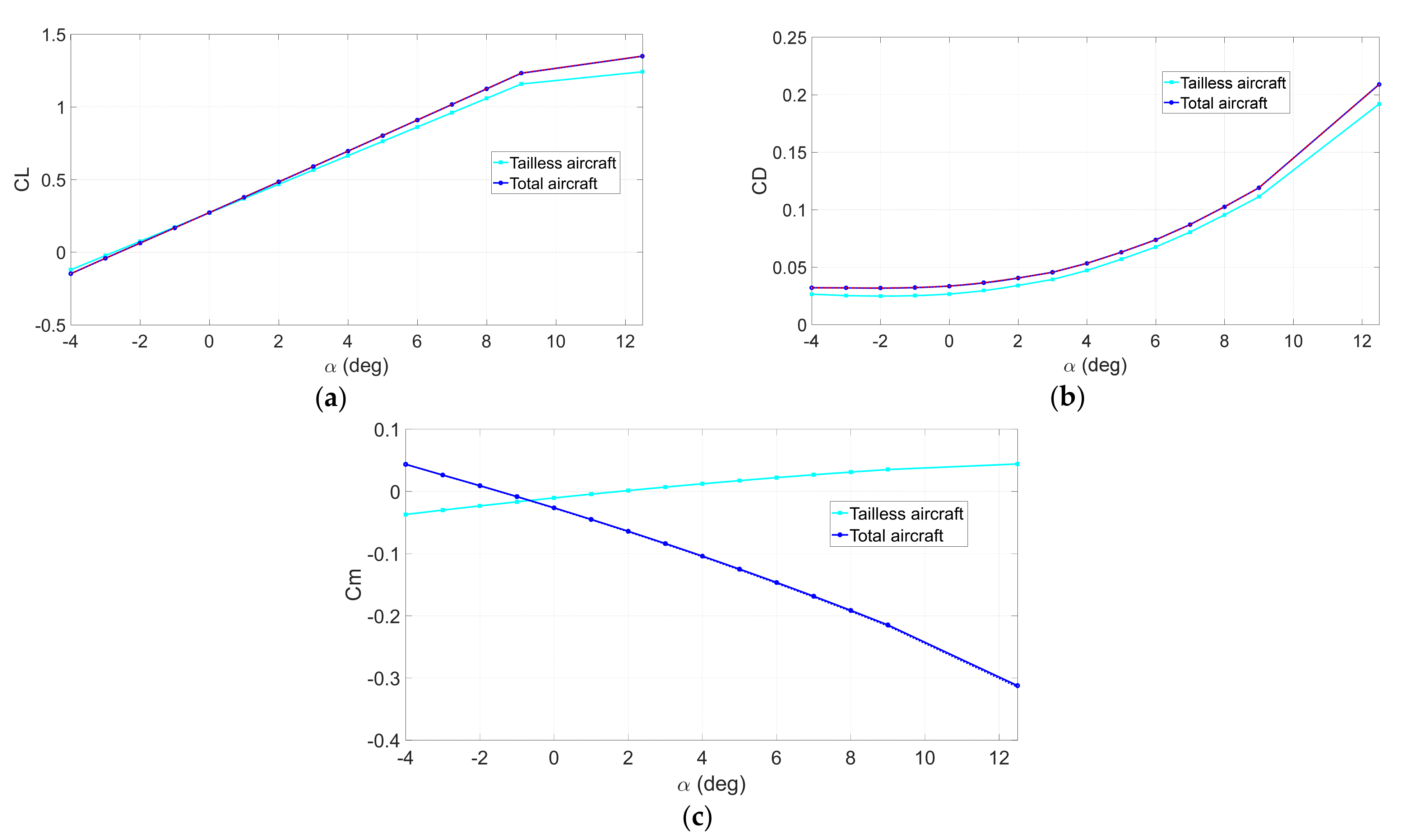
4.2. Aerodynamics Characteristics of the Optimized Aircraft
4.3. Flight Dynamic Stability of the Optimized Aircraft
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Roman Symbols | ||
| Horizontal tail span | ||
| Vertical tail span | ||
| Lift coefficient of the horizontal tail | ||
| Lift coefficient of the vertical tail | ||
| Yawing moment coefficient | ||
| Rate of change of yawing moment coefficient with respect to the change in the sideslip angle | ||
| Nondimensionalized moments about the y-axis | ||
| Rate of change of the pitching moment coefficient with respect to the change in pitch rate | ||
| Tailless aircraft pitching moment coefficient | ||
| Rate of change of the pitching moment coefficient with respect to the change in the angle of attack | ||
| Yawing moment coefficient | ||
| Tailless aircraft yawing moment coefficient | ||
| Rate of change of yawing moment coefficient with respect to the change in the yaw rate | ||
| Rate of change of yawing moment coefficient with respect to the change in the sideslip angle | ||
| Right engine thrust coefficient | ||
| Mean aerodynamic chord | ||
| Forces in the x-, y- and z-direction | ||
| f | Objective function | |
| Gi | Constraint boundary | |
| Horizontal tail incidence angle | ||
| Counter used in the optimization process | ||
| Moments about the x-axis | ||
| Tailless aircraft rolling moment | ||
| Vertical tail contribution to the total rolling moment | ||
| Distance from the aerodynamic centre of the horizontal tail to the CG | ||
| Distance from aerodynamic center of the vertical tail to the aircraft CG | ||
| Pitching moment | ||
| Moments about the -axis | ||
| Horizontal tail contribution to pitching moment | ||
| Tail mass | ||
| Pitching moment generated by the tailless aircraft | ||
| Moments about the -axis | ||
| Vertical tail contribution to the total yawing moment | ||
| p | Uncertain parameters | |
| Target probability of feasibility | ||
| Pitch rate | ||
| Surface area of the wing | ||
| Surface area of the horizontal tail | ||
| Surface area of the vertical tail | ||
| Aircraft without the empennage | ||
| Normalized uncertain variable vector | ||
| Aircraft empty weight | ||
| volume coefficient of the vertical tail | ||
| Volume coefficient of the horizontal tail | ||
| Distance between the thrust line and the aircraft CG within the -plane | ||
| Coupling variable vector | ||
| Global variable vector | ||
| Distance from the aerodynamic centre of the horizontal tail to the aircraft CG | ||
| Distance from the aerodynamic centre of the vertical tail to the aircraft CG | ||
| Greek Symbols | ||
| Angle of attack | ||
| Sideslip angle | ||
| Elevator deflection | ||
| Rudder deflection | ||
| Aerodynamics error ratio | ||
| Asymmetric blade effect error ratio | ||
| Empty mass error ratio | ||
| Tail efficiency factor | ||
| Leading edge sweep angle of horizontal tail | ||
| Taper ratio of the horizontal tail | ||
| Change in the pitching moment coefficient | ||
| Change in the yawing moment coefficient | ||
| Change in the pitch rate | ||
| Change in the yaw rate | ||
| Change in the angle of attack | ||
| Change in the sideslip angle | ||
References
- Antoine, N.E.; Kroo, I.M. Framework for Aircraft Conceptual Design and Environmental Performance Studies. AIAA J. 2005, 43, 2100–2109. [Google Scholar] [CrossRef]
- Perez, R.E.; Chung, J.; Behdinan, K. Aircraft Conceptual Design Using Genetic Algorithms. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000. [Google Scholar] [CrossRef]
- Bos, A.H.W. Aircraft Conceptual Design by Genetic/Gradient-Guided Optimization. Eng. Appl. Artif. Intell. 1998, 11, 377–382. [Google Scholar] [CrossRef]
- Chudoba, B. Development of a Generic Stability and Control Methodology for the Conceptual Design of Conventional and Unconventional Aircraft Configurations. Ph.D. Thesis, Cranfield University, Cranfield, UK, March 2001. [Google Scholar]
- Peigin, S.; Epstein, B. Multiconstrained Aerodynamic Design of Business Jet by CFD Driven Optimization Tool. Aerosp. Sci. Technol. 2008, 12, 125–134. [Google Scholar] [CrossRef]
- Takemiya, T. Aerodynamic Design Applying Automatic Differentiation and Using Robust Variable Fidelity Optimization. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, December 2008; p. 237. [Google Scholar]
- Gumbert, C.R.; Hou, G.J.W.; Newman, P.A. High-Fidelity Computational Optimization for 3-D Flexible Wings: Part I—Simultaneous Aero-Structural Design Optimization (SASDO). Optim. Eng. 2005, 6, 117–138. [Google Scholar] [CrossRef]
- Gumbert, C.R.; Newman, P.A.; Hou, G.J.W. High-Fidelity Computational Optimization for 3-D Flexible Wings: Part II—Effect of Random Geometric Uncertainty on Design. Optim. Eng. 2005, 6, 139–156. [Google Scholar] [CrossRef]
- González, L.; Whitney, E.; Srinivas, K.; Périaux, J. Optimum Multidisciplinary and Multi-Objective Wing Design in CFD Using Evolutionary Techniques. In Computational Fluid Dynamics 2004; Springer: Berlin/Heidelberg, Germany, 2006; pp. 681–686. [Google Scholar] [CrossRef]
- Mavrist, D.N.; Delaurentis, D.A.; Bandte, O.; Hale, M.A. A stochastic approach to multi-disciplinary aircraft analysis and design. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Scharl, J.; Mavris, D.N.; Burdun, I.Y. Use of flight simulation in early design: Formulation and application of the virtual testing and evaluation methodology. In Proceedings of the 2000 World Aviation Conference, San Diego, CA, USA, 10–12 October 2000. [Google Scholar]
- Giesing, J.P.; Barthelemy, J.F.M. A summary of industry mdo applications and needs. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, St. Louis, MO, USA, 2–4 September 1998. [Google Scholar]
- Fernandez, F.T. Applying mdo to classical conceptual aircraft design methodologies. Ph.D. Thesis, Instituto Tecnol’ of Aeronautical Design; Aerospace Systems and Structures, Campo Montenegro, São José dos Campos, Brazil, 2019. [Google Scholar]
- Choi, S.; Alonso, J.J.; Kroo, U.M.; Wintzer, M. Multifidelity Design Optimization of Low-Boom Supersonic Jets. J. Aircr. 2008, 45, 106–118. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S. Review of Meta-Heuristics and Generalised Evolutionary Walk Algorithm. Int. J. Bio-Inspired Comput. 2011, 3, 77–84. [Google Scholar] [CrossRef]
- Kay, J.; Mason, W.H.; Durham, W. Control Authority Assessment in Aircraft Conceptual Design. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 1993. [Google Scholar] [CrossRef] [Green Version]
- Howe, D. Aircraft Conceptual Design Synthesis; Cranfield University: Cranfield, UK; Professional Engineering Publishing Limited: London, UK; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Raymer, D. Aircraft Design. A Conceptual Approach; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1999. [Google Scholar]
- Torenbeek, E. Synthesis of Subsonic Airplane Design. Synthesis of Subsonic Airplane Design; Delft University Press: Delft, The Netherlands, 1976; Volume 80, p. 370. [Google Scholar]
- Martins, J.R.R.A.; Lambe, A.B. Multidisciplinary design optimization: A survey of architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef] [Green Version]
- Simpson, T.W.; Mauery, T.M.; Korte, J.; Mistree, F. Kriging models for global approximation in simulation-based multidisciplinary design optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef] [Green Version]
- Van Gent, I.; Aigner, B.; Beijer, B.; Jepsen, J.; La Rocca, G. Knowledge Architecture Supporting the next Generation of MDO in the AGILE Paradigm. Prog. Aerosp. Sci. 2020, 119, 100642. [Google Scholar] [CrossRef]
- Agte, J.; De Weck, O.; Sobieszczanski-Sobieski, J.; Arendsen, P.; Morris, A.; Spieck, M. MDO: Assessment and Direction for Advancement-an Opinion of One International Group. Struct. Multidiscip. Optim. 2010, 40, 17–33. [Google Scholar] [CrossRef]
- Shahpar, S. Challenges to Overcome for Routine Usage of Automatic Optimisation in the Propulsion Industry. Aeronaut. J. 2011, 115, 615–625. [Google Scholar] [CrossRef]
- Ciampa, P.D.; Nagel, B. AGILE Paradigm: The next Generation Collaborative MDO for the Development of Aeronautical Systems. Prog. Aerosp. Sci. 2020, 119, 100643. [Google Scholar] [CrossRef]
- Lefebvre, T.; Bartoli, N.; Dubreuil, S.; Panzeri, M.; Lombardi, R.; Della Vecchia, P.; Stingo, L.; Nicolosi, F.; De Marco, A.; Ciampa, P.D.; et al. Enhancing Optimization Capabilities Using the AGILE Collaborative MDO Framework with Application to Wing and Nacelle Design. Prog. Aerosp. Sci. 2020, 119, 100649. [Google Scholar] [CrossRef]
- Ciampa, P.D.; Nagel, B. The AGILE Paradigm: The next Generation of Collaborative MDO. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–18. [Google Scholar] [CrossRef]
- Lefebvre, T.; Bartoli, N.; Dubreuil, S.; Panzeri, M.; Lombardi, R.; Della Vecchia, P.; Nicolosi, F.; Ciampa, P.D.; Anisimov, K.; Savelyev, A. Methodological Enhancements in MDO Process Investigated in the AGILE European Project. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–23. [Google Scholar] [CrossRef] [Green Version]
- Ciampa, P.D.; Nagel, B. Towards the 3 rd generation mdo collaborative environment. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences, DCC, Daejeon, Korea, 25–30 September 2016; pp. 1–12. [Google Scholar]
- Papageorgiou, A.; Tarkian, M.; Amadori, K.; Ölvander, J. Multidisciplinary Design Optimization of Aerial Vehicles: A Review of Recent Advancements. Int. J. Aerosp. Eng. 2018. [Google Scholar] [CrossRef]
- Gazaix, A.; Gallard, F.; Gachelin, V.; Druot, T.; Grihon, S.; Ambert, V.; Guénot, D.; Lafage, R.; Vanaret, C.; Pauwels, B.; et al. Towards the Industrialization of New MDO Methodologies and Tools for Aircraft Design. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef] [Green Version]
- Yi, S.I.; Shin, J.K.; Park, G.J. Comparison of MDO methods with mathematical examples. Struct. Multidiscip. Optim. 2008, 35, 391–402. [Google Scholar] [CrossRef]
- Aronstein, D.C.; Schueler, K.L. Two Supersonic Business Aircraft Conceptual Designs, with and without Sonic Boom Constraint. J. Aircr. 2005, 42, 775–786. [Google Scholar] [CrossRef]
- Giunta, A.A.; Golividov, O.; Knill, D.L.; Grossman, B.; Mason, W.H.; Watson, L.T.; Haftka, R.T. Multidisciplinary Design Optimization of Advanced Aircraft Configurations. In Fifteenth International Conference on Numerical Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 0203, pp. 14–34. [Google Scholar] [CrossRef]
- Antoine, N.E.; Kroo, I.M. Aircraft Optimization for Minimal Environmental Impact. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Striz, A.G.; Kennedy, B.; Siddique, Z.; Neeman, H. A Roadmap for Moderate Fidelity Conceptual Design with Multilevel Analysis and MDO. In Proceedings of the Collection of Technical Papers—AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Newport, UK, 1–4 May 2006; Volume 1, pp. 222–232. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Yang, G.; Sun, Q.; Ge, J. An Interval Uncertain Optimization Method Using Back-Propagation Neural Network Differentiation. Comput. Methods Appl. Mech. Eng. 2020, 366, 113065. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Jensen, H.A. Computational Methods in Optimization Considering Uncertainties—An Overview. Comput. Methods Appl. Mech. Eng. 2008, 198, 2–13. [Google Scholar] [CrossRef]
- Hajela, P. Soft Computing in Multidisciplinary Aerospace Design—New Directions for Research. Prog. Aerosp. Sci. 2002, 38, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Vittal, S.; Hajela, P. Probabilistic Design Using Empirical Distributions. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar] [CrossRef]
- Sobieszczanski-Sobieski, J.; Haftka, R.T. Multidisciplinary Aerospace Design Optimization: Survey of Recent Developments. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996. [Google Scholar] [CrossRef] [Green Version]
- Oberkampf, W.L.; DeLand, S.M.; Rutherford, B.M.; Diegert, K.V.; Alvin, K.F. Error and Uncertainty in Modeling and Simulation. Reliab. Eng. Syst. Saf. 2002, 75, 333–357. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Helton, J.C.; Joslyn, C.A.; Wojtkiewicz, S.F. Challenge Problems: Uncertainty in System; CiteSeer: Pennsylvania, PA, USA, 2001; pp. 1–18. [Google Scholar]
- Parry, G.W. The Characterization of Uncertainty in Probabilistic Risk Assessments of Complex Systems. Reliab. Eng. Syst. Saf. 1996, 54, 119–126. [Google Scholar] [CrossRef]
- Haldar, A.; Mahadevan, S. Probability, Reliability and Statistical Methods in Engineering Design; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Du, L.; Choi, K.K.; Youn, B.D.; Gorsich, D. Possibility-Based Design Optimization Method for Design Problems with Both Statistical and Fuzzy Input Data. J. Mech. Des. Trans. ASME 2006, 128, 928–935. [Google Scholar] [CrossRef]
- Struett, R.C. Empennage Sizing and Aircraft Stability Using Matlab Empennage Sizing and Aircraft Stability Using Matlab; The Faculty of the Aerospace Engineering, Department California Polytechnic State University: San Luis Obispo, CA, USA, 2012; pp. 1–37. [Google Scholar]
- Ciliberti, D.; Della Vecchia, P.; Nicolosi, F.; De Marco, A. Aircraft Directional Stability and Vertical Tail Design: A Review of Semi-Empirical Methods. Prog. Aerosp. Sci. 2017, 95, 140–172. [Google Scholar] [CrossRef]
- Rathay, N.W.; Boucher, M.J.; Amitay, M.; Whalen, E. Performance Enhancement of a Vertical Tail Using Synthetic Jet Actuators. AIAA J. 2014, 52, 810–820. [Google Scholar] [CrossRef]
- Stojaković, P.; Velimirović, K.; Rašuo, B. Power optimization of a single propeller airplane take-off run on the basis of lateral maneuver limitations. Aerosp. Sci. Technol. 2018, 72, 553–563. [Google Scholar] [CrossRef]
- Stojakovic, P.; Rasuo, B. Single propeller airplane minimal flight speed based upon the lateral maneuver condition. Aerosp. Sci. Technol. 2016, 49, 239–249. [Google Scholar] [CrossRef]
- Sadraey, M.H. AIRCRAFT DESIGN A Systems Engineering Approach; Daniel Webster College: Nashua, NH, USA, 2013; pp. 255–340. [Google Scholar]
- Rostami, M.; Bagherzadeh, S.A. Development and Validation of an Enhanced Semi-Empirical Method for Estimation of Aerodynamic Characteristics of Light, Propeller-Driven Airplanes. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 638–648. [Google Scholar] [CrossRef]
- Rostami, M.; Chung, J. Multidisciplinary Analysis Program for Light Aircraft (MAPLA). In Proceedings of the Canadian Society for Mechanical Engineering International Congress, Charlottetown, PE, Canada, 27–30 June 2021. [Google Scholar]
- Rostami, M.; Chung, J.; Neufeld, D. Vertical Tail Sizing of Propeller-Driven Aircraft Considering the Asymmetric Blade Effect. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 1–12. [Google Scholar] [CrossRef]
- Rostami, M.; Chung, J.; Park, H.U. Design Optimization of Multi-Objective Proportional–Integral–Derivative Controllers for Enhanced Handling Quality of a Twin-Engine, Propeller-Driven Airplane. Adv. Mech. Eng. 2020, 12, 1687814020923178. [Google Scholar] [CrossRef]
- Roskam, J. Airplane Flight Dynamics and Automatic Flight Control. Part I; DAR Corporation: Lawrence, KS, USA, 2007. [Google Scholar]
- Nelson, R. Flight Stability and Automatic Control; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Etkin, B.; Reid, L.D. Dynamics of Flight Stability and Control, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Du, X.; Chen, W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design. J. Mech. Des. Trans. ASME 2004, 126, 225–233. [Google Scholar] [CrossRef] [Green Version]
- Du, X.; Guo, J.; Beeram, H. Sequential Optimization and Reliability Assessment for Multidisciplinary Systems Design. Struct. Multidiscip. Optim. 2008, 35, 117–130. [Google Scholar] [CrossRef]
- Youn, B.D.; Choi, K.K.; Du, L. Enriched Performance Measure Approach for Reliability-Based Design Optimization. AIAA J. 2005, 43, 874–884. [Google Scholar] [CrossRef]
- Neufeld, D. Multidisciplinary Aircraft Conceptual Design Optimization Considering Fidelity Uncertainties. Program of Aerospace Engineering. Ph.D. Thesis, Ryerson University, Toronto, ON, Canada, 2010; p. 150. [Google Scholar]
- Chiralaksanakul, A.; Mahadevan, S. First-Order approximation methods in Reliability-Based design optimization. J. Mech. Des. 2005, 127, 851. [Google Scholar] [CrossRef]
- Lambe, A.B.; Martins, J.R.R.A. Extensions to the Design Structure Matrix for the Description of Multidisciplinary Design, Analysis, and Optimization Processes. Struct. Multidiscip. Optim. 2012, 46, 273–284. [Google Scholar] [CrossRef]
- Torenbeek, E. Quick estimation of wing structural weight for preliminary aircraft design. Aircr. Eng. Aerosp. Technol. Int. J. 1993, 44, 18–19. [Google Scholar] [CrossRef]
- ASTM. Standard Specification for Ferrosilicon Practice; ASTM: West Conshohocken, PA, USA, 2000; Volume 93, pp. 2–6. [Google Scholar] [CrossRef]
- ASTM. Standard Specification for Low-Speed Flight Characteristics of Aircraft; ASTM: West Conshohocken, PA, USA, 2021. [Google Scholar] [CrossRef]
- ASTM. Standard Specification for Normal Category Aeroplanes Certification; ASTM: West Conshohocken, PA, USA, 2018; Volume i, pp. 1–8. [Google Scholar] [CrossRef]
- ASTM. Standard Specification for Performance of Engine Oils. In Annual Book of ASTM Standards Aircraft; ASTM: West Conshohocken, PA, USA, 2004; pp. 1–26. [Google Scholar] [CrossRef]
- Brandt, S.A.; Post, M.L.; Hall, D.; Gilliam, F.; Jung, T.; Yechout, T. The Value of Semi-Empirical Analysis Models in Aircraft Design. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Wolowicz, H.; Yancey, R.B. Lateral Directional Aerodynamic Characteristics of Light, Twin-Engine Propeller-Driven Airplanes; NASA-TN-D-6946; NASA Flight Research Center: Edwards, CA, USA, 1972. [Google Scholar]
- Wolowicz, H.; Yancey, R.B. Longitudinal Aerodynamic Characteristics of Light, Twin-Engine Propeller-Driven Airplanes; NASA-TN-D-6800; NASA Flight Research Center: Edwards, CA, USA, 1972. [Google Scholar]
- European Aviation Safety Agency. Certification Specifications for Normal, Utility, Aerobatic, and Commuter Category Aeroplanes—CS-23; Amendment 3; European Aviation Safety Agency: Cologne, Germany, 2012.
- MIL-F-8785C MILITARY; Specification Flying Qualities of Piloted Airplanes. Department of the Air Force: Washington, DC, USA, 5 November 1980.
- Mieloszyk, J.; Goetzendorf-Grabowski, T. Introduction of Full Flight Dynamic Stability Constraints in Aircraft Multidisciplinary Optimization. Aerosp. Sci. Technol. 2017, 68, 252–260. [Google Scholar] [CrossRef]






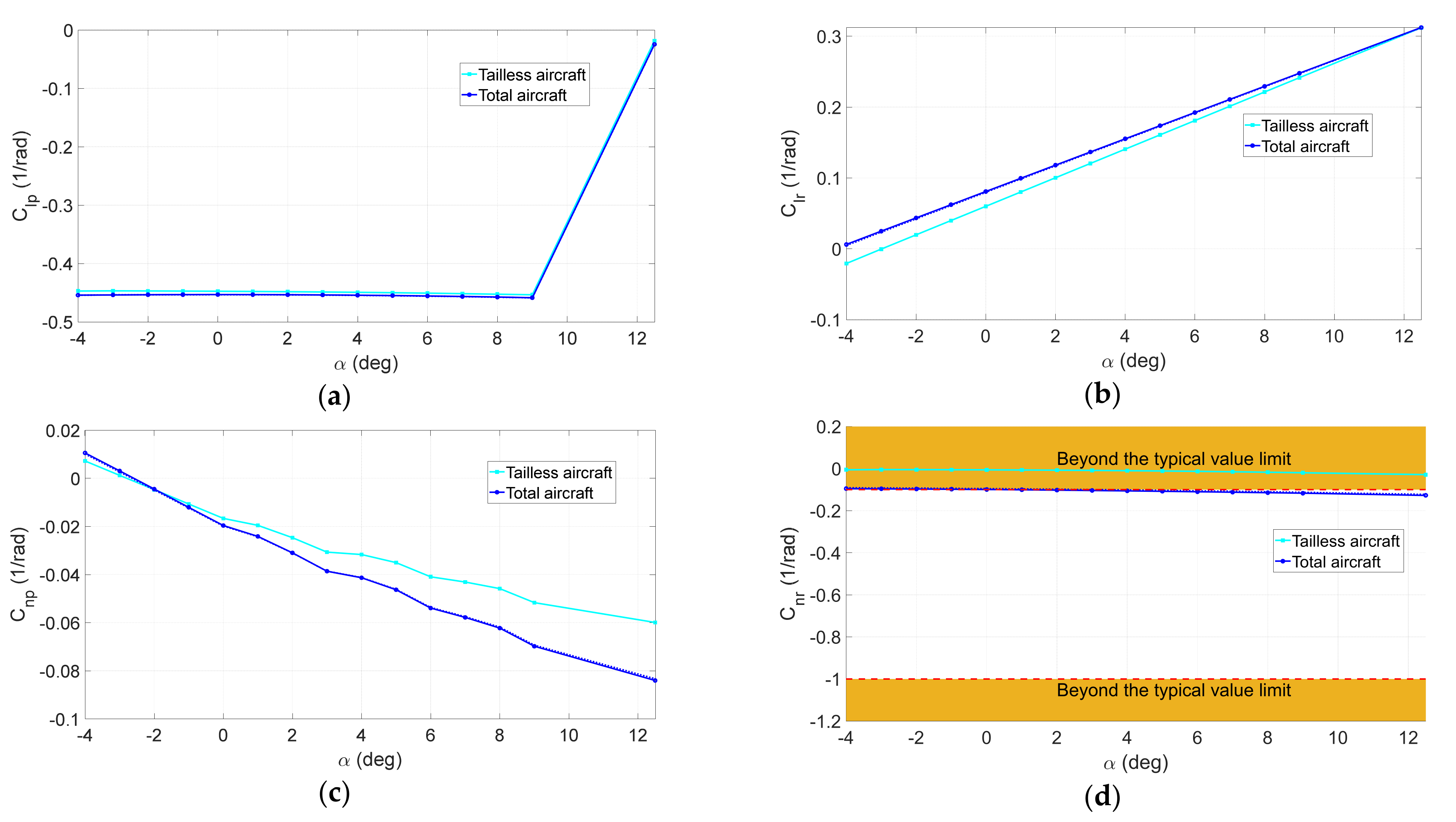
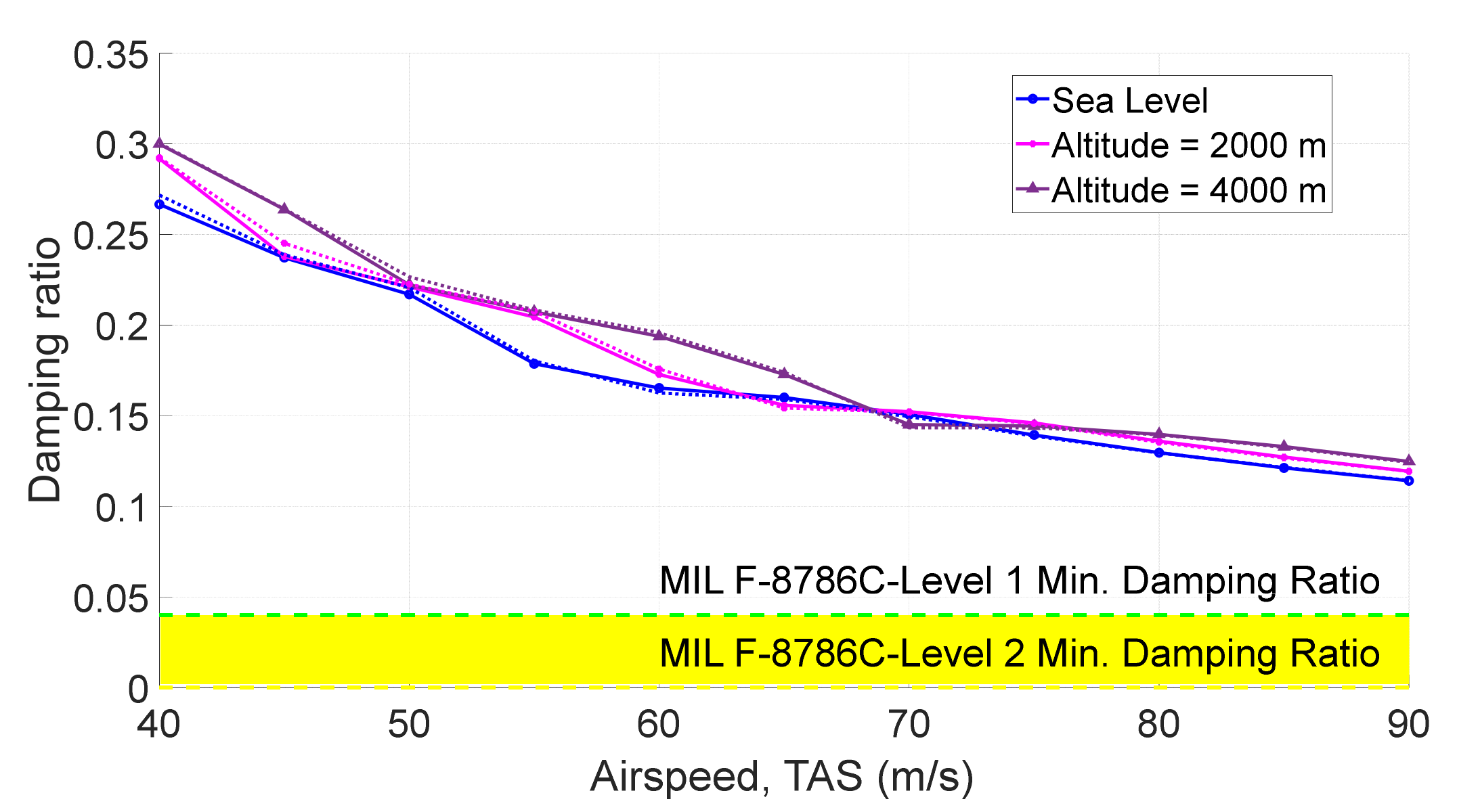
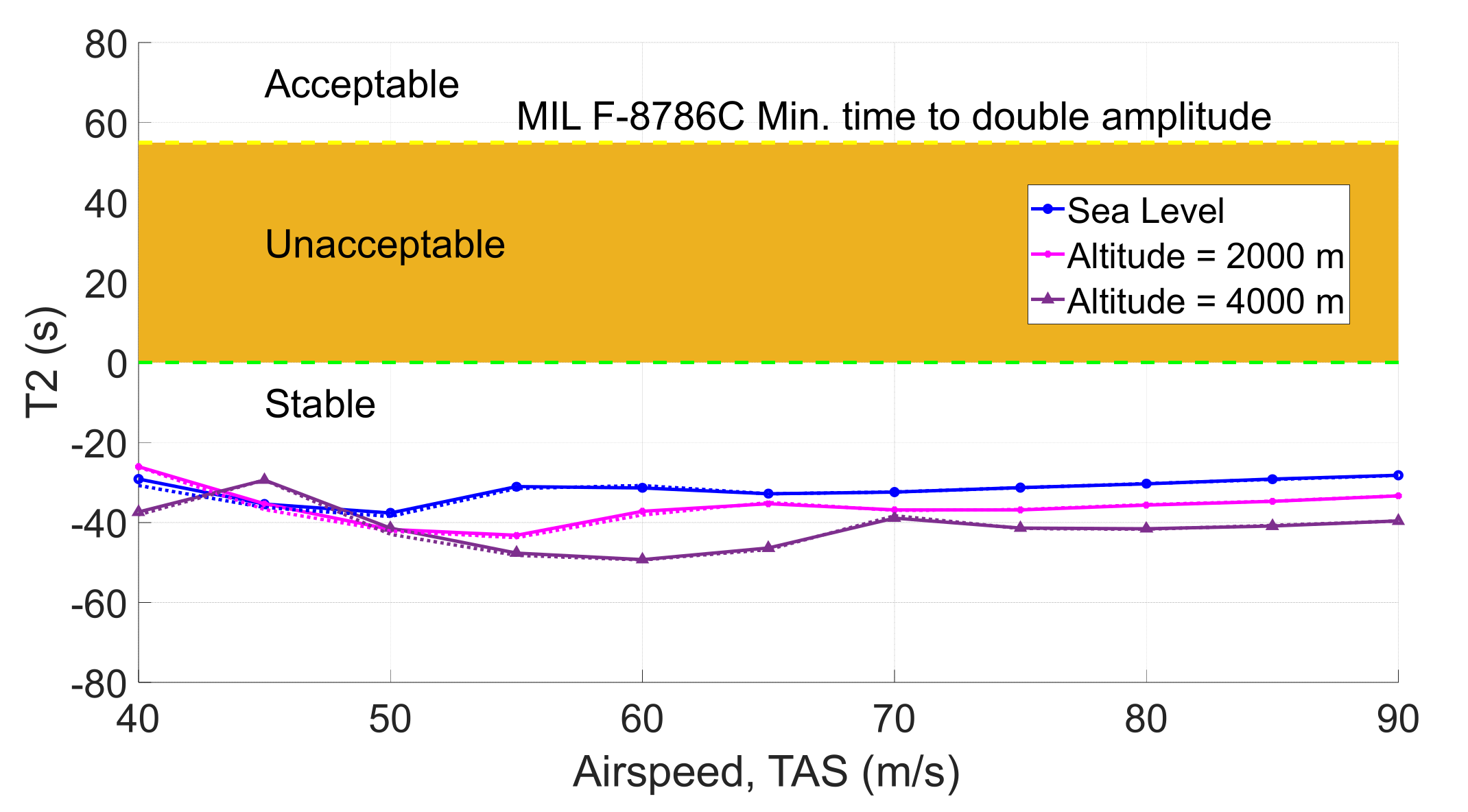
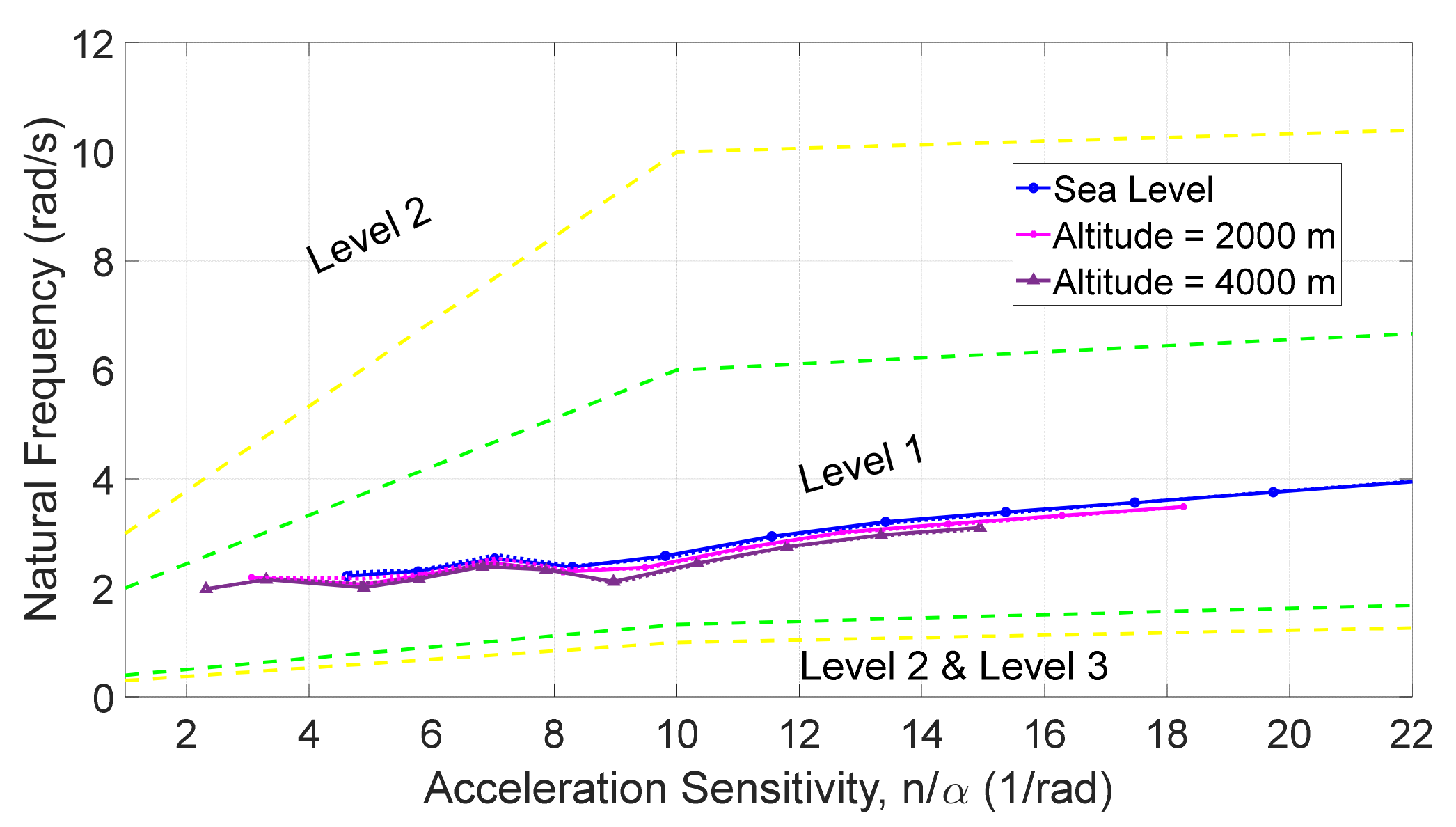

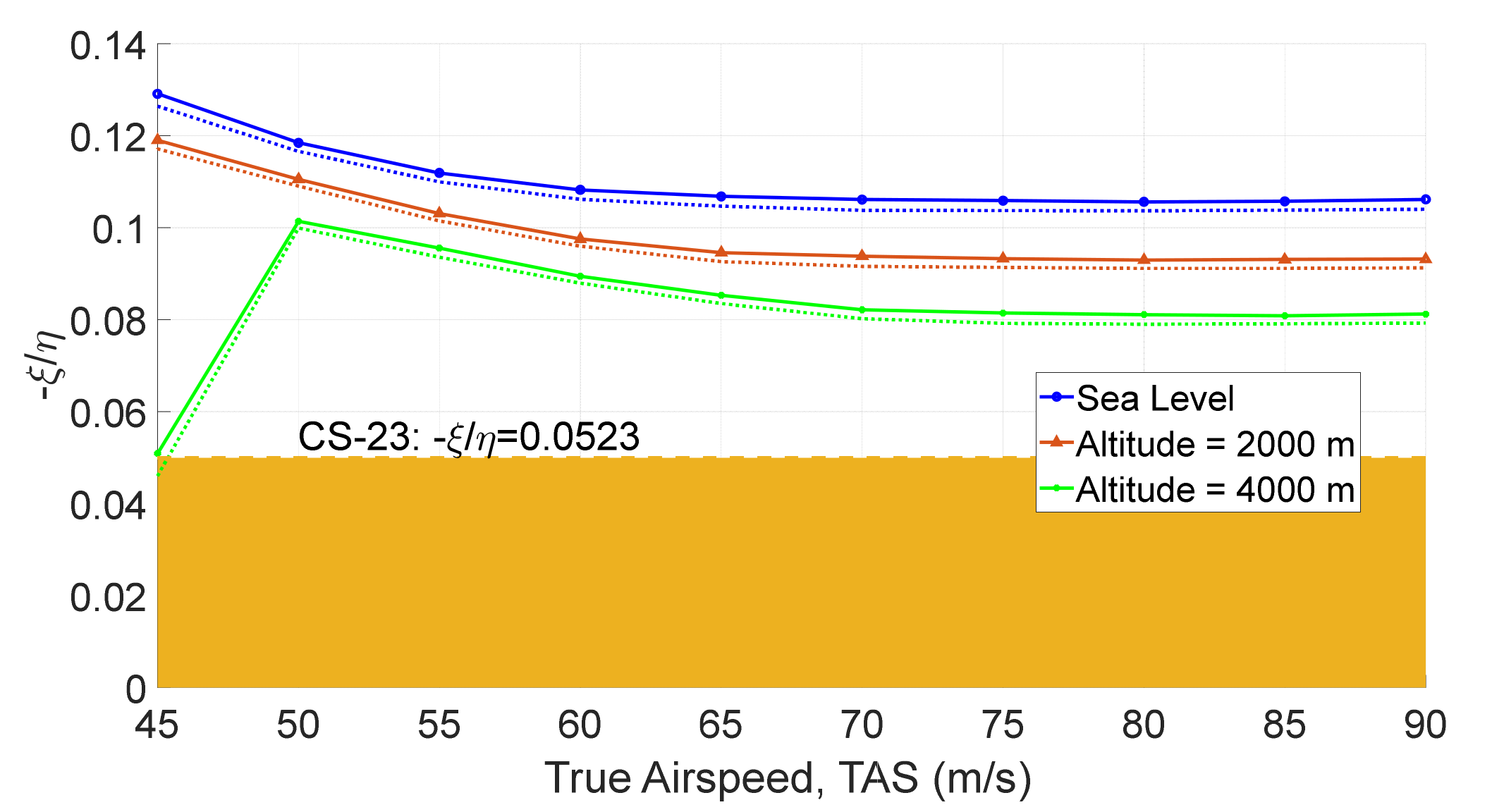
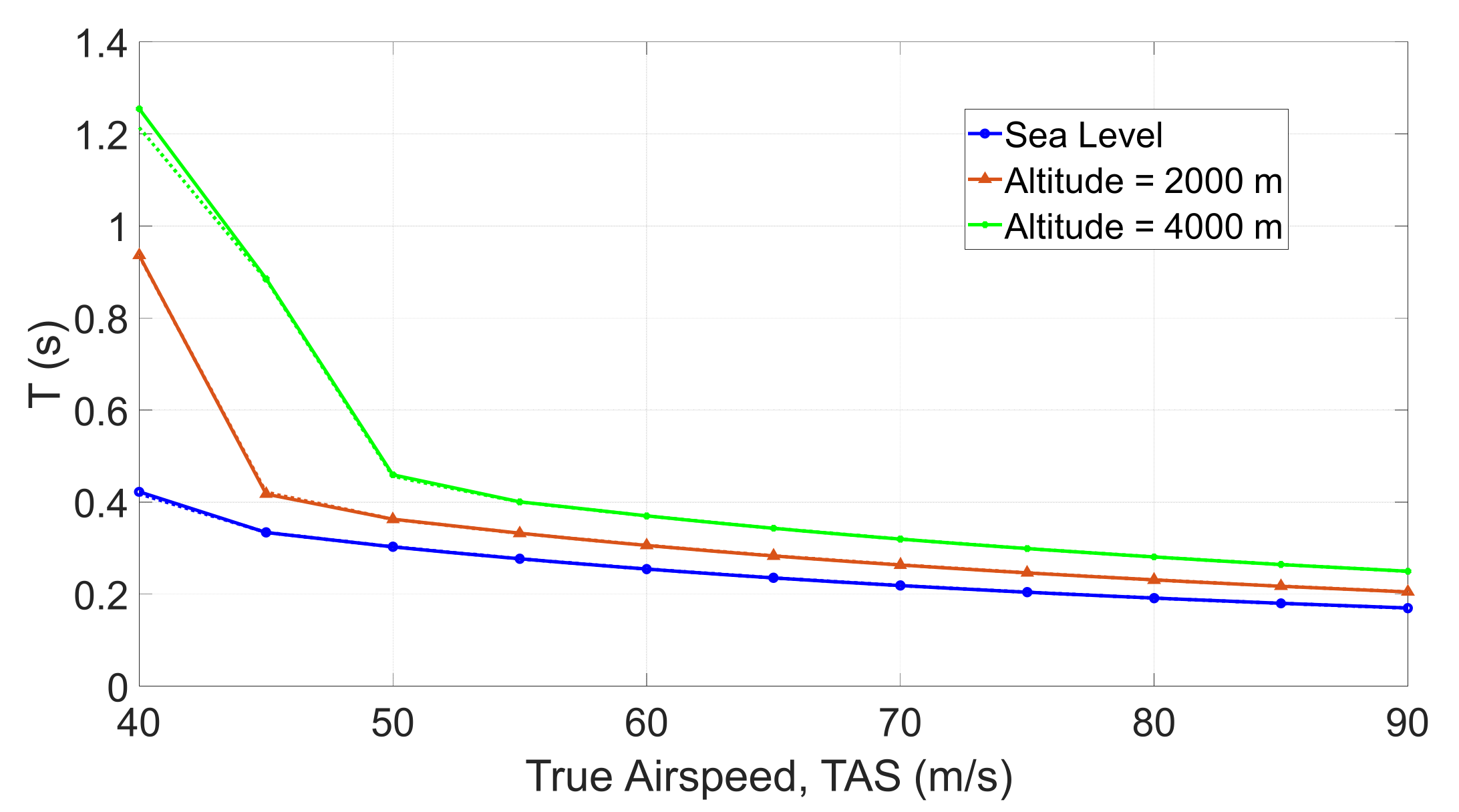
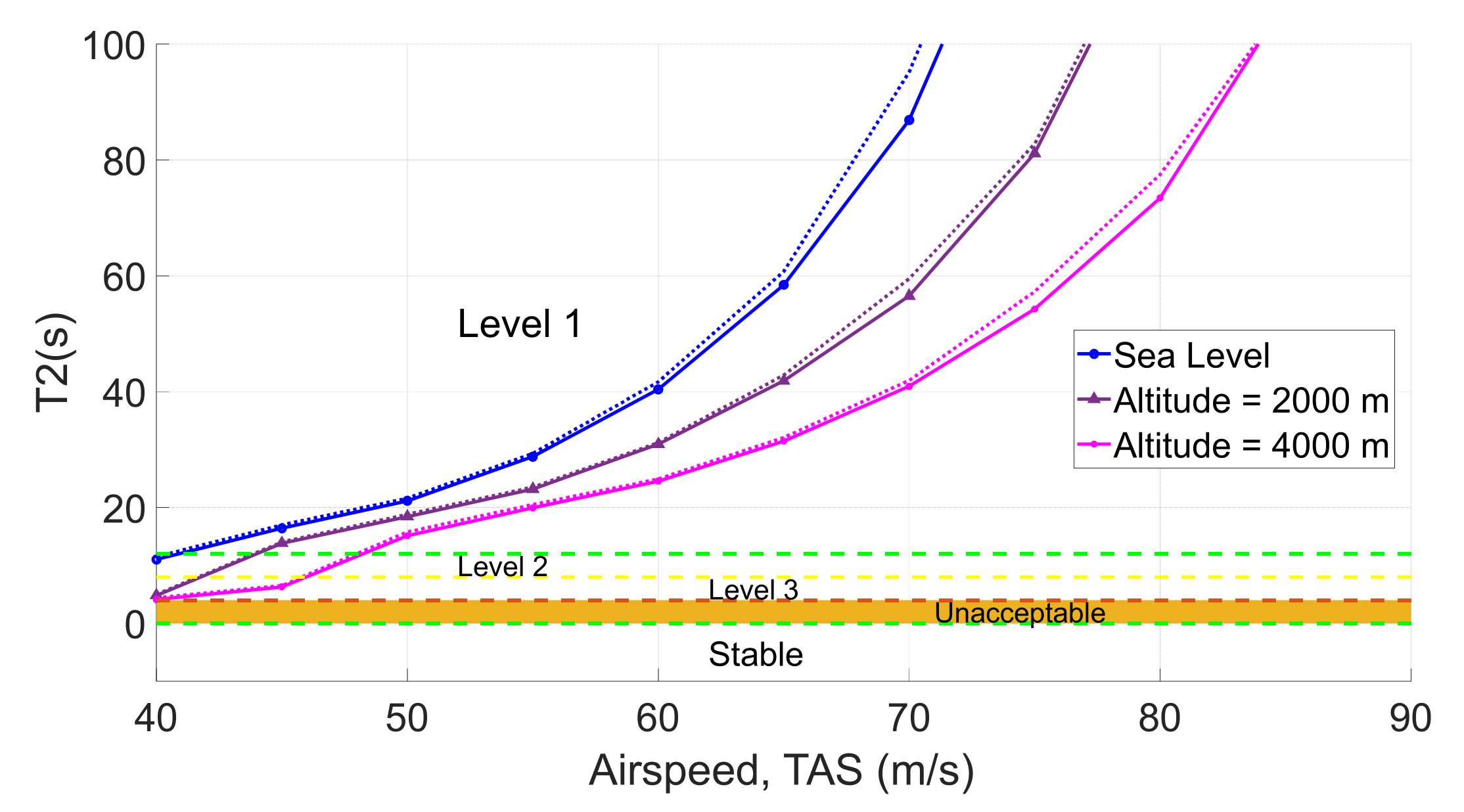
| Method | ||||
|---|---|---|---|---|
| Deterministic | 5.1769 | 3.1134 | 2.0636 | 16 |
| Single Loop | 6.6198 | 3.4413 | 3.2866 | 16 |
| PMA/Sequential | 6.7043 | 3.4506 | 3.2537 | 651 |
| PMA/Double Loop | 6.7043 | 3.4506 | 3.2537 | 1004 |
| RIA/Double Loop | 6.7257 | 3.4391 | 3.2866 | 1530 |
| Method | No. of Failed Runs | Average Error % | Median Error % | Average Time (s) | Average Evals |
|---|---|---|---|---|---|
| Single Loop | 0 | 1.93 | 1.25 | 0.3343 | 145 |
| PMA/Sequential | 5 | 2.54 × 10–5 | 2.54 × 10–5 | 0.5805 | 1648 |
| PMA/Double Loop | 0 | 3.77 | 2.97 × 10–5 | 2.7277 | 3862 |
| RIA/Double Loop | 71 | 6.11 | 0.319 | 4.1316 | 13276 |
| Component | Variable | Description | Limits |
|---|---|---|---|
| Horizontal Tail | Horizontal tail incidence angle, deg | 0 to 3 | |
| bh | Horizontal tail span, m | 3.5 to 5.1 | |
| Horizontal tail root chord, m | 1 to 1.45 | ||
| Horizontal tail tip chord, m | 0.5 to 1 | ||
| Leading edge sweep angle of horizontal tail, deg | 10 to 20 | ||
| lh | Distance, parallel to X-body axis, from the nose of fuselage to the horizontal tail mean aerodynamic chord, m | 8 to 8.7 | |
| zh | Distance, parallel to Z-body axis, from the X-body axis to the quarter chord of the horizontal tail mean aerodynamic chord, positive down, m | –0.4 to –0.1 | |
| celevator | Ratio of elevator chord to horizontal tail chord | 0.2 to 0.5 | |
| Vertical Tail | bv | Vertical tail span, m | 1.8 to 2.2 |
| Vertical tail root chord, m | 1.9 to 2.5 | ||
| Vertical tail tip chord, m | 0.8 to 1.4 | ||
| Trailing edge sweep angle of vertical tail, deg | 10 to 20 | ||
| zv | Perpendicular distance from X-body axis to root chord of vertical-tail, positive down, m | –0.35 to –0.15 | |
| lv | Distance along X-body axis from the nose of fuselage to leading edge of tip chord of vertical tail, m | 8.5 to 9.5 | |
| crudder | Ratio of rudder chord to vertical tail chord, m | 0.2 to 0.5 | |
| Engine | YT | Lateral Distance from X-axis to thrust line, m | 1.6 to 1.9 |
| Constraint | Description | Limits |
|---|---|---|
| Aircraft empty weight, Kg | < 2000 | |
| Pitching moment coefficient, a/rad | ||
| Weathercock stability coefficient, 1/rad | ||
| Effective dihedral coefficient, 1/rad | ||
| Pitching moment coefficient due to pitch rate, 1/rad | ||
| Damping in yaw derivative, 1/rad | ||
| Centre of gravity at its maximum afterwards, % | <27 | |
| SM | Static margin | |
| Maximum rudder deflection, deg | ||
| Maximum elevator deflection, deg | ||
| Handling quality, phugoid mode | ||
| Handling quality, short period mode | ||
| Handling quality, Dutch roll mode | ||
| Handling quality, roll mode | ||
| Handling quality, spiral mode |
| Variable | Optimized Value with Mass Optimization | Optimized Value with Drag Optimization |
|---|---|---|
| (deg) | 1.95 | 1.96 |
| (m) | 4.46 | 4.51 |
| (m) | 1.27 | 1.31 |
| (m) | 0.863 | 0.837 |
| (deg) | 12.18 | 11.23 |
| (m) | 8.338 | 8.327 |
| (m) | –0.275 | –0.281 |
| (m) | 0.37 | 0.37 |
| (m) | 1.855 | 1.83 |
| (m) | 1.969 | 1.966 |
| 0.895 | 0.837 | |
| (deg) | 17.095 | 16.94 |
| (m) | –0.221 | –0.225 |
| (m) | 9.09 | 9.05 |
| (m) | 0.4135 | 0.415 |
| (m) | 1.706 | 1.701 |
| 4.755 | 4.84 | |
| 2.656 | 2.565 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rostami, M.; Bardin, J.; Neufeld, D.; Chung, J. A Multidisciplinary Possibilistic Approach to Size the Empennage of Multi-Engine Propeller-Driven Light Aircraft. Aerospace 2022, 9, 160. https://doi.org/10.3390/aerospace9030160
Rostami M, Bardin J, Neufeld D, Chung J. A Multidisciplinary Possibilistic Approach to Size the Empennage of Multi-Engine Propeller-Driven Light Aircraft. Aerospace. 2022; 9(3):160. https://doi.org/10.3390/aerospace9030160
Chicago/Turabian StyleRostami, Mohsen, Julian Bardin, Daniel Neufeld, and Joon Chung. 2022. "A Multidisciplinary Possibilistic Approach to Size the Empennage of Multi-Engine Propeller-Driven Light Aircraft" Aerospace 9, no. 3: 160. https://doi.org/10.3390/aerospace9030160
APA StyleRostami, M., Bardin, J., Neufeld, D., & Chung, J. (2022). A Multidisciplinary Possibilistic Approach to Size the Empennage of Multi-Engine Propeller-Driven Light Aircraft. Aerospace, 9(3), 160. https://doi.org/10.3390/aerospace9030160







